Enhancing Heat Transfer Behaviour of Ethylene Glycol by the Introduction of Silicon Carbide Nanoparticles: An Experimental and Molecular Dynamics Simulation Study
Abstract
1. Introduction
2. Results and Discussion
2.1. Characterization of SiC Nanoparticle
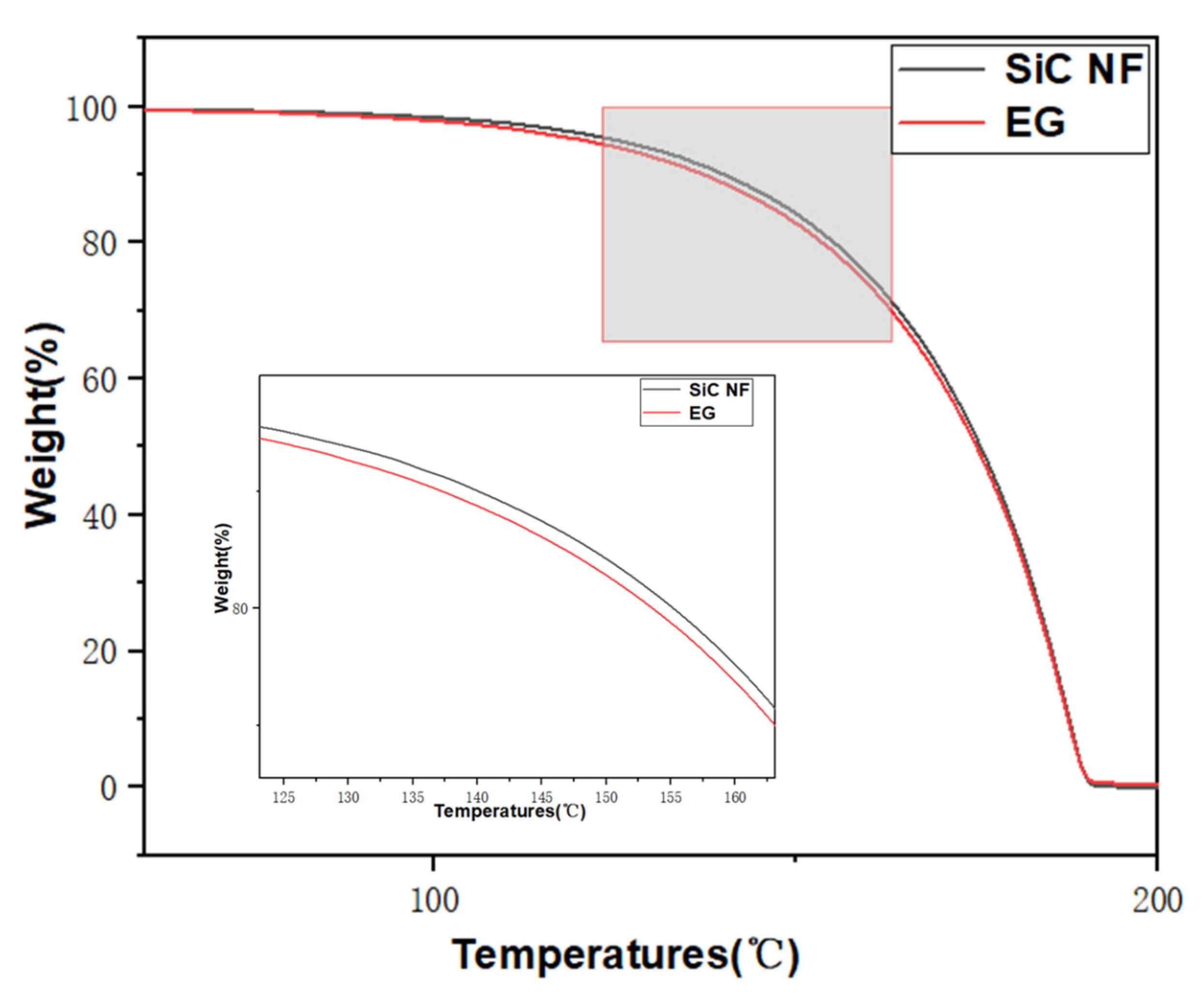
2.2. Thermal Stability of N.F.s
2.3. Thermal Conductivity of E.G./SiC N.F.
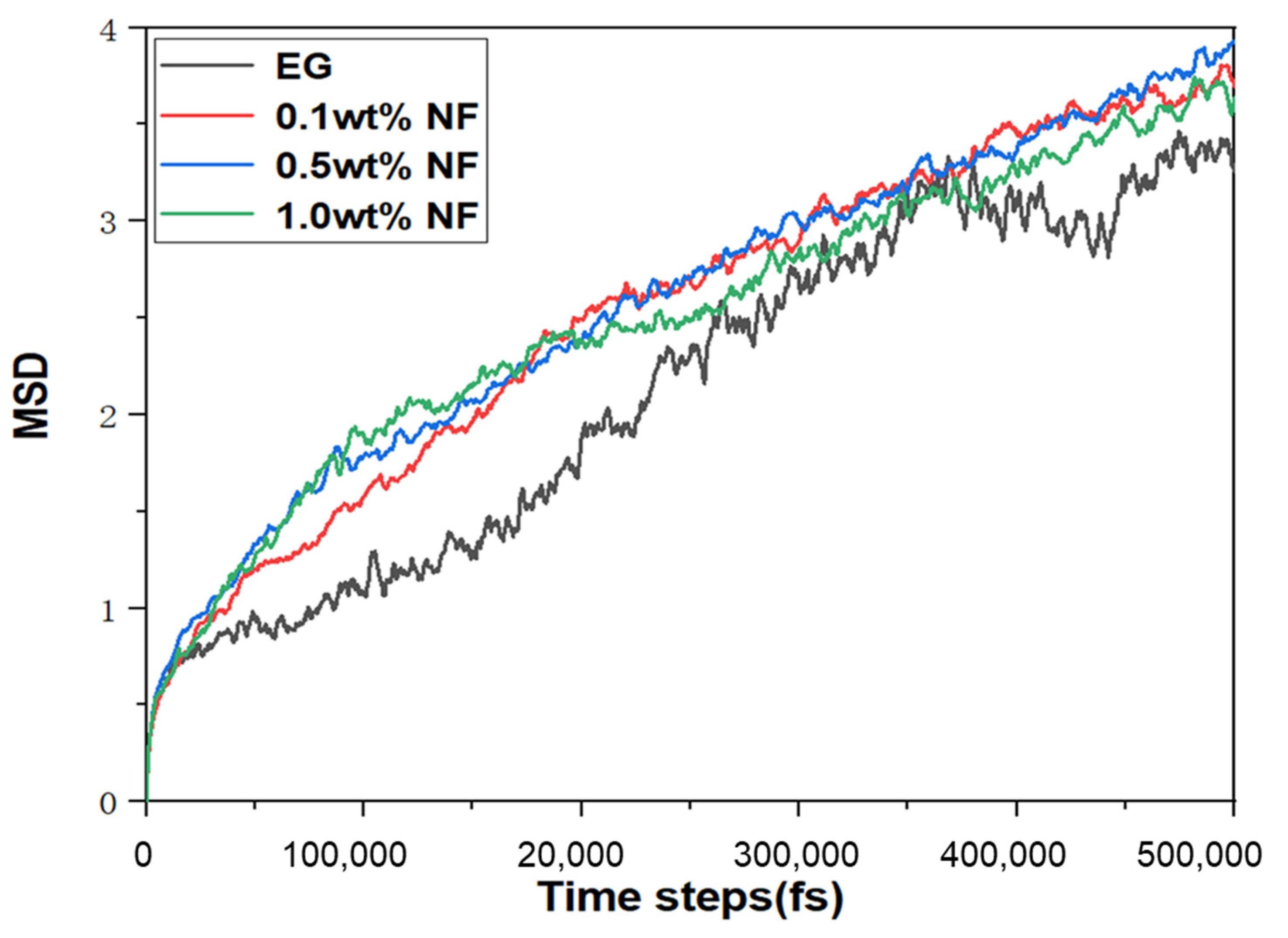
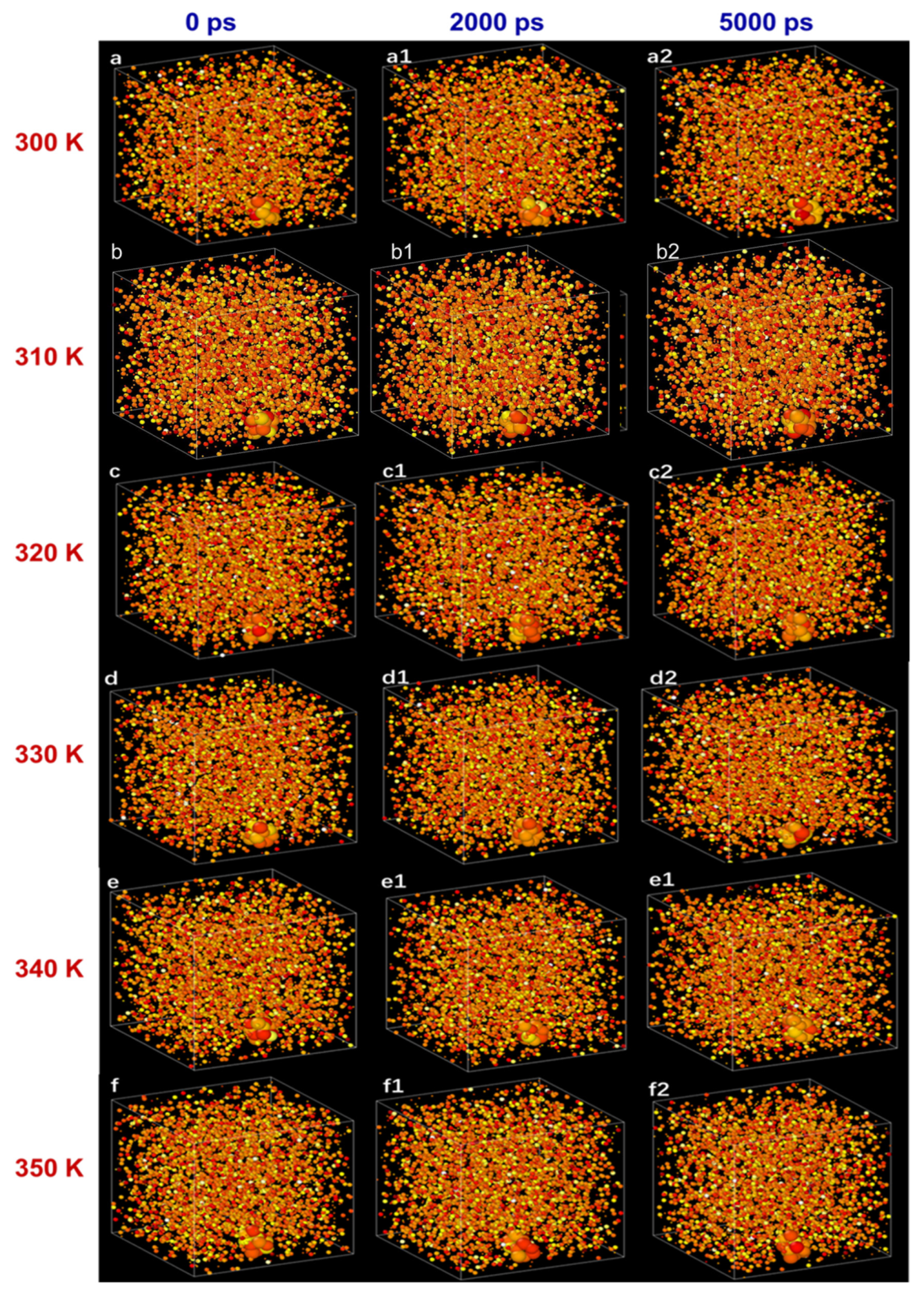
2.4. MSD Analysis of the N.F. Systems
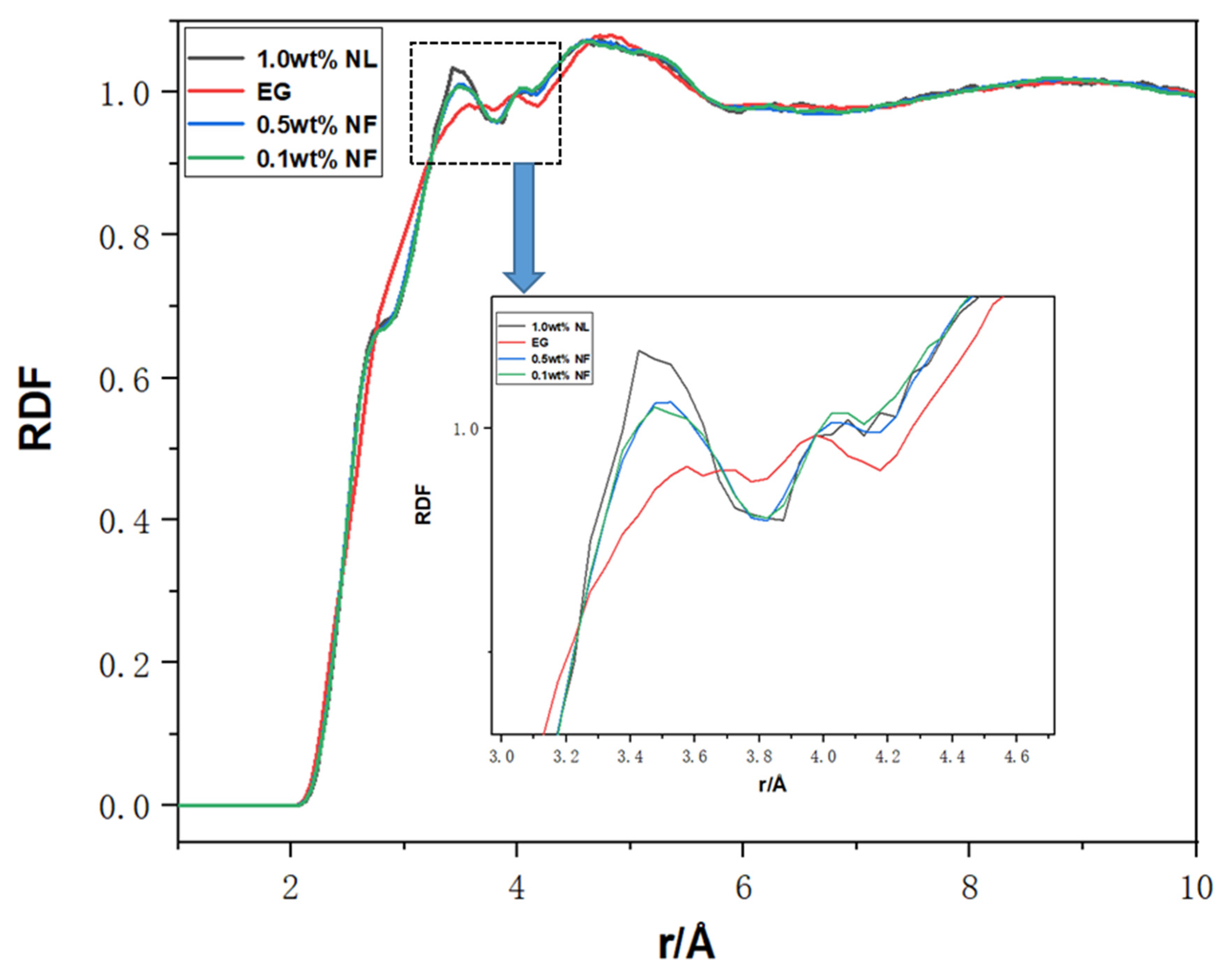
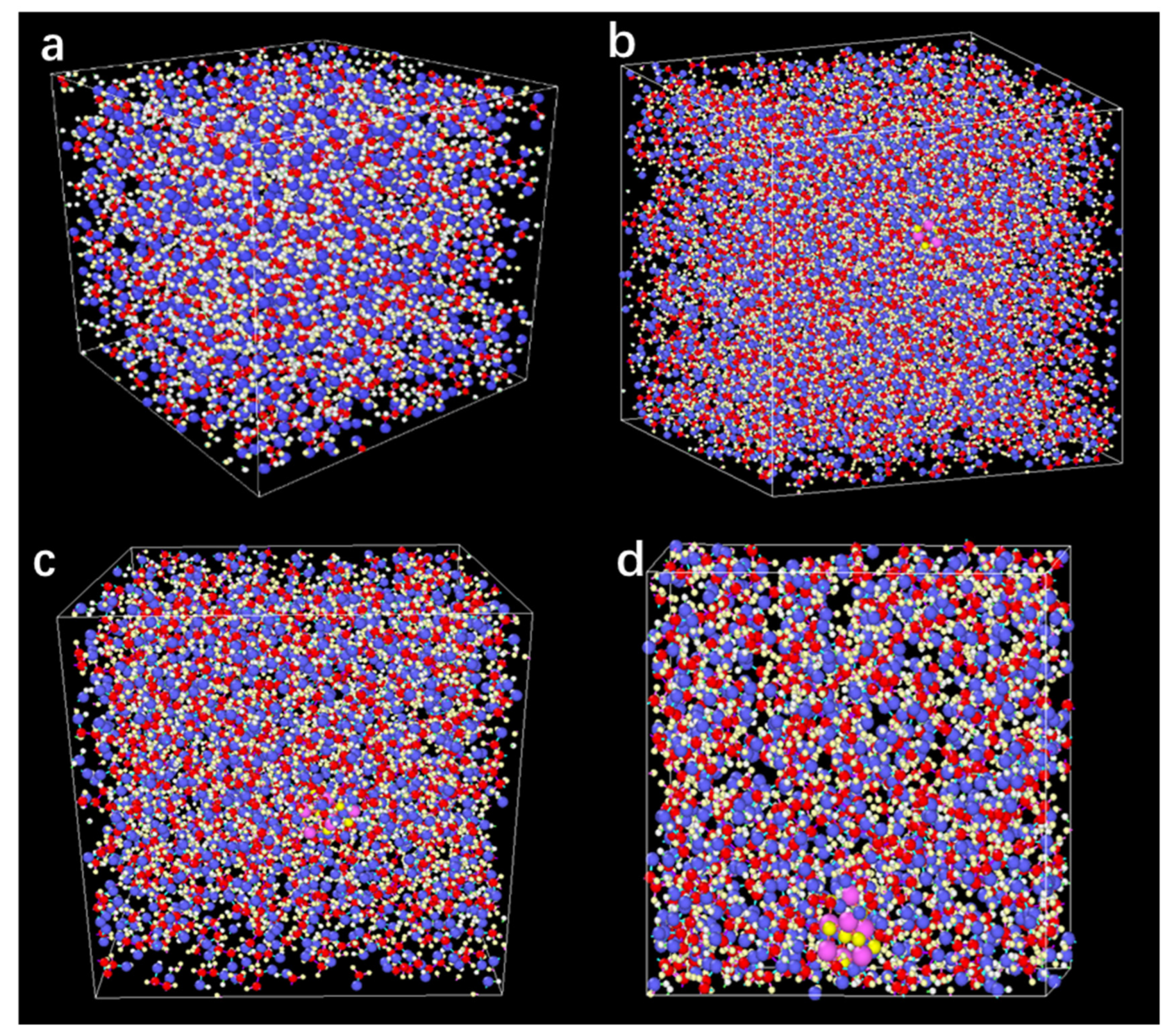
2.5. RDF Analysis and Atom Motion Trajectory for N.F.
3. Computational M.D. Simulation and Experimental Section
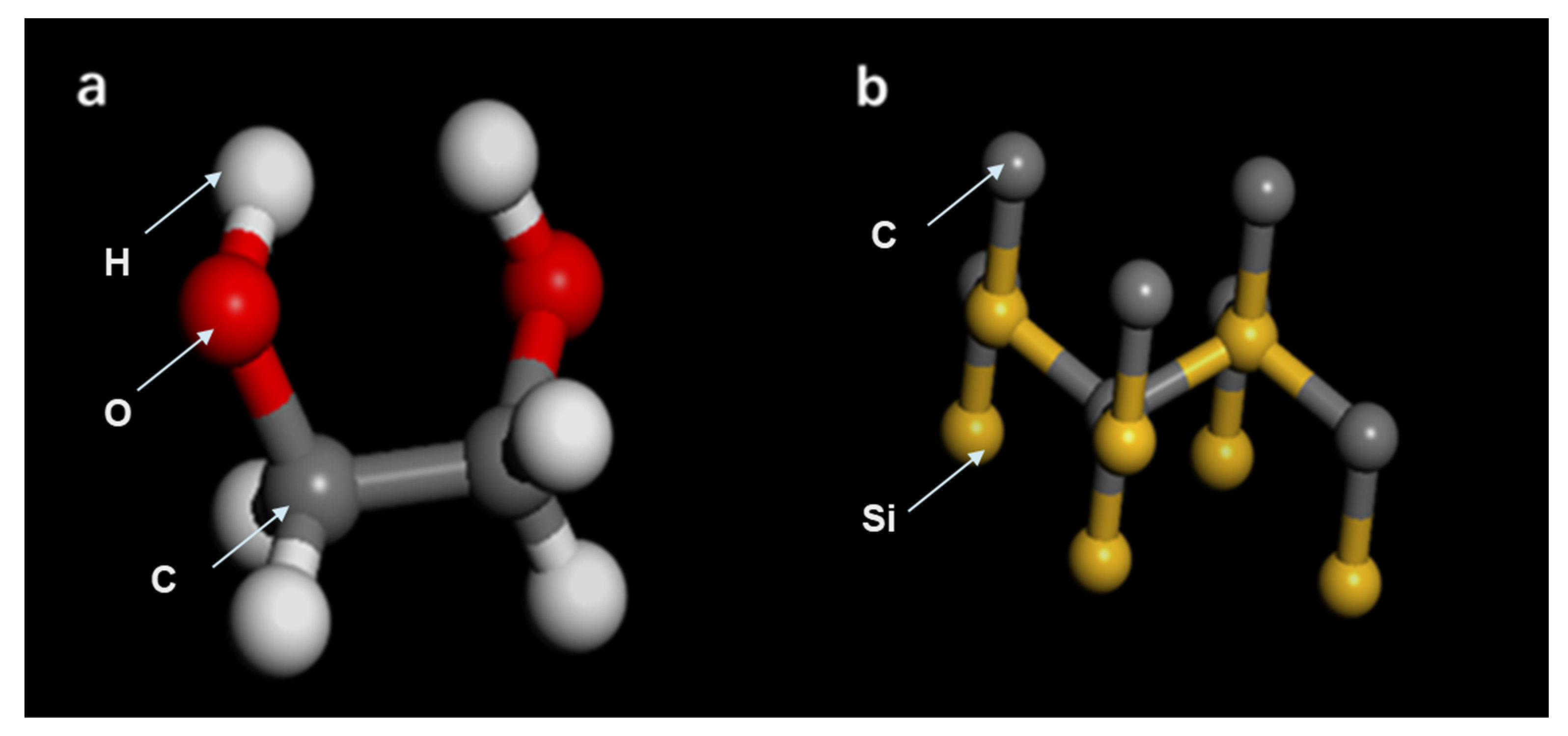
3.1. The Description of the M.D. Simulation
3.2. Inter-Atomic Potentials and Simulation Strategy
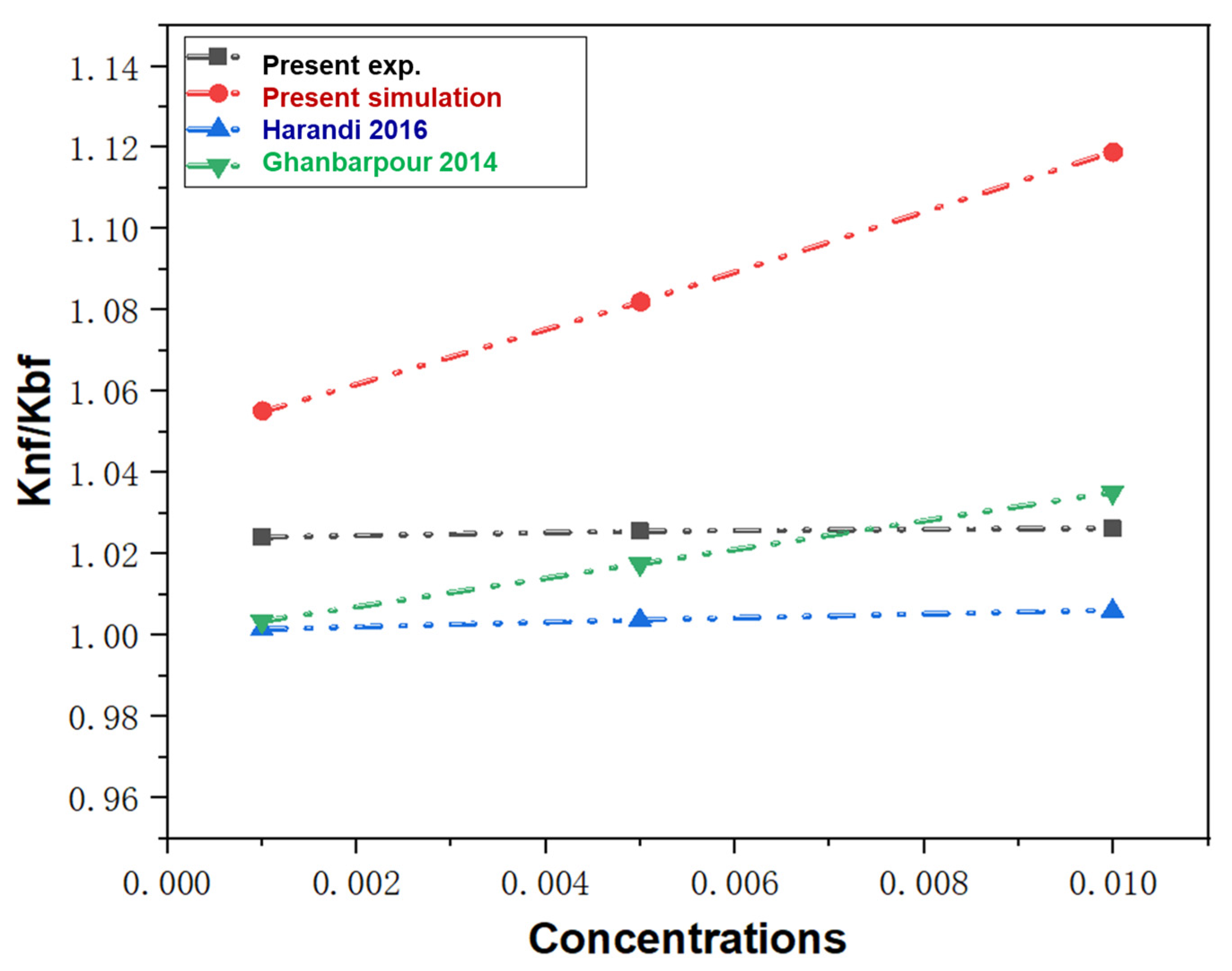
3.3. Verification of the M.D. Simulation Model
3.4. Experimental Section
3.4.1. Materials
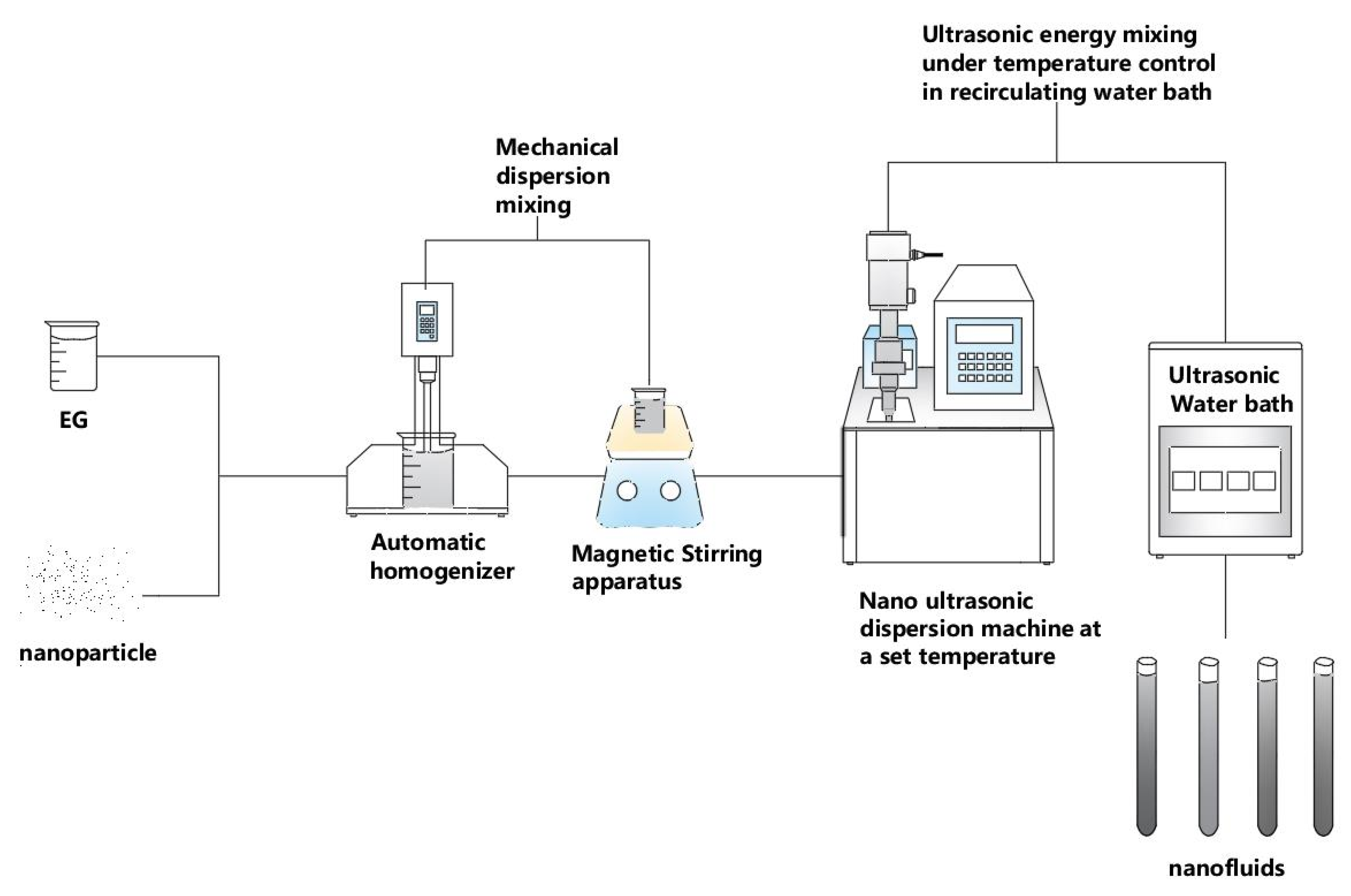
3.4.2. Equipment Employed
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Jiang, H.; Hou, X.; Dearn, K.D.; Su, D.; Ali, M.K.A. Thermal stability enhancement mechanism of engine oil using hybrid MoS2/h-BN nano-additives with ionic liquid modification. Adv. Powder Technol. 2021, 32, 4658–4669. [Google Scholar] [CrossRef]
- Ali, M.K.A.; Hou, X. Improving the heat transfer capability and thermal stability of vehicle engine oils using Al2O3/TiO2 nanomaterials. Powder Technol. 2020, 363, 48–58. [Google Scholar] [CrossRef]
- Leong, K.; Yang, C.; Murshed, S. A model for the thermal conductivity of nanofluids–The effect of interfacial layer. J. Nanoparticle Res. 2006, 8, 245–254. [Google Scholar] [CrossRef]
- Tawfik, M.M. Experimental studies of nanofluid thermal conductivity enhancement and applications: A review. Renew. Sustain. Energy Rev. 2017, 75, 1239–1253. [Google Scholar] [CrossRef]
- Lenin, R.; Joy, P.A.; Bera, C. A review of the recent progress on thermal conductivity of nanofluid. J. Mol. Liq. 2021, 338, 116929. [Google Scholar] [CrossRef]
- Said, Z.; Allagui, A.; Abdelkareem, M.A.; Alawadhi, H.; Elsaid, K. Acid-functionalized carbon nanofibers for high stability, thermoelectrical and electrochemical properties of nanofluids. J. Colloid Interface Sci. 2018, 520, 50–57. [Google Scholar] [CrossRef]
- Lin, X.; Xie, G. Application of Nanofluid Electrochemistry in Heat Dissipation of Permanent Magnet Synchronous Motors. J. Chem. 2022, 2022, 3681749. [Google Scholar] [CrossRef]
- Hassani, S.; Taylor, R.A.; Mekhilef, S.; Saidur, R. A cascade nanofluid-based PV/T system with optimized optical and thermal properties. Energy 2016, 112, 963–975. [Google Scholar] [CrossRef]
- Singh, J.P.; Nandi, T.; Ghosh, S.K. Structure-property relationship of silver decorated functionalized reduced graphene oxide based nanofluids: Optical and thermophysical aspects and applications. Appl. Surf. Sci. 2021, 542, 148410. [Google Scholar] [CrossRef]
- Fatima, N.; Alayyash, K.; Alfwzan, W.F.; Ijaz, N.; Riaz, A.; Saleem, N.; El-Din, E.M.T. Mathematical model for numerical simulations of thermal energy of nano-fluid in a complex peristaltic transport within a curved passage: Pharmacological and engineering biomedical application. Case Stud. Therm. Eng. 2023, 45, 102897. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Miglietta, P.; Milanese, M.; Risi, A. Thermal conductivity, viscosity and stability of Al2O3-diathermic oil nanofluids for solar energy systems. Energy 2016, 95, 124–136. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.; Lou, W.; Hao, J. Gold-ionic liquid nanofluids with preferably tribological properties and thermal conductivity. Nanoscale Res. Lett. 2011, 6, 259. [Google Scholar] [CrossRef]
- Thrush, S.J.; Comfort, A.S.; Dusenbury, J.S.; Xiong, Y.; Qu, H.; Han, X.; Schall, J.D.; Barber, G.C.; Wang, X. Stability, Thermal Conductivity, Viscosity, and Tribological Characterization of Zirconia Nanofluids as a Function of Nanoparticle Concentration. Tribol. Trans. 2020, 63, 68–76. [Google Scholar] [CrossRef]
- Jiang, H.; Hou, X.; Ma, Y.; Su, D.; Qian, Y.; Ali, M.K.A.; Dearn, K.D. The tribological performance evaluation of steel-steel contact surface lubricated by polyalphaolefins containing surfactant-modified hybrid MoS2/h-BN nano-additives. Wear 2022, 504, 204426. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, Y.; Chen, L. Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry. Powder Technol. 2013, 239, 409–414. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. Experimental determination of thermal conductivity of three nanofluids and development of new correlations. Int. J. Heat Mass Transf. 2009, 52, 4675–4682. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, H.; Sasmito, A.P.; Mujumdar, A.S. Measurement and modeling of thermal conductivity of graphene nanoplatelet water and ethylene glycol base nanofluids. Int. J. Heat Mass Transf. 2018, 123, 97–109. [Google Scholar] [CrossRef]
- Satti, J.R.; Das, D.K.; Ray, D. Investigation of the thermal conductivity of propylene glycol nanofluids and comparison with correlations. Int. J. Heat Mass Transf. 2017, 107, 871–881. [Google Scholar] [CrossRef]
- Shukla, K.N.; Koller, T.M.; Rausch, M.H.; Fröba, A.P. Effective thermal conductivity of nanofluids—A new model taking into consideration Brownian motion. Int. J. Heat Mass Transf. 2016, 99, 532–540. [Google Scholar] [CrossRef]
- Esfahani, M.R.; Languri, E.M.; Nunna, M.R. Effect of particle size and viscosity on thermal conductivity enhancement of graphene oxide nanofluid. Int. Commun. Heat Mass Transf. 2016, 76, 308–315. [Google Scholar] [CrossRef]
- Alawi, O.A.; Sidik, N.A.C.; Xian, H.W.; Kean, T.H.; Kazi, S. Thermal conductivity and viscosity models of metallic oxides nanofluids. Int. J. Heat Mass Transf. 2018, 116, 1314–1325. [Google Scholar] [CrossRef]
- Jiang, H.; Hou, X.; Su, D.; Liu, H.; Ali, M.K.A. Elucidation of the thermophysical mechanism of hexagonal boron nitride as nanofluids additives. Adv. Powder Technol. 2021, 32, 2816–2827. [Google Scholar] [CrossRef]
- Toghraie, D.; Chaharsoghi, V.A.; Afrand, M. Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid. J. Therm. Anal. Calorim. 2016, 125, 527–535. [Google Scholar] [CrossRef]
- Li, Y.; Kalbasi, R.; Nguyen, Q.; Afrand, M. Effects of sonication duration and nanoparticles concentration on thermal conductivity of silica-ethylene glycol nanofluid under different temperatures: An experimental study. Powder Technol. 2020, 367, 464–473. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, J.; Zhao, Y.; Ma, H. A molecular dynamics study on thermal conductivity enhancement mechanism of nanofluids–Effect of nanoparticle aggregation. Int. J. Heat Mass Transf. 2022, 183, 122124. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Bantan, R.A.; Golmohammadzadeh, A.; Toghraie, D. The thermal properties of water-copper nanofluid in the presence of surfactant molecules using molecular dynamics simulation. J. Mol. Liq. 2021, 325, 115149. [Google Scholar] [CrossRef]
- Mutuku, W.N. Ethylene glycol (EG)-based nanofluids as a coolant for automotive radiator. Asia Pac. J. Comput. Eng. 2016, 3, 1. [Google Scholar] [CrossRef]
- Goudarzi, K.; Jamali, H. Heat transfer enhancement of Al2O3-EG nanofluid in a car radiator with wire coil inserts. Appl. Therm. Eng. 2017, 118, 510–517. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal Conductivity of Nanoparticle-Fluid Mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- Pinto, R.V.; Fiorelli, F.A.S. Review of the mechanisms responsible for heat transfer enhancement using nanofluids. Appl. Therm. Eng. 2016, 108, 720–739. [Google Scholar] [CrossRef]
- Shah, N.A.; Animasaun, I.L.; Chung, J.D.; Wakif, A.; Alao, F.I.; Raju, C.S.K. Significance of nanoparticle’s radius, heat flux due to concentration gradient, and mass flux due to temperature gradient: The case of Water conveying copper nanoparticles. Sci. Rep. 2021, 11, 1882. [Google Scholar] [CrossRef]
- Moghaieb, H.S.; Padmanaban, D.B.; Kumar, P.; Haq, A.U.; Maddi, C.; McGlynn, R.; Arredondo, M.; Singh, H.; Maguire, P.; Mariotti, D. Efficient solar-thermal energy conversion with surfactant-free Cu-oxide nanofluids. Nano Energy 2023, 108, 108112. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Simulation of combined convective-radiative heat transfer of hybrid nanofluid flow inside an open trapezoidal enclosure considering the magnetic force impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Interacting influences of Lorentz force and bleeding on the hydrothermal behaviors of nanofluid flow in a trapezoidal recess with the second law of thermodynamics analysis. Int. Commun. Heat Mass Transf. 2019, 110, 104411. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, H.; He, X.; Yang, W. Mesporous 3C-SiC hollow fibers. Sci. Rep. 2017, 7, 1893. [Google Scholar] [CrossRef]
- Fan, J.; Li, H.; Jiang, J.; So, L.K.Y.; Lam, Y.W.; Chu, P.K. 3C-SiC Nanocrystals as Fluorescent Biological Labels. Small 2008, 4, 1058–1062. [Google Scholar] [CrossRef]
- Harandi, S.S.; Karimipour, A.; Afrand, M.; Akbari, M.; Orazio, A.D. An experimental study on thermal conductivity of F-MWCNTs–Fe3O4/EG hybrid nanofluid: Effects of temperature and concentration. Int. J. Heat Mass Transf. 2016, 76, 171–177. [Google Scholar] [CrossRef]
- Ghanbarpour, M.; Haghigi, E.B.; Khodabandeh, R. Thermal properties and rheological behavior of water based Al2O3 nanofluid as a heat transfer fluid. Exp. Therm. Fluid Sci. 2014, 53, 227–235. [Google Scholar] [CrossRef]
- Essajai, R.; Mzerd, A.; Hassanain, N.; Qjani, M. Thermal conductivity enhancement of nanofluids composed of rod-shaped gold nanoparticles: Insights from molecular dynamics. J. Mol. Liq. 2019, 293, 111494. [Google Scholar] [CrossRef]
- Mohebbi, A. Prediction of specific heat and thermal conductivity of nanofluids by a combined equilibrium and non-equilibrium molecular dynamics simulation. J. Mol. Liq. 2012, 175, 51–58. [Google Scholar] [CrossRef]
- Cui, W.; Shen, Z.; Yang, J.; Wu, S. Molecular dynamics simulation on the microstructure of absorption layer at the liquid–solid interface in nanofluids. Int. Commun. Heat Mass Transf. 2016, 71, 75–85. [Google Scholar] [CrossRef]






| Nanoparticles Used | Density (g/cm3) | Average Size (nm) | Specific Surface Area (m2/g) | Crystal Form |
|---|---|---|---|---|
| SiC | 0.11 | 40–60 | 39.8 | Cubic |
| SiC Molar Fraction | E.G. Molecule | Si Atom | C Atom | Total Atoms |
|---|---|---|---|---|
| 0% | 1000 | 0 | 0 | 10,000 |
| 0.1% | 4470 | 7 | 7 | 44,714 |
| 0.5% | 899 | 7 | 7 | 9004 |
| 1% | 447 | 7 | 7 | 4884 |
| Atom | (Å) | Ε (kJ/mol) | Molar Mass | Charge q (|e|) | Notes |
|---|---|---|---|---|---|
| C1 (SiC) | 3.4745 | 0.159 | 12.0100 | 0.000000 | C atom from SiC |
| Si | 4.0534 | 0.2000 | 28.0860 | 0.000000 | \ |
| C2 (E.G.) | 3.8754 | 0.1577 | 12.0100 | −0.170000 | C atom from E.G. |
| H1 (C) | 2.4499 | 0.3038 | 1.0080 | 0.100000 | H atom from -CH2 |
| H2 (O) | 2.4499 | 0.1569 | 1.0080 | 0.350000 | H atom from -OH |
| O | 2.8597 | 0.5803 | 16.0000 | −0.380000 | \ |
| Chemical Bond | K1 | r (Distance) |
|---|---|---|
| C2-C2 | 322.7158 | 1.5260 |
| C2-O | 384.0000 | 1.4200 |
| C2-H1 | 340.6175 | 1.1050 |
| O-H2 | 540.6336 | 0.9600 |
| C1-Si | 238.0000 | 1.8090 |
| Angle | K2 | θ (Degrees) |
|---|---|---|
| C2-C2-O | 70.0000 | 109.5000 |
| C2-C2-H1 | 44.4000 | 110.0000 |
| O-C2-H1 | 57.0000 | 109.5000 |
| H1-C2-H1 | 39.5000 | 106.4000 |
| C2-O-H2 Si-C1-Si C1-Si-C1 | 58.5000 42.2000 44.4000 | 106.0000 122.5000 113.5000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Chu, C.; Jiang, H.; Ali, M.K.A.; Dearn, K.D. Enhancing Heat Transfer Behaviour of Ethylene Glycol by the Introduction of Silicon Carbide Nanoparticles: An Experimental and Molecular Dynamics Simulation Study. Molecules 2023, 28, 3011. https://doi.org/10.3390/molecules28073011
Hou X, Chu C, Jiang H, Ali MKA, Dearn KD. Enhancing Heat Transfer Behaviour of Ethylene Glycol by the Introduction of Silicon Carbide Nanoparticles: An Experimental and Molecular Dynamics Simulation Study. Molecules. 2023; 28(7):3011. https://doi.org/10.3390/molecules28073011
Chicago/Turabian StyleHou, Xianjun, Chen Chu, Hua Jiang, Mohamed Kamal Ahmed Ali, and Karl D. Dearn. 2023. "Enhancing Heat Transfer Behaviour of Ethylene Glycol by the Introduction of Silicon Carbide Nanoparticles: An Experimental and Molecular Dynamics Simulation Study" Molecules 28, no. 7: 3011. https://doi.org/10.3390/molecules28073011
APA StyleHou, X., Chu, C., Jiang, H., Ali, M. K. A., & Dearn, K. D. (2023). Enhancing Heat Transfer Behaviour of Ethylene Glycol by the Introduction of Silicon Carbide Nanoparticles: An Experimental and Molecular Dynamics Simulation Study. Molecules, 28(7), 3011. https://doi.org/10.3390/molecules28073011








