Next Article in Journal
Repurposing FIASMAs against Acid Sphingomyelinase for COVID-19: A Computational Molecular Docking and Dynamic Simulation Approach
Next Article in Special Issue
Facile Attachment of Halides and Pseudohalides to Dodecaborate(2-) via Pd-catalyzed Cross-Coupling
Previous Article in Journal
Controllable Synthesis of N2-Intercalated WO3 Nanorod Photoanode Harvesting a Wide Range of Visible Light for Photoelectrochemical Water Oxidation
Previous Article in Special Issue
Thermal Polymorphism in CsCB11H12
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 7
10.3390/molecules28072988
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Polyhedral Dicobaltadithiaboranes and Dicobaltdiselenaboranes as Examples of Bimetallic Nido Structures without Bridging Hydrogens

by
Amr A. A. Attia
1,
Alexandru Lupan
1,* and
Robert Bruce King
2,*
1
Faculty of Chemistry and Chemical Engineering, Babeş-Bolyai University, 400347 Cluj-Napoca, Romania
2
Department of Chemistry and Center for Computational Quantum Chemistry, University of Georgia, Athens, GA 30602, USA
*
Authors to whom correspondence should be addressed.
Molecules 2023, 28(7), 2988; https://doi.org/10.3390/molecules28072988
Submission received: 11 March 2023 / Revised: 24 March 2023 / Accepted: 26 March 2023 / Published: 27 March 2023
(This article belongs to the Special Issue New Developments in Boron Chemistry: From Oxidoborates to Hydrido(hetero)borane Derivatives – in Celebration of Professor John D. Kennedy’s 80th Birthday)
Browse Figures
Versions Notes

Abstract

:
The geometries and energetics of the n-vertex polyhedral dicobaltadithiaboranes and dicobaltadiselenaboranes Cp2Co2E2Bn−4Hn−4 (E = S, Se; n = 8 to 12) have been investigated via the density functional theory. Most of the lowest-energy structures in these systems are generated from the (n + 1)-vertex most spherical closo deltahedra by removal of a single vertex, leading to a tetragonal, pentagonal, or hexagonal face depending on the degree of the vertex removed. In all of these low-energy structures, the chalcogen atoms are located at the vertices of the non-triangular face. Alternatively, the central polyhedron in most of the 12-vertex structures can be derived from a Co2E2B8 icosahedron with adjacent chalcogen (E) vertices by breaking the E–E edge and 1 or more E–B edges to create a hexagonal face. Examples of the arachno polyhedra with two tetragonal and/or pentagonal faces derived from the removal of two vertices from isocloso deltahedra were found among the set of lowest-energy Cp2Co2E2Bn−4Hn−4 (E = S, Se; n = 8 and 12) structures.

1. Introduction

The structures of the polyhedral borane dianions BnHn2− as well as those of the isoelectronic carborane monoanions CBn−1Hn− and neutral dicarbaboranes C2Bn−2Hn are based on the most spherical deltahedra, which are known as the closo deltahedra (Figure 1) [1,2]. Except for the 13-vertex systems, the most spherical deltahedra have exclusively triangular faces with vertex degrees as nearly similar as possible. The 11- and 13-vertex systems contain 1 and 2 degree-6 vertices, respectively, whereas the other closo polyhedra have exclusively degree-4 and -5 vertices, for which the degree of a vertex is defined as the number of edges meeting at the vertex in question. The chemical bonding in these polyhedral boranes and carboranes is based on 2n + 2 skeletal electrons for an n-vertex system, with each BH and CH vertex contributing 2 and 3 skeletal electrons, respectively, after providing an electron for the external B–H or C–H bond. This is a key aspect of the Wade–Mingos rules [3,4,5] relating polyhedral geometry to skeletal electron count. A reasonable chemical bonding model for these deltahedra consists of a resonance hybrid of canonical structures containing a single n-center bond composed of orbitals from each of the n-vertex atoms overlapping at the center of the polyhedron supplemented by n two-center, two-electron bonds on the surface of the polyhedron [6]. This structural model accounts for the 2n + 2 skeletal electrons in the stable closo deltahedral borane structures. The delocalization implicit in this bonding model, particularly the presence of the multicenter core bond, is consistent with the interpretation of these species as three-dimensional aromatic systems [7,8].
The research groups of Hawthorne [9] and Grimes [10] were the first to show that the boron vertices in these polyhedral boranes could be replaced by transition metal units. The cyclopentadienylcobalt unit (CpCo) was especially useful for this purpose due to the robustness of the linkage between the cyclopentadienyl ring and the cobalt atom. Furthermore, a CpCo vertex is a donor of two skeletal electrons like a BH vertex so that it can replace a BH unit in the polyhedral structures. The research of the Hawthorne group [9] focused on metallaboranes that can be obtained from decaborane (B10H14) as a precursor, whereas the research of the Grimes group [10] studied metallaboranes obtained from pentaborane (B5H9) as a precursor. The chemistry of polyhedral boranes and their transition metal derivatives remains of interest even after approximately half a century following the discovery of the original metallaboranes with the possibilities of applications in medicine [11,12] and catalysis [13].
Further development of metallaborane chemistry, especially by Kennedy and his co-workers, by using a variety of metal vertices, particularly those containing second- and third-row transition metals, resulted in the discovery of alternative so-called isocloso deltahedra in 9- and 10-vertex metallaborane structures with a degree-6 vertex for the metal atom (Figure 2) [14,15,16,17]. The 11-vertex closo deltahedron can also be an isocloso deltahedron since it necessarily has a degree 6 vertex. A reasonable chemical bonding model for an n-vertex isocloso metallaborane deltahedron consists exclusively of n 3-center, 2-electron (3c-2e) bonds in n of the 2n − 4 faces of the deltahedron without the n-center core bond found in the closo chemical bonding [18]. Thus, the isocloso metallaboranes are 2n rather than 2n + 2 skeletal electron systems.
Electron-richer polyhedral borane derivatives with n-vertices are obtained by removing a vertex from an (n + 1)-vertex closo or isocloso deltahedron to give a so-called n-vertex nido polyhedron. Such a vertex removal process creates a smaller polyhedron with a non-triangular face at the site of vertex removal. This non-triangular face can be regarded as a “hole” in an otherwise triangulated polyhedral surface. Williams [2] introduced a convenient notation for nido polyhedra as ni-n〈h〉, where n is the number of vertices, and h is the number of vertices in the non-triangular face as indicated by a Roman numeral. For example, by using this notation, the square pyramid can be designated as a ni-5〈IV〉 polyhedron. Since the original (n + 1)-vertex closo deltahedron has 2(n + 1) + 2 skeletal electrons, the n-vertex nido polyhedron derived from it has 2n + 4 skeletal electrons.
The discovery of neutral binary boranes BnHn+4 (n = 2, 5, 6, 8, 9, 10) exhibiting nido structures, of which B10H14 is the most stable [19,20], predates that of the more stable closo boranes by going back to the original boron hydride syntheses of Stock. The structures of B5H9 and B6H10 are derived by the removal of a degree-4 vertex from an octahedron and a degree-5 vertex from a pentagonal bipyramid, respectively, thereby generating a square and a pentagonal face, respectively (Figure 3). The structures of the larger BnHn+4 (n = 8, 9, 10) boranes are derived by removal of the unique degree-6 vertex from the corresponding (n + 1) vertex isocloso deltahedron. The polyhedral frameworks of all of the BnHn+4 boranes (n = 5, 6, 8, 9, 10) all have n BH vertices with the four “extra” hydrogen atoms bridging the B–B edges surrounding the non-triangular face. A relatively large non-triangular face such as a hexagonal hole versus a pentagonal or tetragonal face provides more space for the four hydrogen atoms bridging the hole B–B edges.
A topic of interest is the design of viable n-vertex nido borane structures that have the necessary 2n + 4 skeletal electrons without the need for bridging hydrogen atoms. Tetracarbaborane structures of the type C4Bn−4Hn provide the required 2n + 4 skeletal electrons. In this connection, species of the type C4Bn−4Rn (R = H or alkyl) are known experimentally to have such structures with 6 [21,22], 8 [23,24], 10 [25,26,27,28], 11 [29], and 12 [30,31,32,33,34,35,36] vertices. Furthermore, the structures and energetics of the tetracarbaboranes have been studied by using modern density functional theory methods [37].
Generating a nido polyhedral borane with the requisite 2n + 4 skeletal electrons by using electron-richer carbon atoms in CH vertices to replace boron atoms in BH vertices requires four such carbon heteroatoms in the carborane polyhedron. Using bare sulfur or selenium vertex atoms as heteroatoms in polyhedral borane structures to provide the 2n + 4 skeletal electrons for nido geometry requires only two heteroatoms in an E2Bn−2Hn−2 (E = S, Se) structure since bare sulfur or selenium vertices are each donors of four skeletal electrons after diverting 2 of their 6 valence electrons to an external lone pair. In this connection, the 11-vertex nido-B9H9E2 (E = S, Se) structures have been synthesized and shown via X-ray crystallography to have a central polyhedron obtained via the removal of one vertex from an icosahedron [38].
Dithiaboranes and diselenaboranes with one or two CpCo vertices have been synthesized and structurally characterized via X-ray crystallography (Figure 4). The 12-vertex cobaltadiselenaborane CpCoSe2B9H9 has been synthesized and shown to have a ni-13〈VI〉 structure derived via the removal of a degree-6 vertex from a docosahedron, which is the 13-vertex closo deltahedron [35]. This structure can also be derived from a central CoSe2B9 icosahedron with a Se–Se edge by breaking the Se–Se edge and an adjacent Se–B edge to generate an SeCoSeBB pentagonal face, leaving a degree-3 selenium vertex. This structure is shown by density functional theory to be 1 of the 3 lowest-energy structures lying within 1 kcal/mol of each other [39].
In total, 3 isomeric structures of the 11-vertex dicobaltadithiaborane Cp*2Co2S2B7H7 with 2 pentamethylcyclopentadienylcobalt vertices (Cp*Co) have been isolated by Kang and Sneddon [40] from the mixture that was obtained from the reaction between LiCp*, NaS2B7H8, and CoCl2 (Figure 5). Attempts to obtain definitive structural information on these species via X-ray crystallography were prevented by disorder problems. However, the poor X-ray data were sufficient to indicate the relative positions of the cobalt atom and 11-vertex Co2S2B7 geometries obtained via removal from a vertex from a central icosahedron. Furthermore, 1 of the 3 structures appears to be an ultimate pyrolysis product at 300 °C. The structures were assigned on the basis of the 11B NMR spectra. In addition, trace quantities of a 10-vertex Cp*2Co2S2B6H6 structure were obtained, which was suggested to have a decaborane-like structure on the basis of its 11B NMR.
In view of the difficulty in obtaining definitive structural information on the dicobaltadithiaboranes, we have undertaken density functional theory studies on the complete series of Cp2Co2E2Bn−4Hn−4 (E = S, Se; n = 8, 9, 10, 11, 12) systems with unsubstituted cyclopentadienyl rings. In addition, we have included the Cp*2Co2S2B7H7 system with pentamethylcyclopentadienyl (Cp*) rings in this study for comparison with the reported experimental data. This theoretical study extends the previous study [36] of the dicobaltadiselenaboranes by introducing a second cobalt atom into the metallaborane polyhedron. This provides an opportunity to assess preferences for a pair of cobalt atoms in these structures to occupy adjacent bonding positions or to be as far removed from each other as possible or something in between. The dicobaltadithiaboranes and dicobaltadiselena boranes are of interest in representing the first examples of nido structures without bridging hydrogen atoms containing two transition metal vertices in the underlying polyhedron.

2. Results and Discussion

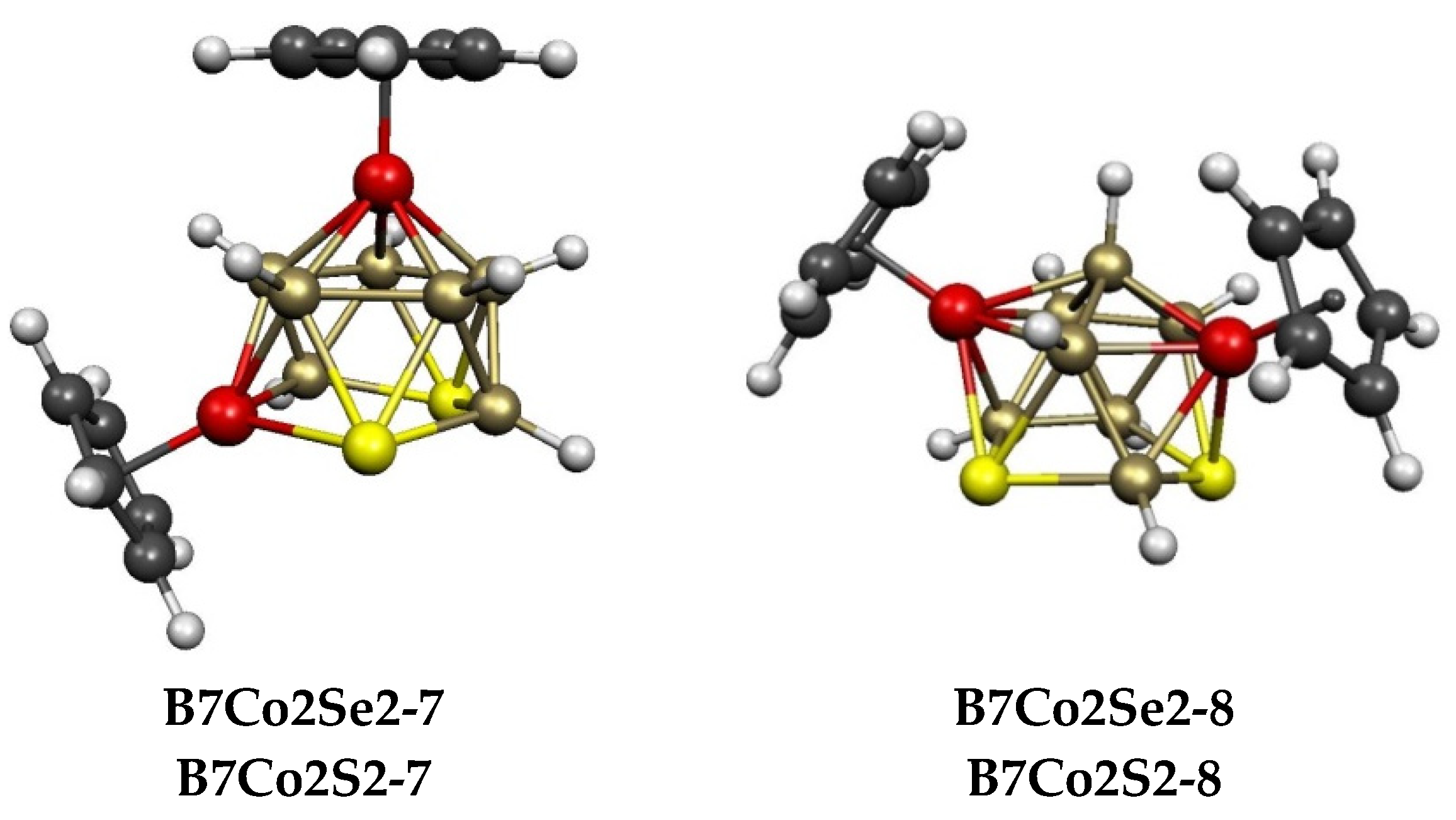
2.1. The 11-Vertex Systems Cp2Co2E2B7H7 (E = S, Se)

In total, 8 structures were found for each of the 11-vertex Cp2Co2E2B7H7 (E = S, Se) systems within 15 kcal/mol of the lowest-energy structure (Figure 6 and Table 1). The central ni-11〈V〉 polyhedron in all of the eight structures can be derived from an icosahedron via the removal of one vertex, leaving a pentagonal face that is similar to the dicarbollide anion C2B9H12− that was originally used by Hawthorne and co-workers [9] to synthesize a variety of transition metal complexes having a central MC2B9 icosahedron. For both Cp2Co2E2B7H7 (E = S, Se) systems, the lowest-energy structures B7Co2E2-1 (E = S, Se) have both cobalt atoms and both chalcogen atoms at the surface of the pentagonal face and, thus, at degree-4 vertices. This is the most prevalent example of generating an n-vertex nido polyhedral borane by the removal of a vertex from an (n + 1)-vertex closo deltahedral borane. Furthermore, in each of the 8 low-energy Cp2Co2E2B7H7 structures, both chalcogen atoms are located at the degree-4 pentagonal face vertices rather than at interior degree-5 vertices. This is consistent with the preference of chalcogen atoms for lower degree vertices in polyhedral selena- and thiaboranes.
Three isomeric pentamethylcyclopentadienyl Cp*2Co2S2B7H7 complexes have been isolated by Kang and Sneddon in small quantities from the reaction between LiCp*, NaS2B7H8, and CoCl2 which they designated by the Roman numerals III, IV, and V in their paper (Figure 5) [37]. Extensive disorder prevented complete X-ray structure determinations on these molecules beyond location of the cobalt atoms. On the basis of 11B NMR and 2D 11B-11B COSY NMR, Kang and Sneddon assigned structures analogous to B7Co2S-1, B7Co2S-2, and B7Co2S-3 to III, IV, and V, respectively. We found that complete substitution of hydrogen atoms with methyl groups did not affect the relative energy ordering of the 3 lowest-energy structures with the relative energies of the Cp* structures B7Co2S-1*, B7Co2S-2*, and B7Co2S-3* being 0.0, 0.6, and 6.7 kcal/mol, respectively. What is strange is the observation that the Kang/Sneddon isomer III, which has the assigned structure B7Co2S2-1* and has both cobalt atoms as well as both sulfur atoms located on pentagonal face vertices, is converted ultimately upon heating to 300 °C to the Kang/Sneddon isomer V (Figure 5), which was assigned the higher-energy structure B7Co2S2-3*, as it has both cobalt atoms located at degree-5 interior vertices. This is contrary to expectation because pyrolysis, particularly to a temperature as high as 300 °C, would be expected to give a lower-energy isomer rather than a higher-energy isomer. Our theoretical studies cast some doubt about the structure assignments of III, IV, and V that were given by Kang and Sneddon in their 1988 study [37]. Note that the predicted Co…Co distances in B7Co2S-1, B7Co2S-2, and B7Co2S-3 are all approximately 3.8 to 3.9 Å, so the determination of these distances by an otherwise incomplete X-ray crystallography study on an extensively disordered system would not be sufficient to distinguish between these three structures. The improvements in X-ray crystallography methodology in the 35 years since the Kang/Sneddon report of the 3 Cp*2Co2S2B7H7 isomers might provide a resolution to this dilemma.

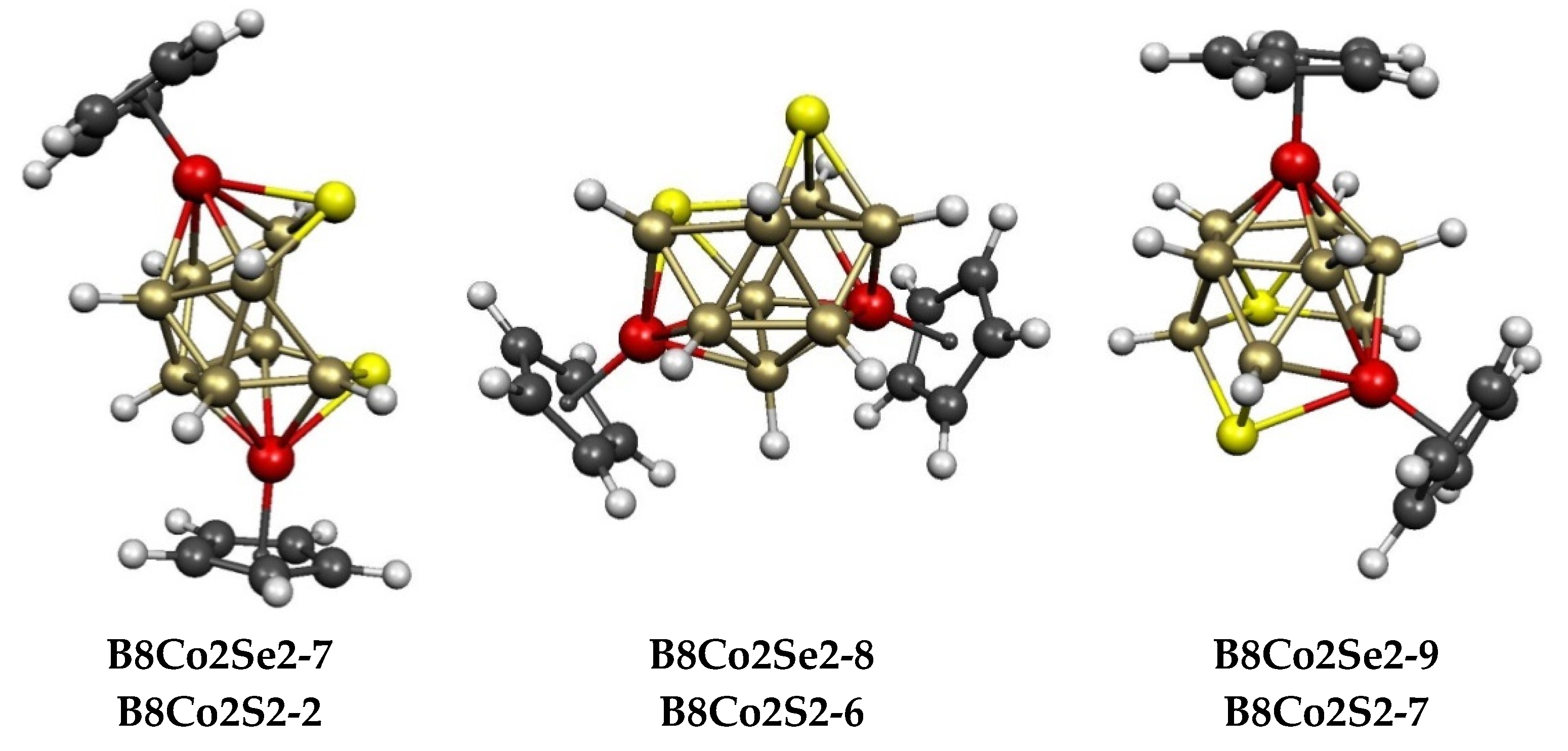
2.2. The 12-Vertex Systems Cp2Co2E2B8H8 (E = S, Se)

In total, 9 structures were found for the 12-vertex Cp2Co2E2B8H8 (E = S, Se) systems up to 9 kcal/mol (E = S) and 12 kcal/mol (E = Se) in energy (Figure 7 and Table 2). These structures are of three types. The polyhedra for the lowest-energy Cp2Co2S2B8H8 structure B8Co2S2-1, as well as those for 4 of the 5 next higher-energy structures B8Co2S2-2, B8Co2S2-3, B8Co2S2-5, and B8Co2S2-6, lying 3.0, 3.1, 3.8, and 5.6 kcal/mol in energy above B8Co2S2-1, respectively, can be derived from a Co2E2B8 icosahedron with an S–S edge by breaking the S–S edge and at least one S–B edge to create typically a gaping, bent hexagonal face. These five structures can be divided in two categories. In B8Co2S2-1, B8Co2S2-5, and B8Co2S2-6, the cobalt atoms are located in meta (non-adjacent, non-antipodal) positions of the original octahedron. However, in B8Co2S2-2 and B8Co2S2-4, the cobalt atoms are located in para (antipodal) positions in the original icosahedron.
Substituting selenium for sulfur in the 12-vertex system to give Cp2Co2Se2B8H8 derivatives leads to a different energy ordering of the 9 lowest-energy structures (Table 2). The lowest-energy Cp2Co2Se2B8H8 structure B8Co2Se2-1 and the higher-energy structure B8Co2Se2-4, which lies 4.0 kcal/mol higher in energy, are exceptional among the complete series of Cp2Co2E2Bn−4Hn−4 (n = 8 to 12) structures in exhibiting ideal C2v symmetry, whereas all of the remaining structures of this type have the lower-symmetry point groups of C1, C2, or Cs. These 2 structures are ni-12〈IV〉 structures derived from the 13-vertex closo deltahedron, namely, the docosahedron (Figure 1), by the removal of the unique degree-4 vertex, thereby creating a tetragonal face with alternating degree-5 and degree-4 vertices. In both B8Co2Se2-1 and B8Co2Se-4, the tetragonal face has alternating cobalt and sulfur vertices. The Cp2Co2S2B8H8 structures corresponding to B8Co2Se2-1 and B8Co2Se2-4 are B8Co2S-9 and B8Co2S-8, respectively, which lie 9.0 and 7.9 kcal/mol in energy above B8Co2S-1.
The remaining 2 of the 9 lowest-energy Cp2Co2E2B8H8 (E = S, Se), structures, namely, B8Co2S-3 and B8Co2S-7 for E = S, which lie 3.1 and 7.1 kcal/mol, respectively, in energy above B8Co2S-1, and B8Co2Se-5 and B8Co2Se-9, respectively, which lie 8.2 and 12.3 kcal/mol, respectively, in energy above B8Co2Se2-1, can be considered to be arachno ar-12〈V,V〉 structures that are obtained by removing 2 vertices from a 14-vertex deltahedron. However, the central 14-vertex deltahedron from which these structures are derived is not the 14-vertex closo deltahedron, namely, the D6d bicapped hexagonal antiprism with 2 degree-6 vertices in antipodal positions, as well as 12 degree-5 vertices, but instead, it is a less symmetrical 14-vertex deltahedron with 3 degree-6 vertices, 10 degree-5 vertices, and 1 degree-4 vertex (Figure 8). This 14-vertex deltahedron is closely related to the 14-vertex polyhedron in experimentally known Cp*2Ru2C2B10H12 by lengthening an edge connecting a degree-6 vertex with a degree-5 vertex [41,42].

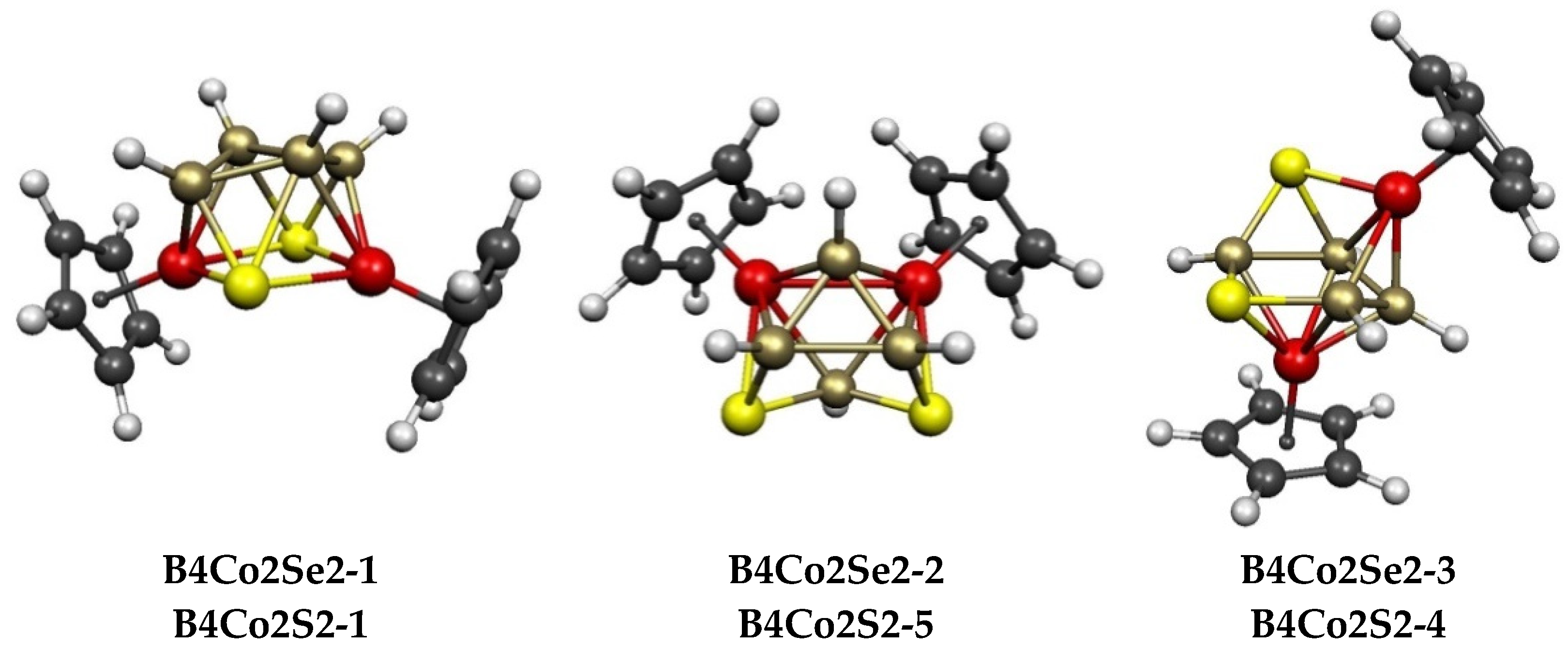
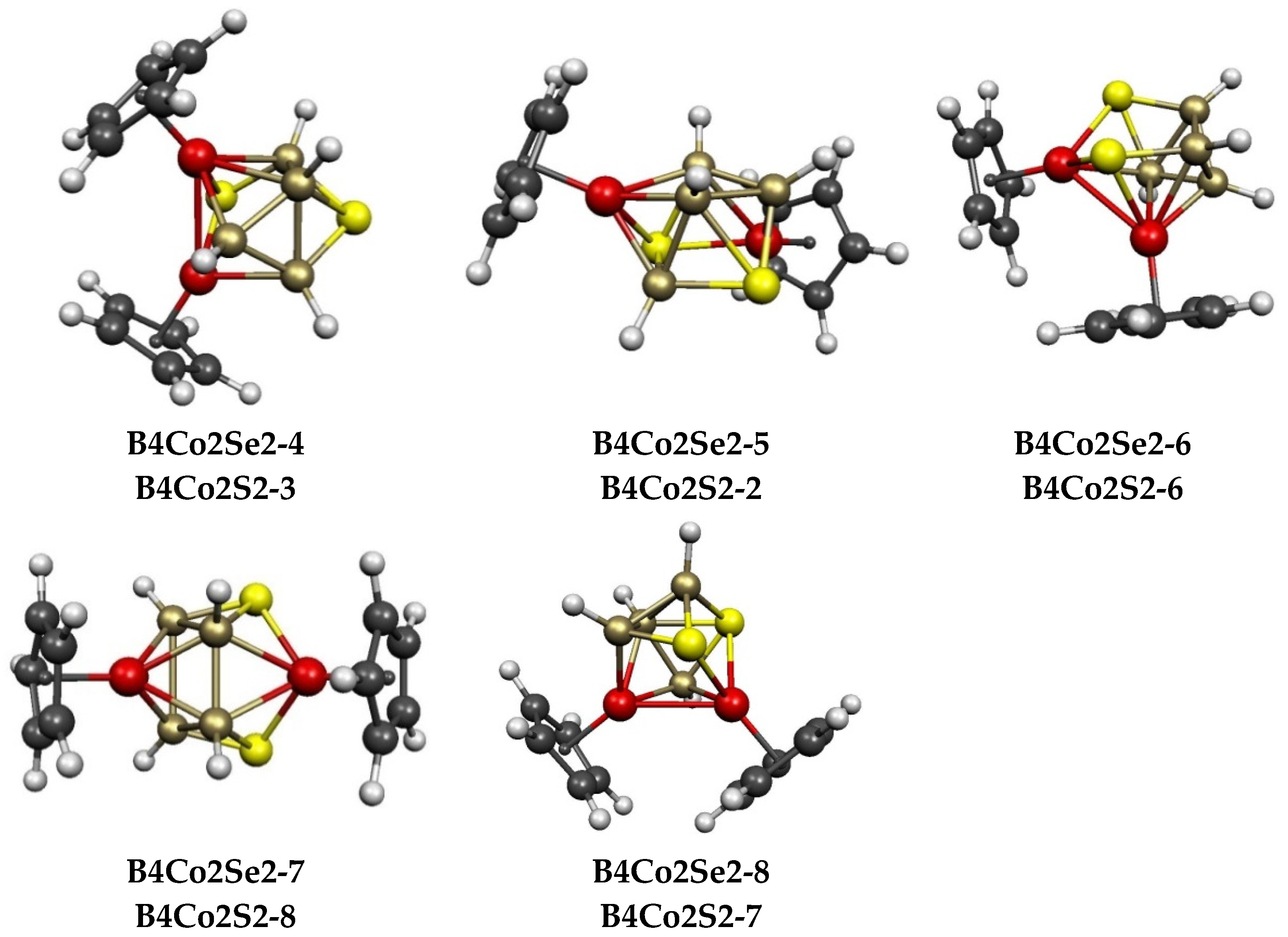
2.3. The Cp2Co2E2Bn−4Hn−4 (E = S, Se) Systems Having 8 to 10 Vertices

The central Co2E2B4 polyhedra in 7 of the 8 lowest-energy structures of the 8-vertex Cp2Co2E2B4H4 (E = S, Se) systems (Figure 9 and Table 3) are all derived by the removal of a vertex from the closo 9-vertex deltahedron, namely, the tricapped trigonal prism (Figure 1). Removal of a degree-4 vertex from the tricapped, trigonal prism gives the bicapped trigonal prism, which is found in the lowest-energy structures B4Co2E2-1 (E = S, Se), as well as the higher-energy structures B4C2S2-2 and B4Co2Se2-5, which lie ~6 kcal/mol in energy above the lowest-energy structures (Table 3). In the lowest-energy structure B4Co2E2-1, the atoms of the open tetragonal face are alternating cobalt and chalcogen atoms with all four boron atoms located at interior vertices. The other bicapped trigonal prismatic Cp2Co2E2B4H4 (E = S, Se) structures have the two sulfur atoms as well as one of the cobalt atoms at the open tetragonal face, with the other cobalt atom at an interior vertex.
For the 8-vertex selenium derivative Cp2Co2Se2B4H4, the 2 low-energy bicapped trigonal prismatic structures B4Co2Se-1 and B4Co2Se-2 are essentially isoenergetic, as they lie within ~1 kcal/mol of each other (Figure 9 and Table 3). The lowest-energy Cp2Co2Se2B4H4 ni-8〈V〉 structure B4Co2Se2-3, which is derived from a tricapped trigonal prism by removing a degree-5 rather than a degree-4 vertex, lies 11.1 kcal/mol above B4Co2Se-1. In total, 4 more ni-8〈V〉 Cp2Co2Se2B4H4 structures, namely, B4Co2Se2-4, B4Co2Se2-5, B4Co2Se2-6, and B4Co2Se2-8, lie in the energy range of 11 to 15 kcal/mol above B4Co2Se2-1. The potential energy surface of the corresponding 8-vertex sulfur system Cp2Co2Se2B4H4 is significantly different since 3 of the 5 ni-8〈V〉 structures B4Co2S2-2, B4Co2S2-3, and B4Co2S2-4 lie within ~2 kcal/mol of the lowest-energy structure B4Co2S2-1 and below the higher-energy, bicapped trigonal prism isomer B4Co2S2-5. In all eight lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures, both sulfur atoms lie on tetragonal or pentagonal face vertices, which is consistent with the preference of sulfur for lower degree vertices in borane polyhedra.
Of the 8 lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures, B4Co2S2-8 and B4Co2Se2-7, which lie at 10.3 and 14.9 kcal/mol in energy, respectively, above the corresponding B4Co2E2-1 structure, are not derived by removing a vertex from a tricapped trigonal prism (Figure 9 and Table 3). Instead, the central Co2S2B4 polyhedron in these structures is generated via the removal of the 2 degree-4 vertices that are bridged by the unique degree-6 vertex from the 10-vertex isocloso deltahedron of ideal C3v symmetry. This leads to an arachno 8-vertex ar-8〈IV,IV〉 structure with 2 tetragonal faces sharing a cobalt atom and a sulfur atom. The process of removing 2 degree-4 vertices from the 10-vertex isocloso deltahedron to give the 8-vertex Cp2Co2E2B4H4 structures B4Co2S2-8 and B4Co2Se2-7 is analogous to the process of removing a degree-4 and a degree-5 vertex from a 14-vertex isocloso 14-vertex deltahedron (Figure 8) to give the 12-vertex ar-14〈IV,V〉 Cp2Co2E2B8H8 structures B8Co2S23 and B8Co2S27 (Figure 7) that are discussed above.
The central polyhedra of the 6 lowest-energy 9-vertex Cp2Co2E2B5H5 (E = S, Se) structures (Figure 10 and Table 4) are all derived from the 10-vertex closo deltahedron, namely, the bicapped square antiprism, by removing either a degree-4 vertex or a degree-5 vertex. Whether a degree-4 vertex is removed to give a capped square antiprism or a degree-5 vertex is removed to give a ni-9〈V〉 structure with a pentagonal face makes relatively little difference in energy since the 6 structures lying within 7 kcal/mol of the lowest-energy structures B5Co2E2-1 (E = S, Se) include 2 representatives of the former type and 4 representatives of the latter type. Both chalcogen vertices are always located at a non-triangular face in all of the low-energy structures.
The potential energy surfaces for the 10-vertex Cp2Co2E2B6H6 (E = S, Se) systems are the simplest of all, with only 3 structures lying within 16 kcal/mol (E = S) or 21 kcal/mol (E = Se) of the lowest-energy structures B6Co2E2-1 (Figure 11 and Table 5). The central Co2E2B6 framework of all three structures is that of the very stable decaborane, B10H14, which is obtained via the removal of the unique degree-6 vertex of the closo 11-vertex deltahedron (sometimes called by the confusing name of “edge-coalesced icosahedron”) to create a bent hexagonal face. The structures B6Co2E2-1, in which the hexagonal face has only boron and sulfur atoms with the sulfur atoms in opposite (“para”) positions, is favored energetically over the next lowest-energy structures B6Co2E2-1 by significant margins of ~11 kcal/mol (E = S) and ~12 kcal/mol (E = Se).

3. Theoretical Methods

The chemical models that were investigated in this study are based on various BnHn2− polyhedra, for which a systematic substitution of 2 BH vertices with 2 CpCo units, followed by the substitution of 2 BH vertices with 2 chalcogen atoms (sulfur or selenium) led to the generation of a total of 5389 different starting structures for each of the Cp2Co2S2Bn−4Hn−4 and Cp2Co2Se2Bn−4Hn−4 systems (n = 8 to 12) (see the Supporting Information).
Full geometry optimizations were carried out on all systems by using the PBE0 DFT functional [43], coupled with the def2-TZVP basis set [44], as implemented in the Gaussian 09 package [45]. The natures of the stationary points after optimization were checked via calculations of the harmonic vibrational frequencies to ensure genuine minima. Furthermore, single-point energy calculations were performed on the lowest-energy optimized structures by using the DLPNO-CCSD(T) method [46,47,48,49,50,51,52,53,54,55,56,57,58,59] coupled with the def2-QZVP basis set, as implemented in the ORCA 3.0.3 software package [60,61,62,63,64,65,66,67,68]. Zero-point corrections taken from the PBE0/def2-TZVP computations were then added to the final energies.
The polyhedral dicobaltadithiaborane and dicobaltadiselenaborane structures Cp2Co2E2Bn4Hn−4 (E = S, Se; n = 8 to 12) are designated as B(n−4)Co2E2-x throughout the text, where n is the total number of polyhedral vertices, and x is the relative ordering of the structure on the energy scale. Only the lowest-energy and, thus, potentially chemically significant structures are considered in detail in this paper. More comprehensive structural information including higher-energy structures, connectivity information not readily seen in the figures, and orbital energies and HOMO-LUMO gaps are provided in the Supporting Information.

4. Summary

The central Co2E2Bn−4 polyhedra in the low-energy structures of the n-vertex polyhedral dicobaltadithiaboranes and dicobaltadiselenaboranes Cp2Co2E2Bn−4Hn−4 (E = S, Se; n = 8 to 12) in general are generated from the (n + 1)-vertex most spherical closo deltahedra via the removal of a single vertex, leading to a tetragonal, pentagonal, or hexagonal face, depending on the degree of the vertex removed. In all of these low-energy structures, both chalcogen atoms are located on the non-triangular face vertices, reflecting the energetic preference of chalcogens for lower degree vertices. For the 8- and 9-vertex systems, the structures obtained via the removal of a degree-4 or degree-5 vertex from the corresponding (n + 1)-vertex closo deltahedra, namely, the tricapped trigonal prism and the bicapped square antiprism, have similar energies. The low-energy structures for the 10-vertex Cp2Co2E2B6H6 (E = S, Se) systems all have the framework of the most stable BnHn+4 borane, namely, B10H14 with a bent hexagonal face. The lowest-energy of these 10-vertex Cp2Co2E2B6H6 structures by significant margins exceeding 10 kcal/mol has only boron and both sulfur atoms located at the 6 hexagonal face vertices. The central polyhedra of all of the 11-vertex Cp2Co2E2B7H7 structures are similar to the polyhedron of the dicarbollide anion C2B9H12− in being generated by loss of a vertex from a regular icosahedron to generate a pentagonal face.
In principle, the central polyhedra in most of the low-energy 12-vertex Cp2Co2E2B8H8 (E = S, Se) structures can be derived via the removal of a vertex from the 13-vertex closo deltahedron, namely, the docosahedron. However, the central polyhedron in most of the 12-vertex structures can also be derived from a Co2E2B8 icosahedron with adjacent chalcogen vertices by breaking the E–E edge and 1 or more E–B edges to create a hexagonal hole.
Two examples of arachno polyhedra were found among the set of lowest-energy Cp2Co2E2Bn−4Hn−4 (E = S, Se; n = 8 to 12) structures. The central polyhedron of one structure within 15 kcal/mol of the lowest-energy structure in each of the 8-vertex Cp2Co2E2B4H4 (E = S, Se) systems is an arachno polyhedron with 2 tetragonal faces sharing an edge that is derived from the 10-vertex isocloso deltahedron via the removal of the 2 degree-4 vertices bridged by the unique degree-6 vertex. In addition, 2 of the structures in each of the 12-vertex Cp2Co2E2B8H8 (E = S, Se) systems are ar12〈IV,V〉 structures that are derived from the 14-vertex isocloso deltahedron that is found in the experimentally known Cp*2Ru2C2B10H12 by removing the unique degree-4 vertex as well as a degree-5 vertex.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28072988/s1, Initial structures, distance, and energy ranking tables, orbital energies and HOMO/LUMO gaps, complete Gaussian09 reference; concatenated .xyz file containing the Cartesian coordinates of the lowest-energy optimized structure. Table S1A: Initial 8-vertex starting structures. Table S1B: Distance matrices and energy rankings for the lowest energy Cp2Co2S2B4H4 structures. Table S1C: Distance matrices and energy rankings for the lowest energy Cp2Co2Se2gB4H4 structures. Table S2A: Initial 9-vertex starting structures. Table S2B: Distance matrices and energy rankings for the lowest energy Cp2Co2S2B5H5 structures. Table S2C: Distance matrices and energy rankings for the lowest energy Cp2Co2Se5B5H5 structures. Table S3A: Initial 10-vertex starting structures. Table S3B: Distance matrices and energy rankings for the lowest energy Cp2Co2S2B6H6 structures. Table S3C: Distance matrices and energy rankings for the lowest energy Cp2Co2Se2B6H6 structures. Table S4A: Initial 11-vertex starting structures. Table S4B: Distance matrices and energy rankings for the lowest energy Cp2Co2S2B7H7 structures. Table S4C: Distance matrices and energy rankings for the lowest energy Cp2Co2Se2B7H7 structures. Table S5A: Initial 12-vertex starting structures. Table S5B: Distance matrices and energy rankings for the lowest energy Cp2Co2S2B8H8 structures. Table S5C: Distance matrices and energy rankings for the lowest energy Cp2Co2Se2B8H8 structures. Table S6A: Distance matrices and energy rankings for the lowest energy permethylated Cp*2Co2S2B7H7 structures. Table S6B: Distance matrices and energy rankings for the lowest energy permethylated Cp*2Co2Se2B7H7 structures. Table S7: Orbital energies and HOMO-LUMO gaps for the lowest Cp2Co2S2Bn−4Hn−4 (n = 8 to 12) structures. Table S8: Orbital energies and HOMO-LUMO gaps for the lowest Cp2Co2Se2Bn−4Hn−4 (n = 8 to 12) structures. Table S9: Orbital energies and HOMO-LUMO gaps for the lowest permethylated Cp*2Co2E2B7H7 (E = S, Se) structures

Author Contributions

R.B.K. and A.L. conceived the project; A.A.A.A. performed the calculations and initially organized the results; A.L. supervised the computations and curated the data; R.B.K. generated the initial draft of the manuscript; R.B.K. and A.L. generated the final draft of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

The computational facilities were provided by the Babeş-Bolyai University under project POC/398/1/1/124155, which is co-financed by the European Regional Development Fund (ERDF) through the Competitiveness Operational Program for Romania 2014–2020.

Data Availability Statement

The data presented in this study are available in supplementary material.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Muetterties, E.L. (Ed.) Boron Hydride Chemistry; Academic Press: New York, NY, USA, 1975. [Google Scholar]
  2. Williams, R.E. The polyborane, carborane, carbocation continuum—Architectural patterns. Chem. Rev. 1992, 92, 177–207. [Google Scholar] [CrossRef]
  3. Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds. J. Chem. Soc. D Chem. Commun. 1971, 15, 792–793. [Google Scholar] [CrossRef]
  4. Mingos, D.M.P. A General theory for cluster and ring compounds of the main group and transition elements. Nat. Phys. Sci. 1972, 236, 99–102. [Google Scholar] [CrossRef]
  5. Mingos, D.M.P. Polyhedral skeletal electron pair approach. Accts. Chem. Res. 1984, 17, 311–319. [Google Scholar] [CrossRef]
  6. King, R.B.; Rouvray, D.H. A graph-theoretical interpretation of the bonding topology in polyhedral boranes, carboranes, and metal clusters. J. Am. Chem. Soc. 1977, 99, 7834–7840. [Google Scholar] [CrossRef]
  7. Aihara, J.-I. 3-Dimensional aromaticity of polyhedral boranes. J. Am. Chem. Soc. 1978, 100, 3339–3342. [Google Scholar]
  8. King, R.B. Three-dimensional aromaticity in polyhedral boranes and related molecules. Chem. Revs. 2001, 101, 1119–1152. [Google Scholar] [CrossRef]
  9. Callahan, K.P.; Hawthorne, M.F. Ten years of metallocarboranes. Adv. Organometal. Chem. 1976, 14, 145. [Google Scholar]
  10. Grimes, R.N. The role of metals in borane clusters. Accts. Chem. Res. 1983, 16, 22–26. [Google Scholar] [CrossRef]
  11. Kuan, H.; Yang, Z.; Zhang, L.; Xie, L.; Wang, L.; Xu, H.; Josephson, L.; Liang, S.H.; Zhang, M.-R. Boron agents for neutron capture therapy. Coord. Chem. Revs. 2020, 405, 213139. [Google Scholar]
  12. Avdeeva, V.V.; Garaev, T.M.; Malinina, E.A.; Zhizhin, K.Y.; Kuznetsov, N.T. Physiologically active compounds based on membranotropic cage carriers—Derivatives of adamantane and polyhedral boron clusters. Russ. J. Inorg. Chem. 2022, 67, 33–53. [Google Scholar] [CrossRef]
  13. Sivaev, I.B. Functional group directed B–H activation of polyhedral boron hydrides by transition metal complexes. Russ. J. Inorg. Chem. 2021, 66, 1192–1246. [Google Scholar] [CrossRef]
  14. Bould, J.; Kennedy, J.D.; Thornton-Pett, M. Ten-vertex metallaborane chemistry. Aspects of the iridadecaborane closo→isonido→isocloso structural continuum. J. Chem. Soc. Dalton 1992, 4, 563–576. [Google Scholar] [CrossRef]
  15. Kennedy, J.D.; Štibr, B. Current Topics in the Chemistry of Boron; Kabalka, G.W., Ed.; Royal Society of Chemistry: Cambridge, UK, 1994; pp. 285–292. [Google Scholar]
  16. Kennedy, J.D. The Borane-Carborane-Carbocation Continuum; Casanova, J., Ed.; Wiley: New York, NY, USA, 1998; Chapter 3; pp. 85–116. [Google Scholar]
  17. Štibr, B.; Kennedy, J.D.; Drdáková, E.; Thornton-Pett, M. Nine-vertex polyhedral iridamonocarbaborane chemistry. Products of thermolysis of [(CO)(PPh3)2IrCB7H8] and emerging alternative cluster-geometry patterns. J. Chem. Soc. Dalton 1994, 2, 229–236. [Google Scholar] [CrossRef]
  18. King, R.B. The oblate deltahedra in dimetallaboranes: Geometry and chemical bonding. Inorg. Chem. 2006, 45, 8211–8216. [Google Scholar] [CrossRef]
  19. Parry, R.W.; Walter, M.K.; Jolly, W.L. (Eds.) Preparative Inorganic Reactions; Interscience: New York, NY, USA, 1968; Volume 5, pp. 45–102. [Google Scholar]
  20. Kasper, J.S.; Lucht, C.M.; Harker, D. The structure of the decaborane molecule. J. Am. Chem. Soc. 1948, 70, 881–882. [Google Scholar] [CrossRef]
  21. Onak, T.P.; Wong, G.T.F. Preparation of the pentagonal pyramidal carborane, 2,3,4,5-tetracarba-nido-hexaborane(6). J. Am. Chem. Soc. 1970, 92, 5226. [Google Scholar] [CrossRef]
  22. Pasinski, J.P.; Beaudet, R.A. Microwave spectrum, structure, and dipole moment of 2,3,4,5-tetracarbahexaborane(6). J. Chem. Phys. 1974, 61, 683–691. [Google Scholar] [CrossRef]
  23. Wrackmeyer, B.; Schang, H.-J.; Hofmann, M.; Schleyer, P.v.R. A new carborane cage: Hexacarba-arachno-dodecaborane(12). Angew. Chem. Int. Ed. 1998, 37, 1245–1247. [Google Scholar] [CrossRef]
  24. Wrackmeyer, B.; Schanz, H.-J.; Hofmann, M.; Schleyer, P.v.R.; Boese, R. The structures of a tetracarba-nido-octaborane(8) and a novel spiro derivative of a 2,3,5-tricarba-nido-hexaborane(7). Eur. J. Inorg. Chem. 1999, 3, 533–537. [Google Scholar] [CrossRef]
  25. Köster, R.; Seidel, G.; Wrackmeyer, B.; Bläser, D.; Boese, R.; Bühl, M.; Schleyer, P.v.R. Decaethyl-2,6,8,10-tetracarba-nido-decaborane(10)—Preparation, structure in the solid state, and stability. Chem. Ber. 1991, 124, 2715–2724. [Google Scholar] [CrossRef]
  26. Rayment, T.; Shearer, H.M.M. Crystal structure of 2,4,6,8,9,10-hexamethyl-2,4,6,8,9,10-hexabora-adamantane. J. Chem. Soc. Dalton 1977, 2, 136–138. [Google Scholar] [CrossRef]
  27. Köster, R.; Seidel, G.; Wrackmeyer, B. Dimerization of a C2B3-closo-carbaborane(5) to the C4B6-adamantane and its 2Z/3Z valence isomerization to the C4B6-nido-carbaborane(10). Angew. Chem. Int. Ed. 1985, 24, 326–328. [Google Scholar] [CrossRef]
  28. Wrackmeyer, B.; Schanz, H.-J. Tetracarba-nido-hexa-, octa-, and –decaborane derivatives. NMR study and DFT calculations. J. Organomet. Chem. 2015, 798, 268–273. [Google Scholar] [CrossRef]
  29. Štíbr, B.; Jelínek, T.; Drdáková, E.; Heřmánek, S.; Plešek, J. A new family of stable parent nido-tetracarbaboranes 5,6,8,9-C4B6H10, 2,7,8,11-C4B7H11, and 7,8,9,10-C4B7H11. Polyhedron 1988, 7, 669–670. [Google Scholar] [CrossRef]
  30. Grimes, R.N. Carbon-rich carboranes and their metal derivatives. Adv. Inorg. Chem. Radiochem. 1983, 26, 55–117. [Google Scholar]
  31. Maynard, R.B.; Grimes, R.N. Oxidative fusion of carborane ligands in iron and cobalt complexes—A systematic study. J. Am. Chem. Soc. 1982, 104, 5983–5986. [Google Scholar] [CrossRef]
  32. Maxwell, W.M.; Miller, V.R.; Grimes, R.N. 4-Carbon carboranes—Synthesis of tetra-C-methyltetracarba-dodecaborane(12) and its metallocarborane derivatives. J. Am. Chem. Soc. 1974, 99, 7116–7117. [Google Scholar] [CrossRef]
  33. Maxwell, W.M.; Miller, V.R.; Grimes, R.N. Iron-hydrogen and iron-cobalt metallocarboranes—Synthesis and chemistry of [(CH3)2C2B4H4]2FeIIH2 and a novel tetracarbon carborane system (CH3)4C4B8H8. Inorg. Chem. 1976, 15, 1343–1348. [Google Scholar] [CrossRef]
  34. Freyberg, D.P.; Weiss, R.; Sinn, E.; Grimes, R.N. Crystal and molecular structure of a tetracarbon carborane, (CH3)4C4B8H8, a new type of nido cage system. Inorg. Chem. 1977, 16, 1847–1851. [Google Scholar] [CrossRef]
  35. Venable, T.L.; Maynard, R.B.; Grimes, R.N. Crystal and molecular structure of a tetracarbon carborane, (CH3)4B8H8, a new type of nido cage system. J. Am. Chem. Soc. 1984, 106, 6187–6193. [Google Scholar] [CrossRef]
  36. Spencer, J.T.; Pourlan, M.R.; Butcher, R.J.; Sinn, E.; Grimes, R.N. Pi-complexation of nido-(PhCH2)2C2B4H6 at the C2B3 and C6 rings—Synthesis and crystal structures of nido-2,3-(CO)3Cr[(.eta.6-C6H5)CH2]2-2,3,-C2B4H6 and (PhCH2)4C4B8H8, a nonfluxional C4B8 cluster. Organometallics 1987, 6, 335–343. [Google Scholar] [CrossRef]
  37. Attia, A.A.A.; Lupan, A.; King, R.B. Tetracarbaboranes: nido structures without bridging hydrogens. Dalton Trans. 2016, 45, 18541–18551. [Google Scholar] [CrossRef] [PubMed]
  38. Friesen, G.D.; Barriola, A.; Daluga, P.; Ragatz, P.; Huffman, J.; Todd, L. Chemistry of dithiaboranes, selenathiaboranes, and diselenaboranes. Inorg. Chem. 1980, 19, 458–462. [Google Scholar] [CrossRef]
  39. Attia, A.A.A.; Lupan, A.; King, R.B. Polyhedral cobaltadiselenaboranes: Nido strucures without bridging hydrogens. RSC Adv. 2016, 6, 53635–53642. [Google Scholar] [CrossRef]
  40. Kang, S.O.; Sneddon, L.G. Synthesis of new dithiacobaltaborane clusters derived from arachno-6,8-S2B7H9. Inorg. Chem. 1988, 27, 3769–3772. [Google Scholar] [CrossRef]
  41. Robertson, A.P.M.; Beattie, N.A.; Scott, C.; Man, W.Y.; Jones, J.J.; Macgregor, S.A.; Rosair, G.M.; Welch, A.J. 14-Vertex heteroboranes with 14 skeletal electron pairs: An experimental and computational study. Angew. Chem. Int. Ed. 2016, 55, 8706–8710. [Google Scholar] [CrossRef]
  42. Szabolcs, J.; Lupan, A.; Kun, A.-Z.; King, R.B. Isocloso versus closo deltahedra in slightly hypoelectronic supraicosahedral 14-vertex dimetallaboranes with 28 skeletal electrons; Relationship to icosahedral dimetallaboranes. New J. Chem. 2020, 44, 16977–16984. [Google Scholar]
  43. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  44. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  45. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA. 2016. Available online: https://gaussian.com/g09citation/ (accessed on 10 February 2023).
  46. Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of intermolecular interaction energies within the local pair natural orbital coupled cluster framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef] [PubMed]
  47. Riplinger, C.; Pinski, P.; Becker, U.; Valeev, E.F.; Neese, F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. [Google Scholar] [CrossRef]
  48. Pavošević, F.; Pinski, P.; Riplinger, C.; Neese, F.; Valeev, E.F. SparseMaps—A systematic infrastructure for reduced-scaling electronic structure methods. IV. Linear-scaling second-order explicitly correlated energy with pair natural orbitals. J. Chem. Phys. 2016, 144, 144109. [Google Scholar] [CrossRef] [PubMed]
  49. Kubas, A.; Berger, D.; Oberhofer, H.; Maganas, D.; Reuter, K.; Neese, F. Surface adsorption energetics studied with “gold standard” wave-function-based ab initio methods: Small-molecule binding to TiO2 (110). J. Phys. Chem. Lett. 2016, 7, 4207–4212. [Google Scholar] [CrossRef] [PubMed]
  50. Isegawa, M.; Neese, F.; Pantazis, D.A. Ionization energies and aqueous redox potentials of organic molecules: Comparison of DFT, correlated ab initio theory and pair natural orbital approaches. J. Chem. Theory Comput. 2016, 12, 2272–2284. [Google Scholar] [CrossRef]
  51. Guo, Y.; Sivalingam, K.; Valeev, E.F.; Neese, F. SparseMaps—A systematic infrastructure for reduced-scaling electronic structure methods. III. Linear-scaling multireference domain-based pair natural orbital N-electron valence perturbation theory. J. Chem. Phys. 2016, 144, 094111. [Google Scholar] [CrossRef]
  52. Dutta, A.K.; Neese, F.; Izsák, R. Towards a pair natural orbital coupled cluster method for excited states. J. Chem. Phys. 2016, 145, 034102. [Google Scholar] [CrossRef]
  53. Datta, D.; Kossmann, S.; Neese, F. Analytic energy derivatives for the calculation of the first-order molecular properties using the domain-based local pair-natural orbital coupled-cluster theory. J. Chem. Phys. 2016, 145, 114101. [Google Scholar] [CrossRef]
  54. Pinski, P.; Riplinger, C.; Valeev, E.F.; Neese, F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. I. An efficient and simple linear scaling local MP2 method that uses an intermediate basis of pair natural orbitals. J. Chem. Phys. 2015, 143, 034108. [Google Scholar] [CrossRef] [Green Version]
  55. Mondal, B.; Neese, F.; Ye, S. Control in the rate-determining step provides a promising strategy to develop new catalysts for CO2 hydrogenation: A local pair natural orbital coupled cluster theory study. Inorg. Chem. 2015, 54, 7192–7198. [Google Scholar] [CrossRef]
  56. Liakos, D.G.; Sparta, M.; Kesharwani, M.K.; Martin, J.M.L.; Neese, F. Exploring the accuracy limits of local pair natural orbital coupled-cluster theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. [Google Scholar] [CrossRef] [PubMed]
  57. Liakos, D.G.; Neese, F. Domain based pair natural orbital coupled cluster studies on linear and folded alkane chains. J. Chem. Theory Comput. 2015, 11, 2137–2143. [Google Scholar] [CrossRef] [PubMed]
  58. Liakos, D.G.; Neese, F. Is it possible to obtain coupled cluster quality energies at near density functional theory cost? domain-based local pair natural orbital coupled cluster vs. modern density functional theory. J. Chem. Theory Comput. 2015, 11, 4054–4063. [Google Scholar] [CrossRef] [PubMed]
  59. Demel, O.; Pittner, J.; Neese, F. A local pair natural orbital-based multireference Mukherjee’s coupled cluster method. J. Chem. Theory Comput. 2015, 11, 3104–3114. [Google Scholar] [CrossRef]
  60. Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  61. Izsák, R.; Neese, F. Speeding up spin-component-scaled third-order pertubation theory with the chain of spheres approximation: The COSX-SCS-MP3 method. Mol. Phys. 2013, 111, 1190–1195. [Google Scholar] [CrossRef]
  62. Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
  63. Kossmann, S.; Neese, F. Efficient structure optimization with second-order many-body perturbation theory: The RIJCOSX-MP2 Method. J. Chem. Theory Comput. 2010, 6, 2325–2338. [Google Scholar] [CrossRef]
  64. Kossmann, S.; Neese, F. Comparison of two efficient approximate Hartee–Fock approaches. Chem. Phys. Lett. 2009, 481, 240–243. [Google Scholar] [CrossRef]
  65. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A “chain-of-spheres” algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  66. Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
  67. Dutta, A.K.; Neese, F.; Izsák, R. Speeding up equation of motion coupled cluster theory with the chain of spheres approximation. J. Chem. Phys. 2016, 144, 034102. [Google Scholar] [CrossRef] [PubMed]
  68. Christian, G.J.; Neese, F.; Ye, S. Unravelling the molecular origin of the regiospecificity in extradiol catechol dioxygenases. Inorg. Chem. 2016, 55, 3853–3864. [Google Scholar] [CrossRef] [PubMed]
Molecules 28 02988 g001 550
Figure 1. The most spherical closo deltahedra having 9 to 13 vertices from which the nido structures discussed in this paper are generated. Vertices of degrees 4, 5, and 6 are indicated in red, black, and green, respectively, in Figures 1, 2, and 8.
Figure 1. The most spherical closo deltahedra having 9 to 13 vertices from which the nido structures discussed in this paper are generated. Vertices of degrees 4, 5, and 6 are indicated in red, black, and green, respectively, in Figures 1, 2, and 8.
Molecules 28 02988 g001
Molecules 28 02988 g002 550
Figure 2. The isocloso deltahedra from which the nido polyhedra with hexagonal holes are generated.
Figure 2. The isocloso deltahedra from which the nido polyhedra with hexagonal holes are generated.
Molecules 28 02988 g002
Molecules 28 02988 g003 550
Figure 3. Generation of the binary BnHn+4 borane structures from closo and isocloso deltahedra by the removal of the starred vertices.
Figure 3. Generation of the binary BnHn+4 borane structures from closo and isocloso deltahedra by the removal of the starred vertices.
Molecules 28 02988 g003
Molecules 28 02988 g004 550
Figure 4. Alternative ways of generating the central 12-vertex polyhedron of the experimentally known CpCoSe2B9H9 from the 12-vertex icosahedron by breaking edges and from the 13-vertex docosahedron by removing the starred degree-5 vertex.
Figure 4. Alternative ways of generating the central 12-vertex polyhedron of the experimentally known CpCoSe2B9H9 from the 12-vertex icosahedron by breaking edges and from the 13-vertex docosahedron by removing the starred degree-5 vertex.
Molecules 28 02988 g004
Molecules 28 02988 g005 550
Figure 5. The 11-vertex frameworks suggested for the 3 Cp*2Co2S2B7H7 isomers isolated by Kang and Sneddon from the reaction between LiCp*, NaS2B7H9, and CoCl2.
Figure 5. The 11-vertex frameworks suggested for the 3 Cp*2Co2S2B7H7 isomers isolated by Kang and Sneddon from the reaction between LiCp*, NaS2B7H9, and CoCl2.
Molecules 28 02988 g005
Molecules 28 02988 g006a 550Molecules 28 02988 g006b 550
Figure 6. The eight lowest-energy Cp2Co2E2B7H7 (E = S, Se) structures oriented to have the open pentagonal face at the bottom.
Figure 6. The eight lowest-energy Cp2Co2E2B7H7 (E = S, Se) structures oriented to have the open pentagonal face at the bottom.
Molecules 28 02988 g006aMolecules 28 02988 g006b
Molecules 28 02988 g007a 550Molecules 28 02988 g007b 550
Figure 7. The nine lowest-energy Cp2Co2E2B8H8 (E = S, Se) structures.
Figure 7. The nine lowest-energy Cp2Co2E2B8H8 (E = S, Se) structures.
Molecules 28 02988 g007aMolecules 28 02988 g007b
Molecules 28 02988 g008 550
Figure 8. The D6d bicapped hexagonal antiprism as the 14-vertex closo deltahedron and a 14-vertex isocloso deltahedron derived from it via a diamond-square-diamond process that is the polyhedron found in the experimentally known Cp*2Ru2C2B10H12. The 12-vertex arachno Cp2Co2E2B8H8 (E = S, Se) structures B8Co2S2-3, B8Co2S2-7, B8Co2Se2-5, and B8Co2eS2-9 are obtained from this 14-vertex isocloso deltahedron by the removal of a degree-4 vertex and a degree-5 vertex, which are so situated that the resulting tetragonal and pentagonal faces share an edge.
Figure 8. The D6d bicapped hexagonal antiprism as the 14-vertex closo deltahedron and a 14-vertex isocloso deltahedron derived from it via a diamond-square-diamond process that is the polyhedron found in the experimentally known Cp*2Ru2C2B10H12. The 12-vertex arachno Cp2Co2E2B8H8 (E = S, Se) structures B8Co2S2-3, B8Co2S2-7, B8Co2Se2-5, and B8Co2eS2-9 are obtained from this 14-vertex isocloso deltahedron by the removal of a degree-4 vertex and a degree-5 vertex, which are so situated that the resulting tetragonal and pentagonal faces share an edge.
Molecules 28 02988 g008
Molecules 28 02988 g009a 550Molecules 28 02988 g009b 550
Figure 9. The eight lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures.
Figure 9. The eight lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures.
Molecules 28 02988 g009aMolecules 28 02988 g009b
Molecules 28 02988 g010 550
Figure 10. The six lowest-energy Cp2Co2E2B5H5 (E = S, Se) structures.
Figure 10. The six lowest-energy Cp2Co2E2B5H5 (E = S, Se) structures.
Molecules 28 02988 g010
Molecules 28 02988 g011 550
Figure 11. The three lowest-energy Cp2Co2E2B6H6 (E = S, Se) structures are oriented so that the bent hexagonal face is at the top.
Figure 11. The three lowest-energy Cp2Co2E2B6H6 (E = S, Se) structures are oriented so that the bent hexagonal face is at the top.
Molecules 28 02988 g011
Table
Table 1. Relative energies (kcal/mol) and geometries of the lowest-energy 11-vertex Cp2Co2E2B7H7 (E = Se, S) structures. In all 8 structures, the central Co2E2B7 polyhedron is derived from an 11-vertex polyhedron that is obtained via the removal of a vertex from the 12-vertex regular icosahedron, leaving a pentagonal face.
Table 1. Relative energies (kcal/mol) and geometries of the lowest-energy 11-vertex Cp2Co2E2B7H7 (E = Se, S) structures. In all 8 structures, the central Co2E2B7 polyhedron is derived from an 11-vertex polyhedron that is obtained via the removal of a vertex from the 12-vertex regular icosahedron, leaving a pentagonal face.
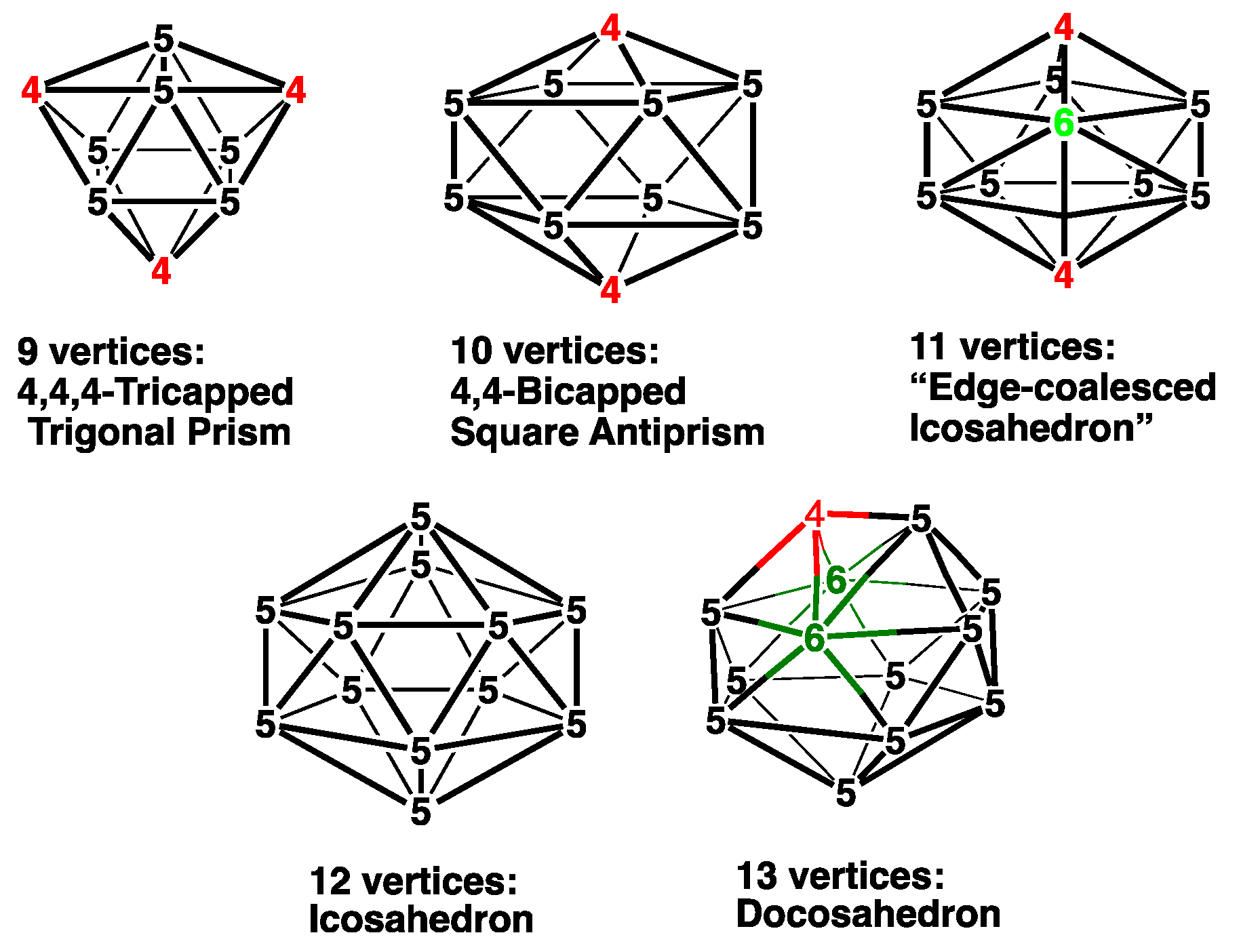
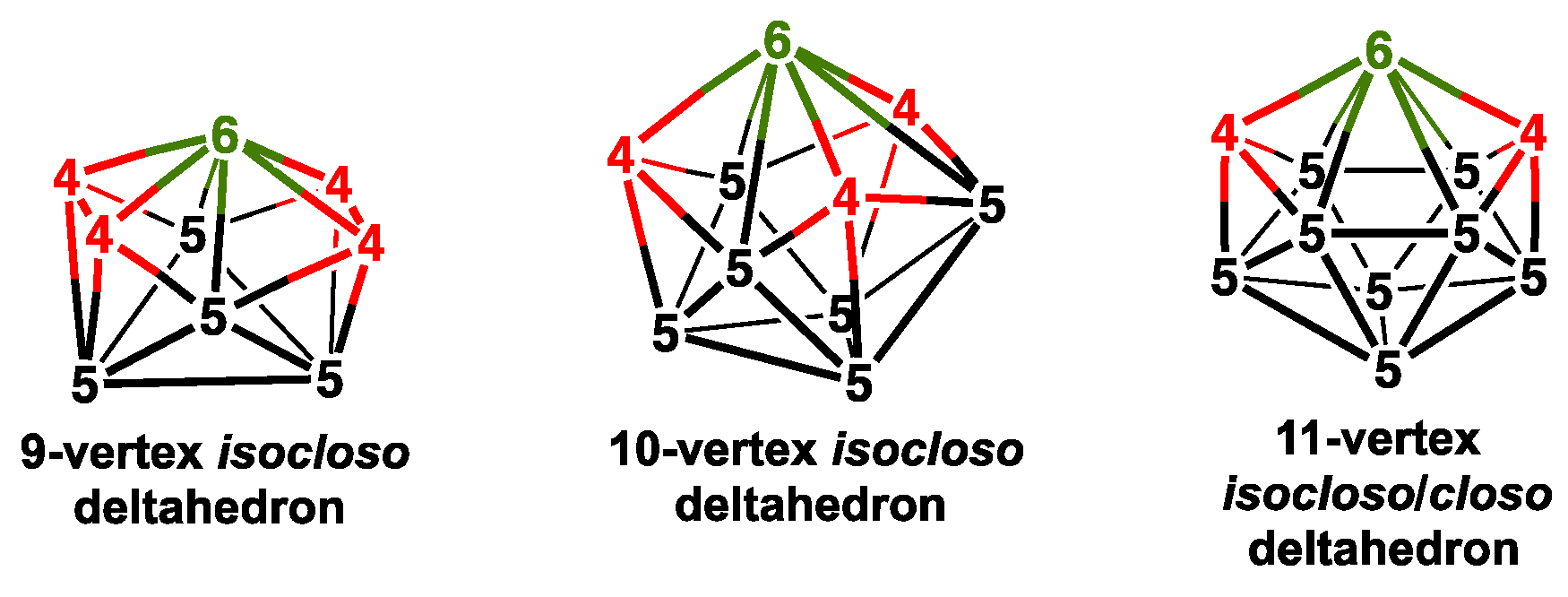
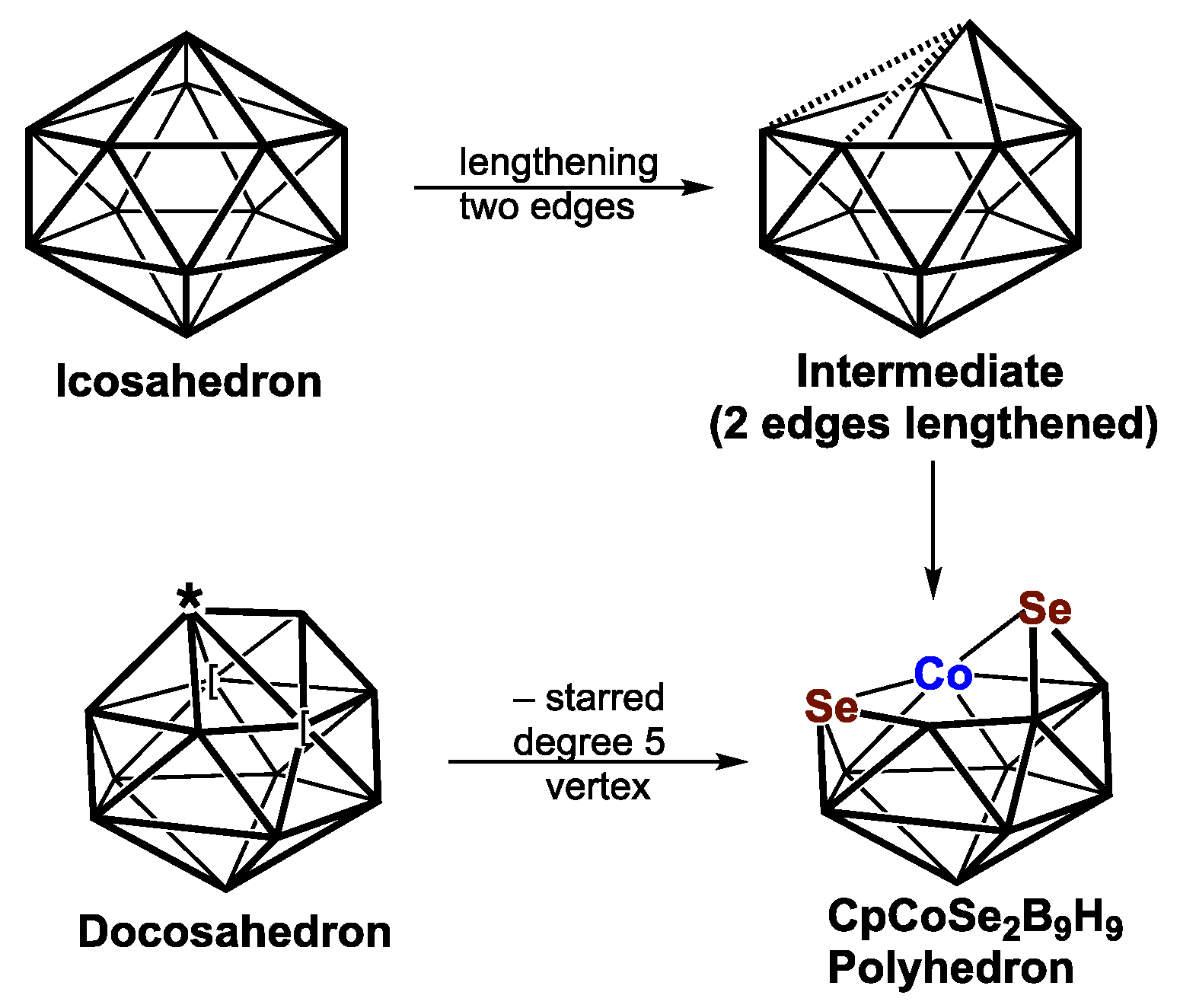
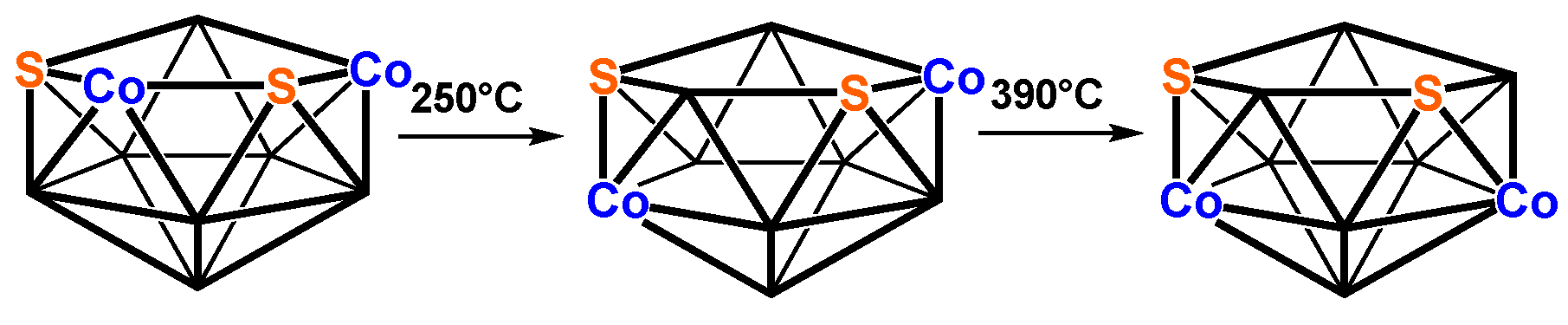
Cp2Co2Se2B7H7Cp2Co2S2B7H7Vertex
Degrees		Co…SCo…Co (E = Se) Pentagonal
Structure (sym)∆EStructure∆ESCoEdgesDist (Å)WBIFace Atoms
B7Co2Se2-1 (C1)0.0B7Co2S2-10.04, 44, 433.910.10SCoSBCo
B7Co2Se2-2 (C1)2.5B7Co2S2-21.84, 44, 533.810.10SCoSBB
B7Co2Se2-3 (C1)8.1B7Co2S2-36.24, 44, 523.790.09SCoBSB
B7Co2Se2-4 (C1)9.4B7Co2S2-47.74, 44, 523.710.10SCoBSB
B7Co2Se2-5 (Cs)10.1B7Co2S2-518.24, 44, 523.680.09SCoSBB
B7Co2Se2-6 (Cs)11.8B7Co2S2-619.94, 45, 523.730.09SBSBB
B7Co2Se2-7 (C1)13.5B7Co2S2-710.74, 44, 513.670.08SCoBSB
B4Co2Se2-8 (C1)14.7B7Co2S2-812.64, 45, 523.730.08SBSBB
Table
Table 2. Relative energies (kcal/mol) and geometries of the lowest-energy 12-vertex Cp2Co2E2B8H8 (E = S, Se) structures.
Table 2. Relative energies (kcal/mol) and geometries of the lowest-energy 12-vertex Cp2Co2E2B8H8 (E = S, Se) structures.
Cp2Co2Se2B8H8Cp2Co2S2B8H8Vertex
Degrees		Co…SCo…Co (E = Se)
Structure (sym)∆EStructure∆ESCoEdgesDist (Å)WBIPolyhedron
B8Co2Se2-1 (C2v)0.0B8Co2S2-99.05, 54, 443.180.17ni-12〈IV〉
B8Co2Se2-2 (C1)4.0B8Co2S2-10.03, 35, 523.850.12meta Co2 open icosahedron
B8Co2Se2-3 (C1)4.5B8Co2S2-53.83, 44, 523.830.09meta Co2 open icosahedron
B8Co2Se2-4 (C2v)5.3B8Co2S2-87.94, 45, 543.480.15ni-12〈IV〉
B8Co2Se2-5 (C1)8.2B8Co2S2-33.13, 45, 513.610.09ar-12〈IV,V〉
B8Co2Se2-6 (C2)8.2B8Co2S2-43.53, 35, 524.220.05para Co2 open icosahedron
B8Co2Se2-7 (C2)9.3B8Co2S2-23.03, 35, 524.820.08para Co2 open icosahedron
B8Co2Se2-8 (C1)11.8B8Co2S2-65.63, 45, 513.730.11meta Co2 open icosahedron
B8Co2Se2-9 (C1)12.3B8Co2S2-77.13, 45, 513.720.10ar-12〈IV,V〉
Table
Table 3. Relative energies (kcal/mol) and geometries of the lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures.
Table 3. Relative energies (kcal/mol) and geometries of the lowest-energy Cp2Co2E2B4H4 (E = S, Se) structures.
Cp2Co2Se2B4H4Cp2Co2S2B4H4Vertex
Degrees		Co…SCo…Co (E = Se) Non-Triang
Face
Structure (sym)∆EStructure∆ESCoEdgesDist (Å)WBIAtomsPolyhedron
B4Co2Se2-1 (C2)0.0B4Co2S2-10.04, 44, 443.390.12SCoSCobicap trig prism
B4Co2Se2-2 (Cs)7.1B4Co2S2-55.24, 44, 433.750.14SCoSBbicap trig prism
B4Co2Se2-3 (C1)11.1B4Co2S2-41.93, 34, 522.550.38SCoBBBni-8〈V〉
B4Co2Se2-4 (C1)11.4B4Co2S2-30.73, 34, 523.440.10SCoBSBni-8〈V〉
B4Co2Se2-5 (Cs)12.5B4Co2S2-20.13, 35, 522.640.24SCoBSBni-8〈V〉
B4Co2Se2-6 (C1)13.5B4Co2S2-66.53, 34, 532.590.40SCoSBBni-8〈V〉
B4Co2Se2-7 (C1)14.9B4Co2S2-810.33, 44, 422.650.442 × SCoSBar-8〈IV,IV〉
B4Co2Se2-8 (Cs)15.3B4Co2S2-78.33, 34, 422.620.09SCoSBBni-8〈V〉
Table
Table 4. Relative energies (kcal/mol) and geometries of the lowest-energy 9-vertex Cp2Co2E2B5H5 (E = S, Se) structures.
Table 4. Relative energies (kcal/mol) and geometries of the lowest-energy 9-vertex Cp2Co2E2B5H5 (E = S, Se) structures.
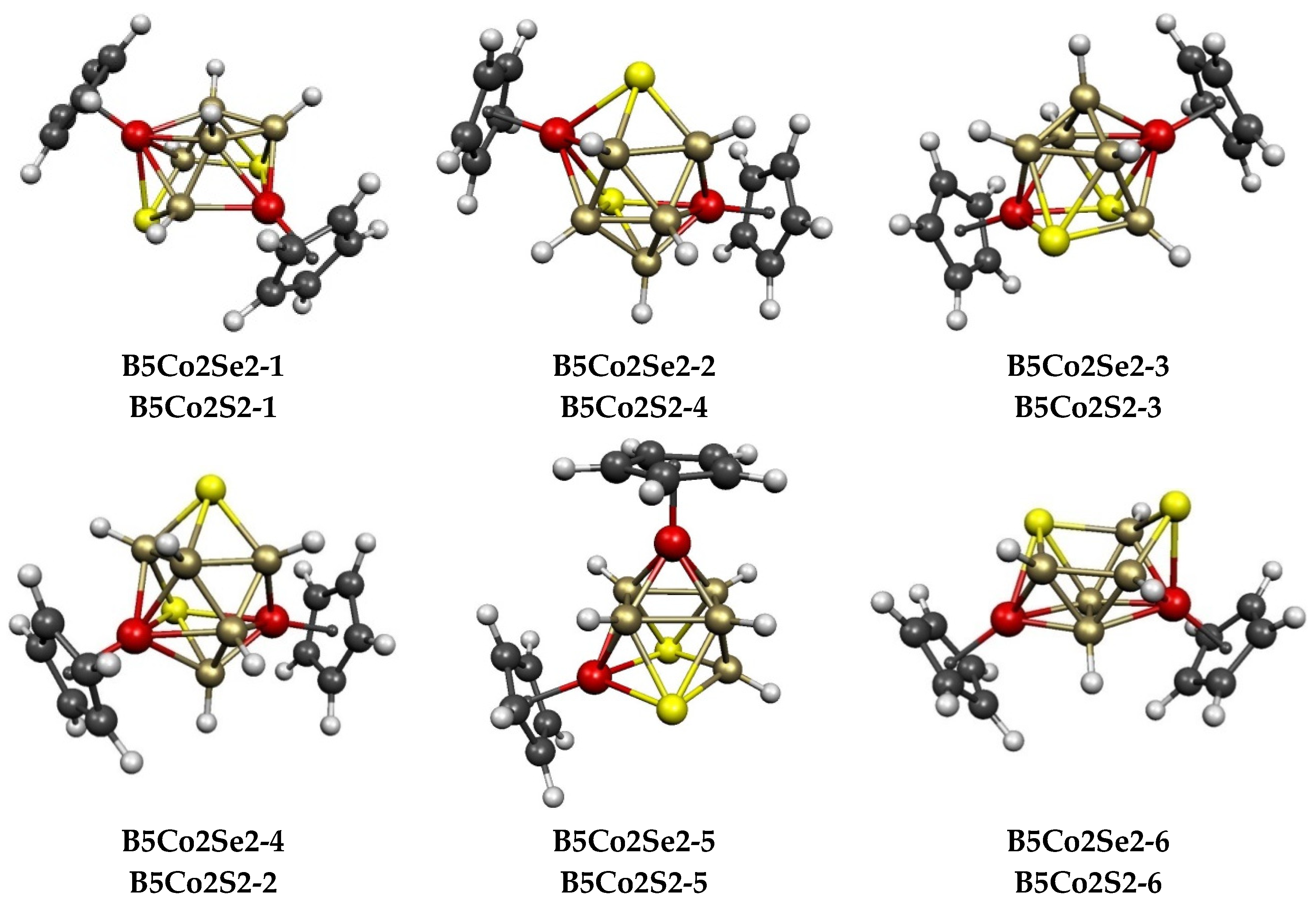
Cp2Co2Se2B5H5Cp2Co2S2B5H5Vertex
Degrees		Co…SCo…Co (E = Se) Non-Triang
Face
Structure (sym)∆EStructure∆ESCoEdgesDist(Å)WBIAtomsPolyhedron
B5Co2Se2-1 (C1)0.0B5Co2S2-10.03, 44, 523.670.11SCoBSBni-9〈V〉
B5Co2Se2-2 (C1)0.7B5Co2S2-43.93, 44, 533.820.07SCoBSConi-9〈V〉
B5Co2Se2-3 (C1)0.9B5Co2S2-33.64, 44, 533.770.12SCoSBcapped square antiprism
B5Co2Se2-4 (C1)2.7B5Co2S2-22.83, 44, 533.400.07SCoBSBni-9〈V〉
B5Co2Se2-5 (Cs)3.7B5Co2S2-56.04, 44, 423.650.11SCoSBcapped square antiprism
B5Co2Se2-6 (C1)6.9B5Co2S2-66.23, 44, 523.720.12SBBSBni-9〈V〉
Table
Table 5. Relative energies (kcal/mol) and geometries of the lowest-energy 10-vertex Cp2Co2E2B6H6 (E = S, Se) structures. In all 3 structures, the central Co2E2B6 polyhedron has the same geometry as the B10 polyhedron in decaborane-14 with a hexagonal face.
Table 5. Relative energies (kcal/mol) and geometries of the lowest-energy 10-vertex Cp2Co2E2B6H6 (E = S, Se) structures. In all 3 structures, the central Co2E2B6 polyhedron has the same geometry as the B10 polyhedron in decaborane-14 with a hexagonal face.
Cp2Co2Se2B6H6Cp2Co2S2B6H6Vertex
Degrees		Co…SCo…Co (E = Se)Hexagonal
Face
Structure (sym)∆EStructure∆ESCoEdgesDist (Å)WBIAtomsPolyhedron
B6Co2Se2-1 (C2v)0.0B6Co2S2-10.03, 35, 523.770.10SBBBBSB10H14 framework
B6Co2Se2-2 (C1)10.6B6Co2S2-212.43, 34, 523.780.09SBBSCoBSB10H14 framework
B6Co2Se2-3 (C1)15.7B6Co2S2-318.13, 34, 522.490.41SBBSCoBSB10H14 framework
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Attia, A.A.A.; Lupan, A.; King, R.B. Polyhedral Dicobaltadithiaboranes and Dicobaltdiselenaboranes as Examples of Bimetallic Nido Structures without Bridging Hydrogens. Molecules 2023, 28, 2988. https://doi.org/10.3390/molecules28072988

AMA Style

Attia AAA, Lupan A, King RB. Polyhedral Dicobaltadithiaboranes and Dicobaltdiselenaboranes as Examples of Bimetallic Nido Structures without Bridging Hydrogens. Molecules. 2023; 28(7):2988. https://doi.org/10.3390/molecules28072988

Chicago/Turabian Style

Attia, Amr A. A., Alexandru Lupan, and Robert Bruce King. 2023. "Polyhedral Dicobaltadithiaboranes and Dicobaltdiselenaboranes as Examples of Bimetallic Nido Structures without Bridging Hydrogens" Molecules 28, no. 7: 2988. https://doi.org/10.3390/molecules28072988

APA Style

Attia, A. A. A., Lupan, A., & King, R. B. (2023). Polyhedral Dicobaltadithiaboranes and Dicobaltdiselenaboranes as Examples of Bimetallic Nido Structures without Bridging Hydrogens. Molecules, 28(7), 2988. https://doi.org/10.3390/molecules28072988

Article Metrics

Back to TopTop