Abstract
Inorganic halide perovskites of the type AMX3, where A is an inorganic cation, M is a metal cation, and X is a halide anion, have attracted attention for optoelectronics applications due to their better optical and electronic properties, and stability, under a moist and elevated temperature environment. In this contribution, the electronic, optical, thermoelectric, and elastic properties of cesium lead bromide, CsPbBr3, and Rb-doped CsPbBr3, were evaluated using the density functional theory (DFT). The generalized gradient approximation (GGA) in the scheme of Perdew, Burke, and Ernzerhof (PBE) was employed for the exchange–correlation potential. The calculated value of the lattice parameter is in agreement with the available experimental and theoretical results. According to the electronic property results, as the doping content increases, so does the energy bandgap, which decreases after doping 0.75. These compounds undergo a direct band gap and present an energies gap values of about 1.70 eV (x = 0), 3.76 eV (x = 0.75), and 1.71 eV (x = 1). The optical properties, such as the real and imaginary parts of the dielectric function, the absorption coefficient, optical conductivity, refractive index, and extinction coefficient, were studied. The thermoelectric results show that after raising the temperature to 800 K, the thermal and electrical conductivities of the compound RbxCs1−xPbBr3 increases (x = 0, 0.25, 0.50 and 1). Rb0.75Cs0.25PbBr3 (x = 0.75), which has a large band gap, can work well for applications in the ultraviolet region of the spectrum, such as UV detectors, are potential candidates for solar cells; whereas, CsPbBr3 (x = 0) and RbPbBr3 (x = 1), have a narrow and direct band gap and outstanding absorption power in the visible ultraviolet energy range.
1. Introduction
Material scientists have discovered that energy collection from low-cost sources utilizing the most effective methods has gained significant importance. As a result, it is necessary to define the materials’ fundamental characteristics, in order to understand how they function in real-world working devices. Solar energy and unused heat can both be harvested with a great potential. Therefore, the goal of fundamental material research is to investigate innovative materials with optimum optical and thermoelectric properties. Generally, halide perovskite compounds with the general formula AMX3, where A is an organic or inorganic cation (such as ion cesium (Cs+), ion methyl ammonium (MA), or ion formamidinium (FA)), M is a metal cation (such as Pb2+ or Sn2+), and X is a halide anion (such as I−, Br−, and Cl−), have attracted much attention in the past few years due to their potential applications as solar-cell absorbers [1,2,3], light-emitting diodes [4,5], photodetectors [6,7,8,9,10,11], and lasers [12]. They possess numerous important technological applications due to their remarkable optical [13,14], electronic [15], and ferroelectric properties [16,17]. Organic–inorganic hybrid perovskite solar cells (PSC) are still adversely affected by poor stability, which reduces their practical applications, as exemplified by [18,19]. These hybrid perovskites degrade because of the considerable impact that moisture, heat, and UV light have on their organic phase.
One effective way to improve the stability of such perovskite requires the use of inorganic materials to replace labile organic components. Recently, all-inorganic halide perovskites of the type CsMX3 have attracted great attention for their usefulness in perovskite solar cell PSC stability improvement. Cesium-based inorganic perovskites have gained popularity due to their significantly increased thermal stability. Formamidinium- or methylammonium-based perovskite films degrade quickly above 200 °C, but the inorganic CsPbI3 and CsPbBr3 perovskite absorbers can maintain their original composition and crystal structure under high temperatures of up to 400 °C, effectively preventing the decomposition of organic groups and further enhancing the performance and stability of the device. In addition, compared to organic–inorganic hybrid perovskite materials, inorganic perovskite materials exhibit superior photoelectric properties, such as high carrier mobility and a long carrier lifetime. When formed from cold-pressed pellets of annealed CsSnI3 polycrystalline material, cesium-based inorganic perovskites have been shown to have a high hole mobility (520 cm2 V/s) and electron mobility (530 cm2 V/s), whereas CsPbBr3 halide single-crystals could achieve an electron lifetime of 2.5 s and an estimated electron mobility of 1000 cm2 V/s [20].
According to the current research, component engineering could change the perovskite crystal surface or integrate new ions into the crystalline structure to replace one of its substituents [21,22,23]. According to ab initio calculations of the electronic structure of perovskites, the outer shell orbitals of the M-site and X-site are significantly responsible for determining the energy levels (conduction band and valence band), depending on their electronegativity difference [24,25,26]. Therefore, element substitution on the A-, M- and/or X-sites can drastically change the band structure and the accompanying optical and electrical properties, such as the light absorption coefficient, bandgap, and charge carrier diffusion length.
Inorganic cations doping in perovskite materials have proven to be a successful tactic for achieving passivation faults, enhancing stability, and improving device performance [27,28,29]. Zhao et al. investigated the impact of A-site ion doping on perovskites [30]. The results demonstrated that alkali metal cations (K+ and Na+) can enhance perovskite film quality and perovskite solar cells photovoltaic performance. The poor carrier transport properties of inorganic perovskite materials severely restrict the development of the corresponding perovskite solar cell solar performance. Nam et al. partially substituted out Cs+ for K+, which reduced the PbX6 octahedron volume and increased phase stability [31].
There are several cesium lead halide CsPbX3 perovskites that have been created and can be utilized for perovskite solar cells, including CsPbBr3 and CsPbCl3 [32,33,34,35,36]. Additionally, all-inorganic perovskite solar cells, such as CsSnI3 [37] and CsPbI3 [38], have been used. Trots et al. [39] investigated the RbPbI3 and CsPbI3 compounds by the means of synchrotron powder diffraction experiments and Rietveld refinement technique. They have shown that both compounds crystallize in orthorhombic Pnma symmetry, revealing almost the same relative change of the lattice parameters upon heating, with an expansion isotropically close to 600 K. Moreover, they have observed that CsPbI3 undergoes first-order reversible phase transformation, whereas no transitions in RbPbI3 were detected. Zhao et al. [40] incorporated the Rb+ ions into the lattice of CsPbCl3 quantum dots by partially substituting the sites of Cs+ ions by the modified hot injection method. They observed that the high photoluminescence yields of CsPbCl3 were improved from 5.7% to 13% with Rb+ doping. It was observed that the emission and absorption peaks of CsPbCl3 quantum dots shifted to the shorter wavelength, and with the increase of Rb+ doping concentration, the lifetime of CsPbCl3 quantum dots was prolonged.
Due to the suppressed luminescence from the deep-level defects, CsPbX3 (X = Br or Cl) perovskites produced with a single crystalline nature have been demonstrated to be desirable for high-resolution detection at room temperature (RT) [41]. Further, it has been reported that the bulk-recrystallized CsPbBr3 emits bright green radiation at room temperature and provides a greater space for the free carriers, which lowers the recombination rates and, consequently, the poor quantum yield [42]. Fatty acids have been shown to inhibit the formation of CsPbBr3 nanocrystals, providing a novel technique to adjust the visible optical properties [43]. The obvious function of CsPbBr3 for optical devices is also covered in numerous additional experimental publications that are readily available [44,45]. Babu et al. [13] calculated the optical, electronic, structural and elastic properties of CsCaCl3 using the full potential linearized augmented plane wave method in the density functional theory. They found that this compound has an indirect energy band gap with a mixed ionic–covalent bonding, optically isotropic and structurally anisotropic property. The values of the band gaps found with different methods are 5.29, 5.35, 5.43, and 6.93 eV using LDA, GGA-PBE, GGA-WC, and mBJ pseudopotentials, respectively. Chang and Park [15] explored the electronic and structural properties of an inorganic perovskite, CsPbX3 (where X = Cl, Br and I), and the lead-halide-based inorganic–organic (CH3NH3)PbX3 perovskites, using the first-principles calculations within the local density approximation. They found that the lattice constants for the cubic structure of CsPbX3 were smaller than the corresponding values for (CH3NH3)PbX3; however, the electronic structures of both kinds of perovskites were found to be similar. Murtaza et al. [46] studied the optical, electronic and structural properties of cubic CsPbX3 (X = Cl, Br and I) using DFT calculations. They found that all of these compounds are direct, with a wide bandgap located at the R-symmetry point, which decreases from Cl to I. The refractive index, reflectivity and zero frequency limits of dielectric function increase with the decrease in bandgap (from Cl to Br to I), while the absorption coefficient and maximum optical conductivity decrease. Duong et al. [47] have demonstrated a novel multiplication method with methylammonium (MA), formamidinium (FA), Cesium (Cs) and Rb, to achieve high efficiency 1.73 eV bandgap perovskite cells, with negligible hysteresis. Mahmood et al. [48] investigated the thermoelectric, optical and mechanical properties of CsPbX3 (X = F, Cl, Br) using DFT calculations. They found that the thermal (k) and electrical (σ) conductivities increase with the increasing of temperature, and the ratio remains at a minimum. When the mechanical and thermodynamic stabilities decrease from CsPbF3 to CsPbBr3, the structural stability increases.
All-inorganic lead APbI3 perovskites (with A = K, Li, Na or Cs cations), made via a self-organization process approach at room temperature, were experimentally explored by Dimesso et al. They discovered that the A cation size has a small impact on how these APbI3 perovskites’ bandgap energies change. Rb and K atoms have similar atomic radii to Cs, thus the correlation effect may be minimal [49]. The bandgap energy for CsPbBr3 with a cubic crystal structure was calculated by Qian et al., using the density functional theory (DFT) approach. They determined that this bandgap energy is 1.75 eV [50]. The anion electronegativity is a significant additional consequence of anion exchange. The calculations for CsPbX3 have also been done by Castelli et al., where X is changed for every halide group [51]. Their calculations revealed that the bandgap energy increased as the electronegativity of the anions increased. However, it appeared that the lattice constant, rather than the electronegativity, had a greater impact on the bandgap energy in the case of organometal perovskites. This explains why a perovskite with an formamidinium cation has a higher bandgap energy than one with a methyl ammonium cation. It is crucial to look into the role of the A cations and the X anions in the formation of the electronic structure of APbX3 perovskites, particularly the valence band and conduction band, as well as crystal binding properties, which are in charge of the processes of light absorption and photo generation of charge carriers.
In the cubic perovskite structure with space group , cesium–lead halides have been observed experimentally [52,53]. While the lattice constants of CsPbCl3 and CsPbBr3 were predicted using the ionic radii of the respective ions, the structural, electrical, thermodynamic, and optical aspects of these compounds were experimentally examined [39,54]. Using the first-principles pseudopotential method with a local density approximation and an empirical tight binding scheme, the structural and electrical characteristics of these compounds were also computed [15].
The aforementioned discussion makes it clear that there is only a limited amount of theoretical research on the optical, elastic, thermoelectric, and electronic properties of Rb-doped cesium lead bromide compounds. However, to our knowledge, no research has been reported on the optoelectronic and thermoelectric properties of this perovskite by density functional theory (DFT).
The aim of the present work was to investigate the electronic, optical, elastic and thermoelectric properties of CsPbBr3 (CPB) and Rb-doped CsPbBr3, using density functional theory and the Boltzmann Transport Equation (BTE) simulations. The differences between a pure CsPbBr3 and doped CPB (RbxCs1−xPbBr3), as well as the influence of Rb doping on these properties, are also discussed.
2. Results and Discussion
2.1. Structural Properties
According to earlier research, AMX3-type compounds display several phases at various temperatures, although at high temperatures, they all take on a cubic perovskite structure, where a three-dimensional framework of MX6 octahedrons with shared corners is provided.
The cubic structure phase of the perovskite CsPbBr3 compound has a space group (221) and lattice parameter a = 5.605 Å.
Figure 1 shows the crystal structure of CsPbBr3. The structure of the cubic CsPbBr3 compound was optimized. The optimization results for the lattice parameter are shown in Table 1 and are proved to be in reasonable agreement with experimental and theoretical values.
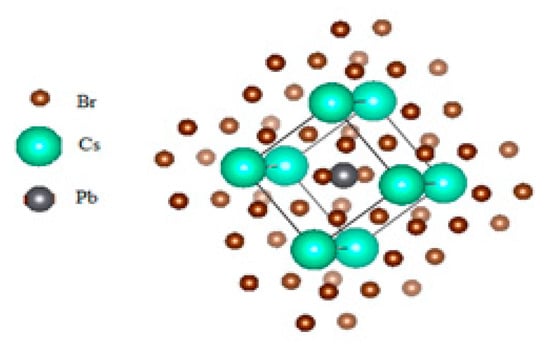
Figure 1.
Crystal structure of CsPbBr3.

Table 1.
Lattice parameter of CsPbBr3 compared to other calculations.
2.2. Elastic and Electronic Properties
For describing the mechanical properties of materials, the elastic constants are essential and basic. The elastic constants are significant factors that describe how macroscopic stress is responded to. In addition to defining how a material is deformed under stress and subsequently recovered and returned to its original shape after tension is removed, the elastic constants of solids also serve as a link between the mechanical and dynamical behavior of crystals. The elastic constants are significant material characteristics that can provide vital details about a material’s structural stability, the nature of its atomic bonds, and its anisotropic properties. There are three distinct elastic constants for a cubic system: B11, B12, and B44.
The state and behavior of the electrons in the material are completely described by a collection of characteristics and representations known as the electronic properties. Such a representation is, for instance, the electronic band structure, which characterizes the state of the electrons in terms of their energy, E, and momentum, k. The electric and optical characteristics, which define how a material reacts to electromagnetic radiation, are both closely related to the electronic properties. Examples of these are electrical conductivity and dielectric response.
The elastic and electronic properties of CsPbBr3, and Rb-doped CsPbBr3, including density of states and band structures, are calculated after the optimization of the lattice parameters. Table 2 lists the values of the elastic constants calculated via DFT calculations. Figure 2 shows the calculated electronic band structures of CsPbBr3 and Rb-doped CsPbBr3 along the higher symmetry directions G, R, X, and M. From the investigation results of CsPbBr3, Castelli et al. [51] reported that the bandgap energy for this perovskite is 1.63 eV, while Qian et al. [55] reported 1.75 eV. The present calculation results for CsPbBr3 (Figure 2a), which was 1.70 eV, gave a closer value to their computational results. Experimentally, Kulbak et al. [56] reported 2.32 eV regarding the bandgap energy of CsPbBr3, whereas Stoumpos et al. [45] reported 2.25 eV. On the other hand, the band structures of RbxCs1−xPbBr3 (x = 0.75 and 1) were calculated and shown in Figure 2b,c, respectively. It is clearly seen that these perovskites exhibited a direct band gap (Figure 2a–c), and achieved around 1.70, 3.76, and 1.71 eV, respectively, upon an increase in Rb content. Distinctions regarding the band gap energies are attributed to the atomic level and size. Furthermore, the gap energy observed in Figure 2c is lowered compared to the previous figures after an increase in the Rb-doping (x = 1), due to several mechanisms, such as the size of Rb. The results for CsPbBr3 (Figure 2a) are in good agreement with the experimental values [45,56,57]. The increase in the energy band gap, followed by a decrease as the doping content increases, is due to either octahedron tilting or a decrease in the overlap of the electron wave function, due to crystal structure contraction and distortion caused by the doping rubidium (Rb) atom [58,59]. To understand the electronic band gap nature, the densities of states (DOSs) of RbxCs1−xPbBr3 (x = 0, 0.75 and 1) were calculated and displayed in Figure 3. As can be appreciated, the valence bands in CsPbBr3 (x = 0) and RbPbBr3 (x = 1) are mostly composed of Brs, Brp, Pbs, Pbp, and Pbd orbitals, with a small contribution from Css, Csp, and Csd states. The conduction bands in both systems are mainly dominated by Pbp and Css orbitals, with small contributions of Brd and Brp. While in Rb0.75Cs0.25PbBr3 (x = 0.75), the valence band consists mainly of the orbital contributions Br-s, Pb-s, and Pb-d. The conduction band consists of the Pbp, Brp, and Brd orbitals, with small Css, Csp, and Csd states. It has been noted that the p orbitals of Pb and Br in the conduction band maximum have an effect on increasing the band gap in the 0.75 doping of Rb.

Table 2.
Elastic properties of CsPbBr3 and gap energies of RbxCs1−xPbBr3 (x = 0, 0.75 and 1).
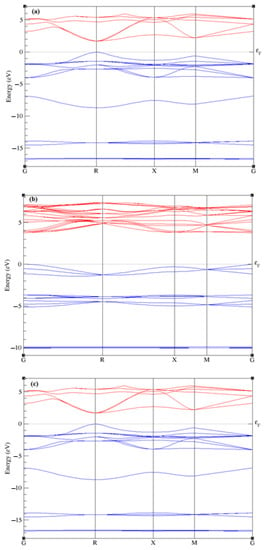
Figure 2.
Band structures of CsPbBr3 and RbxCs1−xPbBr3 (x = 0 (a), 0.75 (b), 1 (c)). Valence bands (blue lines) and conduction bands (red lines).
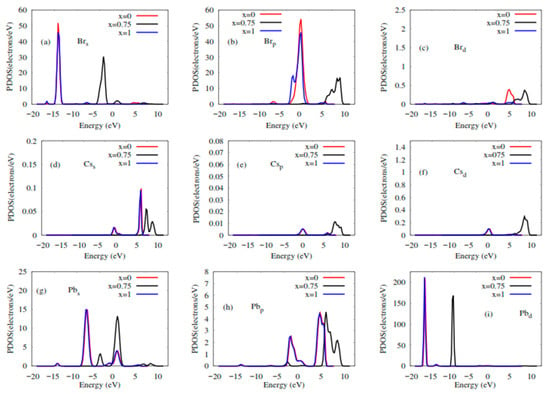
Figure 3.
Partial density of states (PDOSs) of RbxCs1−xPbBr3 (x = 0, 0.75 and 1). (a) Brs orbitals; (b) Brp orbitals; (c) Brd orbitals; (d) Css orbitals; (e) Csp orbitals; (f) Csd orbitals; (g) Pbs orbitals; (h) Pbp orbitals; (i) Pbd orbitals vs. energy.
2.3. Optical Properties
Using solar cells and other optoelectronic devices, it is possible to directly convert the impinging photons into electricity. This capability has motivated scientists to look for materials with higher energy conversion efficiency. Direct inter-band transitions in direct band gap semiconductors are crucial, because indirect band gap semiconductors with intra-band transitions cause heating from phonons. This is because the optical properties of a typical semiconductor depend on the band gap, making transition or recombination rates crucial.
From the complex dielectric function, the optical properties of the halide perovskite materials CsPbBr3 and RbPbBr3 were theoretically studied. At a lower energy expression of complex, the dielectric function is:
where and are the real and imaginary part of the dielectric function, respectively.
The real and imaginary part of the dielectric tensor can be estimated using the Kramer–Kronig relation:
The absorption coefficient α can be expressed as a function of the extinction coefficient k:
The imaginary part of the complex dielectric function, , is related to the band structure of the material and describes its absorption behavior. From Figure 4a,b, the spectra of for CsPbBr3 and RbPbBr3 had similar features: the critical points (onset) in the spectra of were found at 1.66 eV for CsPbBr3 and RbPbBr3. These points are closely related to the band gap 1.70 eV for CsPbBr3 and RbPbBr3. Different characteristic peaks, beyond the critical points, could be identified by the density of states (Figure 3). The first peaks were due to the transition of electrons from Brp states of the VB to the Pbp states in the CB. The other peaks originated because of the electronic transition from Brp states of VB to the unoccupied Cs(s;d) and Rb(s;d) states, and its mixed states with Pbp states in CB. Interestingly, similar features were found in the spectra (Figure 4e) of the extinction coefficients,.
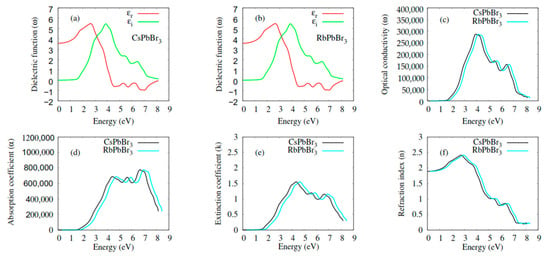
Figure 4.
Optical properties of CsPbBr3 and RbPbBr3: (a,b) Dielectric function ( and ); (c) optical conductivity ; (d) absorption coefficient ; (e) extinction coefficient ; (f) refaction index .
The real part of the complex dielectric function, , is shown in Figure 4a,b. The most important quantity in the spectra is the zero-frequency limit , which is the electronic part part of the static dielectric constant. The value , for CsPbBr3 and RbPbBr3 was 3.5. The , of CsPbBr3 and RbPbBr3 started to increase from the zero-frequency limit, reached its maximum value, then decreased, and in certain energy ranges, went below zero. The optical conductivity spectra, presented in Figure 4c, showed that the optical conductance started at around 1.52 and 1.58 eV for CsPbBr3 and RbPbBr3, respectively. Beyond these points, reached its maxima and then, again, decreased gradually. These compounds had a similar highest . Similar features were observed regarding the absorption coefficients (Figure 4d) in the range 0–6 eV, but the highest peaks were observed in the absorption range 6–9 eV of . Furthermore, the absorption range 2–8 eV showed the usefulness of CsPbBr3 and RbPbBr3 for various optical and optoelectronic devices working in this range. For an optical material to be used in optical devices, such photonic crystals, waveguides, solar cells, and detectors, it is crucial to understand the refractive index it has. The variation in the refractive indexes (n) for CsPbBr3 and RbPbBr3, as a function of incident photon energy, is shown in Figure 4f. The most important quantity in the spectra is the zero-frequency limit n(0), and its value is 2 for both CsPbBr3 and RbPbBr3. The for these compounds increased gradually from the zero-frequency limit, reaching its maximal value, before decreasing. The theoretical analysis of CsPbBr3′s optical characteristics were equivalent to experimental analysis [63,64,65].
2.4. Thermoelectric Properties
The exponential growth of technology has led to enormous energy waste as a result of rising energy demands. Researchers have also been forced to create unique systems that can recycle waste heat into electrical energy due to the lower capacity of the available energy sources. One of the finest options is a thermoelectric generator, which can transform temperature gradients (phonons) directly into potential differences. The computed electrical conductivity measures the free carrier motion that results from temperature gradients that increase the carriers’ kinetic energy. A higher electrical conductivity is required to realize the commercial uses of thermoelectric devices, since it reduces the joule heating effect.
By comparing the ratio of heat efflux per area per unit time to the temperature gradient, it is possible to assess the flow of thermal energy. The two categories of thermal conductivity are electronic and phononic. Due to the importance of intra-band transitions in metals, as compared to semiconductors, lattice vibrations (phonons) have a greater influence in metals than they do in semiconductors. Additionally, whereas the phonon energy has little significance for direct bandgap semiconductors, it is significant for indirect bandgap semiconductors. In order to increase the efficiency of thermoelectric devices, the Wiedemann–Franz law specifies the minimal thermal-to-electrical conductivity ratio [66].
In the present work, to discuss the transport behavior of CsPbBr3 and Rb-doped CsPbBr3 compounds, the thermal and electrical conductivities were calculated in the temperature range of 400–800 K, as displayed in Figure 5. It was observed that the electrical and thermal conductivities increased with increasing temperature until 800 K for pure and Rb-doped CPB. The decreasing slope of the electrical and thermal conductivity curves corresponding to Rb0.25Cs0.75PbBr3 and Rb0.5Cs0.5PbBr3 could be related to the increase of the band gap at T = 800 K, hence, the electrical conductivities at this temperature were 0.25 × 1017, 1.9 × 1017, 3.37 × 1017, and 3.75 × 1017 Ω−1 m−1s−1 for Rb0.25Cs0.75PbBr3, Rb0.5Cs0.5PbBr3, RbPbBr3, and CsPbBr3, respectively. At T = 800 K the thermal conductivities were 1.5 × 1013, 2.4 × 1013, 4.4 × 1013, and 9 × 1013 WK−1 m−1s−1 for Rb0.25Cs0.75PbBr3, Rb0.5Cs0.5PbBr3, RbPbBr3, and CsPbBr3, respectively. Our results are in good agreement with the experimental and theoretical studies reported in by [48,67,68,69], notably electrical conductivity. The increasing slope of the electrical conductivity curves from Rb0.25Cs0.75PbBr3 to RbPbBr3 is justified by the variation in the size of the atomic by effect of doping, which varies the free charge carriers.
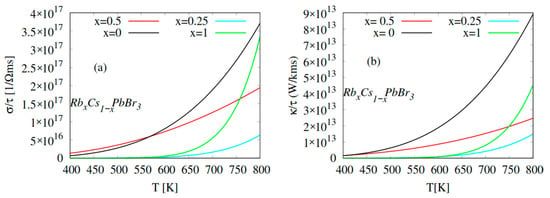
Figure 5.
Thermoelectric properties of RbxCs1−xPbBr3 (x = 0, 0.25, 0.5, 1). (a) Electrical conductivity () vs. temperature; (b) thermal conductivity () vs. temperature.
3. Materials and Methods
New perovskite materials and their properties must be efficiently discovered using computational tools. Considering the wealthy amount of data, it is reasonable that this trend of employing computational methods will continue. Calculating the characteristics of materials is now possible without using experimental methods, because of the density functional theory (DFT). In physics and material science, DFT is a quantum mechanical modeling technique, that is employed to look into the electronic structure of many-body systems. In DFT, the exchange–correlation function, which is a mathematical approximation of the many-body effects of electron correlation, is used to treat electron correlation. In contrast, electron correlation is not included in HF, which reduces accuracy, but simplifies computation. As a result, it is probable that DFT is generally more accurate for many different calculations than HF, especially for systems with strong electron correlations [70]. DFT was realized in the 1980s by Pierre Hohenberg and Walter Kohn [71]. It is a commonly used computational method in material science for quickening the development of new materials and performing high-throughput simulations [72].
The electronic and optical properties of CsPbBr3 and Rb-doped CsPbBr3 perovskite were studied using DFT calculations, implemented in the ABINIT software package [73,74], with generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof function, proposed in [75], using the plane wave pseudo-potential formalism, in order to obtain the response function calculations [76,77]. An energy cut-off of 45 Ha was used for the plane wave expansion, which are well converged. The Monkhorst Pack Mesh scheme [78] k-point grid sampling was set at 5 × 5 × 5, to perform the irreducible Brillouin zone integrations. We use a starting point for CsPbBr3 according to the reported data in the literature [79]. The thermoelectric properties were calculated using BoltzTraP code [80].
4. Conclusions
In this work, a systematic investigation of the electronic, optical, thermoelectric, and elastic properties of cesium lead bromide CsPbBr3 and RbxCs1−xPbBr3 (x = 0, 0.25, 0.50, 0.75, and 1) was carried out, using the density functional theory within the generalized gradient approximation and the Boltzmann transport equation simulations. The optical properties, such as dielectric function, optical conductivity, absorption coefficient, refractive index, and extinction coefficient, were studied in the energy range of 0–10 eV. The calculated band gap energy agrees well with the available theoretical and experimental values, and it increased then decreased as the Rb doping content increased. Our calculations revealed that Rb0.75Cs0.25PbBr3 is a wide band gap material, which indicates that it is a better candidate for high-frequency UV device applications.
CsPbBr3 (x = 0) and RbPbBr3 (x = 1), which have excellent absorption powers in the visible ultraviolet energy range and a short and direct band gap, could be used in solar cells.
Author Contributions
Conceptualization, E.O.; methodology, E.O.; investigation, E.O. and M.A.; resources, E.O.; data curation, E.O., M.A., A.B. and F.C.; writing—original draft preparation, E.O.; writing—review and editing, E.O., M.A. and F.C.; supervision, E.O., M.A. and F.C.; project administration, E.O. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported through computational resources of High Performance Computing-Moroccan Academic and Research Wide Area Network (HPC-MARWAN) provided by the National Center for Scientific and Technical Research (CNRST), Rabat, Morocco.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Samples of the compounds are not available from the authors.
References
- Gao, Y.; Wu, Y.; Lu, H.; Chen, C.; Liu, Y.; Bai, X.; Yang, L.; Yu, W.W.; Dai, Q.; Zhang, Y. CsPbBr3 perovskite nanoparticles as additive for environmentally stable perovskite solar cells with 20.46% efficiency. Nano Energy 2019, 59, 517–526. [Google Scholar] [CrossRef]
- Chung, I.; Lee, B.; He, J.; Chang, R.P.H.; Kanatzidis, M.G. All-solid-state dye-sensitized solar cells with high efficiency. Nature 2012, 485, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Ye, F.; Xiao, M.; Wang, H.; Wang, C.; Liang, J.; Hu, X.; Guan, H.; Cui, H.; Ke, W.; et al. Internal Encapsu-lation for Lead Halide Perovskite Films for Efficient and Very Stable Solar Cells. Adv. Energy Mater. 2022, 12, 2200361. [Google Scholar] [CrossRef]
- Kim, Y.H.; Cho, H.; Heo, J.H.; Kim, T.S.; Myoung, N.; Lee, C.L.; Im, S.H.; Lee, T.W. Multicolored Organic/Inorganic Hybrid Perovskite Light-Emitting Diodes. Adv. Mater. 2015, 27, 1248. [Google Scholar] [CrossRef] [PubMed]
- Stranks, S.D.; Snaith, H.J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 2015, 10, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Saidaminov, M.I.; Adinolfi, V.; Comin, R.; Abdelhady, A.L.; Peng, W.; Dursun, I.; Yuan, M.; Hoogland, S.; Sargent, E.H.; Bakret, O.M. Planar-integrated single-crystalline perovskite photodetectors. Nat. Commun. 2015, 6, 8724. [Google Scholar] [CrossRef] [PubMed]
- Hong, E.; Li, Z.; Yan, T.; Fang, X. Surface-Tension-Dominant Crystallization of 2D Perovskite Single Crystals for Vertically Oriented Hetero-/Homo-Structure Photodetectors. Nano Lett. 2022, 22, 8662. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Zhou, H.; Xiao, M.; Gui, P.; Gao, Z.; Yao, F.; Shao, W.; Liu, C.; Tao, C.; Ke, W.; et al. Semi-transparent, high-performance lead-free Cs3Bi2I9 single crystal self-driven photodetector. Appl. Phys. Lett. 2022, 120, 191102. [Google Scholar] [CrossRef]
- Li, Z.; Hong, E.; Zhang, X.; Deng, M.; Fang, X. Perovskite-Type 2D Materials for High-Performance Photodetectors. J. Phys. Chem. Lett. 2022, 13, 1215–1225. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Zuo, C.; Yang, W.; Fang, X. Supersaturation-Controlled Growth of Monolithically Integrated Lead-Free Halide Perovskite Single-Crystalline Thin Film for High-Sensitivity Photodetectors. Adv. Mater. 2021, 33, 2103010. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Yang, Z.; Yang, D.; Ren, X.; Xu, H.; Yang, Z.; Liu, S.F. 20-mm-Large Single-Crystalline Formamidinium-Perovskite Wafer for Mass Production of Integrated Photodetectors. Adv. Opt. Mater. 2016, 4, 1829–1837. [Google Scholar] [CrossRef]
- Chen, S.; Roh, K.; Lee, J.; Chong, W.K.; Lu, Y.; Mathews, N.; Sum, T.C.; Nurmikko, A. A Photonic Crystal Laser from Solution Based Organo-Lead Iodide Perovskite Thin Films. ACS Nano 2016, 10, 3959–3967. [Google Scholar] [CrossRef] [PubMed]
- Babu, K.E.; Murali, N.; Babu, K.V.; Shibeshi, P.T.; Veeraiah, V. Structural, Elastic, Electronic, and Optical Properties of Cubic Perovskite CsCaCl3 Compound: An ab initio Study. Act. Phys. Pol. A 2014, 125, 1179. [Google Scholar] [CrossRef]
- Clark, S.J.; Donaldson, J.D.; Harvey, J.A. Evidence for the Direct Population of Solid-state Bands by Nonbonding Electron Pairs in Compounds of the Type CsM”X, (M” = Ge, Sn, Pb; X=CI, Br, I). J. Mater. Chem. 1995, 5, 1813. [Google Scholar] [CrossRef]
- Chang, Y.H.; Park, C.H.; Matsuishi, K. First-principles study of the Structural and the electronic properties of the lead-Halide-based inorganic-organic perovskites (CH3NH3) PbX3 and CsPbX3 (X = Cl, Br, I). Korean Phys. Soc. 2004, 44, 889. [Google Scholar]
- Zhao, Y.Q.; Ma, Q.R.; Liu, B.; Yu, Z.L.; Cai, M.Q. Pressure-induced strong ferroelectric polarization in tetra-phase perovskite CsPbBr3. Phys. Chem. Chem. Phys. 2018, 20, 14718. [Google Scholar] [CrossRef] [PubMed]
- Stroppa, A.; Quarti, C.; Angelis, F.D.; Picozzi, S. Ferroelectric Polarization of CH3NH3PbI3: A Detailed Study Based on Density Functional Theory and Symmetry Mode Analysis. J. Phys. Chem. Lett. 2015, 6, 2223. [Google Scholar] [CrossRef]
- Yang, Y.; You, J. Make perovskite solar cells stable. Nature 2017, 544, 155–156. [Google Scholar] [CrossRef]
- Han, Y.; Meyer, S.; Dkhissi, Y.; Weber, K.; Pringle, J.M.; Bach, U.; Spiccia, L.; Cheng, Y.B. Degradation observations of en-capsulated planar CH3NH3PbI3 perovskite solar cells at high temperatures and humidity. J. Mater. Chem. A 2015, 3, 8139. [Google Scholar] [CrossRef]
- Xiao, C.; Li, Z.; Guthrey, H.; Moseley, J.; Yang, Y.; Wozny, S.; Moutinho, H.; To, B.; Berry, J.J.; Gorman, B.; et al. Mechanisms of Electron-Beam-Induced Damage in Perovskite Thin Films Revealed by Cathodoluminescence Spectroscopy. J. Phys. Chem. C 2015, 119, 26904–26911. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C.; Wang, D.; Liu, G.; Zhang, Q.; Luo, W.; Qi, X.; Guo, X.; Zhang, Y.; Lao, Y.; et al. Im-provement of Cs2AgBiBr6 double perovskite solar cell by rubidium doping. Org. Electron. 2019, 74, 204. [Google Scholar] [CrossRef]
- Machiba, H.; Oku, T.; Kishimoto, T.; Ueoka, N.; Suzuki, A. Fabrication and evaluation of K-doped MA0.8FA0.1K0.1PbI3(Cl) perovskite solar cells. Chem. Phys. Lett. 2019, 730, 117–123. [Google Scholar] [CrossRef]
- Fan, Y.; Qin, H.; Ye, W.; Liu, M.; Huang, F.; Zhong, D. Improving the stability of methylammonium lead iodide perovskite solar cells by cesium doping. Thin Solid Films 2018, 667, 40–47. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, R.; Xu, H.T.; Hong, F.; Xu, F.; Wang, L.J. Nature of the band gap of halide perovskites ABX3 (A = CH3NH3, Cs; B = Sn, Pb; X = Cl, Br, I): First-principles calculations. Chin. Phys. B 2015, 24, 116302. [Google Scholar] [CrossRef]
- Yi, C.; Luo, J.; Meloni, S.; Boziki, A.; Ashari-Astani, N.; Graetzel, C.; Zakeeruddin, S.M.; Roethlisberger, U.; Graetzel, M. En-tropic stabilization of mixed A-cation ABX3 metal halide perovskites for high performance perovskite solar cells. Energy Environ. Sci. 2016, 9, 656. [Google Scholar] [CrossRef]
- Lang, L.; Yang, J.-H.; Liu, H.-R.; Xiang, H.; Gong, X. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. A 2014, 378, 290–293. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, Z.; Li, T.; Chen, Y.; Huang, W. Stability of Perovskite Solar Cells: A Prospective on the Substitution of the A Cation and X Anion. Angew. Chem. Int. Ed. 2017, 56, 1190–1212. [Google Scholar] [CrossRef]
- Bu, T.; Liu, X.; Zhou, Y.; Yi, J.; Huang, X.; Luo, L.; Xiao, J.; Ku, Z.; Peng, Y.; Huang, F.; et al. A novel quad-ruple-cation absorber for universal hysteresis elimination for high efficiency and stable perovskite solar cells. Energy Environ. Sci. 2017, 10, 2509. [Google Scholar] [CrossRef]
- Shai, X.; Zuo, L.; Sun, P.; Liao, P.; Huang, W.; Yao, E.-P.; Li, H.; Liu, S.; Shen, Y.; Yang, Y.; et al. Efficient planar perovskite solar cells using halide Sr-substituted Pb perovskite. Nano Energy 2017, 36, 213–222. [Google Scholar] [CrossRef]
- Zhao, W.G.; Yao, Z.; Yu, F.Y.; Yang, D.; Liu, S.Z. Alkali metal doping for improved CH3NH3PbI3 perovskite solar cells. Adv. Sci. 2018, 5, 1700131. [Google Scholar] [CrossRef]
- Nam, J.K.; Chai, S.U.; Cha, W.; Choi, Y.J.; Kim, W.; Jung, M.S.; Kwon, J.; Kim, D.; Park, J.H. Potassium Incorporation for Enhanced Performance and Stability of Fully Inorganic Cesium Lead Halide Perovskite Solar Cells. Nano Lett. 2017, 17, 2028–2033. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.Y.; Lin, H.Y.; Chiang, K.M.; Tsai, W.L.; Huang, Y.C.; Tsao, C.S.; Lin, H.W. All-Vacuum-Deposited Stoichiometrically Balanced Inorganic Cesium Lead Halide Perovskite Solar Cells with Stabilized Efficiency Exceeding 11%. Adv. Mater. 2017, 29, 1605290. [Google Scholar] [CrossRef] [PubMed]
- Lau, C.F.J.; Deng, X.; Ma, Q.; Zheng, J.; Yun, J.S.; Green, M.A.; Huang, S.; Ho-Baillie, A.W.Y. CsPbIBr2 Perovskite Solar Cell by Spray Assisted Deposition. ACS. Energy Lett. 2016, 1, 573. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, S.; Wen, X.; Green, M.A.; Ho-Baillie, A.W.Y. Hole Transport Layer Free Inorganic CsPbIBr2 Perovskite Solar Cell by Dual Source Thermal Evaporation. Adv. Energy Mater. 2016, 6, 1502202. [Google Scholar] [CrossRef]
- Kulbak, M.; Gupta, S.; Kedem, N.; Levine, I.; Bendikov, T.; Hodes, G.; Cahen, D. Cesium Enhances Long-Term Stability of Lead Bromide Perovskite-Based Solar Cells. J. Phys. Chem. Lett. 2016, 7, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zhou, Y.; Xing, G.; Xu, Q.; Garces, H.F.; Solanki, A.; Goh, T.W.; Padture, N.P.; Sum, T.C. Long Minority-Carrier Dif-fusion Length and Low Surface-Recombination Velocity in Inorganic Lead-Free CsSnI3 Perovskite Crystal for Solar Cells. Adv. Funct. Mater. 2017, 27, 1604818. [Google Scholar] [CrossRef]
- Frolova, L.A.; Anokhin, D.V.; Piryazev, A.A.; Luchkin, S.Y.; Dremova, N.N.; Stevenson, K.J.; Troshin, P.A. Highly Efficient All-Inorganic Planar Heterojunction Perovskite Solar Cells Produced by Thermal Coevaporation of CsI and PbI2. J. Phys. Chem. Lett. 2017, 8, 67–72. [Google Scholar] [CrossRef]
- Kim, Y.G.; Kim, T.-Y.; Oh, J.H.; Choi, K.S.; Kim, Y.-J.; Kim, S.Y. Cesium lead iodide solar cells controlled by annealing temperature. Phys. Chem. Chem. Phys. 2017, 19, 6257–6263. [Google Scholar] [CrossRef]
- Trots, D.M.; Myagkota, S.V. High-temperature structural evolution of cesium and rubidium triiodoplumbates. J. Phys. Chem. Solids 2008, 69, 2520–2526. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, W.; Pan, G.; Liu, Y.; Yang, M.; Hua, S.; Chen, X.; Peng, H.; Song, H. Enhancing the exciton emission of CsPbCl3 perovskite quantum dots by incorporation of Rb+ ions. Mater. Res. Bull. 2019, 112, 142–146. [Google Scholar] [CrossRef]
- Sebastian, M.; Peters, J.A.; Stoumpos, C.C.; Im, J.; Kostina, S.S.; Liu, Z.; Kanatzidis, M.G.; Freeman, A.J.; Wessels, B.W. Excitonic emissions and above-band-gap luminescence in the single-crystal perovskite semiconductors CsPbBr3 and CsPbCl3. Phys. Rev. B 2015, 92, 235210. [Google Scholar] [CrossRef]
- Park, J.P.; Lee, T.K.; Kwak, S.K.; Kim, S.-W. Formation of bright-green-color-emitting perovskite CsPbBr3 in a bulk state using a simple recrystallization process. Dye. Pigment. 2017, 144, 151–157. [Google Scholar] [CrossRef]
- He, H.; Tang, B.; Ma, Y. Controlled synthesis of quantum confined CsPbBr3 perovskite nanocrystals under ambient conditions. Nanotechnology 2018, 29, 055601. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Wu, G.; Cheng, J.; Dang, H.; Ma, K.; Zhang, Y.-W.; Tan, P.-F.; Chen, S. High-quality CsPbBr3 perovskite nanocrystals for quantum dot light-emitting diodes. RSC Adv. 2017, 7, 10391–10396. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Peters, J.A.; Liu, Z.; Sebastian, M.; Im, J.; Chasapis, T.C.; Wibowo, A.C.; Chung, D.Y.; Freeman, A.J.; et al. Crystal Growth of the Perovskite Semiconductor CsPbBr3: A New Material for High-Energy Radiation Detection. Cryst. Growth Des. 2013, 13, 2722–2727. [Google Scholar] [CrossRef]
- Murtaza, G.; Ahmad, I. First principle study of the structural and optoelectronic properties of cubic perovskites CsPbM3 (M = Cl, Br, I). Phys. B 2011, 406, 3222. [Google Scholar] [CrossRef]
- Duong, T.; Wu, Y.; Shen, H.; Peng, J.; Fu, X.; Jacobs, D.; Wang, E.C.; Kho, T.C.; Fong, K.C.; Stocks, M.; et al. Rubidium Multication Perovskite with Op-timized Bandgap for Perovskite-Silicon Tandem with over 26% Efficiency. Adv. Energy Mater. 2017, 7, 1700228. [Google Scholar] [CrossRef]
- Mahmood, Q.; Hassan, M.; Rashid, M.; Haq, B.U.; Laref, A. The systematic study of mechanical, thermoelectric and optical properties of lead based halides by first principle approach. Phys. B Condens. Matter 2019, 571, 87–92. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Q.; Li, R.; Lin, C.; Huang, D.; Cheng, Y. The mechanism of alkali doping in CsPbBr3: A first-principles per-spective. J. Appl. Phys. 2021, 129, 165110. [Google Scholar] [CrossRef]
- Zheng, F.; Takenaka, H.; Wang, F.; Koocher, N.Z.; Rappe, A.M. First-principles calculation of the bulk photovoltaic effect in CH3NH3PbI3 and CH3NH3PbI3-xClx. J. Phys. Chem. Lett. 2015, 6, 31. [Google Scholar] [CrossRef]
- Castelli, I.E.; García-Lastra, J.M.; Thygesen, K.S.; Jacobsen, K.W. Bandgap calculations and trends of organometal halide perovskites. APL Mater. 2014, 2, 081514. [Google Scholar] [CrossRef]
- Myagkota, S.; Gloskovskii, A.; Gladyshevskii, R.; Voloshynovskii, A. Luminescent kinetic characteristics of CsPbCl3 aggregates dispersed in Rb1-xCsxCl matrices. Condens. Matter Phys. 2003, 6, 325. [Google Scholar] [CrossRef]
- Moreira, R.L.; Dias, A. Comment on “Prediction of lattice constant in cubic perovskites”. J. Phys. Chem. Solids 2007, 68, 1617. [Google Scholar] [CrossRef]
- Nikl, M.; Nitsch, K.; Chval, J.; Somma, F.; Phani, A.R.; Santucci, S. Optical and structural properties of ternary nanoaggregates in CsI-PbI2 co-evaporated thin films. J. Phys. Condens. Matter. 2000, 12, 1939. [Google Scholar] [CrossRef]
- Qian, J.; Xu, B.; Tian, W. A comprehensive theoretical study of halide perovskites ABX3. Org. Electron. 2016, 37, 61–73. [Google Scholar] [CrossRef]
- Kulbak, M.; Cahen, D.; Hodes, G. How Important Is the Organic Part of Lead Halide Perovskite Photovoltaic Cells? Efficient CsPbBr3 Cells. J. Phys. Chem. Lett. 2015, 6, 2452–2456. [Google Scholar] [CrossRef]
- Beal, R.E.; Slotcavage, D.J.; Leijtens, T.; Bowring, A.R.; Belisle, R.A.; Nguyen, W.H.; Burkhard, G.F.; Hoke, E.T.; McGehee, M.D. Cesium Lead Halide Perovskites with Improved Stability for Tandem Solar Cells. J. Phys. Chem. Lett. 2016, 7, 746. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, R.; Jin, M.; Zhang, Z.; Yu, Y.; Xiang, W.; Liang, X. Rb+-doped CsPbBr3 quantum dots with multi-color stabilized in borosilicate glass via crystallization. J. Eur. Ceram. Soc. 2020, 40, 94–102. [Google Scholar] [CrossRef]
- Shi, Y.; Xi, J.; Lei, T.; Yuan, F.; Dai, J.; Ran, C.; Dong, H.; Jiao, B.; Hou, X.; Wu, Z. Rubidium Doping for Enhanced Perfor-mance of Highly Efficient Formamidinium-Based Perovskite Light-Emitting Diodes. ACS Appl. Mater. Interfaces 2018, 10, 9849–9857. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, J.; Liu, H.; Zhu, M.; Zhou, X.; Wu, P.; Li, C. Prediction of lattice constant in cubic perovskites. J. Phys. Chem. Solids 2006, 67, 1531–1536. [Google Scholar] [CrossRef]
- Pitriana, P.; Wungu, T.D.K.; Herman; Hidayat, R. The characteristics of band structures and crystal binding in all-inorganic perovskite APbBr3 studied by the first principle calculations using the Density Functional Theory (DFT) method. Results Phys. 2019, 15, 102592. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, K.-D.; Lee, H.S. Growth Kinetics and Optical Properties of CsPbBr3 Perovskite Nanocrystals. Energies 2021, 14, 275. [Google Scholar] [CrossRef]
- Yan, W.; Mao, L.; Zhao, P.; Mertens, A.; Dottermusch, S.; Hu, H.; Jin, Z.; Richards, B.S. Determination of complex optical constants and photovoltaic device design of all-inorganic CsPbBr3 perovskite thin films. Opt. Express 2020, 28, 15706–15717. [Google Scholar] [CrossRef]
- Zhao, M.; Shi, Y.; Dai, J.; Lian, J. Ellipsometric study of the complex optical constants of a CsPbBr3 perovskite thin film. J. Mater. Chem. C 2018, 6, 10450–10455. [Google Scholar] [CrossRef]
- Yang, D.; Cheng, X.; Liu, Y.; Shen, C.; Xu, Z.; Zheng, X.; Jiang, T. Dielectric properties of a CsPbBr3 quantum dot solution in the terahertz region. Appl. Opt. 2017, 56, 2878–2885. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.F.; Bohn, H.G.; Schenk, W. Ionic Wiedemann–Franz law. Appl. Phys. Lett. 2000, 77, 2599. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, C.; Fan, S.; Deng, Y.; Zhang, W.; Ye, B.; Xie, Y. Dual vacancies: An effective strategy realizing synergistic optimi-zation of thermoelectric property in BiCuSeO. J. Am. Chem. Soc. 2015, 137, 6587. [Google Scholar] [CrossRef]
- Pei, Y.; May, A.F.; Snyder, G.J. Self-tuning the carrier concentration of PbTe/Ag2Te composites with excess Ag for high ther-moelectric performance. Adv. Energy Mater. 2011, 1, 291. [Google Scholar] [CrossRef]
- Fu, J.; Su, X.; Xie, H.; Yan, Y.; Liu, W.; You, Y.; Cheng, X.; Uher, C.; Tang, X. Understanding the combustion process for the synthesis of mechanically robust SnSe thermoelectrics. Nano Energy 2018, 44, 53–62. [Google Scholar] [CrossRef]
- Yu, H.S.; Li, S.L.; Truhlar, D.G. Perspective: Kohn-Sham density functional theory descending a stair-case. J. Chem. Phys. 2016, 145, 130901. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Becke, A.D.; Parr, R.G. Density functional theory of electronic structure. J. Phys. Chem. 1996, 100, 12974. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
- Gonze, X.; Amadond, B.; Anglade, P.M.; Beuken, J.M.; Bottin, F.; Boulangera, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple John. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Sakata, M.; Nishiwaki, T.; Harada, J. Neutron Diffraction Study of the Structure of Cubic CsPbBr3. J. Phys. Soc. Jpn. 1979, 47, 232–233. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).