Next Article in Journal
Chemical Composition and Biological Activities of Essential Oils of Four Asarum Species Growing in Vietnam
Previous Article in Journal
Excited-State Polarizabilities: A Combined Density Functional Theory and Information-Theoretic Approach Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 6
10.3390/molecules28062577
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tetrel-Bond Interactions Involving Metallylenes TH2 (T = Si, Ge, Sn, Pb): Dual Binding Behavior

by
Yishan Chen
*,
Lifeng Yao
and
Fan Wang
School of Chemistry & Environmental Science, Qujing Normal University, Qujing 655011, China
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(6), 2577; https://doi.org/10.3390/molecules28062577
Submission received: 22 February 2023 / Revised: 7 March 2023 / Accepted: 11 March 2023 / Published: 12 March 2023
(This article belongs to the Section Computational and Theoretical Chemistry)
Browse Figures
Versions Notes

Abstract

:
The dual binding behavior of the metallylenes TH2 (T = Si, Ge, Sn, Pb) with some selected Lewis acids (T’H3F, T’ = Si, Ge, Sn, Pb) and bases (N2, HCN, CO, and C6H6) has been investigated by using the high-level quantum chemical method. Two types (type-A and type-B) of tetrel-bonded complexes can be formed for TH2 due to their ambiphilic character. TH2 act as Lewis bases in type-A complexes, and they act as Lewis acids in type-B ones. CO exhibits two binding modes in the type-B complexes, one of which is TH2···CO and the other is TH2···OC. The TH2···OC complexes possess a weaker binding strength than the other type-B complexes. The TH2···OC complexes are referred to as the type-B2 complexes, and the other type-B complexes are referred to as the type-B1 complexes. The type-A complexes exhibit a relatively weak binding strength with Eint (interaction energy) values ranging from –7.11 to –15.55 kJ/mol, and the type-B complexes have a broad range of Eint values ranging from −9.45 to −98.44 kJ/mol. The Eint values of the type-A and type-B1 complexes go in the order SiH2 > GeH2 > SnH2 > PbH2. The AIM (atoms in molecules) analysis suggests that the tetrel bonds in type-A complexes are purely closed-shell interactions, and those in most type-B1 complexes have a partially covalent character. The EDA (Energy decomposition analysis) results indicate that the contribution values of the three energy terms go in the order electrostatic > dispersion > induction for the type-A and type-B2 complexes, and this order is electrostatic > induction > dispersion for the type-B1 complexes.

1. Introduction

Intermolecular interactions are a key issue for supermolecular chemistry because of their central role in molecular recognition [1,2,3]. A hydrogen bond is the most important intermolecular interaction and has been extensively applied in supermolecular systems [4]. A tetrel bond (TB) is another important intermolecular interaction, and the tetrel atoms, such as C and Si, serve as electron acceptors in TB interactions [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Its formation is ascribed to the areas of lower electronic density around tetrel atoms, and these areas are called σ-holes [29,30,31,32,33] or π-holes [34,35,36,37]. A σ-hole is an area of lower electronic density on the extension of a bond, and a π-hole is an area of a lower electronic density above and below a planar portion of a molecule. A number of investigations have been performed to understand the interplay between tetrel bonds and tetrel bonds or other types of noncovalent interactions [38,39,40,41,42,43,44,45,46,47,48]. The electron-rich species, such as lone pairs and π-systems, can be served as electron donors in TB interactions. The singlet carbenes can be expected to act as electron donors in TB interactions due to the existence of a lone-pair electron on the carbene C atom [49,50].
The simplest carbene is methylene (CH2), and CH2 is too reactive to be isolated. The heavy-atom analogues of methylene, i.e., silylene (SiH2), germylene (GeH2), stannylene (SnH2), and plumbylene (PbH2), are the so-called metallylenes [51]. Figure 1 gives the ground-state structures of CH2 and TH2 (T = Si, Ge, Sn, Pb), and CH2 has a triplet ground state. Unlike CH2, the ground state is a singlet state for TH2. The singlet TH2 possesses two binding sites, namely, the lone pair electrons and the vacant p-orbital on the T atom. The lone pair can act as an electron donor (Lewis base), and the vacant p-orbital can serve as an electron acceptor (Lewis acid). Like CH2, TH2 is difficult to be isolated due to its especially high reactivity with other molecules [52,53,54,55,56,57,58,59,60,61,62,63,64]. This high reactivity is ascribed to the vacant p-orbital of TH2, and metallylenes serve as Lewis acids in these reactions. On the other hand, the lone pair of TH2 is generally expected to be relatively inert because the lone pair of TH2 exhibits higher s-character compared with CH2 [51]. A theoretical study of the possible dual binding behavior of metallylenes in TB interactions is necessary. First, the theoretical studies of TB interactions in which metallylenes act as Lewis bases are absent. Second, the theoretical studies of TB interactions in which metallylenes act as Lewis acids are sparse [65,66,67,68], and systematic studies involving all four metallylenes are still absent. Finally, it is informative to explore how the binding strength of TB interactions changes when the tetrel atoms become heavier. A comprehensive study of TB interactions involving metallylenes should be interesting and can be expected to provide some new insights into TB interactions.
In this study, we investigate the possible dual-binding behavior of metallylenes in TB interactions. We select T’H3F (T’ = Si, Ge, Sn, Pb) as electron acceptors to form the TB complexes with TH2 (T = Si, Ge, Sn, Pb). On the other hand, we select N2, HCN, CO, and C6H6 as electron donors to form the TB complexes with TH2. The molecular electrostatic potential (MEP) surface is useful for searching the approximate binding sites for intermolecular interactions. We first examine the MEP maps of the monomers to locate the possible binding sites for TB interactions, and then we discuss the geometries and binding strength of the TB complexes.

2. Results and Discussion

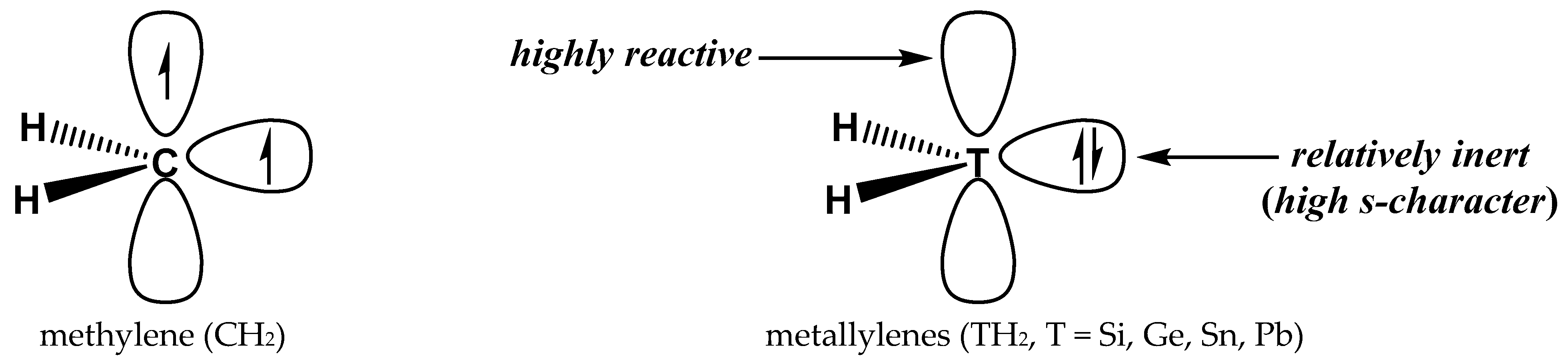
2.1. Geometries and MEP Surfaces of Monomers

The optimized geometries of TH2 with the percentage of s-character of the corresponding lone pairs based on the Natural bond orbital (NBO) analysis are displayed in Figure 2. The values of H-T-H angles in metallylenes range from 90.2° to 92.1°, which are very close to 90° and are obviously smaller than that (101.6°) of H-C-H angle in singlet methylene. Additionally, the percentage of s-character of the lone pairs in metallylenes ranges from 74.2% to 85.1%, which is much larger than that in methylene (56.2%). These differences between metallylenes and methylene indicate that the heavier tetrel atoms, in contrast with the carbon atom, exhibit a weak ability to form hybrid orbitals and prefer to keep the ns2np2 valence electron configurations in metallylenes. It can also be observed that the s-character values increase with the increase of the T atomic number, suggesting that the lone pairs of metallylenes become more inert when the tetrel atoms become heavier. In other words, the electron-donating ability of TH2 should go in the order SiH2 > GeH2 > SnH2 > PbH2.
The MEP surfaces of TH2 are illustrated in Figure 3, and the values of positive maxima (VS,max) and negative minima (VS,min) are also labeled. It can be observed that there exist two possible binding areas around T atoms, one of which is the π-hole area with a positive surface potential, and the other is the lone-pair (LP) area with a negative surface potential. The VS,max values in different TH2 molecules are very close to each other, ranging from 239.5 to 253.3 kJ/mol. Unlike VS,max values, the VS,min values exhibit obvious differences, ranging from −15.9 to −64.4 kJ/mol. It should be noted that the absolute values of VS,max are much larger than those of VS,min, which suggests that the electron-accepting ability of TH2 are much stronger than their electron-donating ability. The VS,min values of TH2 go in the order SiH2 > GeH2 > SnH2 > PbH2, implying that the electron-donating ability of TH2 goes in the same order, which is consistent with the previous conclusion based on the s-character values of lone pairs. A similar phenomenon was observed for the N-heterocyclic carbene and its heavy-atom analogues [69].
Two types of TB complexes can be formed for metallylenes due to their ambiphilic character, which we refer to as type-A and type-B for convenience. Metallylenes act as Lewis bases in type-A complexes, and they act as Lewis acids in type-B ones. T’H3F possess σ-holes and can act as Lewis acids in TB interactions, which can be expected to form the type-A TB complexes with TH2. Figure 3 gives the MEP surfaces of T’H3F, and their VS,max values go in the order PbH3F ≈ SnH3F > GeH3F > SiH3F. We select N2, HCN, CO, and C6H6 as Lewis bases to form the type-B TB complexes with TH2, and their MEP surfaces are illustrated in Figure 4. N2, HCN, and CO possess the lone pairs, and C6H6 possesses the π-system, which can be served as electron donors in TB interactions. It can be observed that the VS,min value (−131.7 kJ/mol) of HCN is much larger than that (−34.3 kJ/mol) of N2. Unlike N2, CO is a heteronuclear diatomic molecule and possesses two negative areas, one of which is around the C atom with a VS,min value of −57.3 kJ/mol, and the other is around the O atom with a VS,min value of −18.0 kJ/mol. The negative area of C6H6 is parallel to the benzene ring with a VS,min value of −68.1 kJ/mol.

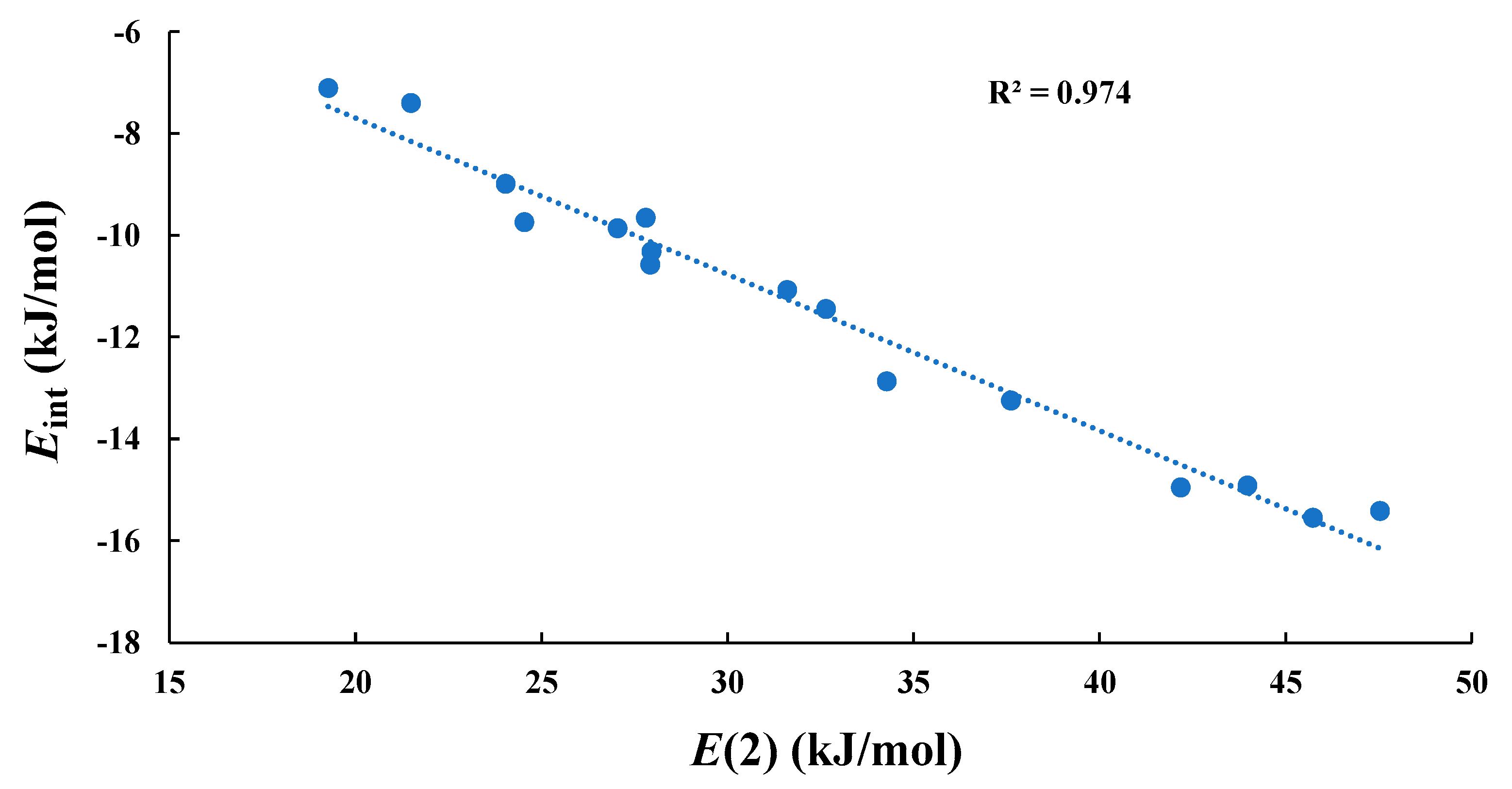
2.2. Type-A (σ-Hole Tetrel Bond) Complexes: TH2 Act as Lewis Bases

The type-A complexes are formed between TH2 and T’H3F, and the corresponding intermolecular interactions exist between two tetrel atoms, which are the σ-hole tetrel bonds. The geometries of the type-A complexes (A1–A16) optimized at the MP2/aug-cc-pVDZ level with the binding distances are displayed in Figure 5, and the corresponding Wiberg bond index (WBI) based on the NBO analysis are also labeled. Our previous studies indicate that the MP2/aug-cc-pVDZ level is more reasonable than MP2/aug-cc-pVTZ level for exploring the intermolecular interactions involving the heavy tetrel atoms. As a comparison, the geometries of these complexes were reoptimized at the MP2/aug-cc-pVTZ level, and the binding distances at the two levels are collected in Table 1. Additionally, the interaction energies (Eint) of these complexes at the four different computational levels are also collected in Table 1. These four levels are referred to as L1 (MP2/aug-cc-pVDZ), L2 (CCSD (T)/aug-cc-pVTZ//MP2/aug-cc-pVDZ), L3 (MP2/aug-cc-pVTZ), and L4 (CCSD (T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ), respectively.
It can be observed from Table 1 that the binding distances of all the sixteen type-A complexes at the L1 level are longer than those at the L3 level, which means that the complexes at the L3 level are overbound compared with the L1 level. It can also be found that the interaction energies at the L1 level are smaller than the corresponding values at the L2 level for all the type-A complexes, which indicates the L1 level underestimates the interaction energies compared with the L2 level. On the other hand, the L3 level overestimates the interaction energies compared with the L4 level. Furthermore, the interaction energies at the L2 level are larger than those at the L4 level in most cases, which suggests that the geometries optimized at the L1 level are more stable than those at the L3 level. The optimized geometries at the L1 level and the Eint values at the L2 level are employed in the following discussion.
Our preceding discussion indicates that the lone pairs of TH2 are relatively inert due to their high s-character, and the electron-donating ability of TH2 is expected to be weak. As expected, the type-A complexes indeed exhibit relatively weak binding strength with Eint values ranging from −7.11 to −15.55 kJ/mol. The type-A complexes possess relatively long T···T’ binding distances ranging from 3.618 to 3.910 Å and relatively small WBI values ranging from 0.050 to 0.104, suggesting that the tetrel bonds in TH2···T’H3F systems should be the noncovalent interactions, which is consistent with the Atoms in molecules (AIM) analysis as discussed below. The F-T’···T binding angles are linear for all the type-A complexes, ranging from 179° to 180°. For a given T’H3F, the Eint values of the type-A complexes go in the order SiH2 > GeH2 > SnH2 > PbH2. For example, the Eint values of the complexes A4, A8, A12, and A16 are −15.42, −14.92, −13.25, and −9.86 kJ/mol, respectively. This order is in agreement with the LP VS,min values of TH2, as shown in Figure 3. On the other hand, for a given TH2, the Eint values of the type-A complexes go in the order PbH3F ≈ SnH3F > GeH3F > SiH3F. For example, the Eint values of the complexes A5, A6, A7, and A8 are −10.32, −11.08, −14.96, and −14.92 kJ/mol, respectively. This order is in agreement with the σ-hole VS,max values of T’H3F, as shown in Figure 3.
The NBO and AIM analysis results of the type-A complexes are listed in Table 2. NBO analysis shows that the dominant orbital interactions for the type-A complexes are LP (T)→σ* (T’-F), with the second-order perturbation stabilization energy E(2) values ranging from 19.27 to 47.53 kJ/mol. In fact, there exists a linear relationship between the Eint and E(2) values, with R2 = 0.974, as shown in Figure 6. In this study, the value of charge transfer (qCT) is the sum of the natural atomic charge over the TH2 molecule in the complexes. A positive qCT represents that the direction of charge transfer is from TH2 to another molecule, and a negative qCT represents the reverse direction. The qCT values are positive for all the type-A complexes, indicating that TH2 act as Lewis bases in type-A complexes. AIM analysis indicates that there exist the intermolecular T···T’ bond critical points (BCP) in all the type-A complexes, and the electron density (ρ), Laplacian (∇2ρ), and energy density (H) at the BCP are listed in Table 2. The ρ values are smaller than 0.01 a.u. for all the type-A complexes. It can also be found that both ∇2ρ and H are positive for all the type-A complexes, suggesting that the tetrel bonds in type-A complexes are the purely closed-shell (noncovalent) interactions. The local kinetic energy density (G) and the local potential energy density (V) also might be used to analyze the electronic behavior at the intermolecular BCP. The values of G and V are listed in Table 2. The previous study indicates that the G and |V| values are increased with an increase of the stabilization energy (the absolute value of interaction energy) for the halogen-bonded complexes, implying that G and V might be considered as a measure of the strength of the intermolecular interaction [70]. Similar relations can also be found for most type-A complexes. For instance, there exist linear relationships between the |Eint| and G or |V| values for the SiH2···T’H3F system, as shown in Figure S1.
The symmetry-adapted perturbation theory (SAPT) is a perturbation theory aimed specifically at calculating the interaction energy between two molecules. The result is obtained as a sum of separate corrections accounting for the electrostatic, induction, dispersion, and exchange contributions to interaction energy, so the SAPT decomposition facilitates the understanding and physical interpretation of results. Electrostatic energy arises from the Coulomb interaction between charge densities of isolated molecules. Induction energy is the energetic effect of mutual polarization between the two molecules. Dispersion energy is a consequence of intermolecular electron correlation, usually explained in terms of correlated fluctuations of electron density on both molecules. Exchange energy is a short-range repulsive effect that is a consequence of the Pauli exclusion principle. The Energy decomposition analysis (EDA) results of the type-A complexes are listed in Table 3, and the graphical changing trends of the contribution of the electrostatic, induction, and dispersion energy terms with the increase of the T atomic number are illustrated in Figure 7. The total interaction energy (Etot) values in Table 3 are similar to the Eint values at the L2 level in Table 1 for most complexes, suggesting that the EDA results are reasonable for the systems in this study. It can be observed that the contribution values of the three energy terms go in the order of electrostatic > dispersion > induction for all the type-A complexes. The contribution of the electrostatic term exhibits a decreasing trend, and that of the dispersion term exhibits an increasing trend with the increase of the T atomic number. Additionally, the contribution of the induction term is basically unchanged with the increase of the T atomic number.

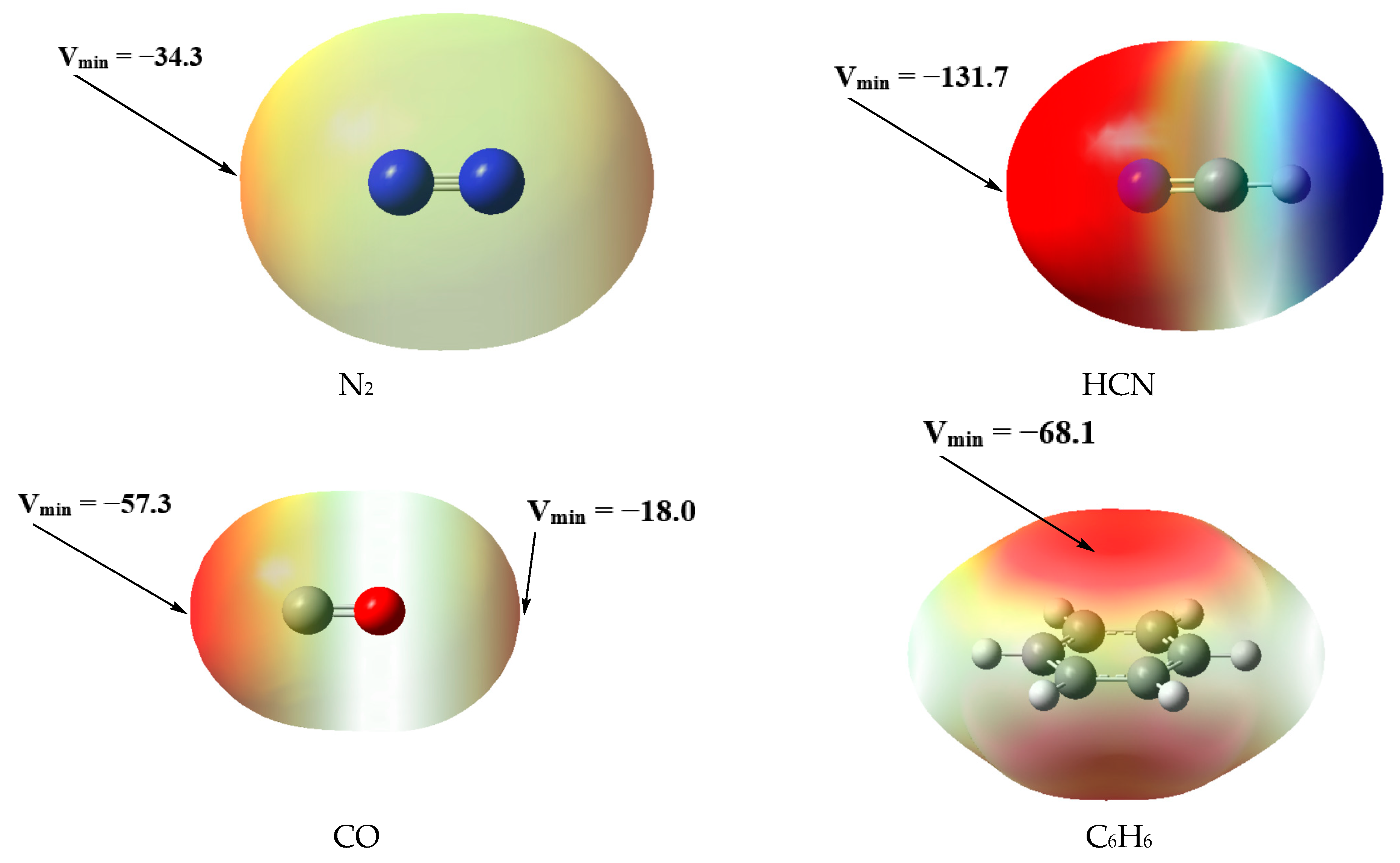
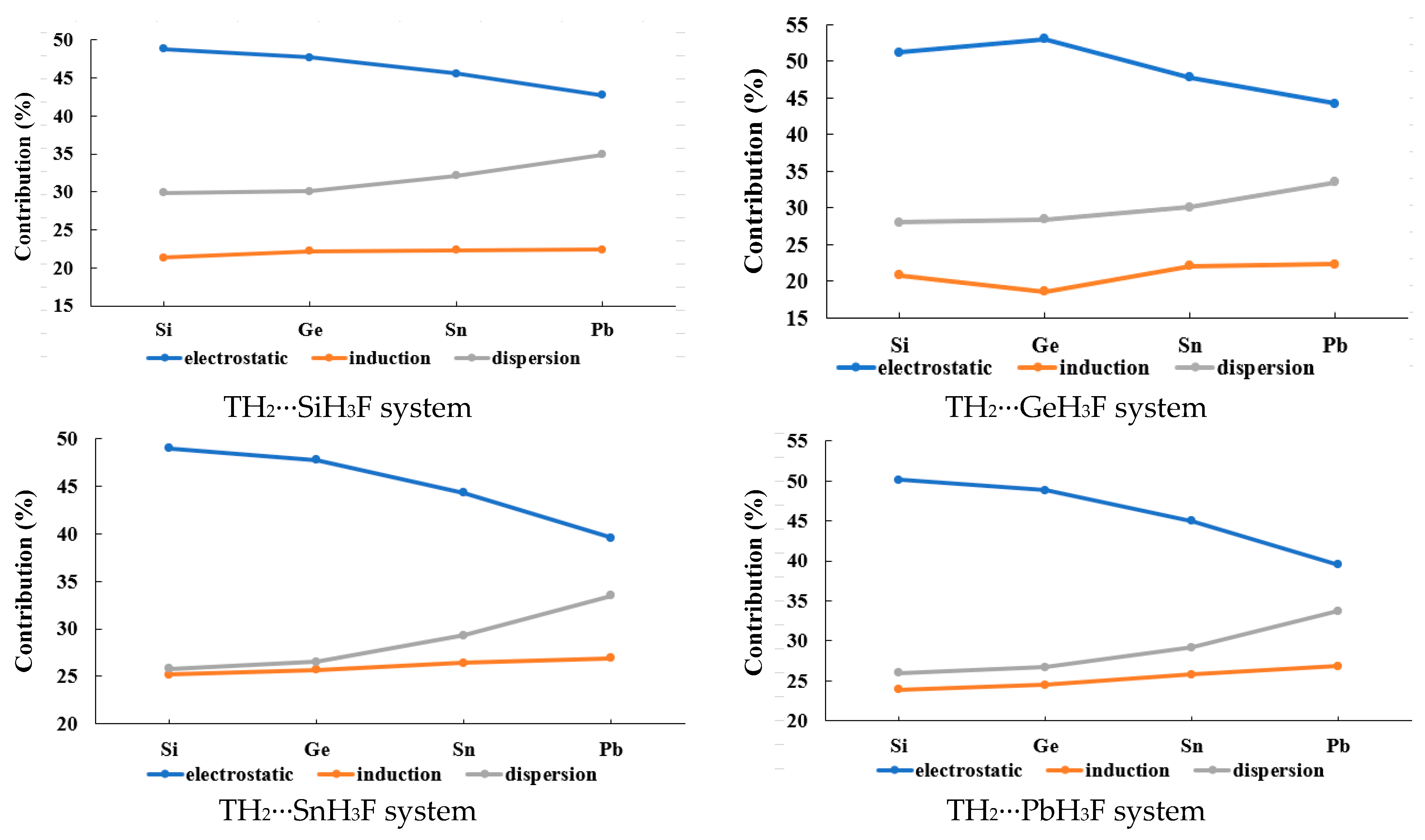
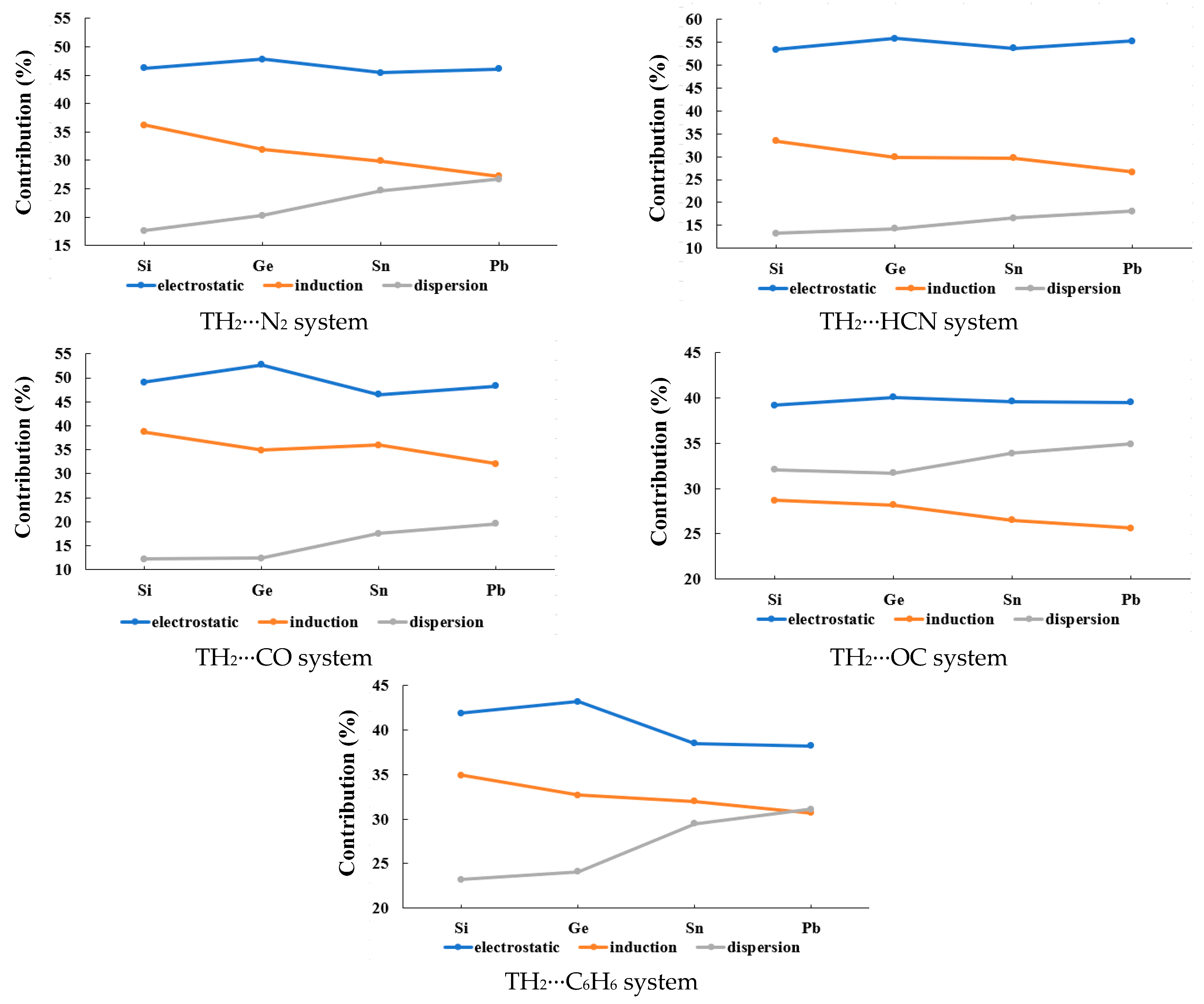
2.3. Type-B (π-Hole Tetrel Bond) Complexes: TH2 Act as Lewis Acids

The metallylenes are the highly reactive Lewis acids and can interact with various Lewis bases. In this section, we select N2, HCN, CO, and C6H6 as Lewis bases to interact with TH2 to form the type-B complexes, which are the π-hole TB complexes. The binding distances and interaction energies of all the twenty type-B complexes (B1–B20) at different levels are collected in Table 4. Like type-A complexes, the binding distances of the type-B complexes at the L1 level are longer than those at the L3 level. It can also be found that the interaction energies of the type-B complexes at the L1 level are similar to those at the L2 level in most cases, but there exist relatively large differences between the L3 and L4 levels. The optimized geometries at the L1 level and the Eint values at the L2 level are employed in the following discussion.
The optimized geometries of the type-B complexes (B1–B8) involving TH2 with N2 and HCN are shown in Figure 8. The formation of the complex SiH2···N2 (B1) was confirmed by the experimental study [61]. It should be noted that N2 is a rather weak Lewis base, and therefore the formation of B1 reflects the high reactivity of SiH2 as a Lewis acid. The T···N binding distances range from 2.175 to 2.736 Å for the TH2···N2 complexes (B1–B4), with the N-N···T binding angles ranging from 171.3° to 179.5°. The complexes B1–B4 possess larger Eint values ranging from −14.59 to −26.08 kJ/mol, with larger WBI values ranging from 0.104 to 0.289, compared with the type-A complexes. Like N2, HCN also uses the lone pair of the N atom as an electron-donor, but HCN is a stronger Lewis base compared with N2. HCN can form the TB complexes with various molecules. The C-N···T binding angles of the TH2···HCN complexes (B5–B8) range from 170.4° to 179.7°, which are similar to those of B1–B4, but B5–B8 possess shorter T···N binding distances ranging from 2.032 to 2.565 Å compared with B1–B4. The Eint values of B5–B8 range from −40.13 to −71.77 kJ/mol, which are nearly three times as large as those of B1–B4, and this difference in Eint values is in agreement with the VS,min values of N2 and HCN, as shown in Figure 4. It can also be found that the WBI values of B5–B8 are larger than the corresponding values of B1–B4. The Eint values of the complexes go in the order SiH2 > GeH2 > SnH2 > PbH2 for both the TH2···N2 and TH2···HCN systems.
The optimized geometries of the type-B complexes (B9–B16) involving TH2 with CO are shown in Figure 9, and the formation of the complex between SiH2 and CO was confirmed by the experimental study [61]. Unlike N2, CO is a heteronuclear diatomic molecule and exhibits two binding modes in the type-B complexes, one of which is TH2···CO and the other is TH2···OC. The fact that CO exhibits two binding modes and that complexes bound on the oxygen side are weaker has been previously reported [71]. The O-C···T binding angles of the TH2···CO complexes (B9–B12) range from 168.7° to 177.6°, which are similar to the C-O···T binding angles (174.8° to 179.4°) of the TH2···OC complexes (B13–B16), but B9–B12 possess obviously shorter T···C binding distances ranging from 1.921 to 2.622 Å compared with the T···O binding distances (2.649 to 2.883 Å) of B13–B16. The WBI values of B9–B12 range from 0.294 to 0.928, which are also much larger than those (0.038 to 0.053) of B13–B16. As expected, the TH2···CO complexes exhibit a stronger binding strength than the TH2···OC complexes, which is in agreement with the VS,min values around C and O atoms of CO, as shown in Figure 4. The Eint value (−98.44 kJ/mol) of the complex SiH2···CO (9) is ten times as large as that (−9.45 kJ/mol) of the complex SiH2···OC (13), and 9 also possesses a rather large WBI value of 0.928, suggesting that 9 has a partially covalent character, which is in agreement with the AIM analysis as discussed below. Considering that the VS,min value (−57.3 kJ/mol) around the C atom of CO is not large, it is somewhat surprising that 9 possesses such a high Eint value. The TH2···CO complexes have a broad range of Eint values ranging from −32.10 to −98.44 kJ/mol, and in contrast, the TH2···OC complexes have a very narrow range of Eint values ranging from −9.45 to −10.07 kJ/mol. The TH2···OC complexes possess a weaker binding strength than the other type-B complexes and exhibit a different binding behavior, as discussed below. We refer to the TH2···OC complexes as the type-B2 complexes and refer to the other type-B complexes as the type-B1 complexes in the following discussions. Like the TH2···N2 and TH2···HCN systems, the Eint values of the TH2···CO system go in the order SiH2 > GeH2 > SnH2 > PbH2.
The optimized geometries of the type-B complexes (B17–B20) involving TH2 with C6H6 are shown in Figure 10. Unlike the other three Lewis bases for which the lone pairs are used as the electron-donors, C6H6 uses the π-system as an electron-donor to form the type-B complexes with TH2. As expected, TH2 molecules are parallel to the benzene ring in these π-hole TB complexes. B17–B20 possess the T···C binding distances ranging from 2.452 to 2.799 Å, with the WBI values ranging from 0.090 to 0.184. The Eint values of B17–B20 range from −32.35 to −43.64 kJ/mol, which are larger than those of the TH2···N2 system but smaller than those of the TH2···HCN system. Like the other type-B1 complexes, the Eint values of the complexes go in the order SiH2 > GeH2 > SnH2 > PbH2 for the TH2···C6H6 system.
As mentioned before, the relative binding strength of the type-A complexes can be clarified by the MEP maps of the corresponding monomers in a reasonable way, but this explanation is not applicable to the type-B1 complexes. Considering that TH2 have a narrow range of VS,max values ranging from 239.5 to 253.3 kJ/mol, one may expect that for a given Lewis base, the Eint values of the type-B complexes should be very close to each other. However, for a given Lewis base, the type-B1 complexes have a relatively broad range of Eint values, and the Eint values go in the order SiH2 > GeH2 > SnH2 > PbH2. Additionally, the Eint values of the type-B1 complexes go in the order CO > HCN > C6H6 > N2 for SiH2 and GeH2; HCN > CO > C6H6 > N2 for SnH2; and HCN > C6H6 ≈ CO > N2 for PbH2. Unlike the type-B1 complexes, the Eint values of the type-B2 complexes are very close to each other, which is consistent with the narrow range of VS,max values of TH2.
The NBO and AIM analysis results of the type-B complexes are listed in Table 5. NBO analysis shows that the dominant orbital interactions for the type-B complexes are LP (B)→LP * (T) (B = N, C, and O) and π (C = C)→LP * (T) with a very broad range of E(2) values ranging from 49.45 to 1488.16 kJ/mol. The E(2) values of the type-B1 complexes are larger than those of the type-B2 and type-A complexes. The qCT values are negative for all the type-B complexes, indicating that TH2 act as Lewis acids in type-B complexes. AIM analysis indicates that there exist the intermolecular T···B (B = N, C, and O) bond critical points in the type-B complexes. Like E(2) values, the ρ values of the type-B1 complexes are larger than those of the type-B2 and type-A complexes. It can also be found that ∇2ρ are positive and H are negative for most type-B1 complexes, suggesting that these complexes have a partially covalent character. There exists a linear relationship between the |Eint| and G values and an approximately linear relationship between the |Eint| and |V| values for the TH2···CO system, as shown in Figure S2.
The EDA results of the type-B complexes are listed in Table 6, and the graphical illustration is shown in Figure 11. The contribution of the electrostatic term exhibits a fluctuating trend (first increase and then decrease) with the increase of the T atomic number. On the other hand, the contribution of the induction term exhibits a decreasing trend, and that of the dispersion term exhibits an increasing trend with the increase of the T atomic number. It can also be observed that the contribution values of the three energy terms go in the order electrostatic > induction > dispersion for the type-B1 complexes, and this order is electrostatic > dispersion > induction for the type-B2 complexes.

3. Computational Methods

The geometries of all the monomers and complexes investigated in this study were fully optimized at the MP2 level of theory using the Gaussian 09 programs [72]. The aug-cc-pVDZ-PP basis set, which uses pseudopotentials to describe the inner core orbitals [73], was applied to Sn and Pb atoms, whereas aug-cc-pVDZ was used for else atoms. The vibrational frequencies were calculated for all the optimized geometries at the same level. As a comparison, the geometries of all the complexes were reoptimized at the MP2/aug-cc-pVTZ (aug-cc-pVTZ-PP for Sn and Pb atoms) level. Single-point energy calculations were performed at the CCSD (T)/aug-cc-pVTZ level to obtain more accurate energies. Interaction energy is defined as the difference between the energy of the complex and the sum of the monomers retaining their internal geometries as in the complex. Basis set superposition error (BSSE) correction was carried out following the counterpoise (CP) method [74]. AIM analysis [75] and MEP calculation were carried out using the Multiwfn program [76], and the MEP maps were generated on a 0.001 a.u. isodensity surface and plotted using GaussView software [77]. NBO analysis [78] was performed via the procedures contained within Gaussian 09. Energy decomposition analysis (EDA) based on symmetry-adapted perturbation theory (SAPT) [79] was performed at the sapt2+dmp2/aug-cc-pVDZ level using the Psi4 package [80].

4. Conclusions

In this study, the dual binding behavior of the metallylenes TH2 with some selected Lewis acids and bases has been investigated. Two types (type-A and type-B) of TB complexes can be formed for TH2 due to their ambiphilic character. TH2 act as Lewis bases in type-A complexes, and they act as Lewis acids in type-B ones. T’H3F possess σ-holes and can act as Lewis acids to form the type-A complexes with TH2, which are the σ-hole TB complexes. N2, HCN, CO, and C6H6 possess the lone pair or π-system and can act as Lewis bases to form the type-B complexes with TH2, which are the π-hole TB complexes. CO exhibits two binding modes in the type-B complexes, one of which is TH2···CO and the other is TH2···OC. The TH2···OC complexes possess a weaker binding strength than the other type-B complexes. The TH2···OC complexes are referred to as the type-B2 complexes, and the other type-B complexes are referred to as the type-B1 complexes. The type-A complexes exhibit a relatively weak binding strength with Eint values ranging from −7.11 to −15.55 kJ/mol. The type-B complexes have a broad range of Eint values ranging from −9.45 to −98.44 kJ/mol, and the Eint values of the type-B1 complexes are larger than those of the type-B2 and type-A complexes. For a given T’H3F, the Eint values of the type-A complexes go in the order SiH2 > GeH2 > SnH2 > PbH2, and for a given TH2, the Eint values of the type-A complexes go in the order PbH3F ≈ SnH3F > GeH3F > SiH3F, which can be clarified by the MEP maps of TH2 and T’H3F in a reasonable way. For a given Lewis base, the type-B1 complexes have a relatively broad range of Eint values, and the Eint values go in the order SiH2 > GeH2 > SnH2 > PbH2. Additionally, the Eint values of the type-B1 complexes go in the order CO > HCN > C6H6 > N2 for SiH2 and GeH2; HCN > CO > C6H6 > N2 for SnH2; and HCN > C6H6 ≈ CO > N2 for PbH2. Unlike the type-B1 complexes, the Eint values of the type-B2 complexes are very close to each other, which is consistent with the narrow range of VS,max values of TH2. The AIM analysis suggests that the tetrel bonds in type-A complexes are the purely closed-shell interactions, and those in most type-B1 complexes have a partially covalent character. The EDA results indicate that the contribution values of the three energy terms go in the order of electrostatic > dispersion > induction for the type-A and type-B2 complexes, and this order is electrostatic > induction > dispersion for the type-B1 complexes.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28062577/s1. Figure S1. Correlation between the |Eint| and G or |V| values for the SiH2···T’H3F system, and Figure S2. Correlation between the |Eint| and G or |V| values for the TH2···CO system.

Author Contributions

Conceptualization, Y.C.; software, L.Y.; validation, Y.C; formal analysis, L.Y.; investigation, Y.C.; resources, F.W.; data curation, L.Y.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C.; visualization, L.Y.; supervision, F.W.; project administration, L.Y.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Scientific Research Funds from the Educational Department of Yunnan Province, China, grant number [2020J0634].

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wheeler, S.E.; Seguin, T.J.; Guan, Y.; Doney, A.C. Noncovalent interactions in organocatalysis and the prospect of computational atalyst design. Acc. Chem. Res. 2016, 49, 1061–1069. [Google Scholar] [CrossRef]
  2. Vallavoju, N.; Sivaguru, J. Supramolecular photocatalysis: Combining confinement and non-covalent interactions to control light initiated reactions. Chem. Soc. Rev. 2014, 43, 4084–4101. [Google Scholar] [CrossRef] [PubMed]
  3. Georgakilas, V.; Tiwari, J.N.; Kemp, K.C.; Perman, J.A.; Bourlinos, A.B.; Kim, K.S.; Zboril, R. Noncovalent functionalization of graphene and graphene oxide for energy materials, biosensing, catalytic, and biomedical applications. Chem. Rev. 2016, 116, 5464–5519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Scheiner, S. Hydrogen Bonding, A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
  5. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-bonding interaction: Rediscovered supramolecular force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef]
  6. Alkorta, I.; Rozas, I.; Elguero, J. Molecular complexes between silicon derivatives and electron-rich groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
  7. Chen, Y.S.; Yao, L.F.; Wang, F. Intermolecular Interactions Involving Heavy Alkenes H2Si=TH2 (T = C, Si, Ge, Sn, Pb) with H2O and HCl: Tetrel Bond and Hydrogen Bond. ACS Omega 2020, 5, 30210–30225. [Google Scholar] [CrossRef] [PubMed]
  8. Chen, Y.S.; Yao, L.F.; Wang, F. Intermolecular interactions between the heavy alkenes H2Si = TH2 (T = C, Si, Ge, Sn, Pb) and acetylene. J. Mol. Model. 2021, 27, 110. [Google Scholar] [CrossRef] [PubMed]
  9. Chen, Y.S.; Yao, L.F.; Wang, F. Intermolecular interactions between the heavy-atom analogues of acetylene T2H2 (T = Si, Ge, Sn, Pb) and HCN. J. Mol. Model. 2023, 29, 52. [Google Scholar] [CrossRef]
  10. Scheiner, S. Origins and Properties of the Tetrel Bond. Phys. Chem. Chem. Phys. 2021, 23, 5702–5717. [Google Scholar] [CrossRef]
  11. Scheiner, S. The ditetrel bond noncovalent bond between neutral tetrel atoms. Phys. Chem. Chem. Phys. 2020, 22, 16606–16614. [Google Scholar] [CrossRef]
  12. Thomas, S.P.; Pavan, M.S.; Row, T.N.G. Experimental evidence for ‘carbon bonding’ in the solid state from charge density analysis. Chem. Commun. 2014, 50, 49–51. [Google Scholar] [CrossRef] [PubMed]
  13. Mani, D.; Arunan, E. The X-C···π (X = F, Cl, Br, CN) carbon bond. J. Phys. Chem. A 2014, 118, 10081–10089. [Google Scholar] [CrossRef] [PubMed]
  14. Southern, S.A.; Bryce, D.L. NMR investigations of noncovalent carbon tetrel bonds. Computational assessment and initial experimental observation. J. Phys. Chem. A 2015, 119, 11891–11899. [Google Scholar] [CrossRef] [PubMed]
  15. Scheiner, S. Comparison of CH···O, SH···O, chalcogen, and tetrel bonds formed by neutral and cationic sulfur-containing compounds. J. Phys. Chem. A 2015, 119, 9189–9199. [Google Scholar] [CrossRef] [Green Version]
  16. Azofra, L.M.; Scheiner, S. Tetrel, chalcogen, and CH···O hydrogen bonds in complexes pairing carbonyl-containing molecules with 1, 2, and 3 molecules of CO2. J. Chem. Phys. 2015, 142, 034307. [Google Scholar] [CrossRef] [Green Version]
  17. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel bonding interactions. Chem. Rec. 2016, 16, 473–487. [Google Scholar] [CrossRef]
  18. Bauzá, A.; Frontera, A.; Mooibroek, T.J. 1,1,2,2-Tetracyanocyclopropane (TCCP) as supramolecular synthon. Phys. Chem. Chem. Phys. 2016, 18, 1693–1698. [Google Scholar] [CrossRef] [Green Version]
  19. Liu, M.X.; Li, Q.Z.; Cheng, J.B.; Li, W.Z.; Li, H.B. Tetrel bond of pseudohalide anions with XH3F (X = C, Si, Ge, and Sn) and its role in SN2 reaction. J. Chem. Phys. 2016, 145, 224310. [Google Scholar] [CrossRef]
  20. Liu, M.X.; Li, Q.Z.; Scheiner, S. Comparison of tetrel bonds in neutral and protonated complexes of pyridineTF3 and furanTF3 (T = C, Si, and Ge) with NH3. Phys. Chem. Chem. Phys. 2017, 19, 5550–5559. [Google Scholar] [CrossRef] [Green Version]
  21. Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef]
  22. Scheiner, S. Comparison of various means of evaluating molecular electrostatic potentials for noncovalent interactions. J. Comput. Chem. 2018, 39, 500–510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Implications of monomer deformation for tetrel and pnicogen bonds. Phys. Chem. Chem. Phys. 2018, 20, 8832–8841. [Google Scholar] [CrossRef] [Green Version]
  24. Remyaa, K.; Suresh, C.H. Intermolecular carbon–carbon, nitrogen–nitrogen and oxygen–oxygen non-covalent bonding in dipolar molecules. Phys. Chem. Chem. Phys. 2015, 17, 18380–18392. [Google Scholar] [CrossRef]
  25. Varadwaj, P.R.; Varadwaja, A.; Jin, B.Y. Significant evidence of C···O and C···C long-range contacts in several heterodimeric complexes of CO with CH3–X, should one refer to them as carbon and dicarbon bonds! Phys. Chem. Chem. Phys. 2014, 16, 17238–17252. [Google Scholar] [CrossRef] [PubMed]
  26. Li, Q.Z.; Zhuo, H.Y.; Li, H.B.; Liu, Z.B.; Li, W.Z.; Cheng, J.B. Tetrel-hydride interaction between XH3F (X = C, Si, Ge, Sn) and HM (M = Li, Na, BeH, MgH). J. Phys. Chem. A 2015, 119, 2217–2224. [Google Scholar] [CrossRef] [PubMed]
  27. Sethio, D.; Oliveira, V.; Kraka, E. Quantitative assessment of tetrel bonding utilizing vibrational spectroscopy. Molecules 2018, 23, 2763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Scheiner, S. Systematic Elucidation of Factors That Influence the Strength of Tetrel Bonds. J. Phys. Chem. A 2017, 121, 5561–5568. [Google Scholar] [CrossRef] [Green Version]
  29. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The sigma-hole. Proceedings of “Modeling interactions in biomolecules II”, Prague, 5–9 September 2005. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  30. Murray, J.S.; Lane, P.; Politzer, P. Expansion of the sigma-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef]
  31. Li, Q.Z.; Guo, X.; Yang, X.; Li, W.Z.; Cheng, J.B.; Li, H.B. A σ-hole interaction with radical species as electron donors: Does single-electron tetrel bonding exist? Phys. Chem. Chem. Phys. 2014, 16, 11617–11625. [Google Scholar] [CrossRef]
  32. McDowell, S.A.C.; Joseph, J.A. The effect of atomic ions on model σ-hole bonded complexes of AH3Y(A = C, Si, Ge; Y = F, Cl, Br). Phys. Chem. Chem. Phys. 2014, 16, 10854–10860. [Google Scholar] [CrossRef]
  33. Quiñonero, D. Sigma-hole carbon-bonding interactions in carbon–carbon double bonds: An unnoticed contact. Phys. Chem. Chem. Phys. 2017, 19, 15530–15540. [Google Scholar] [CrossRef] [PubMed]
  34. Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef]
  35. Wei, Y.X.; Li, Q.Z.; Scheiner, S. The π-tetrel bond and its influence on hydrogen bonding and proton transfer. ChemPhysChem 2018, 19, 736–743. [Google Scholar] [CrossRef] [PubMed]
  36. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Comparison between Tetrel Bonded Complexes Stabilized by σ and π Hole Interactions. Molecules 2018, 23, 1416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Li, W.; Zeng, Y.; Li, X.; Sun, Z.; Meng, L. Insight into the pseudo π-hole interactions in the M3H6(NCF)n (M = C, Si, Ge, Sn, Pb; n = 1, 2, 3) complexes. Phys. Chem. Chem. Phys. 2016, 18, 24672–24680. [Google Scholar] [CrossRef] [PubMed]
  38. Yourdkhani, S.; Korona, T.; Hadipour, N.L. Interplay between tetrel and triel bonds in RC6H4CN···MF3CN···BX3 complexes: A combined symmetry-adapted perturbation theory, Møller-Plesset, and quantum theory of atoms-in-molecules study. J. Comput. Chem. 2015, 36, 2412–2428. [Google Scholar] [CrossRef] [PubMed]
  39. Marín-Luna, M.; Alkorta, I.; Elguero, J. Cooperativity in tetrel bonds. J. Phys. Chem. A 2016, 120, 648–656. [Google Scholar] [CrossRef] [Green Version]
  40. Esrafili, M.D.; Mohammadian-Sabet, F. Cooperativity of tetrel bonds tuned by substituent effects. Mol. Phys. 2016, 114, 1528–1538. [Google Scholar] [CrossRef]
  41. Rezaei, Z.; Solimannejad, M.; Esrafili, M.D. Interplay between hydrogen bond and single-electron tetrel bond: H3C···COX2···HY and H3C···CSX2···HY (X = F, Cl; Y = CN, NC) complexes as a working model. Comput. Theor. Chem. 2015, 1074, 101–106. [Google Scholar] [CrossRef]
  42. Xu, H.L.; Cheng, J.B.; Yang, X.; Liu, Z.B.; Xiao, B.; Li, Q.Z. Interplay between the σ-tetrel bond and σ-halogen bond in PhSiF3 ···4-iodopyridine···N-base. RSC Adv. 2017, 7, 21713–21720. [Google Scholar] [CrossRef] [Green Version]
  43. Chen, Y.S.; Yao, L.F.; Wang, F. Synergistic and antagonistic interplay between tetrel bond and pnicogen bond in complexes involving ring compounds. J. Mol. Model. 2019, 25, 351. [Google Scholar] [CrossRef] [PubMed]
  44. Liu, M.X.; Yang, L.; Li, Q.Z.; Li, W.Z.; Cheng, J.B.; Xiao, B.; Yu, X.F. Modulating the strength of tetrel bonding through beryllium bonding. J. Mol. Model. 2016, 22, 192. [Google Scholar] [CrossRef]
  45. McDowell, S.A.C. Sigma-hole cooperativity in anionic [FX···CH3···YF]− (X, Y = Cl, Br) complexes. Chem. Phys. Lett. 2014, 598, 1–4. [Google Scholar] [CrossRef]
  46. Esrafili, M.D.; Mohammadirad, N.; Solimannejad, M. Tetrel bond cooperativity in open-chain (CH3CN)n and (CH3NC)n clusters (n = 2–7): An ab initio study. Chem. Phys. Lett. 2015, 628, 16–20. [Google Scholar] [CrossRef]
  47. Solimannejad, M.; Orojloo, M.; Amani, S. Effect of cooperativity in lithium bonding on the strength of halogen bonding and tetrel bonding: (LiCN)n···ClYF3 and (LiCN)n···YF3Cl (Y = C, Si and n = 1-5) complexes as a working model. J. Mol. Model. 2015, 21, 183. [Google Scholar] [CrossRef] [PubMed]
  48. Scheiner, S. Relative Strengths of a Pnicogen and a Tetrel Bond and Their Mutual Effects upon One Another. J. Phys. Chem. A 2021, 125, 2631–2641. [Google Scholar] [CrossRef]
  49. Liu, M.X.; Li, Q.Z.; Li, W.Z.; Cheng, J.B. Carbene tetrel-bonded complexes. Struct. Chem. 2017, 28, 823–831. [Google Scholar] [CrossRef]
  50. Bene, J.E.D.; Alkorta, I.; Elguero, J. Carbon-Carbon Bonding between Nitrogen Heterocyclic Carbenes and CO2. J. Phys. Chem. A 2017, 121, 8136–8146. [Google Scholar] [CrossRef]
  51. Mizuhata, Y.; Sasamori, T.; Tokitoh, N. Stable Heavier Carbene Analogues. Chem. Rev. 2009, 109, 3479–3511. [Google Scholar] [CrossRef]
  52. Guo, Y.; Fikri, M.; Friedrichs, G.; Temps, F. An Extended Simultaneous Kinetics and Ringdown Model: Determination of the Rate Constant for the Reaction SiH2 + O2. Phys. Chem. Chem. Phys. 2003, 5, 4622–4630. [Google Scholar] [CrossRef]
  53. Becerra, R.; Goldberg, N.; Cannady, J.P.; Almond, M.J.; Ogden, J.S.; Walsh, R. Experimental and Theoretical Evidence for Homogeneous Catalysis in the Gas-Phase Reaction of SiH2 with H2O (and D2O): A Combined Kinetic and Quantum Chemical Study. J. Am. Chem. Soc. 2004, 126, 6816–6824. [Google Scholar] [CrossRef] [PubMed]
  54. Becerra, R.; Cannady, J.P.; Walsh, R. Time-Resolved GasPhase Kinetic and Quantum Chemical Studies of Reactions of Silylene with Chlorine-Containing Species. 1. HCl. J. Phys. Chem. A 2004, 108, 3987–3993. [Google Scholar] [CrossRef]
  55. Becerra, R.; Cannady, J.P.; Walsh, R. Reactions of Silylene with Unreactive Molecules. I: Carbon Dioxide; Gas-Phase Kinetic and Theoretical Studies. J. Phys. Chem. A 2002, 106, 4922–4927. [Google Scholar] [CrossRef]
  56. Becerra, R.; Cannady, J.P.; Walsh, R. The Gas-Phase Reaction of Silylene with Acetaldehyde. 2. Theoretical Calculations of Isotope Effects for SiH2 versus SiD2 Addition. J. Phys. Chem. A 2002, 106, 11558–11564. [Google Scholar] [CrossRef]
  57. Becerra, R.; Carpenter, I.W.; Gutsche, G.J.; King, K.D.; Lawrance, W.D.; Staker, W.S.; Walsh, R. The Gas-Phase Reaction of SiH2 with Dimethylether: Kinetic Evidence for Direct Formation of a Donor-Acceptor Adduct. Chem. Phys. Lett. 2001, 333, 83–90. [Google Scholar] [CrossRef]
  58. Friedrichs, G.; Fikri, M.; Guo, Y.; Temps, F. Time-Resolved Cavity Ringdown Measurements and Kinetic Modeling of the Pressure Dependences of the Recombination Reactions of SiH2 with the Alkenes C2H4, C3H6, and t-C4H8. J. Phys. Chem. A 2008, 112, 5636–5646. [Google Scholar] [CrossRef]
  59. Al-Rubaiey, N.; Becerra, R.; Walsh, R. A Gas-Phase Kinetic Study of the Silylene Addition Reaction SiH2 + C2D4 as a Function of Temperature and Pressure: Isotope Effects and Mechanistic Complexities. Phys. Chem. Chem. Phys. 2002, 4, 5072–5078. [Google Scholar] [CrossRef]
  60. Becerra, R.; Cannady, J.P.; Dormer, G.; Walsh, R. The Addition Reaction between Silylene and Ethyne: Further Isotope Studies, Pressure Dependence Studies, and Quantum Chemical Calculations. J. Phys. Chem. A 2008, 112, 8665–8677. [Google Scholar] [CrossRef]
  61. Maier, G.; Reisenauer, H.P.; Glatthaar, J.; Zetzmann, R. Complex of Silylene with Nitrogen: A Combined Matrix-Spectroscopic and Density Functional Theory Study. Chem.—Asian J. 2006, 1, 195–202. [Google Scholar] [CrossRef]
  62. Becerra, R.; Bowes, S.-J.; Ogden, J.S.; Cannady, J.P.; Almond, M.J.; Walsh, R. Time-Resolved Gas-Phase Kinetic and Quantum Chemical Studies of the Reaction of Silylene with Nitric Oxide. J. Phys. Chem. A 2005, 109, 1071–1080. [Google Scholar] [CrossRef] [PubMed]
  63. Becerra, R.; Carpenter, I.W.; Gordon, M.S.; Roskop, L.; Walsh, R. Gas Phase Kinetic and Quantum Chemical Studies of the Reactions of Silylene with the Methylsilanes. Absolute Rate Constants, Temperature Dependences, RRKM Modelling and Potential Energy Surfaces. Phys. Chem. Chem. Phys. 2007, 9, 2121–2129. [Google Scholar] [CrossRef] [PubMed]
  64. Becerra, R.; Boganov, S.E.; Egorov, M.P.; Faustov, V.I.; Promyslov, V.M.; Nefedov, O.M.; Walsh, R. An Investigation of the Prototype Germylene Addition Reaction, GeH2 + C2H4: Time-Resolved Gas-Phase Kinetic Studies and Quantum Chemical Calculations of the Reaction Energy Surface. Phys. Chem. Chem. Phys. 2002, 4, 5079–5087. [Google Scholar] [CrossRef]
  65. Bharatam, P.V.; Moudgil, R.; Kaur, D. Lewis Donor and Acceptor Interactions of Silylenes: A Theoretical Study. Organometallics 2002, 21, 3683–3690. [Google Scholar] [CrossRef]
  66. Matczak, P. Theoretical insight into the interaction between SnX2 (X=H, F, Cl, Br, I) and benzene. J. Mol. Model. 2016, 22, 208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  67. Grabowski, S.J. π-Hole Tetrel Bonds—Lewis Acid Properties of Metallylenes. Crystals 2022, 12, 112. [Google Scholar] [CrossRef]
  68. Bankiewicz, B.; Matczak, P. Controlling the preferred nitrogen site in 1,2,3-triazine to bind with stannylenes. Polyhedron 2022, 225, 116056. [Google Scholar] [CrossRef]
  69. Chen, Y.S.; Yao, L.F.; Wang, F. Hydrogen-bonding interactions involving the Imidazol-2-ylidene and its Heavy-atom analogues, Comput. Theor. Chem. 2023, 1220, 114020. [Google Scholar] [CrossRef]
  70. Buralli, G.J.; Petelski, A.N.; Peruchena, N.M.; Sosa, G.L.; Duarte, D.J.R. Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction. Molecules 2017, 22, 2034. [Google Scholar] [CrossRef] [Green Version]
  71. Blanco, F.; Alkorta, I.; Solimannejad, J.; Elguero, J. Theoretical Study of the 1:1 Complexes between Carbon Monoxide and Hypohalous Acids. J. Phys. Chem. A 2009, 113, 3237–3244. [Google Scholar] [CrossRef] [Green Version]
  72. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, UK, 2013. [Google Scholar]
  73. Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
  74. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  75. Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
  76. Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  77. Dennington, R.; Keith, T.; Millam, J.S. GaussView, Version 5; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
  78. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  79. Hohenstein, E.G.; Sherrill, C.D. Density fitting and Cholesky decomposition approximations in symmetry-adapted perturbation theory: Implementation and application to probe the nature of pi-pi interactions in linear acenes. J. Chem. Phys. 2010, 132, 184111–184120. [Google Scholar] [CrossRef] [Green Version]
  80. Turney, J.M.; Simmonett, A.C.; Parrish, R.M.; Hohenstein, E.G.; Evangelista, F.A.; Fermann, J.T.; Mintz, B.J.; Burns, L.A.; Wilke, J.J.; Abrams, M.L.; et al. PSI4: An open-source ab initio electronic structure program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556–565. [Google Scholar] [CrossRef]
Molecules 28 02577 g001 550
Figure 1. Ground-state structures of methylene and metallylenes.
Figure 1. Ground-state structures of methylene and metallylenes.
Molecules 28 02577 g001
Molecules 28 02577 g002 550
Figure 2. Optimized geometries of the metallylenes TH2 at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and the percentage of s-character of the lone pairs.
Figure 2. Optimized geometries of the metallylenes TH2 at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and the percentage of s-character of the lone pairs.
Molecules 28 02577 g002
Molecules 28 02577 g003 550
Figure 3. MEP surfaces of the monomers TH2 and T’H3F at the MP2/aug-cc-pVDZ level, VS,max, and VS,min in kJ/mol.
Figure 3. MEP surfaces of the monomers TH2 and T’H3F at the MP2/aug-cc-pVDZ level, VS,max, and VS,min in kJ/mol.
Molecules 28 02577 g003
Molecules 28 02577 g004 550
Figure 4. MEP surfaces of the selected Lewis bases at the MP2/aug-cc-pVDZ level, VS,min in kJ/mol.
Figure 4. MEP surfaces of the selected Lewis bases at the MP2/aug-cc-pVDZ level, VS,min in kJ/mol.
Molecules 28 02577 g004
Molecules 28 02577 g005 550
Figure 5. Optimized geometries of the type-A complexes at the MP2/aug-cc-pVDZ level, distances in Å, and WBI values (in parenthesis).
Figure 5. Optimized geometries of the type-A complexes at the MP2/aug-cc-pVDZ level, distances in Å, and WBI values (in parenthesis).
Molecules 28 02577 g005
Molecules 28 02577 g006 550
Figure 6. Correlation between the interaction energies (Eint) and E(2) for the type-A complexes.
Figure 6. Correlation between the interaction energies (Eint) and E(2) for the type-A complexes.
Molecules 28 02577 g006
Molecules 28 02577 g007 550
Figure 7. The changing trends of the contribution of the electrostatic, induction, and dispersion energy terms with the increase of the T atomic number for the type-A complexes.
Figure 7. The changing trends of the contribution of the electrostatic, induction, and dispersion energy terms with the increase of the T atomic number for the type-A complexes.
Molecules 28 02577 g007
Molecules 28 02577 g008 550
Figure 8. Optimized geometries of the type-B complexes involving N2 and HCN at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Figure 8. Optimized geometries of the type-B complexes involving N2 and HCN at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Molecules 28 02577 g008
Molecules 28 02577 g009 550
Figure 9. Optimized geometries of the type-B complexes involving CO at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Figure 9. Optimized geometries of the type-B complexes involving CO at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Molecules 28 02577 g009
Molecules 28 02577 g010 550
Figure 10. Optimized geometries of the type-B complexes involving C6H6 at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Figure 10. Optimized geometries of the type-B complexes involving C6H6 at the MP2/aug-cc-pVDZ level, distances in Å, angles in °, and WBI values (in parenthesis).
Molecules 28 02577 g010
Molecules 28 02577 g011 550
Figure 11. The changing trends of the contribution of the electrostatic, induction, and dispersion energy terms with the increase of the T atomic number for the type-B complexes.
Figure 11. The changing trends of the contribution of the electrostatic, induction, and dispersion energy terms with the increase of the T atomic number for the type-B complexes.
Molecules 28 02577 g011
Table
Table 1. Binding distance at MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ (in parentheses) levels (R, in Å) and interaction energy at various levels (Eint, in kJ/mol) for type-A complexes.
Table 1. Binding distance at MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ (in parentheses) levels (R, in Å) and interaction energy at various levels (Eint, in kJ/mol) for type-A complexes.
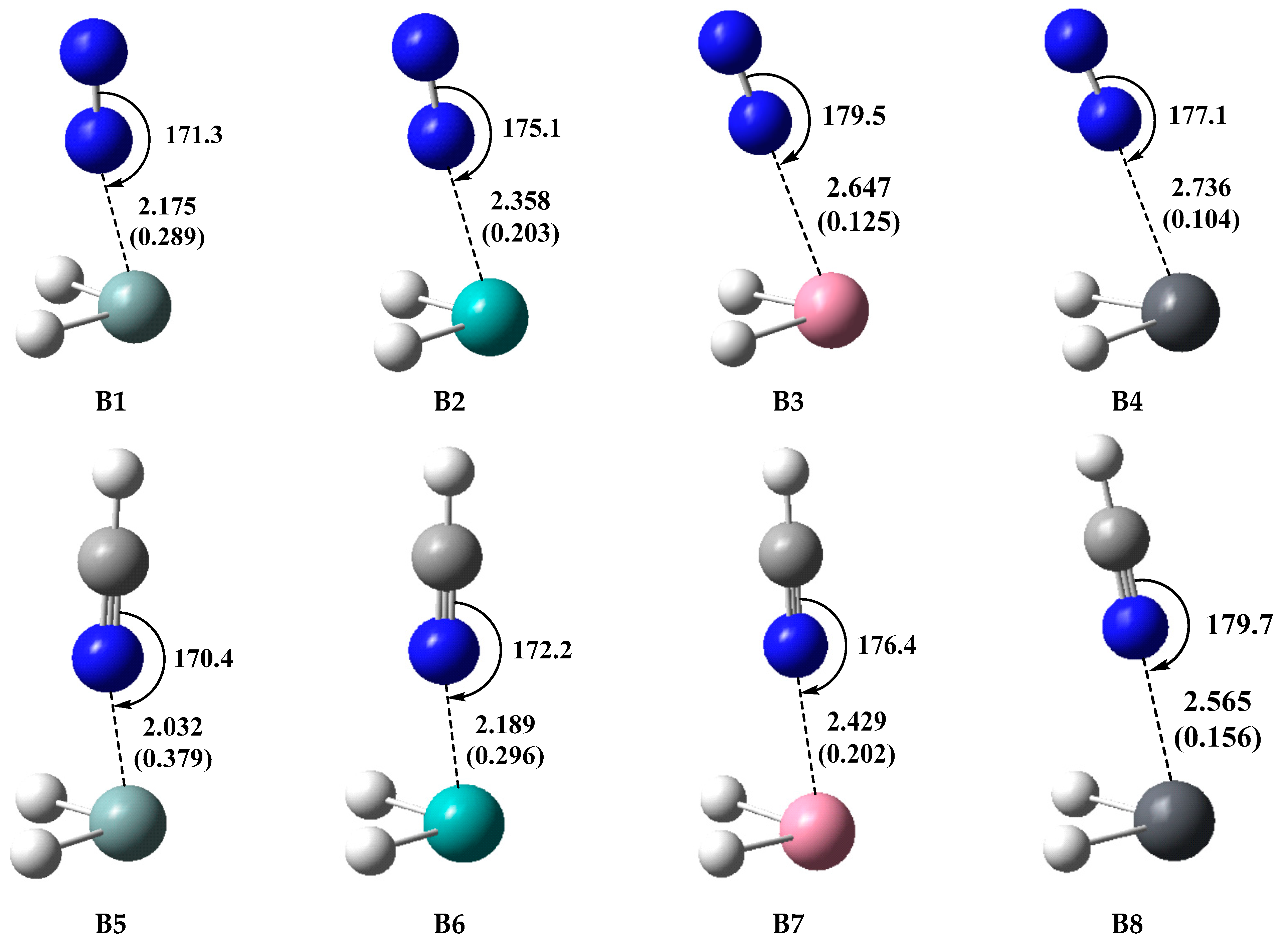
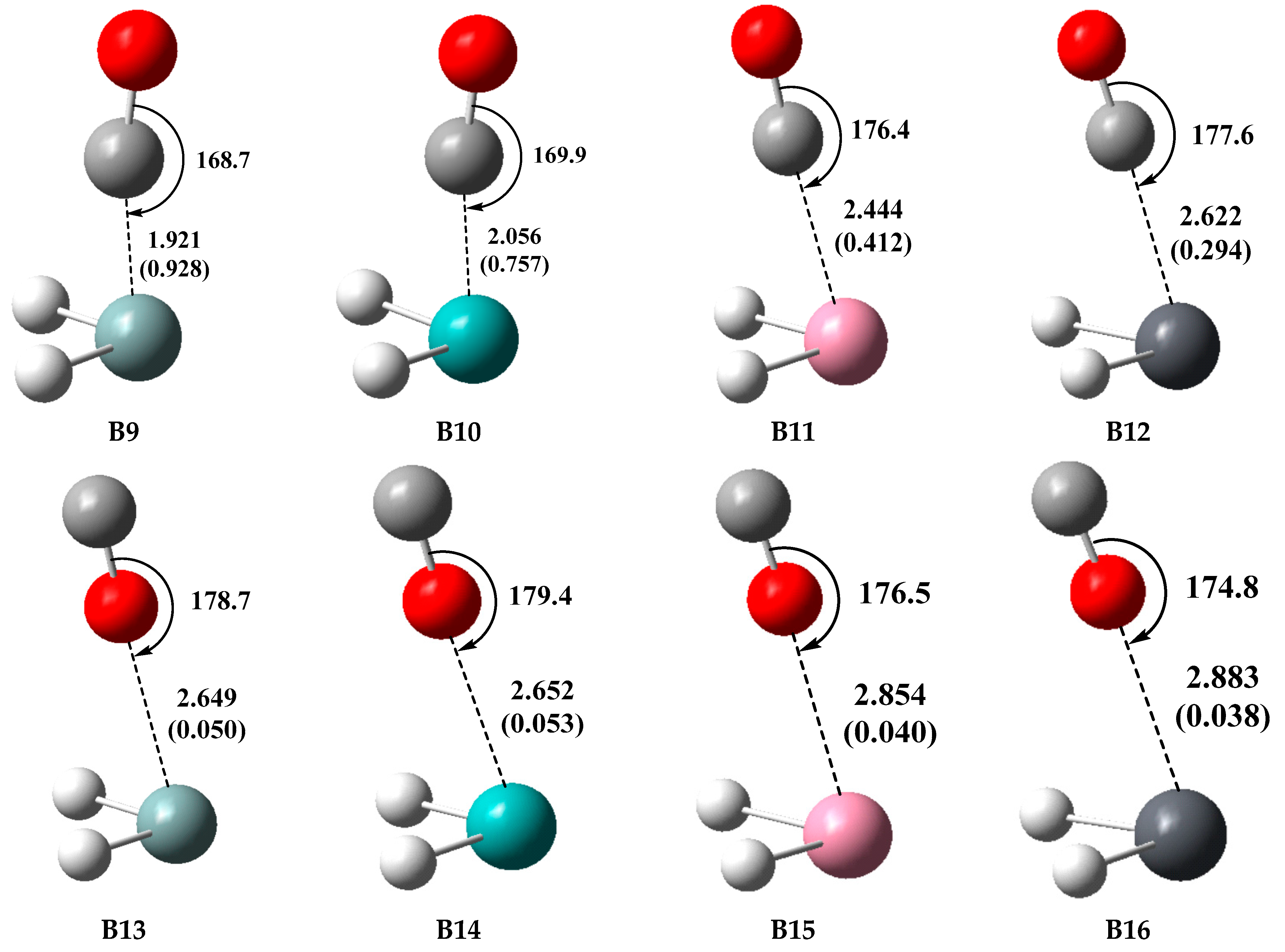
ComplexREint a
L1L2L3L4
A1 (SiH2···SiH3F)3.618 (3.505)−9.07−10.58−10.91−9.95
A2 (SiH2···GeH3F)3.632 (3.516)−10.37−11.45−12.00−10.78
A3 (SiH2···SnH3F)3.624 (3.493)−14.25−15.55−17.68−15.68
A4 (SiH2···PbH3F)3.683 (3.575)−14.46−15.42−17.68−15.38
A5 (GeH2···SiH3F)3.591 (3.437)−8.32−10.32−10.53−9.41
A6 (GeH2···GeH3F)3.618 (3.465)−9.53−11.08−11.45−10.07
A7 (GeH2···SnH3F)3.638 (3.463)−13.13−14.96−16.89−14.92
A8 (GeH2···PbH3F)3.695 (3.545)−13.38−14.92−17.01−14.71
A9 (SnH2···SiH3F)3.770 (3.634)−6.94−8.99−8.82−7.90
A10 (SnH2···GeH3F)3.790 (3.660)−7.98−9.66−9.66−8.53
A11 (SnH2···SnH3F)3.852 (3.672)−10.91−12.87−13.88−12.29
A12 (SnH2···PbH3F)3.887 (3.709)−11.45−13.25−14.67−12.54
A13 (PbH2···SiH3F)3.742 (3.537)−4.68−7.11−5.81−4.93
A14 (PbH2···GeH3F)3.775 (3.556)−5.27−7.40−5.64−4.51
A15 (PbH2···SnH3F)3.875 (3.661)−7.40−9.74−9.82−8.53
A16 (PbH2···PbH3F)3.910 (3.700)−7.69−9.86−10.49−8.61
a L1: MP2/aug-cc-pVDZ; L2: CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVDZ; L3: MP2/aug-cc-pVTZ; L4: CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ.
Table
Table 2. Second-order perturbation stabilization energy (E(2), in kJ/mol), charge transfer (qCT, in e), electron density (ρ, in a.u.), Laplacian (∇2ρ, in a.u.), energy density (H, in a.u.), local kinetic energy density (G, in a.u.) and potential energy density (V, in a.u.) at the BCP for type-A complexes.
Table 2. Second-order perturbation stabilization energy (E(2), in kJ/mol), charge transfer (qCT, in e), electron density (ρ, in a.u.), Laplacian (∇2ρ, in a.u.), energy density (H, in a.u.), local kinetic energy density (G, in a.u.) and potential energy density (V, in a.u.) at the BCP for type-A complexes.
ComplexOrbital InteractionE(2)qCTρ ∇ 2ρHGV
A1 (SiH2···SiH3F)LP (Si)→σ* (Si-F)27.920.03400.00770.01790.00050.0040−0.0035
A2 (SiH2···GeH3F)LP (Si)→σ* (Ge-F)32.650.03890.00800.01830.00050.0041−0.0036
A3 (SiH2···SnH3F)LP (Si)→σ* (Sn-F)45.730.06140.00980.02040.00040.0047−0.0043
A4 (SiH2···PbH3F)LP (Si)→σ* (Pb-F)47.530.05950.00990.02190.00060.0048−0.0043
A5 (GeH2···SiH3F)LP (Ge)→σ* (Si-F)27.960.03550.00820.01890.00050.0043−0.0038
A6 (GeH2···GeH3F)LP (Ge)→σ* (Ge-F)31.600.03930.00830.01900.00050.0042−0.0037
A7 (GeH2···SnH3F)LP (Ge)→σ* (Sn-F)42.180.05870.00970.02030.00040.0047−0.0042
A8 (GeH2···PbH3F)LP (Ge)→σ* (Pb-F)43.970.05710.00980.02190.00060.0049−0.0043
A9 (SnH2···SiH3F)LP (Sn)→σ* (Si-F)24.040.03390.00740.01620.00040.0036−0.0032
A10 (SnH2···GeH3F)LP (Sn)→σ* (Ge-F)27.800.03850.00760.01630.00040.0036−0.0032
A11 (SnH2···SnH3F)LP (Sn)→σ* (Sn-F)34.280.05400.00830.01620.00040.0037−0.0033
A12 (SnH2···PbH3F)LP (Sn)→σ* (Pb-F)37.620.05550.00860.01800.00050.0040−0.0035
A13 (PbH2···SiH3F)LP (Pb)→σ* (Si-F)19.270.02980.00740.01730.00050.0039−0.0034
A14 (PbH2···GeH3F)LP (Pb)→σ* (Ge-F)21.490.03270.00750.01710.00050.0038−0.0033
A15 (PbH2···SnH3F)LP (Pb)→σ* (Sn-F)24.540.04230.00770.01610.00040.0036−0.0032
A16 (PbH2···PbH3F)LP (Pb)→σ* (Pb-F)27.040.04370.00800.01790.00060.0039−0.0034
Table
Table 3. Decomposition of the total interaction energy (Etot) for type-A complexes into electrostatic (Eele), induction (Eind), dispersion (Edisp), and exchange (Eex) energy terms. All energies in kJ/mol. The relative values in percent represent the contribution of electrostatic, induction, and dispersion energy terms to the sum of all the three energy terms.
Table 3. Decomposition of the total interaction energy (Etot) for type-A complexes into electrostatic (Eele), induction (Eind), dispersion (Edisp), and exchange (Eex) energy terms. All energies in kJ/mol. The relative values in percent represent the contribution of electrostatic, induction, and dispersion energy terms to the sum of all the three energy terms.
ComplexEele%EeleEind%EindEdisp%EdispEexEtot
A1 (SiH2···SiH3F)−20.5248.8−8.9521.3−12.5829.931.94−10.12
A2 (SiH2···GeH3F)−23.0351.2−9.3620.8−12.5828.033.94−11.04
A3 (SiH2···SnH3F)−26.7549.0−13.7525.2−14.0425.838.87−15.68
A4 (SiH2···PbH3F)−25.4150.1−12.1223.9−13.2126.035.11−15.63
A5 (GeH2···SiH3F)−21.2347.7−9.8622.2−13.3830.134.82−9.66
A6 (GeH2···GeH3F)−24.4953.0−8.6118.6−13.1328.435.82−10.41
A7 (GeH2···SnH3F)−25.3347.8−13.6325.7−14.0426.538.29−14.71
A8 (GeH2···PbH3F)−24.1248.8−12.1224.5−13.2126.734.74−14.71
A9 (SnH2···SiH3F)−19.0645.6−9.3222.3−13.4232.133.61−8.19
A10 (SnH2···GeH3F)−21.0747.8−9.7422.1−13.2930.135.28−8.82
A11 (SnH2···SnH3F)−20.3644.3−12.1226.4−13.4629.333.61−12.33
A12 (SnH2···PbH3F)−20.0645.0−11.5025.8−13.0029.231.94−12.62
A13 (PbH2···SiH3F)−16.2242.7−8.4922.4−13.2534.932.02−5.94
A14 (PbH2···GeH3F)−17.0144.2−8.6122.3−12.9233.532.35−6.19
A15 (PbH2···SnH3F)−14.6739.6−9.9926.9−12.4133.528.38−8.69
A16 (PbH2···PbH3F)−14.1339.5−9.5726.8−12.0433.726.96−8.78
Table
Table 4. Binding distance at MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ (in parentheses) levels (R, in Å) and interaction energy at various levels (Eint, in kJ/mol) for type-B complexes.
Table 4. Binding distance at MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ (in parentheses) levels (R, in Å) and interaction energy at various levels (Eint, in kJ/mol) for type-B complexes.
ComplexREint a
L1L2L3L4
B1 (SiH2···N2)2.175 (2.042)−24.95−26.08−35.70−25.83
B2 (GeH2···N2)2.358 (2.211)−19.98−19.73−25.16−17.10
B3 (SnH2···N2)2.647 (2.549)−16.34−15.84−20.06−14.55
B4 (PbH2···N2)2.736 (2.643)−14.50−14.59−17.77−12.67
B5 (SiH2···HCN)2.032 (1.951)−68.09−71.77−85.06−73.36
B6 (GeH2···HCN)2.189 (2.087)−55.22−55.64−65.42−54.97
B7 (SnH2···HCN)2.429 (2.373)−47.23−46.77−54.51−46.61
B8 (PbH2···HCN)2.565 (2.485)−40.46−40.13−45.85−38.54
B9 (SiH2···CO)1.921 (1.889)−93.30−98.44−113.11−97.77
B10 (GeH2···CO)2.056 (1.989)−64.83−68.55−81.26−67.26
B11 (SnH2···CO)2.444 (2.347)−38.00−40.80−48.53−40.00
B12 (PbH2···CO)2.622 (2.498)−29.80−32.10−37.29−29.93
B13 (SiH2···OC)2.649 (2.581)−8.03−9.45−9.95−9.03
B14 (GeH2···OC)2.652 (2.593)−7.86−9.61−9.66−8.95
B15 (SnH2···OC)2.854 (2.769)−7.65−9.70−9.24−8.95
B16 (PbH2···OC)2.883 (2.785)−7.65−10.07−9.28−8.86
B17 (SiH2···C6H6)2.452 (2.381)−47.15−43.64−57.06−42.64
B18 (GeH2···C6H6)2.537 (2.446)−42.76−39.29−51.21−36.74
B19 (SnH2···C6H6)2.761 (2.700)−37.75−34.99−44.73−32.65
B20 (PbH2···C6H6)2.799 (2.746)−34.49−32.35−41.72−28.47
a L1: MP2/aug-cc-pVDZ; L2: CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVDZ; L3: MP2/aug-cc-pVTZ; L4: CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ.
Table
Table 5. Second-order perturbation stabilization energy (E(2), in kJ/mol), charge transfer (qCT, in e), electron density (ρ, in a.u.), Laplacian ( ∇ 2ρ, in a.u.), energy density (H, in a.u.), local kinetic energy density (G, in a.u.) and potential energy density (V, in a.u.) at the BCP for type-B complexes.
Table 5. Second-order perturbation stabilization energy (E(2), in kJ/mol), charge transfer (qCT, in e), electron density (ρ, in a.u.), Laplacian ( ∇ 2ρ, in a.u.), energy density (H, in a.u.), local kinetic energy density (G, in a.u.) and potential energy density (V, in a.u.) at the BCP for type-B complexes.
ComplexOrbital InteractionE(2)qCTρ ∇ 2ρHGV
B1 (SiH2···N2)LP (N)→LP* (Si)362.57−0.05920.04010.0605−0.01240.0275−0.0399
B2 (GeH2···N2)LP (N)→LP* (Ge)238.01−0.05380.03410.1253−0.00210.0334−0.0354
B3 (SnH2···N2)LP (N)→LP* (Sn)135.10−0.03840.02330.08800.00070.0213−0.0205
B4 (PbH2···N2)LP (N)→LP* (Pb)113.78−0.03460.02260.08950.00170.0207−0.0191
B5 (SiH2···HCN)LP (N)→LP* (Si)520.33−0.08980.05220.1647−0.01440.0556−0.0700
B6 (GeH2···HCN)LP (N)→LP* (Ge)379.46−0.08600.05140.1808−0.00970.0549−0.0645
B7 (SnH2···HCN)LP (N)→LP* (Sn)229.69−0.06390.03870.1529−0.00140.0397−0.0411
B8 (PbH2···HCN)LP (N)→LP* (Pb)178.74−0.05340.03430.13570.00070.0332−0.0325
B9 (SiH2···CO)LP (C)→LP* (Si)1488.16−0.10090.07620.3377−0.02150.1059−0.1274
B10 (GeH2···CO)LP (C)→LP* (Ge)1092.61−0.12940.07900.2162−0.03050.0846−0.1151
B11 (SnH2···CO)LP (C)→LP* (Sn)465.11−0.11250.04240.1484−0.00380.0409−0.0446
B12 (PbH2···CO)LP (C)→LP* (Pb)317.68−0.09730.03410.1218−0.00010.0306−0.0307
B13 (SiH2···OC)LP (O)→LP* (Si)63.16−0.01870.01470.0385−0.00120.0108−0.0119
B14 (GeH2···OC)LP (O)→LP* (Ge)68.01−0.01970.01580.05680.00030.0139−0.0137
B15 (SnH2···OC)LP (O)→LP* (Sn)49.78−0.01500.01300.04930.00070.0116−0.0109
B16 (PbH2···OC)LP (O)→LP* (Pb)49.45−0.01480.01420.05740.00100.0133−0.0123
B17 (SiH2···C6H6)π (C = C)→LP* (Si)221.92−0.07260.03740.0137−0.01040.0139−0.0243
B18 (GeH2···C6H6)π (C = C)→LP* (Ge)185.55−0.07190.03350.0501−0.00530.0178−0.0231
B19 (SnH2···C6H6)π (C = C)→LP* (Sn)106.21−0.06110.02490.0518−0.00190.0149−0.0168
B20 (PbH2···C6H6)π (C = C)→LP* (Pb)82.85−0.05860.02510.0634−0.00100.0169−0.0179
Table
Table 6. Decomposition of the total interaction energy (Etot) for type-B complexes into electrostatic (Eele), induction (Eind), dispersion (Edisp), and exchange (Eex) energy terms. All energies in kJ/mol. The relative values in percent represent the contribution of electrostatic, induction, and dispersion energy terms to the sum of all the three energy terms.
Table 6. Decomposition of the total interaction energy (Etot) for type-B complexes into electrostatic (Eele), induction (Eind), dispersion (Edisp), and exchange (Eex) energy terms. All energies in kJ/mol. The relative values in percent represent the contribution of electrostatic, induction, and dispersion energy terms to the sum of all the three energy terms.
ComplexEele%EeleEind%EindEdisp%EdispEexEtot
B1 (SiH2···N2)−98.0646.2−76.6636.2−37.2417.6187.68−24.29
B2 (GeH2···N2)−66.1347.8−44.0631.9−28.1320.3118.96−19.35
B3 (SnH2···N2)−36.7445.4−24.1629.9−20.0224.764.33−16.59
B4 (PbH2···N2)−30.6846.1−18.1427.2−17.8126.752.04−14.59
B5 (SiH2···HCN)−207.7553.4−129.7933.4−51.5413.2323.70−65.38
B6 (GeH2···HCN)−158.7155.8−85.2329.9−40.7614.3231.74−52.96
B7 (SnH2···HCN)−101.2453.7−55.9729.7−31.2216.6140.82−47.61
B8 (PbH2···HCN)−78.5855.3−37.8726.6−25.7118.1101.57−40.59
B9 (SiH2···CO)−301.2949.1−237.6338.7−74.4012.2516.90−96.43
B10 (GeH2···CO)−256.4852.7−169.5034.9−60.5312.4419.05−67.47
B11 (SnH2···CO)−95.5146.5−74.0336.0−35.9117.5162.77−42.68
B12 (PbH2···CO)−68.4348.3−45.5232.1−27.7619.6108.72−32.98
B13 (SiH2···OC)−15.8039.2−11.5828.7−12.9232.132.27−8.03
B14 (GeH2···OC)−16.9740.1−11.9128.2−13.4231.734.53−7.77
B15 (SnH2···OC)−13.2539.6−8.8626.5−11.3333.925.67−7.77
B16 (PbH2···OC)−12.5439.5−8.1125.6−11.0834.924.08−7.65
B17 (SiH2···C6H6)−113.9941.9−94.8434.9−63.0323.2231.70−40.17
B18 (GeH2···C6H6)−104.8843.2−79.5532.7−58.4424.1206.24−36.62
B19 (SnH2···C6H6)−65.0438.5−54.2132.0−49.9129.5135.06−34.11
B20 (PbH2···C6H6)−58.3138.2−46.8630.7−47.3631.1121.89−30.64
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, Y.; Yao, L.; Wang, F. Tetrel-Bond Interactions Involving Metallylenes TH2 (T = Si, Ge, Sn, Pb): Dual Binding Behavior. Molecules 2023, 28, 2577. https://doi.org/10.3390/molecules28062577

AMA Style

Chen Y, Yao L, Wang F. Tetrel-Bond Interactions Involving Metallylenes TH2 (T = Si, Ge, Sn, Pb): Dual Binding Behavior. Molecules. 2023; 28(6):2577. https://doi.org/10.3390/molecules28062577

Chicago/Turabian Style

Chen, Yishan, Lifeng Yao, and Fan Wang. 2023. "Tetrel-Bond Interactions Involving Metallylenes TH2 (T = Si, Ge, Sn, Pb): Dual Binding Behavior" Molecules 28, no. 6: 2577. https://doi.org/10.3390/molecules28062577

APA Style

Chen, Y., Yao, L., & Wang, F. (2023). Tetrel-Bond Interactions Involving Metallylenes TH2 (T = Si, Ge, Sn, Pb): Dual Binding Behavior. Molecules, 28(6), 2577. https://doi.org/10.3390/molecules28062577

Article Metrics

Back to TopTop