Abstract
Accurate and efficient determination of excited-state polarizabilities (α) is an open problem both experimentally and computationally. Following our previous work, (Phys. Chem. Chem. Phys. 2023, 25, 2131−2141), in which we employed simple ground-state (S0) density-related functions from the information-theoretic approach (ITA) to accurately and efficiently evaluate the macromolecular polarizabilities, in this work we aimed to predict the lowest excited-state (S1) polarizabilities. The philosophy is to use density-based functions to depict excited-state polarizabilities. As a proof-of-principle application, employing 2-(2′-hydroxyphenyl)benzimidazole (HBI), its substituents, and some other commonly used ESIPT (excited-state intramolecular proton transfer) fluorophores as model systems, we verified that either with S0 or S1 densities as an input, ITA quantities can be strongly correlated with the excited-state polarizabilities. When transition densities are considered, both S0 and S1 polarizabilities are in good relationships with some ITA quantities. The transferability of the linear regression model is further verified for a series of molecules with little or no similarity to those molecules in the training set. Furthermore, the excitation energies can be predicted based on multivariant linear regression equations of ITA quantities. This study also found that the nature of both the ground-state and excited-state polarizabilities of these species are due to the spatial delocalization of the electron density.
1. Introduction
Molecular polarizability, especially static electric dipole polarizability (α), is a fundamental physicochemical property. It reflects the change of a molecule’s dipole moment in a linear-response manner resulting from an external electric field perturbation [1]. It is a fundamental dielectric property important in many disciplines, especially in materials science [2,3]. Experimental determination of excited-state electrostatic properties is mainly determined using Stark spectroscopy, the electronic absorption/emission [4,5] method, and the flash photolysis time-resolved microwave-conductivity (FP-TMRC) [6,7] technique.
In classical physics, polarizability can be approximately obtained in terms of the volume of a system [8,9]. For example, many strong correlations have been observed for both atoms and molecules [10,11,12,13,14,15,16,17,18]. Tkatchenko and Scheffler (TS) [19] proposed use of atomic volumes and atomic polarizabilities to predict the ground-state polarizabilities for small molecules. Recent progress can be found in [20]. However, performance for excited-state systems has not been reported.
In quantum mechanics, polarizability can be obtained by iteratively solving the coupled-perturbed Hartree–Fock (CPHF) equation [21,22] or its Kohn–Sham DFT (density functional theory) counterpart [23]. This protocol requires a sufficiently large basis set with polarization and diffuse functions and huge computational costs, but the computational barriers can be partly overcome by using some linear-scaling methods [24,25,26]. In addition, machine learning (ML)-based [27,28,29] methods and a regression-based [30] model have been applied to predict the S0 polarizabilities. Polarizability can be related to the band gap of HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) in an inverse manner [31,32,33].
In the literature, only a few studies [34,35,36,37,38,39,40] have reported excited-state polarizabilities. This is likely because accurate predictions of excited-state geometries and molecular properties of large molecules are difficult, especially when there are perturbations such as external fields.
Following our previous work, used information-theoretic approach (ITA) quantities to predict the S0 polarizabilities of both small and large molecules [41,42]. Here, we aim to predict the S1 polarizabilities of 2-(2′-hydroxyphenyl)benzimidazole (HBI, 1) and its derivatives as shown in Scheme 1. For 1, it is well-documented [43] that the S0 (Scheme 1a) intramolecular proton transfer (IPT) reaction takes place with difficulty, whereas the S1 (Scheme 1b) or T1 (triplet, not shown) intramolecular proton transfer (ESIPT) process can easily happen. Thus, in this work, only S0 and S1 were considered to reduce computational cost without compromising the results. We have found that with S0 or S1 electron densities as inputs, ITA quantities had good correlations with the excited-state polarizabilities. When transition densities were considered, both S0 and S1 polarizabilities had good relationships with ITA quantities. Furthermore, excitation energies could be predicted based on multiple linear regression equations of ITA quantities. For the first time, we applied the ITA quantities to predict excited-state polarizabilities. It is anticipated that this protocol can be readily applied to condensed-phase systems.
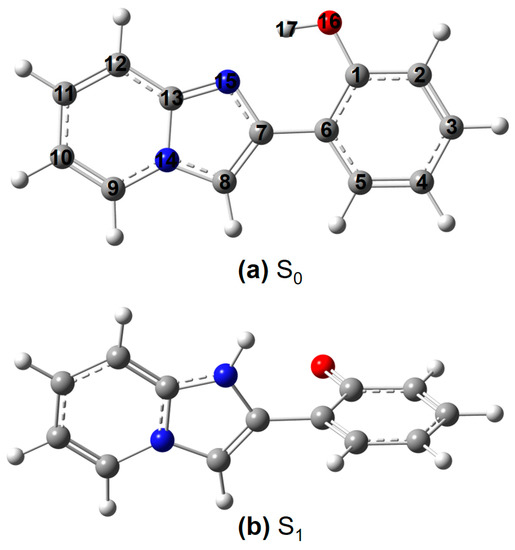
Scheme 1.
(a) Ground-state (S0) and (b) excited-state (S1) of 2-(2′-hydroxyphenyl)benzimidazole (HBI), structure and atomic numbering. A total of 27 substituted HBI structures were generated, including 1: HBI, 2: 3-Br-HBI, 3: 3-Et2N-HBI, 4: 3-HO-HBI, 5: 3-MeO-HBI, 6: 4-F-HBI, 7: 4-Cl-HBI, 8: 4-Br-HBI, 9: 4-CN-HBI, 10: 4-Me-HBI, 11: 4-MeO-HBI, 12: 10-Cl-HBI, 13: 10-Br-HBI, 14: 10-CN-HBI, 15: 10-Me-HBI, 16: 10-CF3-HBI, 17: 10-Ph-HBI, 18: 12-Ph-HBI, 19: 10-(p-MeO-Ph)-HBI, 20: 10-(p-MeCO2-Ph)-HBI, 21: 12-(p-MeO-Ph)-HBI, 22: 12-(p-MeCO2-Ph)-HBI, 23: 4-Me-10-Cl-HBI, 24: 4-Me-10-CF3-HBI, 25: 10-Ph-12-Ph-HBI, 26: 2-(CH2CH2CH=CH2)-8-(CH2CH2Ph)-HBI, 27: 2-F-3-F-4-F-5-F-HBI. Color code: hydrogen in white, carbon in grey, nitrogen in blue, and oxygen in red.
2. Results
Shown in Table 1 are the correlation coefficients (R2) between the S0 polarizabilities (αiso) and ITA quantities, molecular volumes, and quadrupole moments, which were obtained at the CAM-B3LYP/6-311+G(d) level for all the molecular systems shown in Scheme 1 and Scheme 2. The linear regression equations can be found in Table S1. It is clear from Table 1 that the Ghosh−Berkowitz−Parr (GBP) entropy (SGBP), 2nd and 3rd relative Rényi entropy (rR2 and rR3), information gain (IG), G1, G2, and G3, and quadrupole moments (Θiso) have strong linear relationships with αiso, with R2 > 0.8. Of note, the G3 data were shown to be strongly correlated with αiso for various systems, among which were 30 planar or quasi-planar bases [41], and 20/40/8000 amino acids, dipeptides and tripeptides [41,42]. The Θiso values had a good relationship with αiso, the theoretical rationale for which can be found in [42]. However, a solid and sound theoretical verification between G3 and αiso was lacking. Additionally, molecular volumes had only reasonably good correlation with αiso, with R2 = 0.705, indicating that it is not a good descriptor of αiso. For Shannon entropy and Fisher information, there exist three exceptions for 2, 8, and 13. It was found that these three molecules are Br-containing, indicating that there may be some regions for heavy atoms where the electron density and/or its gradients are numerically inconsistent. Taking the three outliers away, much stronger correlations were found for Shannon entropy (better than Fisher information). Here, the nature of ground-state polarizabilities was due to the spatial delocalization of the electron density. Overall, the strong correlations indicate that our computational results are sound.


Scheme 2.
Representative examples of commonly used ESIPT fluorophores.
Table 2 shows S1 polarizabilities, S1 ITA quantities, including Shannon entropy (SS), Fisher information (IF), 2nd and 3rd relative Rényi entropy (rR2 and rR3), G2 and G3, molecular volumes (Vol), and quadrupole moments (Θiso), obtained at the TD-CAM-B3LYP/6-311+G(d) level. Table 2 also shows the correlation coefficients (R2) between the S1 polarizabilities and other quantities at S1. The linear regression equations can be found in Table S2. Note that some ITA quantities, well-defined at S0, are numerically inconsistent (for example, negative occupancy) at S1, and are thus missing. One can see that G2, G3, and Vol have good correlations with αiso at S1, with R2 > 0.8. It is intriguing that at S1 and G3 still have good correlations with αiso. This is the first time such a phenomenon has been observed. However, admittedly, the theoretical foundation lags behind the numerical evidence found in this work. Moreover, we have found that for Vol, the R2 value was much larger at S1 (0.818) than that at S0 (0.705). One possible reason is that the excited-state relaxation expands the volume and polarizability space. Finally, in Columns 3 and 4 of SS and IF, 2, 8, and 13 seem to have abnormal values compared with the others. They are all Br-containing, indicating that there may be some regions for heavy atoms where density gradients are numerically inconsistent at S1. Overall, we showed that excited-state densities and molecular polarizabilities αiso are mutually entangled.

After showing that ITA quantities can be correlated with αiso either at S0 or S1, it is important to ask if one can use ITA quantities at S0 to predict αiso at S1. The answer is definitely yes. Table 3 shows the correlation coefficients (R2) between the αiso values at S1 and ITA quantities, molecular volumes, and quadrupole moments at S0 introduced in Table 1. More details can be found in Table S3. The linear regression equations can be found in Table S4. One can see that the αiso@S0, IG, G1, G2, and G3 have good relationships with αiso@S1, with R2 > 0.8. Moving forward, we ask if one can use the transition density (matrix) as an input for ITA quantities to correlate with αiso either at S0 or S1. The answer again is yes. Table 4 shows strong correlations between αiso either at S0 or S1 and ITA quantities with the transition density matrix as an input. The linear regression equations can be found in Table S5. Except for Shannon entropy (SS) and Fisher information (IF), the other ITA quantities have reasonably good or strong correlations with αiso, either at S0 or S1, with R2 ranging from 0.72 to 0.94. The implication of this is that electron-density-based quantities can be used to predict excited-state properties, such as molecular polarizabilities.


Table 4.
Correlation coefficients (R2) between the ground-state (αiso@S0, in Bohr3) or the first excited-state (αiso@S1, in Bohr3) molecular polarizability, and molecular volume (Vol, in Bohr3/mol), the isotropic quadrupole moment (Θiso, in a.u.), and ITA quantities (in a.u.) based on the transition density matrix as an input for all the systems in Scheme 1 and Scheme 2.
To further showcase the transferability of the linear regression models, we compared both the S0 and S1 polarizabilities for all systems in Scheme 3, as shown in Table 5 and Table 6, respectively. Since Shannon entropy and Fisher information have exceptions for the linear regressions, they were not used for predicting the polarizabilities of all systems in Scheme 3. From Table 5, one can see that, SGBP, rR2, rR3, and G3 perform well in reproducing the conventional S0 polarizabilities, as evidenced by the mean unsigned errors (MUEs) and mean signed errors (MSEs). The other five quantities show reasonably good predictions. From Table 6, one can observe that the predicted S1 polarizabilities are in reasonably good agreement with the conventional data. All the quantities show comparable performance. Taken together, we have shown that the transferability of the linear regression models is convincing, as the systems in Scheme 3 show little or low similarity to those in Scheme 1 and Scheme 2.

Scheme 3.
Molecules used to validate the transferability of the linear regression models. 37: 7-hydroxy-2,3-dihydro-1H-inden-1-one, 38: 1-hydroxy-9H-fluoren-9-one, 39: 1-hydroxy-11H-benzo[b]flu oren-11-one, 40: methyl salicylate, 41: 7-(2-pyridyl)indole, 42: 4,6-dimethyl-2-mercaptopyrimidine, 43: 10-malononitrile-benzo[h]quinoline.


Next, we compared the αiso data (either at S0 or S1) predicted by the TS formulas with conventional results as a reference, as shown in Table 7. The predicted αiso results are shown in Tables S6 and S7. Employing the original Tkatchenko–Scheffler (TS) formula [19] with Becke [44] or Hirshfeld [45] partitions, the αiso data (either at S0/S1) were either strongly underestimated or overestimated, with MUE(%) up to −26.44/−24.94 and 7.92/8.93, respectively. It was found that a mean value could reduce the MSE(%) to 14.40/15.53. Moreover, with the new TS formula [20], the results were not improved but worsened, as shown in Table 7. Taken together, we found that the TS formulas have room to improve in predicting S1 polarizabilities.

Finally, we found that excitation energies can be predicted in addition to multivariant linear regression equations of ITA quantities. For example, one can use the S0 density matrix as an input for ITA quantities to correlate with excitation energies. Similarly, if the transition density matrix is used for ITA quantities, the excitation energies can also be predicted. Based on the two regression equations constructed from all the systems in Scheme 1 and Scheme 2, we collected predicted excitation energies, and those from conventional calculations, for all the systems in Scheme 3, as shown in Table 8. The MUEs and MSEs were −0.84/1.08 eV and −0.76/1.21 eV, respectively, for the excitation energies. This indicates that the inaccuracy of this protocol is comparable to that of underlying approximations of DFT [46,47].

Table 8.
Comparison of the excitation energies (in eV), as predicted with the multivariant linear regression equations for all the systems in Scheme 3, with conventional data as a reference.
3. Discussion
To accurately and efficiently predict excited-state polarizabilities is an ongoing issue. Solving standard CPHF/CPKS equations is computationally intensive, and the computational costs can be excessive for macromolecular systems. Other algorithms and models available in the literature are normally concerned with ground-state polarizabilities. Within this context, we applied density-based ITA quantities to correlate with αiso at S0/S1. This was inspired by our previous work on predicting the ground-state polarizabilities for small and macromolecular systems. Our tentative results show that the protocol is a promising theoretical tool. More systems along this line need to be considered to make this protocol more robust and applicable. We have to point out that when the system under study increases in size, the molecular wavefunctions (thus electron density) become difficult to assess and sometimes computationally unfeasible. Under these circumstances, we have to resort to linear-scaling electronic structure methods, such as GEBF (generalized energy-based fragmentation method) [48,49,50,51], where only small subsystems of a few atoms or groups are treated.
Next, we adopted the TS method, as mentioned previously. We had found previously that, based upon the Hirshfeld or Becke partition scheme, the original TS formula had unsatisfactory performance either by overestimating or underestimating the S1 polarizabilities. An apparent reduction of the deviations can be obtained by averaging the two sets of results. The reason behind this is unclear at the moment. From the original formula,
one can argue that the weights may be the root cause of its poor performance, mainly because the atomic polarizabilities are experimentally determined and computationally verified, as summarized in ref [52]. In the same way, a revised TS formula,
improved performance of predicting S0 polarizabilities. However, its predicting power was shown to be far from satisfactory for macromolecules. In this work, we further found that both the original and new TS formulas fail to give a satisfactory description of the S1 polarizability. This indicates that the two formulas are oversimplified and may be system-dependent. Overall, the volume-based TS equations are inferior to the density-based ITA regression equations.
4. Materials and Methods
4.1. Information-Theoretic Approach Quantities
Shannon entropy SS [53] and Fisher information IF [54] are two cornerstone quantities in information theory. They are defined as Equations (1) and (2), respectively:
where is the electron density and is the density gradient. The physical picture of and is clear; the former measures the spatial delocalization of the electron density and the latter gauges the sharpness or localization of the same.
Apart from total density, components such as kinetic-energy density can be used to define an ITA quantity. With both electron density and the kinetic energy density, Ghosh, Berkowitz, and Parr developed a formula for entropy (SGBP) [55]:
where t(r; ρ) and tTF(r; ρ) represent the non-interacting and Thomas–Fermi (TF) kinetic energy density, respectively. Here k, c, and cK are three constants (k, the Boltzmann constant, c = (5/3) + ln(4πcK/3), and cK = (3/10)(3π2)2/3). Full integration of kinetic energy density t(r; ρ) leads to the total kinetic energy TS via
while t(r; ρ) can be obtained from the canonical orbital densities,
and tTF(r; ρ) is simply cast in terms of ,
Of note, the kinetic-energy density can differ in its form, and can be used in different contexts [56,57,58,59,60,61,62,63]. However, SGBP satisfies the maximum-entropy requirement from a mathematical viewpoint [55].
Moving forward, some ITA quantities were introduced for chemical reactions. As new reactivity descriptors in conceptual density functional theory (CDFT) [64,65,66,67], one example is relative Rényi entropy [68] of order n
Information gain [69] (also called Kullback−Leibler divergence or relative Shannon entropy) IG is expressed as follows,
In Equations (7) and (8), ρ0(r) and ρ(r) satisfy the same normalization condition, and ρ0(r) denotes the reference-state density.
Recently, in [70] one of the present authors proposed three functions G1, G2, and G3, at both atomic and molecular levels. These are defined as below:
Equations (9)–(11) have been theoretically derived, numerically verified, and used in many applications, as in refs [41,42,70,71]. As one of our major achievements over the past decade, we aimed to combine density functional theory and information theory in a seamless manner, since the two theories can have electron density as an input. Our recent progress along this line can be found in two reviews [72,73]. As another prominent example, we have applied the ITA to assess homochirality [74,75].
Finally, the Hirshfeld’s stockholder approach [45,76,77,78,79] is often introduced to partition atoms in a molecule in the literature, as defined in Equation (12),
Here, is the atomic Hirshfeld density, is a sharing function, and is the atomic density of B centered at RA. The sum over all the free atom densities, typically spherically averaged S0 atomic densities, is usually termed the promolecular density. The Stockholder approach is used in the context of ITA because it is also based on information-theoretic arguments. Alternative partitioning schemes include Becke’s fuzzy atom approach [44] and Bader’s zero-flux atoms-in-molecules (AIM) method [80].
4.2. Computational Details
All density functional theory (DFT) calculations were performed with the Gaussian 16 [81] package. Default options included ultrafine integration grids and tight self-consistent field convergence, which were adopted to eliminate numerical noises. The ground- and excited-state structural relaxation was carried out at the CAM-B3LYP/6-311+G(d) [82,83] and TD-CAM-B3LYP/6-311+G(d) [82,83,84,85,86] level, respectively, for 36 molecular systems, as shown in Scheme 1, Scheme 2 and Scheme 3. Optimized atomic Cartesian coordinates are supplied in the Supplementary Materials. Harmonic vibrational frequency calculations were executed at the same level, and no imaginary frequencies were observed by direct visual inspection. Isotropic polarizabilities (αiso = (αxx + αyy + αzz)/3) and isotropic quadrupole moments (Θiso = (Θxx + Θyy + Θzz)/3), molecular volumes (at 0.001 e/Bohr3 contour surface of electronic density), and molecular wavefunctions, were obtained at the CAM-B3LYP/6-311+G(d) level. The Multiwfn 3.8 [87] program was utilized to calculate all ITA quantities at S0 and S1 using the molecular wavefunction file as an input. Of note, except for the S0 state, the keyword “density=current” in Gaussian 16 was used to dump the density matrix in a wavefunction file. The stockholder Hirshfeld partition scheme of atoms in molecules was employed when atomic contributions were concerned. The reference-state density was the neutral atom calculated at the same level of theory as molecules.
5. Conclusions
In this work, we extended the information-theoretic approach (ITA) to treat excited-state polarizabilities. With the ground-state, the first excited-state, or the transition density matrix as an input for ITA quantities, strong linear correlations were observed between molecular polarizabilities and ITA quantities. Based upon these regression equations for molecules in the training set, one can further predict the molecular polarizabilities for other systems in the test set. We verified that good accuracy and transferability of the linear regression models can be obtained. In addition, we found that the nature of both ground-state and excited-state polarizabilities is due to the electron delocalization of the electron density. Finally, we revealed that excitation energies can be predicted on top of a multivariant linear regression equation of ITA quantities. We mention in passing that the ITA quantities were applied to ground-state macromolecules in our previous work and excited-state systems in this work. More work along this line is underway for condensed-phase systems, and the results will be presented elsewhere.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28062576/s1, Excited-state ITA quantities with the transition density matrix as input, all the linear regression equations, molecular polarizabilities predicted by the original and new TS formulas, and the optimized (S0 and S1) Cartesian coordinates of all the systems in Scheme 1, Scheme 2 and Scheme 3.
Author Contributions
Conceptualization, S.L., P.W.A. and D.Z.; data curation, X.H. and D.Z.; formal analysis, X.H. and D.Z.; funding acquisition, P.W.A. and D.Z.; project administration, S.L., P.W.A. and D.Z.; supervision, S.L., P.W.A. and D.Z.; writing—original draft, D.Z.; writing—review and editing, S.L., P.W.A. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the start-up funding of Yunnan University and the Yunnan Fundamental Research Projects (grant NO. 202101AU070012), NSERC, Canada Research Chairs, and the Digital Research Alliance of Canada.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
Ewa D. Raczyńska is acknowledged for this invitation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Buckingham, A.D. Polarizability and hyperpolarizability. Phil. Trans. R. Soc. Lond. A 1979, 293, 239–248. [Google Scholar]
- Tian, T.; Scullion, D.; Hughes, D.; Li, L.H.; Shih, C.-J.; Coleman, J.; Chhowalla, M.; Santos, E.J.G. Electronic Polarizability as the Fundamental Variable in the Dielectric Properties of Two-Dimensional Materials. Nano Lett. 2020, 20, 841–851. [Google Scholar] [CrossRef] [PubMed]
- Rupasinghe, T.P.; Hutchins, K.M.; Bandaranayake, B.S.; Ghorai, S.; Karunatilake, C.; Bučar, D.-K.; Swenson, D.C.; Arnold, M.A.; MacGillivray, L.R.; Tivanski, A.V. Mechanical Properties of a Series of Macro-and Nanodimensional Organic Cocrystals Correlate with Atomic Polarizability. J. Am. Chem. Soc. 2015, 137, 12768–12771. [Google Scholar] [CrossRef] [PubMed]
- Liess, M.; Jeglinski, S.; Vardeny, Z.; Ozaki, M.; Yoshino, K.; Ding, Y.; Barton, T. Electroabsorption Spectroscopy of Luminescent and Nonluminescent π-Conjugated Polymers. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 56, 15712–15724. [Google Scholar] [CrossRef]
- Ponder, M.; Mathies, R. Excited-State Polarizabilities and Dipole Moments of Diphenylpolyenes and Retinal. J. Phys. Chem. 1983, 87, 5090–5098. [Google Scholar] [CrossRef]
- Gelinck, G.H.; Piet, J.J.; Wegewijs, B.R.; Müllen, K.; Wildeman, J.; Hadziioannou, G.; Warman, J.M. Measuring the Size of Excitons on Isolated Phenylene-Vinylene Chains: From Dimers to Polymers. Phys. Rev. B Condens. Matter Mater. Phys. 2000, 62, 1489–1491. [Google Scholar] [CrossRef]
- De Haas, M.P.; Warman, J.M. Photon-Induced Molecular Charge Separation Studied by Nanosecond Time-Resolved Microwave Conductivity. Chem. Phys. 1982, 73, 35–53. [Google Scholar] [CrossRef]
- Condon, E.U. Handbook of Physics, 1st ed.; Condon, E.U., Odishaw, H., Eds.; McGraw-Hill: New York, NY, USA, 1958; pp. 4–22. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; Wiley: New York, NY, USA, 1975; pp. 60–62. [Google Scholar]
- Dmitrieva, I.K.; Plindov, G.I. Dipole Polarizability, Radius and Ionization Potential for Atomic Systems. Phys. Scr. 1983, 27, 402. [Google Scholar] [CrossRef]
- Gough, K.M. Theoretical analysis of molecular polarizabilities and polarizability derivatives in hydrocarbons. J. Chem. Phys. 1989, 91, 2424–2432. [Google Scholar] [CrossRef]
- Laidig, K.E.; Bader, R.F.W. Properties of atoms in molecules: Atomic polarizabilities. J. Chem. Phys. 1990, 93, 7213–7224. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Polarizability and volume. J. Chem. Phys. 1993, 98, 4305–4306. [Google Scholar] [CrossRef]
- Politzer, P.; Jin, P.; Murray, J.S. Atomic polarizability, volume and ionization energy. J. Chem. Phys. 2002, 117, 8197–8202. [Google Scholar] [CrossRef]
- Blair, S.A.; Thakkar, A.J. Relating polarizability to volume, ionization energy, electronegativity, hardness, moments of momentum, and other molecular properties. J. Chem. Phys. 2014, 141, 074306. [Google Scholar] [CrossRef] [PubMed]
- Blair, S.A.; Thakkar, A.J. Additive models for the molecular polarizability and volume. Chem. Phys. Lett. 2014, 610–611, 163–166. [Google Scholar] [CrossRef]
- Miller, K.J. Additivity Methods in Molecular Polarizability. J. Am. Chem. Soc. 1990, 112, 8533–8542. [Google Scholar] [CrossRef]
- Miller, K.J. Calculation of the Molecular Polarizability Tensor. J. Am. Chem. Soc. 1990, 112, 8543–8551. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Szabó, P.; Góger, S.; Charry, J.; Karimpour, M.R.; Fedorov, D.V.; Tkatchenko, A. Four-Dimensional Scaling of Dipole Polarizability in Quantum Systems. Phys. Rev. Lett. 2022, 128, 070602. [Google Scholar] [CrossRef] [PubMed]
- McWeeny, R. Some recent advances in density matrix theory. Rev. Mod. Phys. 1960, 32, 335–369. [Google Scholar] [CrossRef]
- Langhoff, W.; Karplus, M.; Hurst, R.P. Approximations to Hartree—Fock Perturbation Theory. J. Chem. Phys. 1966, 44, 505–514. [Google Scholar] [CrossRef]
- Colwell, S.M.; Murray, C.W.; Handy, N.C.; Amos, R.D. The determination of hyperpolarisabilities using density functional theory. Chem. Phys. Lett. 1993, 210, 261–268. [Google Scholar] [CrossRef]
- Collins, M.A.; Bettens, R.P. Energy-Based Molecular Fragmentation Methods. Chem. Rev. 2015, 115, 5607–5642. [Google Scholar] [CrossRef]
- Niklasson, A.M.; Challacombe, M. Density Matrix Perturbation Theory. Phys. Rev. Lett. 2004, 92, 193001. [Google Scholar] [CrossRef] [PubMed]
- Weber, V.; Niklasson, A.M.N.; Challacombe, M. Ab Initio Linear Scaling Response Theory: Electric Polarizability by Perturbed Projection. Phys. Rev. Lett. 2004, 92, 193002. [Google Scholar] [CrossRef] [PubMed]
- Grisafi, A.; Wilkins, D.M.; Csányi, G.; Ceriotti, M. Symmetry-Adapted Machine Learning for Tensorial Properties of Atomistic Systems. Phys. Rev. Lett. 2018, 120, 036002. [Google Scholar] [CrossRef]
- Wilkins, D.M.; Grisafi, A.; Yang, Y.; Lao, K.U.; DiStasio, R.A., Jr.; Ceriotti, M. Accurate molecular polarizabilities with coupled cluster theory and machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 3401–3406. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.H.A.; Lunghi, A. Predicting tensorial molecular properties with equivariant machine learning models. Phys. Rev. B 2022, 105, 165131. [Google Scholar] [CrossRef]
- Amin, M.; Samy, H.; Küpper, J. Robust and Accurate Computational Estimation of the Polarizability Tensors of Macromolecules. J. Phys. Chem. Lett. 2019, 10, 2938–2943. [Google Scholar] [CrossRef] [PubMed]
- Unsöld, A. Quantentheorie des Wasserstoffmolekülions und der Born-Landéschen Abstoßungskräfte. Z. Für Phys. 1927, 43, 563–574. [Google Scholar] [CrossRef]
- Simón-Manso, Y.; Fuentealba, P. On the Density Functional Relationship between Static Dipole Polarizability and Global Softness. J. Phys. Chem. A 1998, 102, 2029–2032. [Google Scholar] [CrossRef]
- Ayers, P.W. The physical basis of the hard/soft acid/base principle. Faraday Discuss. 2007, 135, 161–190. [Google Scholar] [CrossRef] [PubMed]
- Grozema, F.C.; Telesca, R.; Jonkman, H.T.; Siebbeles, L.D.A.; Snijders, J.G. Excited State Polarizabilities of Conjugated Molecules Calculated Using Time Dependent Density Functional Theory. J. Chem. Phys. 2001, 115, 10014–10021. [Google Scholar] [CrossRef]
- Improta, R.; Ferrante, C.; Bozio, R.; Barone, V. The Polarizability in Solution of Tetra-Phenyl-Porphyrin Derivatives in Their Excited Electronic States: A PCM/TD-DFT Study. Phys. Chem. Chem. Phys. 2009, 11, 4664–4673. [Google Scholar] [CrossRef] [PubMed]
- Van Der Horst, J.W.; Bobbert, P.A.; De Jong, P.H.L.; Michels, M.A.J.; Siebbeles, L.D.A.; Warman, J.M.; Gelinck, G.H.; Brocks, G. Predicting Polarizabilities and Lifetimes of Excitons on Conjugated Polymer Chains. Chem. Phys. Lett. 2001, 334, 303–308. [Google Scholar] [CrossRef]
- Hinchliffe, A.; Sosćun, H.J. Ab Initio Studies of the Dipole Moment and Polarizability of Azulene in Its Ground and Excited Singlet States. Chem. Phys. Lett. 2005, 412, 365–368. [Google Scholar] [CrossRef]
- Christiansen, O.; Hättig, C.; Jørgensen, P. Ground and Excited State Polarizabilities and Dipole Transition Properties of Benzene from Coupled Cluster Response Theory. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1999, 55, 509–524. [Google Scholar] [CrossRef]
- Ye, J.F.; Chen, H.; Note, R.; Mizuseki, H.; Kawazoe, Y. Excess Polarizabilities Upon Excitation from the Ground State to the First Dipole-Allowed Excited State of Diphenylpolyenes. Int. J. Quantum Chem. 2007, 107, 2006–2014. [Google Scholar] [CrossRef]
- Orian, L.; Pilot, R.; Bozio, R. In Silico Stark Effect: Determination of Excited-State Polarizabilities of Squaraine Dyes. J. Phys. Chem. A 2017, 121, 1587–1596. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.B.; Liu, S.B.; Chen, D.H. A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides. Pharmaceuticals 2022, 15, 938. [Google Scholar] [CrossRef]
- Zhao, D.B.; Zhao, Y.L.; He, X.; Ayers, P.W.; Liu, S.B. Efficient and accurate density-based prediction of macromolecular polarizabilities. Phys. Chem. Chem. Phys. 2023, 25, 2131–2141. [Google Scholar] [CrossRef]
- Purkayastha, P.; Chattopadhyay, N. Role of rotamerisation and excited state intramolecular proton transfer in the photophysics of 2-(2′-hydroxyphenyl)benzoxazole, 2-(2′-hydroxyphenyl)benzimidazole and 2-(2′-hydroxyphenyl)benzothiazole: A theoretical study. Phys. Chem. Chem. Phys. 2000, 2, 203–210. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theoret. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W.T. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Teale, A.M.; Helgaker, T.; Savin, A.; Adamo, C.; Aradi, B.; Arbuznikov, A.V.; Ayers, P.W.; Baerends, E.J.; Barone, V.; Calaminici, P.; et al. DFT exchange: Sharing perspectives on the workhorse of quantum chemistry and materials science. Phys. Chem. Chem. Phys. 2022, 24, 28700–28781. [Google Scholar] [CrossRef] [PubMed]
- Li, S.H.; Li, W.; Fang, T. An Efficient Fragment-Based Approach for Predicting the Ground-State Energies and Structures of Large Molecules. J. Am. Chem. Soc. 2005, 127, 7215–7226. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Li, S.H.; Jiang, Y.S. Generalized Energy-Based Fragmentation Approach for Computing the Ground-State Energies and Properties of Large Molecules. J. Phys. Chem. A 2007, 111, 2193–2199. [Google Scholar] [CrossRef]
- Li, S.H.; Li, W.; Ma, J. Generalized Energy-Based Fragmentation Approach and Its Applications to Macromolecules and Molecular Aggregates. Acc. Chem. Res. 2014, 47, 2712–2720. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Dong, H.; Ma, J.; Li, S.H. Structures and Spectroscopic Properties of Large Molecules and Condensed-Phase Systems Predicted by Generalized Energy-Based Fragmentation Approach. Acc. Chem. Res. 2021, 54, 169–181. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Nagle, J.K. Table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 2018, 117, 1200–1225. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Berkowitz, M.; Parr, R.G. Transcription of ground-state density-functional theory into a local thermodynamics. Proc. Natl. Acad. Sci. USA 1984, 81, 8028–8031. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Preston, H.J.T. The kinetic energy of molecular charge distributions and molecular stability. Int. J. Quantum Chem. 1969, 3, 327–347. [Google Scholar] [CrossRef]
- Tal, Y.; Bader, R.F.W. Studies of the energy density functional approach. 1. Kinetic energy. Int. J. Quantum Chem. 1978, 14, 153–168. [Google Scholar] [CrossRef]
- Cohen, L. Local kinetic energy in quantum mechanics. J. Chem. Phys. 1979, 70, 788–789. [Google Scholar] [CrossRef]
- Cohen, L. Representable local kinetic energy. J. Chem. Phys. 1984, 80, 4277–4279. [Google Scholar] [CrossRef]
- Yang, Z.Z.; Liu, S.B.; Wang, Y.A. Uniqueness and Asymptotic Behavior of the Local Kinetic Energy. Chem. Phys. Lett. 1996, 258, 30–36. [Google Scholar] [CrossRef]
- Ayers, P.W.; Parr, R.G.; Nagy, Á. Local kinetic energy and local temperature in the density-functional theory of electronic structure. Int. J. Quantum Chem. 2002, 90, 309–326. [Google Scholar] [CrossRef]
- Anderson, J.S.M.; Ayers, P.W.; Hernandez, J.I.R. How Ambiguous Is the Local Kinetic Energy? J. Phys. Chem. A 2010, 114, 8884–8895. [Google Scholar] [CrossRef] [PubMed]
- Berkowitz, M. Exponential approximation for the density matrix and the Wigner distribution. Chem. Phys. Lett. 1986, 129, 486–488. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.A.; Bartolotti, L.J.; Ayers, P.W.; Fievez, T.; Geerlings, P. Charge density and chemical reactivity: A unified view from conceptual DFT. In Modern Charge Density Analysis; Gatti, C., Macchi, P., Eds.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Liu, S.B. Conceptual Density Functional Theory and Some Recent Developments. Acta Phys.-Chim. Sin. 2009, 25, 590–600. [Google Scholar]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.B.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P.W. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139, 36. [Google Scholar] [CrossRef]
- Liu, S.B.; Rong, C.Y.; Wu, Z.M.; Lu, T. Rényi entropy, Tsallis entropy and Onicescu information energy in density functional reactivity theory. Acta Phys.-Chim. Sin. 2015, 31, 2057–2063. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Liu, S.B. Identity for Kullback-Leibler divergence in density functional reactivity theory. J. Chem. Phys. 2019, 151, 141103. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhao, D.B.; Lu, T.; Liu, S.B.; Rong, C.Y. Quantifications and Applications of Relative Fisher Information in Density Functional Theory. J. Phys. Chem. A 2021, 125, 3802–3811. [Google Scholar] [CrossRef] [PubMed]
- Rong, C.Y.; Wang, B.; Zhao, D.B.; Liu, S.B. Information-Theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 2020, 10, e1461. [Google Scholar] [CrossRef]
- Rong, C.Y.; Zhao, D.B.; He, X.; Liu, S.B. Development and Applications of the Density-Based Theory of Chemical Reactivity. J. Phys. Chem. Lett. 2022, 13, 11191–11200. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.B. Homochirality Originates from Handedness of Helices. J. Phys. Chem. Lett. 2020, 11, 8690–8696. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.B. Principle of Chirality Hierarchy in Three-Blade Propeller Systems. J. Phys. Chem. Lett. 2021, 12, 8720–8725. [Google Scholar] [CrossRef] [PubMed]
- Nalewajski, R.F.; Parr, R.G. Information theory, atoms in molecules, and molecular similarity. Proc. Natl. Acad. Sci. USA 2000, 97, 8879–8882. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.W. Information Theory, the Shape Function, and the Hirshfeld Atom. Theor. Chem. Acc. 2006, 115, 370–378. [Google Scholar] [CrossRef]
- Parr, R.G.; Ayers, P.W.; Nalewajski, R.F. What Is an Atom in a Molecule? J. Phys. Chem. A 2005, 109, 3957–3959. [Google Scholar] [CrossRef] [PubMed]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vohringer-Martinez, E.; Bultinck, P. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. 2nd row atoms, Z = 11 − 18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R. Adiabatic time-dependent density functional methods for excited state properties. J. Chem. Phys. 2002, 117, 7433–7447. [Google Scholar] [CrossRef]
- Liu, J.; Liang, W. Analytical Hessian of electronic excited states in time-dependent density functional theory with Tamm-Dancoff approximation. J. Chem. Phys. 2011, 135, 014113. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).