Abstract
Density functional theory (DFT) benchmark studies of 1H and 13C NMR chemical shifts often yield differing conclusions, likely due to non-optimal test molecules and non-standardized data acquisition. To address this issue, we carefully selected and measured 1H and 13C NMR chemical shifts for 50 structurally diverse small organic molecules containing atoms from only the first two rows of the periodic table. Our NMR dataset, DELTA50, was used to calculate linear scaling factors and to evaluate the accuracy of 73 density functionals, 40 basis sets, 3 solvent models, and 3 gauge-referencing schemes. The best performing DFT methodologies for 1H and 13C NMR chemical shift predictions were WP04/6-311++G(2d,p) and ωB97X-D/def2-SVP, respectively, when combined with the polarizable continuum solvent model (PCM) and gauge-independent atomic orbital (GIAO) method. Geometries should be optimized at the B3LYP-D3/6-311G(d,p) level including the PCM solvent model for the best accuracy. Predictions of 20 organic compounds and natural products from a separate probe set had root-mean-square deviations (RMSD) of 0.07 to 0.19 for 1H and 0.5 to 2.9 for 13C. Maximum deviations were less than 0.5 and 6.5 ppm for 1H and 13C, respectively.
1. Introduction
Prediction of NMR chemical shifts using computational quantum chemistry, including density functional theory (DFT), is a well-established methodology that can significantly decrease the likelihood of structure determination errors [1,2,3,4,5,6,7,8]. Such calculations can aid in NMR peak assignments [9,10], as highlighted in our recent example of misassigned beta-lactam carbonyl chemical shifts [11]. They have been used to confirm organic [12,13,14,15], inorganic [16,17], and organometallic [18,19] reaction products, particularly those with unexpected or unusual molecular structures [20,21,22], and they have been applied in complex speciation studies [23,24,25]. Perhaps most notably, chemical shift calculations were used to revise incorrectly reported natural product structures: aquatolide [26], vannusal B [27], glabramycin C [28], and hexacyclinol [29]. For elucidation of spectroscopically challenging natural products, Buevich and Elyashberg demonstrated that DFT NMR calculations could enhance the performance of computer-assisted structure elucidation (CASE) [30,31,32]. More recently, such calculations have been used to determine the conformations of cyclic peptides in solution [33,34], and they have been applied to biomolecules, such as nucleic acids [35,36,37], carbohydrates [38,39,40], and proteins [41,42,43]. Calculations of chemical shifts, via shielding tensors, have also been combined with solid-state NMR to help refine X-ray diffraction data of proteins [44] and to determine the packing arrangements of microcrystalline material [45], a practice referred to as NMR crystallography [46].
DFT is among the most widely used computational chemistry tools for chemical shift calculations due to the combination of accuracy and efficiency [3,7,47]. Application of DFT for structure problem solution involves judicious choice of both a density functional and basis set, which can be obtained from benchmark studies on a test set of compounds, often from 20 to 100 small- to medium-sized, rigid molecules that have readily available experimental data. A multitude of DFT benchmark studies have been reported in the literature (Table 1), yet these studies have presented conflicting conclusions regarding the most accurate method. For instance, Konstantinov and Broadbelt found BMK to be the best performing functional for chemical shift predictions [48], while Toomsalu and Burk found it to be the worst performing [49]. Granted, these two studies used different solvent conditions (viz., toluene-d8 and CDCl3), but even for the same solvent system there have been significantly different findings, such as Benassi recommending WP04 for δC predictions in CDCl3 based on a benchmark test set of 104 diverse, small organic molecules [50], while Buß and Koch found the performance of WP04, for a test set of 24 heterocycles in CDCl3, to be the second worst performing density functional for δC [51]. Paradoxically, the worst performing functional, WC04, from Buß and Koch’s study [51] was specifically parameterized for accurate δC predictions by Wiitala and coworkers [52]. More to this point, Stoychev, Auer, and Neese found double-hybrid density functionals, such as DSD-PBEP86, to provide superior performance for δH predictions that were most comparable to extremely costly coupled cluster calculations [53], while de Oliveria et al. recently reported no benefit for the use of double hybrids over conventional density functionals (i.e., GGAs, meta-GGAs, and hybrids) [54]. Additionally, most authors found that the gauge-independent atomic orbital (GIAO) method provides the best accuracy, but there have been two contemporary reports on improved accuracy using the continuous set of gauge transformations (CSGT) method [49,55]. Thus, it is difficult to choose which model chemistry to apply for spectral data predictions. One possible reason for these discrepancies is the use of vastly different experimental data sets for benchmarking.
One of the earliest and most comprehensive compound sets comprising 80 structures of proton (1H) chemical shifts was curated by Rablen et al. [1] in 1999 and later augmented by Tantillo and coworkers [3] with the inclusion of carbon (13C) chemical shift data (Figure 1a) and an additional 24 compounds in a separate probe set (Figure 1b). Although the test and probe sets of Rablen and Tantillo have been used for several benchmarking studies [1,3,50,56] with various density functionals, basis sets, and solvent effect studies, they are not without challenges: (1) relativistic effects from elements in rows three and beyond of the periodic table must be included for accurate δC predictions of carbons bound to the heavy atom (Figure 1c) [57]; (2) molecules such as furfural (Figure 1c) and dimethyl acetal exhibit multiple low-lying conformers in solution whose Boltzmann-weighting factors are highly dependent on the level of theory employed; (3) compounds such as methanol and indole contain hydrogen bond donors that will exhibit concentration-, pH-, and temperature-dependent chemical shifts in solution; (4) aromatic, olefinic, and alkynyl compounds may also exhibit concentration-dependent chemical shifts due to aggregation from π–π stacking [58,59]; and 5) experimental data were not measured in a single solvent system (instead, either CDCl3 or CCl4 was used, which may yield significant differences [60]). Experimental NMR chemical shift data used by Rablen and Tantillo were from eight sources [61,62,63,64,65,66,67,68] with sample concentrations for carbon NMR spectra, which at times reached up to 10% weight/volume (solid) or volume/volume (liquid). At such high concentrations, interactions between solute molecules may also lead to chemical shift differences [58].

Table 1.
Comparison of different benchmark studies for 1H and 13C NMR chemical shift predictions.
Table 1.
Comparison of different benchmark studies for 1H and 13C NMR chemical shift predictions.
| Best δH Method a | Best δC Method a | Orig. b | Geom. Optimization | Solv./Model c | Conv. d | Benchmark Set | Ref. |
|---|---|---|---|---|---|---|---|
| mPW1LYP/6-311+G(2d,p) | WP04/DGTZVP | GIAO | B3LYP/6-311+G(2d,p) | CDCl3/SMD | linear | 104 small organics | [50] |
| BMK/6-311G(d) | BMK/6-31G(d) | GIAO | B3LYP/6-31+G(d,p) | toluene/none | linear | 37 small organics | [48] |
| B97-2/pcS-3 | B97-2/pcS-3 | GIAO | B3LYP-D3/def2-TZVP | water/CPCM | MOSS | 176 metabolites | [69] |
| B3LYP/6-31G(d,p) | B3LYP/6-31G(d,p) | GIAO | B3LYP/6-31G(d,p) | gas/none | linear | 28 small organics | [70] |
| B97-2/pcS-2 | B97-2/6-311G(d,p) | GIAO | CCSD(T)/cc-pVTZ | gas/none | TMS | 29 CCSD(T) calcs. | [71] |
| δH not evaluated | B3LYP/6-311+G(d) B3LYP/MIDI! | GIAO | B3LYP/MIDI! | gas/none CDCl3/none | linear | 15 gas cmpds. 37 solution cmpds. | [72] |
| not recommended e | LC-TPSS/cc-pVTZ | CSGT | LC-TPSS/def2-SVP | CDCl3/COSMO | linear | 39 small molecules | [55] |
| WP04/pcS-2 PBE0/6-31G(d) | PBE0/pcS-2 PBE0/6-31G(d) | GIAO | δH: B3LYP/6-31(d) δC: ωB97X-D/6-31G(d) | CDCl3/PCM | linear | 24 heterocycles | [51] |
| WP04/aug-cc-pVDZ | mPW1PW91/ 6-311+G(2d,p) | GIAO | B3LYP/6-31+G(d,p) | CDCl3/PCM | linear | 23 small organics | [73] |
| B3LYP/6-311++G(2df,p) | δC not evaluated | GIAO | B3LYP/6-31+G(d) | CDCl3/none | linear | 80 small organics | [1] |
| WP04/aug-cc-pVDZ | δC not evaluated | GIAO | B3LYP/6-31G(d) | CDCl3/PCM | linear | 80 small organics | [56] |
| B3LYP/cc-pVDZ | B3LYP/cc-pVDZ | GIAO | B3LYP/6-31G(d) | CDCl3/COSMO | linear | 312 small molecules | [74] |
| SSB-D/ET-pVQZ | SSB-D/ET-pVQZ | GIAO | SSB-D/ET-pVQZ | gas/none | TMS | 33 small molecules | [75] |
| PBE0/cc-pVTZ | PBE0/aug-cc-pVDZ | CSGT | B3LYP/6-311++G(d,p) | CDCl3/none | TMS | 25 small organics | [49] |
| B3LYP/6-311++G(d,p) | δC not evaluated | GIAO | B3LYP/6-31G(d,p) | CDCl3/none | C6H6 | 14 aromatics | [76] |
| δH not evaluated | B3LYP/cc-pVDZ | GIAO | B3LYP/6-311++G(2d,p) | DMSO/CPCM | linear | 51 organics | [77] |
| LH20t/pcSseg-4 | mPSTS/pcSseg-4 | curr. f | CCSD(T)/cc-pVTZ | gas/none | TMS | 23 small organics f | [78] |
| DSD-PBEP86/ps4 | DSD-PBEP86/ps4 | GIAO | CCSD(T)/cc-pVTZ | gas/none | CH4 | 15 gas cmpds. | [53] |
| mPW1PW91/6-311G(d) | same as δH method | GIAO | B3LYP/6-31G(d,p) | CDCl3/PCM | TMS | 25 organics | [79] |
| revTPSS/cc-pVTZ | δC not evaluated | GIAO | M06-2X/6-311+G(2d,p) | gas/none | TMS | 72 small organics | [54] |
| DSD-PBEP86/pcSseg-3 | MP2/pcSseg-3 | GIAO | CCSD(T)/cc-pVQZ | gas/none | N/A g | 117 gas cmpds. | [80] |
a In cases where two methods are listed, no definitive conclusion on the best model chemistry was provided in the study. b Method for treating gauge origin dependence. c Solvent refers to the solvent (or gas phase) that the experimental NMR data were measured in, while model refers to the implicit solvent model used, if any. d Method to convert isotropic shielding tensors to chemical shifts. Linear = linear scaling factors; MOSS = motif-specific scaling (six linear scaling factors for different functionalities); TMS, C6H6, and CH4 = uses these compounds as single point references. e Errors with respect to experiment were found to be too large for δH predictions. f Benchmarking relative to theoretical results from CCSD(T)/def2-TZVP; gauge–origin invariance from current density approach [81]. g Benchmarking relative to absolute shieldings obtained from high-level in vacuo GIAO-CCSD(T)/pcSseg-3//CCSD(T)/cc-pVQZ calculations.
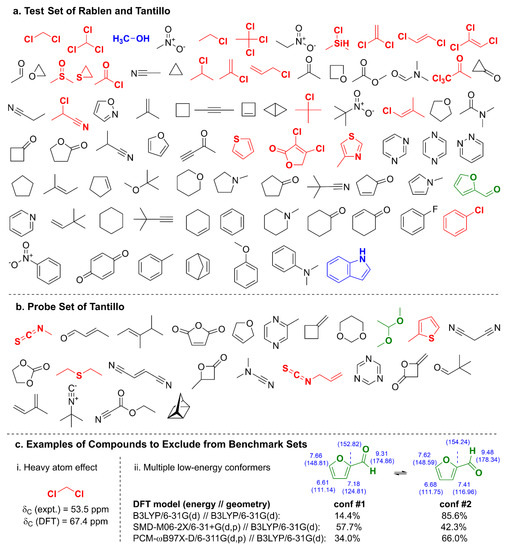
Figure 1.
(a) Benchmark test set used by Rablen et al. [1] and Tantillo et al. [3] to generate linear scaling factors per Equation (1). Bold-faced, colored structures are modeling challenges due to row three atoms (red), H-bond donors (blue), or multiple low-energy conformers (green). (b) Probe set used by Tantillo et al. [3] to examine accuracy of DFT model chemistries for δH and δC predictions. (c) Examples of problematic structures for benchmarking: (i) attachment of Cl, a row three heavy atom, to carbon results in a 13.9 ppm δC overprediction by DFT; and (ii) difficulties with accurately determining conformer energetics, as shown for several different energy calculations both with and without dispersion corrections using the same B3LYP/6-31G(d) geometries, can lead to vastly different Boltzmann populations and chemical shift predictions. Both 1H and 13C chemical shifts (δC in parentheses) were calculated using the DP4+ model (PCM-mPW1PW91/6-31+G**//B3LYP/6-31G*) [82].
When considering curation of a well-behaved test set, several compounds should be eliminated from the test set for the reasons indicated above (i.e., colored structures in Figure 1), such as those that contain row three elements or hydrogen bond donors or exhibit multiple low-lying conformers. Moreover, the experimental NMR data should be fully verified, including peak assignments, at a sufficiently low concentration in a single solvent system (viz., CDCl3), and spectra should be appropriately and consistently referenced to ensure reliability. In addition, because several molecules in the test set are highly reactive and thus not easily obtainable (i.e., bicyclobutane, cyclopropanone, and cyclobutene), they should also be excluded from consideration.
An additional plausible reason for the differing conclusions from various DFT chemical shift benchmarking studies is the varying referencing schemes used to convert isotropic shielding tensors into chemical shifts. The simplest method of subtracting the calculated isotropic shielding tensor, σ, for tetramethylsilane (TMS), according to the equation, δ = σTMS − σcmpd, is also the least accurate due to poor cancellation of errors, especially when comparing carbon atoms with different hybridization [83]. A better approach that improves error cancellation is to replace TMS with a structurally similar reference compound relative to the molecule of interest [84,85,86,87]. Alternatively, the most frequently applied methodology, which also improves error cancellation over TMS and does not require experimental data for specific reference compounds, is to calculate and apply linear scaling factors for a given computational model according to Equation (1) [1,3]. However, the downside is that such linear scaling factors must be determined from a large training set of experimental data, often as part of a comprehensive benchmarking study.
The goal of this research was to re-measure and verify experimental NMR assignments for a set of compounds, hereafter referred to as DELTA50, that can be used to provide a reliable benchmark for existing and new DFT methodologies as they are developed. In addition, a majority of currently available functionals, basis sets, and solvation models as implemented in Gaussian 16 [88] were tested to determine which is the most appropriate for 1H and 13C NMR chemical shift predictions. The DELTA50 set was then used to calculate (per Equation (1)) linear scaling factors for conversion of isotropic shielding tensors to chemical shifts. Finally, the performance of the optimal methods and linear scaling factors were assessed using 20 natural products and small- to medium-sized organic compounds, which represents a probe set.
2. Results and Discussion
2.1. DELTA50 Compound Curation and Experimental Measurements
DELTA50 (Figure 2) contains 50 compounds, comprising 114 proton and 143 carbon chemical shifts, which is a subset of the compounds from the test and probe sets of Rablen [1] and Tantillo [3] (Figure 1) that avoids the previously mentioned problem cases. A wide variety of functional groups (nitro, fluoro, nitrile, aldehyde, ketone, ester, alkyne, amide, amine, olefin, aliphatic, aromatic, and ether), ring sizes (three- to six-membered), and bond hybridizations are present, resulting in 1H and 13C NMR chemical shifts ranging from 0.25 to 9.80 ppm and −2.9 to 219.4 ppm, respectively.
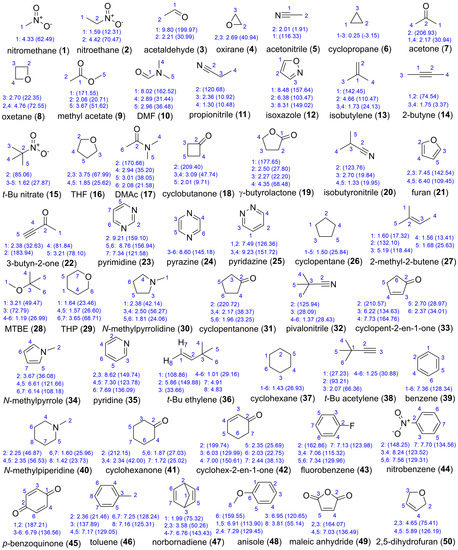
Figure 2.
DELTA50 benchmark set of 50 small molecules that avoid the issues described in Figure 1. Experimental 1H chemical shifts are provided for numbered carbon atoms with 13C chemical shifts listed in parentheses. Numbering corresponds to that used in calculations. Experimental data were acquired on a 600 MHz NMR in CDCl3 and referenced to TMS at 0.00 ppm for both 1H and 13C.
Proton and carbon NMR spectra were acquired at 298 K for ≤10 mM solutions of each compound dissolved in CDCl3 with 0.03% TMS as internal reference using a 600 MHz spectrometer. A concentration of 10 mM in a 5 mm NMR tube (~1–2 mg) allowed for collection of 13C NMR spectra in reasonable overall acquisition times (e.g., approximately 2–4 h on a Bruker 600 MHz AVANCE III spectrometer equipped with a liquid N2-cooled broadband Prodigy™ probe) with all resonances detectable (signal-to-noise ratio ≥ 3:1). Proton NMR spectra were acquired using a 2.73 s acquisition time, 20 ppm spectral width, 6.175 ppm transmitter frequency, 16 scans, and a 1 s relaxation delay. Carbon NMR spectra were acquired using a 0.9 s acquisition time, 240 ppm spectral width, 100 ppm transmitter frequency, 3072 to 4096 scans, and a 2 s relaxation delay. Spectral data were processed in MestReNova, version 14.2. using 0.3 and 1.0 Hz exponential line broadenings applied to 1H and 13C, respectively. Both proton (δH) and carbon (δC) chemical shifts were referenced to TMS at 0.00 ppm and recorded to two decimal places. Individual proton and carbon spectra for each molecule are provided in the Supplementary Materials with expansions for individual multiplets or congested spectral regions, and the assigned chemical shifts are shown for each spectrum; these are also shown in Figure 2.
A concentration-dependent study was undertaken to ensure that samples were sufficiently dilute to avoid deleterious aggregation using a representative subset of compounds with diverse functionalities from DELTA50: benzene, pyridazine, tetrahydrofuran (THF), 3-butyn-2-one, and fluorobenzene (Figure 3). Here, it was found that proton chemical shifts were stable within a variance of ±0.3% at concentrations up to 50 mM. The largest concentration effects were observed for pyridazine and 3-butyn-2-one, which were also found to exhibit the largest proton chemical shift deviations from theoretical predictions in Rablen’s study [1]. THF did not show any chemical shift changes up to a concentration of 50 mM, as would be expected for an aliphatic compound, while the chemical shifts of benzene and fluorobenzene deviated by less than 0.02%, indicating that π–π interactions were not appreciable at these concentrations. The alkyne proton chemical shift (3.21 ppm) of 3-butyn-2-one proportionally increased up to 0.1% with increasing concentration, while the methyl proton resonance (2.38 ppm) showed no change, indicating slight π interactions. The protons meta to nitrogen of pyridazine (7.49 ppm) showed the largest concentration dependence, and it was also noticed in the pyridazine samples that the peak width and chemical shift of residual water varied considerably (υ1/2 12 to 23 Hz and δH 1.54 to 1.80 ppm). This pointed to the presence of DCl in CDCl3 that could protonate basic nitrogens, especially at low concentrations. Thus, a few solid crystals of anhydrous K2CO3 were added to the CDCl3 solvent to neutralize DCl, and this resulted in more consistent chemical shifts as well as markedly improved pyridazine peak shape. Based on these results, anhydrous K2CO3 was used for all sample preparations of basic compounds, and a 10 mM concentration was considered acceptable for the compounds in the DELTA50 test set.
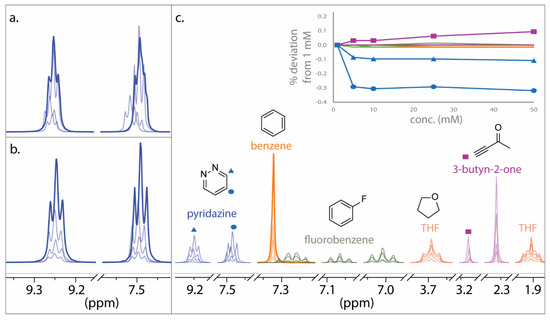
Figure 3.
Proton chemical shift dependence as a function of concentration in CDCl3. (a) Pyridazine without K2CO3. (b) Pyridazine with K2CO3 to neutralize residual DCl. (c) 600 MHz NMR spectral overlays for individual compounds. Concentrations were varied from 1 to 50 mM. The largest chemical shift deviations with respect to concentration are highlighted for pyridazine (blue triangles and circles) and the alkyne proton of 3-butyn-2-one (pink squares).
In some cases where chemical shift assignments were not sufficiently obvious from chemical shifts, scalar coupling, and integration, additional one- and two-dimensional (NOE, gCOSY, multiplicity-edited gHSQC, and/or gHMBC) spectra were acquired for confirmation. In particular, selective NOEs (300 to 700 ms mixing times) were used to determine the assignment of the methyl peaks in 2-methyl-2-butene, N,N-dimethylacetamide (DMAc), and N,N-dimethylformamide (DMF).
The differences between the previous experimental data and those recorded in the present study are shown as histogram plots (Figure 4). While 76 proton chemical shifts (67%) were within ±0.05 ppm of the previously reported experimental data, there were 19 outliers (17%) with greater than a ±0.10 ppm deviation. The largest difference of 0.21 ppm was for the α-ether protons of tetrahydropyran. Linear scaling factors calculated at the B3LYP/cc-pVTZ//B3LYP/6-31G(d) level using the previous experimental data were approximately 0.2% different than using the newly acquired data (slope = −1.0429, intercept = 31.6499 versus slope = −1.0450, intercept = 31.6889, respectively), resulting in a maximum 0.04 ppm difference in predicted proton chemical shifts. For δC, 88 out of 143 measurements (62%) were within ±0.25 ppm of the previously reported experimental data; 8 outliers (6%) were found with greater than a ±0.50 ppm difference. The largest carbon chemical shift difference of 2.45 ppm was for the keto carbon of cyclohexanone. Linear scaling factors, at the B3LYP/cc-pVTZ//B3LYP/6-31G(d), differed by approximately 0.1% (slope = −1.0372, intercept = 181.5955 using the previous experimental data, and slope = −1.0364, intercept = 181.5727 using the newly acquired data). This resulted in differences of up to 0.15 ppm.
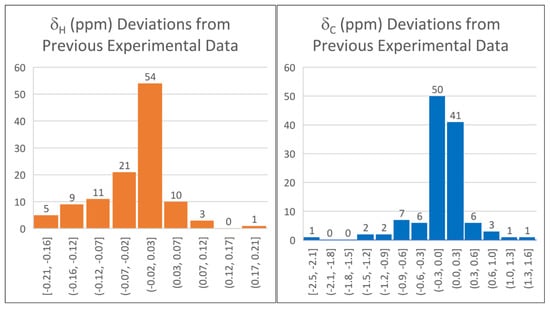
Figure 4.
Histogram plots showing frequency of measured differences between experimental data available in the literature compared with re-measured values in this study for 114 proton chemical shifts and 143 carbon chemical shifts.
To ensure that only a single low-energy conformer comprised at least 98% of the Boltzmann distribution, a conformer search was performed for each molecule in the DELTA50 set using a mixed torsional, low-mode sampling search in MacroModel and the OPLS4 force field [89] as implemented in the Schrödinger software suite, version 2021-1 [90]. In some cases, multiple conformers were found, such as boat and chair forms of cyclohexane, and these were analyzed further by DFT energy calculations using the M06-2X/6-31+G(d,p) model chemistry (including vibrational energy corrections) and the SMD solvent model for chloroform, as implemented in Gaussian 16 [88]. This model chemistry was chosen because the M06-2X functional combined with the SMD solvent model has been shown to be particularly effective for prediction of relative energies [91,92,93,94]. Minimum energy conformations were initially verified by lack of imaginary vibrational modes (i.e., the second derivative matrix of energy with respect to displacement was positive definite). Boltzmann probabilities were calculated (see Supplementary Materials for additional details), and the dominant conformer (≥98% probability weighting) was included in the DELTA50 set (as was the case for the chair conformation of cyclohexane).
For each molecule in the DELTA50 set, geometries were optimized at the B3LYP/6-31G(d) level. The Cartesian coordinates and atom numbering for optimized geometries are provided in the Supplementary Materials along with the experimentally measured chemical shifts. A relatively low level of theory was chosen for molecular geometry optimizations because: (1) geometries are reasonably well predicted at this level; (2) geometry optimization is one of the most time-consuming steps in a DFT calculation; and (3) predicted chemical shift dependencies on molecular geometry should be correctable via linear scaling factors [3]. Moreover, the impact of geometry optimization on overall accuracy was further assessed after evaluating the performance of various functionals, basis sets, and solvent models.
2.2. DFT Benchmark Study
The performance of 73 density functionals implemented in Gaussian 16 [88] was evaluated for GIAO isotropic shielding predictions using a large, correlation-consistent, triple-zeta basis set, cc-pVTZ, ultrafine integration grid, and the polarizable continuum model (PCM) for solvent effects. Hartree–Fock (HF) theory was also evaluated for comparison purposes. A wide variety of different classes of functionals (Table 2) were included: those based on either the local density approximation (LDAs), generalized gradient approximation (GGAs), meta-GGAs, or hybrids, such as the popular B3LYP functional, that include an empirically derived contribution of HF exchange. In addition, range-separated functionals, which are often denoted with the prefix ‘LC’ for long-range correction, were also evaluated. Range-separated functionals vary the contributions from the various exchange terms based on pairwise electronic spatial distance to overcome problems from long-range density over-delocalization [95]. Finally, the impact of including an empirical dispersion correction, denoted as either ‘D’ or ‘D3′, was also considered. While most of these functionals were designed for reproduction of electronic energies, two functionals, WP04 and WC04, were specifically parameterized for accurate proton and carbon chemical shift prediction, respectively [52].

Table 2.
Performance of density functionals and HF for 1H and 13C chemical shift predictions.
Isotropic shielding tensors, σ, were converted to chemical shifts through linear regression analysis in Excel. To evaluate performance of each functional, residuals (deviations) were plotted as a function of chemical shift, and root-mean-square deviations (RMSD) and maximum deviations (MD) were calculated (Table 2). Particular focus was placed on evaluation of systematic errors with respect to hybridization and functional groups.
In general, a systematic improvement in accuracy was seen in going from HF theory to LDAs and then to more advanced functionals, e.g., HF < LDAs < GGAs ≈ meta-GGAs < hybrids. However, range separation showed minimal improvement in accuracy, and in most cases, except ωB97X-D, no difference was observed upon including an empirical dispersion correction. Maximum deviations for proton and carbon chemical shifts were typically from 0.2 to 0.5 ppm and 5 to 8 ppm, respectively. HF, SOGGA11, and several of the Minnesota functionals performed particularly poorly. The best performing functionals in the present study were found to be ωB97X-D for carbon chemical shifts and WP04 for proton chemical shifts.
Figure 5 shows an example of carbon chemical shift deviations from experiment for several representative functionals from each class versus Hartree–Fock theory. Deviations were typically smaller for proton and carbon chemical shifts that resonate upfield (i.e., less than approximately 4.5 and 60 ppm for δH and δC, respectively), which corresponds to sp3-hybridized carbons. The largest deviations for carbon chemical shift predictions were typically carbonyls, olefins, and sp-hybridized carbons. Systematic errors were observed among several functional groups across the board for most density functionals. For instance, mPW1PW91, PBE0, B3LYP, and B97-D overpredicted the more electron-rich carbon in olefins by 2–5 ppm and underpredicted the amide carbonyl in DMF and DMAc by 3–6 ppm. Alkynes and nitriles were overpredicted by several ppm for mPW1PW91 and PBE0, underpredicted by 1–2 ppm for B97-D, or exhibited no noticeable bias for B3LYP.
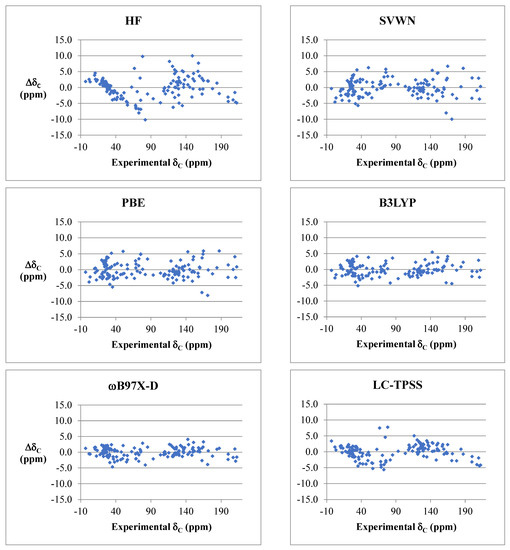
Figure 5.
Comparison of deviations for carbon chemical shift predictions for representative density functionals and HF (cc-pVTZ basis sets, B3LYP/6-31G* optimized geometries, and PCM solvation model for chloroform was used in all instances).
Following functional evaluation, the basis set size was investigated. In principle, larger, more complete basis sets should have the flexibility to better approximate the electronic density and thereby yield higher accuracy, but this has not always been found to be the case with DFT-based methods [96,97,98]. Importantly, the size of the basis set can dramatically increase computational time. A medium-sized basis set would be most appropriate for larger molecules of greater than 600–700 Da, while the most accurate basis set should be utilized for calculations of small molecules or fragment structures and for critical compounds, such as newly discovered natural products with unusual scaffolds (e.g., homodimericin A [99]). Table 3 shows the errors and computation times for 40 basis sets from double to quadruple zeta, including polarization and diffuse functions on both heavy atoms and hydrogens. While counterintuitive (yet similar to other benchmark studies), smaller basis sets were found to provide more accurate carbon chemical shift predictions [48,51,71], with def2-SVP identified as the best performing basis set when paired with the ωB97X-D functional. Conversely, proton chemical shift predictions typically require larger basis sets, and diffuse functions appear to be productive for reducing errors. The best performing basis set was 6-311++G(2df,p); however, the computational time was found to be more than six times longer for calculation of nitromethane compared to the next smaller Pople-type basis set, 6-311++G(2d,p). Because 6-311++G(2d,p) performed nearly as well, this was chosen as the preferred basis set when paired with WP04 for proton chemical shift predictions.

Table 3.
Impact of basis set on accuracy of 1H and 13C NMR chemical shift predictions a.
In general, δH predictions exhibited substantially fewer systematic errors than δC. There were still a few notable cases: the aldehyde proton of DMF was often underpredicted by 0.1 to 0.5 ppm, cyclopropane was overpredicted by 0.1 to 0.3 ppm, and the alkyne protons in t-butyl acetylene and 3-butyn-2-one were underpredicted by 0.1 to 0.3 ppm.
Chemical shift calculations require that the Hamiltonian include interaction terms from the external magnetic field vector, which under a finite basis set leads to a dependence on the choice of the vector origin or gauge [100]. While all gauge methods converge to the same limit at increasing basis set size, most chemical shift calculations are typically handled via GIAO [101,102,103,104,105] due to faster convergence; however, Iron [55] found that the CSGT [105,106,107] method provides more accurate results when paired with long-range corrected (LC) functionals (i.e., the CSGT method with LC-TPSS/cc-pVTZ and the COSMO solvation model was recommended). To test if alternative gauge procedures showed improvement in predictability, CSGT and individual gauges for atoms in molecules (IGAIM) [106,107] were compared to GIAO. Because the accuracy of the gauge method is dependent on basis set size, the basis set was also varied from double- to triple-zeta with inclusion of varying amounts of diffuse and polarization functions. Table 4 shows that, as expected, GIAO converged much more quickly than CSGT and IGAIM. For carbon chemical shift predictions, GIAO produced the lowest RMSD error at only a double-zeta basis set, def2-SVP, and predictions became worse at larger basis sets. The CSGT and IGAIM predictions were nearly equivalent and required triple-zeta basis sets augmented with diffuse functions (viz., aug-cc-pVTZ and jul-cc-pVTZ), which were more than an order of magnitude longer in computation time, to yield comparable levels of accuracy to GIAO with def2-SVP. For proton chemical shifts, GIAO was slower to converge compared to carbon, yet GIAO still exhibited significantly improved accuracy at smaller basis set sizes versus CSGT and IGAIM. Based on these results, GIAO should be the preferred method when considering both speed and accuracy.

Table 4.
Impact of gauge-referencing method and basis set on δH and δC predictions a.
Chemical shifts strongly depend on the molecular geometry and internuclear bond distances. Fortunately, the ground state geometry of most compounds has been shown to be well predicted at relatively low levels of theory using a wide variety of density functionals and even Hartree–Fock theory. At the start of this benchmarking study, geometries were optimized in vacuo at the B3LYP/6-31G(d) level, which is a frequently used methodology for computations of spectroscopic properties as well as energetics. The appropriateness of that choice was investigated by holding the NMR chemical shift calculation method constant [PCM-ωB97X-D/def2-SVP for δC and PCM-WP04/6-311++G(2d,p) for δH] while varying the geometry optimization method. Four different functionals (B3LYP, B3LYP-D3, M06-2X, and ωB97X-D), which are often used for geometry optimizations, were tested when paired with Pople-type basis sets from double- to triple-zeta. In addition, implicit solvation models, PCM or SMD, were applied to the optimizations of B3LYP, B3LYP-D3, and M06-2X because they exhibited the best accuracy for gas phase calculations. Finally, several computationally economical methods, such as HF, PBE, BLYP, and two semi-empirical methods, PM7 and AM1, were also investigated. Data in Table 5 show that the choice of geometry optimization method led to similar accuracy, which validates the choice of using a relatively low level of theory for the bulk of this benchmarking study. B3LYP performed better than M06-2X and ωB97X-D. Inclusion of dispersion correction resulted in a slight improvement in accuracy, at the expense of a negligible increase in computational time. Thus, B3LYP-D3 was used rather than B3LYP, with the additional benefit that the impact of the D3 correction should also enhance the accuracy of the energy prediction for Boltzmann-weighting. Adding an implicit solvation model also resulted in a moderate improvement in accuracy, with the PCM model slightly outperforming SMD. The most accurate predictions for carbon chemical shifts were found when using PCM-B3LYP-D3 with the 6-311G(d,p) basis set, while proton chemical shifts were very slightly less accurate with that basis set compared to 6-31G(d,p).

Table 5.
Impact of molecular geometry on chemical shift predictions a.
Finally, the impact of the solvent model on the accuracy of chemical shifts was studied. Three implicit solvation models implemented in Gaussian 16 were tested with the DELTA50 set using either ωB97X-D/def2-SVP for δC or WP04/6-311++G(2d,p) for δH. The integral equation formalism (IEF) version of the polarizable continuum model (PCM) is the recommended (default) model in Gaussian 16 [108]. The SMD model of Truhlar et al. [109] is a revised version of the PCM model that was developed specifically for reproducing solvation energies. Finally, the polarizable conductor calculation model, CPCM, [110,111] was also evaluated. Results in Table 6 show a marked improvement with the use of any solvation model but only a slight improvement in accuracy when using PCM versus CPCM or SMD.

Table 6.
Impact of implicit solvent model on chemical shift predictions a.
Table 6.
Impact of implicit solvent model on chemical shift predictions a.
| δH (ppm) | δC (ppm) | |||
|---|---|---|---|---|
| Solvent Model b | RMSD c | MD c | RMSD c | MD c |
| PCM | 0.079 | 0.21 | 1.50 | 4.61 |
| CPCM | 0.080 | 0.20 | 1.50 | 4.57 |
| SMD | 0.087 | 0.29 | 1.51 | 4.69 |
| none | 0.107 | 0.33 | 1.84 | 5.31 |
a Calculations using PCM (chloroform) solvent model and B3LYP/6-31G(d) geometries. b Recommended implicit solvation model highlighted in blue, bold font. c RMSD = root-mean-square deviation; MD = maximum deviation.
Based on the totality of the previous results, the best performing density functional for carbon chemical shift prediction was found to be ωB97X-D when paired with the def2-SVP basis set. For proton chemical shift predictions, the WP04 functional exhibited the lowest error when combined with the 6-311++G(2df,p) basis set, but calculation times were unreasonably long. In contrast, the smaller 6-311++G(2d,p) basis set gave nearly comparable accuracy at a six-fold reduced computational cost. For both proton and carbon chemical shift predictions, the GIAO method was most accurate at these basis set sizes. Molecular geometries should be optimized at the B3LYP-D3/6-311G(d,p) level. Implicit solvent effects from the PCM model should be included at all stages of the calculation. The best performing models were δH: GIAO-PCM-WP04/6-311++G(2d,p)//PCM-B3LYP-D3/6-311G(d,p) and δC: GIAO-PCM-ωB97X-D/def2-SVP//PCM-B3LYP-D3/6-311G(d,p). When it is necessary to reduce calculation times for larger molecules, the geometry optimization step can be changed to B3LYP/6-31G(d) with a moderate reduction in accuracy for carbon chemical shift predictions while maintaining the same level of accuracy for protons after changing the basis set to jul-cc-pVDZ for proton NMR calculations. Importantly, dispersion corrections should still be used for electronic energy calculations with this faster method. In cases where dispersive interactions may be critical to the optimized geometry, such as inclusion of explicit solvent and studies of organometallic complexes, then the high-accuracy method should be used. The recommended methods and linear scaling factors are listed in Table 7.

Table 7.
Recommended DFT methods and linear scaling factors.
Table 7.
Recommended DFT methods and linear scaling factors.
| Calculation Step | Method 1: Speed + Efficiency | Method 2: High Accuracy |
|---|---|---|
| Geometry Optimization | B3LYP/6-31G(d) a | PCM-B3LYP-D3/6-311G(d,p) |
| Energy Calculation | PCM-B3LYP-D3/6-31G(d) | PCM-B3LYP-D3/6-311G(d,p) |
| δH Calculation | GIAO-PCM-WP04/jul-cc-pVDZ | GIAO-PCM-WP04/6-311++G(2d,p) |
| δH Scaling Factors b | m = −1.0309, b = 31.8883 | m = −1.0311, b = 32.2654 |
| δC Calculation | GIAO-PCM-ωB97X-D/def2-SVP | GIAO-PCM-ωB97X-D/def2-SVP |
| δC Scaling Factors b | m = −1.0081, b = 195.6683 | m = −1.0065, b = 196.0386 |
a The “fine” integration grid will also improve calculation speed with a negligible impact on accuracy at this level of theory (note: a larger grid is needed for meta-GGAs [112]). b slope = m, y-intercept = b; to be used in Equation (1).
2.3. Probe Set Evaluation
Next, the performance of each method from Table 7 was evaluated for chemical shift predictions of small- to medium-sized complex synthetic organic compounds and natural products. In this fashion, DELTA50 can be considered a training set for generation of linear scaling factors or optimization of new empirical density functionals, while the series of complex structures and natural products represents a probe set. Twenty relatively rigid, well-studied compounds ranging in molecular weights from 96 to 854 g mol−1 with experimental NMR data measured in deuterated chloroform were included in this probe set. These structures and calculation results are listed in Figure 6 and Table 8, respectively. Most of the compounds in the probe set have existing single-crystal X-ray diffraction (SCXRD) data, and/or their structures have been verified via total synthesis. Additionally, for 18 out of 20 compounds, previous DFT chemical shift calculations have been performed. For several cases, multiple high-quality computational NMR studies have been performed (see Supplementary Materials for data from additional reports). This allows for direct comparison to the best performing methods in this study. Also noteworthy is that for most of these compounds, extensive 2D NMR data have been collected, such that the proton and carbon chemical shift assignments are unlikely to be misassigned. A few proton and carbon assignments are still ambiguous, such as the carbons resonating from 40 to 50 ppm of ingenane diterpene 8, and these have been left out of the probe set (further details can be found in the Supplementary Materials).
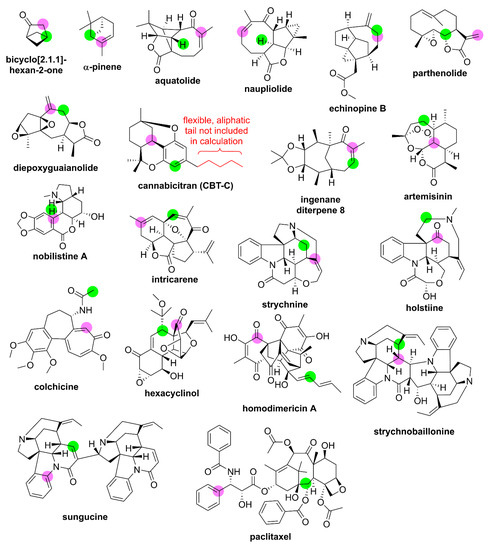
Figure 6.
Probe set structures. Atomic locations of maximum chemical shift deviations compared to experiment for method two calculations from this study are highlighted for δC and δH in magenta and lime green, respectively.
Several trends are immediately noticeable. As expected, method two generally exhibited the most accurate performance as evident by the lowest RMSD for 14 out of 20 proton chemical shift predictions and 16 out of 20 carbon chemical shift predictions. Moreover, the maximum δC deviation across all compounds, representing 424 carbon chemical shift predictions, was only 6.5 ppm for a ketone carbon of homodimericin A, which provides a relatively low upper limit upon which putative NMR structure proposals could be called into question following DFT calculations using the prescribed model chemistry in this paper. It should also be noted that in a few cases where existing literature DFT methods were found to outperform method two, such as the δH predictions of strychnine or the δC predictions of artemisinin, these were from studies where the DFT procedures were specifically optimized for these classes of compounds rather than being a general-purpose chemical shift model chemistry for organic compounds.
From Figure 6, there also appears to be a spatial relationship between the least accurate predicted proton and carbon chemical shift from method two, which is highlighted by the colored circles. This was unexpected considering that markedly different optimal density functionals and basis set sizes were used for carbon (GIAO-PCM-ωB97X-D/def2-SVP) versus proton [GIAO-PCM-WP04/6-311++G(2d,p)] chemical shift predictions, although they share the same geometry optimization method [PCM-B3LYP-D3/6-311G(d,p)]. In all cases except echinopine B, the least accurately predicted proton is not attached to the least accurately predicted carbon. Rather, while both nuclei are in close spatial proximity, they are separated by approximately 2.5 to 5 Å. This is most pronounced for olefinic carbons that are often overpredicted by approximately 3 to 5 ppm leading to an underprediction, or over-shielding effect, on nearby protons by approximately 0.1 to 0.3 ppm. It is also noteworthy that a few investigators have found that isotropic shielding tensors are particularly sensitive to the molecular geometry [113,114], and this may indicate that future improvements in density functional performance for chemical shift predictions might come indirectly from improvements in the geometry optimization method rather than from the functional used for GIAO shielding tensor calculations.

Table 8.
DFT method performances for chemical shift predictions of probe compounds.
Table 8.
DFT method performances for chemical shift predictions of probe compounds.
| Compound | MW (g mol−1) | Confs c | δ (ppm) | This Study a | Previous DFT Studies | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method 1 | Method 2 | |||||||||
| RMSD d | MD d | RMSD d | MD d | RMSD d | MD d | Ref. e | ||||
| bicyclo [2.1.1]-hexan-2-one | 96 | 1 | δH: δC: | 0.03 0.6 | 0.05 0.8 | 0.07 0.5 | 0.12 0.7 | 0.12 1.1 | 0.20 1.7 | [26] |
| α-pinene | 136 | 1 | δH: δC: | 0.08 1.6 | 0.19 3.5 | 0.08 1.5 | 0.15 3.6 | 0.63 3.6 | 1.14 7.4 | [115] |
| aquatolide | 246 | 3 | δH: δC: | 0.10 1.7 | 0.26 4.1 | 0.05 1.5 | 0.11 3.2 | 0.11 1.8 | 0.27 4.1 | [26] |
| naupliolide | 246 | 4 | δH: δC: | 0.14 2.3 | 0.33 5.5 | 0.10 1.9 | 0.20 5.6 | 0.23 3.0 | 0.58 7.8 | [26] |
| echinopine B | 246 | 9 | δH: δC: | 0.07 1.4 | 0.17 2.6 | 0.08 1.4 | 0.22 2.5 | 0.10 2.5 | 0.22 5.5 | [26] |
| parthenolide | 248 | 3 | δH: δC: | 0.08 1.5 | 0.14 3.0 | 0.02 1.4 | 0.04 2.8 | not available | ||
| diepoxy-guaianolide | 262 | 5 | δH: δC: | 0.12 1.7 | 0.21 4.1 | 0.05 1.8 | 0.12 4.1 | 0.18 1.3 | 0.44 2.6 | [116] |
| cannabicitran (CBT-C) | 258 b | 2 | δH: δC: | 0.11 0.9 | 0.17 2.2 | 0.07 1.0 | 0.17 2.2 | 0.12 1.1 | 0.31 2.0 | [117] |
| ingenane diterpene 8 | 278 | 2 | δH: δC: | 0.17 2.7 | 0.39 4.5 | 0.06 2.2 | 0.14 4.7 | 0.08 2.2 | 0.20 3.9 | [26] |
| artemisinin | 282 | 1 | δH: δC: | 0.10 1.1 | 0.25 2.1 | 0.12 1.1 | 0.24 2.3 | -- f 0.8g | -- f 1.4 g | [118] |
| nobilistine A | 317 | 20 | δH: δC: | 0.14 1.7 | 0.25 3.6 | 0.12 1.5 | 0.25 3.5 | 0.27 1.6 | 0.65 3.1 | [119] |
| intricarene | 326 | 2 | δH: δC: | 0.10 2.3 | 0.24 4.0 | 0.09 2.1 | 0.21 3.8 | 0.12 2.2 | 0.27 4.9 | [26] |
| strychnine | 334 | 3 | δH: δC: | 0.15 1.5 | 0.41 4.0 | 0.10 1.4 | 0.25 3.8 | 0.08 1.8 | 0.18 6.7 | [120] |
| holstiine | 382 | 4 | δH: δC: | 0.16 2.4 | 0.30 7.7 | 0.10 1.9 | 0.23 5.1 | 0.21 2.9 | 0.47 11.3 | [121] |
| colchicine | 399 | 81 | δH: δC: | 0.10 2.1 | 0.21 3.8 | 0.11 2.2 | 0.20 4.0 | 0.16 2.3 | 0.25 5.0 | [59] |
| hexacyclinol | 416 | 23 | δH: δC: | 0.15 2.4 | 0.38 7.0 | 0.13 2.1 | 0.30 5.9 | 0.29 4.6 | 0.62 9.0 | [122] |
| homodimericin A | 491 | 9 | δH: δC: | 0.10 3.4 | 0.21 7.7 | 0.10 2.9 | 0.19 6.5 | not available | ||
| strychnobaillonine | 613 | 12 | δH: δC: | 0.19 3.0 | 0.46 10.4 | 0.16 2.4 | 0.34 6.4 | 0.22 2.9 | 0.62 6.7 | [123] |
| sungucine | 635 | 11 | δH: δC: | 0.18 1.9 | 0.51 4.4 | 0.14 1.8 | 0.31 4.5 | 0.18 1.8 | 0.64 5.4 | [124] |
| paclitaxel | 854 | >157 | δH: δC: | 0.17 2.8 | 0.43 7.2 | 0.19 2.3 | 0.52 6.3 | -- f 3.7 | -- f 9.1 | [125] |
a Results from performance of methods one and two from Table 7. b For cannabicitran, calculations were performed on a truncated structure (MW 258). c Number of conformers within 5 kcal mol−1 of the DFT-calculated global energy minimum. d RMSD = root-mean-square deviation; MD = maximum deviation, in ppm. (Best performance for each compound is highlighted in blue, bold font). e Reference to previous DFT prediction results if available. See SI for calculation details. f The only DFT predictions available were for δC. g Only 6 out of 15 δC calculations were reported [118].
3. Materials and Methods
The following solvents and standard reagents were purchased from Sigma-Aldrich: chloroform-d (99.96 atom %D) with 0.03% (v/v) TMS, tetrahydrofuran (anhydrous, inhibitor-free, ≥99%), 1-methyl pyrrole (99%), γ-butyrolactone (99+%), nitroethane (99.5%), pyrazine (99+%), bicyclo [2.2.1]hepta-2,5-diene (98%), cyclopentane (analytical standard), pyridazine (98%), fluorobenzene (analytical standard), pyrimidine (≥98.0%), acetaldehyde (ACS reagent grade, ≥99.5%, in a sealed ampule), trimethylene oxide (97%), 2-butyne (98%), ethylene oxide (2000 μg/mL dissolved in dichloromethane, a certified reference material, in a sealed ampule), furan (≥99%), cyclopropane (≥99%, in a gas cylinder), 2-methyl propene (99%, in a gas cylinder), N,N-dimethylacetamide (99.8%, extra dry), cyclohexane (99.5%, anhydrous), methyl acetate (99.5%, anhydrous), nitromethane (≥99.0%), acetonitrile (99.8%, anhydrous), N,N-dimethylformamide (99.8%, anhydrous), 2,5-dihydrofuran (97%), toluene (99.8%, anhydrous), isobutyronitrile (99%), acetone (≥99.9%, HPLC grade), tert-butyl methyl ether (99.8%, anhydrous), tetrahydropyran (99%, anhydrous), propionitrile (analytical standard), 2-methyl-2-butene (99+%), and N-methylpyrrolidine (97%). 3-Butyn-2-one (98+%) was obtained from Lancaster Synthesis. The following reagent standards were purchased from Oakwood Chemicals: cyclobutanone, cyclopent-2-enone, 3,3-dimethyl-1-butene, 2-methyl-2-nitropropane, benzene (ACS grade), nitrobenzene, 3,3-dimethyl-1-butyne, pyridine, anisole, cyclohex-2-enone, cyclohexanone, 1-methyl piperidine, maleic anhydride, p-benzoquinone, pivalonitrile, cyclopentanone, and isoxazole.
Dissolved solutions of gaseous reagents, cyclopropane and isobutylene (2-methyl propene), were prepared by bubbling them through CDCl3 and then serially diluting until acceptable NMR spectra were obtained (i.e., chemical shifts were stable upon dilution, indicating no aggregation).
Homodimericin A was provided by Aili Fan (Peking University, Beijing, China).
A variety of density functionals, as implemented in Gaussian 16 [88], were evaluated as part of the benchmarking study. The exchange and correlation components of LDAs, GGAs, and meta-GGAs as well as standalone combinations are listed in the Supplementary Materials along with primary references. In addition, the long-range correction method of Hirao and co-workers was also applied to the non-hybrid functionals, BP86, BPW91, N12, TPSS, revTPSS, and M06-L, which were noted in Table 1 with the prefix ‘LC’.
4. Conclusions
Experimental proton and carbon NMR chemical shift data for 50 structurally diverse compounds dissolved in deuterated chloroform were carefully measured in this study, enabling a comprehensive benchmark of DFT methods. Linear scaling factors to convert isotropic shielding tensors to chemical shifts were generated for two recommended methodologies that balance speed and accuracy. These two best performing methods were then evaluated against 20 probe organic compounds and natural products with high accuracy observed particularly when compared to previously reported DFT predictions for proton and carbon chemical shifts of these well-studied structures.
Of particular importance, this chemical shift test set can be used for performance evaluation of newly developed model chemistries as well as future design and optimization of empirical density functionals. Such work will be a focus for future research conducted in our laboratory.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28062449/s1, fully assigned experimental NMR spectra for DELTA50 compounds, optimized xyz coordinates for all calculated molecules, tables of chemical shifts for probe compounds, and an Excel file containing linear scaling factors and individual results for all model chemistries evaluated. References [2,3,26,29,52,59,88,89,90,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233] are cited in the supplementary materials.
Author Contributions
R.D.C., J.S.W. and Y.-H.L. performed the calculations. R.D.C. and J.S.W. performed the experimental measurements; A.V.B., E.C.S., M.R., R.T.W. and G.E.M. participated in the study design and manuscript writing. All authors contributed to the design of the study, figure construction, and manuscript preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available in Electronic Supporting Information (ESI), and for additional details, please contact the authors.
Acknowledgments
We thank Aili Fan of Peking University in Beijing, China, for providing homodimericin A. We are grateful to Qi Gao and Yunyi Wang for reviewing the manuscript, as well as Caroline McGregor and Jenna Leschek of Analytical Research & Development (AR&D) at Merck & Co., Inc., Rahway, NJ, USA for their continued support and encouragement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rablen, P.R.; Pearlman, S.A.; Finkbiner, J. A Comparison of Density Functional Methods for the Estimation of Proton Chemical Shifts with Chemical Accuracy. J. Phys. Chem. A 1999, 103, 7357–7363. [Google Scholar] [CrossRef]
- Bagno, A.; Rastrelli, F.; Saielli, G. Toward the Complete Prediction of the 1H and 13C NMR Spectra of Complex Organic Molecules by DFT Methods: Application to Natural Substances. Chem. A Eur. J. 2006, 12, 5514–5525. [Google Scholar] [CrossRef] [PubMed]
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry. Chem. Rev. 2012, 112, 1839–1862. [Google Scholar] [CrossRef] [PubMed]
- Willoughby, P.H.; Jansma, M.J.; Hoye, T.R. A Guide to Small-Molecule Structure Assignment through Computation of (1H and 13C) NMR Chemical Shifts. Nat. Protoc. 2014, 9, 643–660. [Google Scholar] [CrossRef] [PubMed]
- Grimblat, N.; Sarotti, A.M. Computational Chemistry to the Rescue: Modern Toolboxes for the Assignment of Complex Molecules by GIAO NMR Calculations. Chem. Eur. J. 2016, 22, 12246–12261. [Google Scholar] [CrossRef] [PubMed]
- Hehre, W.; Klunzinger, P.; Deppmeier, B.; Driessen, A.; Uchida, N.; Hashimoto, M.; Fukushi, E.; Takata, Y. Efficient Protocol for Accurately Calculating 13C Chemical Shifts of Conformationally Flexible Natural Products: Scope, Assessment, and Limitations. J. Nat. Prod. 2019, 82, 2299–2306. [Google Scholar] [CrossRef]
- Marcarino, M.O.; Zanardi, M.M.; Cicetti, S.; Sarotti, A.M. NMR Calculations with Quantum Methods: Development of New Tools for Structural Elucidation and Beyond. Acc. Chem. Res. 2020, 53, 1922–1932. [Google Scholar] [CrossRef]
- Costa, F.L.; de Albuquerque, A.C.; Fiorot, R.G.; Lião, L.M.; Martorano, L.H.; Mota, G.V.; Valverde, A.L.; Carneiro, J.W.; dos Santos Junior, F.M. Structural Characterisation of Natural Products by Means of Quantum Chemical Calculations of NMR Parameters: New Insights. Org. Chem. Front. 2021, 8, 2019–2058. [Google Scholar] [CrossRef]
- Castro, A.C.; Balcells, D.; Repisky, M.; Helgaker, T.; Cascella, M. First-Principles Calculation of 1H NMR Chemical Shifts of Complex Metal Polyhydrides: The Essential Inclusion of Relativity and Dynamics. Inorg. Chem. 2020, 59, 17509–17518. [Google Scholar] [CrossRef]
- Chierotti, M.R.; Garlaschelli, L.; Gobetto, R.; Nervi, C.; Peli, G.; Sironi, A.; Della Pergola, R. An Unusual Carbonyl Chemical Shift in a Carbonylhexairidium Cluster: A Combined Solid-State NMR and DFT Approach. Eur. J. Inorg. Chem. 2007, 3477–3483. [Google Scholar] [CrossRef]
- Cohen, R.D.; Wang, X.; Sherer, E.C.; Martin, G.E. Application of 1,1-ADEQUATE and DFT to Correct 13C Misassignments of Carbonyl Chemical Shifts for Carbapenem Antibiotics. Magn. Reson. Chem. 2022, 60, 963–969. [Google Scholar] [CrossRef]
- Losacco, G.L.; Cohen, R.D.; DaSilva, J.O.; Haidar Ahmad, I.A.; Sherer, E.C.; Mangion, I.; Regalado, E.L. Deuterated Modifiers in Sub/Supercritical Fluid Chromatography for Streamlined NMR Structure Elucidation. Anal. Chem. 2022, 94, 12176–12184. [Google Scholar] [CrossRef]
- Basu, K.; Lehnherr, D.; Martin, G.E.; Desmond, R.A.; Lam, Y.-H.; Peng, F.; Chung, J.Y.; Arvary, R.A.; Zompa, M.A.; Zhang, S.-W.; et al. Development of a Green and Sustainable Manufacturing Process for Gefapixant Citrate (MK-7264) Part 3: Development of a One-Pot Formylation-Cyclization Sequence to the Diaminopyrimidine Core. Org. Process Res. Dev. 2020, 24, 2462–2477. [Google Scholar] [CrossRef]
- Meanwell, M.; Silverman, S.M.; Lehmann, J.; Adluri, B.; Wang, Y.; Cohen, R.; Campeau, L.-C.; Britton, R. A Short de novo Synthesis of Nucleoside Analogs. Science 2020, 369, 725–730. [Google Scholar] [CrossRef]
- Song, Z.J.; Zhou, G.; Cohen, R.; Tan, L. Preparation of ABNO on Scale and Analysis by Quantitative Paramagnetic NMR. Org. Process Res. Dev. 2018, 22, 1257–1261. [Google Scholar] [CrossRef]
- Vankova, N.; Heine, T.; Kortz, U. NMR Chemical Shifts of Metal Centres in Polyoxometalates: Relativistic DFT Predictions. Eur. J. Inorg. Chem. 2009, 5102–5108. [Google Scholar] [CrossRef]
- Martel, L.; Capelli, E.; Body, M.; Klipfel, M.; Beneš, O.; Maksoud, L.; Raison, P.E.; Suard, E.; Visscher, L.; Bessada, C. Insight into the Crystalline Structure of ThF4 with the Combined use of Neutron Diffraction, 19F Magic-Angle Spinning-NMR, and Density Functional Theory Calculations. Inorg. Chem. 2018, 57, 15350–15360. [Google Scholar] [CrossRef]
- Novotný, J.; Sojka, M.; Komorovsky, S.; Nečas, M.; Marek, R. Interpreting the Paramagnetic NMR Spectra of Potential Ru(III) Metallodrugs: Synergy Between Experiment and Relativistic DFT Calculations. J. Am. Chem. Soc. 2016, 138, 8432–8445. [Google Scholar] [CrossRef]
- Vícha, J.; Novotný, J.; Straka, M.; Repisky, M.; Ruud, K.; Komorovsky, S.; Marek, R. Structure, Solvent, and Relativistic Effects on the NMR Chemical Shifts in Square-Planar Transition-Metal Complexes: Assessment of DFT Approaches. Phys. Chem. Chem. Phys. 2015, 17, 24944–24955. [Google Scholar] [CrossRef]
- Sim, Y.E.; Nwajiobi, O.; Mahesh, S.; Cohen, R.D.; Reibarkh, M.Y.; Raj, M. Secondary Amine Selective Petasis (SASP) Bioconjugation. Chem. Sci. 2020, 11, 53–61. [Google Scholar] [CrossRef]
- Joyce, L.A.; Nawrat, C.C.; Sherer, E.C.; Biba, M.; Brunskill, A.; Martin, G.E.; Cohen, R.D.; Davies, I.W. Beyond Optical Rotation: What’s Left is not Always Right in Total Synthesis. Chem. Sci. 2018, 9, 415–424. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.D.; Saurí, J.; Huff, C.A.; Krska, S.W.; Martin, G.E. Additional pitfalls of using 1,1-ADEQUATE for structure elucidation. Magn. Reson. Chem. 2016, 54, 897–900. [Google Scholar] [CrossRef]
- Rivera, N.R.; Cohen, R.D.; Zhang, S.-W.; Dance, Z.E.; Halsey, H.M.; Song, S.; Bu, X.; Reibarkh, M.; Ren, H.; Lee, A.Y. Gefapixant Citrate (MK-7264) Sulfonamide Step Speciation Study: Investigation into Precipitation-Dissolution Events during Addition of Chlorosulfonic Acid. Org. Process Res. Dev. 2023, 27, 286–294. [Google Scholar] [CrossRef]
- Koch, K.R.; Burger, M.; Kramer, J.; Westra, A. 195Pt NMR and DFT Computational Methods as Tools Towards the Understanding of Speciation and Hydration/Solvation of [PtX6]2− (X = Cl−, Br−) Anions in Solution. Dalton Trans. 2006, 37, 3277–3284. [Google Scholar] [CrossRef] [PubMed]
- Gordon, L.W.; Wang, J.; Messinger, R.J. Revealing Impacts of Electrolyte Speciation on Ionic Charge Storage in Aluminum-Quinone Batteries by NMR Spectroscopy. J. Magn. Reson. 2023, 348, 107374. [Google Scholar] [CrossRef]
- Lodewyk, M.W.; Soldi, C.; Jones, P.B.; Olmstead, M.M.; Rita, J.; Shaw, J.T.; Tantillo, D.J. The Correct Structure of Aquatolide—Experimental Validation of a Theoretically-Predicted Structural Revision. J. Am. Chem. Soc. 2012, 134, 18550–18553. [Google Scholar] [CrossRef]
- Saielli, G.; Nicolaou, K.C.; Ortiz, A.; Zhang, H.; Bagno, A. Addressing the Stereochemistry of Complex Organic Molecules by Density Functional Theory-NMR: Vannusal B in Retrospective. J. Am. Chem. Soc. 2011, 133, 6072–6077. [Google Scholar] [CrossRef]
- Li, Y. Structural Revision of Glabramycins B and C, Antibiotics from the Fungus Neosartorya glabra by DFT Calculations of NMR Chemical Shifts and Coupling Constants. RSC Adv. 2015, 5, 36858–36864. [Google Scholar] [CrossRef]
- Rychnovsky, S.D. Predicting NMR Spectra by Computational Methods: Structure Revision of Hexacyclinol. Org. Lett. 2006, 8, 2895–2898. [Google Scholar] [CrossRef]
- Buevich, A.V.; Elyashberg, M.E. Synergistic Combination of CASE Algorithms and DFT Chemical Shift Predictions: A Powerful Approach for Structure Elucidation, Verification, and Revision. J. Nat. Prod. 2016, 79, 3105–3116. [Google Scholar] [CrossRef]
- Buevich, A.V.; Elyashberg, M.E. Towards Unbiased and More Versatile NMR-Based Structure Elucidation: A Powerful Combination of CASE Algorithms and DFT Calculations. Magn. Reson. Chem. 2018, 56, 493–504. [Google Scholar] [CrossRef]
- Buevich, A.V.; Elyashberg, M.E. Enhancing Computer-Assisted Structure Elucidation with DFT Analysis of J-Couplings. Magn. Reson. Chem. 2020, 58, 594–606. [Google Scholar] [CrossRef]
- Zaretsky, S.; Hickey, J.L.; Denis, M.A.S.; Scully, C.C.; Roughton, A.L.; Tantillo, D.J.; Lodewyk, M.W.; Yudin, A.K. Predicting Cyclic Peptide Chemical Shifts using Quantum Mechanical Calculations. Tetrahedron 2014, 70, 7655–7663. [Google Scholar] [CrossRef]
- Nguyen, Q.N.N.; Schwochert, J.; Tantillo, D.J.; Lokey, R.S. Using 1H and 13C NMR Chemical Shifts to Determine Cyclic Peptide Conformations: A Combined Molecular Dynamics and Quantum Mechanics Approach. Phys. Chem. Chem. Phys. 2018, 20, 14003–14012. [Google Scholar] [CrossRef]
- Fonville, J.M.; Swart, M.; Vokáčová, Z.; Sychrovský, V.; Šponer, J.E.; Šponer, J.; Hilbers, C.W.; Bickelhaupt, F.M.; Wijmenga, S.S. Chemical Shifts in Nucleic Acids Studied by Density Functional Theory Calculations and Comparison with Experiment. Chem. Eur. J. 2012, 18, 12372–12387. [Google Scholar] [CrossRef]
- Victora, A.; Möller, H.M.; Exner, T.E. Accurate Ab Initio Prediction of NMR Chemical Shifts of Nucleic Acids and Nucleic Acids/Protein Complexes. Nucleic Acids Res. 2014, 42, e173. [Google Scholar] [CrossRef]
- Jin, X.; Zhu, T.; Zhang, J.Z.; He, X. A Systematic Study on RNA NMR Chemical Shift Calculation Based on the Automated Fragmentation QM/MM Approach. RSC Adv. 2016, 6, 108590–108602. [Google Scholar] [CrossRef]
- Taubert, S.; Konschin, H.; Sundholm, D. Computational Studies of 13C NMR Chemical Shifts of Saccharides. Phys. Chem. Chem. Phys. 2005, 7, 2561–2569. [Google Scholar] [CrossRef]
- Toukach, F.V.; Ananikov, V.P. Recent Advances in Computational Predictions of NMR Parameters for the Structure Elucidation of Carbohydrates: Methods and Limitations. Chem. Soc. Rev. 2013, 42, 8376–8415. [Google Scholar] [CrossRef]
- Palivec, V.; Pohl, R.; Kaminský, J.; Martinez-Seara, H. Efficiently Computing NMR 1H and 13C Chemical Shifts of Saccharides in Aqueous Environment. J. Chem. Theory Comput. 2022, 18, 4373–4386. [Google Scholar] [CrossRef]
- Larsen, A.S.; Bratholm, L.A.; Christensen, A.S.; Channir, M.; Jensen, J.H. ProCS15: A DFT-Based Chemical Shift Predictor for Backbone and Cβ Atoms in Proteins. PeerJ 2015, 3, e1344. [Google Scholar] [CrossRef] [PubMed]
- Bratholm, L.A.; Jensen, J.H. Protein Structure Refinement Using a Quantum Mechanics-Based Chemical Shielding Predictor. Chem. Sci. 2017, 8, 2061–2072. [Google Scholar] [CrossRef] [PubMed]
- Přecechtělová, J.P.; Mladek, A.; Zapletal, V.; Hritz, J. Quantum Chemical Calculations of NMR Chemical Shifts in Phosphorylated Intrinsically Disordered Proteins. J. Chem. Theory Comput. 2019, 15, 5642–5658. [Google Scholar] [CrossRef] [PubMed]
- Mueller, L.J.; Dunn, M.F. NMR Crystallography of Enzyme Active Sites: Probing Chemically Detailed, Three-Dimensional Structure in Tryptophan Synthase. Acc. Chem. Res. 2013, 46, 2008–2017. [Google Scholar] [CrossRef]
- Hodgkinson, P. NMR Crystallography of Molecular Organics. Prog. Nucl. Magn. Reson. Spectrosc. 2020, 118, 10–53. [Google Scholar] [CrossRef]
- Ashbrook, S.E.; McKay, D. Combining Solid-State NMR Spectroscopy with First-Principles Calculations—A Guide to NMR Crystallography. Chem. Commun. 2016, 52, 7186–7204. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Konstantinov, I.A.; Broadbelt, L.J. Regression Formulas for Density Functional Theory Calculated 1H and 13C NMR Chemical Shifts in Toluene-d8. J. Phys. Chem. A 2011, 115, 12364–12372. [Google Scholar] [CrossRef]
- Toomsalu, E.; Burk, P. Critical Test of Some Computational Methods for Prediction of NMR 1H and 13C Chemical Shifts. J. Mol. Model. 2015, 21, 244. [Google Scholar] [CrossRef]
- Benassi, E. Benchmarking of Density Functionals for a Soft but Accurate Prediction and Assignment of 1H and 13C NMR Chemical Shifts in Organic and Biological Molecules. J. Comput. Chem. 2017, 38, 87–92. [Google Scholar] [CrossRef]
- Buß, A.; Koch, R. Simulation of NMR Chemical Shifts in Heterocycles: A Method Evaluation. J. Mol. Model. 2017, 23, 9. [Google Scholar] [CrossRef]
- Wiitala, K.W.; Hoye, T.R.; Cramer, C.J. Hybrid Density Functional Methods Empirically Optimized for the Computation of 13C and 1H Chemical Shifts in Chloroform Solution. J. Chem. Theory Comput. 2006, 2, 1085–1092. [Google Scholar] [CrossRef]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Efficient and Accurate Prediction of Nuclear Magnetic Resonance Shielding Tensors with Double-Hybrid Density Functional Theory. J. Chem. Theory Comput. 2018, 14, 4756–4771. [Google Scholar] [CrossRef]
- De Oliveira, M.T.; Alves, J.M.A.; Braga, A.A.C.; Wilson, D.J.D.; Barboza, C.A. Do Double-Hybrid Exchange–Correlation Functionals Provide Accurate Chemical Shifts? A Benchmark Assessment for Proton NMR. J. Chem. Theory Comput. 2021, 17, 6876–6885. [Google Scholar] [CrossRef]
- Iron, M.A. Evaluation of the Factors Impacting the Accuracy of 13C NMR Chemical Shift Predictions using Density Functional Theory—The Advantage of Long-Range Corrected Functionals. J. Chem. Theory Comput. 2017, 13, 5798–5819. [Google Scholar] [CrossRef]
- Jain, R.; Bally, T.; Rablen, P.R. Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets. J. Org. Chem. 2009, 74, 4017–4023. [Google Scholar] [CrossRef]
- Kaupp, M. Relativistic Effects on NMR Chemical Shifts. In Relativistic Electronic Structure Theory, Part 2: Applications; Schwerdtfeger, P., Ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2004; Volume 14, pp. 552–597. [Google Scholar]
- Mitra, A.; Seaton, P.J.; Assarpour, R.A.; Williamson, T. Unprecedented Concentration Dependent Chemical Shift Variation in 1H-NMR Studies: A Caveat in the Investigations of Molecular Recognition and Structure Elucidation. Tetrahedron 1998, 54, 15489–15498. [Google Scholar] [CrossRef]
- Pierens, G.K.; Venkatachalam, T.; Reutens, D.C. NMR and DFT Investigations of Structure of Colchicine in Various Solvents Including Density Functional Theory Calculations. Sci. Rep. 2017, 7, 5605. [Google Scholar] [CrossRef]
- Stadelmann, T.; Balmer, C.; Riniker, S.; Ebert, M.-O. Impact of Solvent Interactions on 1H and 13C Chemical Shifts Investigated Using DFT and a Reference Dataset Recorded in CDCl3 and CCl4. Phys. Chem. Chem. Phys. 2022, 24, 23551–23560. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Lavanish, J.M. Formation and Thermal Decomposition of Bicyclo[1.1.0]butane-2-exo-d11. J. Am. Chem. Soc. 1966, 88, 5272–5275. [Google Scholar] [CrossRef]
- Collins, S.W.; Alger, T.D.; Grant, D.M.; Kuhlmann, K.F.; Smith, J.C. Carbon-13 Spin Relaxation and Methyl Rotation Barriers in the Methylethylenes. J. Phys. Chem. 1975, 79, 2031–2037. [Google Scholar] [CrossRef]
- Simons, W.W. The Sadtler Handbook of Proton NMR Spectra; Sadtler: Philadelphia, PA, USA, 1978. [Google Scholar]
- Silverstein, R.M.; Bassler, G.C.; Morrill, T.C. Spectrometric Identification of Organic Compounds; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Properties of Organic Compounds Database, version 5.0; CRC Press: Boca Raton, FL, USA, 1996.
- Bos, R.; Barnett, N.W.; Dyson, G.A.; Lim, K.F.; Russell, R.A.; Watson, S.P. Studies on the Mechanism of the Peroxyoxalate Chemiluminescence Reaction: Part 1. Confirmation of 1,2-Dioxetanedione as an Intermediate using 13C Nuclear Magnetic Resonance Spectroscopy. Anal. Chim. Acta 2004, 502, 141–147. [Google Scholar] [CrossRef]
- Spectral Database for Organic Compounds, SDBS. National Institute of Advanced Industrial Science and Technology (AIST): Japan. Available online: https://sdbs.db.aist.go.jp (accessed on 7 December 2022).
- Bellina, F.; Rossi, R. An Efficient and Inexpensive Multigram Synthesis of 3,4-Dibromo- and 3,4-Dichlorofuran-2(5H)-one. Synthesis 2007, 1887–1889. [Google Scholar] [CrossRef]
- Hoffmann, F.; Li, D.-W.; Sebastiani, D.; Brüschweiler, R. Improved Quantum Chemical NMR Chemical Shift Prediction of Metabolites in Aqueous Solution Toward the Validation of Unknowns. J. Phys. Chem. A 2017, 121, 3071–3078. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, H.P.; Shaghaghi, H.; Tafazzoli, M. Gauge Invariant Atomic Orbital-Density Functional Theory Prediction of Accurate Gas Phase 1H and 13C NMR Chemical Shifts. Concepts Magn. Reson. Part A 2011, 38, 269–279. [Google Scholar] [CrossRef]
- Flaig, D.; Maurer, M.; Hanni, M.; Braunger, K.; Kick, L.; Thubauville, M.; Ochsenfeld, C. Benchmarking Hydrogen and Carbon NMR Chemical Shifts at HF, DFT, and MP2 Levels. J. Chem. Theory Comput. 2014, 10, 572–578. [Google Scholar] [CrossRef]
- Giesen, D.J.; Zumbulyadis, N. A Hybrid Quantum Mechanical and Empirical Model for the Prediction of Isotropic 13C Shielding Constants of Organic Molecules. Phys. Chem. Chem. Phys. 2002, 4, 5498–5507. [Google Scholar] [CrossRef]
- Pierens, G.K. 1H and 13C NMR Scaling Factors for the Calculation of Chemical Shifts in Commonly Used Solvents Using Density Functional Theory. J. Comput. Chem. 2014, 35, 1388–1394. [Google Scholar] [CrossRef]
- Yesiltepe, Y.; Nuñez, J.R.; Colby, S.M.; Thomas, D.G.; Borkum, M.I.; Reardon, P.N.; Washton, N.M.; Metz, T.O.; Teeguarden, J.G.; Govind, N. An Automated Framework for NMR Chemical Shift Calculations of Small Organic Molecules. J. Cheminform. 2018, 10, 52. [Google Scholar] [CrossRef]
- Armangue, L.; Solà, M.; Swart, M. Nuclear Shieldings with the SSB-D Functional. J. Phys. Chem. A 2011, 115, 1250–1256. [Google Scholar] [CrossRef]
- Wang, B.; Fleischer, U.; Hinton, J.F.; Pulay, P. Accurate Prediction of Proton Chemical Shifts. I. Substituted Aromatic Hydrocarbons. J. Comput. Chem. 2001, 22, 1887–1895. [Google Scholar] [CrossRef]
- Xin, D.; Sader, C.A.; Chaudhary, O.; Jones, P.-J.; Wagner, K.; Tautermann, C.S.; Yang, Z.; Busacca, C.A.; Saraceno, R.A.; Fandrick, K.R. Development of a 13C NMR Chemical Shift Prediction Procedure Using B3LYP/cc-pVDZ and Empirically Derived Systematic Error Correction Terms: A Computational Small Molecule Structure Elucidation Method. J. Org. Chem. 2017, 82, 5135–5145. [Google Scholar] [CrossRef]
- Holzer, C.; Franzke, Y.J.; Kehry, M. Assessing the Accuracy of Local Hybrid Density Functional Approximations for Molecular Response Properties. J. Chem. Theory Comput. 2021, 17, 2928–2947. [Google Scholar] [CrossRef]
- Ermanis, K.; Parkes, K.E.B.; Agback, T.; Goodman, J.M. The Optimal DFT Approach in DP4 NMR Structure Analysis-Pushing the Limits of Relative Configuration Elucidation. Org. Biomol. Chem. 2019, 17, 5886–5890. [Google Scholar] [CrossRef]
- Schattenberg, C.J.; Kaupp, M. Extended Benchmark Set of Main-Group Nuclear Shielding Constants and NMR Chemical Shifts and Its Use to Evaluate Modern DFT Methods. J. Chem. Theory Comput. 2021, 17, 7602–7621. [Google Scholar] [CrossRef]
- Bates, J.E.; Furche, F. Harnessing the Meta-Generalized Gradient Approximation for Time-Dependent Density Functional Theory. J. Chem. Phys. 2012, 137, 164105. [Google Scholar] [CrossRef]
- Grimblat, N.; Zanardi, M.M.; Sarotti, A.M. Beyond DP4: An Improved Probability for the Stereochemical Assignment of Isomeric Compounds Using Quantum Chemical Calculations of NMR Shifts. J. Org. Chem. 2015, 80, 12526–12534. [Google Scholar] [CrossRef]
- Baldridge, K.K.; Siegel, J.S. Correlation of Empirical δ(TMS) and Absolute NMR Chemical Shifts Predicted by ab initio Computations. J. Phys. Chem. A 1999, 103, 4038–4042. [Google Scholar] [CrossRef]
- Schuler, R.H.; Albarran, G.; Zajicek, J.; George, M.; Fessenden, R.W.; Carmichael, I. On the Addition of •OH Radicals to the Ipso Positions of Alkyl-Substituted Aromatics: Production of 4-Hydroxy-4-methyl-2, 5-cyclohexadien-1-one in the Radiolytic Oxidation of p-Cresol. J. Phys. Chem. A 2002, 106, 12178–12183. [Google Scholar] [CrossRef]
- Wipf, P.; Kerekes, A.D. Structure Reassignment of the Fungal Metabolite TAEMC161 as the Phytotoxin Viridiol. J. Nat. Prod. 2003, 66, 716–718. [Google Scholar] [CrossRef]
- Timmons, C.; Wipf, P. Density Functional Theory Calculation of 13C NMR Shifts of Diazaphenanthrene Alkaloids: Reinvestigation of the Structure of Samoquasine A. J. Org. Chem. 2008, 73, 9168–9170. [Google Scholar] [CrossRef] [PubMed]
- Sarotti, A.M.; Pellegrinet, S.C. A Multi-standard Approach for GIAO 13C NMR Calculations. J. Org. Chem. 2009, 74, 7254–7260. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Von Bargen, C.D. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef] [PubMed]
- MacroModel, Schrödinger Release 2021-1; MacroModel, Schrödinger, LLC: New York, NY, USA, 2021.
- Walker, M.; Harvey, A.J.; Sen, A.; Dessent, C.E. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef]
- Kang, Y.K.; Park, H.S. Conformational Preferences of Cationic β-Peptide in Water Studied by CCSD(T), MP2, and DFT Methods. Heliyon 2020, 6, e04721. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Performance of SM6, SM8, and SMD on the SAMPL1 Test Set for the Prediction of Small-Molecule Solvation Free Energies. J. Phys. Chem. B 2009, 113, 4538–4543. [Google Scholar] [CrossRef]
- Brémond, É.; Pérez-Jiménez, Á.J.; Sancho-García, J.C.; Adamo, C. Range-Separated Hybrid Density Functionals Made Simple. J. Chem. Phys. 2019, 150, 201102. [Google Scholar] [CrossRef]
- Jensen, F. How Large is the Elephant in the Density Functional Theory Room? J. Phys. Chem. A 2017, 121, 6104–6107. [Google Scholar] [CrossRef]
- Feller, D.; Dixon, D.A. Density Functional Theory and the Basis Set Truncation Problem with Correlation Consistent Basis Sets: Elephant in the Room or Mouse in the Closet? J. Phys. Chem. A 2018, 122, 2598–2603. [Google Scholar] [CrossRef]
- Jensen, F. Method Calibration or Data Fitting? J. Chem. Theory Comput. 2018, 14, 4651–4661. [Google Scholar] [CrossRef]
- Mevers, E.; Saurí, J.; Liu, Y.; Moser, A.; Ramadhar, T.R.; Varlan, M.; Williamson, R.T.; Martin, G.E.; Clardy, J. Homodimericin A: A Complex Hexacyclic Fungal Metabolite. J. Am. Chem. Soc. 2016, 138, 12324–12327. [Google Scholar] [CrossRef]
- Facelli, J.C. Calculations of Chemical Shieldings: Theory and Applications. Concepts Magn. Reson. Part A 2004, 20, 42–69. [Google Scholar] [CrossRef]
- London, F. Théorie Quantique des Courants Interatomiques dans les Combinaisons Aromatiques (Quantum Theory of Interatomic Currents in Aromatic Compounds). J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- McWeeny, R. Perturbation Theory for the Fock-Dirac Density Matrix. Phys. Rev. 1962, 126, 1028. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-Consistent Perturbation Theory of Diamagnetism: I. A Gauge-Invariant LCAO Method for NMR Chemical Shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Keith, T.; Bader, R. Calculation of Magnetic Response Properties Using Atoms in Molecules. Chem. Phys. Lett. 1992, 194, 1–8. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F. Calculation of Magnetic Response Properties Using a Continuous Set of Gauge Transformations. Chem. Phys. Lett. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E.; Houk, K. Integration Grid Errors for Meta-GGA-Predicted Reaction Energies: Origin of Grid Errors for the M06 Suite of Functionals. J. Chem. Theory Comput. 2010, 6, 395–404. [Google Scholar] [CrossRef]
- Böhm, M.C.; Schulte, J.; Ramírez, R. On the Influence of Nuclear Fluctuations on Calculated NMR Shieldings of Benzene and Ethylene: A Feynman Path Integral—Ab initio Investigation. Int. J. Quantum Chem. 2002, 86, 280–296. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Chemical Accuracy in the Computation of NMR Shieldings: The PBE0 Model. Chem. Phys. Lett. 1998, 298, 113–119. [Google Scholar] [CrossRef]
- Deng, Q.; Jiang, L.; Yu, Y.; Yang, Y. Theoretical Exploration of the Mechanism of α-Pinene Hydrogenation. J. Organomet. Chem. 2022, 980–981, 122513. [Google Scholar] [CrossRef]
- Kutateladze, A.G.; Kuznetsov, D.M.; Beloglazkina, A.A.; Holt, T. Addressing the Challenges of Structure Elucidation in Natural Products Possessing the Oxirane Moiety. J. Org. Chem. 2018, 83, 8341–8352. [Google Scholar] [CrossRef]
- Wood, J.S.; Gordon, W.H.; Morgan, J.B.; Williamson, R.T. Calculated and Experimental 1H and 13C NMR Assignments for Cannabicitran. Magn. Reson. Chem. 2022, 60, 196–202. [Google Scholar] [CrossRef]
- Galasso, V.; Kovač, B.; Modelli, A. A Theoretical and Experimental Study on the Molecular and Electronic Structures of Artemisinin and Related Drug Molecules. Chem. Phys. 2007, 335, 141–154. [Google Scholar] [CrossRef]
- Lodewyk, M.W.; Tantillo, D.J. Prediction of the Structure of Nobilisitine A Using Computed NMR Chemical Shifts. J. Nat. Prod. 2011, 74, 1339–1343. [Google Scholar] [CrossRef]
- Semenov, V.A.; Krivdin, L.B. DFT Computational Schemes for 1H and 13C NMR Chemical Shifts of Natural Products, Exemplified by Strychnine. Magn. Reson. Chem. 2020, 58, 56–64. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. 1H and 13C NMR Spectra of Strychnos Alkaloids: Selected NMR Updates. Int. J. Quantum Chem. 2020, 120, e26348. [Google Scholar] [CrossRef]
- Saielli, G.; Bagno, A. Can Two Molecules have the same NMR Spectrum? Hexacyclinol Revisited. Org. Lett. 2009, 11, 1409–1412. [Google Scholar] [CrossRef]
- Semenov, V.A.; Krivdin, L.B. Computational 1H and 13C NMR of Strychnobaillonine: On the Way to Larger Molecules Calculated at Lower Computational Costs. Magn. Reson. Chem. 2021, 59, 108–116. [Google Scholar] [CrossRef]
- Semenov, V.A.; Krivdin, L.B. Simple and Versatile Scheme for the Stereochemical Identification of Natural Products and Diverse Organic Compounds with Multiple Asymmetric Centers. J. Phys. Chem. A 2021, 125, 10359–10372. [Google Scholar] [CrossRef]
- Aliev, A.E.; Courtier-Murias, D.; Zhou, S. Scaling Factors for Carbon NMR Chemical Shifts Obtained from DFT B3LYP Calculations. J. Mol. Struct. THEOCHEM 2009, 893, 1–5. [Google Scholar] [CrossRef]
- Kelly, D.P.; Giansiracusa, J.J.; Leslie, D.R.; McKern, I.D.; Sinclair, G.C. 13C-1H Coupling Constants in Carbocations. 5.1 Trishomocyclopropenium Cations Generated from Bicyclo [3.1.0]hex-3-yl, Tricyclo [3.2.1.02,4]oct-8-yl, and Pentacyclo [4.3.0.02,4.03,8.05,7]non-9-yl Precursors. J. Org. Chem. 1988, 53, 2497–2504. [Google Scholar] [CrossRef]
- Guan, Y.; Sowndarya, S.S.; Gallegos, L.C.; St. John, P.C.; Paton, R.S. Real-Time Prediction of 1H and 13C Chemical Shifts with DFT Accuracy Using a 3D Graph Neural Network. Chem. Sci. 2021, 12, 12012–12026. [Google Scholar] [CrossRef]
- Lee, S.G. α-Pinene and Myrtenol: Complete 1H NMR Assignment. Magn. Reson. Chem. 2002, 40, 311–312. [Google Scholar] [CrossRef]
- Akssira, M.; Mellouki, F.; Salhi, A.; Alilou, H.; Saouf, A.; El Hanbali, F.; Arteaga, J.F.; Barrero, A.F. Naupliolide, a Sesquiterpene Lactone with a Novel Tetracyclic Skeleton from Nauplius graveolens Subsp. odorus. Tet. Lett. 2006, 47, 6719–6721. [Google Scholar] [CrossRef]
- Dong, M.; Cong, B.; Yu, S.-H.; Sauriol, F.; Huo, C.-H.; Shi, Q.-W.; Gu, Y.-C.; Zamir, L.O.; Kiyota, H. Echinopines A and B: Sesquiterpenoids Possessing an Unprecedented Skeleton from Echinops spinosus. Org. Lett. 2008, 10, 701–704. [Google Scholar] [CrossRef] [PubMed]
- Tiuman, T.S.; Ueda-Nakamura, T.; Garcia Cortez, D.A.; Dias Filho, B.P.; Morgado-Díaz, J.A.; de Souza, W.; Nakamura, C.V. Antileishmanial Activity of Parthenolide, a Sesquiterpene Lactone Isolated from Tanacetum parthenium. Antimicrob. Agents Chemother. 2005, 49, 176–182. [Google Scholar] [CrossRef]
- Kutateladze, A.G.; Reddy, D.S. High-Throughput in silico Structure Validation and Revision of Halogenated Natural Products is Enabled by Parametric Corrections to DFT-Computed 13C NMR Chemical Shifts and Spin–Spin Coupling Constants. J. Org. Chem. 2017, 82, 3368–3381. [Google Scholar] [CrossRef]
- Valdez-Calderón, A.; Torres-Valencia, J.M.; Manríquez-Torres, J.J.; Velázquez-Jiménez, R.; Román-Marín, L.U.; Hernández-Hernández, J.D.; Cerda-García-Rojas, C.M.; Joseph-Nathan, P. An Unusual Diepoxyguaianolide from Stevia Tomentosa. Tet. Lett. 2013, 54, 3286–3289. [Google Scholar] [CrossRef]
- Rigby, J.H.; de Sainte Claire, V.; Cuisiat, S.V.; Heeg, M.J. Synthetic Studies on the Ingenane Diterpenes. Direct Conversion of the out,out-Bicyclo [4.4.1]undecane System into a Highly Strained In,out Stereoisomer. J. Org. Chem. 1996, 61, 7992–7993. [Google Scholar] [CrossRef]
- Zhongshan, W.; Nakashima, T.T.; Kopecky, K.R.; Molina, J. Qinghaosu: 1H and 13C Nuclear Magnetic Resonance Spectral Assignments and Luminescence. Can. J. Chem. 1985, 63, 3070–3074. [Google Scholar] [CrossRef]
- Evidente, A.; Abou-Donia, A.H.; Darwish, F.A.; Amer, M.E.; Kassem, F.F.; Hammoda, H.A.; Motta, A. Nobilisitine A and B, Two Masanane-Type Alkaloids from Clivia nobilis. Phytochemistry 1999, 51, 1151–1155. [Google Scholar] [CrossRef]
- Marrero, J.; Rodríguez, A.D.; Barnes, C.L. Intricarene, an Unprecedented Trispiropentacyclic Diterpene from the Caribbean Sea Plume Pseudopterogorgia kallos. Org. Lett. 2005, 7, 1877–1880. [Google Scholar] [CrossRef]
- Martin, G.E.; Hadden, C.E.; Crouch, R.C.; Krishnamurthy, V. ACCORD-HMBC: Advantages and Disadvantages of Static Versus Accordion Excitation. Magn. Reson. Chem. 1999, 37, 517–528. [Google Scholar] [CrossRef]
- Cherif, A.; Martin, G.E.; Soltero, L.R.; Massiot, G. Configuration and Total Assignment of the 1H- and 13C-NMR Spectra of the Alkaloid Holstiine. J. Nat. Prod. 1990, 53, 793–802. [Google Scholar] [CrossRef]
- Williams, A.; Elyashberg, M.; Blinov, K.; Lankin, D.; Martin, G.; Reynolds, W.; Porco Jr, J.; Singleton, C.; Su, S. Applying Computer-Assisted Structure Elucidation Algorithms for the Purpose of Structure Validation: Revisiting the NMR Assignments of Hexacyclinol. J. Nat. Prod. 2008, 71, 581–588. [Google Scholar] [CrossRef]
- Tchinda, A.T.; Jansen, O.; Nyemb, J.-N.; Tits, M.; Dive, G.; Angenot, L.; Frederich, M. Strychnobaillonine, an Unsymmetrical Bisindole Alkaloid with an Unprecedented Skeleton from Strychnos icaja Roots. J. Nat. Prod. 2014, 77, 1078–1082. [Google Scholar] [CrossRef]
- Frederich, M.; De Pauw, M.-C.; Llabres, G.; Tits, M.; Hayette, M.-P.; Brandt, V.; Penelle, J.; De Mol, P.; Angenot, L. New Antimalarial and Cytotoxic Sungucine Derivatives from Strychnos icaja Roots. Planta Med. 2000, 66, 262–269. [Google Scholar] [CrossRef]
- Lamotte, J.; Dupont, L.; Dideberg, O.; Kambu, K.; Angenot, L. Isolation and Structure of Sungucine: A New Type of Bisindoline Alkaloid. Tet. Lett. 1979, 20, 4227–4228. [Google Scholar] [CrossRef]
- Chmurny, G.N.; Hilton, B.D.; Brobst, S.; Look, S.A.; Witherup, K.M.; Beutler, J.A. 1H- and 13C-NMR Assignments for Taxol, 7-epi-Taxol, and Cephalomannine. J. Nat. Prod. 1992, 55, 414–423. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Slater, J.C. Quantum Theory of Molecules and Solids Vol. 4: The Self-Consistent Field for Molecules and Solids; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Electronic Structure of Solids ’91; Ziesche, P., Eschrig, H., Eds.; Akademie Verlag: Berlin, Germany, 1991; p. 11. [Google Scholar]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687, Erratum in Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized Gradient Approximation for the Exchange-Correlation Hole of a Many-Electron System. Phys. Rev. B 1996, 54, 16533. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange Functionals with Improved Long-Range Behavior and Adiabatic Connection Methods without Adjustable Parameters: The mPW and mPW1PW Models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
- Gill, P.M. A New Gradient-Corrected Exchange Functional. Mol. Phys. 1996, 89, 433–445. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Implementation and Validation of the Lacks-Gordon Exchange Functional in Conventional Density Functional and Adiabatic Connection Methods. J. Comput. Chem. 1998, 19, 418–429. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Constantin, L.A.; Sun, J. Workhorse Semilocal Density Functional for Condensed Matter Physics and Quantum Chemistry. Phys. Rev. Lett. 2009, 103, 026403, Erratum in Phys. Rev. Lett. 2011, 106, 179902. [Google Scholar] [CrossRef]
- Perdew, J.P.; Kurth, S.; Zupan, A.; Blaha, P. Accurate Density Functional with Correct Formal Properties: A Step Beyond the Generalized Gradient Approximation. Phys. Rev. Lett. 1999, 82, 2544. [Google Scholar] [CrossRef]
- Becke, A.D.; Roussel, M.R. Exchange Holes in Inhomogeneous Systems: A Coordinate-Space Model. Phys. Rev. A 1989, 39, 3761–3767. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Peverati, R.; Zhao, Y.; Truhlar, D.G. Generalized Gradient Approximation that Recovers the Second-Order Density-Gradient Expansion with Optimized Across-the-Board Performance. J. Phys. Chem. Lett. 2011, 2, 1991–1997. [Google Scholar] [CrossRef]
- Hamprecht, F.A.; Cohen, A.J.; Tozer, D.J.; Handy, N.C. Development and Assessment of New Exchange-Correlation Functionals. J. Chem. Phys. 1998, 109, 6264–6271. [Google Scholar] [CrossRef]
- Boese, A.D.; Doltsinis, N.L.; Handy, N.C.; Sprik, M. New Generalized Gradient Approximation Functionals. J. Chem. Phys. 2000, 112, 1670–1678. [Google Scholar] [CrossRef]
- Boese, A.D.; Handy, N.C. A New Parametrization of Exchange-Correlation Generalized Gradient Approximation Functionals. J. Chem. Phys. 2001, 114, 5497–5503. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Exchange-Correlation Functional with Good Accuracy for Both Structural and Energetic Properties While Depending Only on the Density and its Gradient. J. Chem. Theory Comput. 2012, 8, 2310–2319. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Adiabatic Connection Models Free from Adjustable Parameters. Chem. Phys. Lett. 1997, 274, 242–250. [Google Scholar] [CrossRef]
- Cohen, A.J.; Handy, N.C. Dynamic Correlation. Mol. Phys. 2001, 99, 607–615. [Google Scholar] [CrossRef]
- Xu, X.; Goddard III, W.A. The X3LYP Extended Density Functional for Accurate Descriptions of Nonbond Interactions, Spin States, and Thermochemical Properties. Proc. Natl. Acad. Sci. USA 2004, 101, 2673–2677. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Austin, A.; Petersson, G.A.; Frisch, M.J.; Dobek, F.J.; Scalmani, G.; Throssell, K. A Density Functional with Spherical Atom Dispersion Terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Communication: A Global Hybrid Generalized Gradient Approximation to the Exchange-Correlation Functional that Satisfies the Second-Order Density-Gradient Constraint and has Broad Applicability in Chemistry. J. Chem. Phys. 2011, 135, 191102. [Google Scholar] [CrossRef]
- Wilson, P.J.; Bradley, T.J.; Tozer, D.J. Hybrid Exchange-Correlation Functional Determined from Thermochemical Data and ab initio Potentials. J. Chem. Phys. 2001, 115, 9233–9242. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Optimized Density Functionals from the Extended G2 Test Set. J. Chem. Phys. 1998, 108, 9624–9631. [Google Scholar] [CrossRef]
- Van Voorhis, T.; Scuseria, G.E. A Novel Form for the Exchange-Correlation Energy Functional. J. Chem. Phys. 1998, 109, 400–410. [Google Scholar] [CrossRef]
- Boese, A.D.; Handy, N.C. New Exchange-Correlation Density Functionals: The Role of the Kinetic-Energy Density. J. Chem. Phys. 2002, 116, 9559–9569. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. M11-L: A Local Density Functional that Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics. J. Phys. Chem. Lett. 2012, 3, 117–124. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. An Improved and Broadly Accurate Local Approximation to the Exchange-Correlation Density Functional: The MN12-L Functional for Electronic Structure Calculations in Chemistry and Physics. Phys. Chem. Chem. Phys. 2012, 14, 13171–13174. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Truhlar, D.G. MN15-L: A New Local Exchange-Correlation Functional for Kohn-Sham Density Functional Theory with Broad Accuracy for Atoms, Molecules, and Solids. J. Chem. Theory Comput. 2016, 12, 1280–1293. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a Long-Range Corrected Hybrid Functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Heyd, J.; Krukau, A.V.; Scuseria, G.E. Importance of Short-Range Versus Long-Range Hartree-Fock Exchange for the Performance of Hybrid Density Functionals. J. Chem. Phys. 2006, 125, 074106. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E.; Perdew, J.P. Tests of Functionals for Systems with Fractional Electron Number. J. Chem. Phys. 2007, 126, 154109. [Google Scholar] [CrossRef] [PubMed]
- Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can Short-Range Hybrids Describe Long-Range-Dependent Properties? J. Chem. Phys. 2009, 131, 044108. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Double-Hybrid Density Functionals. J. Chem. Phys. 2009, 131, 174105. [Google Scholar] [CrossRef]
- Henderson, T.M.; Izmaylov, A.F.; Scuseria, G.E.; Savin, A. Assessment of a Middle-Range Hybrid Functional. J. Chem. Theory Comput. 2008, 4, 1254–1262. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Assessment and Validation of a Screened Coulomb Hybrid Density Functional. J. Chem. Phys. 2004, 120, 7274–7280. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Efficient Hybrid Density Functional Calculations in Solids: Assessment of the Heyd-Scuseria-Ernzerhof Screened Coulomb Hybrid Functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef]
- Heyd, J.; Peralta, J.E.; Scuseria, G.E.; Martin, R.L. Energy Band Gaps and Lattice Parameters Evaluated with the Heyd-Scuseria-Ernzerhof Screened Hybrid Functional. J. Chem. Phys. 2005, 123, 174101. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Erratum: "Hybrid Functionals Based on a Screened Coulomb Potential". J. Chem. Phys. 2006, 124, 219906. [Google Scholar] [CrossRef]
- Izmaylov, A.F.; Scuseria, G.E.; Frisch, M.J. Efficient Evaluation of Short-Range Hartree-Fock Exchange in Large Molecules and Periodic Systems. J. Chem. Phys. 2006, 125, 104103. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics. Phys. Chem. Chem. Phys. 2012, 14, 16187–16191. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. IV. A New Dynamical Correlation Functional and Implications for Exact-Exchange Mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals that are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Exchange-Correlation Functional with Broad Accuracy for Metallic and Nonmetallic Compounds, Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2005, 123, 161103. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Comparative DFT Study of van der Waals Complexes: Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef] [PubMed]
- Haoyu, S.Y.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Dobbs, K.; Hehre, W. Molecular Orbital Theory of the Properties of Inorganic and Organometallic Compounds 4. Extended Basis Sets for Third- and Fourth-Row, Main-Group Elements. J. Comput. Chem. 1986, 7, 359–378. [Google Scholar] [CrossRef]
- Gordon, M.S.; Binkley, J.S.; Pople, J.A.; Pietro, W.J.; Hehre, W.J. Self-Consistent Molecular-Orbital Methods. 22. Small Split-Valence Basis Sets for Second-Row Elements. J. Am. Chem. Soc. 1982, 104, 2797–2803. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- McLean, A.; Chandler, G. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Pietro, W.J.; Francl, M.M.; Hehre, W.J.; DeFrees, D.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods. 24. Supplemented Small Split-Valence Basis Sets for Second-Row Elements. J. Am. Chem. Soc. 1982, 104, 5039–5048. [Google Scholar] [CrossRef]
- Binkley, J.S.; Pople, J.A.; Hehre, W.J. Self-Consistent Molecular Orbital Methods. 21. Small Split-Valence Basis Sets for First-Row Elements. J. Am. Chem. Soc. 1980, 102, 939–947. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian Basis Sets for use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Barone, V. Structure, Magnetic Properties and Reactivities of Open-Shell Species from Density Functional and Self-Consistent Hybrid Methods. In Recent Advances in Density Functional Methods, Part I; Chong, D.P., Ed.; World Scientific Publishing Co.: Singapore, 1996. [Google Scholar]
- Easton, R.E.; Giesen, D.J.; Welch, A.; Cramer, C.J.; Truhlar, D.G. The MIDI! Basis Set for Quantum Mechanical Calculations of Molecular Geometries and Partial Charges. Theor. Chim. Acta 1996, 93, 281–301. [Google Scholar] [CrossRef]
- Dunning, T.H.; Hay, P.J. Gaussian Basis Sets for Molecular Calculations. In Methods of Electronic Structure Theory. Modern Theoretical Chemistry; Schaefer, H.F., Ed.; Springer: Boston, MA, USA, 1977; Volume 3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).