Figure 1.
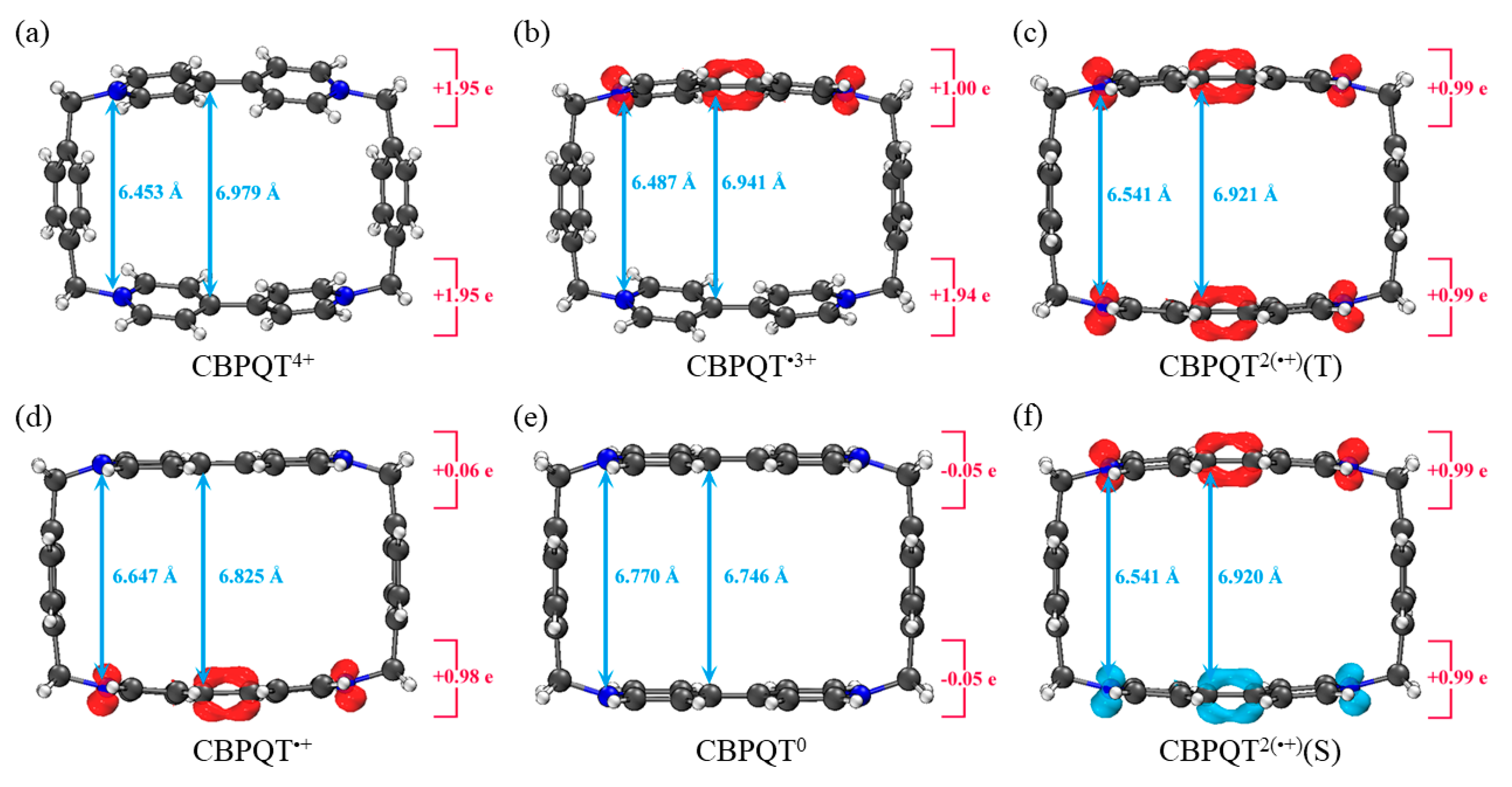
Geometries, NPA charge distribution and spin density distribution of (a) CBPQT4+, (b) CBPQT•3+, (c) CBPQT2(•+)(Triplet), (d) CBPQT•+, (e) CBPQT0, (f) CBPQT2(•+)(Singlet) obtained by ωB97X-D/6-31G* in MeCN solvent. The white, gray and blue spheres represent H, C and N atoms, respectively. The red isosurface represents positive spin density and the blue isosurface is negative.
Figure 1.
Geometries, NPA charge distribution and spin density distribution of (a) CBPQT4+, (b) CBPQT•3+, (c) CBPQT2(•+)(Triplet), (d) CBPQT•+, (e) CBPQT0, (f) CBPQT2(•+)(Singlet) obtained by ωB97X-D/6-31G* in MeCN solvent. The white, gray and blue spheres represent H, C and N atoms, respectively. The red isosurface represents positive spin density and the blue isosurface is negative.
Figure 2.
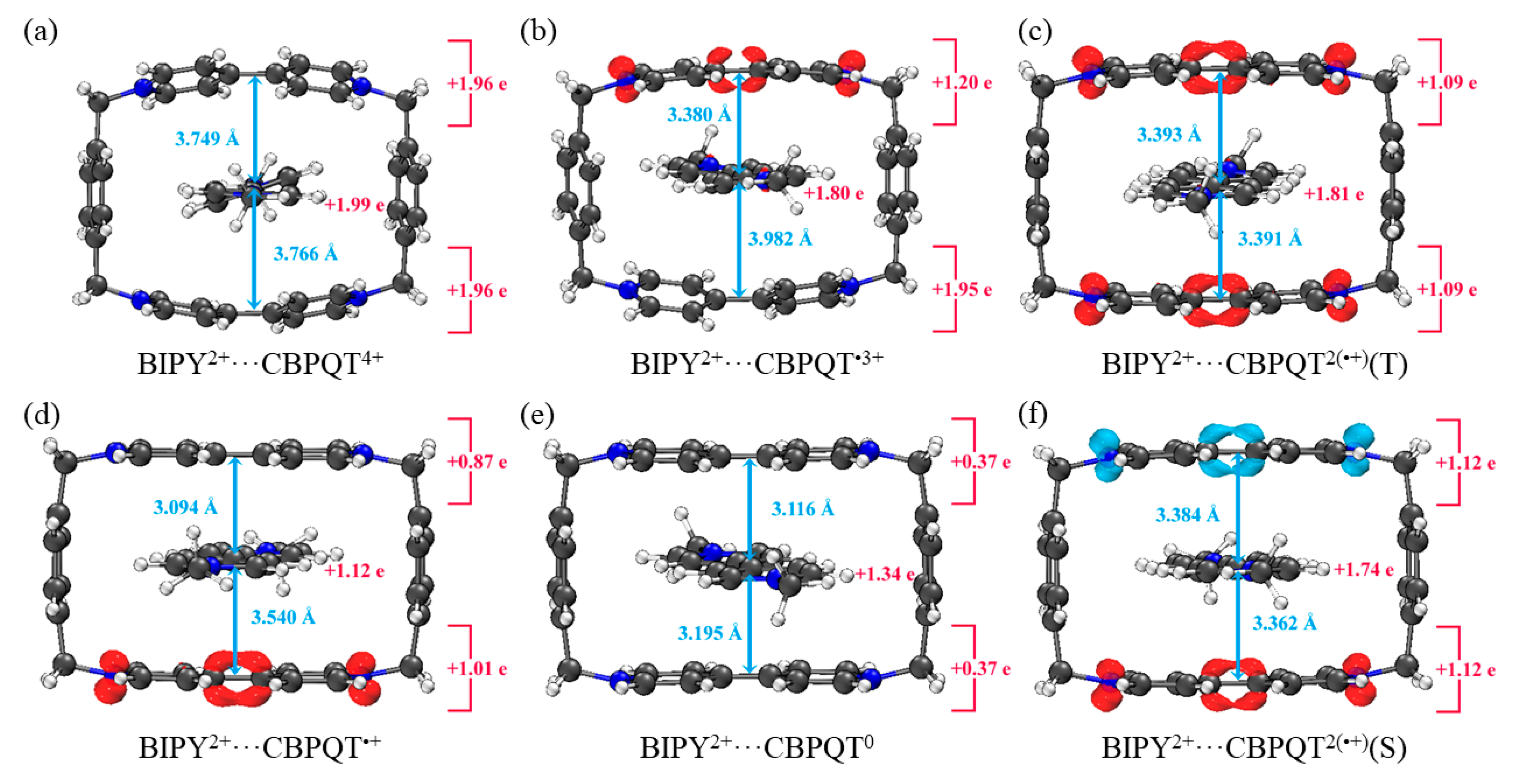
Geometries, NPA charge distribution and spin density distribution of (a) BIPY2+···CBPQT4+, (b) BIPY2+···CBPQT•3+, (c) BIPY2+···CBPQT2(•+)(T), (d) BIPY2+···CBPQT•+, (e) BIPY2+···CBPQT0, (f) BIPY2+···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 2.
Geometries, NPA charge distribution and spin density distribution of (a) BIPY2+···CBPQT4+, (b) BIPY2+···CBPQT•3+, (c) BIPY2+···CBPQT2(•+)(T), (d) BIPY2+···CBPQT•+, (e) BIPY2+···CBPQT0, (f) BIPY2+···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 3.
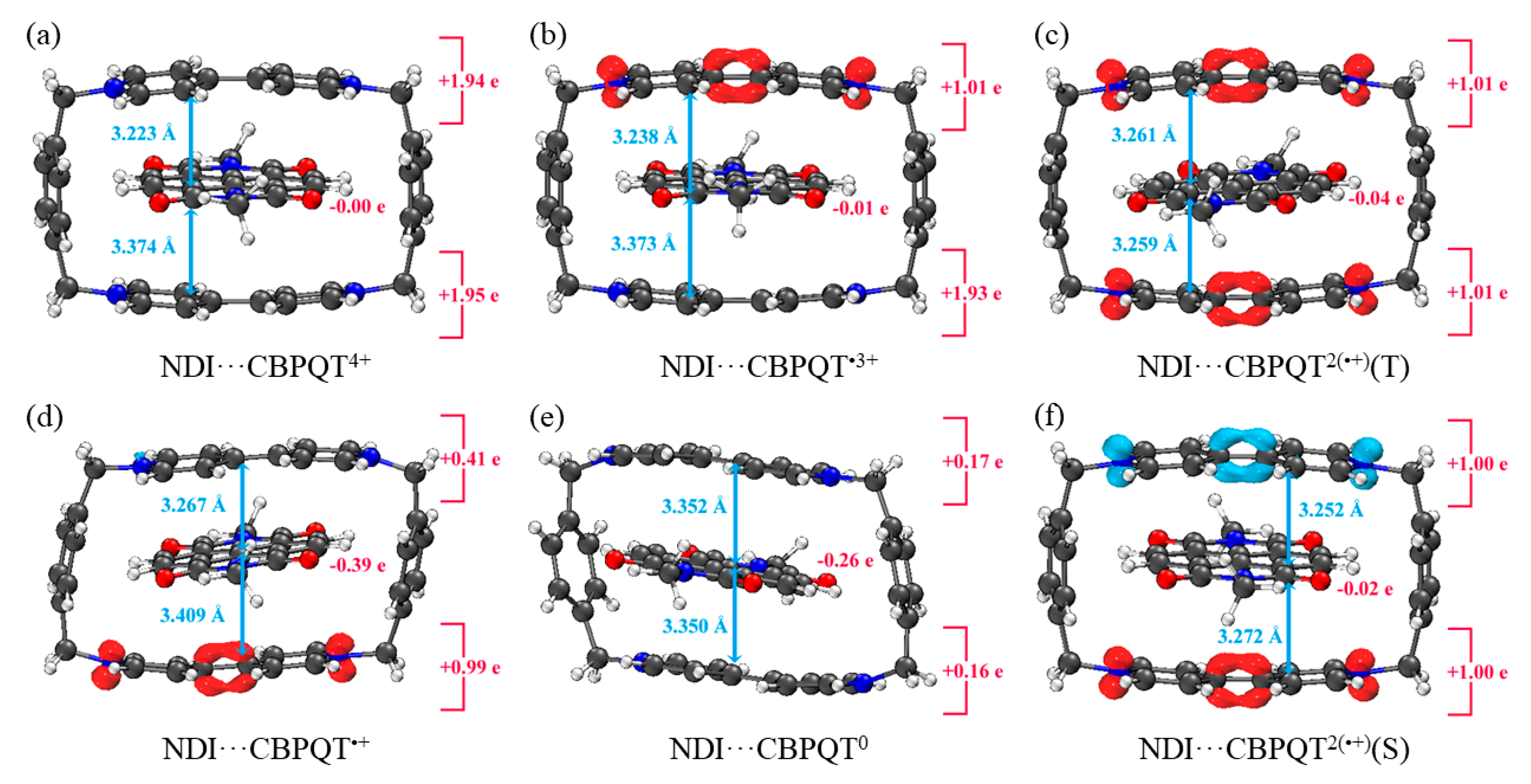
Geometries, NPA charge distribution and spin density distribution of (a) NDI···CBPQT4+, (b) NDI···CBPQT•3+, (c) NDI···CBPQT2(•+)(T), (d) NDI···CBPQT•+, (e) NDI···CBPQT0, (f) NDI···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 3.
Geometries, NPA charge distribution and spin density distribution of (a) NDI···CBPQT4+, (b) NDI···CBPQT•3+, (c) NDI···CBPQT2(•+)(T), (d) NDI···CBPQT•+, (e) NDI···CBPQT0, (f) NDI···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 4.
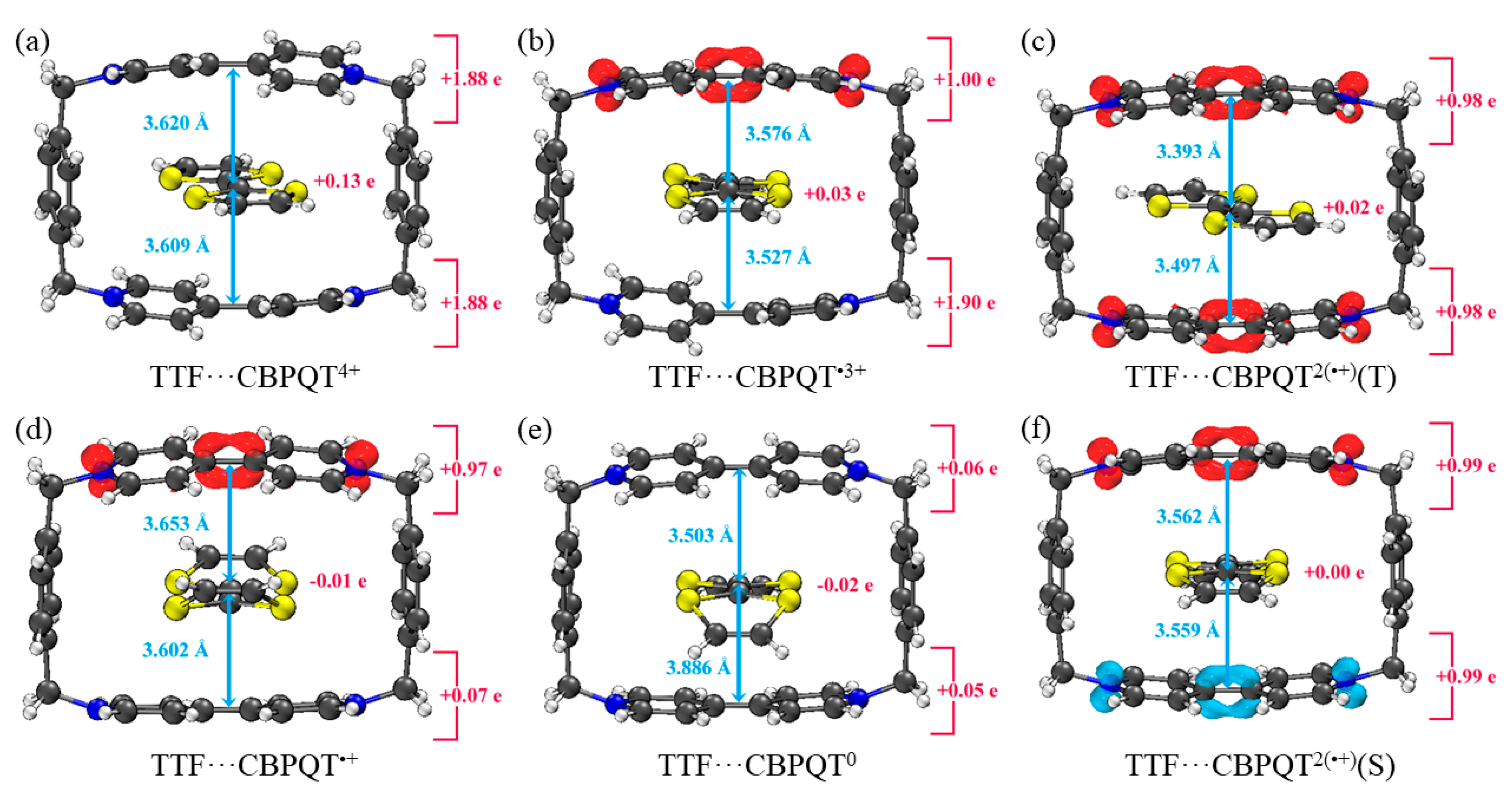
Geometries, NPA charge distribution and spin density distribution of (a) TTF···CBPQT4+, (b) TTF···CBPQT•3+, (c) TTF···CBPQT2(•+)(T), (d) TTF···CBPQT•+, (e) TTF···CBPQT0, (f) TTF···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 4.
Geometries, NPA charge distribution and spin density distribution of (a) TTF···CBPQT4+, (b) TTF···CBPQT•3+, (c) TTF···CBPQT2(•+)(T), (d) TTF···CBPQT•+, (e) TTF···CBPQT0, (f) TTF···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
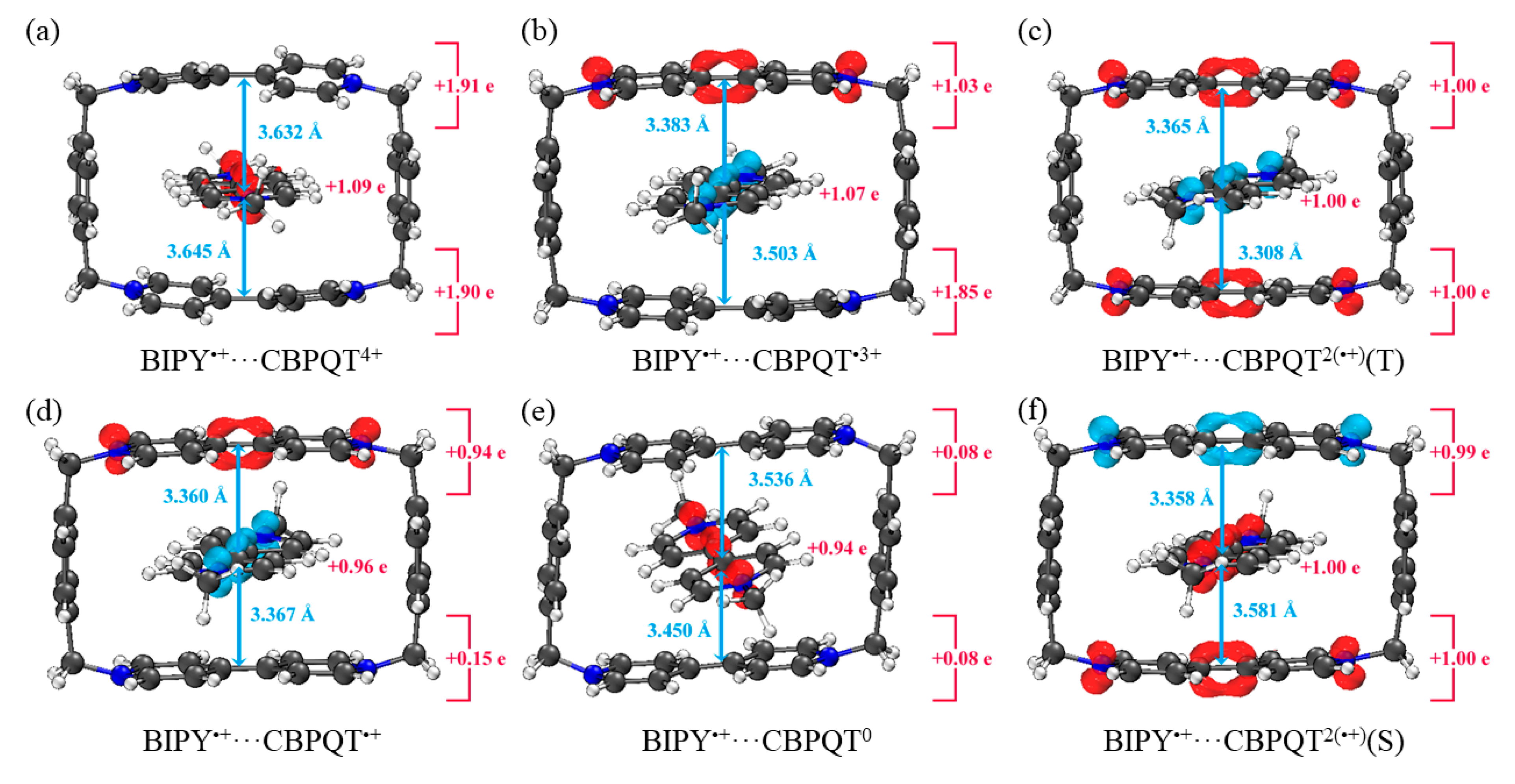
Figure 5.
Geometries, NPA charge distribution and spin density distribution of (a) BIPY•+···CBPQT4+, (b) BIPY•+···CBPQT•3+, (c) BIPY•+···CBPQT2(•+)(T), (d) BIPY•+···CBPQT•+, (e) BIPY•+···CBPQT0, (f) BIPY•+···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 5.
Geometries, NPA charge distribution and spin density distribution of (a) BIPY•+···CBPQT4+, (b) BIPY•+···CBPQT•3+, (c) BIPY•+···CBPQT2(•+)(T), (d) BIPY•+···CBPQT•+, (e) BIPY•+···CBPQT0, (f) BIPY•+···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 6.
Geometries, NPA charge distribution and spin density distribution of (a) NDI•−···CBPQT4+, (b) NDI•−···CBPQT•3+, (c) NDI•−···CBPQT2(•+)(T), (d) NDI•−···CBPQT•+, (e) NDI•−···CBPQT0, (f) NDI•−···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 6.
Geometries, NPA charge distribution and spin density distribution of (a) NDI•−···CBPQT4+, (b) NDI•−···CBPQT•3+, (c) NDI•−···CBPQT2(•+)(T), (d) NDI•−···CBPQT•+, (e) NDI•−···CBPQT0, (f) NDI•−···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in MeCN solvent.
Figure 7.
Geometries, NPA charge distribution and spin density distribution of (a) BTA•···CBPQT4+, (b) BTA•···CBPQT•3+, (c) BTA•···CBPQT2(•+)(T), (d) BTA•···CBPQT•+, (e) BTA•···CBPQT0, (f) BTA•···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in CPCM solvent.
Figure 7.
Geometries, NPA charge distribution and spin density distribution of (a) BTA•···CBPQT4+, (b) BTA•···CBPQT•3+, (c) BTA•···CBPQT2(•+)(T), (d) BTA•···CBPQT•+, (e) BTA•···CBPQT0, (f) BTA•···CBPQT2(•+)(S) obtained by ωB97X-D/6-31G* in CPCM solvent.
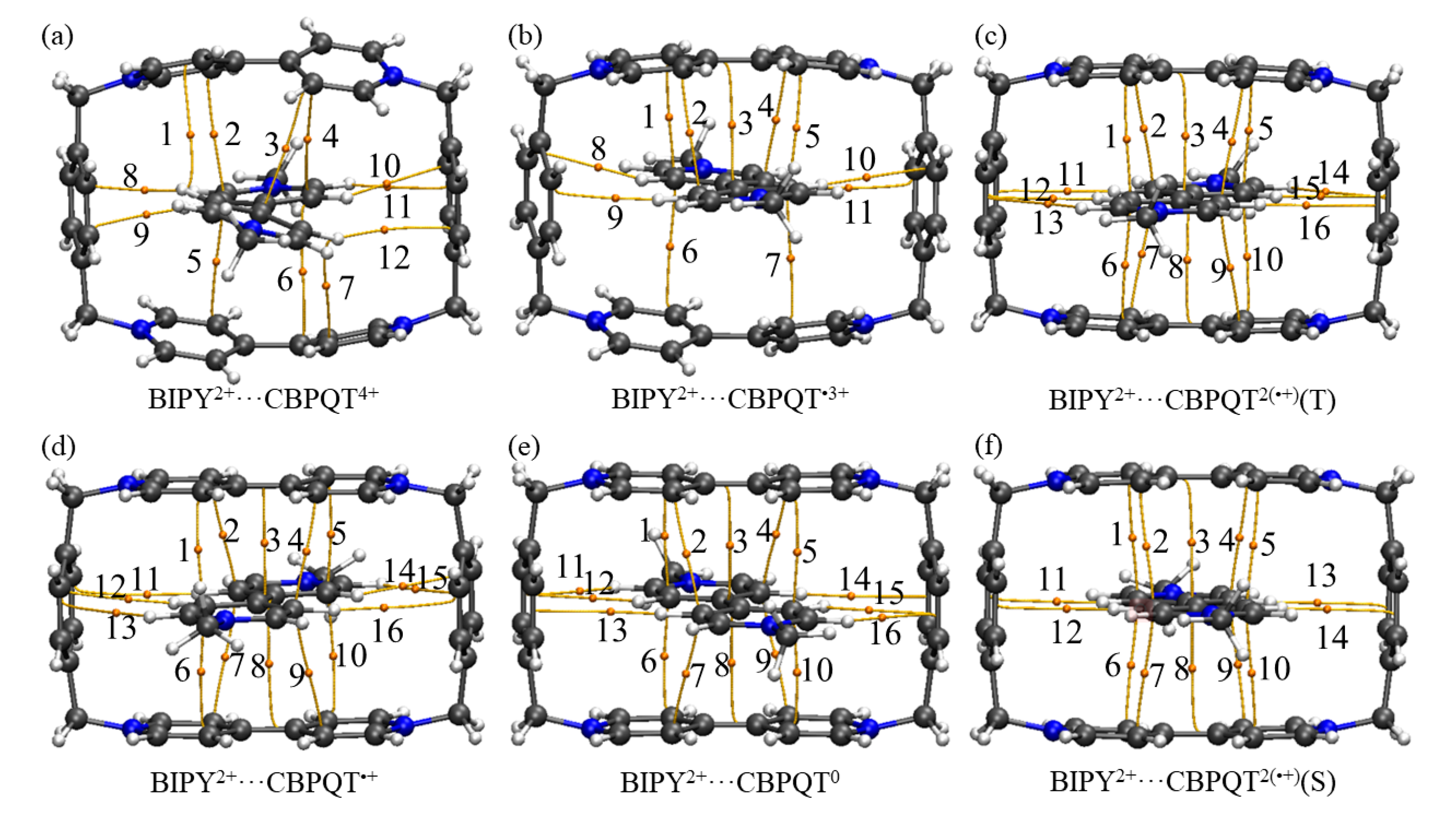
Figure 8.
Intermolecular BCPs found in the (a) BIPY2+···CBPQT4+, (b) BIPY2+···CBPQT•3+, (c) BIPY2+···CBPQT2(•+)(T), (d) BIPY2+···CBPQT•+, (e) BIPY2+···CBPQT0, (f) BIPY2+···CBPQT2(•+)(S) complexes.
Figure 8.
Intermolecular BCPs found in the (a) BIPY2+···CBPQT4+, (b) BIPY2+···CBPQT•3+, (c) BIPY2+···CBPQT2(•+)(T), (d) BIPY2+···CBPQT•+, (e) BIPY2+···CBPQT0, (f) BIPY2+···CBPQT2(•+)(S) complexes.
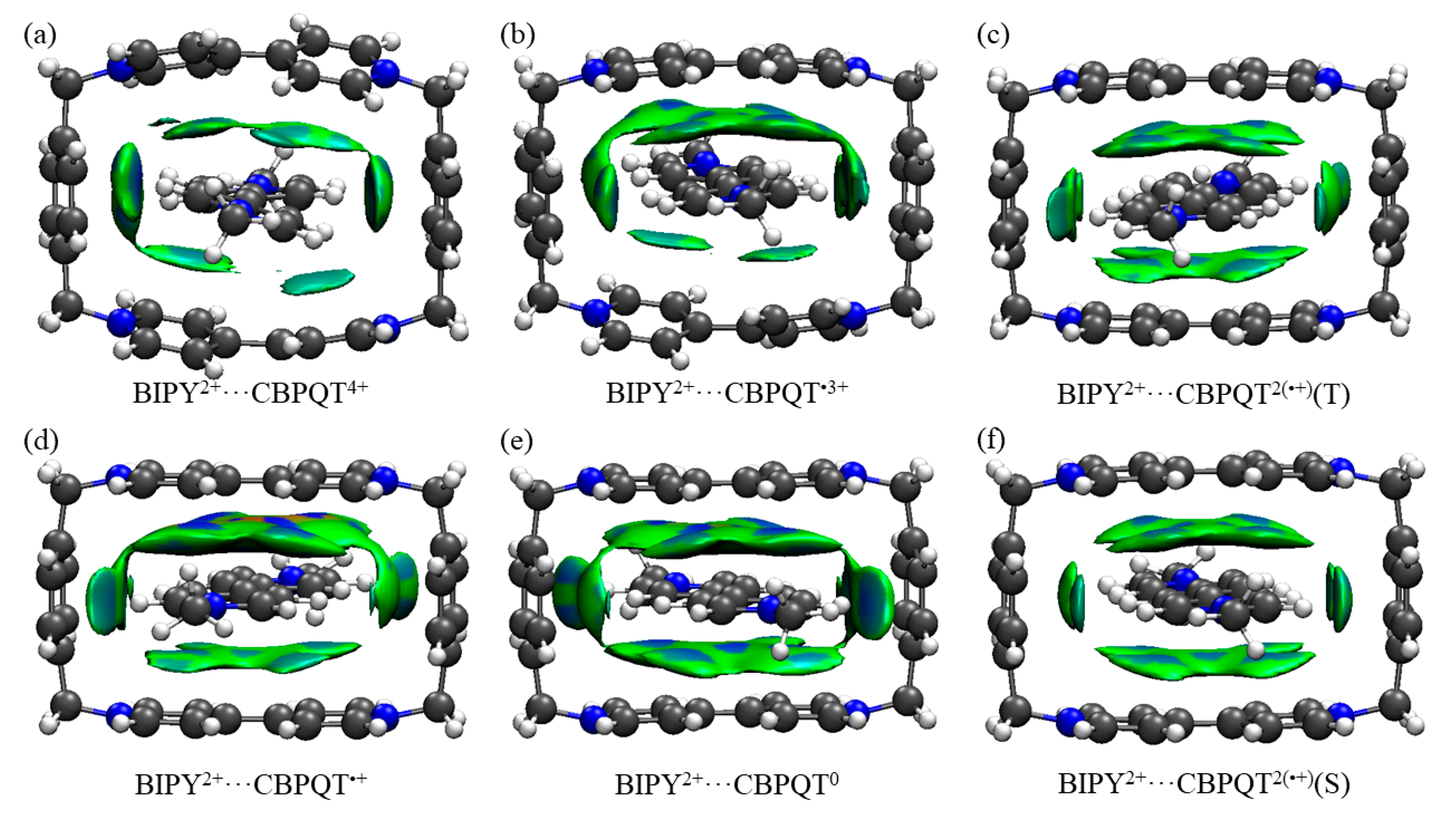
Figure 9.
(a–f) IGM plot iso-surfaces of BIPY2+···CBPQTn+ (n = 0–4) complexes. δginter = 0.005 a.u. All iso-surfaces are colored according to a BGR scheme over the range −0.03 < sign(λ2)ρ < +0.05 a.u.
Figure 9.
(a–f) IGM plot iso-surfaces of BIPY2+···CBPQTn+ (n = 0–4) complexes. δginter = 0.005 a.u. All iso-surfaces are colored according to a BGR scheme over the range −0.03 < sign(λ2)ρ < +0.05 a.u.
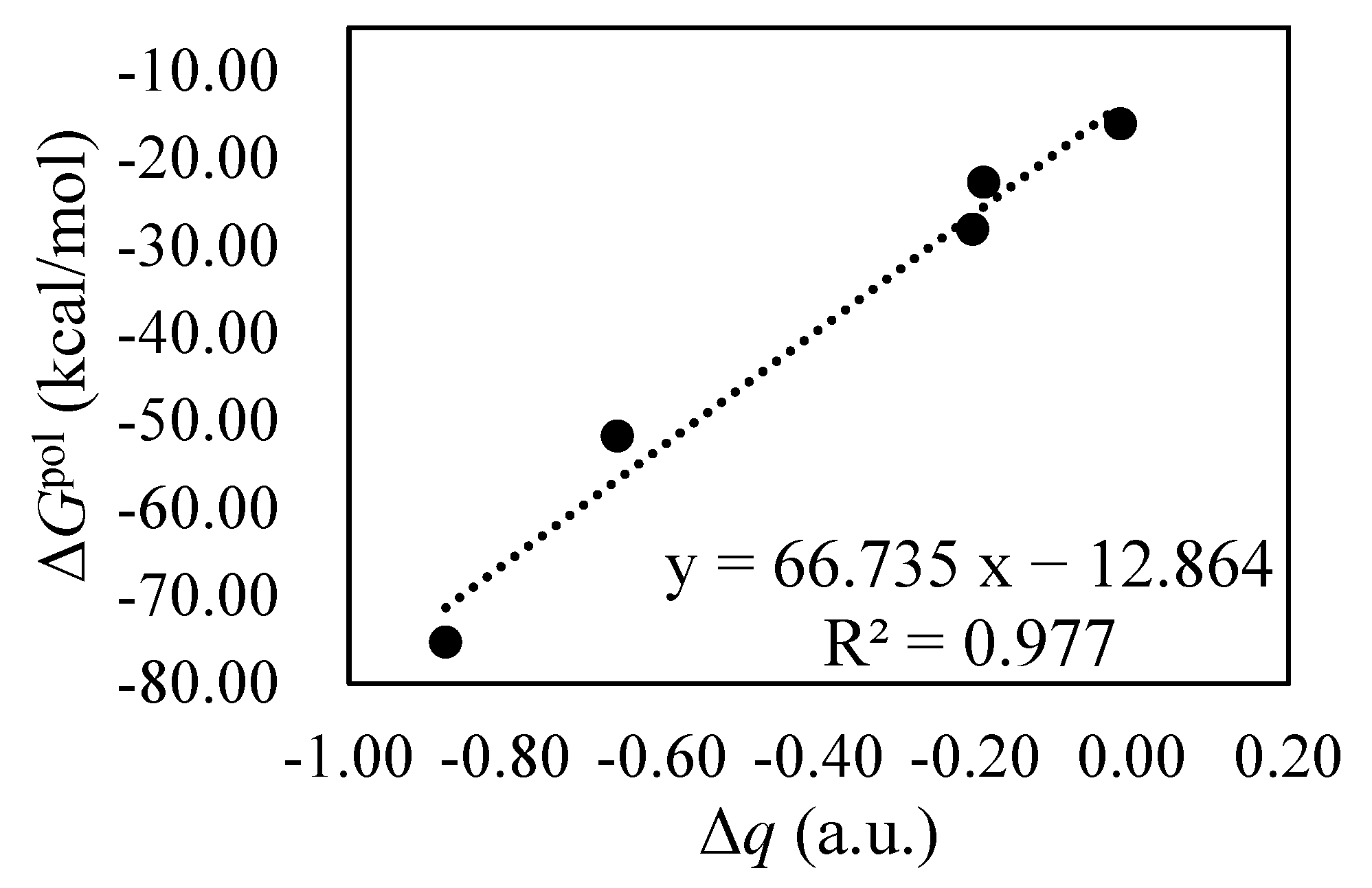
Figure 10.
Correlation between the variation in charge (∆q) on BIPY2+ and polarization interactions of the BIPY2+···CBPQTn+ complexes in the solution.
Figure 10.
Correlation between the variation in charge (∆q) on BIPY2+ and polarization interactions of the BIPY2+···CBPQTn+ complexes in the solution.
Figure 11.
MO diagrams of (a) BIPY2+···CBPQT0, (b) BIPY•+···CBPQT0, (c) BIPY2+···CBPQT•3+, (d) BIPY•+···CBPQT•3+ complexes.
Figure 11.
MO diagrams of (a) BIPY2+···CBPQT0, (b) BIPY•+···CBPQT0, (c) BIPY2+···CBPQT•3+, (d) BIPY•+···CBPQT•3+ complexes.
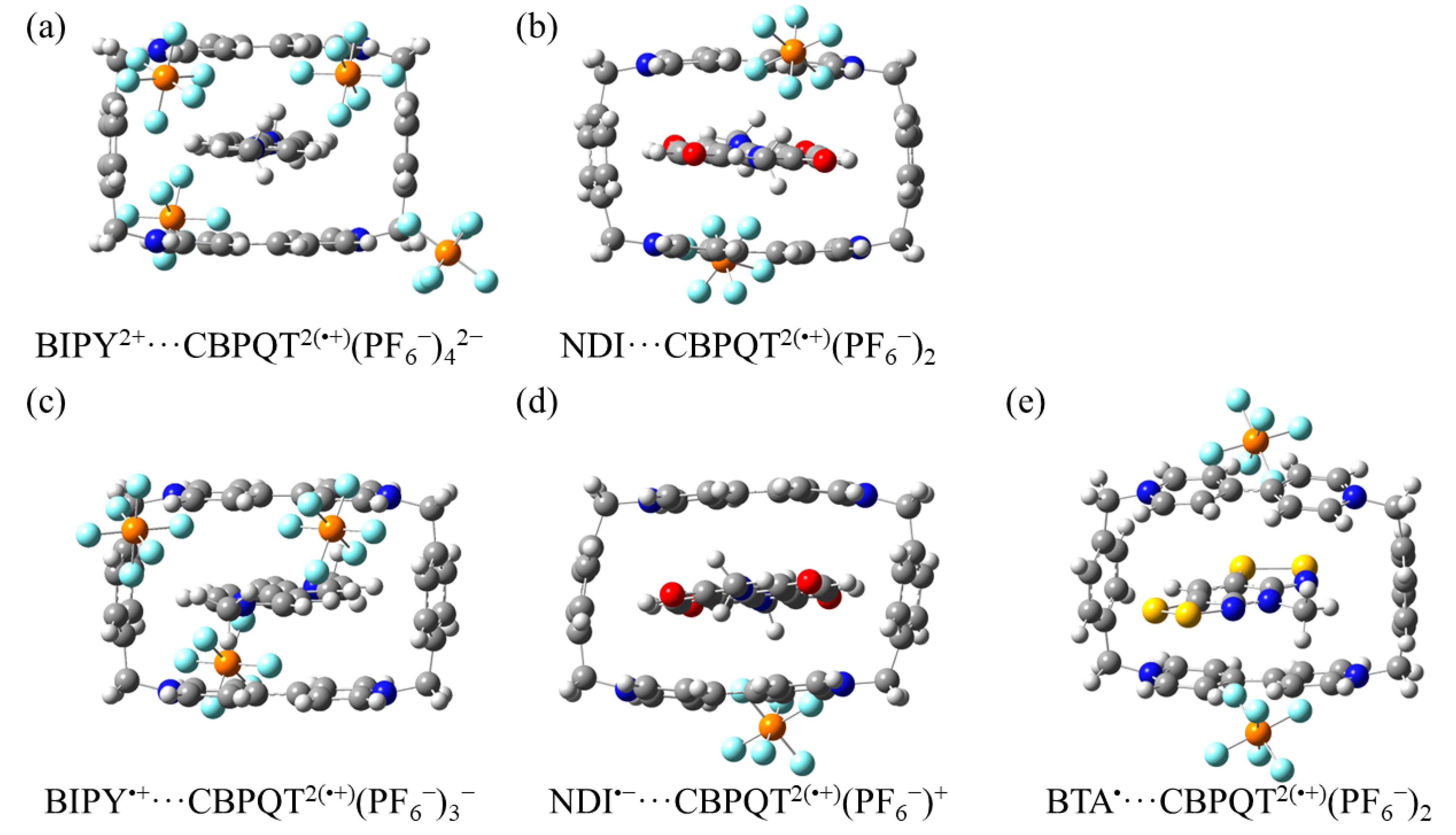
Figure 12.
Geometries of (a) BIPY2+···CBPQT2(•+)(PF6−)42−, (b) NDI···CBPQT2(•+)(PF6−)2, (c) BIPY•+···CBPQT2(•+)(PF6−)3−, (d) NDI•−···CBPQT2(•+)(PF6−)+, and (e) BTA•···CBPQT2(•+)(PF6−)2 obtained by ωB97X-D/6-31G* in CPCM MeCN solvent.
Figure 12.
Geometries of (a) BIPY2+···CBPQT2(•+)(PF6−)42−, (b) NDI···CBPQT2(•+)(PF6−)2, (c) BIPY•+···CBPQT2(•+)(PF6−)3−, (d) NDI•−···CBPQT2(•+)(PF6−)+, and (e) BTA•···CBPQT2(•+)(PF6−)2 obtained by ωB97X-D/6-31G* in CPCM MeCN solvent.
Table 1.
The GKS-EDA results of BIPY2+···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 1.
The GKS-EDA results of BIPY2+···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| BIPY2+···CBPQT4+ | 405.32 | 19.49 | −16.03 | −373.66 | −34.27 | 0.85 |
| BIPY2+···CBPQT•3+ | 296.62 | 30.41 | −28.09 | −270.29 | −48.01 | −19.37 |
| BIPY2+···CBPQT2(•+)(T) | 190.54 | 34.06 | −22.70 | −182.87 | −50.13 | −31.11 |
| BIPY2+···CBPQT2(•+)(S) | 189.98 | 36.97 | −23.22 | −181.52 | −53.56 | −31.34 |
| BIPY2+···CBPQT•+ | 70.56 | 57.56 | −75.26 | −69.95 | −52.53 | −69.61 |
| BIPY2+···CBPQT0 | −40.63 | 62.87 | −51.70 | 22.78 | −66.08 | −72.77 |
Table 2.
The GKS-EDA results of NDI···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 2.
The GKS-EDA results of NDI···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| NDI···CBPQT4+ | −22.99 | 79.11 | −15.30 | 2.71 | −69.72 | −26.19 |
| NDI···CBPQT•3+ | −27.04 | 81.93 | −14.63 | 2.48 | −70.44 | −27.70 |
| NDI···CBPQT2(•+)(T) | −35.53 | 101.94 | −14.21 | 0.82 | −76.87 | −23.85 |
| NDI···CBPQT2(•+)(S) | −28.93 | 82.65 | −11.77 | −0.01 | −70.26 | −28.33 |
| NDI···CBPQT•+ | −35.93 | 95.28 | −20.63 | 0.29 | −76.97 | −37.97 |
| NDI···CBPQT0 | −37.99 | 95.14 | −17.22 | 0.27 | −77.22 | −37.02 |
Table 3.
The GKS-EDA results of TTF···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 3.
The GKS-EDA results of TTF···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| TTF···CBPQT4+ | −34.31 | 50.09 | −8.72 | 6.11 | −44.84 | −31.67 |
| TTF···CBPQT•3+ | −24.43 | 38.48 | −7.69 | 5.42 | −40.54 | −28.77 |
| TTF···CBPQT2(•+)(T) | −26.45 | 56.43 | −7.26 | 2.83 | −48.45 | −22.90 |
| TTF···CBPQT2(•+)(S) | −19.11 | 36.29 | −4.86 | 2.98 | −39.44 | −24.14 |
| TTF···CBPQT•+ | −14.43 | 37.88 | −7.12 | 1.35 | −40.39 | −22.71 |
| TTF···CBPQT0 | −10.92 | 35.15 | −6.26 | 0.45 | −38.11 | −19.69 |
Table 4.
The GKS-EDA results of BIPY•+···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 4.
The GKS-EDA results of BIPY•+···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| BIPY•+···CBPQT4+ | 187.20 | 31.77 | −8.09 | −186.23 | −43.82 | −19.17 |
| BIPY•+···CBPQT•3+ | 135.20 | 37.84 | −11.37 | −138.20 | −51.08 | −27.61 |
| BIPY•+···CBPQT2(•+)(T) | 83.16 | 42.48 | −11.37 | −93.51 | −54.53 | −33.77 |
| BIPY•+···CBPQT2(•+)(S) | 83.86 | 41.82 | −10.13 | −93.22 | −51.00 | −28.67 |
| BIPY•+···CBPQT•+ | 31.16 | 47.04 | −14.18 | −42.96 | −56.91 | −35.84 |
| BIPY•+···CBPQT0 | −19.77 | 44.44 | −13.18 | 3.43 | −51.35 | −36.42 |
Table 5.
The GKS-EDA results of NDI•−···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 5.
The GKS-EDA results of NDI•−···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| NDI•−···CBPQT4+ | −263.17 | 117.52 | −23.10 | 207.67 | −83.67 | −44.75 |
| NDI•−···CBPQT•3+ | −208.11 | 123.56 | −12.20 | 147.48 | −86.41 | −35.67 |
| NDI•−···CBPQT2(•+)(T) | −136.96 | 92.25 | −14.36 | 99.68 | −75.67 | −35.06 |
| NDI•−···CBPQT2(•+)(S) | −136.56 | 90.66 | −13.77 | 99.75 | −73.19 | −33.10 |
| NDI•−···CBPQT•+ | −92.29 | 111.79 | −16.96 | 53.08 | −80.92 | −25.30 |
| NDI•−···CBPQT0 | −26.00 | 86.89 | −12.03 | 0.03 | −70.36 | −21.46 |
Table 6.
The GKS-EDA results of BTA•···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 6.
The GKS-EDA results of BTA•···CBPQTn+ complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| Complexes | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| BTA•···CBPQT4+ | −21.78 | 55.56 | −10.11 | 4.54 | −57.84 | −29.64 |
| BTA•···CBPQT•3+ | −23.00 | 58.80 | −10.75 | 3.83 | −58.75 | −29.87 |
| BTA•···CBPQT2(•+)(T) | −23.40 | 60.15 | −8.56 | 1.07 | −59.21 | −29.94 |
| BTA•···CBPQT2(•+)(S) | −24.10 | 61.56 | −8.51 | 1.34 | −59.53 | −29.23 |
| BTA•···CBPQT•+ | −25.95 | 64.72 | −11.46 | 1.49 | −59.86 | −31.07 |
| BTA•···CBPQT0 | −25.03 | 61.80 | −11.14 | −0.38 | −56.88 | −31.63 |
Table 7.
Host–guest interactions after the addition of counterions in BIPY2+···CBPQT2(•+), NDI···CBPQT2(•+), BIPY•+···CBPQT2(•+),NDI•−···CBPQT2(•+), and BTA•···CBPQT2(•+) complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
Table 7.
Host–guest interactions after the addition of counterions in BIPY2+···CBPQT2(•+), NDI···CBPQT2(•+), BIPY•+···CBPQT2(•+),NDI•−···CBPQT2(•+), and BTA•···CBPQT2(•+) complexes obtained by ωB97X-D/6-31+G* in MeCN solvent (kcal/mol).
| | ΔGele | ΔGexrep | ΔGpol | ΔGdesol | ΔGdisp/corr | ΔGTOT |
|---|
| BIPY2+···CBPQT2(•+)(PF6−)42− | −224.84 | 63.06 | −28.08 | 179.19 | −67.61 | −78.28 |
| NDI···CBPQT2(•+)(PF6−)2 | −37.99 | 94.10 | −14.16 | 2.33 | −80.15 | −35.87 |
| BIPY•+···CBPQT2(•+)(PF6−)3− | −86.48 | 65.25 | −16.72 | 53.83 | −70.55 | −54.67 |
| NDI•−···CBPQT2(•+)(PF6−)+ | −86.84 | 95.94 | −17.82 | 53.55 | −80.37 | −35.54 |
| BTA•···CBPQT2(•+)(PF6−)2 | −20.39 | 54.86 | −7.74 | 0.89 | −59.19 | −31.59 |