Identifying Systematic Force Field Errors Using a 3D-RISM Element Counting Correction
Abstract
1. Introduction
2. Theory
2.1. PMV Correction
2.2. vdW Volume Correction
2.3. Element Count Correction
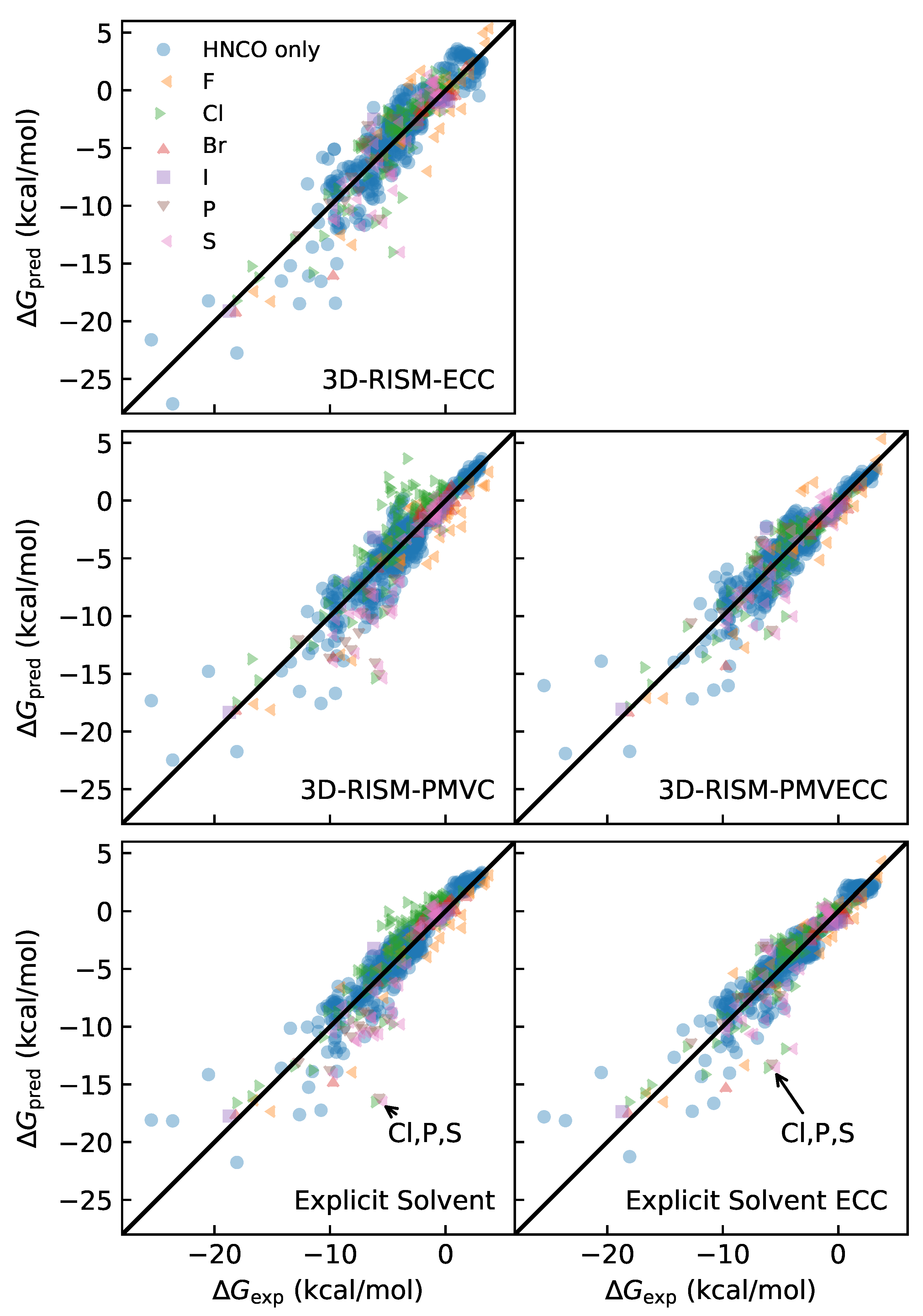
3. Results
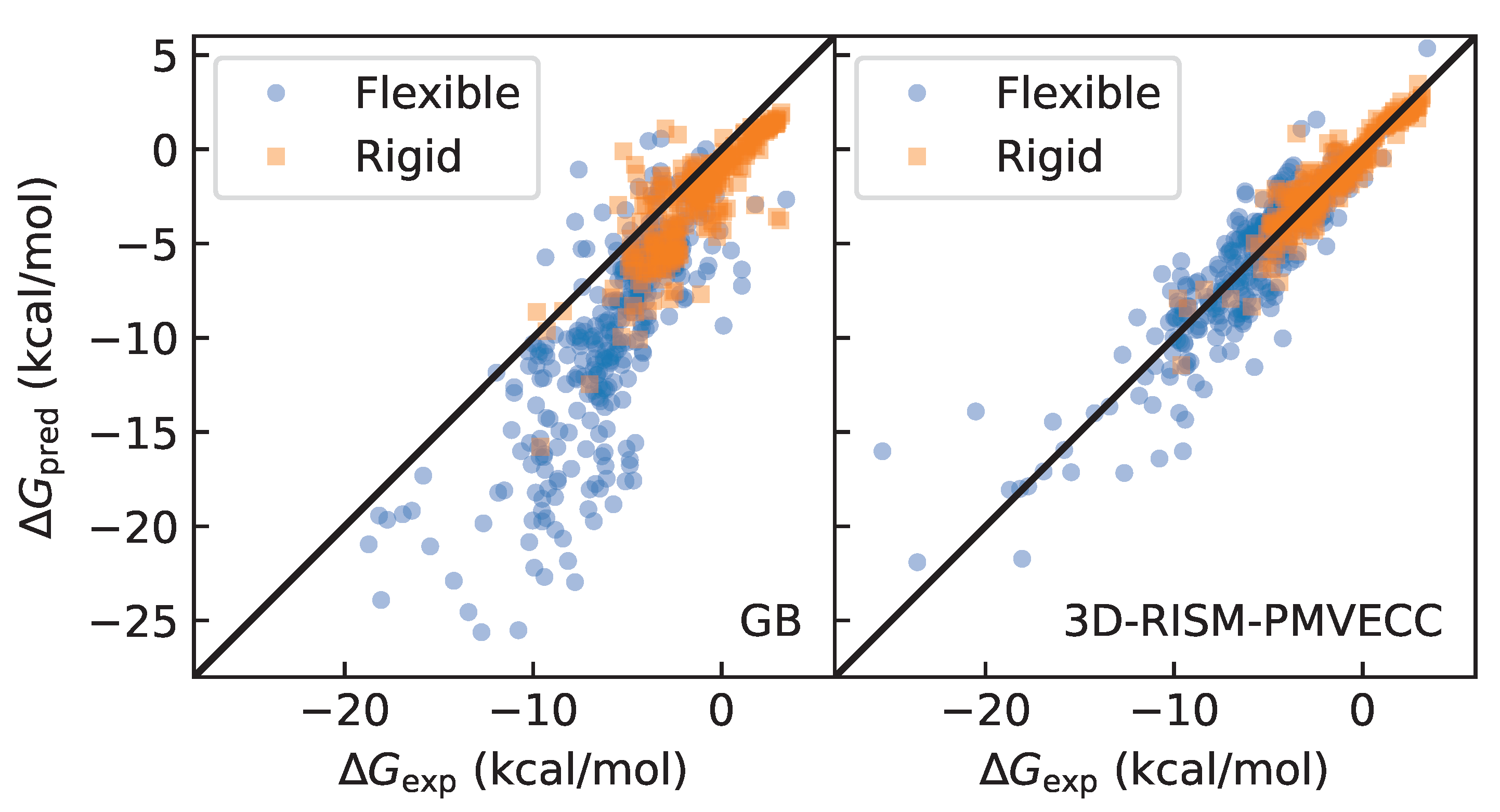
3.1. Identifying Rigid and Flexible Molecules Using Molecular Dynamics with GB Solvent
3.2. Fitting PMVC, ECC, and PMVECC Parameters
3.3. Quality of Fit
4. Discussion
4.1. Dealing with Conformational Sampling
4.2. Accuracy and Computational Efficiency of 3D-RISM/PMVECC
4.3. Force Field Parameters
5. Materials and Methods
5.1. Structure Preparation
5.2. GB HFE
5.3. 1D-RISM
5.4. 3D-RISM Calculations
5.5. Parameter Fitting
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skyner, E.R.; McDonagh, L.J.; Groom, R.C.; Mourik, T.V.; Mitchell, O.J.B. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef] [PubMed]
- Sharp, K.A.; Honig, B. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 1990, 94, 7684–7692. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Self-consistent description of a metal–water interface by the Kohn–Sham density functional theory and the three-dimensional reference interaction site model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. An Integral Equation to Describe the Solvation of Polar Molecules in Liquid Water. J. Phys. Chem. B 1997, 101, 7821–7826. [Google Scholar] [CrossRef]
- Ornstein, L.S.; Zernike, F. Accidental deviations of density and opalescence at the critical point of a single substance. Proc. Akad. Sci. 1914, 17, 793. [Google Scholar]
- Truchon, J.F.; Pettitt, B.M.; Labute, P. A Cavity Corrected 3D-RISM Functional for Accurate Solvation Free Energies. J. Chem. Theory Comput. 2014, 10, 934–941. [Google Scholar] [CrossRef]
- Sergiievskyi, V.P.; Jeanmairet, G.; Levesque, M.; Borgis, D. Fast Computation of Solvation Free Energies with Molecular Density Functional Theory: Thermodynamic-Ensemble Partial Molar Volume Corrections. J. Phys. Chem. Lett. 2014, 5, 1935–1942. [Google Scholar] [CrossRef]
- Palmer, D.S.; Frolov, A.I.; Ratkova, E.L.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matter 2010, 22, 492101. [Google Scholar] [CrossRef]
- Robert, A.; Luukkonen, S.; Levesque, M. Pressure correction for solvation theories. J. Chem. Phys. 2020, 152, 191103. [Google Scholar] [CrossRef]
- Borgis, D.; Luukkonen, S.; Belloni, L.; Jeanmairet, G. Accurate prediction of hydration free energies and solvation structures using molecular density functional theory with a simple bridge functional. J. Chem. Phys. 2021, 155, 024117. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Case, D.A.; Yamazaki, T.; Gusarov, S.; Kovalenko, A.; Luchko, T. Small molecule hydration energy and entropy from 3D-RISM. J. Phys. Condens. Matter 2016, 28, 344002. [Google Scholar] [CrossRef] [PubMed]
- Luchko, T.; Blinov, N.; Limon, G.C.; Joyce, K.P.; Kovalenko, A. SAMPL5: 3D-RISM partition coefficient calculations with partial molar volume corrections and solute conformational sampling. J. Comput. Aided Mol. Des. 2016, 30, 1115–1127. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kovalenko, A. A molecular solvation theory simulation of liquid alkyl esters of acetic acid with the 3D Reference Interaction Site Model. J. Mol. Liq. 2021, 344, 117763. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Application of the Approximate 3D-RISM Molecular Solvation Theory to Acetonitrile as Solvent. J. Phys. Chem. B 2020, 124, 4590–4597. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Performance of 3D-RISM-KH in Predicting Hydration Free Energy: Effect of Solute Parameters. J. Phys. Chem. A 2019, 123, 4087–4093. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kovalenko, A. Benchmarking Free Energy Calculations in Liquid Aliphatic Ketone Solvents Using the 3D-RISM-KH Molecular Solvation Theory. J 2021, 4, 604–613. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Application of the 3D-RISM-KH molecular solvation theory for DMSO as solvent. J. Comput. Aided Mol. Des. 2019, 33, 905–912. [Google Scholar] [CrossRef]
- Roy, D.; Blinov, N.; Kovalenko, A. Predicting Accurate Solvation Free Energy in n-Octanol Using 3D-RISM-KH Molecular Theory of Solvation: Making Right Choices. J. Phys. Chem. B 2017, 121, 9268–9273. [Google Scholar] [CrossRef]
- Sumi, T.; Mitsutake, A.; Maruyama, Y. A solvation-free-energy functional: A reference-modified density functional formulation. J. Comput. Chem. 2015, 36, 1359–1369. [Google Scholar] [CrossRef]
- Luukkonen, S.; Belloni, L.; Borgis, D.; Levesque, M. Predicting Hydration Free Energies of the FreeSolv Database of Drug-like Molecules with Molecular Density Functional Theory. J. Chem. Inf. Model. 2020, 60, 3558–3565. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.L.; Guthrie, J.P. FreeSolv: A database of experimental and calculated hydration free energies, with input files. J. Comput. Aided Mol. Des. 2014, 28, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Duarte Ramos Matos, G.; Kyu, D.Y.; Loeffler, H.H.; Chodera, J.D.; Shirts, M.R.; Mobley, D.L. Approaches for Calculating Solvation Free Energies and Enthalpies Demonstrated with an Update of the FreeSolv Database. J. Chem. Eng. Data 2017, 62, 1559–1569. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A. Three-dimensional RISM Theory for Molecular Liquids and Solid-Liquid Interfaces. In Molecular Theory of Solvation; Hirata, F., Ed.; Number 24 in Understanding Chemical Reactivity; Springer: Dordrecht, The Netherlands, 2004; pp. 169–275. [Google Scholar]
- Luchko, T.; Joung, I.S.; Case, D.A. Chapter 4 Integral Equation Theory of Biomolecules and Electrolytes. In Innovations in Biomolecular Modeling and Simulations; Royal Society of Chemistry: Cambridge, UK, 2012. [Google Scholar]
- Joung, I.S.; Luchko, T.; Case, D.A. Simple electrolyte solutions: Comparison of DRISM and molecular dynamics results for alkali halide solutions. J. Chem. Phys. 2013, 138, 044103. [Google Scholar] [CrossRef]
- Tsednee, T.; Luchko, T. Closure for the Ornstein-Zernike equation with pressure and free energy consistency. Phys. Rev. E 2019, 99, 032130. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Potential of Mean Force between Two Molecular Ions in a Polar Molecular Solvent: A Study by the Three-Dimensional Reference Interaction Site Model. J. Phys. Chem. B 1999, 103, 7942–7957. [Google Scholar] [CrossRef]
- Kast, S.M.; Kloss, T. Closed-form expressions of the chemical potential for integral equation closures with certain bridge functions. J. Chem. Phys. 2008, 129, 236101. [Google Scholar] [CrossRef]
- Kobryn, A.E.; Gusarov, S.; Kovalenko, A. A closure relation to molecular theory of solvation for macromolecules. J. Phys. Condens. Matter 2016, 28, 404003. [Google Scholar] [CrossRef]
- Morita, T.; Hiroike, K. A New Approach to the Theory of Classical Fluids. I. Prog. Theor. Phys. 1960, 23, 1003–1027. [Google Scholar] [CrossRef]
- Verlet, L.; Levesque, D. On the theory of classical fluids II. Physica 1962, 28, 1124–1142. [Google Scholar] [CrossRef]
- Sergiievskyi, V.; Jeanmairet, G.; Levesque, M.; Borgis, D. Solvation free-energy pressure corrections in the three dimensional reference interaction site model. J. Chem. Phys. 2015, 143, 184116. [Google Scholar] [CrossRef] [PubMed]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Mobley, D.L.; Shirts, M.; Lim, N.; Chodera, J.; Beauchamp, K.; Lee-Ping. MobleyLab/FreeSolv: Version 0.52. 2018. Available online: https://zenodo.org/record/1161245#.Y8YTVxVByUk (accessed on 16 June 2018).
- Mobley, D.L.; Dill, K.A.; Chodera, J.D. Treating Entropy and Conformational Changes in Implicit Solvent Simulations of Small Molecules. J. Phys. Chem. B 2008, 112, 938–946. [Google Scholar] [CrossRef]
- Knapp, B.; Ospina, L.; Deane, C.M. Avoiding False Positive Conclusions in Molecular Simulation: The Importance of Replicas. J. Chem. Theory Comput. 2018, 14, 6127–6138. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. Enhanced solvation force extrapolation for speeding up molecular dynamics simulations of complex biochemical liquids. J. Chem. Phys. 2019, 151, 214102. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. MTS-MD of Biomolecules Steered with 3D-RISM-KH Mean Solvation Forces Accelerated with Generalized Solvation Force Extrapolation. J. Chem. Theory Comput. 2015, 11, 1875–1895. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. Multiple time step molecular dynamics in the optimized isokinetic ensemble steered with the molecular theory of solvation: Accelerating with advanced extrapolation of effective solvation forces. J. Chem. Phys. 2013, 139, 244106. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. Generalised canonical–isokinetic ensemble: Speeding up multiscale molecular dynamics and coupling with 3D molecular theory of solvation. Mol. Simul. 2013, 39, 25–48. [Google Scholar] [CrossRef]
- Miyata, T.; Hirata, F. Combination of molecular dynamics method and 3D-RISM theory for conformational sampling of large flexible molecules in solution. J. Comput. Chem. 2008, 29, 871–882. [Google Scholar] [CrossRef]
- Luchko, T.; Gusarov, S.; Roe, D.R.; Simmerling, C.; Case, D.A.; Tuszynski, J.; Kovalenko, A. Three-Dimensional Molecular Theory of Solvation Coupled with Molecular Dynamics in Amber. J. Chem. Theory Comput. 2010, 6, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Anandakrishnan, R.; Drozdetski, A.; Walker, R.C.; Onufriev, A.V. Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations. Biophys. J. 2015, 108, 1153–1164. [Google Scholar] [CrossRef] [PubMed]
- Wilson, L.; Krasny, R.; Luchko, T. Accelerating the 3D reference interaction site model theory of molecular solvation with treecode summation and cut-offs. J. Comput. Chem. 2022, 43, 1251–1270. [Google Scholar] [CrossRef]
- Miyata, T.; Hikasa, Y. Sigma enlarging bridge correction of three dimensional Ornstein–Zernike theory for solvation free energy of polyatomic solutes immersed in Lennard-Jones monatomic solvent. AIP Adv. 2022, 12, 085206. [Google Scholar] [CrossRef]
- Mobley, D.L.; Bayly, C.I.; Cooper, M.D.; Shirts, M.R.; Dill, K.A. Small Molecule Hydration Free Energies in Explicit Solvent: An Extensive Test of Fixed-Charge Atomistic Simulations. J. Chem. Theory Comput. 2009, 5, 350–358. [Google Scholar] [CrossRef]
- Riquelme, M.; Lara, A.; Mobley, D.L.; Verstraelen, T.; Matamala, A.R.; Vöhringer-Martinez, E. Hydration Free Energies in the FreeSolv Database Calculated with Polarized Iterative Hirshfeld Charges. J. Chem. Inf. Model. 2018, 58, 1779–1797. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Greene, D.; Homeyer, N.; et al. AMBER 2017; University of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.; Beauchamp, K.; Naden, L.; Chodera, J.; Rodríguez-Guerra, J.; Martiniani, S.; Stern, C.; Henry, M.; Fass, J.; Gowers, R.; et al. Choderalab/Pymbar: 3.1.1. 2022. Available online: https://zenodo.org/record/7383197#.Y8YTchVByUk (accessed on 1 December 2022).
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E.I.; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; et al. Amber 2021; University of California: San Francisco, CA, USA, 2021. [Google Scholar]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Perkyns, J.; Pettitt, B.M. A site–site theory for finite concentration saline solutions. J. Chem. Phys. 1992, 97, 7656–7666. [Google Scholar] [CrossRef]
- Perkyns, J.S.; Montgomery Pettitt, B. A dielectrically consistent interaction site theory for solvent—Electrolyte mixtures. Chem. Phys. Lett. 1992, 190, 626–630. [Google Scholar] [CrossRef]
- Kovalenko, A.; Ten-no, S.; Hirata, F. Solution of three-dimensional reference interaction site model and hypernetted chain equations for simple point charge water by modified method of direct inversion in iterative subspace. J. Comput. Chem. 1999, 20, 928–936. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June 2010; pp. 92–96. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June 2010; pp. 56–61. [Google Scholar] [CrossRef]

| PMVC | ECC | PMVECC | Explicit Solvent ECC | |
|---|---|---|---|---|
| a | −0.15 | −0.130(1) | ||
| b | −0.04(1) | 0.00(1) | ||
| H | −1.199(1) | −0.225(5) | −0.098(1) | |
| N | −1.573(6) | −0.392(7) | 0.091(5) | |
| C | −1.667(1) | −0.148(8) | 0.114(1) | |
| O | −1.277(3) | 0.069(9) | 0.088(3) | |
| F | −2.082(4) | −0.05(1) | 0.076(2) | |
| Cl | −4.695(4) | −1.19(2) | −0.456(2) | |
| Br | −5.544(7) | −1.06(2) | −0.412(6) | |
| I | −6.27(1) | −0.79(3) | −0.25(1) | |
| P | −1.03(3) | 2.04(3) | 2.93(3) | |
| S | −3.18(1) | 0.09(2) | 0.32(1) |
| Slope | MUE | MSE | RMSE | Max Error | |||
|---|---|---|---|---|---|---|---|
| Rigid | |||||||
| 3D-RISM/PMVC | 0.93(4) | 0.86(6) | −0.29(7) | 1.3(1) | 0.75(4) | 6.6 | |
| 3D-RISM/ECC | 0.92(4) | 1.02(6) | −0.51(8) | 1.37(8) | 0.76(3) | 5.9 | |
| 3D-RISM/PMVECC | 0.92(2) | 0.61(3) | 0.05(5) | 0.83(6) | 0.89(2) | 4.4 | |
| Explicit solvent | 0.96(3) | 0.85(4) | −0.59(6) | 1.11(6) | 0.86(2) | 4.6 | |
| Explicit solvent, ECC | 0.91(2) | 0.66(3) | −0.14(5) | 0.86(4) | 0.88(1) | 3.1 | |
| Flexible | |||||||
| 3D-RISM/PMVC | 0.98(4) | 1.53(8) | 0.2(1) | 2.1(1) | 0.75(3) | 9.6 | |
| 3D-RISM/ECC | 1.07(4) | 1.56(7) | 0.0(1) | 2.1(1) | 0.78(3) | 9.8 | |
| 3D-RISM/PMVECC | 0.95(5) | 1.35(6) | −0.04(9) | 1.8(1) | 0.79(3) | 9.4 | |
| Explicit solvent | 0.97(4) | 1.34(7) | −0.09(0) | 1.8(1) | 0.79(3) | 10.8 | |
| Explicit solvent, ECC | 0.91(4) | 1.17(6) | −0.13(9) | 1.7(1) | 0.81(3) | 7.8 | |
| Total | |||||||
| 3D-RISM/PMVC | 1.01(3) | 1.22(5) | 0.00(7) | 1.77(9) | 0.83(2) | 9.6 | |
| 3D-RISM/ECC | 1.06(2) | 1.32(5) | −0.21(7) | 1.80(8) | 0.84(2) | 9.8 | |
| 3D-RISM/PMVECC | 0.96(3) | 1.01(4) | 0.00(6) | 1.44(7) | 0.87(1) | 9.4 | |
| Explicit solvent | 1.02(3) | 1.11(4) | −0.32(6) | 1.53(8) | 0.87(1) | 10.8 | |
| Explicit solvent, ECC | 0.94(2) | 0.94(4) | −0.13(5) | 1.35(8) | 0.88(1) | 7.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casillas, L.; Grigorian, V.M.; Luchko, T. Identifying Systematic Force Field Errors Using a 3D-RISM Element Counting Correction. Molecules 2023, 28, 925. https://doi.org/10.3390/molecules28030925
Casillas L, Grigorian VM, Luchko T. Identifying Systematic Force Field Errors Using a 3D-RISM Element Counting Correction. Molecules. 2023; 28(3):925. https://doi.org/10.3390/molecules28030925
Chicago/Turabian StyleCasillas, Lizet, Vahe M. Grigorian, and Tyler Luchko. 2023. "Identifying Systematic Force Field Errors Using a 3D-RISM Element Counting Correction" Molecules 28, no. 3: 925. https://doi.org/10.3390/molecules28030925
APA StyleCasillas, L., Grigorian, V. M., & Luchko, T. (2023). Identifying Systematic Force Field Errors Using a 3D-RISM Element Counting Correction. Molecules, 28(3), 925. https://doi.org/10.3390/molecules28030925





