Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions
Abstract
1. Introduction
2. The Models
2.1. The Lattice Model
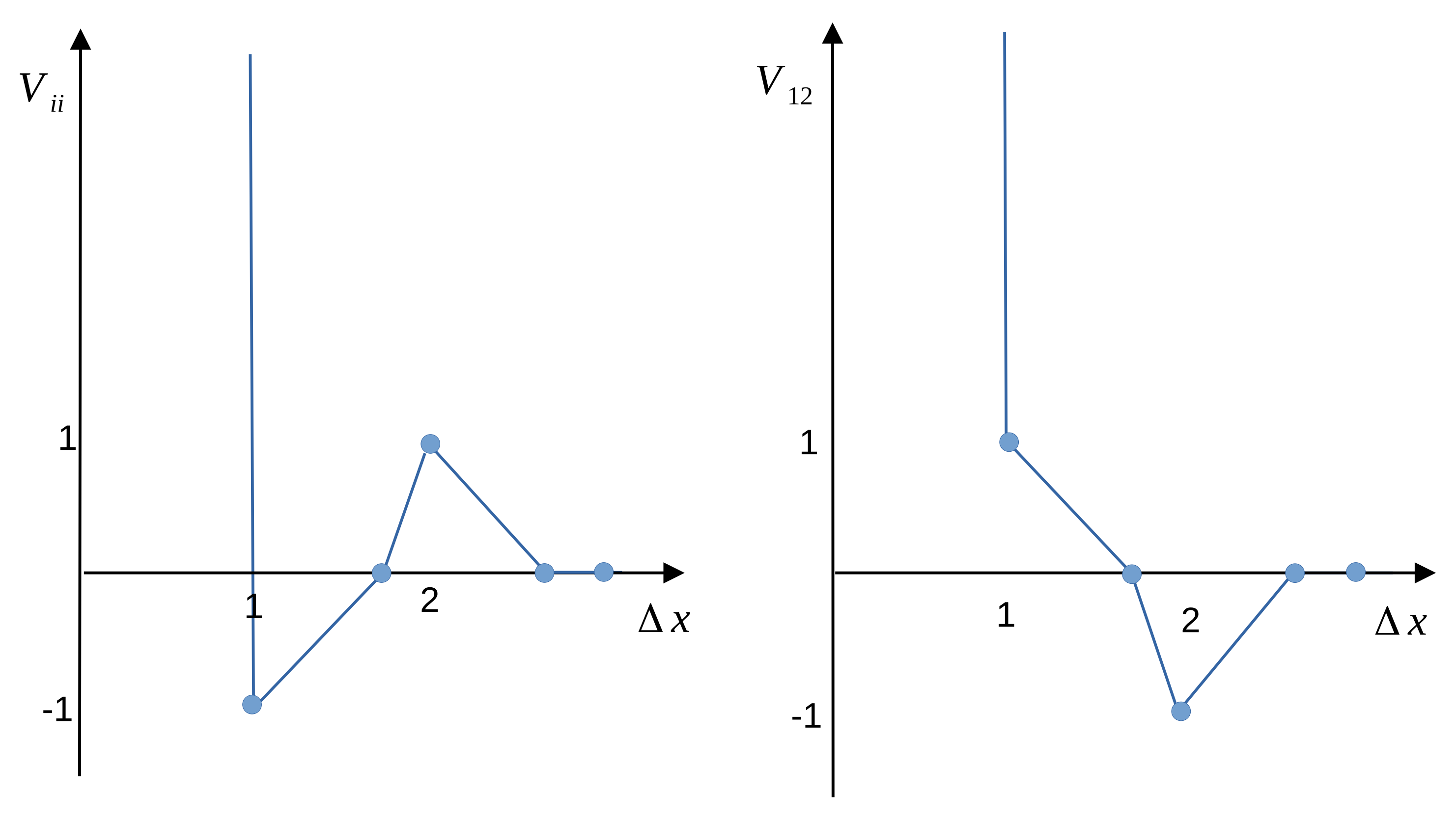
2.2. The Continuous Model
3. Methods
3.1. The Lattice Model Calculations and Simulations
3.2. The Continuous Model Simulations
4. Results and Discussion
4.1. The Lattice Model
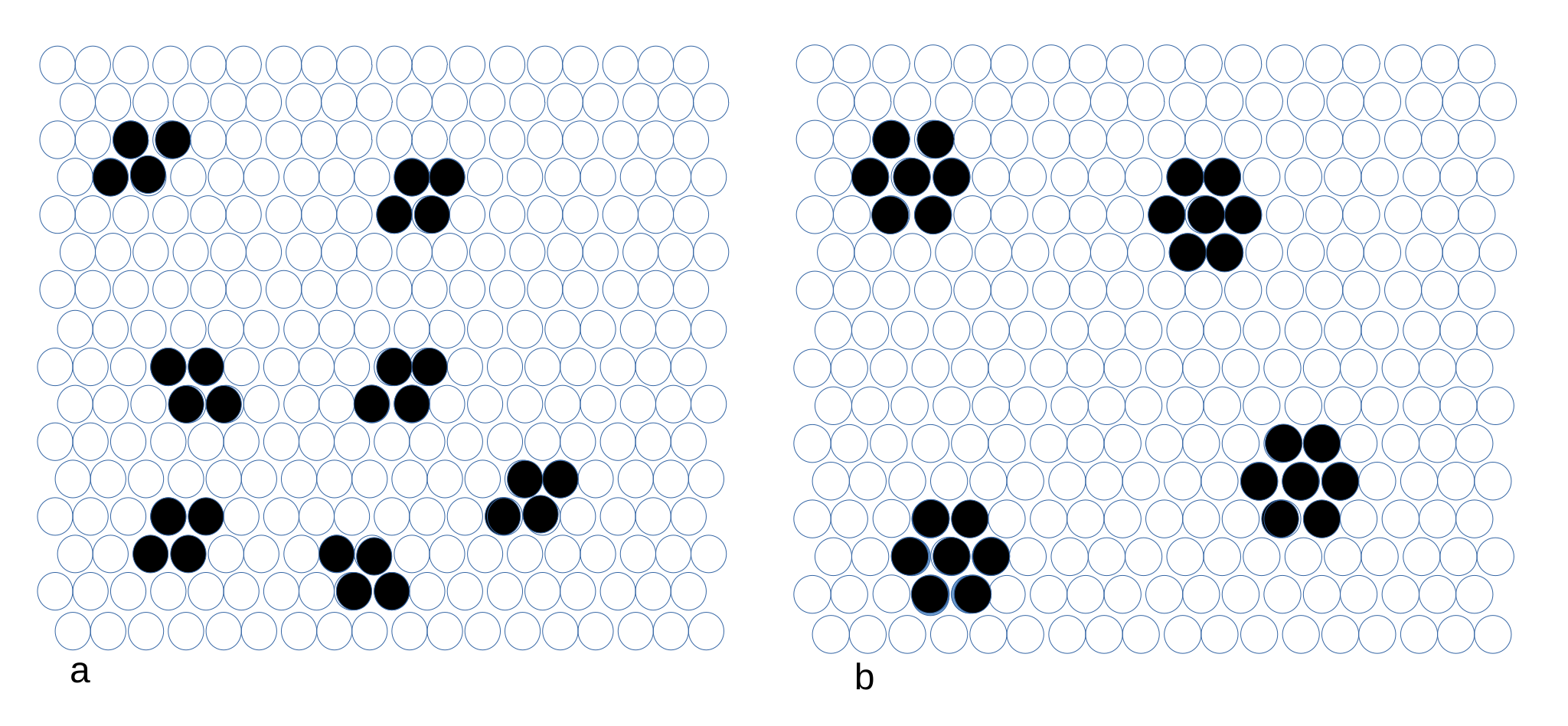
4.1.1. The Case of Fixed Numbers of Particles
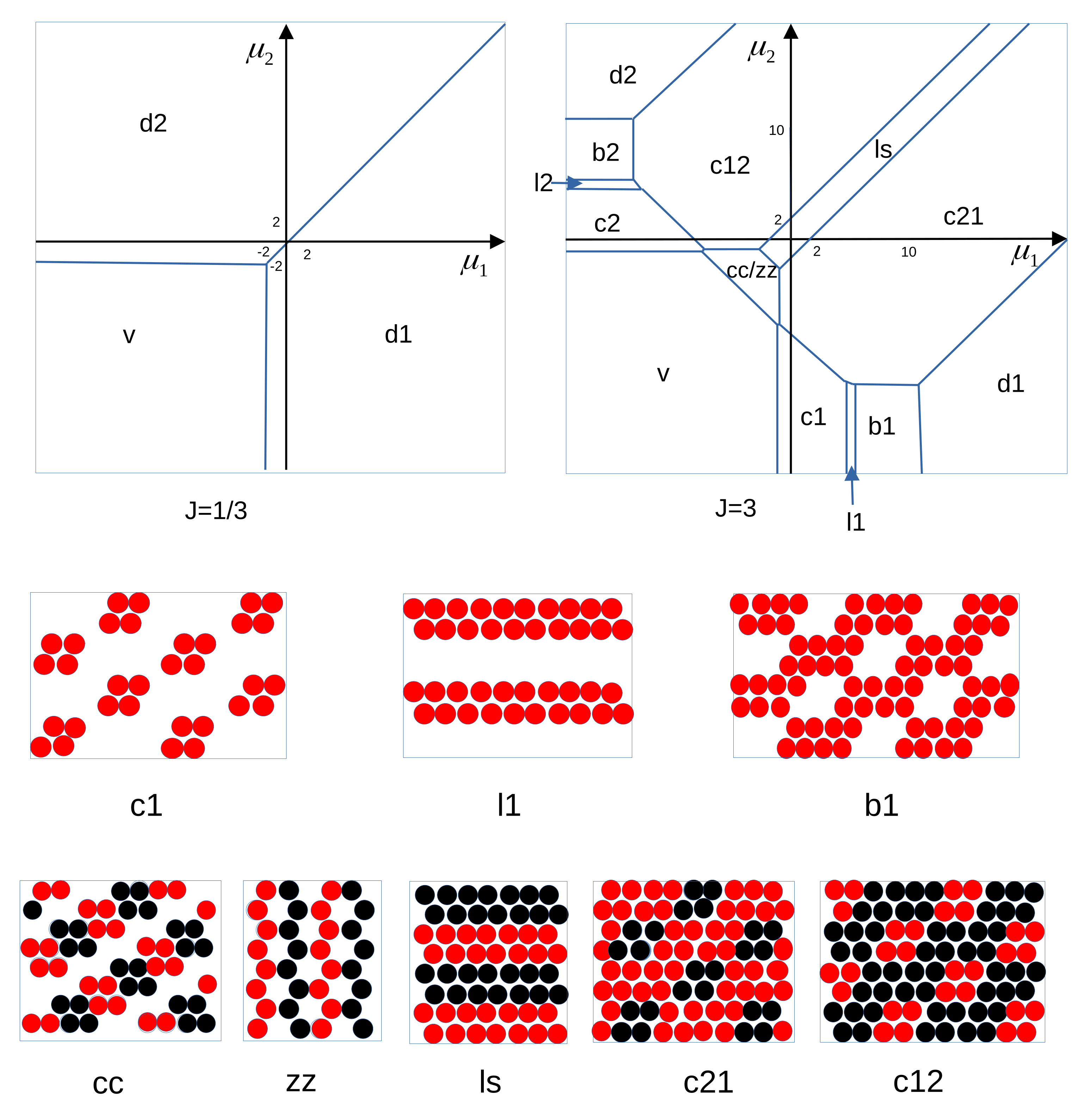
4.1.2. The Case of the Open System—Calculations
- vacuum, v (dilute gas for );
- all cells occupied by the first, d1, or by the second, d2, component (disordered liquid rich in the first or the second component, respectively for );
- hexagonal arrangement of one-component clusters, c1, c2;
- one-component stripes, l1, l2;
- one-component dense phase with hexagonally ordered bubbles, b1, b2;
- chains of alternating clusters of the two types separated by empty layers, cc;
- alternating zig-zag chains of the first and the second component, zz;
- alternating adjacent bilayers of the first and the second component, ls;
- hexagonal lattice of clusters of one-component particles in the dense liquid formed by the particles of the other type, c12, c21.
- d2-b2-c12: ;
- b2-c12-l2: ;
- c12-l2-c2: ;
- c2-c12-cc: ;
- c2-cc-v: ;
- c12-cc-ls: .
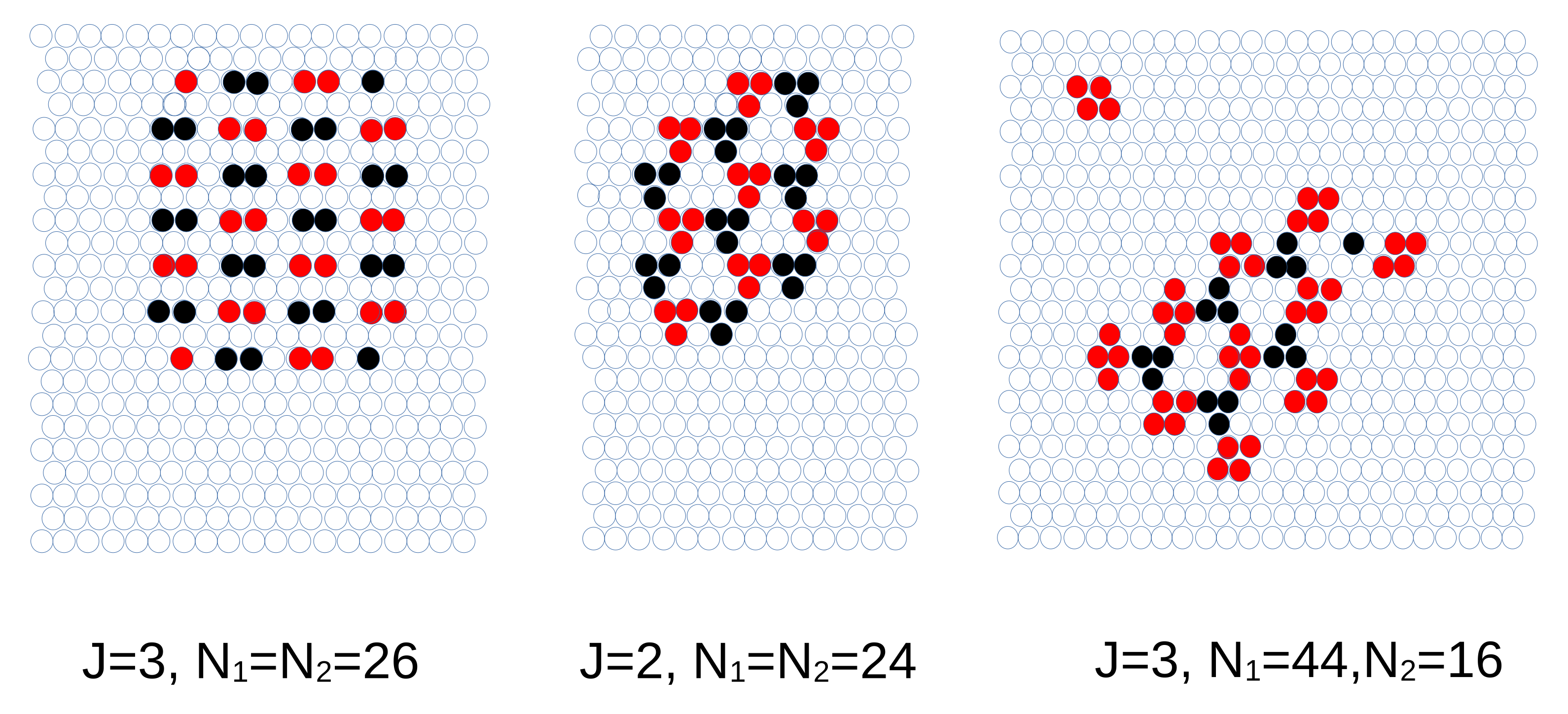
4.1.3. The Case of the Open System—MC Simulations
4.2. The Continuous Model
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Veatch, S.L.; Soubias, O.; Keller, S.L.; Gawrisch, K. Critical fluctuations in domain-forming lipid mixtures. Proc. Nat. Acad. Sci. USA 2007, 104, 17650–17655. [Google Scholar] [CrossRef]
- Honerkamp-Smith, A.R.; Veatch, S.L.; Keller, S.L. An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochim. Biophys. Acta 2009, 1788, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp-Smith, A.R.; Veatch, S.L.; Keller, S.L. Critical Fluctuations in Plasma Membrane Vesicles. ACS Chem. Biol. 2008, 3, 287–293. [Google Scholar]
- Machta, B.B.; Veatch, S.L.; Sethna, J.P. Critical Casimir Forces in Cellular Membranes. Phys. Rev. Lett. 2012, 109, 138101. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E.; de Gennes, P.G. Wall phenomena in a critical binary mixture. C. R. Acad. Sci. Ser. B 1978, 287, 207. [Google Scholar]
- Krech, M. Fluctuation-induced forces in critical fluids. J. Phys. Condens. Matter 1999, 11, R391. [Google Scholar] [CrossRef]
- Brankov, G.; Tonchev, N.S.; Danchev, D.M. Theory of Critical Phenomena in Finite-Size Systems; World Scientific: Singapore, 2000. [Google Scholar]
- Hertlein, C.; Helden, L.; Gambassi, A.; Dietrich, S.; Bechinger, C. Direct measurement of critical Casimir forces. Nature 2008, 451, 172. [Google Scholar] [CrossRef]
- Gambassi, A.; Maciołek, A.; Hertlein, C.; Nellen, U.; Helden, L.; Bechinger, C.; Dietrich, S. Critical Casimir effect in classical binary liquid mixtures. Phys. Rev. E 2009, 80, 061143. [Google Scholar] [CrossRef]
- Nellen, U.; Dietrich, J.; Helden, L.; Chodankar, S.; Nygard, K.; van der Veen, J.F.; Bechinger, C. Salt-induced changes of colloidal interactions in critical mixtures. Soft Matter 2011, 80, 061143. [Google Scholar] [CrossRef]
- Vasilyev, O.A.; Marino, E.; Kluft, B.B.; Schall, P.; Kondrat, S. Debye vs. Casimir: Controlling the structure of charged nanoparticles deposited on a substrate. Nanoscale 2021, 113, 6475. [Google Scholar] [CrossRef]
- Pousaneh, F.; Ciach, A.; Maciołek, A. Effect of ions on confined near-critical binary aqueous mixture. Soft Matter 2012, 8, 7567. [Google Scholar] [CrossRef]
- Ciach, A. Competition Between Electrostatic and Thermodynamic Casimir Potentials in Near-Critical Mixtures with Ions. Adv. Biomembr. Lipid Self-Assem. 2016, 23, 61–100. [Google Scholar]
- Stradner, A.; Sedgwick, H.; Cardinaux, F.; Poon, W.; Egelhaaf, S.; Schurtenberger, P. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 2004, 432, 492. [Google Scholar] [CrossRef]
- Bartlett, P.; Campbell, A.I. Three-Dimensional Binary Superlattices of Oppositely Charged Colloids. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Imperio, A.; Reatto, L. Microphase separation in two-dimensional systems with competing interactions. J. Chem. Phys. 2006, 124, 164712. [Google Scholar] [CrossRef]
- Archer, A.J.; Wilding, N.B. Phase behavior of a fluid with competing attractive and repulsive interactions. Phys. Rev. E 2007, 76, 31501. [Google Scholar] [CrossRef]
- Archer, A.J. Two-dimensional fluid with competing interactions exhibiting microphase separation: Theory for bulk and interfacial properties. Phys. Rev. E 2008, 78, 031402. [Google Scholar] [CrossRef]
- Pȩkalski, J.; Ciach, A.; Almarza, N.G. Periodic ordering of clusters and stripes in a two-dimensional lattice model. I. Ground state, mean-field phase diagram and structure of the disordered phases. J. Chem. Phys. 2014, 140, 114701. [Google Scholar] [CrossRef]
- Almarza, N.G.; Pȩkalski, J.; Ciach, A. Two-dimensional lattice model for periodic ordering of clusters and stripes. II. Monte Carlo simulations. J. Chem. Phys. 2014, 140, 164708. [Google Scholar] [CrossRef]
- Sweatman, M.B.; Fartaria, R.; Lue, L. Cluster formation in fluids with competing short-range and long-range interactions. J. Chem. Phys. 2014, 140, 124508. [Google Scholar] [CrossRef]
- Lindquist, B.A.; Jadrich, R.B.; Truskett, T.M. Assembly of nothing: Equilibrium fluids with designed structrued porosity. Soft Matter 2016, 12, 2663–2667. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Zhang, K.; Charbonneau, P. Equilibrium Phase Behavior of a Continuous-Space Microphase Former. Phys. Rev. Lett. 2016, 116, 098301. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Charbonneau, P. Equilibrium phase behavior of the square-well linear microphase-forming model. J. Phys. Chem. B 2016, 120, 6178–6188. [Google Scholar] [CrossRef] [PubMed]
- Edelmann, M.; Roth, R. Gyroid phase of fluids with spherically symmetric competing interactions. Phys. Rev. E 2016, 93, 062146. [Google Scholar] [CrossRef]
- Pini, D.; Parola, A. Pattern formation and self-assembly driven by competing interactions. Soft Matter 2017, 13, 9259. [Google Scholar] [CrossRef]
- Royall, C.P. Hunting mermaids in real space: Known knowns, known unknowns and unknown unknowns. Soft Matter 2018, 14, 4020. [Google Scholar] [CrossRef]
- Marolt, K.; Zimmermann, M.; Roth, R. Microphase separation in a two-dimensional colloidal system with competing attractive critical Casimir and repulsive magnetic dipole interactions. Phys. Rev. E 2019, 100, 052602. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, Y. Colloidal systems with a short-range attraction and long-range repulsion: Phase diagrams, structures, and dynamics. Curr. Opin. Colloid Interface Sci. 2019, 39, 123. [Google Scholar] [CrossRef]
- Hatlo, M.M.; Karatrantos, A.; Lue, L. One-component plasma of point charges and of charged rods. Phys. Rev. E 2009, 80, 061107. [Google Scholar] [CrossRef]
- Ruiz-Franco, J.; Zaccarelli, E. On the Role of Competing Interactions in Charged Colloids with Short-Range Attraction. Annu. Rev. Condens. Matter Phys. 2021, 12, 51. [Google Scholar] [CrossRef]
- Ciach, A.; Pȩkalski, J.; Góźdź, W.T. Origin of similarity of phase diagrams in amphiphilic and colloidal systems with competing interactions. Soft Matter 2013, 9, 6301. [Google Scholar] [CrossRef]
- Litniewski, M.; Ciach, A. Adsorption in Mixtures with Competing Interactions. Molecules 2021, 26, 4532. [Google Scholar] [CrossRef]
- Ferreiro-Rangel, C.A.; Sweatman, M.B. Cluster formation in binary fluids with competing short-range and long-range interactions. Mol. Phys 2018, 116, 3231–3244. [Google Scholar] [CrossRef]
- Tan, J.; Afify, N.D.; Ferreiro-Rangel, C.A.; Fan, X.; Sweatman, M.B. Cluster formation in symmetric binary SALR mixtures. J. Chem. Phys. 2021, 154, 074504. [Google Scholar] [CrossRef]
- Ciach, A.; Patsahan, O.; Meyra, A. Effects of fluctuations on correlation functions in inhomogeneous mixtures. Condens. Matter Phys. 2020, 23, 23601. [Google Scholar] [CrossRef]
- Patsahan, O.; Litniewski, M.; Ciach, A. Self-assembly in mixtures with competing interactions. Soft Matter 2021, 17, 2883. [Google Scholar] [CrossRef]
- Patsahan, O.; Meyra, A.; Ciach, A. Correlation functions in mixtures with energetically favoured nearest neighbours of different kind: A size-asymmetric case. Mol. Phys. 2020, 119, 1–16. [Google Scholar] [CrossRef]
- Patsahan, O.; Meyra, A.; Ciach, A. Effect of a confining surface on a mixture with spontaneous inhomogeneities. J. Mol. Liq. 2022, 363, 119844. [Google Scholar] [CrossRef]
- Munao, G.; Prestipino, S.; Bomont, J.M.; Costa, D. Clustering in Mixtures of SALR Particles and Hard Spheres with Cross Attraction. J. Phys. Chem. B 2022, 126, 2027. [Google Scholar] [CrossRef]
- Leunissen, M.; Christova, C.; Hynninen, A.P.; Royal, C.; Campbell, A.; Imhof, A.; Dijkstra, M.; van Roji, R.; van Blaaderen, A. Ionic colloidal crystals of oppositely charged particles. Nature 2005, 437, 235. [Google Scholar] [CrossRef]
- Landau, D.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic Press, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Blume, M.; Emery, V.J.; Griffith, R.B. Ising Model for the lambda Transition and Phase Separation in He3-He4 Mixtures. Phys. Rev. A 1971, 4, 1071. [Google Scholar] [CrossRef]
- Grishina, V.S.; Vikhrenko, V.S.; Ciach, A. Triangular lattice models for pattern formation by core–shell particles with different shell thicknesses. J. Phys. Condens. Matter 2020, 32, 405102. [Google Scholar] [CrossRef] [PubMed]
- Grishina, V.S.; Vikhrenko, V.S.; Ciach, A. Structural and thermodynamic peculiarities of core-shell particles at fluid interfaces from triangular lattice models. Entropy 2020, 32, 405102. [Google Scholar] [CrossRef] [PubMed]
- Rauh, A.; Rey, M.; Barbera, L.; Zanini, M.; Karg, M.; Isa, L. Compression of hard core-soft shell nanoparticles at liquid-liquid interfaces: Influence of the shell thickness. Soft Matter 2017, 13, 158. [Google Scholar] [CrossRef]
- Ickler, M.; Menath, J.; Holstein, L.; Rey, M.; Buzza, D.M.A.; Vogel, N. Interfacial self-assembly of SiO2–PNIPAM core–shell particles with varied crosslinking density. Soft Matter 2022, 18, 5585. [Google Scholar] [CrossRef]
- Groda, Y.; Vikhrenko, V.S.; di Caprio, D. Equilibrium properties of the lattice system with SALR interaction potential on a square lattice: Quasi-chemical approximation versus Monte Carlo simulation. Condens. Matter Phys. 2018, 21, 43002. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciach, A.; De Virgiliis, A.; Meyra, A.; Litniewski, M. Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions. Molecules 2023, 28, 1366. https://doi.org/10.3390/molecules28031366
Ciach A, De Virgiliis A, Meyra A, Litniewski M. Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions. Molecules. 2023; 28(3):1366. https://doi.org/10.3390/molecules28031366
Chicago/Turabian StyleCiach, Alina, Andres De Virgiliis, Ariel Meyra, and Marek Litniewski. 2023. "Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions" Molecules 28, no. 3: 1366. https://doi.org/10.3390/molecules28031366
APA StyleCiach, A., De Virgiliis, A., Meyra, A., & Litniewski, M. (2023). Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions. Molecules, 28(3), 1366. https://doi.org/10.3390/molecules28031366





