The Kurtz–Perry Powder Technique Revisited: A Study of the Effect of Reference Selection on Powder Second-Harmonic Generation Response
(This article belongs to the Section Materials Chemistry)
Abstract
:1. Introduction
2. Results and Discussion
2.1. Experimental Results
2.2. Theoretical Analysis of Second-Harmonic Generation Intensity
2.3. Two Criteria for Selecting Reference Materials
3. Experimental Section
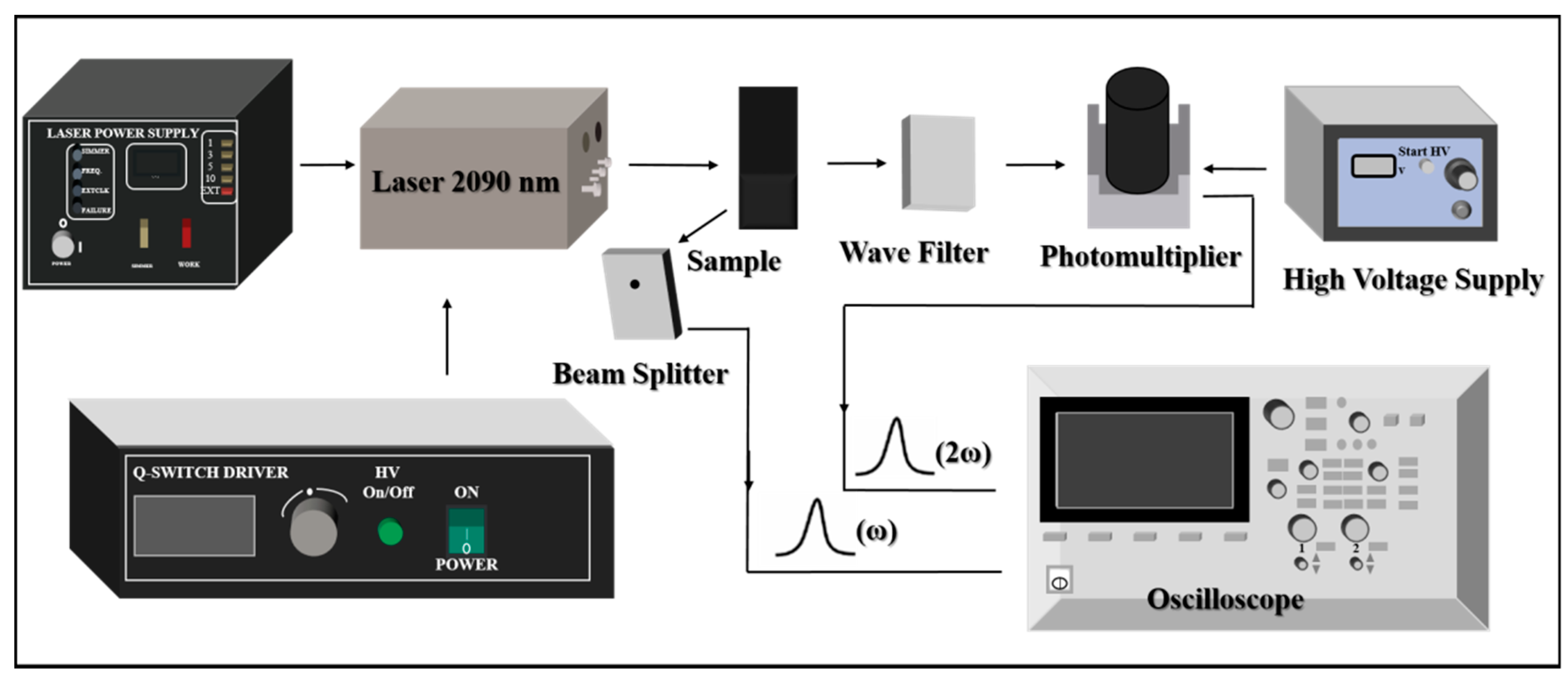
3.1. Experimental Apparatus
3.2. Sample Preparation
3.3. Second-Harmonic Generation Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burland, D.M.; Miller, R.D.; Walsh, C.A. Second-order nonlinearity in poled-polymer systems. Chem. Rev. 1994, 94, 31–75. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Gong, P.; Lin, Z.; Yao, J.; Wu, Y. BaGa2SnSe6: A new phase-matchable IR nonlinear optical material with strong second harmonic generation response. J. Mater. Chem. C 2015, 3, 10998–11004. [Google Scholar] [CrossRef]
- Chen, C.; Wu, Y.; Jiang, A.; Wu, B.; You, G.; Li, R.; Lin, S. New nonlinear-optical crystal: LiB3O5. J. Opt. Soc. Am. B 1989, 6, 616–621. [Google Scholar] [CrossRef]
- Wang, Y.; Ghotbi, M.; Das, S.; Dai, Y.; Li, S.; Hu, X.; Gan, X.; Zhao, J.; Sun, Z. Difference frequency generation in monolayer MoS2. Nanoscale 2020, 12, 19638–19643. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhong, K.; Wang, A.; Zhou, M.; Li, S.; Gao, L.; Zhang, Z. Optical Terahertz Sources Based on Difference Frequency Generation in Nonlinear Crystals. Crystals 2022, 12, 936. [Google Scholar] [CrossRef]
- Sullivan, S.; Thomas, E.L. Optical parametric oscillation in RDA. Opt. Commun. 1975, 14, 419–420. [Google Scholar] [CrossRef]
- Zhou, F.; Lu, X.; Rao, A.; Stone, J.; Moille, G.; Perez, E.; Westly, D.; Srinivasan, K. Hybrid-Mode-Family Kerr Optical Parametric Oscillation for Robust Coherent Light Generation on Chip. Laser Photonics Rev. 2022, 16, 2100582. [Google Scholar] [CrossRef]
- Gong, P.; Liang, F.; Kang, L.; Chen, X.; Qin, J.; Wu, Y.; Lin, Z. Recent advances and future perspectives on infrared nonlinear optical metal halides. Coordin. Chem. Rev. 2019, 380, 83–102. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, F.; Wang, C.; Jia, M.; Zhao, X.; Liu, Z.; Ge, Y.; Zhang, Y.; Zhang, H. Nonlinear Photonics Using Low-Dimensional Metal-Halide Perovskites: Recent Advances and Future Challenges. Adv. Mater. 2021, 33, 2004446. [Google Scholar] [CrossRef]
- Chu, Y.; Li, G.; Su, X.; Wu, K.; Pan, S. A review on the development of infrared nonlinear optical materials with triangular anionic groups. J. Solid State Chem. 2019, 271, 266–272. [Google Scholar] [CrossRef]
- Lin, H.; Wei, W.B.; Chen, H.; Wu, X.T.; Zhu, Q.L. Rational design of infrared nonlinear optical chalcogenides by chemical substitution. Coordin. Chem. Rev. 2020, 406, 213150. [Google Scholar] [CrossRef]
- Li, Z.; Yao, J.; Wu, Y. Chalcophosphates: A Treasure House of Infrared Nonlinear Optical Materials. Cryst. Growth Des. 2020, 20, 7550–7564. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, X.; Li, C.; Liu, W.; Lin, Z.; Yao, J. Highly polarized [GeOTe3] motif-driven structural order promotion and an enhanced second harmonic generation response in the new nonlinear optical oxytelluride Ba3Ge2O4Te3. J. Mater. Chem. C 2022, 10, 150–159. [Google Scholar] [CrossRef]
- Degheidy, A.R.; Elkenany, E.B. Impact of temperature and pressure on mechanical properties of GaxIn1−xAsyP1−y alloy lattice matched to different substrates. J. Alloy. Compd. 2015, 652, 379–385. [Google Scholar] [CrossRef]
- Degheidy, A.R.; Elkenany, E.B.; Alfrnwani, O. Mechanical properties of AlxIn1-xSb ternary alloys under the effect of pressure and temperature. Comput. Condens. Matter 2018, 15, 55–60. [Google Scholar] [CrossRef]
- Armstrong, J.A.; Bloembergen, N.; Ducuing, J.; Pershan, P.S. Interactions between Light Waves in a Nonlinear Dielectric. Phys. Rev. 1962, 127, 1918–1939. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: Hoboken, NJ, USA, 1984; Volume 5. [Google Scholar]
- Maker, P.; Terhune, R.; Nisenoff, M.; Savage, C. Effects of dispersion and focusing on the production of optical harmonics. Phys. Rev. Lett. 1962, 8, 21. [Google Scholar] [CrossRef]
- Terhune, R.; Maker, P.; Savage, C. Optical harmonic generation in calcite. Phys. Rev. Lett. 1962, 8, 404. [Google Scholar] [CrossRef]
- Nikogosyan, D.N. Nonlinear Optical Crystals: A Complete Survey; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kurtz, S.; Perry, T. A powder technique for the evaluation of nonlinear optical materials. J. Appl. Phys. 1968, 39, 3798–3813. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Gong, P.; Li, X.; Zhou, M.; Mar, A.; Lin, Z.; Yao, J.; Wu, Y.; Chen, C. Trigonal Planar [HgSe3]4– Unit: A New Kind of Basic Functional Group in IR Nonlinear Optical Materials with Large Susceptibility and Physicochemical Stability. J. Am. Chem. Soc. 2016, 138, 6135–6138. [Google Scholar] [CrossRef]
- Li, C.; Meng, X.; Li, Z.; Yao, J. Hg-based chalcogenides: An intriguing class of infrared nonlinear optical materials. Coordin. Chem. Rev. 2022, 453, 214328. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, X.; Zhou, M.; Guo, Y.; Luo, X.; Wu, Y.; Lin, Z.; Yao, J. Zn3P2S8: A Promising Infrared Nonlinear-Optical Material with Excellent Overall Properties. Inorg. Chem. 2018, 57, 10503–10506. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, Y.; Guo, Y.; Xing, W.; Luo, X.; Lin, Z.; Yao, J.; Wu, Y. Broadening Frontiers of Infrared Nonlinear Optical Materials with π-Conjugated Trigonal-Planar Groups. Chem. Mater. 2019, 31, 1110–1117. [Google Scholar]
- Li, Z.; Zhang, S.; Guo, Y.; Lin, Z.; Yao, J.; Wu, Y. SnGa2GeSe6, a benign addition to the AMIII2MIVQ6 family: Synthesis, crystal structure and nonlinear optical performance. Dalton T. 2019, 48, 6638–6644. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Huang, Z.; Zhao, L.-D.; Uykur, E.; Xing, W.; Lin, Z.; Yao, J.; Wu, Y. Molecular Construction from AgGaS2 to CuZnPS4: Defect-Induced Second Harmonic Generation Enhancement and Cosubstitution-Driven Band Gap Enlargement. Chem. Mater. 2020, 32, 3288–3296. [Google Scholar] [CrossRef]
- Clark, D.J.; Zhang, J.H.; Craig, A.J.; Weiland, A.; Brant, J.A.; Cho, J.B.; Kim, Y.S.; Jang, J.I.; Aitken, J.A. The Kurtz-Perry powder technique revisited: A case study on the importance of reference quality and broadband nonlinear optical measurements using LiInSe2. J. Alloy. Compd. 2022, 917, 165381. [Google Scholar] [CrossRef]
- Guo, Y.; Liang, F.; Li, Z.; Xing, W.; Lin, Z.S.; Yao, J.; Mar, A.; Wu, Y. AHgSnQ4 (A = Sr, Ba; Q = S, Se): A Series of Hg-Based Infrared Nonlinear-Optical Materials with Strong Second-Harmonic-Generation Response and Good Phase Matchability. Inorg. Chem. 2019, 58, 10390–10398. [Google Scholar] [CrossRef]
- Guo, Y.; Liang, F.; Li, Z.; Xing, W.; Lin, Z.; Yao, J.; Wu, Y. Li4HgSn2Se7: The First Second-Order Nonlinear Optical-Active Selenide in the I4–II–IV2–VI7 Diamond-like Family. Cryst. Growth Des. 2019, 19, 5494–5497. [Google Scholar] [CrossRef]
- Ran, M.Y.; Ma, Z.; Wu, X.T.; Lin, H.; Zhu, Q.L. Ba2Ge2Te5: A ternary NLO-active telluride with unusual one-dimensional helical chains and giant second harmonic-generation tensors. Inorg. Chem. Front. 2021, 8, 4838–4845. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, S.; Han, S.; Yang, Z.; Pan, S. Sn2B5O9Br as an Outstanding Bifunctional Material with Strong Second-Harmonic Generation Effect and Large Birefringence. Adv. Opt. Mater. 2021, 9, 2001734. [Google Scholar] [CrossRef]
- Bonnin, M.A.; Bayarjargal, L.; Wolf, S.; Milman, V.; Winkler, B.; Feldmann, C. GaSeCl5O: A Molecular Compound with Very Strong SHG Effect. Inorg. Chem. 2021, 60, 15653–15658. [Google Scholar] [CrossRef] [PubMed]
- Zou, G.; Lin, C.; Jo, H.; Nam, G.; You, T.S.; Ok, K.M. Pb2BO3Cl: A Tailor-Made Polar Lead Borate Chloride with Very Strong Second Harmonic Generation. Angew. Chem. Int. Edit. 2016, 55, 12078–12082. [Google Scholar] [CrossRef] [PubMed]
- Peng, G.; Lin, C.; Ye, N. NaZnCO3(OH): A High-Performance Carbonate Ultraviolet Nonlinear Optical Crystal Derived from KBe2BO3F2. J. Am. Chem. Soc. 2020, 142, 20542–20546. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Kang, L.; Gong, P.; Lin, Z. LiZn(OH)CO3: A Deep-Ultraviolet Nonlinear Optical Hydroxycarbonate Designed from a Diamond-like Structure. Angew. Chem. Int. Edit. 2021, 60, 13574–13578. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, H.; Yu, H.; Hu, Z.; Wang, J.; Wu, Y. An Effective Strategy for Designing Nonlinear Optical Crystals by Combining the Structure-Directing Property of Oxyfluorides with Chemical Substitution. Angew. Chem. Int. Edit. 2021, 60, 25302–25306. [Google Scholar] [CrossRef]
- Aramburu, I.; Ortega, J.; Folcia, C.; Etxebarria, J. Second harmonic generation by micropowders: A revision of the Kurtz–Perry method and its practical application. Appl. Phys. B 2014, 116, 211–233. [Google Scholar]
- Aramburu, I.; Ortega, J.; Folcia, C.; Etxebarria, J. Second-harmonic generation in dry powders: A simple experimental method to determine nonlinear efficiencies under strong light scattering. Appl. Phys. Lett. 2014, 104, 071107. [Google Scholar] [CrossRef]
- Kiguchi, M.; Kato, M.; Okunaka, M.; Taniguchi, Y. New method of measuring second harmonic generation efficiency using powder crystals. Appl. Phys. Lett. 1992, 60, 1933–1935. [Google Scholar] [CrossRef]
- Aramburu, I.; Ortega, J.; Folcia, C.; Etxebarria, J.; Illarramendi, M.; Breczewski, T. Accurate determination of second order nonlinear optical coefficients from powder crystal monolayers. J. Appl. Phys. 2011, 109, 113105. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Wu, H.; Yu, H.; Lin, Z.; Hu, Z.; Wang, J.; Wu, Y. CsZn2BO3X2 (X2=F2, Cl2, and FCl): A Series of Beryllium-Free Deep-Ultraviolet Nonlinear-Optical Crystals with Excellent Properties. Angew. Chem. Int. Edit. 2020, 59, 19006–19010. [Google Scholar] [CrossRef]
- Wu, C.; Jiang, X.; Lin, L.; Dan, W.; Lin, Z.; Huang, Z.; Humphrey, M.G.; Zhang, C. Strong SHG Responses in a Beryllium-Free Deep-UV-Transparent Hydroxyborate via Covalent Bond Modification. Angew. Chem. Int. Edit. 2021, 60, 27151–27157. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.; Jiang, X.; Wang, Z.; Huang, Z.; Lin, Z.; Long, X.; Humphrey, M.G.; Zhang, C. Giant Second-Harmonic Generation Response and Large Band Gap in the Partially Fluorinated Mid-Infrared Oxide RbTeMo2O8F. J. Am. Chem. Soc. 2021, 143, 12455–12459. [Google Scholar] [CrossRef]
- Guo, Y.; Liang, F.; Yin, W.; Li, Z.; Luo, X.; Lin, Z.S.; Yao, J.; Mar, A.; Wu, Y. BaHgGeSe4 and SrHgGeSe4: Two New Hg-Based Infrared Nonlinear Optical Materials. Chem. Mater. 2019, 31, 3034–3040. [Google Scholar] [CrossRef]
- Sun, M.; Xing, W.; Lee, M.-H.; Yao, J. Bridging oxygen atoms in trigonal prism units driven strong second-harmonic-generation efficiency in Sr3Ge2O4Te3. Chem. Commun. 2022, 58, 11167–11170. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, H.; Xu, F.; Cao, L.; Jiang, X.; Yang, S.; Sun, Y.; Zhao, X.; Lin, C.; Ye, N. Mg2In3Si2P7: A Quaternary Diamond-like Phosphide Infrared Nonlinear Optical Material Derived from ZnGeP2. J. Am. Chem. Soc. 2021, 143, 10309–10316. [Google Scholar] [CrossRef]
- Eckardt, R.C.; Masuda, H.; Fan, Y.X.; Byer, R.L. Absolute and relative nonlinear optical coefficients of KDP, KD*P, BaBO4, LiIO3, MgO: LiNbO3, and KTP measured by phase-matched second-harmonic generation. IEEE J. Quantum Electron. 1990, 26, 922–933. [Google Scholar] [CrossRef]
- Smith, W.L. KDP and ADP transmission in the vacuum ultraviolet. Appl. Opt. 1977, 16, 1798. [Google Scholar] [CrossRef] [PubMed]
- Bierlein, J.D.; Vanherzeele, H. Potassium titanyl phosphate: Properties and new applications. J. Opt. Soc. Am. B 1989, 6, 622–633. [Google Scholar] [CrossRef]
- Chemla, D.; Kupecek, P.; Robertson, D.; Smith, R. Silver thiogallate, a new material with potential for infrared devices. Opt. Commun. 1971, 3, 29–31. [Google Scholar] [CrossRef]
- Boyd, G.; Kasper, H.; McFee, J.; Storz, F. Linear and nonlinear optical properties of some ternary selenides. IEEE J. Quantum Electron. 1972, 8, 900–908. [Google Scholar] [CrossRef]
- Boyd, G.D.; Buehler, E.; Storz, F.G. Linear and Nonlinear Optical Properties of ZnGeP2 and CdSe. Appl. Phys. Lett. 1971, 18, 301–304. [Google Scholar] [CrossRef]
- Petrov, V.; Badikov, V.V.; Badikov, D.V.; Kato, K.; Shevyrdyaeva, G.S.; Miyata, K.; Mero, M.; Wang, L.; Heiner, Z.; Panyutin, V.L. Barium nonlinear optical crystals for the mid-IR: Characterization and some applications. J. Opt. Soc. Am. B 2021, 38, B46–B58. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, G.; Ye, N. Growth and Characterization of BaGa4S7: A New Crystal for Mid-IR Nonlinear Optics. Cryst. Growth Des. 2009, 9, 1186–1189. [Google Scholar] [CrossRef]
- Zhao, X.; Li, C.; Bai, J.; Wang, Z.; Yao, J.; Tan, R.; Xu, X. Recalibration of the nonlinear optical coefficients of BaGa4Se7 crystal using second-harmonic-generation method. Opt. Lett. 2021, 46, 5894–5897. [Google Scholar] [CrossRef] [PubMed]
- Smith, A. Introduction to SNLO software. 2015. Available online: https://www.as-photonics.com/snlo_files/snlo_introduction.pdf (accessed on 8 January 2023).
- Smith, A.V. How to select nonlinear crystals and model their performance using SNLO software. Proc. SPIE 2000, 3928, 62–69. [Google Scholar]
- Guo, Y.; Li, Z.; Lei, Z.; Luo, X.; Yao, J.; Yang, C.; Wu, Y. Synthesis, growth of crack-free large-size BaGa4Se7 crystal, and annealing studies. Cryst. Growth Des. 2018, 19, 1282–1287. [Google Scholar] [CrossRef]
- Aydın, C.; Benhaliliba, M.; Al-Ghamdi, A.A.; Gafer, Z.H.; El-Tantawy, F.; Yakuphanoglu, F. Determination of optical band gap of ZnO: ZnAl2O4 composite semiconductor nanopowder materials by optical reflectance method. J. Electroceram. 2013, 31, 265–270. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Ilican, S.; Caglar, M.; Caglar, Y. The determination of the optical band and optical constants of non-crystalline and crystalline ZnO thin films deposited by spray pyrolysis. J. Optoelectron. Adv. Mater. 2007, 9, 2180. [Google Scholar]


| Compound | S. G. | Eg (eV) | Refractive Index@1045 nm | Transmission Range (μm) | deff (pm/V) a | Reference |
|---|---|---|---|---|---|---|
| LBO | Pna21 | 7.37 | nx = 1.5651 ny = 1.5908 nz = 1.6057 | 0.60–2.6 | deff = 0.64 | [3] |
| β-BBO | R3 | 6.53 | no = 1.6546 ne = 1.5393 | 0.189–3.5 | deff = 2.01 | [20,48] |
| KDP | I-42d | 6.97 | no = 1.4944 ne = 1.4601 | 0.18–1.7 | deff = 0.26 | [48,49] |
| KTP | Pna21 | 3.52 | nx = 1.7391 ny = 1.7464 nz = 1.7902 | 0.35–4.5 | deff = 3.58 | [48,50] |
| AGS | I-42d | 2.75 | no = 2.4549 ne = 2.4021 | 0.50–13 | deff = 13.4 | [51] |
| AGSe | I-42d | 1.82 | no = 2.7044 ne = 2.6838 | 0.73–17 | deff = 28.3 | [52] |
| ZGP | I-42d | 1.75 | no = 3.2759 ne = 3.3313 | 0.70–12 | deff = 34.3 | [52,53] |
| BGS | Pmn21 | 3.59 | nx = 2.2828 ny = 2.3024 nz = 2.3231 | 0.54–9.4 | deff = 5.38 | [54,55] |
| BGSe | Pc | 2.73 | nx = 2.4897 ny = 2.5047 nz = 2.5641 | 0.70–14.8 | deff = 14.7 | [54,56] |
| Compound | SHG Intensity | deff (LBO as Reference) b | deff(AGS as Reference) b | deff (AGSe as Reference) b | deff (ZGP as Reference) b | deff (BGS as Reference) b | deff (BGSe as Reference) b | deff (pm/V) a |
|---|---|---|---|---|---|---|---|---|
| LBO | 1.25 | 0.64 | 10.03 | 26.46 | 14.1 | 1.72 | 7.66 | 0.64 |
| AGS | 2.23 | 0.85 | 13.4 | 35.23 | 18.79 | 2.29 | 10.23 | 13.4 |
| AGSe | 1.43 | 0.68 | 10.74 | 28.3 | 15.09 | 1.83 | 8.18 | 28.3 |
| ZGP | 7.39 | 1.56 | 24.4 | 64.33 | 34.3 | 4.17 | 25.91 | 34.3 |
| BGS | 12.25 | 2.80 | 31.4 | 82.83 | 44.16 | 5.38 | 18.63 | 5.38 |
| BGSe | 4.60 | 1.23 | 19.24 | 50.75 | 27.06 | 3.30 | 14.7 | 14.7 |
| Optical Property | Positive/Negative | Type of PM | PolFact | nFact |
|---|---|---|---|---|
| uniaxial | positive: ne > no | I | 3/8 | |
| II | 1/2 | |||
| negative: ne < no | I | 3/8 | ||
| II | 1/2 | |||
| biaxial | positive: ne > no | I | 3/8 | 1 |
| II | 1/2 | 1 | ||
| negative: ne < no | I | 3/8 | 1 | |
| II | 1/2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Wang, G.; Yao, J. The Kurtz–Perry Powder Technique Revisited: A Study of the Effect of Reference Selection on Powder Second-Harmonic Generation Response. Molecules 2023, 28, 1116. https://doi.org/10.3390/molecules28031116
Sun M, Wang G, Yao J. The Kurtz–Perry Powder Technique Revisited: A Study of the Effect of Reference Selection on Powder Second-Harmonic Generation Response. Molecules. 2023; 28(3):1116. https://doi.org/10.3390/molecules28031116
Chicago/Turabian StyleSun, Mengran, Guili Wang, and Jiyong Yao. 2023. "The Kurtz–Perry Powder Technique Revisited: A Study of the Effect of Reference Selection on Powder Second-Harmonic Generation Response" Molecules 28, no. 3: 1116. https://doi.org/10.3390/molecules28031116
APA StyleSun, M., Wang, G., & Yao, J. (2023). The Kurtz–Perry Powder Technique Revisited: A Study of the Effect of Reference Selection on Powder Second-Harmonic Generation Response. Molecules, 28(3), 1116. https://doi.org/10.3390/molecules28031116






