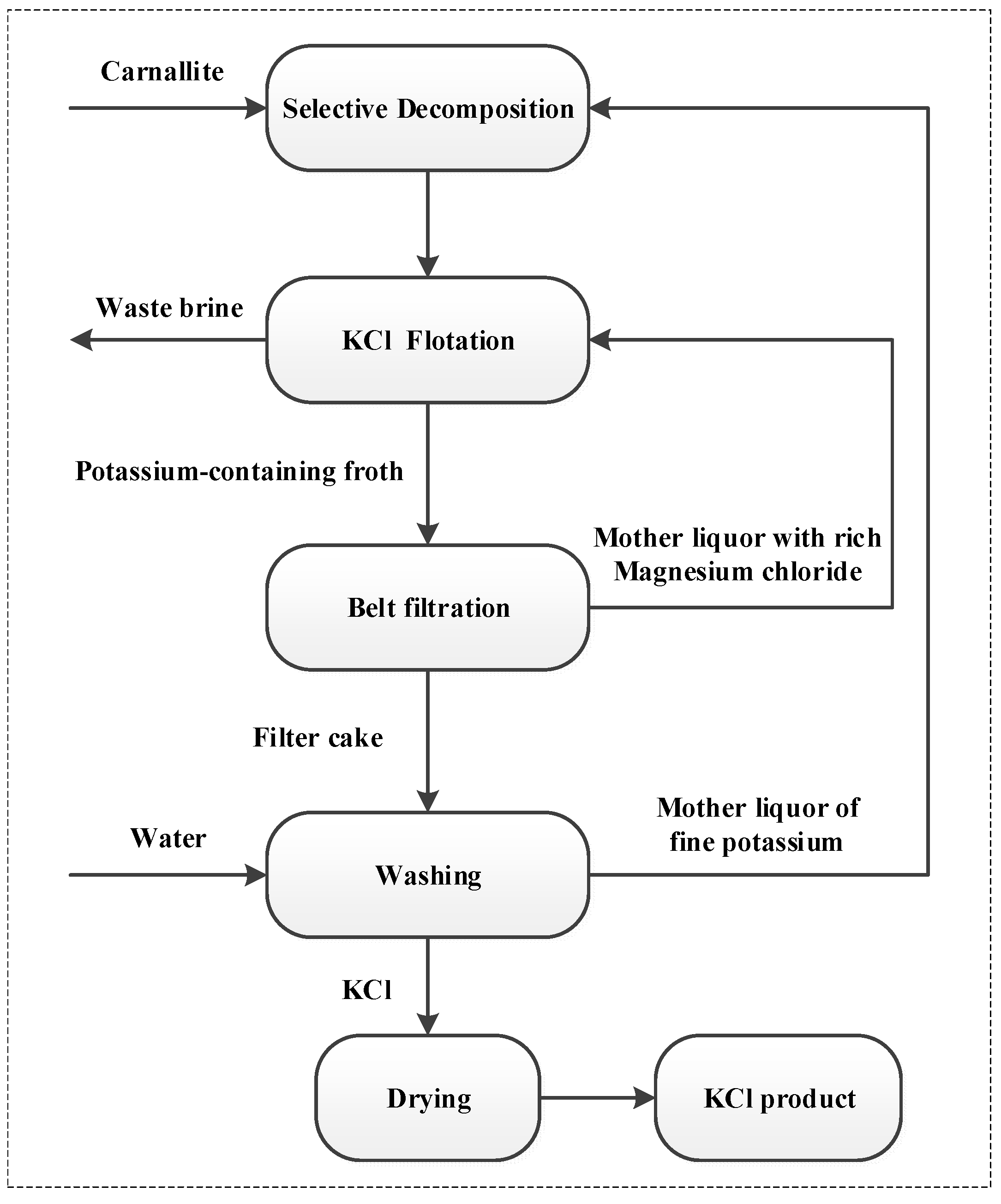
Figure 1.
Process flow chart of cold decomposition–direct flotation technology of potassium chloride.
Figure 1.
Process flow chart of cold decomposition–direct flotation technology of potassium chloride.
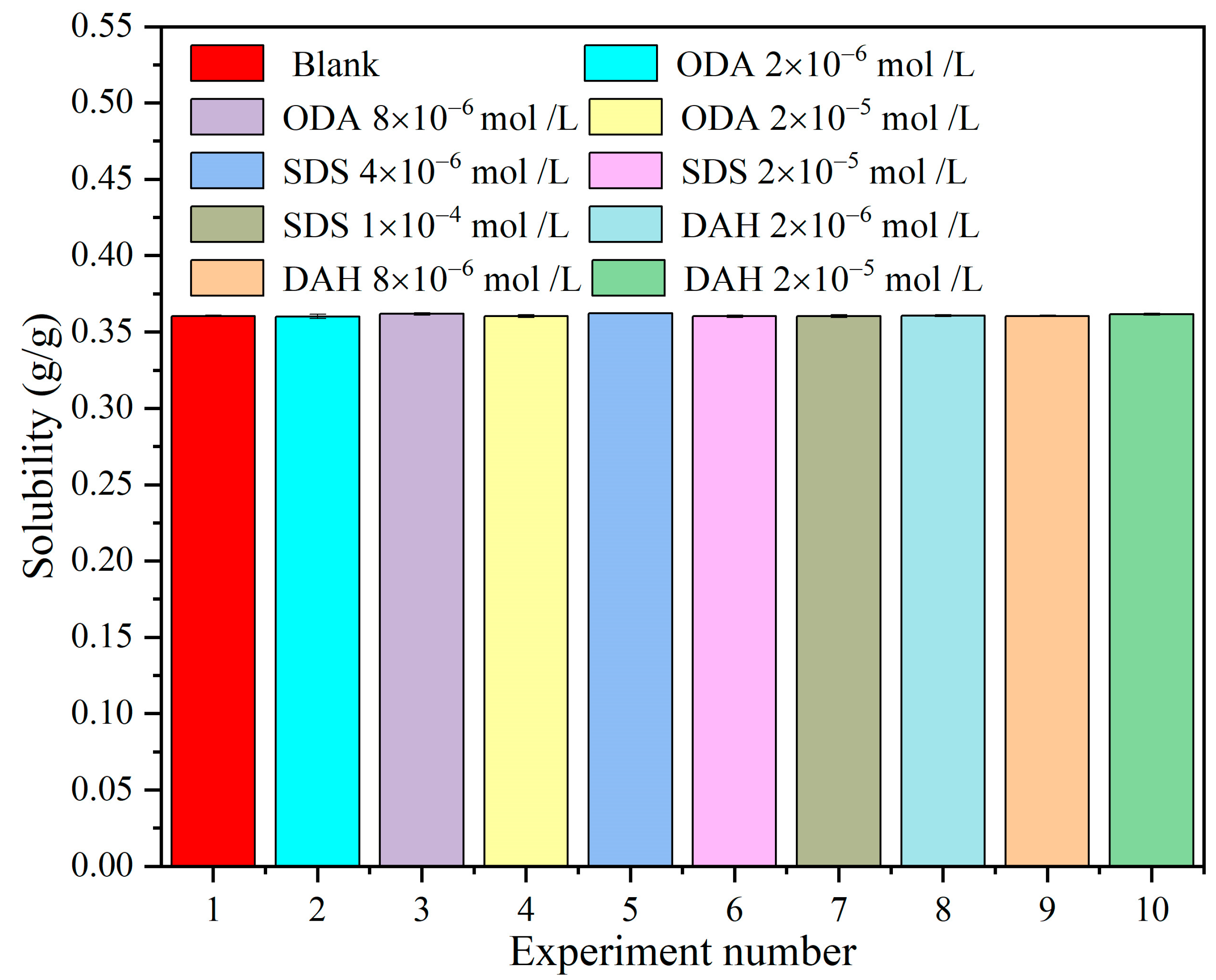
Figure 2.
The effects of different flotation agent concentrations on the solubility of KCl at 298.15 K.
Figure 2.
The effects of different flotation agent concentrations on the solubility of KCl at 298.15 K.
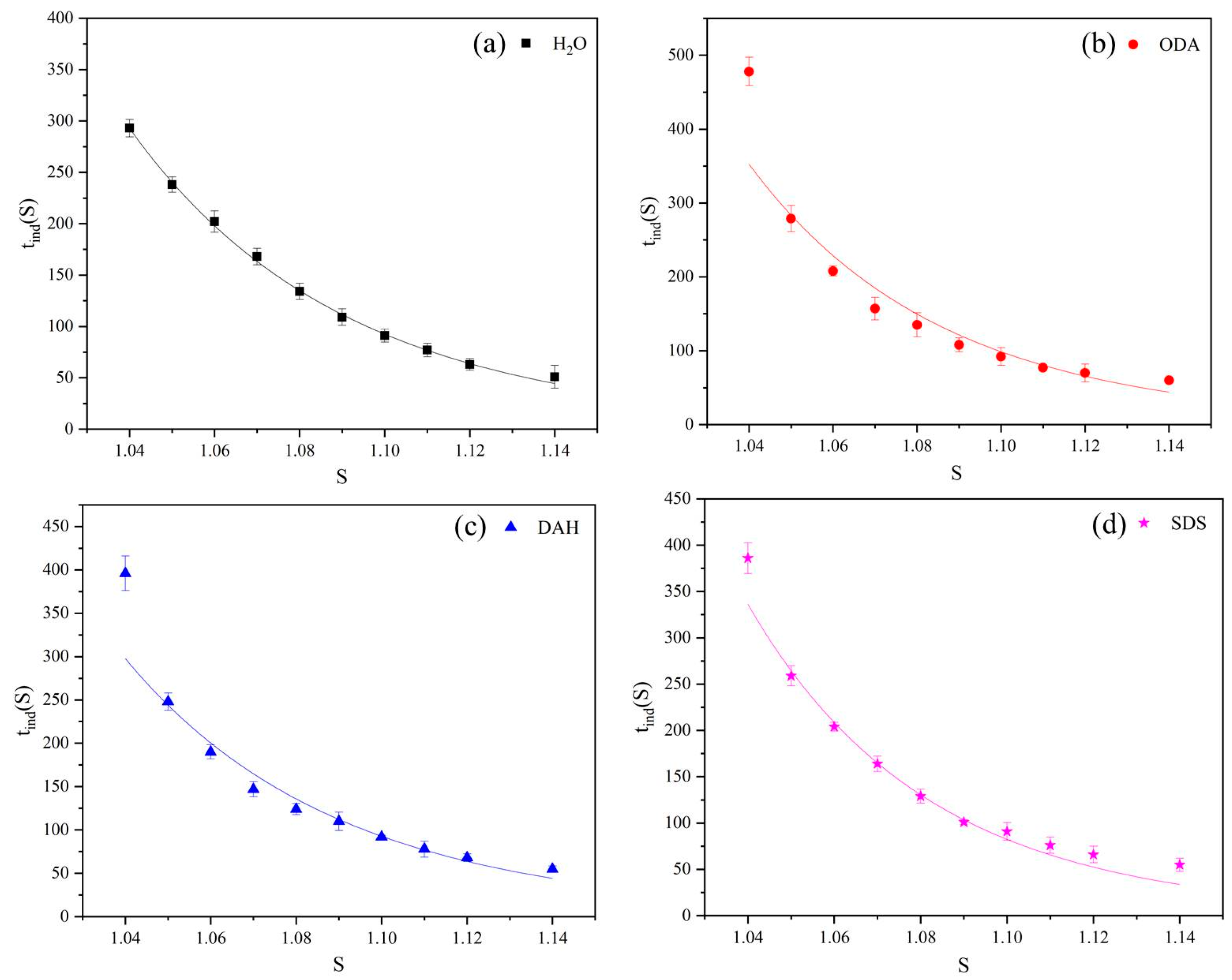
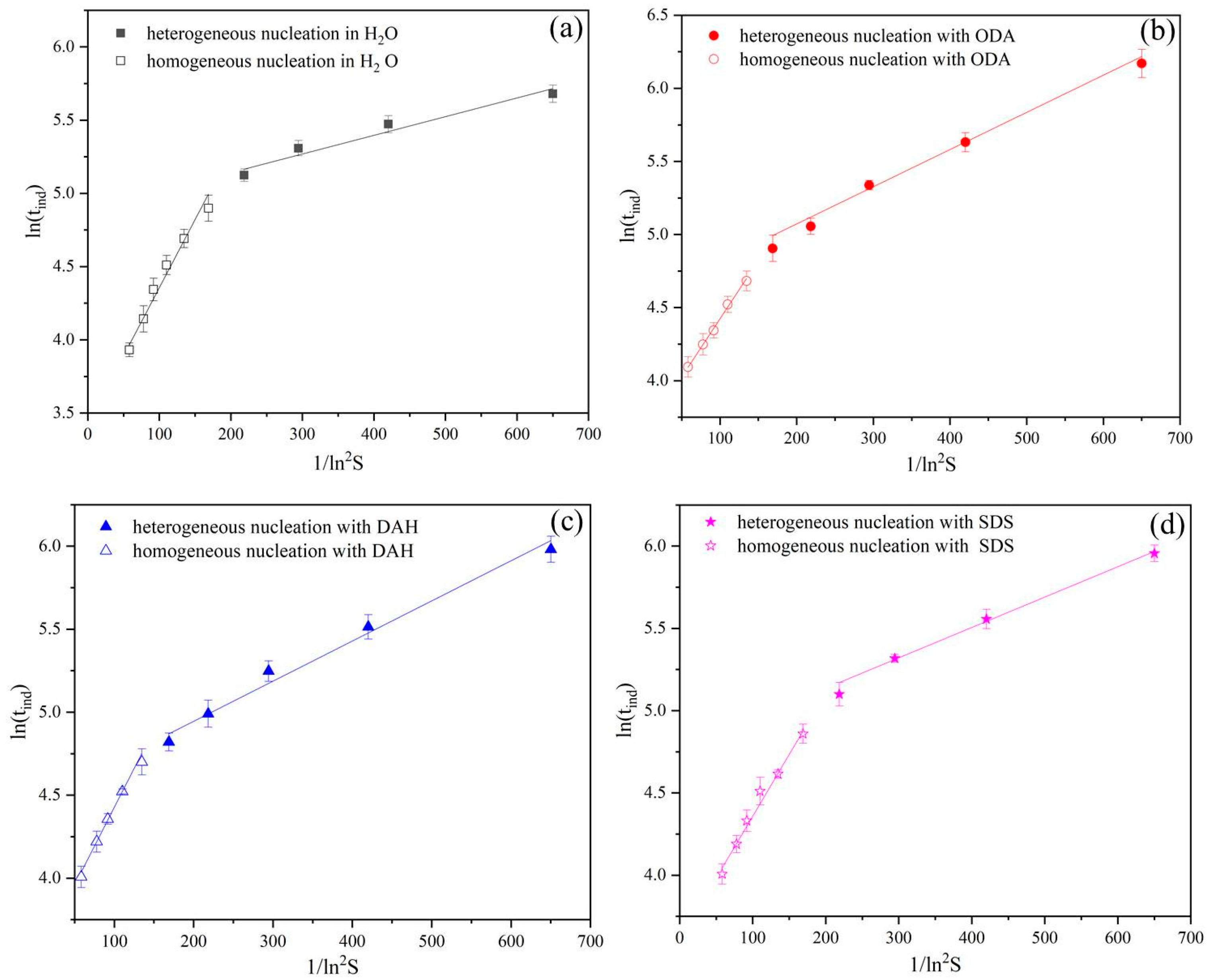
Figure 3.
The relationship between the induction periods of potassium chloride and supersaturation ratios in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
Figure 3.
The relationship between the induction periods of potassium chloride and supersaturation ratios in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
Figure 4.
Plot of and for potassium chloride crystallization in the presence of different flotation agents: (a) H2O, (b) ODA, (c) SDS, (d) DAH.
Figure 4.
Plot of and for potassium chloride crystallization in the presence of different flotation agents: (a) H2O, (b) ODA, (c) SDS, (d) DAH.
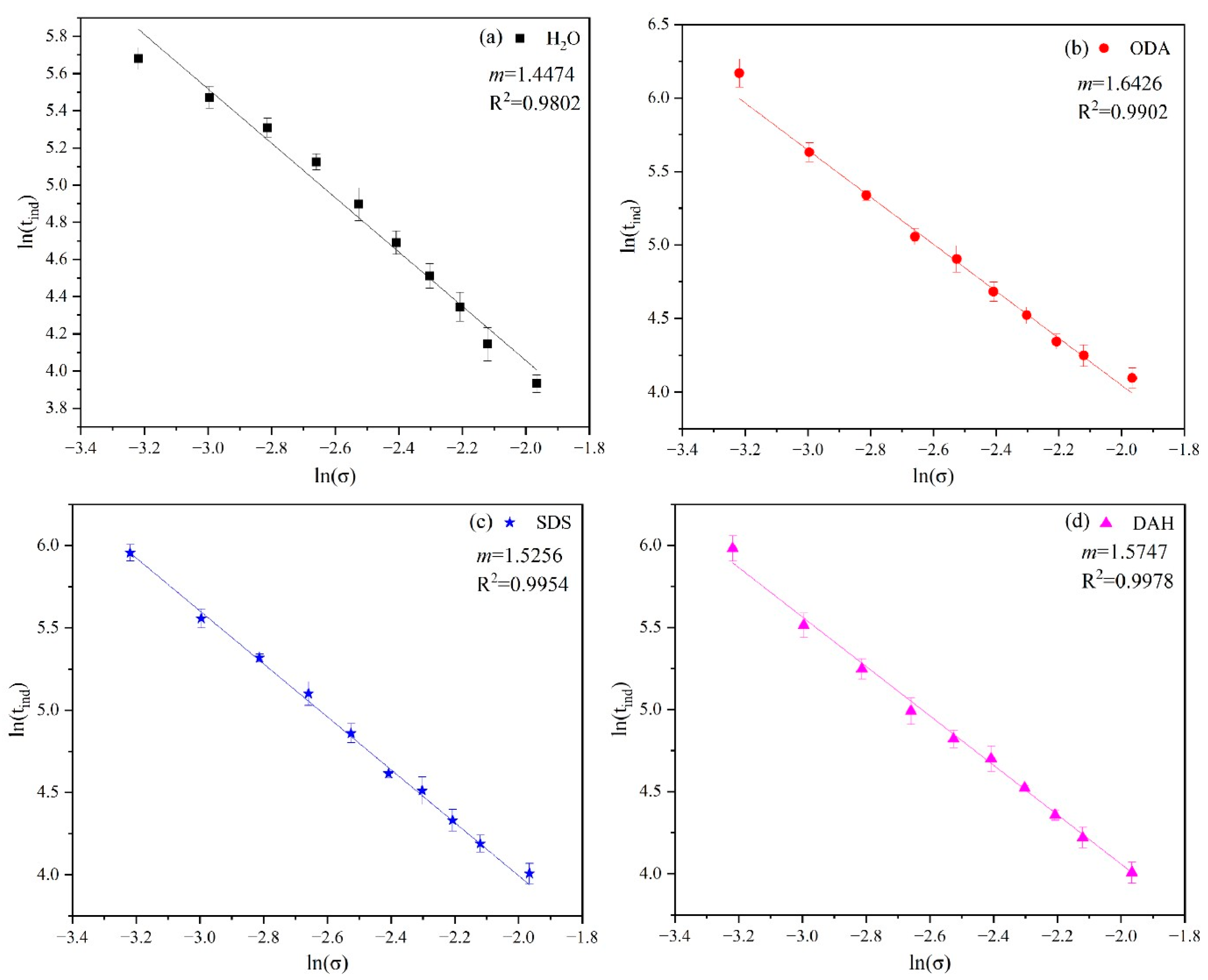
Figure 5.
The relationship between and in the potassium chloride induction period experiment in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
Figure 5.
The relationship between and in the potassium chloride induction period experiment in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
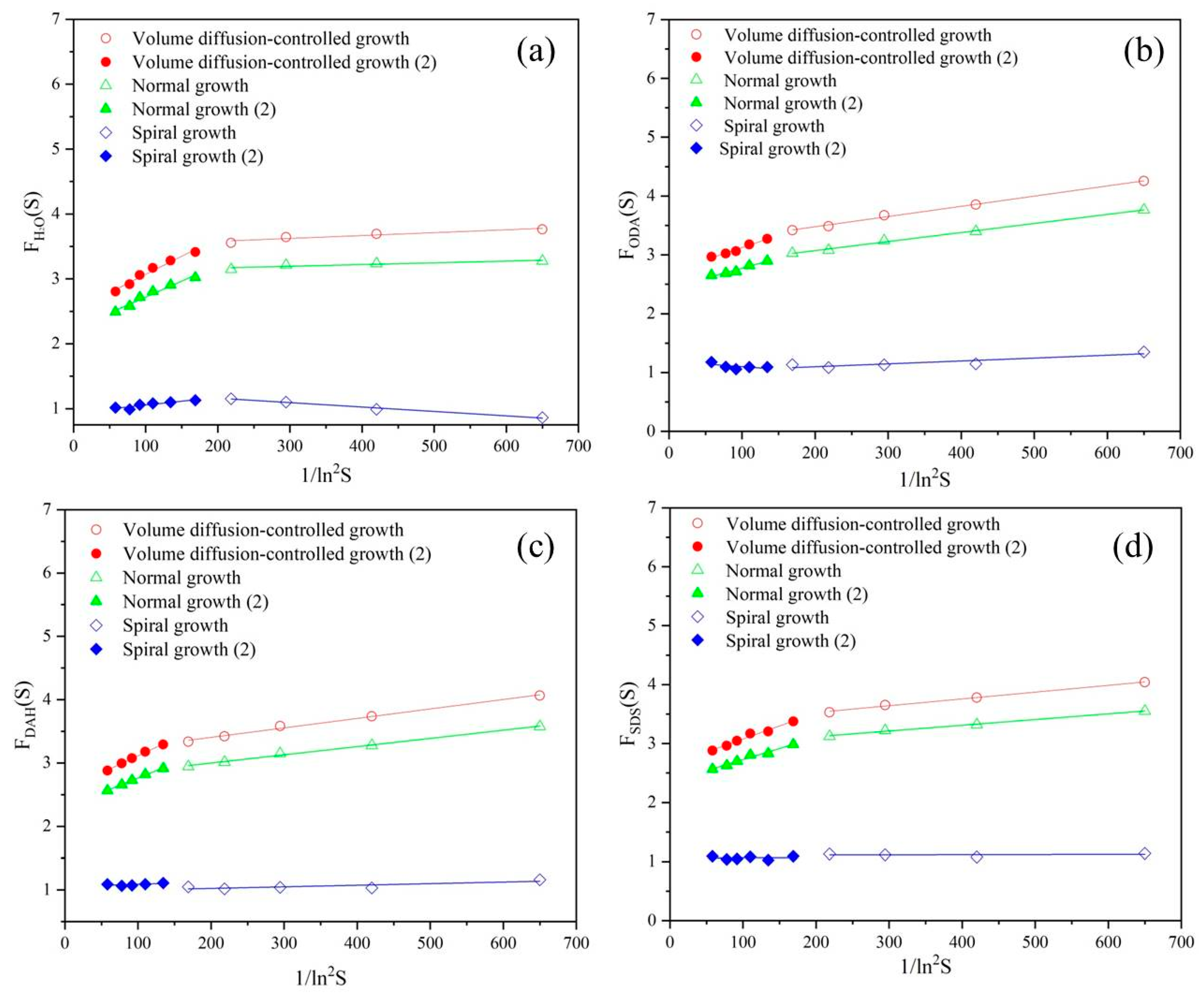
Figure 6.
Dependence of Fu(S) on ln2S under normal growth, spiral growth and diffusion-controlled growth mechanisms in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
Figure 6.
Dependence of Fu(S) on ln2S under normal growth, spiral growth and diffusion-controlled growth mechanisms in the presence of different flotation agents: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
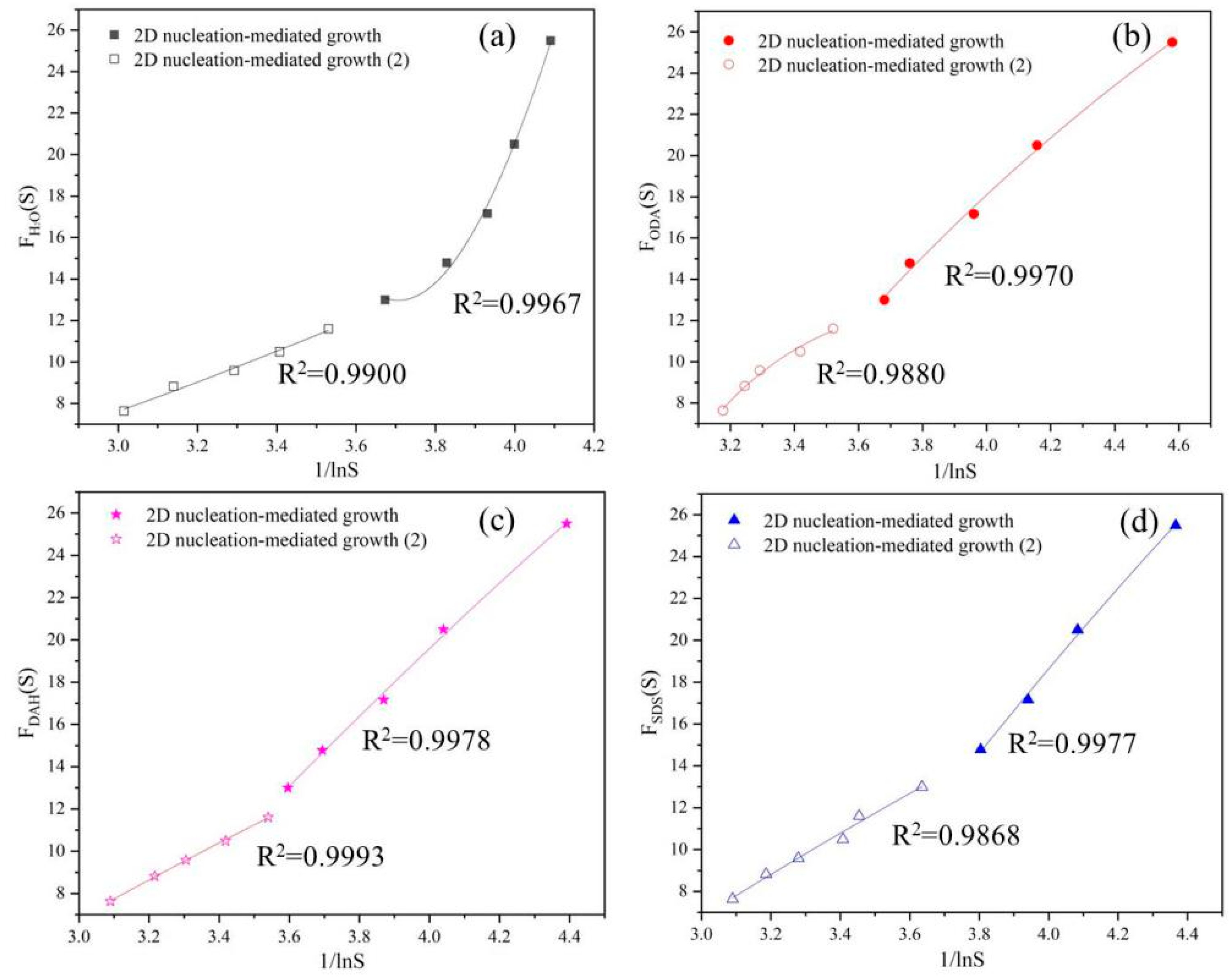
Figure 7.
Dependence of Fu(S) on lnS under 2D nucleation-mediated growth mechanism in the presence of different flotation agent: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
Figure 7.
Dependence of Fu(S) on lnS under 2D nucleation-mediated growth mechanism in the presence of different flotation agent: (a) H2O, (b) ODA, (c) DAH, (d) SDS.
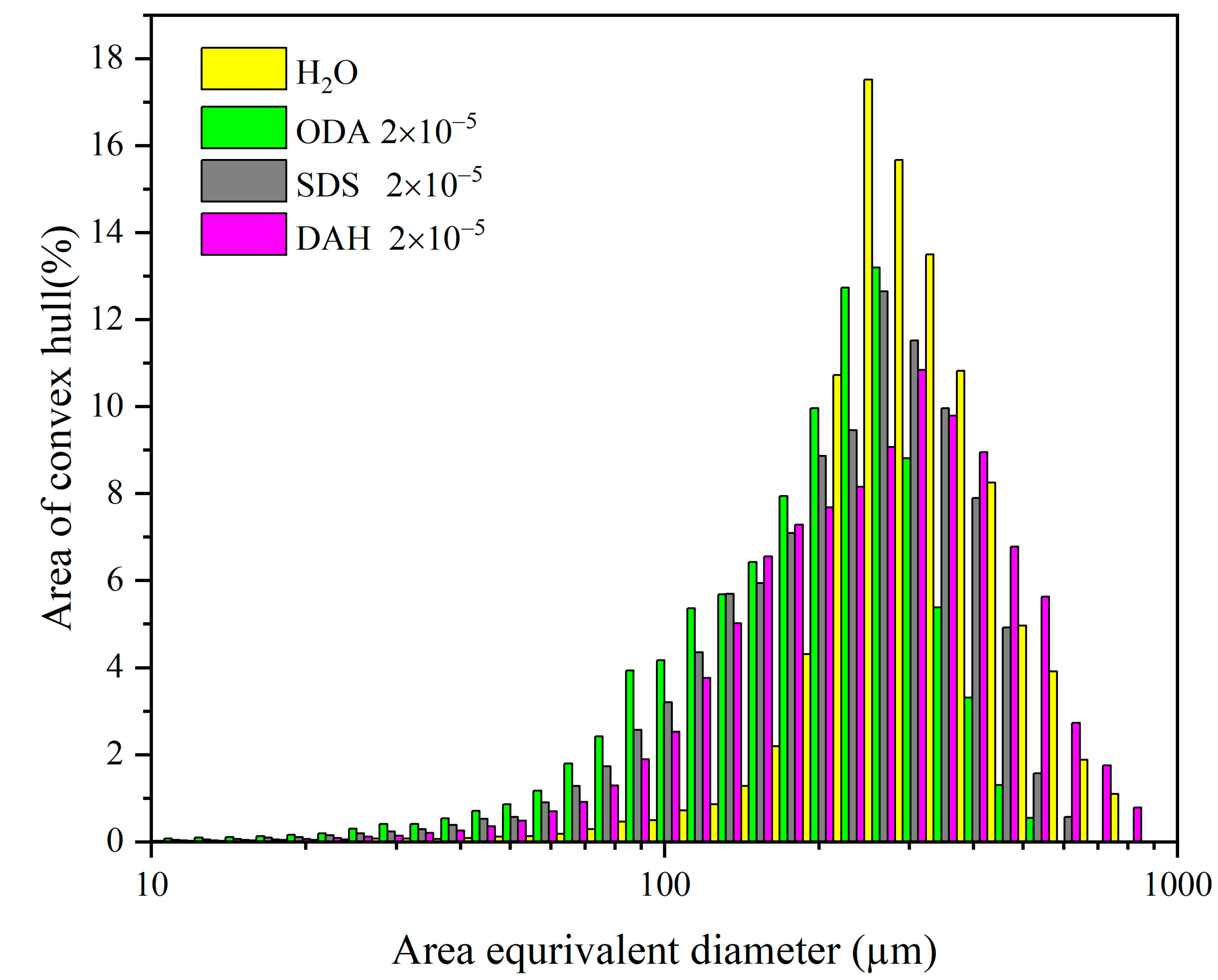
Figure 8.
Particle size distribution of potassium chloride in the presence of different flotation agents (agitation rate 300 rpm, cooling rate 20 °C/h, supersaturation ratio 1.08).
Figure 8.
Particle size distribution of potassium chloride in the presence of different flotation agents (agitation rate 300 rpm, cooling rate 20 °C/h, supersaturation ratio 1.08).
Figure 9.
Crystal morphology of potassium chloride in the presence of different flotation agents: (a) H2O, (b) ODA, (c) SDS, (d) DAH (agitation rate 300 rpm, cooling rate 20 °C/h, supersaturation ratio 1.08, the scale in all figures is 50 µm).
Figure 9.
Crystal morphology of potassium chloride in the presence of different flotation agents: (a) H2O, (b) ODA, (c) SDS, (d) DAH (agitation rate 300 rpm, cooling rate 20 °C/h, supersaturation ratio 1.08, the scale in all figures is 50 µm).
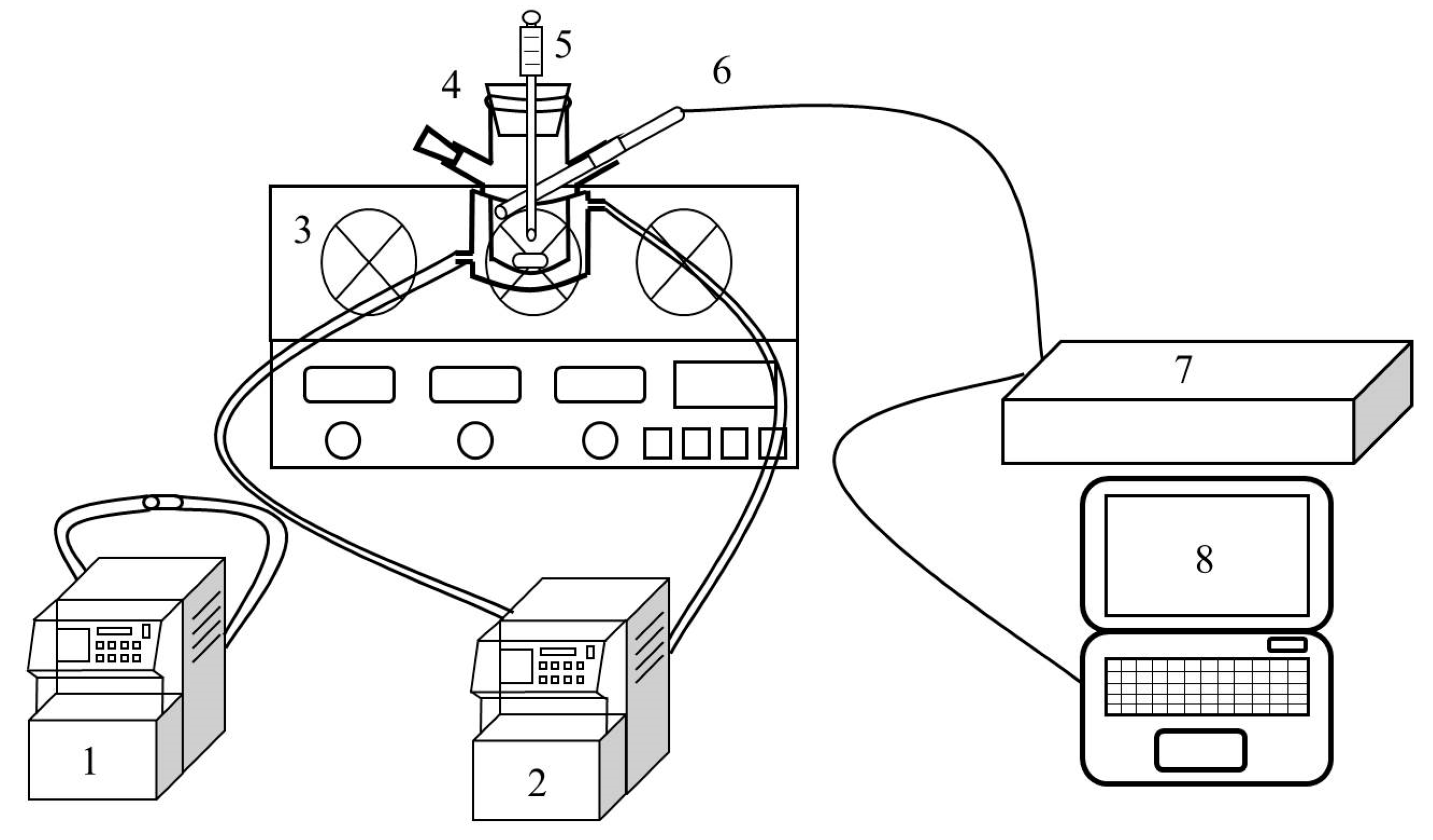
Figure 10.
Experimental device of induction period determination (1: cooling circulating water machine (high temperature), 2: cooling circulating water machine (low temperature), 3: digital magnetic stirrer, 4: crystallizer, 5: electronic thermometer, 6: FBRM probe, 7: FBRM workstation, 8: computer).
Figure 10.
Experimental device of induction period determination (1: cooling circulating water machine (high temperature), 2: cooling circulating water machine (low temperature), 3: digital magnetic stirrer, 4: crystallizer, 5: electronic thermometer, 6: FBRM probe, 7: FBRM workstation, 8: computer).
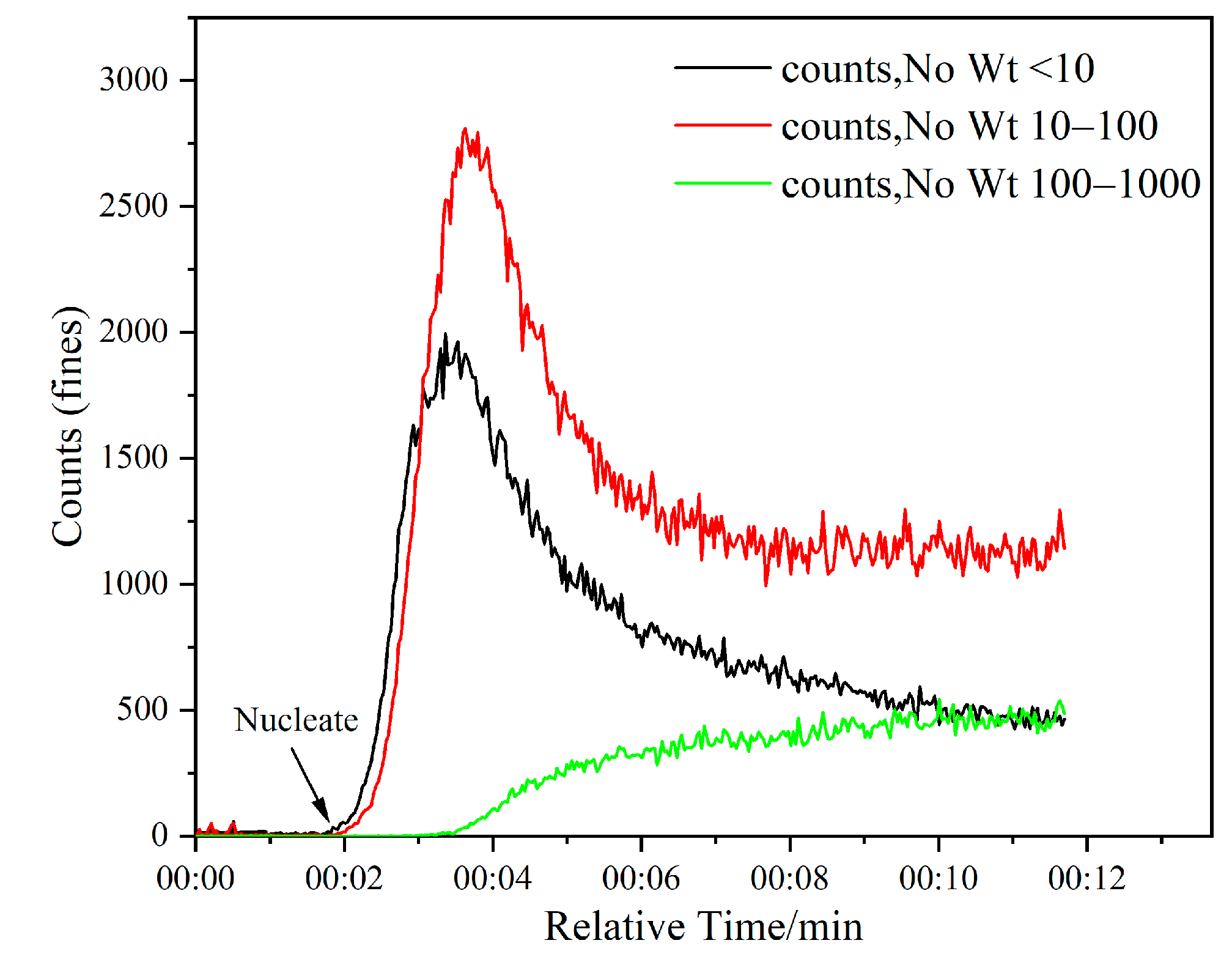
Figure 11.
Monitoring the nucleation point of KCl using FBRM (DAH 2 × 10−5 mol/L, stirring rate 300 rpm, supersaturation 1.08).
Figure 11.
Monitoring the nucleation point of KCl using FBRM (DAH 2 × 10−5 mol/L, stirring rate 300 rpm, supersaturation 1.08).
Table 1.
Empirical parameters obtained from the Formula (2) in the presence of different flotation agents.
Table 1.
Empirical parameters obtained from the Formula (2) in the presence of different flotation agents.
| Flotation Agents | | | R2 |
|---|
| H2O | 651.22 | 20.38 | 0.9984 |
| ODA | 1497.26 | 31.53 | 0.9470 |
| DAH | 1038.16 | 27.02 | 0.9516 |
| SDS | 1010.14 | 26.23 | 0.9765 |
Table 2.
The slopes of the straight lines and the corresponding interfacial energies fitted according to Equation (10).
Table 2.
The slopes of the straight lines and the corresponding interfacial energies fitted according to Equation (10).
| Flotation Agents | Homogeneous Nucleation | Heterogeneous Nucleation |
|---|
| Slope | Intercept | R2 | /mJ·m−2 | /s−1 | Slope | Intercept | R2 | /mJ·m−2 | /s−1 |
|---|
| H2O | 0.0087 | 3.4859 | 0.9740 | 5.3934 | 3.06 × 10−2 | 0.0012 | 4.9105 | 0.9570 | 2.8054 | 7.37 × 10−3 |
| ODA | 0.0078 | 3.6395 | 0.9964 | 5.1949 | 2.63 × 10−2 | 0.0026 | 4.5085 | 0.9921 | 3.6004 | 1.10 × 10−2 |
| DAH | 0.0091 | 3.5037 | 0.9927 | 5.1604 | 3.01 × 10−2 | 0.0024 | 4.4828 | 0.9864 | 3.4860 | 1.13 × 10−2 |
| SDS | 0.0076 | 3.6084 | 0.9826 | 5.1434 | 2.71 × 10−2 | 0.0019 | 4.7179 | 0.9909 | 3.2599 | 8.93 × 10−3 |
Table 3.
The critical nucleation sizes rcrit (Å) calculated according to Equation (11).
Table 3.
The critical nucleation sizes rcrit (Å) calculated according to Equation (11).
| | Homogeneous Nucleation | Heterogeneous Nucleation |
|---|
| S | H2O | ODA | DAH | SDS | H2O | ODA | DAH | SDS |
|---|
| 1.04 | 41.62 | 40.09 | 39.82 | 39.69 | 21.65 | 27.78 | 26.90 | 25.16 |
| 1.05 | 33.46 | 32.22 | 32.01 | 31.91 | 17.40 | 22.33 | 21.62 | 20.22 |
| 1.06 | 28.01 | 26.98 | 26.80 | 26.72 | 14.57 | 18.70 | 18.11 | 16.93 |
| 1.07 | 24.13 | 23.24 | 23.08 | 23.01 | 12.55 | 16.11 | 15.59 | 14.58 |
| 1.08 | 21.21 | 20.43 | 20.29 | 20.23 | 11.03 | 14.16 | 13.71 | 12.82 |
| 1.09 | 18.94 | 18.24 | 18.12 | 18.06 | 9.85 | 12.64 | 12.24 | 11.45 |
| 1.10 | 17.13 | 16.50 | 16.39 | 16.33 | 8.91 | 11.43 | 11.07 | 10.35 |
| 1.11 | 15.64 | 15.07 | 14.97 | 14.92 | 8.14 | 10.44 | 10.11 | 9.45 |
| 1.12 | 14.40 | 13.87 | 13.78 | 13.74 | 7.49 | 9.62 | 9.31 | 8.71 |
| 1.14 | 12.46 | 12.00 | 11.92 | 11.88 | 6.48 | 8.32 | 8.05 | 7.53 |
Table 4.
Expressions of Fu(S) corresponding to different growth mechanisms.
Table 4.
Expressions of Fu(S) corresponding to different growth mechanisms.
| Growth Mechanism | ν | n | Fu(S) |
|---|
| Normal growth | 1 | 4 | |
| Spiral growth | 1 | 4 | |
| Diffusion-controlled growth | 1/2 | 5/2 | |
| 2D nucleation-mediated growth | 1 | 4 | |
Table 5.
The coefficients R2 for different growth mechanisms of KCl in the presence of different flotation agents.
Table 5.
The coefficients R2 for different growth mechanisms of KCl in the presence of different flotation agents.
| Flotation Agents | Growth Mechanisms | R2 |
|---|
| (1) | (2) |
|---|
| H2O | Normal growth | 0.8493 | 0.9714 |
| Spiral growth | 0.9898 | 0.8530 |
| Diffusion-controlled growth | 0.9130 | 0.9729 |
| ODA | Normal growth | 0.9963 | 0.9587 |
| Spiral growth | 0.8217 | 0.3583 |
| Diffusion-controlled growth | 0.9966 | 0.9775 |
| DAH | Normal growth | 0.9951 | 0.9978 |
| Spiral growth | 0.6856 | 0.3683 |
| Diffusion-controlled growth | 0.9938 | 0.9970 |
| SDS | Normal growth | 0.9960 | 0.9756 |
| Spiral growth | 0.0301 | 0.0033 |
| Diffusion-controlled growth | 0.9957 | 0.9798 |
Table 6.
The particle size statistics of potassium chloride in the presence of different flotation agents obtained via particle size analyzer.
Table 6.
The particle size statistics of potassium chloride in the presence of different flotation agents obtained via particle size analyzer.
| Flotation Agents | Mean [µm] | D10 [µm] | D50 [µm] | D90 [µm] |
|---|
| H2O | 357.46 | 221.45 | 328.43 | 549.62 |
| ODA | 284.17 | 166.54 | 263.26 | 437.21 |
| DAH | 291.5 | 118.42 | 283.12 | 479.18 |
| SDS | 289.49 | 115.30 | 290.29 | 460.87 |
Table 7.
Different concentrations of flotation agents selected in the experiment.
Table 7.
Different concentrations of flotation agents selected in the experiment.
| Flotation Agents | Concentration (mol/L) |
|---|
| ODA | 2 × 10−6 | 8 × 10−6 | 2 × 10−5 |
| DAH | 2 × 10−6 | 8 × 10−6 | 2 × 10−5 |
| SDS | 4 × 10−6 | 2 × 10−5 | 1 × 10−4 |
Table 8.
The corresponding to different growth mechanisms.
Table 8.
The corresponding to different growth mechanisms.
| Growth Mechanism | f(S) |
|---|
| Normal growth | (S − 1) |
| Spiral growth | (S − 1)2 |
| Diffusion-controlled growth | (S − 1) |
| 2D nucleation-mediated growth | |