Abstract
The adsorption of nitrogen molecules on a (100) tungsten surface has been studied using a new potential energy surface in which long-range interactions are suitably characterized and represented by the Improved Lennard–Jones function. The new potential energy surface is used to carry out molecular dynamics simulations by adopting a semiclassical collisional method that explicitly includes the interaction with the surface phonons. The results of the sticking probability, evaluated as a function of the collision energy, are in good agreement with those obtained in the experiments and improve the already good comparison recently obtained with calculations performed using interactions from the Density Functional Theory method and corrected for long-range van der Waals contributions. The dependence of trapping probability on the surface temperature for a well-defined collision energy has also been investigated.
1. Introduction
The adsorption of gaseous species on surfaces is of fundamental interest for many processes useful in different applied fields (see, for instance, Refs. [1,2] and the references therein). For this reason, over the years, the complexity of interacting species and the considered substrate has increased.
The reliability of the dynamics and kinetics of the adsorption process, evaluated by computational methods, relies on the accuracy of the used potential energy surface (PES) controlling the evolution of single collision events. In this regard, over the years, with the concomitant advent of powerful supercomputers, it has been possible to determine the PES using increasingly precise and refined methods [3]. The determination of the interaction driving the collisions in heterogeneous gas–surface systems poses different problems, from both the theoretical and computational points of view, primarily for the fact that the involved PES is multidimensional, being dependent on six coordinates. As a consequence, and also due to the large computational time demanded to assure the convergence of calculated energies, complete, fully dimensional electronic structure calculations have been performed for a few elementary systems, notably those involving diatomic molecules on noble and transition metals [4,5]. Among the proposed approximate schemes, the most promising approach is the Density Functional Theory (DFT), which is accurate near the chemisorption potential well, but less accurate for weak long-range interactions. Such weak components are of non-covalent nature and control the gas–surface trapping (physisorption). Therefore, they promote the formation of the precursor (or pre-reactive) state of basic elementary processes, whose role in molecular dynamics is not trivial to identify. In this paper, we have addressed and tried to solve this last point for N2 adsorption on a W(100) surface.
In the last decade, several studies have appeared in the literature [6,7,8] with an aim to explain the steep decrease in the sticking probability, the collision energy increasing up to 0.5 eV, as obtained in the experiments made in the late eighties [9,10,11] for nitrogen molecules impinging a W(100) surface. These experiments, in the same collision energy range, also revealed a different reactivity to the case in which nitrogen molecules impact W(110) [12,13]. Understanding and rationalizing the nitrogen adsorption process on tungsten can help to understand and explain the processes that occur on other metal surfaces of interest in nitrogen industrial processes, the ammonia synthesis in primis, which usually involves the interaction of N2 and H2, mainly with an iron surface [14].
The authors of Ref. [7] succeeded in significantly improving the previous results of simulations reported in Ref. [15] concerning the behavior of the sticking probability as a function of collision energy for N2 on W(100), as obtained in experiments [9,10,11]. This improvement was obtained by adopting a PES determined by DFT calculations, including long-range interactions via the vdW-DF2 functional as implemented in the VASP code [16]. The authors of Ref. [7] ascribe the improvement in comparison with the experimental results to the fact that with the introduction of long-range interactions, the barrier in the entrance channel, revealed in the PES of Ref. [15], disappears.
The same authors investigated the energy dissipation during the adsorption dynamics of nitrogen molecules by the Generalized Langevin Oscillator (GLO) for molecule–surface interaction, whilst the Local Density Friction Approximation (LDFA) is implemented to consider the electron–hole (e–h) pair excitations [8]. From this study, it emerged that the interaction with the surface atoms plays a key role in the reaction energetics, while the e–h excitations rather influence the ratio between dissociative and non-dissociative adsorptions [8].
Recently, we proved that the Improved Lennard–Jones (ILJ) potential function [17] can also be useful and accurate for a proper description of the weak long-range non-covalent interactions between gaseous molecules and surfaces arising from the combination of size repulsion with dispersion attraction and controlling the physisorption state formation [18]. The accuracy of this description is derived from the fact that the adopted parameters relate to the intrinsic chemical–physical properties of the reaction partners. Moreover, by adopting the ILJ potential in conjunction with state-to-state molecular dynamics (MD) simulations based on a semiclassical collisional model [19,20], including the interaction with the surface phonons, treated in a quantum way, we were able to explain and support observations made in molecular beams (MB) experiments [21]. In addition, for each simplest-reference interacting pair, the ILJ function provides an asymptotic dispersion attraction associated with a coefficient, from which the atom/molecule–surface dispersion coefficient can also be evaluated (see next Section 2 and Section 3).
Therefore, this work aims to apply our computational setup to the N2-tungsten system to improve further the comparison between experiment and theory for the sticking probability and, at the same time, to provide an additional contribution to understanding reaction dynamics and the underlying energetics. To do this, we mainly focused on the evaluation of the long-range interaction strength, while also determining the and coefficients.
We built a new PES by grafting the short-range interaction data, taken from the literature, onto the long-range interaction modeled according to the ILJ potential. Then, we used the obtained PES, given in the proper analytical form, for MD simulations of N2 molecules impinging the W(100) surface in the low-collision-energy range. The surface temperature (TS) effect on the sticking probability, due to being related closely to the energy exchange with the phonons, explicitly considered in the adopted method, has also been investigated. The proper inclusion of surface phonons produces an agreement improved with the experimental results, whilst the correct treatment of the long-range interaction determining the precursor state suggests a new picture for the reaction dynamics.
Thus, the paper is organized in the following way: Section 2 focuses on the results obtained for the long-range interaction potential for the three active sites on the W(100) surface and provides the dispersion coefficients, which are also compared with the results available in the literature; in the same section, the results obtained for the sticking probability as a function of collision energy and surface temperature will be presented and discussed. Section 3 provides all basic details of the methods employed to carry out MD simulations and to formulate the PES. Some conclusions are drawn in Section 4.
2. Results and Discussion
2.1. The ILJ Long-Range Potential of N and N2 Interacting with W(100)
Details on the ILJ formulation, representing the weak long-range non-covalent part of each interaction potential, are summarized in the Section 3. Table 1 provides values of the basic ILJ potential parameters and of related and dispersion coefficients. By exploiting high-resolution gas-phase MB experiments, it has been demonstrated [17] that the coefficients, representative of the asymptotic behavior of the ILJ potential, are in good agreement with the results obtained from other experimental sources, semiempirical predictions and/or ab initio calculations. In this section, the focus is on the asymptotic part of the PES affecting the gas–surface trapping and on the comparison between the C3 coefficients, obtained in an internally consistent way from the ILJ coefficients, with the results available in the literature. In particular, the parameters reported in Table 1 have been evaluated, according to Refs. [17,22], by exploiting the polarizability of the single, isolated N atom (1.1 Å3) and the effective polarizability value of N in N2 (0.88 Å3). We also estimated the value of the effective polarizability of each W atom bound in the surface equal to 2.9 Å3 and considered an atomic surface density (ρ) equal to 0.0632 atom/Å3. In Figure 1, the coefficient for the nitrogen atom and molecule is reported as a function of their polarizability (α) in comparison with the values, determined with the same method, for rare gases interacting with W(100). In the same figure, the coefficients for the interaction of rare gases with W(100), obtained with different methods [23], are reported for a useful comparison. Looking at the plot, we can infer both the linear correlation between the coefficient and α, and a good comparison between the data reported in the literature and those calculated in this work for rare gases. Moreover, the right placement of points for N and N2 in the plot makes us confident about the parameters used to obtain the long-range potential of interest for the present investigation.

Table 1.
ILJ adopted parameters and related dispersion coefficients. Note that ε, Rm and represent, respectively, the potential well, the minimum location and the dispersion attraction coefficient of each weak interacting effective atom-effective atom pair. β, related to the hardness of the partners, is a parameter defining the shape of the potential well. The coefficient, defining the long-range atom/molecule–surface dispersion attraction, is proportional to multiplied by the atomic surface density (for further details, see the Section 3).
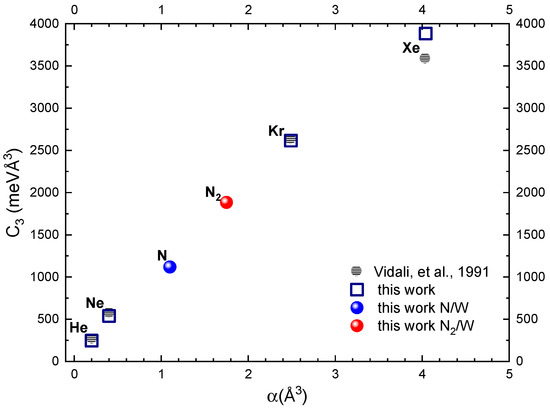
Figure 1.
coefficients calculated for rare gases and nitrogen (atomic and molecular) as a function of polarizability (α) of the gaseous species interacting with W(100) in comparison with the data of Ref. [23]. The polarizability values of rare gas atoms and N2 are taken from Ref. [24] and that of N from Ref. [25]. Note that while the relative values vary almost linearly with the rare gas atoms’ polarizability, their absolute value also depends on the effective polarizability of W atoms bounded in the surface.
In Figure 2, the ILJ potential for the three active sites on the surface, top (T) on a W atom, bridge (B) between two adjacent W atoms and hollow (H) in the center of the bcc unit cell, are reported for N2 impinging with the center of mass (CM) on the given site for two different orientations of the molecular axis with respect to the surface plane, parallel and perpendicular. In the same Figure, the ILJ potential for the N atom is also provided for the three sites.
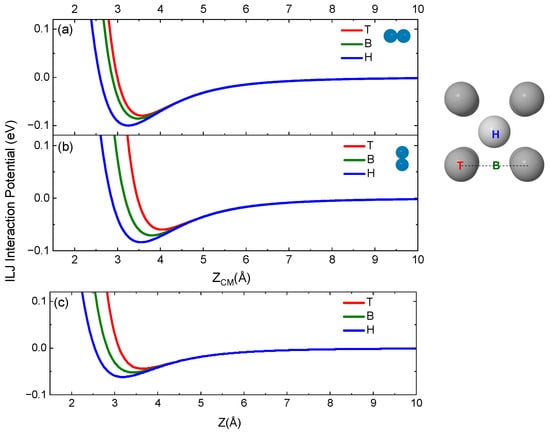
Figure 2.
ILJ potential for N2 impinging with its CM on T, B and H sites and with molecular axis being (a) parallel and (b) perpendicular to the surface plane. (c) ILJ potential for nitrogen atom impinging on the three sites. On the right side of the figure is the top view of the unit cell of W(100) on which the three sites on the surface are located. The color of the curves is associated with that of the site label. In the plot, Z defines the component of R along the normal direction and Z = 0 corresponds to the surface first layer.
From Figure 2, it emerges that the H site is the most attractive and that the minimum is placed at shorter distances from the surface compared with the other sites. Furthermore, for both atom and molecule, the physisorption well depth decreases with the sites according to the H > B > T order. Moreover, for the same site, the molecule in parallel configuration undergoes greater attraction, with the well depth being close to 0.1 eV for the H site.
2.2. Potential Energy Surface Determination
The complete reactive PES has been obtained as a sum of pairwise interactions, according to the consolidated functional form already used for the study of several molecule–surface systems [21] and given in Equation (1).
VN2(R) and VN(R) represent (nitrogen molecule)– and (nitrogen atom)–surface interaction potentials, respectively. R is the distance of impinging species from the surface. The weight function fsw(r) switches the interaction potential between VN2 and VN as r, the interatomic distance between the atoms in the molecule, increases and is given by
This function has been chosen to provide quick switching between 1 and 0, preserving the values of VN2 and VN for r lower and higher, respectively, than the intramolecular distance considered critical for N2 molecule dissociation (3 ÷ 3.5 Å).
VN2(R) has been obtained by combining the interaction potential on the three different sites (see Figure 2) on the surface through a switch function fswhbt, given in Equation (4):
the sum on j runs on the two atoms in the molecule while that on i runs on the atoms Nat in the assumed surface model lattice.
with
Xg and Yg are the molecule CM coordinates on the X–Y plane of the assumed reference frame; a is the lattice constant of W(100), equal to 3.165 Å.
fswbt is another switching function to discriminate between B and T sites and has the following functional form:
The interaction potential for the H site is determined as a pure ILJ potential according to the data available in the literature [6,26] for both orientations of N2 molecule impinging to the surface. Instead, for sites T and B, the ILJ potential was added to the fitting value of the potential determined in Refs. [6,26] for the incidence of N2 in a perpendicular and parallel configuration, respectively. In fact, the authors of both papers determine the interaction potentials for distances up to 4.0 ÷ 5.0 Å, too short to control the asymptotic behavior at longer distances, responsible for the formation of the precursor state.
For VT and VB, the expression, as a function of the CM distance along the normal to the surface of the incident molecule, is
where is the Z coordinate of molecule CM in the assumed reference frame.
The subscript S from here can be T or B. Note that the switch between the two functional expressions of the potential occurs as a function of Z, the component along the normal direction to the X–Y plane of R.
The general expression for the parameter P (P generally indicating the, and Morse function parameters; being the additional long-range correction factor; and denoting the switch value for Z) depends on the site and orientation of the molecular axis (θ) relative to the surface plane. Then, its analytic form is P = A + B (1 − cos(θ)) and the values of the constants for each site are given in Table 2.

Table 2.
Constant for the potential parameters for T and B sites for N2 impacting on W(100).
The complete interaction potential for the N2 molecule impinging with perpendicular and parallel orientation of its molecular axis and with CM on the three active sites on the W(100) surface is reported in Figure 3a,b.
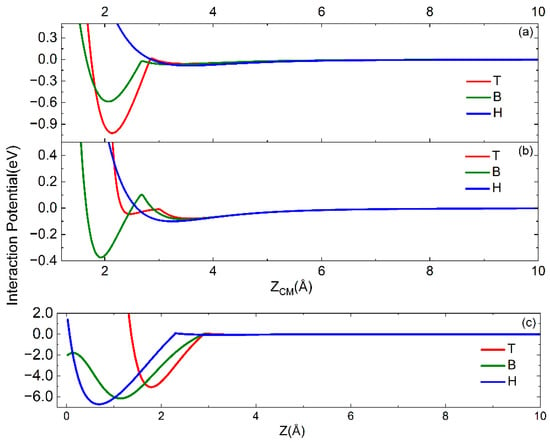
Figure 3.
Interaction potentials for N2 impinging with CM on T, B and H sites and with molecular axis (a) parallel and (b) perpendicular to the surface plane. (c) Interaction potential for nitrogen atom impinging on the three sites. The correspondence between the colors of the curves and the sites is the same as in Figure 2.
The interaction potential for atomic nitrogen for short distances has been obtained by fitting the results of Refs. [6,27]. The analytical form for VN is the same as Equation (3). For atomic nitrogen also, the interaction potential for the H site is obtained as the sum of short- and long-range contributions. The terms corresponding to the different sites are given similarly by the expression of Equation (6), while the corresponding parameters are reported in Table 3. The behavior of the obtained potential is reported in Figure 3c.

Table 3.
Constants for the potential parameters of T, B and H sites for N impacting on W(100).
Looking at Figure 3, it is clear that the PES for the interaction of N and N2 on W(100) results strongly corrugated. It is interesting to note that the molecular approach towards well-defined surface sites can introduce a small barrier for the transition from the physisorption well to the chemisorption well.
2.3. The Sticking Probability for N2 Interacting on W(100)
The values of sticking probability as a function of N2 collision energy (Ecoll) obtained by MD simulations are reported in Figure 4 for TS = 300 K in comparison with experimental data [10] and the results of previous simulations [7]. The values reported in the plot are obtained by including both dissociative and molecular adsorption events. Looking at the plot, it appears that the comparison with experimental results is improved significantly with respect to the comparison with the results of Ref. [7], mainly for the lower collision energies (Ecoll < 0.2 eV). In particular, in this energy range, the slope with which the sticking probability (PSticking) decreases is almost the same as that of the experimental data. These findings, in comparison with those of Ref. [7], could indicate a different mechanism in the interaction dynamics due to the adoption of a dissimilar long-range interaction potential and/or that the treatment of the interaction with the phonons of the surface adopted here is able to describe better the energy exchanges between the incident species and the surface.
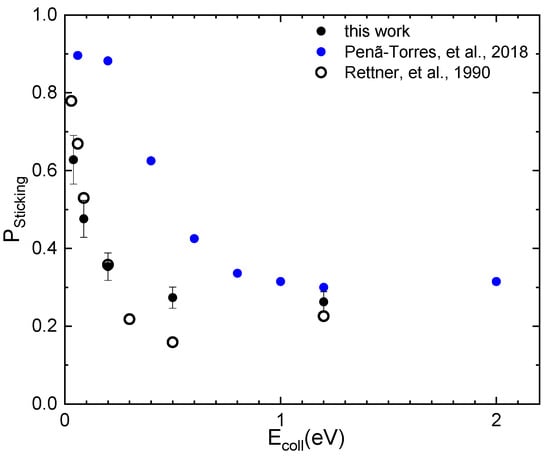
Figure 4.
Sticking probability (PSticking) for N2 interacting in normal direction on W(100) as a function of collision energy in comparison with results of latest calculations [7] and of experiments [10]. TS = 300 K.
To settle the matter, an accurate analysis of the trajectories has been carried out to highlight the energy exchanges occurring between the internal degrees of the molecule and the surface. The analysis revealed that, for low collision energies and with the molecule in the lowest internal state, the interaction is strong mainly when the molecules approach the surface by moving with a cartwheel-type internal motion. In this case, the rotational excitation mechanism, being the most efficient, favors the trapping that, in turn, can promote bounces on the surface, also contributing to the desynchronization of the motion of the two N atoms in the molecule. This behavior has already been observed in the interaction of nitrogen molecules with a graphite surface [21] and related to the surface phonons. In addition, as observed in previous studies for the interaction of molecules with graphite and silica surfaces [20,21,28], the molecule approaching the surface is first slightly accelerated and then undergoes a strong deceleration while transferring energy to the rotational motion. Consequently, a strong increment of the rotational number occurs to which the energy coming from the phonons of the surface also contributes, albeit with a smaller amount. The occurrence of such a trapping mechanism has already been advanced in Ref. [29] to explain the adsorption of hydrogen molecules on a cold Cu surface. Therefore, in light of the above, the obtained results for PSticking can be explained in terms of a dynamic steering mechanism. In our picture of interaction dynamics, the rotational excitation counteracts the steering that favors the molecule path towards a direct dissociation and molecules remain trapped on the surface. In the past, the role of rotational effect in the adsorption of molecules on metals has been observed in the MB experiments [30,31] and studied in Refs. [32,33]. In addition to the dynamic steering, the results for PSticking, for low collision energies, can also be ascribed to either the physisorption well appearing in the assumed PES and having a depth greater than or, at most, of the same order (see Section 2.2) as Ecoll, which prevents the molecule from being immediately scattered in gas-phase, and/or to the existence of a barrier that can be higher than the collisional energy. The dynamic mechanism just described can be observed in Figure 5, which shows one of the trajectories ending with molecular adsorption for Ecoll = 0.04 eV.
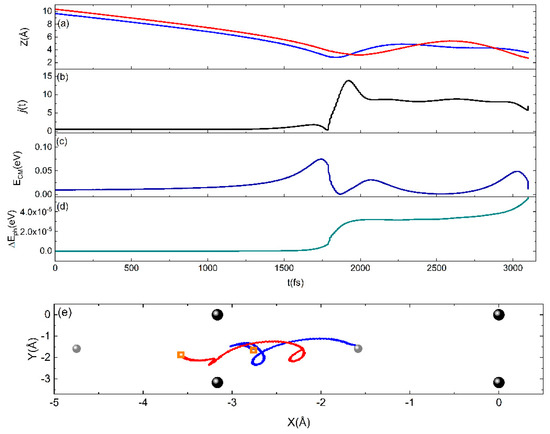
Figure 5.
A typical sticking trajectory for Ecoll = 0.04 eV. Time evolution of (a) the coordinate of the two atoms (lines blue and red) in the N2 molecule, along the Z normal direction, which ends with the adsorption; (b) the rotational state j; (c) the center of mass translational energy (ECM); (d) the energy exchanged with the surface phonons; and (e) the diffusion motion in the X–Y plane, of assumed reference frame, of the trajectory of two atoms (blue and red lines) in the N2 molecule (orange squares indicate the starting point of each trajectory). The W atoms on the first (big black spheres) and second (small grey spheres) layers are also reported.
Thus, the ILJ potential used to treat the long-range interactions exploited by a state-to-state model, including the coupling with the surface phonon motion, is able to highlight molecular excitation governing the process dynamics and, with respect to previous calculations, provides results much closer to those resulting from experimental measurements.
The role of coupling of the N2 molecule with phonons is further extolled by considering, at a selected collision energy, the dependence of the trapping probability (Ptrapping) on TS. Ptrapping represents the probability for a molecule to become trapped on the surface or eventually, after a while spent bouncing on the latter, to be scattered in the gas-phase. We did this, and in Figure 6, we report the results of our study in comparison with those reported in Ref. [10], obtained by adopting a hard cube model with parameters chosen to provide results consistent with experimental measurements. Looking at Figure 6, we can conclude that, even in this case, there is a very good agreement, considering the error of our results and the approximations and parametrization of Ref. [10] to obtain the line in the plot based on experimental measurements.
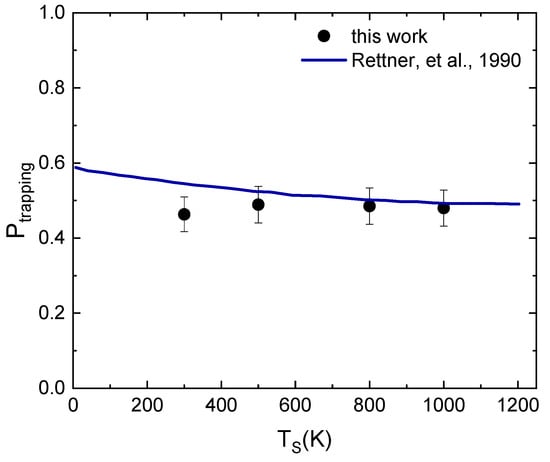
Figure 6.
Trapping probability (Ptrapping) for N2 interacting on W(100) as a function of surface temperature (TS) at Ecoll = 0.088 eV in comparison with results obtained in Ref. [10].
The plot in Figure 6 also suggests a weak dependence on the surface temperature of Ptrapping, which appears to be more strongly correlated to the collision energy of the molecule and the energy exchanges occurring during the interaction. Such almost non-dependence on the surface temperature of Ptrapping can perhaps be attributed to the mass mismatch between the incident species and the substrate.
3. Methods
The computational setup, used to describe the collisions of atomic and molecular nitrogen with W(100) surface, is based on a state-to-state semiclassical collision method, derived and completely exposed in Ref. [19], which has been used in the past for the description of surface processes; therefore, it has already been extensively described elsewhere [34] and more recently in Ref. [20]. For this reason, in the following, only a brief summary of the most important and specific features will be provided.
The method consists of three different operational steps: (1) determination of 3D surface model structure and corresponding surface phonon dynamics; (2) building up of PES for the reaction under study; and (3) propagation of a sufficiently large number of classical trajectories in the adopted framework [19,20].
The 3D surface model, consisting of 255 atoms disposed on six layers, is the one defined in Ref. [34] for which we determined the phonon dynamics by solving the time-dependent Schrödinger equations of motion under the harmonic oscillator approximation—that is, assuming that a set of M = 3Nat − 6 independent harmonic oscillators are perturbed by a linear force exerted between the species approaching the surface from the gas-phase and the solid substrate [19]. Details on the bulk potential and the density of phonon states can be found in Ref. [34].
The PES has been built by adding to the short-range potential (described in Section 2.2) the long-range interactions according to the ILJ potential [17] given by
with
The first term of Equation (7) describes the separation distance dependence of the size repulsion, while the second one is that of the dispersion attraction. The parameters ε and , which represent the potential well depth and its location, respectively, for each considered pair, define at each R the strength of both terms in Equation (7). β is an additional parameter depending on the “hardness” of the two partners. For the neutral–neutral interactions, as in the present ones, m = 6 must be used: in these cases, the ILJ function provides for each interacting pair an asymptotic dispersion attraction contribution associated with a partial coefficient, defined as. The combination of all partial coefficients determines the value of the global atom/molecule–surface attraction coefficient , which controls the capture efficiency and the formation of the precursor state of many gas–surface elementary processes. The C3 coefficient is obtained through the well-known relationship (see Ref. [21] and references therein) that binds it to the coefficient:
The dynamics of the N2 molecule interacting with W(100) surface is followed by solving self-consistently the relevant 3D Hamilton’s equations of motion with those of the lattice phonons, under given initial conditions:
is the momentum of atom i having mass mi and H is the Hamiltonian for a diatomic molecule impinging on a surface, given by
with being the N2 intramolecular interaction potential and the effective potential of mean field type, depending on time and surface temperature, formulated as
where is the “static” interaction potential, given by Equation (1), between the atoms in the gas-phase and the lattice atoms in their equilibrium positions. is the linear driving force exerted on each k-th phonon mode Qk. are the “phonon excitation strengths” given in terms of the Fourier components of the external force:
with , being the frequency of the k-th phonon mode.is the energy exchanged between the impinging molecule and the solid substrate due to the phonon creation and phonon annihilation processes. The energy exchanged with the phonons can be obtained directly from the transition probabilities for the excitation/deexcitation phonon processes [19].
The rotational and vibrational states of N2 molecules, assumed as a Morse oscillator [35], were analyzed in terms of the action-angle variables using the semiclassical quantization rules [36]. Therefore, the roto-vibrational states were determined as continuous variables, as we are unable to predict some features caused by quantum effects and selection rules.
In this computational framework, we took the nitrogen molecule impinging along the normal to the surface planes starting from a distance of 10 Å and with collision energy in the range [0.04–1.2] eV. The starting distance was chosen as a compromise between reasonable calculation times for trajectory propagation and the need to consider the effects of long-range interactions. For each Ecoll value, we propagated 30,000 trajectories, while TS was fixed to 300 K. The initial coordinates of impinging species were randomly generated at the beginning of each trajectory, in an aiming area coinciding with the unit cell. The molecule CM impinges with polar angle θ = 0°, defining the selected normal approach, and azimuthal angle (ϕ) of the molecular axis was randomly chosen at the beginning of each trajectory. We can describe and follow the different elementary surface processes occurring when the N2 molecule impinges on the surface, as the assumed PES is reactive. The impact of a molecule on a surface can give rise to scattering (elastic or inelastic), adsorption of both atoms, desorption of just one atom with the other adsorbed on the surface or desorption of both atoms as a molecule or separated.
The criteria adopted in the analysis of trajectories, leading to the assignment of a given trajectory to one of the listed reaction channels, are similar to those used in Ref. [28]. So, molecular scattering occurs if, after the interaction with the W(100) surface, the intramolecular distance (r) is lower than the distance of dissociation for the N2 molecule and, at the same time, the distance between molecule CM and the surface is larger than 8.0 Å. On the contrary, if after the interaction with the tungsten surface the distance between N2 CM and the surface is comparable to or smaller than the distance (≈5.0 Å) at which the potential approaches its asymptotic value, and r is lower than the dissociation distance, the molecule is considered trapped in the physisorption well. Further, a second “energy” criterion can be followed according to which the molecule is adsorbed when the energy available to escape from the potential well is less than the effective potential, accounting for the interaction with the surface phonons.
The trapped molecule can be subject to a steering process that can produce one of the processes listed above.
4. Conclusions
This study presents a new PES controlling the collision dynamics of N2 molecules impinging on the W(100) surface. The long-range interaction components, defining the asymptotic behavior of the PES, have been properly characterized and represented by an ILJ function. MD simulations, performed with a semiclassical collisional model, have been exploited to characterize basic details of the collision dynamics, including its dependence on collision energy, ranging from sub-thermal up to hyper-thermal conditions. In particular, we focused on the sticking probability, with its dependence on the collision energy; on the trapping probability, with its dependence on the surface temperature for a selected Ecoll; and on their comparison with the corresponding experimental determinations. This study proves that the asymptotic part of the interaction plays a crucial role in the molecular interaction dynamics since defining all relevant features of the precursor state controls the dynamics of basic phenomena occurring at the gas–surface interphase. Furthermore, the description adopted here for long-range forces is found to be more suitable than that obtained by using DFT methods with appropriate corrections.
Author Contributions
Conceptualization, methodology, formal analysis, investigation, writing—original draft preparation, writing—review and editing, M.R.; conceptualization, methodology, investigation, writing—original draft preparation, writing—review and editing, F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dɡbrowski, A. Adsorption-from theory to practice. Adv. Colloid Interface Sci. 2001, 93, 135–224. [Google Scholar] [CrossRef]
- Ptushinskiĭ, Y.G. Low-temperature adsorption of gases on metal surfaces. Low Temp. Phys. 2004, 30, 1–26. [Google Scholar] [CrossRef]
- Groß, A. Adsorption on Surfaces in Theoretical Surface Science—A Microscopic Perspective; Springer: Berlin/Heidelberg, Germany, 2009; pp. 101–160. [Google Scholar]
- Hammer, B.; Norskov, J.K. Theoretical Surface Science and Catalysis—Calculations and Concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar]
- Gao, W.; Chen, Y.; Li, B.; Liu, S.-P.; Liu, X.; Jiang, Q. Determining the adsorption energies of small molecules with the intrinsic properties of adsorbates and substrates. Nat. Commun. 2020, 11, 1196. [Google Scholar] [CrossRef]
- Allouche, A. First principles calculations on nitrogen reactivity on tungsten surfaces. J. Phys. Condens. Matter 2016, 28, 015001. [Google Scholar] [CrossRef]
- Penã-Torres, A.; Busnengo, H.F.; Juaristi, J.I.; Larregaray, P.; Crespos, C. Dynamics of N2 sticking on W(100): The decisive role of van der Waals interactions. Phys. Chem. Chem. Phys. 2018, 20, 19326–19331. [Google Scholar] [CrossRef]
- Peña-Torres, A.; Busnengo, H.F.; Juaristi, J.I.; Larregaray, P.; Crespos, C. Energy Dissipation Effects on the Adsorption Dynamics of N2 on W(100). J. Phys. Chem. C 2019, 123, 2900–2910. [Google Scholar] [CrossRef]
- Rettner, C.T.; Stein, H.; Schweizer, E.K. Effect of collision energy and incidence angle on the precursor-mediated dissociative chemisorption of N2 on W(100). J. Chem. Phys. 1988, 89, 3337–3341. [Google Scholar] [CrossRef]
- Rettner, C.T.; Schweizer, E.K.; Stein, H. Dynamics of the chemisorption of N2 on W(100): Precursor-mediated and activated dissociation. J. Chem. Phys. 1990, 93, 1442–1454. [Google Scholar] [CrossRef]
- Rettner, C.T.; Schweizer, E.K.; Stein, H.; Auerbach, D.J. Role of Surface Temperature in the Precursor-Mediated Dissociative Chemisorption of N2 on W(100). Phys. Rev. Lett. 1988, 61, 986–989. [Google Scholar] [CrossRef]
- Auerbach, D.J.; Pfnur, H.E.; Rettner, C.T.; Schlaegel, J.E.; Lee, J.; Madix, R.J. Kinetic energy and angular dependence of activated dissociative adsorption of N2 on W(110): Observed insensitivity to incidence angle. J. Chem. Phys. 1984, 81, 2515–2516. [Google Scholar] [CrossRef]
- Pfnur, H.E.; Rettner, C.T.; Lee, J.; Madix, R.J.; Auerbach, D.J. Dynamics of the activated dissociative chemisorption of N2 on W(110): A molecular beam study. J. Chem. Phys. 1986, 85, 7452–7466. [Google Scholar] [CrossRef]
- Ertl, G.; Thiele, N. XPS studies with ammonia synthesis catalysts. Appl. Surf. Sci. 1979, 3, 99–112. [Google Scholar] [CrossRef]
- Volpilhac, G.; Salin, A. Dissociative adsorption of N2 on the W(100) surface. Surf. Sci. 2004, 556, 129–144. [Google Scholar] [CrossRef]
- Hafner, J.; Kresse, G. The Vienna ab-initio simulation program VASP: An efficient and versatile tool for studying the structural, dynamic and electronic properties of materials. In Properties of Complex Inorganic Solids; Gonis, A., Meike, A., Turchi, P.E.A., Eds.; Springer: Boston, MA, USA, 1997; pp. 69–82. [Google Scholar] [CrossRef]
- Pirani, F.; Brizi, S.; Roncaratti, L.F.; Casavecchia, P.; Cappelletti, D.; Vecchiocattivi, F. Beyond the Lennard-Jones model: A simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations. Phys. Chem. Chem. Phys. 2008, 10, 5489–5503. [Google Scholar] [CrossRef] [PubMed]
- Rutigliano, M.; Pirani, F. The role of long-range interactions on the selectivity of gaseous molecule-surface scattering. Chem. Phys. Lett. 2021, 770, 138444. [Google Scholar] [CrossRef]
- Billing, G.D. Dynamics of Molecule Surface Interactions, 1st ed.; John-Wiley & Sons: New York, NY, USA, 2000; pp. 112–141. [Google Scholar]
- Rutigliano, M.; Pirani, F. Scattering of N2 Molecules from Silica Surfaces: Effect of Polymorph and Surface Temperature. Molecules 2022, 27, 7445. [Google Scholar] [CrossRef]
- Rutigliano, M.; Pirani, F. Selectivity and Stereodynamics Effects in the Scattering of Nitrogen Molecules from a Graphite Surface. J. Phys. Chem. C 2020, 124, 10470–10482. [Google Scholar] [CrossRef]
- Cambi, R.; Cappelletti, D.; Liuti, G.; Pirani, F. Generalized correlations in terms of polarizability for van der Waals interaction potential parameter calculations. J. Chem. Phys. 1991, 95, 1852–1861. [Google Scholar] [CrossRef]
- Vidali, G.; Ihm, G.; Kim, H.-Y.; Cole, M.W. Potentials of physical adsorption. Surf. Scie. Reports 1991, 12, 133–181. [Google Scholar] [CrossRef]
- Olney, T.N.; Cann, N.M.; Cooper, G.; Brion, C.E. Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum-rules. Chem. Phys. 1997, 223, 59–98. [Google Scholar] [CrossRef]
- Werner, H.-J.; Meyer, W. Finite perturbation calculations for the static dipole polarizabilities of the first-row atoms. Phys. Rev. A 1976, 13, 13–16. [Google Scholar] [CrossRef]
- Ibarguen, C.; Larregaray, P.; Peña-Torres, A.; Crespos, C. Inelastic Scattering of N2 off W(001): Reconciling Experiment and Theory at Low Collision Energies. J. Phys. Chem. C 2018, 122, 28856–28861. [Google Scholar] [CrossRef]
- Ibarguen Becerra, C.; Crespos, C.; Galparsoro, O.; Larregaray, P. Atomic scattering of H and N on W(100): Effect of lattice vibration and electronic excitations on the dynamics. Surf. Sci. 2020, 701, 121678. [Google Scholar] [CrossRef]
- Rutigliano, M.; Pirani, F. Surface processes involving nitrogen molecules and atoms on silica surface at low temperature: The role of energy exchanges. Plasma Sources Sci. Technol. 2022, 31, 094006. [Google Scholar] [CrossRef]
- Andersson, S.; Harris, J. Trapping of molecular hydrogen at surfaces via translational-rotational energy conversion. Phys. Rev. B 1983, 27, 9–14. [Google Scholar] [CrossRef]
- Beutl, M.; Rendulic, K.D.; Castro, G.R. Does the rotational state of a molecule influence trapping in a precursor? An investigation of N2/W(100),CO/FeSi(100) and O2/Ni(111). Surf. Sci. 1997, 385, 97–106. [Google Scholar] [CrossRef]
- Beutl, M.; Riedler, M.; Rendulic, K.D. Strong rotational effects in the adsorption dynamics of H2/Pd(111): Evidence for dynamical steering. Chem. Phys. Lett. 1995, 247, 249–252. [Google Scholar] [CrossRef]
- Kay, M.; Darling, G.R.; Holloway, S.; White, J.A.; Bird, D.M. Steering effects in non-activated adsorption. Chem. Phys. Lett. 1995, 245, 311–318. [Google Scholar] [CrossRef]
- Gross, A.; Wilke, S.; Scheffler, M. Six-dimensional quantum dynamics of adsorption and desorption of H2 at Pd(100) no need for a molecular precursor adsorption state. Surf. Sci. 1996, 357–358, 614–618. [Google Scholar] [CrossRef][Green Version]
- Rutigliano, M.; Cacciatore, M. Eley–Rideal recombination of hydrogen atoms on a tungsten surface. Phys. Chem. Chem. Phys. 2011, 13, 7475–7484. [Google Scholar] [CrossRef] [PubMed]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure: IV. In Constants of Diatomic Molecules; Van Nostrand Reinhold Company: New York, NY, USA, 1979; pp. 412–413. [Google Scholar]
- Muckerman, J.T. Monte Carlo Calculations of Energy Partitioning and Isotope Effects in Reactions of Fluorine Atoms with H2, HD, and D2. J. Chem. Phys. 1971, 54, 1155–1164. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).