Engineering the Electronic Structure towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-Doping: A First-Principles Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Computational Methods
2.2. Crystal Structure and Formation Energy
2.3. Electronic Structure
2.4. Effective Masses of Charge Carriers
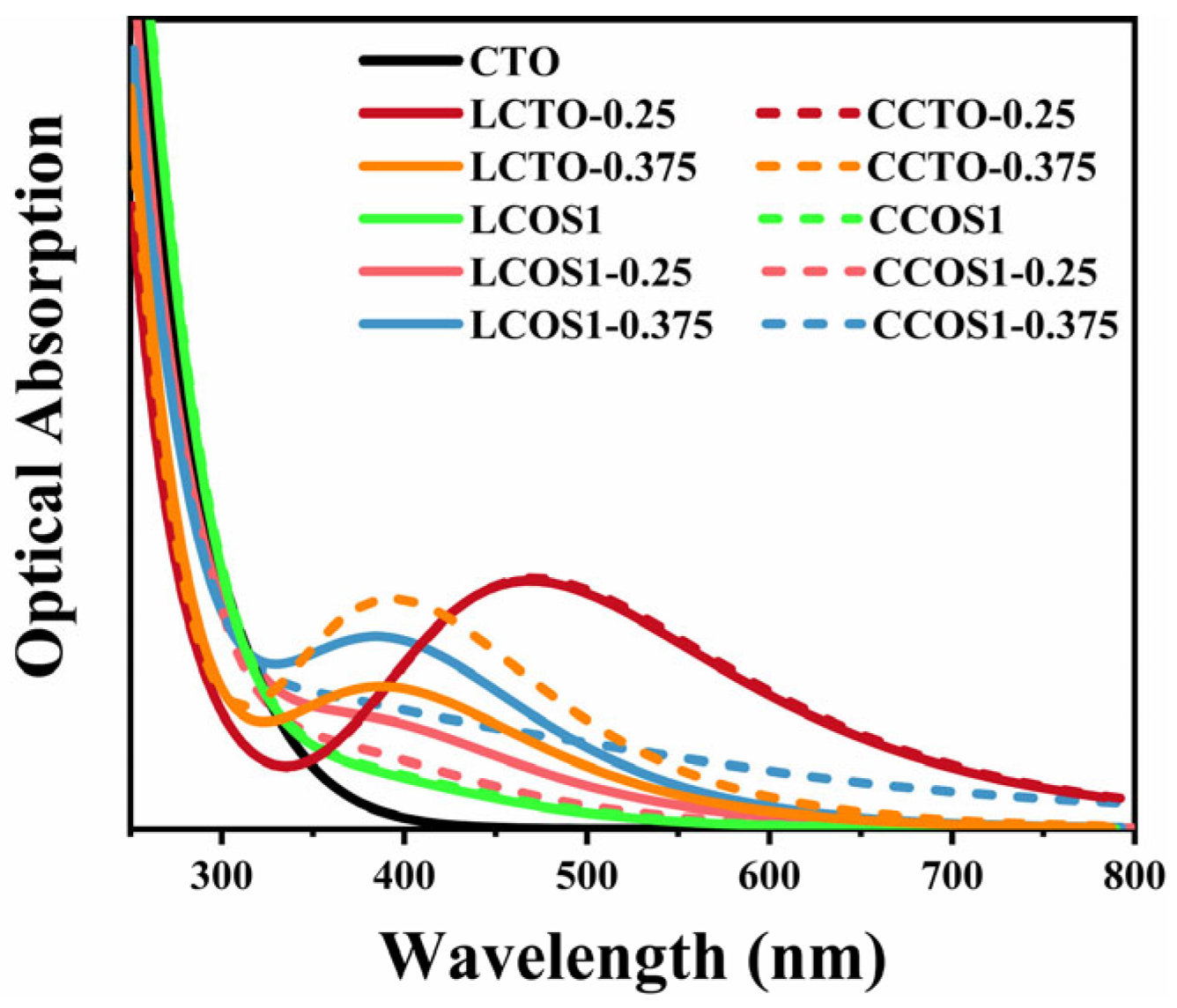
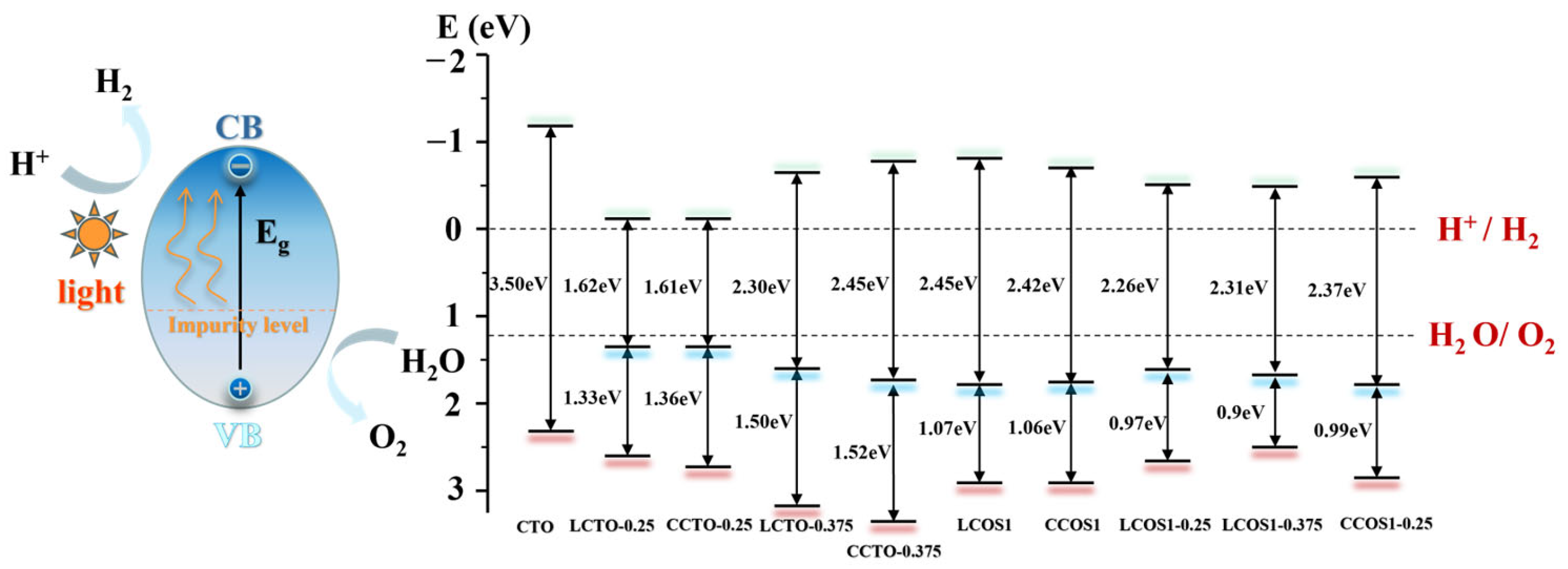
2.5. Optical Properties and Water Redox Potential
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Cao, S.; Piao, L.; Chen, X. Emerging Photocatalysts for Hydrogen Evolution. Trends Chem. 2020, 2, 57–70. [Google Scholar] [CrossRef]
- Phang, S.J.; Wong, V.L.; Tan, L.L.; Chai, S.P. Recent advances in homojunction-based photocatalysis for sustainable environmental remediation and clean energy generation. Appl. Mater. Today 2020, 20, 100741. [Google Scholar] [CrossRef]
- Chen, X.B.; Shen, S.H.; Guo, L.J.; Mao, S.S. Semiconductor-based Photocatalytic Hydrogen Generation. Chem. Rev. 2010, 110, 6503–6570. [Google Scholar] [CrossRef] [PubMed]
- Bafaqeer, A.; Tahir, M.; Khan, A.A.; Saidina Amin, N.A. Indirect Z-Scheme Assembly of 2D ZnV2O6/RGO/g-C3N4 Nanosheets with RGO/pCN as Solid-State Electron Mediators toward Visible-Light-Enhanced CO2 Reduction. Ind. Eng. Chem. Res. 2019, 58, 612–8624. [Google Scholar] [CrossRef]
- Lozano-Sánchez, L.M.; Lee, S.W.; Sekino, T. Practical microwave-induced hydrothermal synthesis of rectangular prism-like CaTiO3. Cryst. Eng. Comm. 2013, 15, 2359–2362. [Google Scholar] [CrossRef]
- Han, C.; Liu, J.; Yang, W.; Wu, Q.; Yang, H.; Xue, X. Enhancement of photocatalytic activity of CaTiO3 through HNO3 acidification. J. Photochem. Photobiol. A Chem. 2016, 322, 1–9. [Google Scholar] [CrossRef]
- Manjusha, P.; Bonamali, P. A review on CaTiO3 photocatalyst: Activity enhancement methods and photocatalytic applications. Powder Technol. 2021, 388, 274–304. [Google Scholar]
- Wang, Y.; Wang, J.; Lian, W.; Liu, Y. Insight into the enhanced photocatalytic activity of Mo and P codoped SrTiO3 from first-principles prediction. RSC Adv. 2020, 10, 40117–40126. [Google Scholar] [CrossRef] [PubMed]
- Goktas, A.; Aslan, F.; Mutlu, I.H. Effect of preparation technique on the selected characteristics of Zn1−xCoxO nanocrystalline thin films deposited by sol–gel and magnetron sputtering. J. Alloys Compd. 2014, 615, 765–778. [Google Scholar] [CrossRef]
- Goktas, S.; Goktas, A. A comparative study on recent progress in efficient ZnO based nanocomposite and heterojunction photocatalysts: A review. J. Alloys Compd. 2021, 863, 158734. [Google Scholar] [CrossRef]
- Lv, M.; Sun, X.; Wei, S.; Shen, C.; Mi, Y.; Xu, X. Ultrathin lanthanum tantalate perovskite nanosheets modified by nitrogen doping for efficient photocatalytic water splitting. ACS Nano 2017, 11, 11441–11448. [Google Scholar] [CrossRef]
- Goktas, A.; Modanlı, S.; Tumbul, A.; Kilic, A. Facile synthesis and characterization of ZnO, ZnO:Co, and ZnO/ZnO:Co nano rod-like homojunction thin films: Role of crystallite/grain size and microstrain in photocatalytic performance. J. Alloys Compd. 2022, 893, 162334. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, X.; Fan, X.; Glinka, Y.D.; Feng, X.; He, Z.; Wei, Z.; Chen, R. Interfacial-Field-Induced Increase of the Structural Phase Transition Temperature in Organic-Inorganic Perovskite Crystals Coated with ZnO Nanoshell. Adv. Mater. Interfaces. 2018, 5, 1800301. [Google Scholar]
- Anderson, T.R.; Hawkins, E.; Jones, P.D. CO2, the greenhouse effect and global warming: From the pioneering work of Arrhenius and Callendar to today’s Earth system models. Endeavour 2016, 40, 178–187. [Google Scholar] [CrossRef]
- Si, C.; Zhang, W.; Lu, Q.; Guo, E.; Yang, Z.; Chen, J.; He, X.; Luo, J. Recent Advances in Perovskite Catalysts for Efficient Overall Water Splitting. Catalysts 2022, 12, 601. [Google Scholar] [CrossRef]
- Nunocha, P.; Kaewpanha, M.; Bongkarn, T.; Eiad-Ua, A.; Suriwong, T. Effect of Nb doping on the structural, optical, and photocatalytic properties of SrTiO3 nanopowder synthesized by sol-gel auto combustion technique. J. Asian Ceram. Soc. 2022, 10, 583–596. [Google Scholar] [CrossRef]
- Lozano-Sánchez, L.M.; Méndez-Medrano, M.G.; Colbeau-Justin, C.; Rodríguez-López, J.L.; Hernández-Uresti, D.B.; Obregón, S. Long-lived photoinduced charge-carriers in Er3+ doped CaTiO3 for photocatalytic H2 production under UV irradiation. Catal. Commun. 2016, 84, 36–39. [Google Scholar] [CrossRef]
- Gao, Q.; Meng, J.; Yang, Y.; Lin, Q.; Lu, Y.; Wei, X.; Li, J.; Han, G.; Zhang, Z. Zirconium doping in calcium titanate perovskite oxides with surface nano step structure for promoting photocatalytic hydrogen evolution. Appl. Surf. Sci. 2021, 542, 148544. [Google Scholar] [CrossRef]
- Bi, Y.; Ehsan, M.F.; Huang, Y.; Jin, J.; He, T. Synthesis of Cr-doped SrTiO3 photocatalyst and its application in visible-light-driven transformation of CO2 into CH4. J. CO2 Util. 2015, 12, 43–48. [Google Scholar] [CrossRef]
- Wang, J.; Yin, S.; Komatsu, M.; Zhang, Q.; Saito, F.; Sato, T. Mechanochemical synthesis and photocatalytic activity of nitrogen doped SrTiO3. J. Ceram. Soc. Jpn. 2004, 5, S1408. [Google Scholar]
- Ran, J.; Wang, T.; Zhang, J.; Liu, Y.; Xu, C.; Xi, S.; Gao, D. Modulation of Electronics of Oxide Perovskites by Sulfur Doping for Electrocatalysis in Rechargeable Zn–Air Batteries. Chem. Mater. 2020, 32, 3439–3446. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, A.; Krishnan, V. Perovskite Oxide Based Materials for Energy and Environment-Oriented Photocatalysis. ACS Catal. 2020, 10, 10253–10315. [Google Scholar] [CrossRef]
- Yang, K.; Dai, Y.; Huang, B. First-principles characterization of ferromagnetism in N-doped SrTiO3 and BaTiO3. Appl. Phys. Lett. 2012, 100, 062409. [Google Scholar] [CrossRef]
- Attou, L.; Al-Shami, A.; Boujemaâ, J.; Mounkachi, O.; Ez-Zahraouy, H. Predicting the structural, optoelectronic, dynamical stability and transport properties of Boron-doped CaTiO3: DFT based study. Phys. Scripta. 2022, 97, 115808. [Google Scholar] [CrossRef]
- Bantawal, H.; Shenoy, U.S.; Bhat, D.K. Vanadium doped CaTiO3 cuboids: Role of vanadium in improving the photocatalytic activity. Nanoscale Adv. 2021, 3, 5301–5311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, G.; Li, Y.; Teng, Y. Electronic structure and photocatalytic properties of copper-doped CaTiO3. Int. J. Hydrogen Energy 2010, 35, 2713–2716. [Google Scholar] [CrossRef]
- Sun, H.; Dong, C.; Huang, A.; Zhan, H.; Wang, G.; Liu, W.; Ma, B.; Wang, W. Transition Metal Doping Induces Ti3+ to Promote the Performance of SrTiO3@TiO2 Visible Light Photocatalytic Reduction of CO2 to Prepare C1 Product. Chem. Eur. J. 2022, 28, e202200019. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.X.; Sang, L.X.; Wang, J.Z.; Yang, Q.H.; Sun, Y.H.; Li, Z.Y.; Zeng, S.L. Photocatalytic activity of perovskite oxides ABO3 and the factors of influence. J. Tianjin Univ. 2001, 34, 229–231. [Google Scholar]
- Anzai, A.; Fujiwara, K.; Yamamoto, A.; Yoshida, H. Platinum-loaded lanthanum-doped calcium titanate photocatalysts prepared by a flux method for photocatalytic steam reforming of methane. Catal. Today. 2020, 352, 1–9. [Google Scholar] [CrossRef]
- Martha, S.; Chandra Sahoo, P.; Parida, K.M. An overview on visible light responsive metal oxide based photocatalysts for hydrogen energy production. RSC Adv. 2015, 5, 61535–61553. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, Y.; Jing, Y.; Yao, Y. New insights into assessing the favorable co-doping dopants with various co-doped cases for the band gap engineering of SrTiO3. Int. J. Hydrogen Energy 2015, 40, 1343–1351. [Google Scholar] [CrossRef]
- Goktas, A. High-quality solution-based Co and Cu co-doped ZnO nanocrystalline thin films: Comparison of the effects of air and argon annealing environments. J. Alloys Compd. 2018, 735, 2038–2045. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhou, W.; Wang, C.; Zhou, L.L.; Wu, P. Electronic structure and optical properties of SrTiO3 codoped by W/Mo on different cationic sites with C/N from hybrid functional calculations. Comput. Mater. Sci. 2018, 146, 150–157. [Google Scholar] [CrossRef]
- Shi, W.J.; Xiong, S.J. Ab initio study on band-gap narrowing in SrTiO3 with Nb–C–Nb cooping. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 1541–1545. [Google Scholar] [CrossRef]
- Wang, Q.; Hisatomi, T.; Jia, Q.; Tokudome, H.; Zhong, M.; Wang, C.; Pan, Z.; Takata, T.; Nakabayashi, M.; Shibata, N.; et al. Scalable water splitting on particulate photocatalyst sheets with a solar-to-hydrogen energy conversion efficiency exceeding 1%. Nat. Mater. 2016, 15, 611–615. [Google Scholar] [CrossRef]
- Jiang, J.; Jia, Y.; Wang, Y.; Chong, R.; Xu, L.; Liu, X. Insight into efficient photocatalytic elimination of tetracycline over SrTiO3(La,Cr) under visible-light irradiation: The relationship of doping and performance. Appl. Surf. Sci. 2019, 486, 93–101. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; He, X.; Xu, J. Electronic structure and photocatalytic properties of Ag–La codoped CaTiO3. J. Alloys Compd. 2012, 516, 91–95. [Google Scholar] [CrossRef]
- Ohno, T.; Tsubota, T.; Nakamura, Y.; Sayama, K. Preparation of S, C cation-codoped SrTiO3 and its photocatalytic activity under visible light. Appl. Catal. A-Gen. 2005, 288, 74–79. [Google Scholar] [CrossRef]
- Niu, M.; Cheng, D.; Cao, D. Enhanced photoelectrochemical performance of anatase TiO2 by metal-assisted SeO coupling for water splitting. Int. J. Hydrogen Energy 2013, 38, 1251–1257. [Google Scholar] [CrossRef]
- Liu, H.F. Effect of nitrogen and carbon doping on electronic properties of SrTiO3. Solid State Commun. 2012, 152, 2063–2065. [Google Scholar] [CrossRef]
- Fo, Y.; Ma, Y.; Dong, H.; Zhou, X. Tuning the electronic structure of BaTiO3 for an enhanced photocatalytic performance using cation–anion codoping: A first-principles study. New J. Chem. 2021, 45, 8228–8239. [Google Scholar] [CrossRef]
- Sulaeman, U.; Yin, S.; Sato, T. Synthesis of La/N Co-Doped SrTiO3 Using Polymerized Complex Method for Visible Light Photocatalysis. Adv. Nanoparticles 2013, 2, 6–10. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, H.; Inoue, T.; Yao, Q. Highly active SrTiO3 for visible light photocatalysis: A first-principles prediction. Solid State Commun. 2014, 181, 5–8. [Google Scholar] [CrossRef]
- Gomathi Devi, L.; Anitha, B.G. Effective band gap engineering by the incorporation of Ce, N and S dopant ions into the SrTiO3 lattice: Exploration of photocatalytic activity under UV/solar light. J. Sol Gel Sci. Technol. 2020, 94, 50–66. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Wang, Z.; Zhang, Z. Homogeneous and heterogeneous reaction mechanisms and kinetics of mercury oxidation in coal-fired flue gas with bromine addition. Proc. Combust. Inst. 2017, 36, 4039–4049. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, N.; Xu, S. Towards high visible light photocatalytic activity in rare earth and N co-doped SrTiO3: A first principles evaluation and prediction. RSC Adv. 2017, 7, 16282–16289. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Wang, Y.; Zhang, X.; Fan, Y.; Liu, Y.; Yi, Z. Role of P in improving V-doped SrTiO3 visible light photocatalytic activity for water splitting: A first-principles study. Int. J. Hydrogen Energy 2021, 46, 20492–20502. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Yang, H.; Han, C.; Xue, X. Photocatalytic activity of Fe-doped CaTiO3 under UV–visible light. J. Environ. Sci. 2014, 26, 1489–1495. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comp. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, M.; Li, Q.; Zhou, J.; Gao, J.; Zhu, Q.; Wang, Y. A DFT Study on Electronic and Optical Properties of La/Ce-Doped CaTiO3 Perovskite. In Proceedings of the 5th International Conference on Energy Storage and Intelligent Vehicles (ICEIV 2022), Online, 3–4 December 2022; Sun, F., Yang, Q., Dahlquist, E., Xiong, R., Eds.; Springer: Singapore, 2022; pp. 161–170. [Google Scholar]
- Ali, R.; Yashima, M. Space group and crystal structure of the Perovskite CaTiO3 from 296 to 1720K. J. Solid State Che. 2005, 178, 2867–2872. [Google Scholar] [CrossRef]
- Rizwan, M.; Usman, Z.; Shakil, M.; Gillani, S.S.A.; Azeem, S.; Jin, H.B.; Cao, C.B.; Mehmood, R.F.; Nabi, G.; Asghar, M.A. Electronic and optical behaviour of lanthanum doped CaTiO3 perovskite. Mater. Res. Express 2020, 7, 015920. [Google Scholar] [CrossRef]
- Yamanaka, T.; Hirai, N.; Komatsu, Y. Structure change of Ca1−xSrxTiO3 perovskite with composition and pressure. Am. Miner. 2002, 87, 1183–1189. [Google Scholar] [CrossRef]
- Yin, W.J.; Wei, S.H.; Al-Jassim, M.M. Double-hole-mediated coupling of dopants and its impact on band gap engineering in TiO2. Phys. Rev. Lett. 2011, 106, 066801. [Google Scholar] [CrossRef]
- Wu, M.C.; Chen, W.C.; Chan, S.H.; Su, W.F. The effect of strontium and barium doping on perovskite-structured energy materials for photovoltaic applications. Appl. Surf. Sci. 2018, 429, 9–15. [Google Scholar] [CrossRef]
- Zeba, I.; Bashir, N.; Ahmad, R.; Shakil, M.; Rizwan, M.; Rafique, M.; Rashid, F.; Gillani, S.S.A. Cubic to pseudo-cubic tetragonal phase transformation with lithium and beryllium doping in CaTiO3 and its impact on electronic and optical properties: A DFT approach. Bull. Mater. 2020, 43, 244. [Google Scholar] [CrossRef]
- Yang, P.-X.; Tai, B.; Wu, W.; Zhang, J.-M.; Wang, F.; Guan, S.; Guo, W.; Lu, Y.; Yang, S.A. Tailoring lanthanide doping in perovskite CaTiO3 for luminescence applications. Phys. Chem. Chem. Phys. 2017, 19, 16189–16197. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Meng, Q.; Huang, J.; Li, Q.; Yang, J. Band structure engineering of anatase TiO2 by metal-assisted P-O coupling. J. Chem. Phys. 2014, 140, 174705. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.M.; Wang, C.; Liu, Y.; Zhou, X. Hybrid density functional theory description of non-metal doping in perovskite BaTiO3 for visible-light photocatalysis. J. Solid State Chem. 2019, 280, 121018. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Weber, D.; Marisa, C.; Marcelo, A.; Renan, A.; Ariadne, C.; Marcio, D.; Gilmar, E.; Mário, G.; Elson, L.; Maria, F. Unraveling the relationship bet65ween bulk structure and exposed surfaces and its effect on the electronic structure and photoluminescent properties of Ba0.5Sr0.5TiO3: A joint experimental and theoretical approach. Mater. Res. Bull. 2021, 143, 111442. [Google Scholar]
- Shaheen, A.; Akhtar, S.; Abbas, S.M.A.; Abbas, S.M.G.; Arshad, M.I.; Batool, J.; Amin, N. First-principles evaluation of electronic and optical properties of (Mo, C) codoped BaHfO3 for applications in photocatalysis. J. Appl. Phys. 2018, 123, 161569. [Google Scholar]
- Park, H.; Syam Kumar, R.; Akande, A.; Sanvito, S.; El-Mellouhi, F. The rise of Nb-, Ta-, and Bi-based oxides/chalcogenides for photocatalytic applications. Int. J. Hydrogen Energy 2022, 47, 3358–3370. [Google Scholar] [CrossRef]
- Hautier, G.; Miglio, A.; Ceder, G.; Rignanese, G.M.; Gonze, X. Identification and design principles of low hole effective mass p-type transparent conducting oxides. Nat. Commun. 2013, 4, 2292. [Google Scholar] [CrossRef]
- Sergey, V.; François, L. Theory of enhancement of thermoelectric properties of materials with nanoinclusions. Phys. Rev. B 2008, 77, 214304. [Google Scholar]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
- Kumar, A.; Schuerings, C.; Kumar, S.; Kumar, A.; Krishnan, V. Perovskite-structured CaTiO3 coupled with g-C3N4 as a heterojunction photocatalyst for organic pollutant degradation. Beilstein J. Nanotechnol. 2018, 9, 671–685. [Google Scholar] [CrossRef]
- García-Mendoza, M.F.; Torres-Ricárdez, R.; Ramírez-Morales, E.; Álvarez-Ramirez, J.G.; Díaz-Flores, L.L.; del Ángel-Meraz, E.; Rojas-Blanco, L.; Pérez-Hernández, G. CaTiO3 perovskite synthesized by chemical route at low temperatures for application as a photocatalyst for the degradation of methylene blue. J. Mater. Sci. Mater. Electron. 2023, 34, 873. [Google Scholar] [CrossRef]
- Dong, W.; Song, B.; Meng, W.; Zhao, G.; Han, G. A simple solvothermal process to synthesize CaTiO3 microspheres and its photocatalytic properties. Appl. Surf. Sci. 2015, 349, 272–278. [Google Scholar] [CrossRef]
- Takata, T.; Pan, C.S.; Domen, K. Recent progress in oxynitride photocatalysts for visible-light-driven water splitting. Sci. Technol. Adv. Mater. 2015, 16, 033506. [Google Scholar] [CrossRef] [PubMed]
- Longo, E.; Orhan, E.; Pontes, F.M.; Pinheiro, C.D.; Leite, E.R.; Varela, J.A.; Pizani, P.S.; Boschi, T.M.; Lanciotti, F.; Beltrán, A.; et al. Photoluminescent properties and structural disorder. Phys. Rev. B 2004, 69, 125115. [Google Scholar] [CrossRef]
- Souza, I.A.; Gurgel, M.F.C.; Santos, L.P.S.; Góes, M.S.; Cava, S.; Cilense, M.; Rosa, I.L.V.; Paiva-Santos, C.O.; Longo, E. Theoretical and Experimental Study of Disordered Ba0.45Sr0.55TiO3 Photoluminescence at Room Temperature. Chem. Phys. 2006, 322, 343–348. [Google Scholar] [CrossRef]
- Ferri, E.A.V.; Sczancoski, J.C.; Cavalcante, L.S.; Paris, E.C.; Espinosa, J.W.M.; de Figueiredo, A.T.; Pizani, P.S.; Mastelaro, V.R.; Varela, J.A.; Longo, E. Photoluminescence Behavior in MgTiO3 Powders with Vacancy/Distorted Clusters and Octahedral Tilting. Mater. Chem. Phys. 2009, 117, 192–198. [Google Scholar] [CrossRef]
- Goktas, A.; Aslan, E.; Arslan, F.; Kilic, A. Characterization of multifunctional solution-processed Sn1−xZnxS nanostructured thin films for photosensitivity and photocatalytic applications. Opt. Mater. 2022, 133, 112984. [Google Scholar] [CrossRef]
- Blasse, G.; Schipper, W.; Hamelink, J.J. On the quenching of the luminescence of the trivalent cerium ion. Inorg. Chim. Acta. 1991, 189, 77–80. [Google Scholar] [CrossRef]
- Lee, J.H.; Do, J.Y.; Park, N.K.; Seo, M.W.; Ryu, H.J.; Hong, J.P.; Kim, Y.S.; Kim, S.K.; Kang, M. Cost-effective and dynamic carbon dioxide conversion into methane using a CaTiO3@Ni-Pt catalyst in a photo-thermal hybrid system. J. Photochem. Photobiol. A Chem. 2018, 364, 219–232. [Google Scholar] [CrossRef]
- Park, B.-G. Photoluminescence of Eu3+-doped CaTiO3 perovskites and their photocatalytic properties with a metal ion loading. Chem. Phys. Lett. 2019, 722, 44–49. [Google Scholar] [CrossRef]
- Qiu, B.; Yan, X.G.; Huang, W.Q.; Huang, G.F.; Jiao, C.; Zhan, S.Q.; Long, J.P.; Yang, Z.M.; Wan, Z.; Peng, P. The electronic and optical properties of X-doped SrTiO3 (X = Rh, Pd, Ag): A first-principles calculations. Int. J. Mod. Phys. B 2014, 28, 1450031. [Google Scholar] [CrossRef]

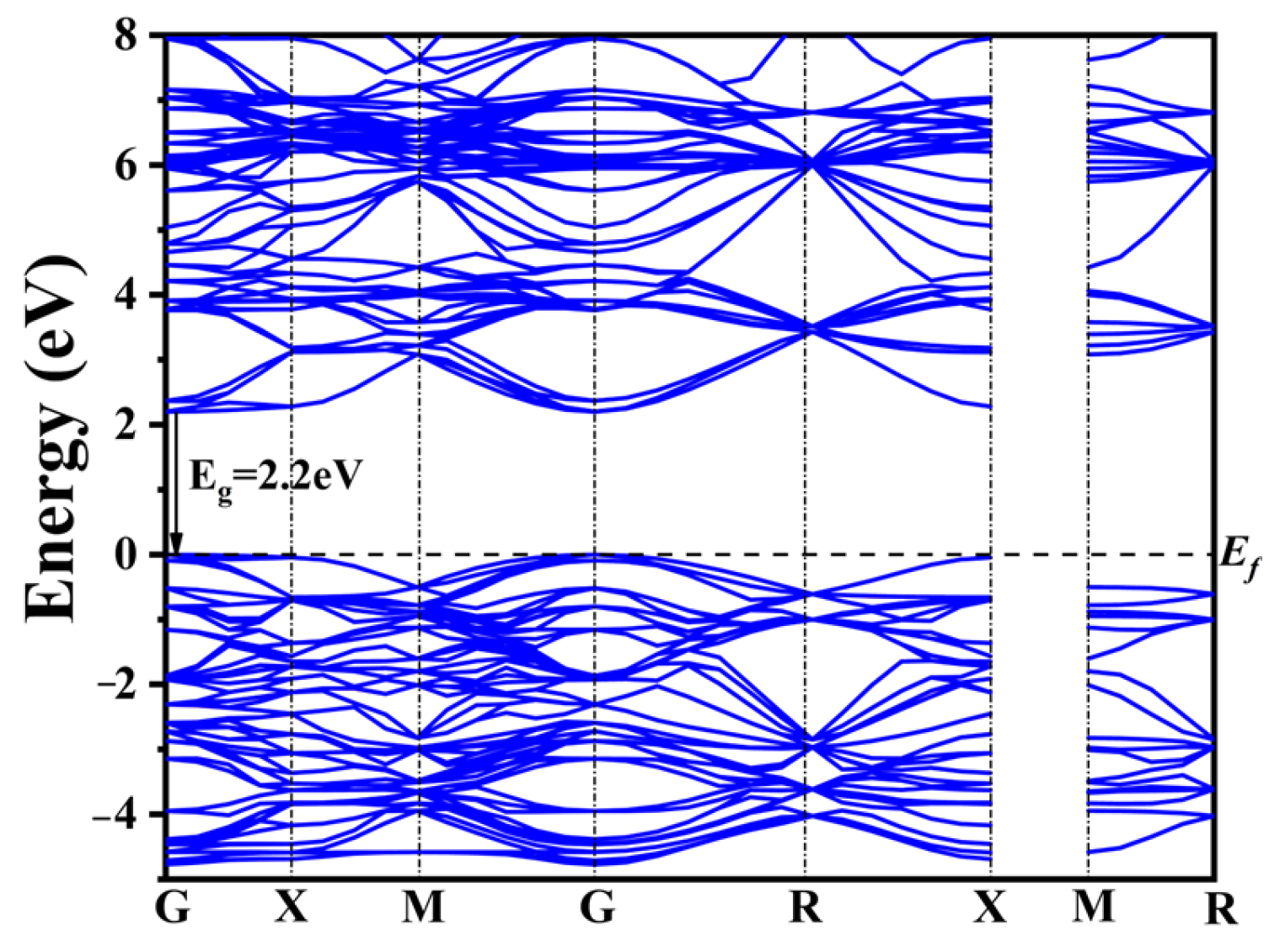
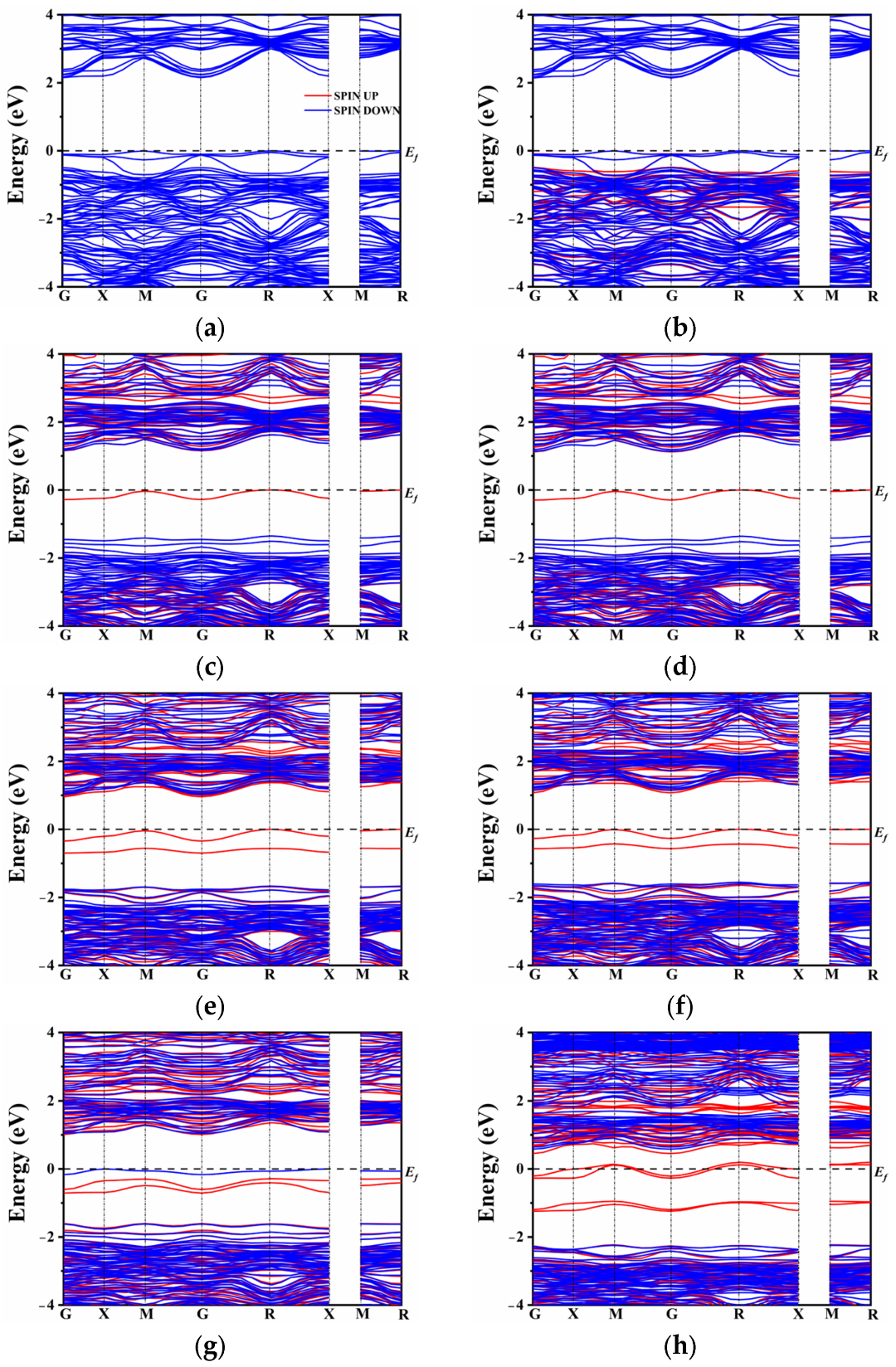
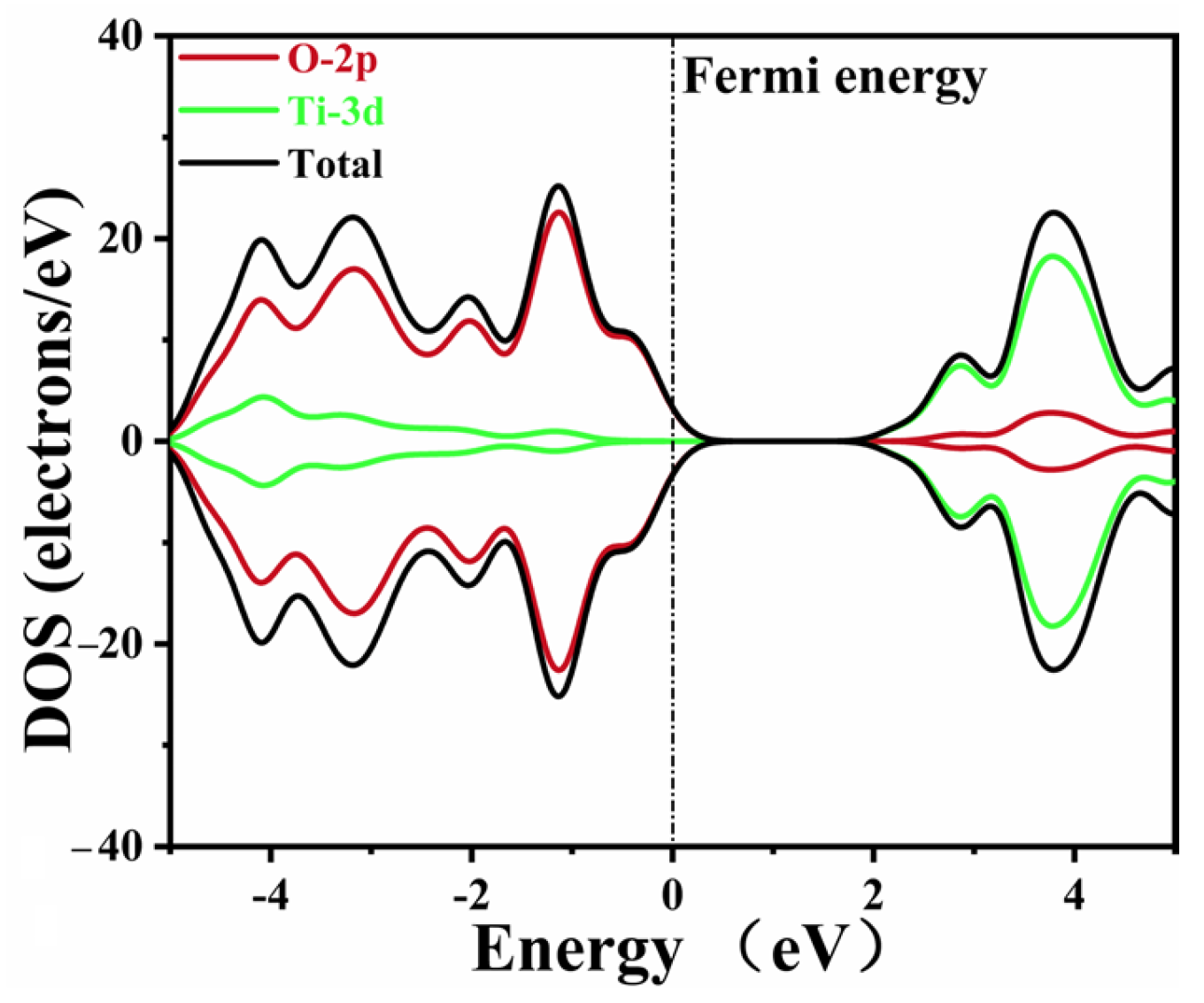
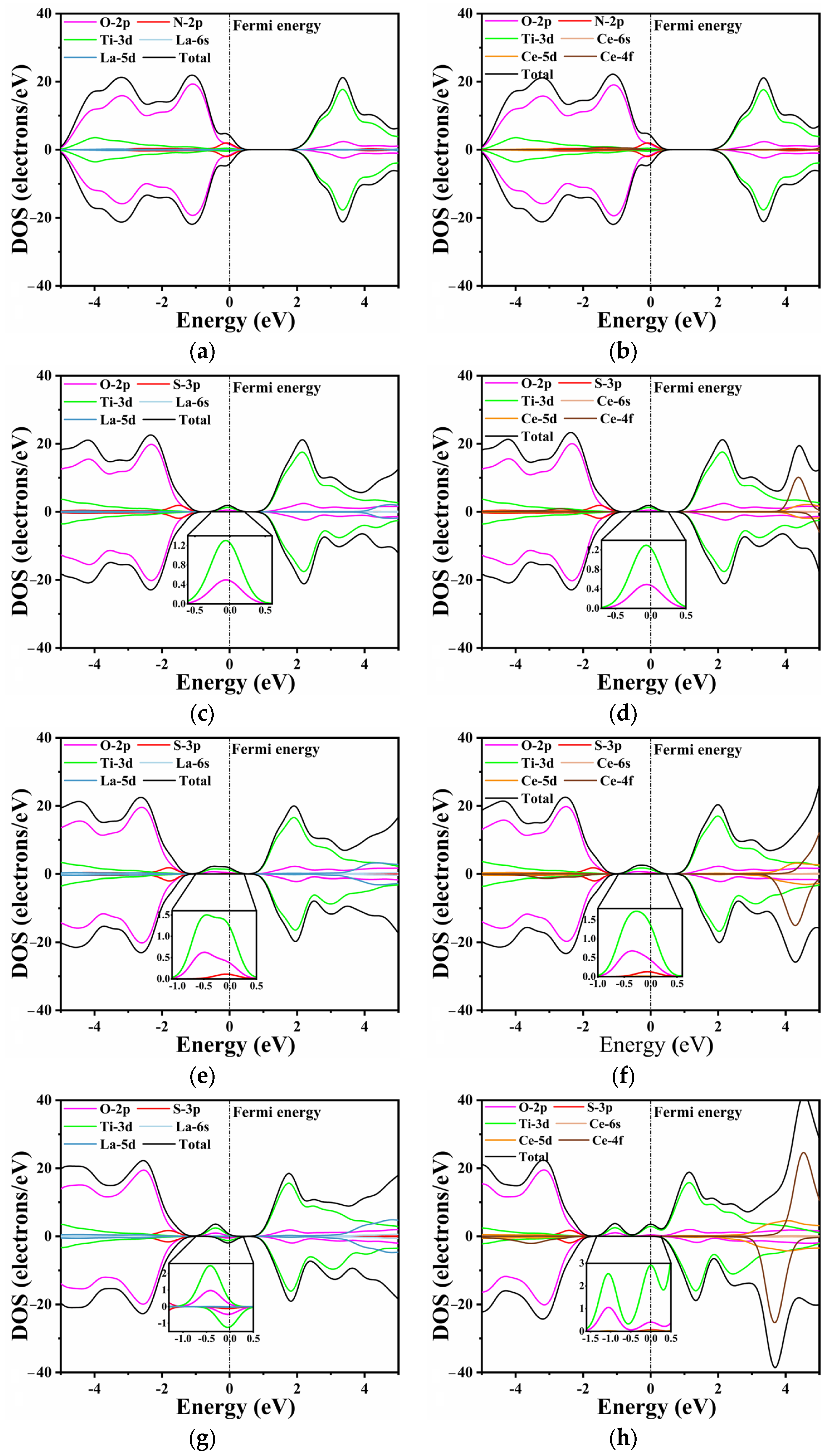

| Co-Doped Model | (eV) | (eV) | Co-Doped Model | (eV) | (eV) |
|---|---|---|---|---|---|
| LCON1 | 1.318 | −4.427 | CCON1 | 1.828 | −3.917 |
| LCON2 | 0.947 | −4.797 | CCON2 | 1.800 | −3.944 |
| LCOS1 | 0.841 | −4.904 | CCOS1 | 1.718 | −4.026 |
| LCOS2 | 1.360 | −4.385 | CCOS2 | 1.845 | −3.900 |
| Co-Doped Model | (eV) | Co-Doped Model | (eV) |
|---|---|---|---|
| LCON1 | 0.793 | CCON1 | 1.378 |
| LCON2 | 1.251 | CCON2 | 1.494 |
| LCOS1 | 3.375 | CCOS1 | 3.593 |
| LCOS2 | 2.856 | CCOS2 | 3.467 |
| Co-Doped Model | (eV) | (eV) | Doped Model | (eV) |
|---|---|---|---|---|
| LCOS1-0.25 | 0.237 | −5.508 | LCTO-0.25 | −0.920 |
| LCOS1-0.375 | −0.428 | −6.173 | LCTO-0.375 | −4.470 |
| CCOS1-0.25 | 1.979 | −3.766 | CCTO-0.25 | 1.005 |
| CCOS1-0.375 | 2.298 | −3.447 | CCTO-0.375 | −1.952 |
| Model | CaTiO3 | LCOS1-0.25 | ||
|---|---|---|---|---|
| Number | Atom Type | Bader Net Atomic Charge | Atom Type | Bader Net Atomic Charge |
| 1 | Ca | 1.33 | Ca | 1.47 |
| 2 | Ca | 1.33 | Ca | 0.48 |
| 3 | Ca | 1.33 | Ca | 0.55 |
| 4 | Ca | 1.33 | La | 1.38 |
| 5 | Ca | 1.33 | Ca | 1.43 |
| 6 | Ca | 1.33 | Ca | 0.91 |
| 7 | Ca | 1.33 | Ca | 0.76 |
| 8 | Ca | 1.33 | La | 1.09 |
| 9 | O | −1.05 | O | −0.60 |
| 10 | O | −1.05 | O | −0.67 |
| 11 | O | −1.04 | O | −0.83 |
| 12 | O | −1.05 | O | −0.71 |
| 13 | O | −1.05 | O | −0.87 |
| 14 | O | −1.05 | O | −0.70 |
| 15 | O | −1.05 | O | −0.84 |
| 16 | O | −1.04 | O | −0.96 |
| 17 | O | −1.05 | O | −0.97 |
| 18 | O | −1.04 | O | −0.66 |
| 19 | O | −1.04 | O | −0.46 |
| 20 | O | −1.05 | O | −0.26 |
| 21 | O | −1.05 | O | −1.38 |
| 22 | O | −1.04 | O | −1.24 |
| 23 | O | −1.04 | O | −1.32 |
| 24 | O | −1.04 | O | −1.45 |
| 25 | O | −1.04 | O | −1.52 |
| 26 | O | −1.04 | O | −1.22 |
| 27 | O | −1.04 | O | −1.51 |
| 28 | O | −1.04 | O | −0.44 |
| 29 | O | −1.04 | O | −0.60 |
| 30 | O | −1.04 | S | −0.62 |
| 31 | O | −1.04 | O | −0.82 |
| 32 | O | −1.04 | O | −1.05 |
| 33 | Ti | 1.80 | Ti | 1.71 |
| 34 | Ti | 1.80 | Ti | 1.58 |
| 35 | Ti | 1.80 | Ti | 1.73 |
| 36 | Ti | 1.80 | Ti | 1.90 |
| 37 | Ti | 1.80 | Ti | 1.77 |
| 38 | Ti | 1.80 | Ti | 1.65 |
| 39 | Ti | 1.80 | Ti | 1.47 |
| 40 | Ti | 1.80 | Ti | 1.82 |
| Model | Electrons in the CB | Holes in the VB | IB | |||
|---|---|---|---|---|---|---|
| Direction | Direction | Direction | ||||
| CTO | 0.069 | M-G | 0.084 | M-G | - | - |
| LCTO-0.25 | 0.063 | M-G | 0.086 | M-G | 0.070 | M-G |
| CCTO-0.25 | 0.065 | M-G | 0.116 | M-G | 0.073 | M-G |
| LCTO-0.375 | 0.079 | G-R | 0.089 | G-R | 0.141 | G-R |
| CCTO-0.375 | 0.130 | M-G | 0.161 | M-G | 0.257 | M-G |
| LCON2 | 0.074 | M-G | 0.149 | M-G | - | - |
| CCON2 | 0.081 | M-G | 0.158 | M-G | - | - |
| LCOS1 | 0.145 | M-G | 0.198 | M-G | 0.114 | M-G |
| CCOS1 | 0.137 | M-G | 0.196 | M-G | 0.108 | M-G |
| LCOS1-0.25 | 0.050 | G-R | 0.119 | G-R | 0.087 | G-R |
| CCOS1-0.25 | 0.095 | M-G | 0.137 | M-G | 0.115 | M-G |
| LCOS1-0.375 | 0.137 | M-G | 0.146 | M-G | 0.164 | G-X |
| Doping Type | Functional | Lattice Parameters (nm) | (eV) | Refs. | |
|---|---|---|---|---|---|
| Pd-doped | LDA | a = 7.75, b = 7.75, c = 7.75 | 0.84 | 425 | [79] |
| N-doped | GGA-PBE | a = 7.79, b = 7.79, c = 8.02 | 2.92 | - | [60] |
| S-doped | GGA-PBE | a = 8.37, b = 8.37, c = 8.01 | 2.55 | - | [60] |
| (La-S)-codoped | GGA-PBE | a = 8.21, b = 7.79, c = 7.83 | 0.96 | 412 | This work |
| (Mo-P)-codoped | GGA-PBE | - | 1.49 | 425 | [8] |
| (P-V)-codoped | GGA-PBE | a = 7.82, b = 7.82, c = 7.80 | 0.95 | 445 | [47] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wang, Y.; Jia, Y.; Yan, W.; Li, Q.; Zhou, J.; Wu, K. Engineering the Electronic Structure towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-Doping: A First-Principles Study. Molecules 2023, 28, 7134. https://doi.org/10.3390/molecules28207134
Zhang Q, Wang Y, Jia Y, Yan W, Li Q, Zhou J, Wu K. Engineering the Electronic Structure towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-Doping: A First-Principles Study. Molecules. 2023; 28(20):7134. https://doi.org/10.3390/molecules28207134
Chicago/Turabian StyleZhang, Qiankai, Yang Wang, Yonggang Jia, Wenchao Yan, Qinghao Li, Jun Zhou, and Kai Wu. 2023. "Engineering the Electronic Structure towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-Doping: A First-Principles Study" Molecules 28, no. 20: 7134. https://doi.org/10.3390/molecules28207134
APA StyleZhang, Q., Wang, Y., Jia, Y., Yan, W., Li, Q., Zhou, J., & Wu, K. (2023). Engineering the Electronic Structure towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-Doping: A First-Principles Study. Molecules, 28(20), 7134. https://doi.org/10.3390/molecules28207134








