Abstract
The tetrel bond between PhXF2Y(TF3) (T = C and Si; X = Cl, Br, and I; Y = F and Cl) and the electron donor MCN (M = Li and Na) was investigated at the M06-2X/aug-cc-pVDZ level of theory. As the electronegativity of the halogen atom X increases, the strength of the tetrel bond also increases, but as the electronegativity of the halogen atom Y increases, the strength of the tetrel bond decreases. The magnitude of the interaction energy in most –CF3 complexes was found to be less than 10 kcal/mol, but to exceed 11 kcal/mol for PhClF2Cl(CF3)⋯NCNa. The tetrel bond is greatly enhanced when the –SiF3 group interacts with LiCN or NaCN, with the largest interaction energy approaching 100 kcal/mol and displaying a covalent Si⋯N interaction. Along with this enhancement, the Si⋯N distance was found to be less than the X–Si bond length, the –SiF3 group to be closer to the N atom, and in most –SiF3 systems, the X–Si–F angle to be less than 90°; the –SiF3 group therefore undergoes inversion and complete transfer in some systems.
1. Introduction
A tetrel bond (TB) is defined as an interaction between a Group 14 element acting as a Lewis acid center and a Lewis base [1]. In recent years, tetrel bonding has become a hot research topic in the fields of materials science, chemistry, and biology [2,3]. Specifically, it has important applications in molecular assembly [4], organic catalysis [5], biological molecular function regulation [6], and so on. When an electron-withdrawing atom or group is covalently-bonded to a Group 14 atom, a positive electrostatic potential region develops on the surface of the tetrel (T) atom. This positive region is dependent on the structure of the Lewis acid itself. When the T atom is sp3 and sp2 hybridized, such regions are called σ-holes and π-holes, respectively [7,8]. All such regions attract electrons.
The earliest TBs were reported for research on the interactions between methane (with electron-withdrawing substituents) and various nucleophilic reagents. After the H atom on methane is replaced by an F atom, the positive sites generated on the extension of the F-C bond and opposite to the F atom can attract Lewis bases, such as H2O [9]. Subsequently, a large amount of crystal data indicates a similar interaction between other Group 14 atoms and Lewis bases [1].
Compared with other congeners, it is generally difficult for C atoms to form TBs, because of their positivity and the low polarizability of their electron clouds [7]. When C atoms participate in TB formation, this interaction is sometimes called a carbon bond [9]. Although the carbon bond is weak, there is still much evidence for its existence [9,10]. For example, when C is adjacent to four strong electron-withdrawing groups (e.g., the –CN group), 1,1,2,2-tetracyanocyclopropane can form a strong carbon bond with tetrahydrofuran, and the interaction energy is 11 kcal/mol [11]. In another study, when the Lewis acid was a cation, the carbon bond was found to be strengthened, resulting in a binding energy of 14–17 kcal/mol [12].
Starting from Si, the strength of the TB increases in the order Si < Ge < Sn. The TB strengths due to Pb and Sn are not significantly different from each other, though their relative stabilities change with the type of base [13]. There is some controversy about their relative magnitudes [14,15], but nevertheless, compared to C, other T atoms are likely to form much stronger TBs. In research by Grabowski on GeF4, it was found that when an F atom is replaced by H, its TB strength decreases because the depth of the σ-hole on Ge is reduced [14]. The commonalities between the TB and other weak interactions can also be revealed by charge transfer and AIM methodologies [16]. Later in-depth investigations further extended the findings on TBs. For example, a more recent study by Scheiner on TB strength variation due to systematic replacement of the H atoms of TH4 by F atoms found that with the addition of the first three F atoms, the binding energy corresponding to a T⋯N interaction kept rising, but a levelling-off was noticed on addition of the fourth F atom, or even a slight weakening of the binding energy [17]. The molecular electrostatic potential (MEP) maximum on Ge was also determined, from which it was concluded that the sequential addition of F atoms systematically deepened the σ-hole [17].
As noted for the triel bond, which was discovered later [18], the deformation of the monomer also plays an important role in the formation of the TB [19,20,21] and is sometimes so great that the deformation energy causes the computed binding energy to have a positive value [22]. Significant deformation of monomers is often accompanied by charge transfer between molecules [23,24]. The formation of a strong TB is usually accompanied by charge transfer from the lone pair on the Lewis base to a nearby orbital on the Lewis acid [16]. Taking FH3Ge as an example, when Ge is replaced by C, the σ*T-F orbital energy increases from 83.46 to 186.37 kcal/mol, thereby reducing the charge-transfer energy and, consequently, the TB strength from 12.7 to 2.16 kcal/mol [25]
TB strength is one of the factors affecting the transfer of –TX3 groups. The transfer of TX3 groups can be important in some chemical reactions, so some studies have focused on the role of TBs in important chemical processes, especially in SN2 reactions. The rotation mechanism of –CH3 in the SN2 reaction Cl– + CH3I was analyzed in detail by molecular beam imaging and chemical kinetics calculations [26]. In this process, a structure similar to a TB complex was found for both reactants and products [26]. Grabowski believed the initial stage of an SN2 reaction to be related to TB formation [16]. The latter stage of the reaction N3− + CH3Br → CH3N3 also involves the TB [27]. The three-center four-electron structure of carbon ([N–C–N]+) is formed by the double-tooth electron donor-capturing carbene ions via a TB, and its structure was found to be similar to the transition state geometry of an SN2 reaction [28].
The idea behind the present study of –TX3 group transfer was suggested by proton transfer, which is due to hydrogen bonding [29]. Therefore, we speculate that TBs may also cause –TX3 transfer. However, it is more difficult to transfer the –TX3 group via a TB, as the molecular weight of the –TX3 group is large compared to the mass of a proton. The transfer of the –TX3 group has, however, been achieved through synergistic effects. For example, the addition of BeCl2 molecules to a binary complex via beryllium bonds can enhance the interaction energy; half-transfer of the –GeF3 group has been observed [30]. The interaction energy of a TB formed by PhTH3 (T = Si, Ge) and a nitrogen heterocyclic carbene (NHC) was found to be less than 4 kcal/mol [31]. When the benzene ring of PhTH3 participates in a cation-π interaction with Be2+, the interaction energy sharply increases to 100 kcal/mol and complete transfer occurs [31].
Hypervalent halogens have strong oxidizing properties and novel structures compared to monovalent halides, making them important species in organic synthesis [32]. Akiba summarized the general situation regarding the structures and bonding of hypervalent halogens [33]. Hypervalent halogens have also been extensively studied in theoretical research [34,35].
The complete transfer of a –TX3 group has been achieved previously through a synergistic effect, and this present work focuses on achieving the complete transfer of the –TX3 group without using a third molecule; i.e., without the synergistic effect. We selected the hypervalent halogen compound PhXF2Y(TF3) as the TB σ-hole donor, where X is a hypervalent halogen atom connected to five atoms or groups; X can be either Cl, Br or I, Ph is a benzene ring, Y is a monovalent halogen atom, and the corresponding molecules are represented as A–XTF3 and B–XTF3, with A and B representing two situations where Y is either F or Cl, respectively (Scheme 1). MCN (M=Li and Na) are the electron donors. In the present work, the structure and properties of the TB formed between PhXF2Y(TF3) and MCN, as well as the conditions for the transfer of the –TF3 group, are explored and discussed.
Scheme 1.
The scheme of A-X-TF3 and B-X-TF3 (X = F, Cl, Br, I, T = C, Si).
2. Results
2.1. Electrostatic Potentials of Monomers
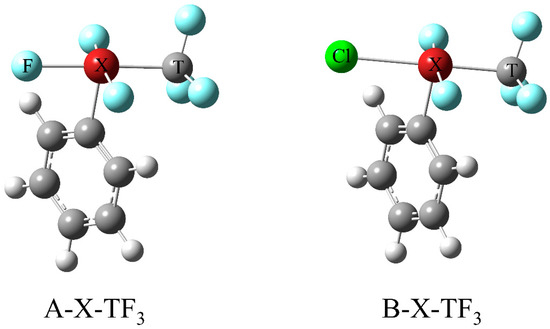
Figure 1 shows the electrostatic potential diagrams for the monomers of the electron acceptors A–XTF3 and B–XTF3. The red positive electrostatic potential region on the extension line of each molecule’s X–T bond is the σ–hole. The figure also shows the positive electrostatic potential values Vs, max on the 0.001 a.u. isosurface. It can be seen from the figure that the Vs, max of B–XTF3 is greater than that of A–XTF3, contrary to the fact that F is more electronegative than Cl (more on this later); however, Vs, max decreases in the order X = Cl > Br > I, consistent with the electronegativity of the halogen atom X. The electrostatic potential for the SiF3-containing monomer is more than twice the value for its CF3-containing analogue.
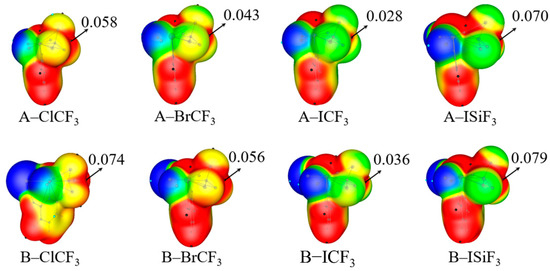
Figure 1.
MEP maps of A–XTF3 and B–XTF3 monomers. Color ranges in a.u are: red, greater than 0.02; yellow, between 0.02 and 0; green, between −0.02 and 0; blue, less than −0.02.
2.2. Geometric Structure and Interaction Energy
Figure 2 shows the structural diagrams of the TB complexes formed by B–XTF3 and the electron donor MCN, while the structural diagrams of the A–XTF3 systems are shown in Figure S1. Some important geometric parameters of the complexes are listed in Table 1. Firstly, the Si⋯N binding distance is much shorter than that of the C⋯N distance and is represented by R1 in the table. The R1 values of the SiF3 complexes are shorter than 2.0 Å, while the R1 values of the CF3 complexes are close to or greater than 3 Å. The X–Si distances in the SiF3 complexes are longer than the X–C distances in the CF3 complexes, represented by R2 in the table. The table also shows the difference between R1 and R2, as well as the change in the X-T bond length on complexation. For the –CF3 systems, R1 > R2, so their difference is positive, indicating that the C⋯N bond is a traditional noncovalent interaction. For the –SiF3 systems, R1 < R2, therefore, the difference is negative, indicating that Si⋯N has become a covalent interaction. The γ1 and γ2 listed in the table are, respectively, the ratio of R1 and R2 to the sum of the Van der Waals radii of the two relevant atoms. For the –CF3 system, γ1 is approximately 0.7, consistent with a weak C⋯N TB, while γ2 is about 0.5, reflecting the covalent properties of the X–C bond. For the –SiF3 system, γ1 is approximately 0.4, while γ2 is about 0.5, indicating that the covalent component of the Si⋯N TB is greater than that of the X–Si bond. This indicates that the –SiF3 group is located in the middle of the X and N atoms and is closer to the N atom. This indirectly indicates that –SiF3 is completely transferred from the X atom of the electron acceptor to the N atom of the electron donor. The last column of Table 1 shows that α(X–T–F) changes from 106° ~ 109° (for the –CF3 systems) to values close to 90o (for the –SiF3 systems), with some angles significantly smaller than 90o, further emphasizing the difference between the tetrel atoms C and Si. It is evident from Figure 2 that the umbrella-like structure of –CF3, which is oriented towards N, is transformed into an umbrella-like structure oriented towards X in the –SiF3 systems. It is worth noting that α for B–ClSiF3⋯NCNa has a relatively small value of 81.6°, indicating the largest transfer.
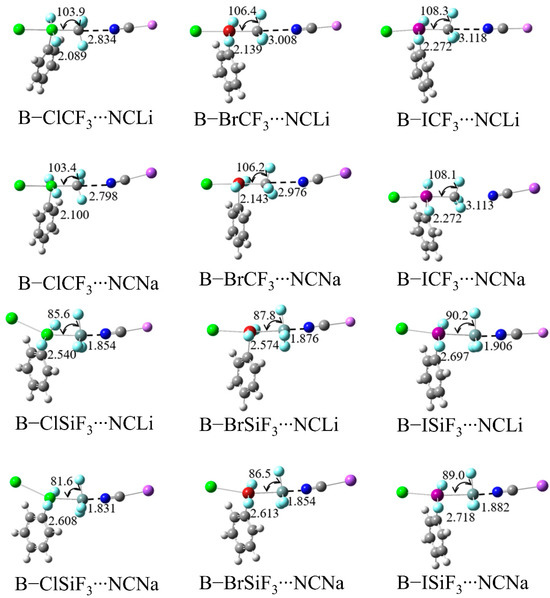
Figure 2.
Optimized structures of B–XTF3⋯NCM, marked with the mean of the three angles X–T–F (α, deg), T⋯N distance (R1, Å) and X–T bond length (R2, Å).

Table 1.
Interaction energy (Eint, kcal/mol), T⋯N distance (R1, Å), X–T bond length (R2, Å) and its change on complexation (ΔR2, Å), and average of the three X–T–F angles (α, deg) in the complexes.
The interaction energy (Eint) of these systems varies widely, from 2 to 97 kcal/mol. Eint changes with the electronegativity of the X atom. The larger the electronegativity of X, the larger the value for Eint; both A–XTF3 and B–XTF3 show this trend, consistent with the order of the electrostatic potential on the electron acceptor. Similarly, the electron donor NaCN forms a stronger TB than does LiCN, the Eint of the –SiF3 system is greater than that of the –CF3 system, and the TB formed by B–XCF3 is stronger than that of A–XCF3 (more on this later). The trend for the change in the interaction energy is opposite to the trend for the variation of the T⋯N distance R1. Figure 3 intuitively reflects this conclusion. From the graph, we found that Eint is correlated with R1, with a correlation coefficient as high as 0.98–0.99.
Figure 3.
Linear graph of the interaction energy (Eint) with the T⋯N distance (R1) in the complexes of A/B–XCF3 (left) and A/B–XSiF3 (right).
2.3. AIM Analysis
Table 2 lists the topological parameters at the bond critical points (BCPs) of T⋯N and X–T, corresponding to the AIM diagrams in Figure 4. These parameters are closely related to the strength of the TB, and Figure 5 shows the relationship between the Eint and the electron density ρ at the T⋯N BCP, revealing a strong positive correlation between the parameters; i.e., with an increase in electron density, the interaction energy also increases, with a correlation coefficient of 0.98–0.99. For the CF3 complexes, the electron density varies from 0.007 to 0.01 a.u. It can also be seen in Figure 4 that there is no obvious bond path between C and N in C⋯N, but three paths from N to F. For the SiF3 complexes, the situation is different. The electron density is one order of magnitude larger than the –CF3 value and it can be seen from the figure that there is an obvious bond path between Si and N in the Si⋯N interaction. In addition to the numerical changes, we also noticed a change in sign. When the C atom is replaced by the Si atom, the energy density H at the T⋯N BCP also changes from positive to negative, indicating a change in the type of T⋯N bond from noncovalent interactions in the –CF3 systems to partially covalent interactions in the –SiF3 systems, resulting in an enhanced TB.

Table 2.
AIM electron density (ρ), its Laplacian (∇2ρ) and total energy density (H) at the T⋯N and X–T BCPs in the binary complexes; all quantities are in a.u.
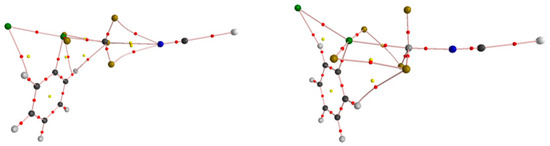
Figure 4.
AIM diagrams of B–ClCF3⋯NCNa (left) and B–ClSiF3⋯NCNa (right). Bond paths are indicated by broken lines with bond critical points represented by small red dots.
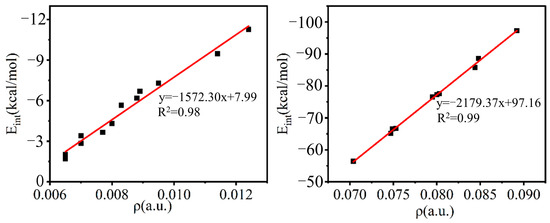
Figure 5.
Linear graph of interaction energy (Eint) and electron density (ρ) at the T⋯N BCP in the complexes of A/B–XCF3 (left) and A/B–XSiF3 (right).
The X–C covalent bond has large electron density values (greater than 0.1 a.u.) and a large Laplacian and total energy density. The ρ at the X–C BCP is approximately 0.1 a.u., ∇2ρ < 0, H < 0, which indicates that the X–C bond is a typical covalent bond. For the –SiF3 system, the electron density at the BCP of the X–Si bond is lower than that of the Si–N bond, indicating that the Si–N bond is more tightly bound than the X–Si bond, which is consistent with the point that the covalent contribution to Si–N is greater than in the X–Si bond, as mentioned earlier. ∇2ρ > 0, H < 0 indicates that the Si–N bond is a partially covalent interaction. There are exceptions, as when X = I, the ∇2ρ at the BCP of the X–Si bond is also negative, but this is still a typical covalent bond.
Figure 6 is the NCI diagram of the B–XTF3⋯NCM system, with an orange-green area sandwiched between C and N that represents the medium strength C⋯N tetrel bond. There is a blue region along the Si⋯N bond axis that represents a strong attraction, surrounded by a red region representing repulsion, which indicates overall a strong Si⋯N TB.
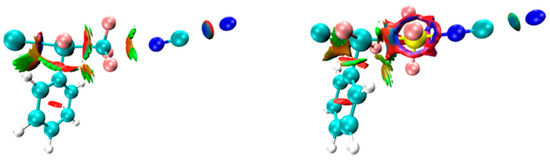
Figure 6.
NCI diagram of B–ClCF3∙∙∙NCNa (left) and B–ClSiF3∙∙∙NCNa (right). Blue, green, and red areas represent strong attraction, weak attraction, and strong repulsion interactions, respectively.
2.4. NOCV Analysis
Table 3 shows the charge transfer (CT) between the interacting monomers of the complex, as well as the change in the charge on the A–X or B–X molecular subunits. For the –CF3 system, the CT value is relatively small, ranging from 0.002 to 0.007 e; This parameter increases significantly in the –SiF3 system, with most values now in the vicinity of 0.2 e. For the B–ClSiF3⋯NCM system, the charge transfer exceeds one electron, which is consistent with the change in the interaction energy of these systems.

Table 3.
Charge transfer between A/B–XTF3 and MCN (CT, e), NOCV orbital energies (E, kcal/mol) and the change in the charge on the A–X or B–X molecular subunit (Δq, e).
The formation of TBs can also be analyzed using the natural orbital for chemical valence (NOCV) method. The NOCV density contour map is shown in Figure 7, which is composed of blue and green contour maps, where blue represents electrons accepted and green represents electrons donated. The area near the N atom is green, while the area near –TF3 is blue, which means that the electron density is transferred from the lone-pair electron orbital of the N atom into the antibonding molecular orbital of X–T. The energy corresponding to this orbital interaction is also given in Table 3.
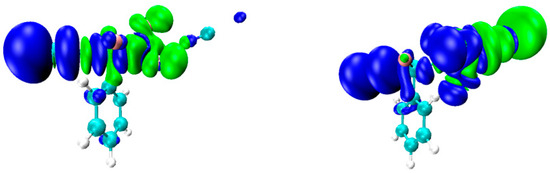
Figure 7.
NOCV pair density map of B–ClCF3⋯NCNa (left) and B–ClSiF3⋯NCNa (right).
We found a good linear relationship between the NOCV orbital energy and the interaction energy. Figure S2 shows the linear relationship between these parameters in the –SiF3 system, with a correlation coefficient of 0.95. The orbital effect in the –CF3 systems is not significant, with the most negative NOCV energy being −0.81 kcal/mol, which is negligible and can therefore be ignored. On the other hand, the orbital effects in the –SiF3 systems are significant, with NOCV energies ranging between −54.86 and −82.60 kcal/mol.
Presumably, the orbital interaction and charge transfer are also facilitated by the previously mentioned change in α(X-T-F) from more to less acute values, consistent with the strong linear correlation between Eint and α shown in Figure 8 above.
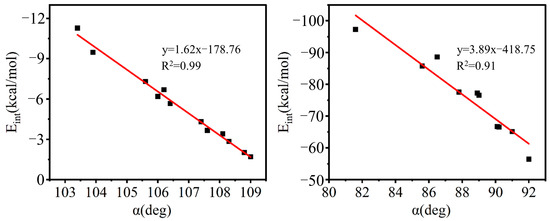
Figure 8.
Linear relationship between the interaction energy (Eint) and the X–T–F angle (α) in the complexes of A/B–XCF3 (left) and A/B–XSiF3 (right).
2.5. Energy Decomposition Analysis
The total interaction energy of the complex is decomposed into electrostatic energy (Ees), exchange energy (Eex), repulsion energy (Erep), polarization energy (Epol), and dispersion energy (Edisp) contributions. The relevant data are presented in Table 4. From the table, it can be seen that the electrostatic energy makes the largest contribution to the attractive energies for most systems. For most –CF3 systems, in addition to the electrostatic energy, the contributions from the dispersion energy and the exchange energy are also relatively large, while the contribution from the polarization energy is the smallest. For the –SiF3 system, these energies increase significantly by several orders of magnitude. In addition to the electrostatic energy, the contribution from the polarization energy is also very important. For example, the polarization energy of the B–ClSiF3⋯NCNa system is as high as 108.94 kcal/mol. The most surprising observation is that the NOCV orbital energy of the B–ClSiF3⋯NCNa system is also very high, attaining a value of 82.60 kcal/mol. Unlike the –CF3 system, the dispersion energy makes the smallest contribution to the interaction energy in the –SiF3 systems, though its value is still quite large. The relationship between the total interaction energy and three attractive terms in the –SiF3 system (Ees, Epol, and Edisp) were plotted and the three parameters are linearly related to the total interaction energy, as shown in Figure S3. The dispersion energy, which hardly changes with a change in the total interaction energy, is depicted in the figure by what is essentially a horizontal straight line. The relationship between the electrostatic energy and the total interaction energy is similar to the relationship between the polarization energy and the total interaction energy, as the slopes of their straight lines are similar.

Table 4.
Electrostatic (Ees), exchange (Eex), repulsion (Erep), polarization (Epol), and dispersion energies (Edisp), as well as the total interaction energy (Etotal), for the complexes; all energies in kcal/mol.
3. Computational Methodology
All calculations were performed at the M06-2X/aug-cc-pVDZ [36,37] level of theory using the Gaussian 09 suite of programs [38], because this method can provide a reliable description of noncovalent bonding in molecular systems, including complexes held together by tetrel bonds [39,40]. In order to ensure that all structures are real minima on their respective potential energy surfaces, vibrational frequency calculations were undertaken at the same level, thereby confirming that there were no imaginary frequencies. The interaction energies were calculated using the supermolecule method, and the basis set superposition error (BSSE) correction was performed using the counterpoise method proposed by Boys and Bernardi [41].
To predict the interaction sites and their magnitudes, wave function surface analysis software (WFA-SAS) [42] was used to calculate the molecular electrostatic potential (MEP) of each monomer and binary complex on the 0.001 a.u. isosurface. The electron density, its Laplacian and total energy density at the bond critical point (BCP), were analyzed by using Bader’s atoms in molecules (AIM) theory [43] and the Multiwfn program [44]. Natural bond orbital (NBO) analyses were performed using NBO 5.0 software [45]. Multiwfn [44] and VMD software [46] were used for natural orbitals for chemical valence (NOCV) [47] and noncovalent interaction (NCI) analyses, and for drawing their diagrams. The localized molecular orbital energy decomposition analysis (LMO-EDA) [48] implemented in the GAMESS suite of programs [49] was used to partition the interaction energy into five different energy components: electrostatic energy, exchange energy, repulsion energy, polarization energy, and dispersion energy.
4. Discussion
Previous studies found that the TB formed by the –CF3 group is weak, and even when the electron donor atom is connected to hydrogen atoms, it is more inclined to form hydrogen bonds. When anions act as electron donors in these types of complexes, their interaction energy rarely exceeds 7 kcal/mol [50]. However, when the –CF3 group is connected to a hypervalent halogen group, it not only forms a TB but also gives rise to relatively large interaction energies in many cases, such as in B–ClCF3⋯NCNa, where the interaction energy exceeds 11 kcal/mol. Therefore, we have found an effective way in the present work to promote strong TB formation with the –CF3 group.
The influence on the TB of the halogen atom X connected to the –TF3 group should not be underestimated, since the strength of the TB increases in the order X = I < Br < Cl. The greater the electronegativity of the X atom, the stronger the TB, since the electron-withdrawing ability of X increases accordingly and, consequently, deepens the σ–hole. This effect on the TB is similar to the effect of the halogen atom X in XTF3 [51].
However, when the halogen atom Y on the electron acceptor PhXF2Y(TF3) changes from Cl to F, the depth of the σ–hole decreases and the corresponding TB weakens, which is inconsistent with the relative electronegativities of the Y halogen atoms. This puzzling finding can be rationalized by considering two similar model complexes, denoted for clarity as Y-FClF2-(CF3)∙∙∙NCLi, where Y=F or Cl, X=Cl, T=C and F replaces the Ph group in the electron acceptor PhXF2Y(TF3). The optimized geometries for these model complexes are similar to the structures shown in Figure S1 (corresponding to A–ClCF3⋯NCLi; Y=F) and Figure 2 (corresponding to B–ClCF3⋯NCLi; Y=Cl), except that the phenyl group, perpendicular to the Y-Cl-C axis, has been replaced by an F atom. The complexes, with and without the phenyl group, have similar computed properties, with the Y=Cl systems being more stable than the Y=F systems.
With reference to Scheme 1, Figure 1, Figure 2 and Figure S1, the electron acceptor B–Cl–CF3 (Y=Cl) has a larger dipole moment than A–Cl–CF3 (Y = F) because the F atom opposite to C, on the extension of the Cl–C axis, gives rise to a larger Cl positive charge in A–Cl–CF3 than the positive charge on the corresponding Cl atom in B–Cl–CF3 when this F atom is replaced by Cl; the M062x/6-31++G(d,p) NBO charges for Cl are +1.676 (Y=Cl) and +1.428e (Y=F), for the electron acceptors with Ph replaced by F. Since the other F atoms perpendicular to the F−Cl−C or Cl−Cl−C axis were found to have similar negative NBO charges in both molecules (ranging between 0.4 and 0.45e in magnitude), the negative charge on the B-ClF3 subunit (q = −0.136; Y = Cl) is larger than the negative charge on the A-ClF3 subunit (q = −0.073; Y = F). Hence, the larger charge separation between the negatively-charged B-ClF3 subunit and the positively-charged CF3 subunit in B–Cl–CF3, along with a longer R2 (i.e., Cl-C bond length, see Table 1), gives rise to a dipole moment larger than the A–Cl–CF3 dipole moment. The larger Vs, max values in Figure 1 for the B-XTF3 monomers, compared to the A-XTF3 monomers, are also consistent with this explanation.
The larger B–Cl–CF3 dipole thus yields more strongly bound complexes with NCLi than does A–Cl–CF3, with the intermolecular interaction dominated by dipole–dipole electrostatic forces (see Table 4), especially since the intermolecular charge transfer for both complexes is small (CT < 0.007 e, see Table 3).
On complexation, the electric field due to the NCLi dipole shifts charge from the CF3 subunit into the Cl–C internuclear region, leading to Cl–C bond extension, a more positive CF3 subunit and a more negative A–Cl or B-Cl subunit. This, in turn, leads to an increase in the net dipole moment (relative to the isolated monomers), which stabilizes the interaction with NCLi to a greater extent in B–Cl–CF3⋯NCLi than in A–Cl–CF3⋯NCLi. Table 1 shows the larger Cl–C bond extension due to complexation (ΔR2) for the B-ClCF3 complex (relative to the A–ClCF3 complex), while Table 3 shows the larger increase in the negative charge on the B–Cl subunit due to complexation (relative to the A-Cl subunit). For T = Si, the significantly larger charge transfer (CT > 0.19 e, Table 3) and polarization (Table 4) in the SiF3 complexes augment the electrostatic forces, leading to complexes that are much more strongly bound than their CF3 counterparts (see Table 1 and Table 4).
The impact of orbital interactions on TB strength thus cannot be ignored. According to the NOCV results, the orbital interaction between the molecules is mainly due to the charge transfer from the lone pair electrons on N into the antibonding molecular orbital of T–X. As mentioned above, the orbital interactions in the –CF3 systems are not significant, while the –SF3 systems involve significant orbital interactions. The polarization energy components obtained from the energy decomposition analysis also indirectly confirm this observation. The difference between orbital interactions in the –SF3 and –CF3 systems plays a decisive role in the differences between their interaction energies. The EDA analysis is also consistent with this finding. In the –CF3 systems, the polarization energy is relatively small and does not exceed −4.69 kcal/mol, which suggests minor orbital interactions. On the contrary, in the –SiF3 systems, the polarization energy has grown significantly and is now more comparable in magnitude to even the electrostatic energy.
In this work, a hypervalent halogen group is adjacent to –TF3, while in the XTF3 molecule, the –TF3 group is adjacent to a monovalent halogen atom X. It is therefore of interest to compare the strengths of the TBs formed in these two different situations. The interaction energy of the ClSiF3⋯NCLi system is approximately 2 kcal/mol [52] and the interaction energy of the FSiF3⋯NCLi system is 8 kcal/mol [16], whereas the interaction energy of the B–ClSiF3⋯NCLi system is 85 kcal/mol, which is significantly larger than for the first two systems. The most positive electrostatic potential of the C atom in ClCF3 is 0.041 a.u., while the most positive electrostatic potentials of the C atom in A–ClCF3 and B–ClCF3 are 0.058 a.u. and 0.074 a.u., respectively, which are both larger in magnitude than the former. Therefore, adding a hypervalent halogen functional group to –TF3 makes it a better σ–hole donor, and it thus forms a stronger TB.
The electron donor used in this work is MCN, where M is an alkali metal. Alkali metal atoms are prone to losing electrons, so when the H atom in HCN is replaced by an alkali metal, the corresponding molecule becomes a stronger electron donor and therefore forms a stronger TB. Such alkali metal substituents can also make methyl C atoms nucleophilic [53]. If the electron donor has more than one alkali metal substituent, its electron-donating ability increases and the resulting TB is further strengthened. For example, the interaction energy between CH3F and C2H2 is only 1 kcal/mol, but two Li/Na substituents increase this amount to 5–6 kcal/mol [54]. Of course, other metals have similar enhancement effects. For example, the TB formed between HCN and SiF4 is weak, with an interaction energy of only 3.45 kcal/mol. However, if HCN is replaced by AgCN, the interaction energy of the TB increases nearly fourfold [55].
In our previous work on tetrel bonds, the same electron donor MCN was used [56], but the strength of the TB formed and the degree of –SiF3 group transfer are different from the corresponding results from the present study. The interaction energy of the TA–SiF3⋯NCNa (TA = tetrazole) system is 53 kcal/mol. When BH3 or BF3 is added to different N atoms of TA to form a triel bond, the interaction energy of the tetrel bond in the ternary complex increases to 60–66 kcal/mol. The interaction energy of the A/B–XSiF3⋯NCNa system can reach 56–97 kcal/mol in magnitude. Therefore, the TB formed by the –TF3 group connected to a hypervalent halogen atom is generally stronger than the TB formed by the –TF3 group connected to an N atom. The most positive electrostatic potential of Si in the A/B–XSiF3 molecule is greater than 0.07 a.u., while it is 0.11 a.u. in the TA–SiF3 molecule. However, the former forms a stronger TB, suggesting that deformation plays an important role in the formation of the former.
The α value in the TA–SiF3⋯NCNa system is 93°, dropping to 91° in the ternary complex, and the overall structure is triangular biconical, with two N atoms occupying the top position of the triangular biconical. Thus the –SiF3 group achieves a half-transfer from tetrazole to NaCN. In A/B–XSiF3⋯NCNa, the range of α is 81–92°. In some systems, the –SiF3 group is closer to NaCN, achieving complete transfer of the –SiF3 group. By utilizing the synergistic effect of cation-π interactions, this group can also achieve half-transfer from the C atom of the benzene ring to the C atom of a nitrogen heterocyclic carbene [31]. In conventional molecules, the bonding energy of the Si–N bond is similar to that of the Cl–Si bond, but in the hypervalent halide compounds, the bonding energy of the latter is lower than in conventional halide compounds. Therefore, the –SiF3 group in A/B–XSiF3 molecules is prone to transfer. The bonding energy of the Si–O bond is greater than that of the Si–N bond, which suggests that if the electron donor MCN is replaced by pyridine oxide, the –SiF3 group in A/B–XSiF3 systems is more likely to undergo transfer, and the extent of transfer likely to be greater. In previous work [57], we achieved half-transfer of SiF3 using the substituent effect; in the present study, we have demonstrated the full transfer of SiF3 without cooperative or substitution effects.
5. Conclusions
The TBs formed between PhXF2Y(TF3) and MCN were investigated at the M06-2X/aug-cc-pVDZ level of theory. When –TF3 is adjacent to a hypervalent halogen atom, the TB formed increases with the electronegativity of the hypervalent halogen atom X and decreases with the electronegativity of the halogen atom Y; both C and Si exhibit this behavior. For the –CF3 systems, the interaction energy ranges in magnitude between 1 and 12 kcal/mol, forming medium strength C⋯N TBs. For the –SiF3 systems, the interaction energy can become as large as 56–97 kcal/mol in magnitude, forming strong Si⋯N TBs. Electrostatic interactions play a dominant role in the formation of T⋯N TBs. In the –SiF3 systems, orbital interactions are more pronounced than in the –CF3 systems, and even comparable in magnitude to electrostatic interactions. The orbital interaction between the molecules is mainly due to the charge transfer from the lone-pair electrons on N into the antibonding molecular orbital of T–X. The C⋯N TBs are largely closed-shell interactions, whereas the Si⋯N TBs are characterized by partially covalent interactions. For the –SiF3 systems, the Si⋯N interaction distance is shorter than the X–Si bond length, and the –SiF3 group is more inclined towards the N atom than the X atom, with α values in most of the –SiF3 systems found to be less than 90°, indicating inversion and complete transfer of the –SiF3 group.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28207087/s1, Figure S1: Optimized structure diagram of A–XTF3∙∙∙MCN, marked with the mean of the three angles X–T–F (α, deg), T∙∙∙N distance (R1, Å) and X–T bond length (R2, Å); Figure S2: Linear diagram of interaction energy (Eint) with NOCV orbital energy (E) in the –SiF3; Figure S3: Linear correlation between the interaction energy (Eint) with three attractive terms (Ees, Epol and Edisp) in the –SiF3 complexes.
Author Contributions
Conceptualization, Q.L.; Data curation, Z.N., S.A.C.M., and Q.L.; Formal analysis, Z.N., S.A.C.M., and Q.L.; Investigation, Z.N. and Q.L.; Methodology, Q.L.; Resources, Q.L.; Software, Q.L.; Supervision, Q.L.; Validation, Z.N., S.A.C.M., and Q.L.; Visualization, Z.N. and Q.L.; Writing—original draft, Z.N. and Q.L.; Writing—review & editing, S.A.C.M., Z.N., and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Shandong Province (ZR2021MB123) and Yantai University Innovation Funding (GGIFYTU2327).
Data Availability Statement
Data is available from the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
References
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-bonding interaction: Rediscovered supramolecular force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef]
- Bauzá, A.; Ramis, R.; Frontera, A. Computational study of anion recognition based on tetrel and hydrogen bonding interaction by calix [4] pyrrole derivatives. Comput. Theor. Chem. 2014, 1038, 67–70. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel bonding interactions. Chem. Rec. 2016, 16, 473–487. [Google Scholar] [CrossRef] [PubMed]
- Daolio, A.; Scilabra, P.; Terraneo, G.; Resnati, G. C (sp3) atoms as tetrel bond donors: A crystallographic survey. Coord. Chem. Rev. 2020, 413, 213265. [Google Scholar] [CrossRef]
- Jena, S.; Dutta, J.; Tulsiyan, K.D.; Sahu, A.K.; Choudhury, S.S.; Biswal, H.S. Noncovalent interactions in proteins and nucleic acids: Beyond hydrogen bonding and π-stacking. Chem. Soc. Rev. 2022, 51, 4261–4286. [Google Scholar] [CrossRef] [PubMed]
- Mundlapati, V.R.; Sahoo, D.K.; Bhaumik, S.; Jena, S.; Chandrakar, A.; Biswal, H.S. Noncovalent carbon-bonding interactions in proteins. Angew. Chem. Int. Ed. 2018, 57, 16496–16500. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. Expansion of the σ-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef]
- Scheiner, S.; Nziko, V.P. Comparison of π-hole tetrel bonding with σ-hole halogen bonds in complexes of XCN (X= F, Cl, Br, I) and NH3. Phys. Chem. Chem. Phys. 2016, 18, 3581. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. The X–C∙∙∙Y (X = O/F, Y = O/S/F/Cl/Br/N/P) ‘carbon bond’and hydrophobic interactions. Phys. Chem. Chem. Phys. 2013, 15, 14377–14383. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. Microwave spectroscopic and atoms in molecules theoretical investigations on the Ar∙∙∙propargyl alcohol complex: Ar∙∙∙H–O, Ar∙∙∙π, and Ar∙∙∙C interactions. ChemPhysChem 2013, 14, 754–763. [Google Scholar] [CrossRef] [PubMed]
- Heywood, V.L.; Alford, T.P.; Roeleveld, J.J.; Deprez, S.J.L.; Verhoofstad, A.; Vlugt, J.V.; Domingos, S.R.; Schnell, M.; Davis, A.P.; Mooibroke, T.J. Observations of tetrel bonding between sp3-carbon and THF. Chem. Sci. 2020, 11, 5289–5293. [Google Scholar] [CrossRef]
- Scheiner, S. Comparison of CH···O, SH···O, chalcogen, and tetrel bonds formed by neutral and cationic sulfur-containing compounds. J. Phys. Chem. 2015, 119, 9189–9199. [Google Scholar] [CrossRef]
- Donald, K.J.; Tawfik, M. The weak helps the strong: Sigma-holes and the stability of MF4· base complexes. J. Phys. Chem. A 2013, 117, 14176–14183. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel bonds, penta-and hexa-coordinated tin and lead centres. Appl. Organomet. Chem. 2017, 31, e3727. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Scheiner, S. Comparison of tetrel bonds in neutral and protonated complexes of pyridineTF3 and furanTF3 (T = C, Si, and Ge) with NH3. Phys. Chem. Chem. Phys. 2017, 19, 5550–5559. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
- Scheiner, S. Systematic elucidation of factors that influence the strength of tetrel bonds. J. Phys. Chem. A 2017, 121, 5561–5568. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. π-Hole bonds: Boron and aluminum Lewis acid centers. ChemPhysChem 2015, 16, 1470–1479. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Aman, Y.; Ji, X.; Mo, Y. Tetrel bonding interaction: An analysis with the block-localized wavefunction (BLW) approach. Phys. Chem. Chem. Phys. 2019, 21, 11776–11784. [Google Scholar] [CrossRef]
- Lin, H.; Meng, L.; Li, X.; Zeng, Y.; Zhang, X. Comparison of pnicogen and tetrel bonds in complexes containing CX2 carbenes (X = F, Cl, Br, OH, OMe, NH2, and NMe2). New J. Chem. 2019, 43, 15596–15604. [Google Scholar] [CrossRef]
- McDowell, S.A.; Wang, R.; Li, Q. Interactions in model ionic dyads and triads containing tetrel Aaoms. Molecules 2020, 25, 4197. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Steric crowding in tetrel bonds. J. Phys. Chem. A 2018, 122, 2550–2562. [Google Scholar] [CrossRef]
- Niu, Z.; McDowell, S.A.; Li, Q. Triel bonds with Au atoms as electron donors. ChemPhysChem 2023, 24, e202200748. [Google Scholar] [CrossRef] [PubMed]
- Amgoune, A.; Bourissou, D. σ-Acceptor, Z-type ligands for transition metals. Chem. Commun. 2011, 47, 859–871. [Google Scholar] [CrossRef]
- Scheiner, S. Origins and properties of the tetrel bond. Phys. Chem. Chem. Phys. 2021, 23, 5702–5717. [Google Scholar] [CrossRef]
- Mikosch, J.; Trippel, S.; Eichhorn, C.; Otto, R.; Lourderaj, U.; Zhang, J.X.; Hase, W.L.; Weidemuller, M.; Wester, R. Imaging nucleophilic substitution dynamics. Science 2008, 319, 183–186. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Cheng, J.; Li, W.; Li, H. Tetrel bond of pseudohalide anions with XH3F (X = C, Si, Ge, and Sn) and its role in SN2 reaction. J. Chem. Phys. 2016, 145, 224310. [Google Scholar] [CrossRef] [PubMed]
- Karim, A.; Schulz, N.; Andersson, H.; Nekoueishahraki, B.; Carlsson, A.; Sarabi, D.; Valkonen, A.; Rissanen, K.; Grafenstein, J.; Keller, S.; et al. Carbon’s three–center, four–electron tetrel bond, treated experimentally. J. Am. Chem. Soc. 2018, 140, 17571–17579. [Google Scholar] [CrossRef]
- Lim, D.W.; Sadakiyo, M.; Kitagawa, H. Proton transfer in hydrogen–bonded degenerate systems of water and ammonia in metal–organic frameworks. Chem. Sci. 2019, 10, 16–33. [Google Scholar] [CrossRef]
- Bauza, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π–hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef]
- Liu, N.; Wu, Q.; Li, Q.; Scheiner, S. Promotion of TH3 (T = Si and Ge) group transfer within a tetrel bond by a cation–π interaction. Phys. Chem. Chem. Phys. 2022, 24, 1113–1119. [Google Scholar] [CrossRef]
- Zhdankin, V.V.; Stang, P.J. Chemistry of polyvalent iodine. Chem. Rev. 2008, 108, 5299–5358. [Google Scholar] [CrossRef]
- Akiba, K. Chemistry of Hypervalent Compounds; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Sikalov, A.A. Hypervalent halogen hydrides HalHn (Hal = Cl, Br, I; n = 3, 5, 7): DFT and ab initio stability prediction. Theor. Chem. Acc. 2020, 139, 8. [Google Scholar] [CrossRef]
- Tian, W.K.; Miao, Q.; Li, Q.Z.; Li, W.; Cheng, J. Superalkali Li3M (M = Cl, Br, I) as a Lewis base in halogen bonding: A heavier halogen is a stronger Lewis base than a lighter halogen. Comput. Theor. Chem. 2013, 1012, 41–46. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B. Gaussian 09, Revision, A.02; Gaussian, Inc.: Wallingford, UK, 2009. [Google Scholar]
- Yang, F.L.; Yang, X.; Wu, R.Z.; Yan, C.X.; Yang, F.; Ye, W.; Zhang, L.W.; Zhou, P.P. Intermolecular interactions between σ- and π-holes of bromopentafluorobenzene and pyridine: Computational and experimental investigations. Phys. Chem. Chem. Phys. 2018, 20, 11386–11395. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Q.; Yang, F.L.; Lu, K.; Yian, C.X.; Dou, W.; Yang, L.; Zhou, P.P. Competition and cooperativity of hydrogen-bonding and tetrel-bonding interactions involving triethylene diamine (DABCO), H2O and CO2 in air. New J. Chem. 2020, 44, 2328–2338. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 2002, 19, 553–566. [Google Scholar] [CrossRef]
- Bulat, F.A.; Toro-Labbé, A.; Brinck, T.; Murray, J.S.; Politzer, P. Quantitative analysis of molecular surfaces: Areas, volumes, electrostatic potentials and average local ionization energies. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital. Chem. Rev. 1998, 88, 899–926. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys. 2009, 131, 014102. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Non–covalent sp3 carbon bonding with ArCF3 is analogous to CH–π interactions. Chem. Commun. 2014, 50, 12626–12629. [Google Scholar] [CrossRef]
- Liu, M.; Yang, L.; Li, Q.; Li, W.; Cheng, J.; Xiao, B.; Yu, X. Modulating the strength of tetrel bonding through beryllium bonding. J. Mol. Model. 2016, 22, 192. [Google Scholar] [CrossRef]
- Solimannejad, M.; Orojloo, M.; Amani, S. Effect of cooperativity in lithium bonding on the strength of halogen bonding and tetrel bonding: (LiCN)n∙∙∙ClYF3 and (LiCN)n∙∙∙YF3Cl (Y= C, Si and n= 1–5) complexes as a working model. J. Mol. Model. 2015, 21, 183. [Google Scholar] [CrossRef]
- Scheiner, S. The ditetrel bond: Noncovalent bond between neutral tetrel atoms. Phys. Chem. Chem. Phys. 2020, 22, 16606–16614. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Li, H.; Cheng, J.; Li, W.; Li, Q. Prominent enhancing effects of substituents on the strength of π···σ–hole tetrel bond. Int. J. Quantum Chem. 2017, 117, e25448. [Google Scholar] [CrossRef]
- Wei, Y.; Cheng, J.; Li, W.; Li, Q. Regulation of coin metal substituents and cooperativity on the strength and nature of tetrel bonds. RSC Adv. 2017, 7, 46321–46328. [Google Scholar] [CrossRef]
- Wu, Q.; Xie, X.; Li, Q.; Scheiner, S. Enhancement of tetrel bond involving tetrazole–TtR3 (Tt = C., Si; R. = H., F). Promotion of SiR3 transfer by a triel bond. Phys. Chem. Chem. Phys. 2022, 24, 25895–25903. [Google Scholar] [CrossRef]
- Niu, Z.H.; Wu, Q.Z.; Li, Q.Z.; Scheiner, S. C∙∙∙O and Si∙∙∙O tetrel bonds: Substituent effects and transfer of the SiF3 group. Int. J. Mol. Sci. 2023, 24, 11884. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).