Next Article in Journal
Recent Advances on Small-Molecule Antagonists Targeting TLR7
Next Article in Special Issue
Ensemble Learning, Deep Learning-Based and Molecular Descriptor-Based Quantitative Structure–Activity Relationships
Previous Article in Journal
Chemical Synthesis and Biological Evaluation of 3-Substituted Estrone/Estradiol Derivatives as 17β-Hydroxysteroid Dehydrogenase Type 1 Inhibitors Acting via a Reverse Orientation of the Natural Substrate Estrone
Previous Article in Special Issue
Comprehensive Survey of Consensus Docking for High-Throughput Virtual Screening
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 2
10.3390/molecules28020633
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Machine Learning Prediction of Mycobacterial Cell Wall Permeability of Drugs and Drug-like Compounds

by
Eugene V. Radchenko
1,2,
Grigory V. Antonyan
1,
Stanislav K. Ignatov
2 and
Vladimir A. Palyulin
1,2,*
1
Department of Chemistry, Lomonosov Moscow State University, 119991 Moscow, Russia
2
Department of Chemistry, Lobachevsky State University of Nizhny Novgorod, 603022 Nizhny Novgorod, Russia
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(2), 633; https://doi.org/10.3390/molecules28020633
Submission received: 18 December 2022 / Revised: 30 December 2022 / Accepted: 30 December 2022 / Published: 7 January 2023
(This article belongs to the Special Issue Drug Design with Advanced Computational Strategies and Artificial Intelligence)
Browse Figures
Versions Notes

Abstract

:
The cell wall of Mycobacterium tuberculosis and related organisms has a very complex and unusual organization that makes it much less permeable to nutrients and antibiotics, leading to the low activity of many potential antimycobacterial drugs against whole-cell mycobacteria compared to their isolated molecular biotargets. The ability to predict and optimize the cell wall permeability could greatly enhance the development of novel antitubercular agents. Using an extensive structure–permeability dataset for organic compounds derived from published experimental big data (5371 compounds including 2671 penetrating and 2700 non-penetrating compounds), we have created a predictive classification model based on fragmental descriptors and an artificial neural network of a novel architecture that provides better accuracy (cross-validated balanced accuracy 0.768, sensitivity 0.768, specificity 0.769, area under ROC curve 0.911) and applicability domain compared with the previously published results.

1. Introduction

Tuberculosis (TB) is a serious infectious disease caused by pathogenic Mycobacterium tuberculosis mycobacteria (or, in some cases, by a number of related mycobacteria species belonging to the Mycobacterium tuberculosis complex) [1,2]. This is a chronic bacterial infection characterized by the development of cell-mediated hypersensitivity and the formation of granulomas in the affected tissues. The disease is usually localized in the respiratory organs, but other organs may be involved in the process. Tuberculosis exhibits a variety of clinical and pathomorphological manifestations, as well as broad abilities for adaptation to changing environmental conditions and the characteristics of the host organism [3].
According to the World Health Organization (WHO), tuberculosis is one of the most widespread and socially significant infections: every year, despite being a preventable and curable disease, about 10.6 million people develop tuberculosis and 1.6 million people die worldwide, making it the leading cause of death from a single infectious agent [4]. The major problem in the treatment is the mycobacterial resistance to antibiotics. Multidrug-resistant (MDR) mycobacteria are resistant to treatment with two first-line anti-TB medications, isoniazid and rifampicin, whereas the forms that are also resistant to second-line medications are called extensively drug-resistant (XDR) [5,6,7,8].
Mycobacterium tuberculosis is a rather complex organism containing a broad variety of targets that can be affected by drug compounds [9,10,11]. The established antimycobacterial targets include specific processes of the cell wall biosynthesis [12,13,14,15], protein synthesis [16], DNA replication and repair [17,18,19], DNA transcription [20], bioenergetic metabolism [21,22,23], and other metabolic pathways [24,25]. In addition, massive and fruitful efforts have been directed in recent years at the identification and exploitation of various emerging and potential targets as the basis for the development of novel antitubercular drugs [26,27,28,29,30,31,32,33], especially with a focus on overcoming the drug resistance [34,35,36]. Besides the enzyme targets, the important roles of mycobacterial membranes [37] and transporters [38,39] as drug targets has been recognized, as well as the opportunities offered by the multi-target approaches [40] and host-directed therapies [35,41]. Promising studies of novel preventive and therapeutic TB vaccines [42,43,44] and nanocarrier-based approaches for the efficient and targeted delivery of anti-TB drugs and vaccines [45,46] are also ongoing.
Nevertheless, the anti-tubercular drug discovery and development projects face many complications that result in high attrition rates, leaving clinical needs unmet [47,48,49]. In particular, the target-based approaches using biochemical screening assays and/or in silico models [50] to identify and optimize inhibitors have so far failed to produce any clinical drug candidates, primarily due to their lack of whole-cell activity [30,48]. It is commonly accepted that one of the key causes for this is the extremely low permeability of the mycobacterial cell envelope [49]. Atypical among bacteria, the M. tuberculosis cell envelope has an elaborate dense multilayered structure devoid of the majority of transporters, with the wax-like outer membrane formed by mycolic acids and their derivatives [12,49]. Its penetration is believed to be facilitated by the relatively higher lipophilicity of anti-TB drugs (compared to other antibacterials), requiring reassessment of the standard drug-likeness rules [38,49,51] and the shift of the overall ADME analysis towards the local (microenvironment-based) drug exposure [52]. Although the whole-cell phenotypic screening followed by target elucidation is presently seen as the most efficient approach to the tuberculosis drug discovery [30,48], the ability to predict and optimize envelope permeability for a potential drug using in silico models would be very valuable in any pipeline.
The first steps towards this goal were made in the 1990s [53,54] by experimental permeability measurements in the model Mycobacteria species for limited sets of antibiotics and nutrients. They were shown to be much lower than in other bacteria, and rough semi-quantitative correlations with lipophilicity and charges were established, highlighting the diffusion-based and porin-assisted permeation mechanisms. In one study [55], the M. tuberculosis cell wall permeabilities for a small congeneric series of antitubercular drugs were estimated simply as their Caco-2 cell membrane permeabilities using correlations with several physico-chemical descriptors. In another study [56], based on the simplistic molecular dynamics simulations of solutes in pseudo-mycolic acid monolayers, the lateral and transverse diffusion coefficients were calculated and the qualitative correlation between the solute molecular shape and permeability was established.
Taking into account the difficulties of direct permeability measurement, later research mostly relied on general-purpose quantitative structure–activity/structure–property relationship (QSAR/QSPR) modeling techniques applied to more or less representative structure–permeability datasets, wherein the permeability estimates were derived from the publicly available activity data. In the MycPermCheck model [57] for permeability classification, the 3727 compounds from the CDD TB database [58] that were active in the cell-based inhibition assays were considered as permeable, whereas the “impermeable” examples were generated by a random sampling of drug-like compounds from the ZINC12 database [59]. Using five previously selected physico-chemical descriptors, a one-dimensional principal component model, and logistic regression, the model achieved a sensitivity of 67.2% at the specificity of 90% (or sensitivity of 72.2% at the specificity of 75%) on the validation set.
In one study [60], the permeability was estimated from the ChEMBL [61] data using the differences in activity between the cell-based and enzyme-based M. tuberculosis inhibition assays. For various subsets of 366 common compounds and additional 273 compounds highly potent in cell-based assays, the Partial Least Squares Regression (PLSR) models based on the subset of PaDEL [62] 1D and 2D descriptors were built and further translated to classification predictions, and the sensitivity of 70–95% and specificity of 8–45% were achieved for the validation set. Developing this approach, the recent work [63] used a ChEMBL-derived dataset of 1114 compounds, PaDEL descriptors, and a variety of machine learning methods to achieve the area under ROC curve (AUC) value of 0.81 for the validation set of 40 compounds.
Inspired by these encouraging results, the goal of the present work was to develop a predictive in silico model of Mycobacterium tuberculosis permeability based on the available Big Data from the cell-based and enzyme-based inhibitory activity assays that would be applicable to diverse drugs and drug-like compounds.

2. Results and Discussion

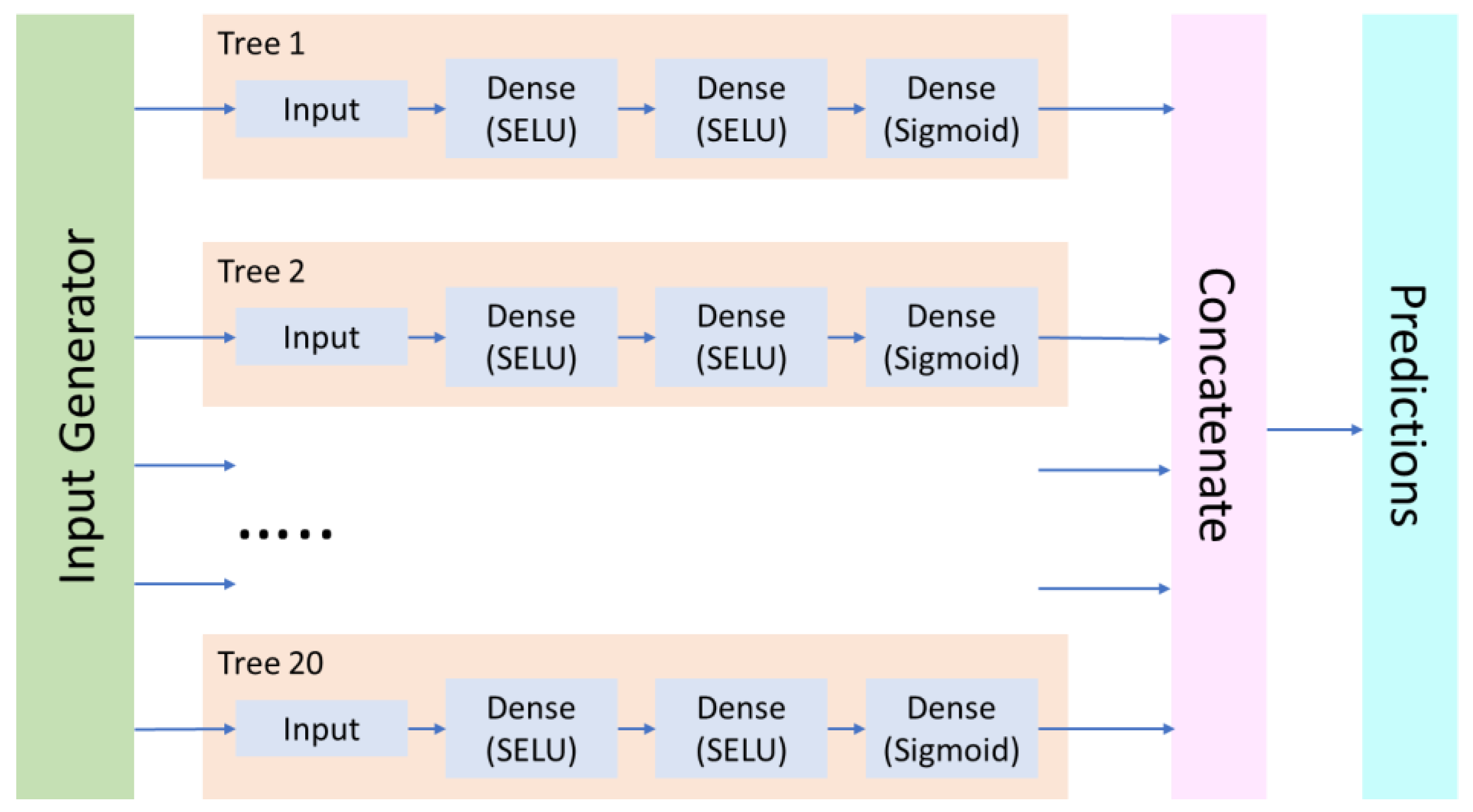
2.1. General Modeling Approach

For a broadly applicable predictive structure–permeability model, a key foundational element is a sufficiently diverse and representative dataset. Following the approach proposed and validated in the previous studies, the permeability data were derived from the differences in the inhibitory activity measurements between the target-based and cell-based assays, as reported in the publicly available Big Data sources (see Section 2.2).
For model construction, we decided to focus on the combination of artificial neural networks and the fragmental (substructural) descriptors representing the occurrence numbers of various substructures. Providing efficient tools for various QSPR and QSAR problems [64,65,66], this approach has been successfully employed to model the structure influence on various pharmacokinetic, toxicity, and physico-chemical endpoints such as human intestinal absorption [67], blood–brain barrier permeability [68,69], hERG-mediated cardiac toxicity [70], lipophilicity [71], etc. Some of these models are available online at our ADMET Prediction Service page (http://qsar.chem.msu.ru/admet/ accessed on 1 December 2022) and have been successfully used to evaluate the key absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties of diverse potential drug compounds in virtual screening and molecular design studies [72,73,74,75,76].

2.2. Mycobacterium tuberculosis Inhibitor Permeability Dataset

As noted above, similar to the previous studies [60,63], the compounds that have shown activity in any of the selected target-based assays were classified as permeable if they were active in any of the selected cell-based assays; otherwise they were taken to be impermeable. To this end, the publicly available PubChem 2022 database [77] was used as the source of (Big) raw data (in particular, it included both the assays synchronized with ChEMBL [61] and a number of additional assays). The Big Data resources offer unprecedented opportunities for deep analysis of the structure–activity and structure–property relationships and for the development of more accurate and broadly applicable predictive models, but require additional efforts for data preparation and curation [78]. On the other hand, one should bear in mind that large diverse datasets, often comprising compounds with different properties and mechanisms of action and based on only partially comparable measurements (commonly approximate by design) that are performed in different laboratories over significant time periods using varying techniques and conditions, usually impose natural limits on the quality of the resulting models.
The detailed data preparation procedures reflecting the established guidelines [79,80,81] are explained in Section 3.1, and only a brief overview of salient points is presented here. Using the automated keyword search in the local database, the assays potentially relevant for the antimycobacterial activity were identified. During the expert analysis of this list, the key cell-based and target-based assays were selected that were required to be sufficiently populated in terms of data point counts as well as sufficiently diverse and representative in the chemical and endpoint spaces. In particular, the chemical space coverage was prioritized over the maximum reliability of specific data points, and this was reflected both in the assay selection and in the downstream standardization of the (binary) activity definitions.
Using custom Web scripts accessing both local and remote databases, the assay and compound data were joined and downloaded as the TSV format files. After manual and automated preprocessing and curation, the cleaned individual datasets were prepared and then merged to produce the united datasets for the selected cell-based and target-based assays. In total, the cell-based dataset contained 557,527 compounds, among which 96,040 compounds were active in at least one out of 11 assays. The target-based dataset contained 926,660 compounds, among which 9450 compounds were active in at least one out of 11 assays.
By matching this target-active dataset against the cell-based results, 8242 compounds were identified that were active in at least one target-based assay and have also been tested in at least one cell-based assay. In particular, 2671 compounds that have shown activity in at least one cell-based assay were classified as penetrating the M. tuberculosis cell wall (MtbPen = 1, positive result) whereas the remaining 5571 compounds (inactive in all 11 cell-based assays) were classified as non-penetrating (MtbPen = 0, negative result). In the present paper, this dataset will be called MtbPen8242.
As can be seen, the MtbPen8242 dataset is moderately imbalanced (the ratio of non-penetrating to penetrating compounds is greater than 2.08). During subsequent structure-property modeling, this imbalance was found to create problems limiting the model quality. Thus, a balanced dataset MtbPen5371ad of 5371 compounds was prepared from it that comprises all (2671) penetrating compounds as well as a diverse subset of 2700 out of 5571 non-penetrating compounds. This dataset is provided in the Supplementary Materials.

2.3. Molecular Descriptors

The fragmental (substructural) descriptors [64,65,66] representing the occurrence numbers of various substructures were calculated in the framework of the NASAWIN 2.0 [82] software. Linear paths, cycles, and branches were generated using multi-level classification that takes into account atom types, valence states, bonding patterns, and number of attached hydrogens as well as bond types. The rare fragments that are present in fewer than 100 compounds and thus cannot be used to detect general predictive relationships were removed. The fragments containing up to eight non-hydrogen atoms were considered in order to provide sufficiently detailed description of the structures without excessive increase in the number of descriptors. In total, several thousands of descriptors (depending on the fragment size) were generated.

2.4. Neural Network Modeling Procedure

As noted above, similar to our studies on the prediction of ADMET properties [67,68,69,70], the combination of fragmental descriptors and artificial neural networks is especially suitable for modeling such primarily non-specific properties in diverse sets of organic and drug-like compounds. Even the specific contributions (e.g., from various active transporters) are implicitly taken into account by the neural network-based fragmental model [69].
Further developing the previously published modeling approach [69], we created a novel network architecture that logically implements the same high-level modeling workflow, integrating the classical feed-forward back-propagation neural network (BPNN) and the repeated double cross-validation [83] approach (Figure 1). The double cross-validation procedure involves two loops, and in each loop a fraction of the dataset is randomly selected as a test subset. During each iteration of the inner loop, a neural network submodel is built using the training subset while the prediction error on the test subset is monitored to provide the early termination while the outer loop test subset is used to validate the resulting model. Usually, the 5 × 4-fold double cross-validation scheme is employed, corresponding to N O = 5 and N I = 4 in Figure 1. That is, in the outer loop, the dataset is split into five subsets of approximately equal sizes and each of them is used to validate four models built in the inner loop by splitting the remaining data into four subsets of approximately the same size and using three of them for training the model and one for early termination. The procedure can be repeated several times ( N R ) to enhance the stability and reliability of the results [69]. The validation subset errors are then consolidated and normalized into the appropriate cross-validation statistics (such as the accuracy, balanced accuracy, sensitivity, and specificity for classification models). To reduce the risk of overfitting and chance correlations, the inner and outer splits are randomly shuffled at each step. This approach not only provides quite reliable estimates of the model predictivity but also generates an ensemble of neural network models based on different subsets of data that can be used to improve prediction quality and evaluate the model applicability.
However, although most commonly the double cross-validation procedure is performed sequentially, in the present work, we implemented a parallelized version that unrolls the loops and integrates the ensemble submodels (“trees”) into a single neural network (“forest”) that is fed with input data from the generator objects. This approach significantly enhanced the modeling performance (Figure 2).
Most of the other key architecture decisions from the earlier study [69] were retained (see the reference for the discussion of other available options). Each “tree” neural subnetwork may include one or more fully connected (Dense) layers with the scaled exponential linear unit (SELU) activation function [84] that provides the best results in terms of model quality and training efficiency. Optionally, the fully connected layers can be interleaved with the AlphaDropout [84] regularization layers in order to prevent overfitting. For the output layer in a classification model, the sigmoid activation function was used, which is expected to provide an estimated probability of the compound penetrating the cell wall (positive result). Binary cross-entropy (BCE) was used as a loss function for model training. For data preprocessing, the MinMaxScaler algorithm was used, which transforms the descriptors by linear scaling to the [ 0 ,   1 ] range. Global descriptor selection (for the entire modeling dataset after scaling) was performed to remove low-variable descriptors (defined as variance below 10–6) and to identify the most relevant descriptor subset using a stepwise descriptor selection procedure wherein the Partial Least Squares regression model is iteratively refined by adding descriptors with the highest F-value score with the residual endpoint. Since these models are sufficiently different from the resulting neural network models, we can be reasonably confident that the descriptor selection procedure does not lead to overfitting or chance correlations.
The neural network models were built using the in-house Python script based on the TensorFlow 2.4.1/Keras 2.4.3 framework on a high-performance NVIDIA RTX3080Ti GPU.
The hyperparameters controlling the machine learning modeling workflow can significantly affect its quality and efficiency. These include the neural network architecture (number and size of the hidden layers) and training parameters as well as the descriptor set (in particular, fragment size, selection algorithm, and the number of selected descriptors) and the prediction and applicability control parameters (see below). In the present study, hyperparameter optimization and model selection were performed using the Optuna 3.0.3 [85] library that implements the tree-structured Parzen Estimator algorithm. The goal function for the maximization was defined as the cross-validated balanced accuracy of the model. For some of the hyperparameters, the optimal values determined in the preliminary tests were kept fixed during the final modeling.
As mentioned above, an ensemble of the neural network submodels generated by the double cross-validation procedure from different subsets of data can be used to improve prediction quality and evaluate the model applicability. In particular, for the classification case, the mean and standard deviation of the individual predicted probability values are computed, and a failed prediction is reported if the standard deviation is greater than a specified fraction of the acceptable range (usually 30%).

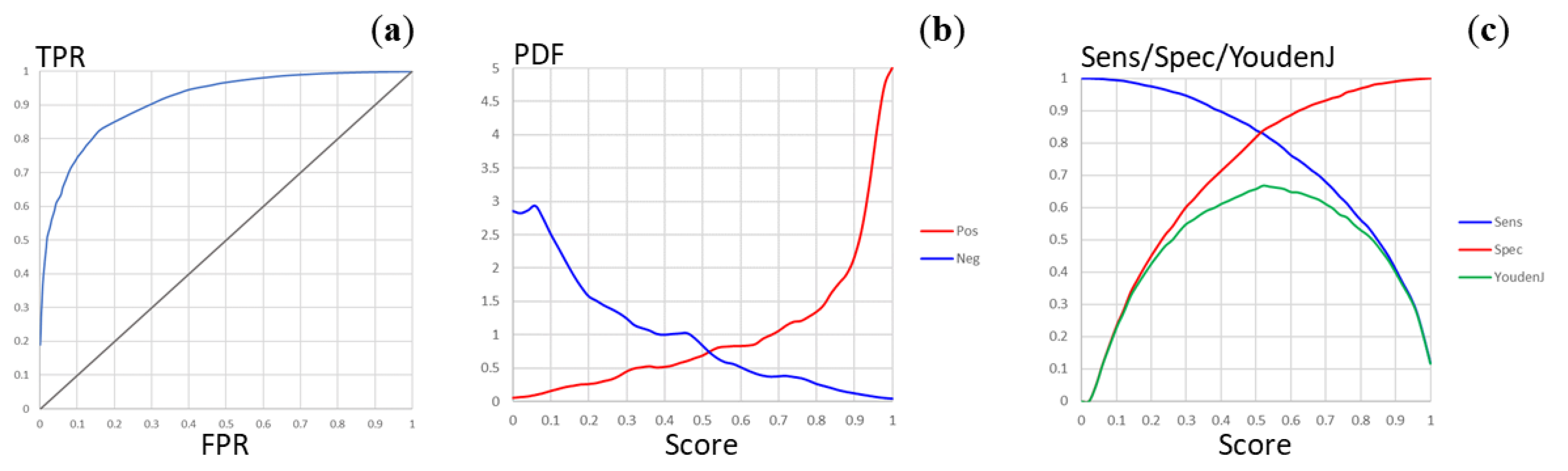
2.5. Predictive Model of Mycobacterium tuberculosis Permeability

For the full MtbPen8242 dataset, three sets of fragmental descriptors were considered during the hyperparameter optimization, containing up to 5, 6, or 8 non-hydrogen atoms. Descriptor subsets of varying size (from 100 to 1000 descriptors) were selected. Two or three hidden layers were considered in the neural network whereas the size of hidden layers relative to the number of descriptors was varied in the ranges 0.80–0.01 and 0.30–0.10 or 0.80–0.01, 0.50–0.01, and 0.30–0.10, respectively. The dropout layers with probability between 0 and 0.5 were used. The optimal model was based on 500 fragmental descriptors containing up to six non-hydrogen atoms, and two hidden layers containing 296 and 75 neurons. Unfortunately, its predictivity was lower than desired (cross-validated accuracy Acccv = 0.752, balanced accuracy BalAcccv = 0.683, sensitivity Senscv = 0.486, and specificity Speccv = 0.880, the confusion matrix is presented in Table 1). These data, as well as the inspection of individual predictions, indicated that the model failed to recognize many of the penetrating compounds, producing many false negatives. It was suggested that this bias could be caused by the dataset imbalance, with excessive non-penetrating compounds implicitly increasing their importance and the model’s preference for them.
For this reason, the balanced MtbPen5371ad dataset was prepared as described in Section 2.2, and the new model was built using hyperparameter optimization with the same search space definition, except that the fragmental descriptors up to eight atoms were not considered. The optimal model was based on 900 fragmental descriptors containing up to six non-hydrogen atoms, and two hidden layers containing 46 and 270 neurons (interestingly, the network architectures with three hidden fully connected layers did not provide significant improvements in model quality). The predictivity of this model was significantly higher, with cross-validated accuracy Acccv = 0.768, balanced accuracy BalAcccv = 0.768, sensitivity Senscv = 0.768, and specificity Speccv = 0.769 (the confusion matrix is presented in Table 1). The ROC curve for this classification is shown in Figure 3A. The area under ROC curve can be calculated as AUCROC = 0.911. The plot of the distribution densities of probability scores for the positive and negative compounds (Figure 3B) demonstrates good separation of the penetrating and the non-penetrating compounds whereas the plots of the sensitivity, specificity, and Youden’s J statistic values vs the score threshold (Figure 3C) show that the natural threshold of 0.5 is close to optimal. These parameters are similar or better than those of the most reliable models available in the literature, whereas a substantially broader applicability domain can be expected thanks to the significantly larger, representative, and diverse training set. The training of the model was completed in about 260 epochs, indicating low risk of overfitting. Nevertheless, one should bear in mind that the uncertainty of the data (stemming from the trade-offs inherent in high-throughput screening as well as from certain heuristics employed in the analysis) could limit the model predictivity.
Overall, the resulting predictive model can provide useful guidance and improve the efficiency of the virtual screening, multiparameter assessment, and lead optimization efforts for the potential antitubercular drugs. However, similar to any in silico model, its predictions should eventually be validated in vitro and/or in vivo since a specific compound of interest might be outside of the model applicability domain or could interact with the M. tuberculosis cell wall components (such as transporters) in some unexpected ways.

3. Materials and Methods

3.1. Mycobacterium tuberculosis Inhibitor Permeability Dataset

As noted above, similar to the previous studies [60,63], the compounds that have shown activity in any of the selected target-based assays were classified as permeable if they were active in any of the selected cell-based assays, otherwise, they were taken to be impermeable. As the source of (Big) raw data, the publicly available PubChem 2022 database [77] was employed. Using the automated keyword search in the local database (assay name or description contain “mycobacter” or “tubercul”), the assays potentially relevant for the antimycobacterial activity were identified. During the expert analysis of this list, the key cell-based and target-based assays for Mycobacterium tuberculosis inhibition were selected that were required to be sufficiently populated in terms of data point counts as well as sufficiently diverse and representative in the chemical and endpoint spaces (Table 2). In particular, the chemical space coverage was prioritized over the maximum reliability of specific data points, and this was reflected both in the assay selection and in the downstream standardization of the (binary) activity definitions that was based preferentially on the primary screening inhibition percentages rather than on more accurate but much less abundant secondary screening data.
DataWarrior 5.5.0 software (Idorsia Pharmaceuticals Ltd., https://openmolecules.org/ accessed on 1 December 2022) was used for the management, search, and analysis of the structure–activity databases.
Using custom PHP Web scripts accessing both local and remote databases, the assay and compound data were joined and downloaded as the TSV format files. The cleaned individual datasets were prepared using manual and automated data preprocessing and curation involving the removal of unnecessary data columns, deduplication of activity records for the compounds (that could contain different activities or equivalent or different results of repeated measurements of the same activity), standardization of the chemical structures (removal of smaller disconnected fragments, neutralization of salts), and standardization of the (binary) activity definitions and representations (see Table 2). Then, the individual datasets were merged to produce the united datasets for the selected cell-based and target-based assays. In total, the cell-based dataset contained 557,527 compounds, among which 96,040 compounds were active in at least one out of 11 assays. The target-based dataset contained 926,660 compounds, among which 9450 compounds were active in at least one out of 11 assays.
By matching this target-active dataset against the cell-based results, 8242 compounds were identified that were active in at least one target-based assay and have also been tested in at least one cell-based assay. In particular, 2671 compounds that have shown activity in at least one cell-based assay were classified as penetrating the M. tuberculosis cell wall (MtbPen = 1, positive result) whereas the remaining 5571 compounds (inactive in all 11 cell-based assays) were classified as non-penetrating (MtbPen = 0, negative result). In the present paper, this dataset is called MtbPen8242.
Since the MtbPen8242 dataset is moderately imbalanced (the ratio of non-penetrating to penetrating compounds is greater than 2.08), a balanced dataset MtbPen5371ad was prepared from it that comprises all (2671) penetrating compounds as well a diverse subset of 2700 out of 5571 non-penetrating compounds. This dataset is provided in the Supplementary Materials.

3.2. Modeling Workflow

The fragmental (substructural) descriptors representing the occurrence numbers of various substructures were calculated in the framework of the NASAWIN 2.0 [82] software. Linear paths, cycles, and branches were generated using multi-level classification that takes into account atom types, valence states, bonding patterns, and number of attached hydrogens as well as bond types. The rare fragments that are present in fewer than 100 compounds and thus cannot be used to detect general predictive relationships were removed. The fragments containing up to 8 non-hydrogen atoms were considered.
Predictive neural network models were built using the in-house Python script based on the TensorFlow 2.4.1/Keras 2.4.3 framework on a high-performance NVIDIA RTX3080Ti GPU. In addition to the standard libraries, the scikit-learn 1.1.3 machine learning framework [86] and the Optuna 3.0.3 [85] hyperparameter optimization library were used.

4. Conclusions

Thus, we have developed a predictive in silico model of the Mycobacterium tuberculosis cell wall permeability (MtbPen) derived from the extensive Big Data-based dataset and applicable to diverse drugs and drug-like compounds. Using the fragmental (substructural) descriptors representing the occurrence numbers of various substructures, we have refined the modeling workflow and evaluated the performance of different options. Playing a key role, the double cross-validation procedure generates an ensemble of neural network models based on different subsets of data that can be used to improve prediction quality and to evaluate the model applicability for a particular compound. Its novel parallelized implementation integrates the ensemble submodels (“trees”) into a single neural network (“forest”) that is fed with input data from the generator objects. This approach significantly enhanced the modeling performance. It was also found that even moderate (2:1) dataset imbalance could degrade the model quality since the excessive non-penetrating compounds implicitly increase their importance and the model’s preference for them.
Our optimal model is based on a balanced dataset of 5371 compounds (including 2671 penetrating compounds as well as a diverse representative subset of 2700 non-penetrating compounds) and 900 fragmental descriptors of up to six non-hydrogen atoms. It has quite good predictivity parameters (cross-validated accuracy Acccv = 0.768, balanced accuracy BalAcccv = 0.768, sensitivity Senscv = 0.768, specificity Speccv = 0.769, and area under ROC curve AUCROC = 0.911) that are similar or better than those of the most reliable models available in the literature, whereas a substantially broader applicability domain can be expected thanks to the significantly larger, representative, and diverse training set. The model can provide useful guidance and improve the efficiency of the virtual screening, multiparameter assessment, and lead optimization efforts for potential antitubercular drugs. However, similar to any in silico model, its predictions should eventually be validated in vitro and/or in vivo since a specific compound of interest might be outside of the model applicability domain or could interact with the M. tuberculosis cell wall components (such as transporters) in some unexpected ways.
This predictive model will be made available online at our ADMET Prediction Service page (http://qsar.chem.msu.ru/admet/ accessed on 1 December 2022), enabling the evaluation and optimization of the Mycobacterium tuberculosis cell wall permeability and other key ADMET properties of potential antitubercular agents and other drug compounds.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28020633/s1, structure–permeability dataset.

Author Contributions

Conceptualization, E.V.R., S.K.I. and V.A.P.; methodology, E.V.R. and V.A.P.; software, E.V.R.; investigation, E.V.R., G.V.A., S.K.I. and V.A.P.; data curation, E.V.R.; writing—original draft preparation, E.V.R., G.V.A. and V.A.P.; writing—review and editing, E.V.R., S.K.I. and V.A.P.; supervision, S.K.I. and V.A.P.; project administration, S.K.I.; funding acquisition, S.K.I. and V.A.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was carried out within the framework of the Strategic Academic Leadership Program “Priority 2030” of the Lobachevsky State University of Nizhny Novgorod (project no. N-473-99). The development of the basic approaches to permeability prediction was supported by State Assignment of the Lomonosov Moscow State University (topic no. 121021000105-7).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Not applicable.

References

  1. Friedman, L.N.; Dedicoat, M.; Davies, P.D.O. (Eds.) Clinical Tuberculosis, 6th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2020; ISBN 978-1-351-24998-0. [Google Scholar]
  2. Sharma, S.K.; Mohan, A. Textbook of Tuberculosis and Nontuberculous Mycobacterial Diseases, 3rd ed.; Jaypee Brothers Medical Publishers: New Delhi, India, 2020; ISBN 978-93-89129-21-2. [Google Scholar]
  3. Chai, Q.; Zhang, Y.; Liu, C.H. Mycobacterium tuberculosis: An adaptable pathogen associated with multiple human diseases. Front. Cell. Infect. Microbiol. 2018, 8, 158. [Google Scholar] [CrossRef]
  4. World Health Organization. Global Tuberculosis Report 2022; World Health Organization: Geneva, Switzerland, 2022; ISBN 978-92-4-006172-9.
  5. Goossens, S.N.; Sampson, S.L.; Van Rie, A. Mechanisms of drug-induced tolerance in Mycobacterium tuberculosis. Clin. Microbiol. Rev. 2020, 34, e00141-20. [Google Scholar] [CrossRef]
  6. Liebenberg, D.; Gordhan, B.G.; Kana, B.D. Drug resistant tuberculosis: Implications for transmission, diagnosis, and disease management. Front. Cell. Infect. Microbiol. 2022, 12, 943545. [Google Scholar] [CrossRef]
  7. Li, H.; Yuan, J.; Duan, S.; Pang, Y. Resistance and tolerance of Mycobacterium tuberculosis to antimicrobial agents–How M. tuberculosis can escape antibiotics. WIREs Mech. Dis. 2022, 14, e1573. [Google Scholar] [CrossRef] [PubMed]
  8. Poulton, N.C.; Rock, J.M. Unraveling the mechanisms of intrinsic drug resistance in Mycobacterium tuberculosis. Front. Cell. Infect. Microbiol. 2022, 12, 997283. [Google Scholar] [CrossRef] [PubMed]
  9. Bendre, A.D.; Peters, P.J.; Kumar, J. Tuberculosis: Past, present and future of the treatment and drug discovery research. Curr. Res. Pharmacol. Drug Discov. 2021, 2, 100037. [Google Scholar] [CrossRef] [PubMed]
  10. Chauhan, A.; Kumar, M.; Kumar, A.; Kanchan, K. Comprehensive review on mechanism of action, resistance and evolution of antimycobacterial drugs. Life Sci. 2021, 274, 119301. [Google Scholar] [CrossRef] [PubMed]
  11. Perveen, S.; Sharma, R. Screening approaches and therapeutic targets: The two driving wheels of tuberculosis drug discovery. Biochem. Pharmacol. 2022, 197, 114906. [Google Scholar] [CrossRef]
  12. Bhat, Z.S.; Rather, M.A.; Maqbool, M.; Lah, H.U.; Yousuf, S.K.; Ahmad, Z. Cell wall: A versatile fountain of drug targets in Mycobacterium tuberculosis. Biomed. Pharmacother. 2017, 95, 1520–1534. [Google Scholar] [CrossRef]
  13. Dulberger, C.L.; Rubin, E.J.; Boutte, C.C. The mycobacterial cell envelope–A moving target. Nat. Rev. Microbiol. 2020, 18, 47–59. [Google Scholar] [CrossRef]
  14. Abrahams, K.A.; Besra, G.S. Synthesis and recycling of the mycobacterial cell envelope. Curr. Opin. Microbiol. 2021, 60, 58–65. [Google Scholar] [CrossRef]
  15. Kuang, W.; Zhang, H.; Wang, X.; Yang, P. Overcoming Mycobacterium tuberculosis through small molecule inhibitors to break down cell wall synthesis. Acta Pharm. Sin. B 2022, 12, 3201–3214. [Google Scholar] [CrossRef]
  16. Kumar, N.; Sharma, S.; Kaushal, P.S. Protein synthesis in Mycobacterium tuberculosis as a potential target for therapeutic interventions. Mol. Aspects Med. 2021, 81, 101002. [Google Scholar] [CrossRef] [PubMed]
  17. Reiche, M.A.; Warner, D.F.; Mizrahi, V. Targeting DNA replication and repair for the development of novel therapeutics against tuberculosis. Front. Mol. Biosci. 2017, 4, 75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Das, S.; Garg, T.; Srinivas, N.; Dasgupta, A.; Chopra, S. Targeting DNA gyrase to combat Mycobacterium tuberculosis: An update. Curr. Top. Med. Chem. 2019, 19, 579–593. [Google Scholar] [CrossRef]
  19. Miggiano, R.; Morrone, C.; Rossi, F.; Rizzi, M. Targeting genome integrity in Mycobacterium tuberculosis: From nucleotide synthesis to DNA replication and repair. Molecules 2020, 25, 1205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Stephanie, F.; Tambunan, U.S.F.; Siahaan, T.J. M. tuberculosis transcription machinery: A review on the mycobacterial RNA polymerase and drug discovery efforts. Life 2022, 12, 1774. [Google Scholar] [CrossRef]
  21. Roy, K.K.; Wani, M.A. Emerging opportunities of exploiting mycobacterial electron transport chain pathway for drug-resistant tuberculosis drug discovery. Expert Opin. Drug Discov. 2020, 15, 231–241. [Google Scholar] [CrossRef]
  22. Urban, M.; Šlachtová, V.; Brulíková, L. Small organic molecules targeting the energy metabolism of Mycobacterium tuberculosis. Eur. J. Med. Chem. 2021, 212, 113139. [Google Scholar] [CrossRef] [PubMed]
  23. Hasenoehrl, E.J.; Wiggins, T.J.; Berney, M. Bioenergetic inhibitors: Antibiotic efficacy and mechanisms of action in Mycobacterium tuberculosis. Front. Cell. Infect. Microbiol. 2020, 10, 611683. [Google Scholar] [CrossRef]
  24. Samuels, A.N.; Wang, E.R.; Harrison, G.A.; Valenta, J.C.; Stallings, C.L. Understanding the contribution of metabolism to Mycobacterium tuberculosis drug tolerance. Front. Cell. Infect. Microbiol. 2022, 12, 958555. [Google Scholar] [CrossRef] [PubMed]
  25. Yelamanchi, S.D.; Surolia, A. Targeting amino acid metabolism of Mycobacterium tuberculosis for developing inhibitors to curtail its survival. IUBMB Life 2021, 73, 643–658. [Google Scholar] [CrossRef] [PubMed]
  26. Saxena, A.K.; Singh, A. Mycobacterial tuberculosis enzyme targets and their inhibitors. Curr. Top. Med. Chem. 2019, 19, 337–355. [Google Scholar] [CrossRef] [PubMed]
  27. Huszár, S.; Chibale, K.; Singh, V. The quest for the holy grail: New antitubercular chemical entities, targets and strategies. Drug Discov. Today 2020, 25, 772–780. [Google Scholar] [CrossRef]
  28. Bahuguna, A.; Rawat, D.S. An overview of new antitubercular drugs, drug candidates, and their targets. Med. Res. Rev. 2020, 40, 263–292. [Google Scholar] [CrossRef] [PubMed]
  29. Shetye, G.S.; Franzblau, S.G.; Cho, S. New tuberculosis drug targets, their inhibitors, and potential therapeutic impact. Transl. Res. 2020, 220, 68–97. [Google Scholar] [CrossRef] [PubMed]
  30. Oh, S.; Trifonov, L.; Yadav, V.D.; Barry, C.E.; Boshoff, H.I. Tuberculosis drug discovery: A decade of hit assessment for defined targets. Front. Cell. Infect. Microbiol. 2021, 11, 611304. [Google Scholar] [CrossRef]
  31. Angula, K.T.; Legoabe, L.J.; Beteck, R.M. Chemical classes presenting novel antituberculosis agents currently in different phases of drug development: A 2010–2020 review. Pharmaceuticals 2021, 14, 461. [Google Scholar] [CrossRef]
  32. Yang, L.; Hu, X.; Chai, X.; Ye, Q.; Pang, J.; Li, D.; Hou, T. Opportunities for overcoming tuberculosis: Emerging targets and their inhibitors. Drug Discov. Today 2022, 27, 326–336. [Google Scholar] [CrossRef]
  33. Mi, J.; Gong, W.; Wu, X. Advances in key drug target identification and new drug development for tuberculosis. Biomed. Res. Int. 2022, 2022, 5099312. [Google Scholar] [CrossRef]
  34. Singh, V.; Chibale, K. Strategies to combat multi-drug resistance in tuberculosis. Acc. Chem. Res. 2021, 54, 2361–2376. [Google Scholar] [CrossRef]
  35. Torfs, E.; Piller, T.; Cos, P.; Cappoen, D. Opportunities for overcoming Mycobacterium tuberculosis drug resistance: Emerging mycobacterial targets and host-directed therapy. Int. J. Mol. Sci. 2019, 20, 2868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Stephanie, F.; Saragih, M.; Tambunan, U.S.F. Recent progress and challenges for drug-resistant tuberculosis treatment. Pharmaceutics 2021, 13, 592. [Google Scholar] [CrossRef] [PubMed]
  37. Modak, B.; Girkar, S.; Narayan, R.; Kapoor, S. Mycobacterial membranes as actionable targets for lipid-centric therapy in tuberculosis. J. Med. Chem. 2022, 65, 3046–3065. [Google Scholar] [CrossRef] [PubMed]
  38. Fullam, E.; Young, R.J. Physicochemical properties and Mycobacterium tuberculosis transporters: Keys to efficacious antitubercular drugs? RSC Med. Chem. 2021, 12, 43–56. [Google Scholar] [CrossRef]
  39. de Oliveira, M.C.B.; Balan, A. The ATP-Binding Cassette (ABC) transport systems in Mycobacterium tuberculosis: Structure, function, and possible targets for therapeutics. Biology 2020, 9, 443. [Google Scholar] [CrossRef]
  40. Stelitano, G.; Sammartino, J.C.; Chiarelli, L.R. Multitargeting compounds: A promising strategy to overcome multi-drug resistant tuberculosis. Molecules 2020, 25, 1239. [Google Scholar] [CrossRef] [Green Version]
  41. Jeong, E.-K.; Lee, H.-J.; Jung, Y.-J. Host-directed therapies for tuberculosis. Pathogens 2022, 11, 1291. [Google Scholar] [CrossRef] [PubMed]
  42. Hu, Z.; Lu, S.-H.; Lowrie, D.B.; Fan, X.-Y. Research advances for virus-vectored tuberculosis vaccines and latest findings on tuberculosis vaccine development. Front. Immunol. 2022, 13, 895020. [Google Scholar] [CrossRef]
  43. Flores-Valdez, M.A.; Kupz, A.; Subbian, S. Recent developments in mycobacteria-based live attenuated vaccine candidates for tuberculosis. Biomedicines 2022, 10, 2749. [Google Scholar] [CrossRef]
  44. Bouzeyen, R.; Javid, B. Therapeutic vaccines for tuberculosis: An overview. Front. Immunol. 2022, 13, 878471. [Google Scholar] [CrossRef] [PubMed]
  45. Rajput, A.; Mandlik, S.; Pokharkar, V. Nanocarrier-based approaches for the efficient delivery of anti-tubercular drugs and vaccines for management of tuberculosis. Front. Pharmacol. 2021, 12, 749945. [Google Scholar] [CrossRef] [PubMed]
  46. Macêdo, D.C.D.S.; Cavalcanti, I.D.L.; Medeiros, S.M.D.F.R.D.S.; de Souza, J.B.; Lira Nogueira, M.C.D.B.; Cavalcanti, I.M.F. Nanotechnology and tuberculosis: An old disease with new treatment strategies. Tuberculosis 2022, 135, 102208. [Google Scholar] [CrossRef] [PubMed]
  47. Dalberto, P.F.; de Souza, E.V.; Abbadi, B.L.; Neves, C.E.; Rambo, R.S.; Ramos, A.S.; Macchi, F.S.; Machado, P.; Bizarro, C.V.; Basso, L.A. Handling the hurdles on the way to anti-tuberculosis drug development. Front. Chem. 2020, 8, 586294. [Google Scholar] [CrossRef] [PubMed]
  48. Abrahams, K.A.; Besra, G.S. Mycobacterial drug discovery. RSC Med. Chem. 2020, 11, 1354–1365. [Google Scholar] [CrossRef]
  49. Craggs, P.D.; de Carvalho, L.P.S. Bottlenecks and opportunities in antibiotic discovery against Mycobacterium tuberculosis. Curr. Opin. Microbiol. 2022, 69, 102191. [Google Scholar] [CrossRef] [PubMed]
  50. Macalino, S.J.Y.; Billones, J.B.; Organo, V.G.; Carrillo, M.C.O. In silico strategies in tuberculosis drug discovery. Molecules 2020, 25, 665. [Google Scholar] [CrossRef] [Green Version]
  51. Machado, D.; Girardini, M.; Viveiros, M.; Pieroni, M. Challenging the drug-likeness dogma for new drug discovery in tuberculosis. Front. Microbiol. 2018, 9, 1367. [Google Scholar] [CrossRef] [Green Version]
  52. Tanner, L.; Denti, P.; Wiesner, L.; Warner, D.F. Drug permeation and metabolism in Mycobacterium tuberculosis: Prioritising local exposure as essential criterion in new TB drug development. IUBMB Life 2018, 70, 926–937. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Jarlier, V.; Nikaido, H. Permeability barrier to hydrophilic solutes in Mycobacterium chelonei. J. Bacteriol. 1990, 172, 1418–1423. [Google Scholar] [CrossRef]
  54. Trias, J.; Benz, R. Permeability of the cell wall of Mycobacterium smegmatis. Mol. Microbiol. 1994, 14, 283–290. [Google Scholar] [CrossRef] [PubMed]
  55. Lee, S.-H.; Choi, M.; Kim, P.; Myung, P.K. 3D-QSAR and cell wall permeability of antitubercular nitroimidazoles against Mycobacterium tuberculosis. Molecules 2013, 18, 13870–13885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Hong, X.; Hopfinger, A.J. Molecular modeling and simulation of Mycobacterium tuberculosis cell wall permeability. Biomacromolecules 2004, 5, 1066–1077. [Google Scholar] [CrossRef]
  57. Merget, B.; Zilian, D.; Müller, T.; Sotriffer, C.A. MycPermCheck: The Mycobacterium tuberculosis permeability prediction tool for small molecules. Bioinformatics 2013, 29, 62–68. [Google Scholar] [CrossRef] [Green Version]
  58. Ekins, S.; Bradford, J.; Dole, K.; Spektor, A.; Gregory, K.; Blondeau, D.; Hohman, M.; Bunin, B.A. A collaborative database and computational models for tuberculosis drug discovery. Mol. Biosyst. 2010, 6, 840–851. [Google Scholar] [CrossRef]
  59. Irwin, J.J.; Shoichet, B.K. ZINC–A free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. [Google Scholar] [CrossRef] [Green Version]
  60. Janardhan, S.; Ram Vivek, M.; Sastry, G.N. Modeling the permeability of drug-like molecules through the cell wall of Mycobacterium tuberculosis: An analogue based approach. Mol. Biosyst. 2016, 12, 3377–3384. [Google Scholar] [CrossRef] [PubMed]
  61. Gaulton, A.; Hersey, A.; Nowotka, M.; Bento, A.P.; Chambers, J.; Mendez, D.; Mutowo, P.; Atkinson, F.; Bellis, L.J.; Cibrián-Uhalte, E.; et al. The ChEMBL database in 2017. Nucleic Acids Res. 2017, 45, D945–D954. [Google Scholar] [CrossRef]
  62. Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
  63. Nagamani, S.; Sastry, G.N. Mycobacterium tuberculosis cell wall permeability model generation using chemoinformatics and machine learning approaches. ACS Omega 2021, 6, 17472–17482. [Google Scholar] [CrossRef] [PubMed]
  64. Zefirov, N.S.; Palyulin, V.A. Fragmental approach in QSPR. J. Chem. Inf. Comput. Sci. 2002, 42, 1112–1122. [Google Scholar] [CrossRef] [PubMed]
  65. Artemenko, N.V.; Baskin, I.I.; Palyulin, V.A.; Zefirov, N.S. Artificial neural network and fragmental approach in prediction of physicochemical properties of organic compounds. Russ. Chem. Bull. 2003, 52, 20–29. [Google Scholar] [CrossRef]
  66. Artemenko, N.V.; Baskin, I.I.; Palyulin, V.A.; Zefirov, N.S. Prediction of physical properties of organic compounds using artificial neural networks within the substructure approach. Dokl. Chem. 2001, 381, 317–320. [Google Scholar] [CrossRef]
  67. Radchenko, E.V.; Dyabina, A.S.; Palyulin, V.A.; Zefirov, N.S. Prediction of human intestinal absorption of drug compounds. Russ. Chem. Bull. 2016, 65, 576–580. [Google Scholar] [CrossRef]
  68. Dyabina, A.S.; Radchenko, E.V.; Palyulin, V.A.; Zefirov, N.S. Prediction of blood-brain barrier permeability of organic compounds. Dokl. Biochem. Biophys. 2016, 470, 371–374. [Google Scholar] [CrossRef]
  69. Radchenko, E.V.; Dyabina, A.S.; Palyulin, V.A. Towards deep neural network models for the prediction of the blood-brain barrier permeability for diverse organic compounds. Molecules 2020, 25, 5901. [Google Scholar] [CrossRef] [PubMed]
  70. Radchenko, E.V.; Rulev, Y.A.; Safanyaev, A.Y.; Palyulin, V.A.; Zefirov, N.S. Computer-aided estimation of the hERG-mediated cardiotoxicity risk of potential drug components. Dokl. Biochem. Biophys. 2017, 473, 128–131. [Google Scholar] [CrossRef]
  71. Artemenko, N.V.; Palyulin, V.A.; Zefirov, N.S. Neural-network model of the lipophilicity of organic compounds based on fragment descriptors. Dokl. Chem. 2002, 383, 114–116. [Google Scholar] [CrossRef]
  72. Berishvili, V.P.; Kuimov, A.N.; Voronkov, A.E.; Radchenko, E.V.; Kumar, P.; Choonara, Y.E.; Pillay, V.; Kamal, A.; Palyulin, V.A. Discovery of novel tankyrase inhibitors through molecular docking-based virtual screening and molecular dynamics simulation studies. Molecules 2020, 25, 3171. [Google Scholar] [CrossRef]
  73. Vasilenko, D.A.; Sadovnikov, K.S.; Sedenkova, K.N.; Karlov, D.S.; Radchenko, E.V.; Grishin, Y.K.; Rybakov, V.B.; Kuznetsova, T.S.; Zamoyski, V.L.; Grigoriev, V.V.; et al. A facile approach to bis(isoxazoles), promising ligands of the AMPA receptor. Molecules 2021, 26, 6411. [Google Scholar] [CrossRef]
  74. Makhaeva, G.F.; Kovaleva, N.V.; Boltneva, N.P.; Rudakova, E.V.; Lushchekina, S.V.; Astakhova, T.Y.; Serkov, I.V.; Proshin, A.N.; Radchenko, E.V.; Palyulin, V.A.; et al. Bis-amiridines as acetylcholinesterase and butyrylcholinesterase inhibitors: N-Functionalization determines the multitarget anti-Alzheimer’s activity profile. Molecules 2022, 27, 1060. [Google Scholar] [CrossRef]
  75. Sedenkova, K.N.; Zverev, D.V.; Nazarova, A.A.; Lavrov, M.I.; Radchenko, E.V.; Grishin, Y.K.; Gabrel’yan, A.V.; Zamoyski, V.L.; Grigoriev, V.V.; Averina, E.B.; et al. Novel nanomolar allosteric modulators of AMPA receptor of bis(pyrimidine) series: Synthesis, biotesting and SAR analysis. Molecules 2022, 27, 8252. [Google Scholar] [CrossRef]
  76. Elkina, N.A.; Grishchenko, M.V.; Shchegolkov, E.V.; Makhaeva, G.F.; Kovaleva, N.V.; Rudakova, E.V.; Boltneva, N.P.; Lushchekina, S.V.; Astakhova, T.Y.; Radchenko, E.V.; et al. New multifunctional agents for potential Alzheimer’s disease treatment based on tacrine conjugates with 2-arylhydrazinylidene-1,3-diketones. Biomolecules 2022, 12, 1551. [Google Scholar] [CrossRef] [PubMed]
  77. Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem in 2021: New data content and improved web interfaces. Nucleic Acids Res. 2021, 49, D1388–D1395. [Google Scholar] [CrossRef]
  78. Tetko, I.V.; Engkvist, O.; Koch, U.; Reymond, J.-L.; Chen, H. BIGCHEM: Challenges and opportunities for Big Data analysis in chemistry. Mol. Inform. 2016, 35, 615–621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  79. Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef] [PubMed]
  80. Fourches, D.; Muratov, E.; Tropsha, A. Trust, but verify: On the importance of chemical structure curation in cheminformatics and QSAR modeling research. J. Chem. Inf. Model. 2010, 50, 1189–1204. [Google Scholar] [CrossRef]
  81. Fourches, D.; Muratov, E.; Tropsha, A. Trust, but verify II: A practical guide to chemogenomics data curation. J. Chem. Inf. Model. 2016, 56, 1243–1252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  82. Baskin, I.I.; Halberstam, N.M.; Artemenko, N.V.; Palyulin, V.A.; Zefirov, N.S. NASAWIN–A universal software for QSPR/QSAR studies. In EuroQSAR 2002 Designing Drugs and Crop Protectants: Processes, Problems and Solutions; Ford, M., Livingstone, D., Dearden, J., van de Waterbeemd, H., Eds.; Blackwell Science Inc.: New York, NY, USA, 2003; pp. 260–263. ISBN 978-1-4051-2516-1. [Google Scholar]
  83. Filzmoser, P.; Liebmann, B.; Varmuza, K. Repeated double cross validation. J. Chemom. 2009, 23, 160–171. [Google Scholar] [CrossRef]
  84. Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems: NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 972–981, ISBN 978-1-5108-6096-4. [Google Scholar] [CrossRef]
  85. Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. Available online: http://arxiv.org/abs/1907.10902 (accessed on 18 December 2022).
  86. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
Molecules 28 00633 g001 550
Figure 1. General modeling workflow.
Figure 1. General modeling workflow.
Molecules 28 00633 g001
Molecules 28 00633 g002 550
Figure 2. Basic architecture of the “forest” neural network model.
Figure 2. Basic architecture of the “forest” neural network model.
Molecules 28 00633 g002
Molecules 28 00633 g003 550
Figure 3. Plots of the model quality parameters for the MtbPen classification model. (a) The ROC curve (TPR, true positive rate; FPR, false positive rate). (b) The distribution densities (PDF, probability density function) of the penetration probability scores for the positive and negative compounds. (c) Dependence of the sensitivity, specificity, and Youden’s J statistic on the score threshold.
Figure 3. Plots of the model quality parameters for the MtbPen classification model. (a) The ROC curve (TPR, true positive rate; FPR, false positive rate). (b) The distribution densities (PDF, probability density function) of the penetration probability scores for the positive and negative compounds. (c) Dependence of the sensitivity, specificity, and Youden’s J statistic on the score threshold.
Molecules 28 00633 g003
Table
Table 1. Confusion matrices for the MtbPen classification models.
Table 1. Confusion matrices for the MtbPen classification models.
DatasetMtbPen8242MtbPen5371ad
PredictedPredicted
PositiveNegativePositiveNegative
ObservedPositive143512362214457
Negative52850434372263
Table
Table 2. PubChem assays used in compiling the MtbPen datasets.
Table 2. PubChem assays used in compiling the MtbPen datasets.
AID 1IDTypeActivity/Compound Count 2DescriptionActivity Condition 3
1332C01Cell1118High throughput screen to identify inhibitors of Mycobacterium tuberculosis H37RvInh30
1626C02Cell215,397High throughput screen to identify inhibitors of Mycobacterium tuberculosis H37RvInh30
1949C03Cell100,697High throughput screen of 100,000 compound library to identify inhibitors of Mycobacterium tuberculosis H37RvInh30
2842C04Cell23,823High throughput screen of a putative kinase compound library to identify inhibitors of Mycobacterium tuberculosis H37RvInh30
449762C05Cell327,669High throughput screening assay used to identify novel compounds that inhibit Mycobacterium tuberculosis in 7H9 mediaInh30
1259343C06Cell6225High throughput screening of small molecules that kill Mycobacterium tuberculosisInh30
1259417C07Cell1105High throughput whole cell screen to identify inhibitors of Mycobacterium tuberculosisInh30
1671161C08Cell96,022/86,588Phenotypic growth assay for Mycobacterium tuberculosis grown for 4 days on DPPC, cholesterol, tyloxapol-based mediaInh30
1671162C09Cell103,984/86,574Phenotypic growth assay for Mycobacterium tuberculosis grown for 3 days on 7H9, glucose tyloxapol-based mediaInh30
1671174C10Cell53,171/53,165Phenotypic assay to identify agents that inhibit growth of Mycobacterium tuberculosisInh30
488890C11Cell324,545Elucidation of physiology of non-replicating, drug-tolerant Mycobacterium tuberculosisInh30
375T01Target10,011/10,009Mycobacterium tuberculosis pantothenate synthetase assayOutcome
1376T02Target216,162/215,860Inhibitors of mycobacterial glucosamine-1-phosphate acetyl transferase (GlmU)Outcome
2606T03Target324,858/324,747Primary biochemical high throughput screening assay to identify inhibitors of the membrane-associated serine protease Rv3671c in M. tuberculosisOutcome
504406T04Target324,148/324,048High throughput screening of inhibitors of Mycobacterium tuberculosis UDP-galactopyranose mutase (UGM) enzymeOutcome
540299T05Target103,205/102,628A screen for compounds that inhibit the MenB enzyme of Mycobacterium tuberculosisOutcome
588335T06Target356,407/356,160Counterscreen for inhibitors of the fructose-bisphosphate aldolase (FBA) of M. tuberculosisOutcome
602481T07Target356,486/353,572Mycobacterium tuberculosis BioA enzyme inhibitorOutcome
1159583T08Target301,203/300,060High throughput screen for small molecule inhibitors of a hypoxia-regulated fluorescent biosensor in Mycobacterium tuberculosisOutcome
1671160T09Target8874/8841Assay for Asp RNA synthetase-1 from Mycobacterium tuberculosisInh30
1671178T10Target67,199/66,591Mycobacterium tuberculosis polyketide synthase 13 thioesterase (PKS13)Inh30
2221T11Target293,466/293,376Cell-free homogenous primary high throughput screen to identify inhibitors of RecA intein splicing activityOutcome
1 PubChem assay ID. 2 Number of raw activity records and (if different) number of compounds after deduplication and preprocessing. 3 Conditions used to identify active compounds: Inh30–Inhibition > 30%; Outcome–Activity Outcome = Active.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Radchenko, E.V.; Antonyan, G.V.; Ignatov, S.K.; Palyulin, V.A. Machine Learning Prediction of Mycobacterial Cell Wall Permeability of Drugs and Drug-like Compounds. Molecules 2023, 28, 633. https://doi.org/10.3390/molecules28020633

AMA Style

Radchenko EV, Antonyan GV, Ignatov SK, Palyulin VA. Machine Learning Prediction of Mycobacterial Cell Wall Permeability of Drugs and Drug-like Compounds. Molecules. 2023; 28(2):633. https://doi.org/10.3390/molecules28020633

Chicago/Turabian Style

Radchenko, Eugene V., Grigory V. Antonyan, Stanislav K. Ignatov, and Vladimir A. Palyulin. 2023. "Machine Learning Prediction of Mycobacterial Cell Wall Permeability of Drugs and Drug-like Compounds" Molecules 28, no. 2: 633. https://doi.org/10.3390/molecules28020633

Article Metrics

Back to TopTop