Ternary Mixed Micelle Hexadecyltrimethylammonium Bromide—Dodecyltrimethylammonium Bromide—Sodium Deoxycholate: Gibbs Free Energy of Mixing and Excess Gibbs Energy of Mixing
Abstract
:1. Introduction
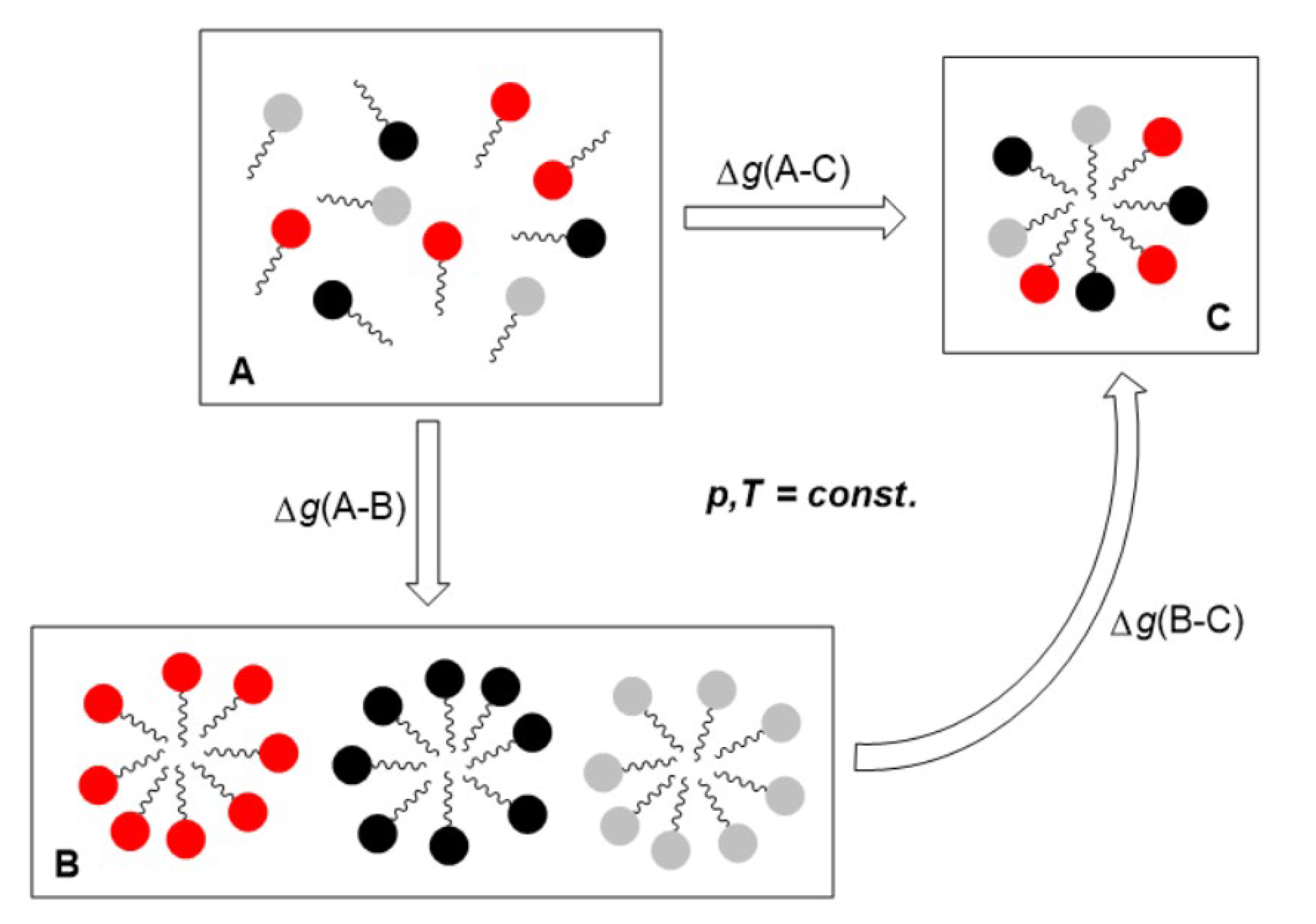
2. Results and Discussion
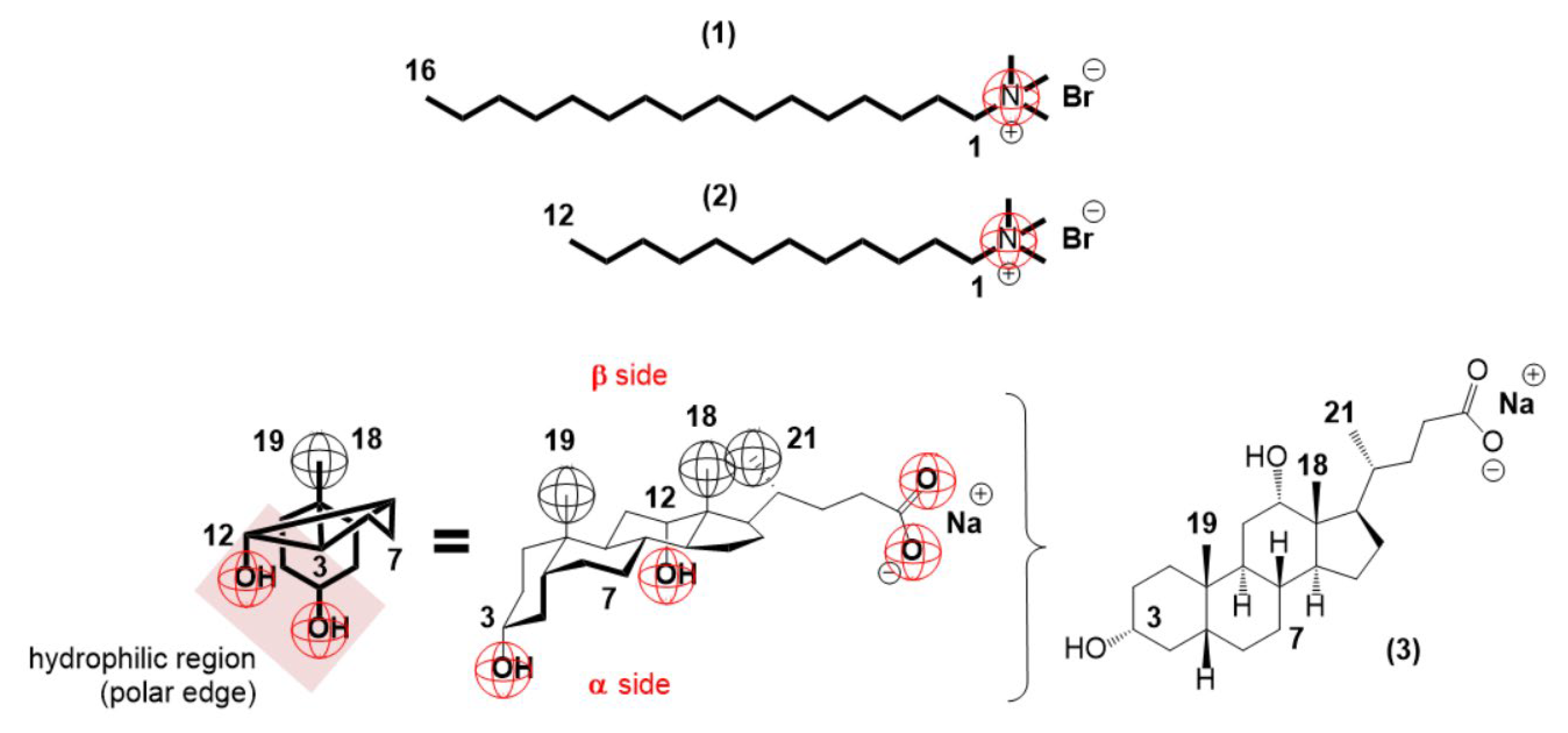
3. Materials and Methods
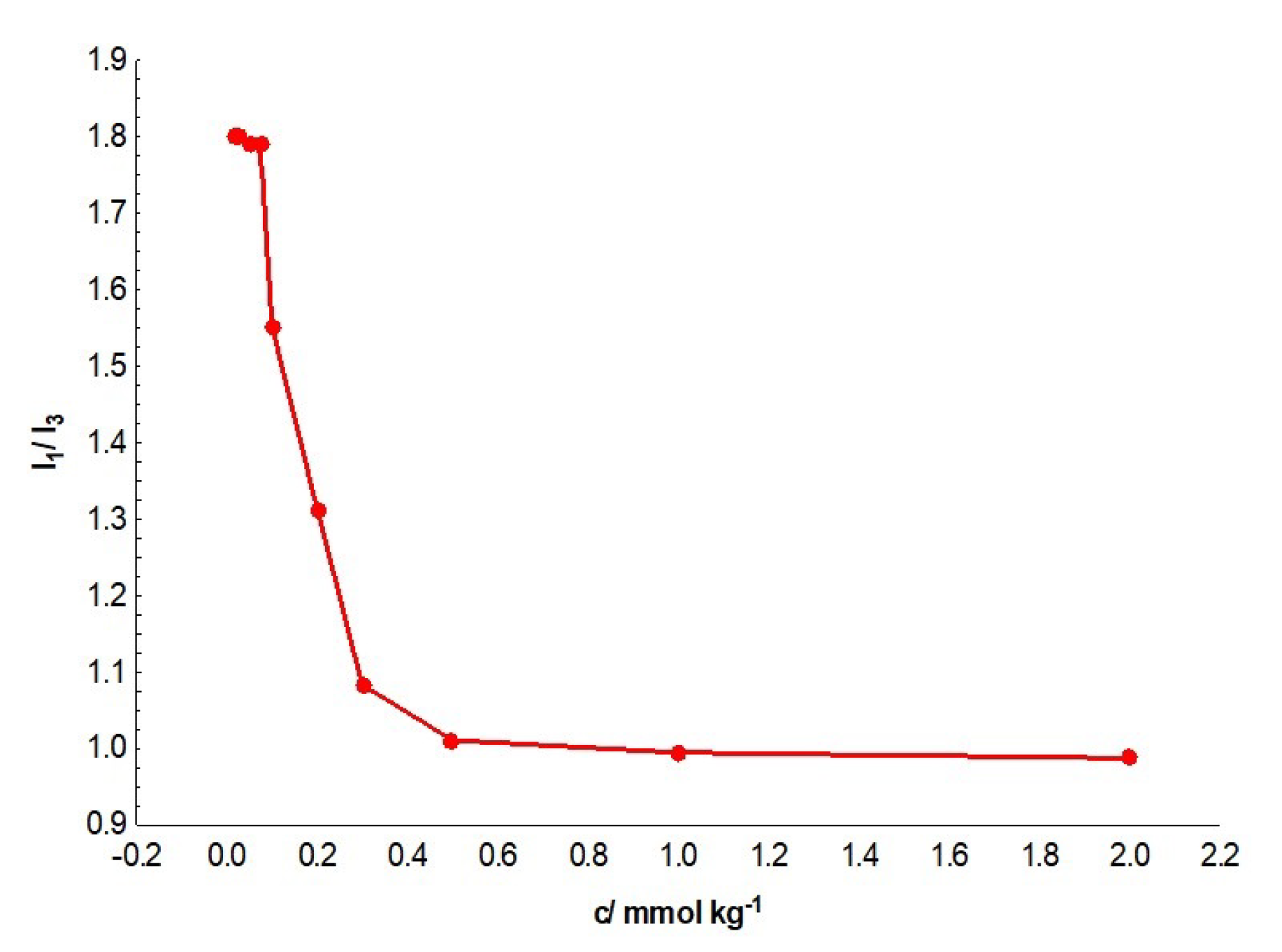
3.1. Determinations of Critical Micellar Concentration
3.2. Conductivity Measurements
3.3. Conductivity Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Appendix A
Appendix B
| 278.1 K | 283.1 K | 288.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 11.541 | 11.336 | 11.968 | ||||||
| 0.125 | 1.1347 | 0.54 | −5.83 | 1.2236 | 0.53 | −5.59 | 1.2373 | 0.53 | −5.82 |
| 0.25 | 1.292 | 0.62 | −3.94 | 1.3209 | 0.61 | −3.93 | 1.3995 | 0.61 | −3.98 |
| 0.5 | 1.3505 | 0.8 | −1.98 | 1.3937 | 0.79 | −1.97 | 1.4857 | 0.78 | −2.03 |
| 0.75 | 1.1186 | 0.92 | −1.44 | 1.1532 | 0.91 | −1.53 | 1.231 | 0.9 | −1.67 |
| 0.875 | 0.6595 | 0.79 | −5.39 | 0.9829 | 0.91 | −2.53 | 0.9342 | 0.85 | −3.75 |
| 1 | 0.9218 | 0.9627 | 1.043 | ||||||
| 293.1 K | 298.1 K | 303.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 13.431 | 14.195 | 14.154 | ||||||
| 0.125 | 1.2769 | 0.54 | −5.98 | 1.29 | 0.53 | −6.36 | 1.3318 | 0.51 | −6.69 |
| 0.25 | 1.5974 | 0.62 | −3.69 | 1.7761 | 0.62 | −3.73 | 1.8451 | 0.59 | −4.12 |
| 0.5 | 1.454 | 0.77 | −2.46 | 1.4785 | 0.73 | −3.04 | 1.5562 | 0.69 | −3.56 |
| 0.75 | 1.4066 | 0.98 | 0.11 | 1.548 | 0.93 | −1.05 | 1.7702 | 0.87 | −1.81 |
| 0.875 | 1.0048 | 0.87 | −3.53 | 1.2032 | 0.88 | −3.13 | 1.0255 | 0.77 | −5.47 |
| 1 | 1.0795 | 1.2513 | 1.5614 | ||||||
| 308.1 K | 313.1 K | ||||||||
| α1 | CMC | x1 | β | CMC | x1 | β | |||
| 0 | 18.59 | 21.161 | |||||||
| 0.125 | 1.4271 | 0.53 | −6.78 | 1.5269 | 0.53 | −6.7 | |||
| 0.25 | 1.964 | 0.62 | −4.12 | 2.0639 | 0.62 | −4.25 | |||
| 0.5 | 1.6482 | 0.73 | −3.41 | 2.028 | 0.77 | −2.68 | |||
| 0.75 | 1.6398 | 0.88 | −2.24 | 1.9487 | 0.96 | −0.65 | |||
| 0.875 | 1.379 | 0.88 | −3.39 | 1.4815 | 0.89 | −3.27 | |||
| 1 | 1.4525 | 1.526 | |||||||
| 278.1 K | 283.1 K | 288.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 62.565 | 59.484 | 59.773 | ||||||
| 0.077 | 0.4622 | 0.47 | −9.08 | 0.4849 | 0.47 | −8.86 | 0.5181 | 0.47 | −8.76 |
| 0.142 | 0.4421 | 0.51 | −8.21 | 0.5314 | 0.50 | −7.46 | 0.5862 | 0.50 | −7.23 |
| 0.25 | 0.2247 | 0.53 | −10.00 | 0.2371 | 0.53 | −9.89 | 0.2359 | 0.53 | −9.98 |
| 0.33 | 0.1204 | 0.54 | −12.11 | 0.1115 | 0.54 | −12.53 | 0.1249 | 0.54 | −12.15 |
| 0.368 | 0.1084 | 0.55 | −12.41 | 0.1208 | 0.55 | −11.98 | 0.1200 | 0.54 | −12.19 |
| 1 | 0.9218 | 0.9627 | 1.043 | ||||||
| 293.1 K | 298.1 K | 303.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 63.919 | 65.737 | 66.675 | ||||||
| 0.077 | 0.5305 | 0.47 | −8.87 | 0.5945 | 0.46 | −8.75 | 0.6029 | 0.45 | −9.13 |
| 0.142 | 0.9253 | 0.50 | −5.61 | 0.9521 | 0.49 | −5.85 | 10.113 | 0.48 | −6.06 |
| 0.25 | 0.2461 | 0.53 | −10.01 | 0.2656 | 0.52 | −10.07 | 0.3052 | 0.51 | −10.00 |
| 0.33 | 0.1319 | 0.54 | −12.13 | 0.1464 | 0.53 | −12.08 | 0.2129 | 0.53 | −11.08 |
| 0.368 | 0.1333 | 0.54 | −11.96 | 0.1708 | 0.54 | −11.33 | 0.2051 | 0.53 | −11.10 |
| 1 | 10.795 | 12.513 | 15.614 | ||||||
| 308.1 K | 313.1 K | ||||||||
| α1 | CMC | x1 | β | CMC | x1 | β | |||
| 0 | 79.129 | 75.430 | |||||||
| 0.077 | 0.6499 | 0.46 | −9.07 | 0.6559 | 0.46 | −9.02 | |||
| 0.142 | 10.336 | 0.49 | −6.19 | 10.376 | 0.49 | −6.17 | |||
| 0.25 | 0.4474 | 0.53 | −8.64 | 0.6196 | 0.53 | −7.35 | |||
| 0.33 | 0.2058 | 0.54 | −11.38 | 0.2682 | 0.54 | −10.33 | |||
| 0.368 | 0.2510 | 0.55 | −10.45 | 0.2682 | 0.54 | −10.20 | |||
| 1 | 14.525 | 1.526 | |||||||
| 278.1 K | 283.1 K | 288.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 62.565 | 59.484 | 59.773 | ||||||
| 0.077 | 10.071 | 0.37 | −10.26 | 10.482 | 0.37 | −10.00 | 10.510 | 0.37 | −10.02 |
| 0.142 | 0.9878 | 0.40 | −9.54 | 0.9926 | 0.39 | −9.37 | 10.065 | 0.39 | −9.41 |
| 0.25 | 0.9773 | 0.42 | −8.96 | 0.9811 | 0.42 | −8.79 | 0.9774 | 0.42 | −8.91 |
| 0.33 | 0.9533 | 0.44 | −8.89 | 0.9928 | 0.44 | −8.59 | 10.072 | 0.43 | −8.64 |
| 0.368 | 0.8739 | 0.45 | −9.12 | 0.8248 | 0.45 | −9.21 | 0.8578 | 0.44 | −9.16 |
| 1 | 11.541 | 11.336 | 11.968 | ||||||
| 293.1 K | 298.1 K | 303.1 K | |||||||
| α1 | CMC | x1 | β | CMC | x1 | β | CMC | x1 | β |
| 0 | 63.919 | 65.737 | 66.675 | ||||||
| 0.077 | 11.182 | 0.37 | −10.12 | 11.360 | 0.37 | −10.21 | 12.982 | 0.36 | −9.67 |
| 0.142 | 10.112 | 0.39 | −9.75 | 10.745 | 0.39 | −9.66 | 11.088 | 0.39 | −9.56 |
| 0.25 | 0.9737 | 0.42 | −9.29 | 0.9962 | 0.42 | −9.36 | 10.693 | 0.42 | −9.09 |
| 0.33 | 0.9777 | 0.44 | −9.10 | 0.9749 | 0.43 | −9.28 | 10.397 | 0.43 | −9.05 |
| 0.368 | 0.8993 | 0.44 | v | 0.8621 | 0.44 | −9.66 | 0.9062 | 0.44 | v |
| 1 | 13.431 | 14.195 | 14.154 | ||||||
| 308.1 K | 313.1 K | ||||||||
| α1 | CMC | x1 | β | CMC | x1 | β | |||
| 0 | 79.129 | 75.430 | |||||||
| 0.077 | 13.316 | 0.37 | −10.46 | 23.629 | 0.33 | −7.99 | |||
| 0.142 | 11.430 | 0.39 | −10.32 | 12.114 | 0.38 | −10.16 | |||
| 0.25 | 10.285 | 0.42 | −10.13 | 11.103 | 0.41 | −9.92 | |||
| 0.33 | 10.085 | 0.44 | −10.02 | 10.266 | 0.43 | −10.07 | |||
| 0.368 | 10.693 | 0.44 | −9.69 | 10.047 | 0.43 | −10.07 | |||
| 1 | 18.59 | 21.161 | |||||||
Appendix C
References
- Rusanov, A.I. The wonderful world of micelles. Colloid J. 2014, 76, 121–126. [Google Scholar] [CrossRef]
- Rusanov, A.I. The mass action law theory of micellar solutions. Adv. Colloid Interface Sci. 1993, 45, 1–78. [Google Scholar] [CrossRef]
- Poša, M. Self-Association of the Anion of 7-Oxodeoxycholic Acid (Bile Salt): How Secondary Micelles Are Formed. Int. J. Mol. Sci. 2023, 24, 11853. [Google Scholar] [CrossRef]
- Kumar, H.; Kaur, G. Scrutinizing Self-Assembly, Surface Activity and Aggregation Behavior of Mixtures of Imidazolium Based Ionic Liquids and Surfactants. A Comprehensive Review. Front. Chem. 2021, 9, 667941. [Google Scholar] [CrossRef] [PubMed]
- Szymczyk, K.; Jańczuk, B. The adsorption at solution–air interface and volumetric properties of mixtures of cationic and nonionic surfactants. Colloids Surf. A 2007, 293, 39–50. [Google Scholar] [CrossRef]
- Song, L.D.; Rosen, M.J. Surface properties, micellization, and premicellar aggregation of gemini surfactants with rigid and flexible spacers. Langmuir 1996, 12, 1149–1151. [Google Scholar] [CrossRef]
- Bhattarai, A.; Rub, M.A.; Posa, M.; Saha, B.; Asiri, A.M.; Kumar, D. Studies of ninhydrin and phenylalanine in cationic dimeric gemini micellar system: Spectrophotometric and conductometric measurements. Colloids Surf. A 2022, 655, 130334. [Google Scholar] [CrossRef]
- Poša, M.; Bhattarai, A.; Khan, J.M.; Saha, B.; Kumar, D. Impact of double headed geminis on leucine and ninhydrin reaction in buffer solvent. Colloids Surf. A 2023, 674, 131951. [Google Scholar] [CrossRef]
- Azum, N.; Rub, M.A.; Asiri, A.M. Bile salt–bile salt interaction in mixed monolayer and mixed micelle formation. J. Chem. Thermodyn. 2019, 128, 406–414. [Google Scholar] [CrossRef]
- Rub, M.A.; Azum, N.; Khan, F.; Asiri, A.M. Aggregation of sodium salt of ibuprofen and sodium taurocholate mixture in different media: A tensiometry and fluorometry study. J. Chem. Thermodyn. 2018, 121, 199–210. [Google Scholar] [CrossRef]
- Ren, Z.H.; Huang, J.; Zheng, Y.C.; Lai, L.; Mei, P.; Yu, X.R.; Chang, Y.L. Micellization and interaction for ternary mixtures of amino sulfonate surfactant and octylphenol polyoxyethylene ethers in aqueous solution: 2 blending with surfactant with a longer or shorter hydrophilic chain. J. Mol. Liq. 2018, 272, 380–386. [Google Scholar] [CrossRef]
- Sheng, R.; Quan, X.F.; Ren, Z.H.; Huang, J.; Li, D.N.; Wang, J.R.; Qian, Z.B.; Zhang, Y.X.; Chai, L.L.; Li, B.B.; et al. Molecular interaction between sodium dodecylbenzene sulfonate and octylphenol polyoxyethylene ether and effect of hydrophilic chain. Colloids Surf. A 2021, 626, 127048. [Google Scholar] [CrossRef]
- Rubingh, D.N. Mixed Micelle Solutions. In Solution Chemistry of Surfactants; Mittal, K.L., Ed.; Springer: New York, NY, USA, 1979; Volume 1, pp. 337–354. [Google Scholar] [CrossRef]
- Holland, P.M.; Rubingh, D.N. Nonideal multicomponent mixed micelle model. J. Phys. Chem. 1983, 87, 1984–1990. [Google Scholar] [CrossRef]
- Holland, P.M. Nonideal mixed micellar solutions. Adv. Colloid Interface Sci. 1986, 26, 111–129. [Google Scholar] [CrossRef]
- Poša, M. Mixed micelles of binary surfactant mixtures: Tween 40—Na-3,12-dioxo-5β-cholanoate; Tween 80—Na-3,12-dioxo-5β-cholanoate and their thermodynamic description-characterization. Chem. Eng. Res. Des. 2014, 92, 1826–1839. [Google Scholar] [CrossRef]
- Shiloach, A.; Blankschtein, D. Prediction of critical micelle concentration and synergism of binary surfactans mixtures containing zwitterionic surfactants. Langmuir 1997, 13, 3968–3981. [Google Scholar] [CrossRef]
- Shiloach, A.; Blankschtein, D. Predicting micellar solution properties of binary surfactants mixtures. Langmuir 1998, 14, 1618–1636. [Google Scholar] [CrossRef]
- Nagarajan, R. Molecular theory for mixed micelles. Langmuir 1985, 1, 331–341. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Mixtures; The Clarendon Press: Oxford, UK, 1952; pp. 23–46. [Google Scholar]
- Poša, M.; Pilipović, A.; Popović, K.; Kumar, D. Thermodynamics of trimethyltetradecylammonium bromide—Sodium deoxycholate binary mixed micelle formation in aqueous solution: Regular Solution Theory with mutual compensation of excess configurational and excess conformational entropy. J. Mol. Liq. 2022, 360, 119473. [Google Scholar] [CrossRef]
- Poša, M. Symmetry (asymmetry) of the molar excess Gibbs free energy function of the binary mixed micelles of bile acid anion and classical cationic surfactant: Influence of sterically shielded and sterically unshielded polar groups of the steroid skeleton. Symmetry 2022, 14, 2337. [Google Scholar] [CrossRef]
- Bagheri, A.; Khalili, P. Synergism between and cationic surfactants in a concentration range of mixed monolayers at an air–water interface. RSC Adv. 2017, 7, 18151–18161. [Google Scholar] [CrossRef]
- Bagheri, A.; Jafari-Chashmi, P. Study of aggregation behavior between N-lauryl sarcosine sodium and Dodecyltrimethylammonium bromide in aqueous solution, using conductometric and spectrophotometric techniques. J. Mol. Liq. 2019, 282, 466–473. [Google Scholar] [CrossRef]
- Maeda, H. Phenomenological approaches in the thermodynamics of mixed micelles with electric charge. Adv. Colloid Interf. Sci. 2010, 156, 70–82. [Google Scholar] [CrossRef]
- Hoffmann, H.; Pössnecker, G. The mixing behavior of surfactants. Langmuir 1994, 10, 381–389. [Google Scholar] [CrossRef]
- Lozar, J. Thermodynamique des Solutions et des Mélanges; Elipses: Paris, France, 2013; pp. 100–116. [Google Scholar]
- Ganguly, J. Thermodynamic modelling of solid solutions. EMU Notes Mineral. 2001, 3, 37–69. [Google Scholar]
- Straikov, B.E.; Norden, B. Enthalpy-entropy compensation: A phantom or something useful? J. Phys. Chem. B 2007, 111, 14431–14435. [Google Scholar] [CrossRef]
- Kumar, D.; Poša, M. Linear hydrophobic congeneric groups of bile acid anion derivatives based on the self-association (micellization) process and the phenomenon of enthalpy-entropy compensation. J. Mol. Liq. 2023, 382, 121925. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Tepavčević, V.; Obradović, S. Micellisation in water solutions of binary mixture of surfactants Na-deoxycholate—Na-decyl-sulphate and Na-hyodeoxycholate—Na-decyl-sulphate: Rational development (selection) of the thermodynamic model for describing GE. J. Chem. Eng. Data 2018, 63, 691–701. [Google Scholar] [CrossRef]
- Pilipović, A.; Ocokoljić, M.; Janev, M.; Poša, M. The ternary mixed micelle of Tween 20- Sodium Deoxycholate- Sodium Cholate: The molar excess thermodynamic potencials. J. Chem. Thermodyn. 2022, 167, 106695. [Google Scholar] [CrossRef]
- Schulz, J.E.P.; Rodriguez, J.L.M.; Minardi, R.M.; Miraglia, D.B.; Schulz, P.C. On the applicability of the regular solution theory to multicomponent systems. J. Surfact Deterg. 2013, 16, 795–803. [Google Scholar] [CrossRef]
- Dongowski, G.; Fritzsch, B.; Giessler, J.; Hartl, A.; Kuhlmann, O.; Neubert, R.H.H. The influence of bile salts and mixed micelles on the pharmacokinetics of quinine in rabbits. Eur. J. Pharm. Biopharm. 2005, 60, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Wiedmann, T.S.; Kamel, L. Examination of the solubilization of drugs by bile salt micelles. J. Pharm. Sci. 2002, 91, 1743–1764. [Google Scholar] [CrossRef]
- Enache, M.; Toader, A.M.; Neacsu, V.; Ionita, G.; Enache, M.I. Spectroscopic investigation of the interaction of the anticancer drug mitoxantrone with sodium taurodeoxycholate (NaTDC) and sodium taurocholate (NaTC) bile salts. Molecules 2017, 22, 1079. [Google Scholar] [CrossRef]
- Toader, A.M.; Dascalu, I.; Neacsu, E.I.; Enache, M. Binding interactions of actinomycin D anticancer drug with bile salts micelles. J. Serb. Chem. Soc. 2023, 88, 367–379. [Google Scholar] [CrossRef]
- Poša, M. Conformationally rigid and flexible surfactant binary (pseudoternary) mixed micelle with mutual synergistic interaction. J. Mol. Liq. 2021, 334, 116158. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Torović, L.; Cvejić Hogervorst, J. Co-solubilisation of a binary mixtures of isoflavones in a water micellar solution of sodium cholate or cetyltrimethylammonium bromide: Influence of the micelle structure. J. Mol. Liq. 2019, 273, 134–146. [Google Scholar] [CrossRef]
- Kamrath, R.F.; Franses, E.I. Mass-action model of mixed micellization. J. Phys. Chem. 1984, 88, 1642–1648. [Google Scholar] [CrossRef]
- Jójárt, B.; Poša, M.; Fisher, B.; Szöri, M.; Farkaš, Z.; Viskolcz, B. Mixed micelles of sodium cholate and sodium dodecylsulphate 1:1 binary mixture at different temperatures—Experimental and theoretical investigations. PLoS ONE 2014, 9, e102114. [Google Scholar] [CrossRef]
- Zana, R. Critical micellization concentration of surfactants in aqueous solution and free energy of micellization. Langmuir 1996, 12, 1208–1211. [Google Scholar] [CrossRef]
- Schulz, P.C.; Rodríguez, J.L.; Minardi, R.M.; Sierra, M.B.; Morini, M.A. Are the mixtures of homologous surfactants ideal? J. Colloid Interface Sci. 2006, 303, 264–271. [Google Scholar] [CrossRef]
- Hore, P.J. Nuclear Magnetic Resonance; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sanders, J.K.M.; Hunter, B.K. Modern NMR Spectroscopy; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Privalov, P.L.; Gill, S.J. The hydrophobic effect: A reappraisal. Pure Appl. Chem. 1989, 61, 1097–1104. [Google Scholar] [CrossRef]
- Garidel, P.; Hildebrand, A. Thermodynamic properties of association of colloids. J. Therm. Anal. Calorim. 2005, 82, 483–489. [Google Scholar] [CrossRef]
- Garidel, P.; Hildebrand, A.; Neubert, R.; Blume, A. Thermodynamic characterization of bile salt aggregation as a function of temperature and ionic strength using isotermal titration calorimetry. Langmuir 2000, 16, 5267–5275. [Google Scholar] [CrossRef]
- Paula, S.; Süs, W.; Tuchtenhagen, J.; Blume, A. Thermodynamics of micelle formation as a function of temperature: A high sensitivity titration calorimetry study. J. Phys. Chem. 1995, 99, 11742–11751. [Google Scholar] [CrossRef]
- Anderson, S.L.; Rovnyak, D.; Strein, T.G. Direct measurement of the thermodynamics of chiral recognition in bile salt micelles. Chirality 2016, 28, 290–298. [Google Scholar] [CrossRef]
- Vázquez-Gómez, S.; Pilar Vázquez-Tato, M.; Seijas, J.A.; Meijide, F.; de Frutos, S.; Vázquez Tato, J. Thermodynamics of the aggregation of the bile anions of obeticholic and chenodeoxycholic acids in aqueous solution. J. Mol. Liq. 2019, 296, 112092. [Google Scholar] [CrossRef]
- Kroflic, A.; Sarac, B.; Bester-Rogac, M. Thermodynamic characterization of 3-[(3- cholamidopropyl)-dimethylammonium]-1-propanesulfonate (CHAPS) micellization using isothermal titration calorimetry: Temperature, salt, and pH dependence. Langmuir 2012, 28, 10363–10371. [Google Scholar] [CrossRef]
- Small, D.M. The physical chemistry of cholanic acids. In The Bile Acids: Chemistry, Physiology and Metabolism; Nair, P.P., Kritchevsky, D., Eds.; Plenum Press: New York, NY, USA, 1971; Volume 3, pp. 249–332. [Google Scholar]
- Mikov, M.; Fawcett, J.P. Bile Acids; Medishet Publisher: Geneva, Switzerland, 2007. [Google Scholar]
- Pártai, L.B.; Sega, M.; Jedlovszky, P. Morphology of bile salts micelles as studied by computer simulation methods. Langmuir 2007, 23, 12322–12328. [Google Scholar] [CrossRef]
- Unpleby, H.C.; Williamson, R.C. The efficacy of agents employed to prevent anastomotic recurrence in colorectal carcinoma. Ann. R. Coll. Surg. Engl. 1984, 66, 192–194. [Google Scholar]
- Smith, A.R.W.; Lambert, P.A.; Hammond, S.M.; Jessup, C. The differing effects of cetyltrimethylammonium bromide and cetrimide B. P. upon growing cultures of Escherichia Coli NCIB 8277. J. Appl. Bacteriol. 1975, 38, 143–149. [Google Scholar] [CrossRef]
- Kasilingam, T.; Thangavelu, C. Biocidal behaviour of (dodecyltrimethylammonium bromide) on carbon steel in well water. Trans. Indian Inst. Met. 2016, 69, 793–803. [Google Scholar] [CrossRef]
- Huang, L.; Somasundaran, P. Theoretical model and phase behavior for binary surfactant mixtures. Langmuir 1997, 13, 6683–6688. [Google Scholar] [CrossRef]
- Kumari, S.; Chauhan, S.; Umar, A.; Fouad, H.; Shaheer Akhtar, M. Conductometric and fluorescence probe analysis to investigate the interaction between bioactive peptide and bile salts: A micellar state study. Molecules 2022, 27, 7561. [Google Scholar] [CrossRef] [PubMed]
- Subuddhi, U.; Mishra, A.K. Micellization of bile salts in aqueous medium: A fluorescence study. Colloids Surf. Biointerfaces 2007, 57, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Pillania, A. Thermodynamic and micellization properties of aqueous cetyltrimethylammonium bromide solution in presence of 1-butyl-2,3-dimethylimidazolium bromide. Fluid Phase Equilib. 2016, 412, 115–122. [Google Scholar] [CrossRef]
- Chauhan, S.; Kaur, M.; Kumar, K.; Chauhan, M.S. Study of the effect of electrolyte and temperature on the critical micelle concentration of dodecyltrimethylammonium bromide in aqueous medium. J. Chem. Thermodyn. 2014, 78, 175–181. [Google Scholar] [CrossRef]
- Mahbub, S.; Rub, M.A.; Hoque, M.A.; Khana, M.A.; Asiri, A.M. Critical Micelle Concentrations of Sodium Dodecyl Sulfate and Cetyltrimethylammonium Bromide Mixtures in Binary Mixtures of Various Salts at Different Temperatures and Compositions. Russ. J. Phys. Chem. A 2019, 93, 2043–2052. [Google Scholar] [CrossRef]
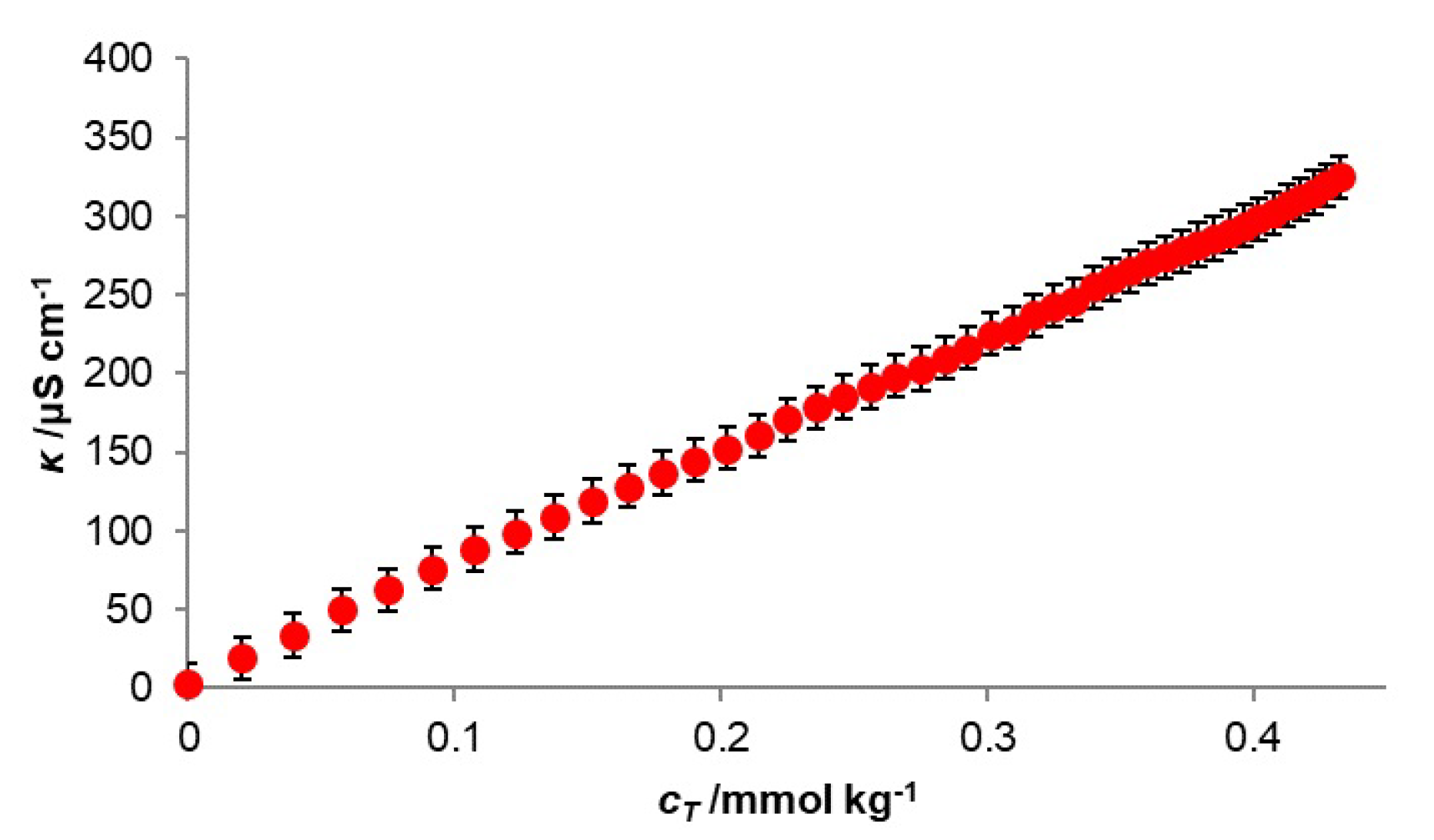
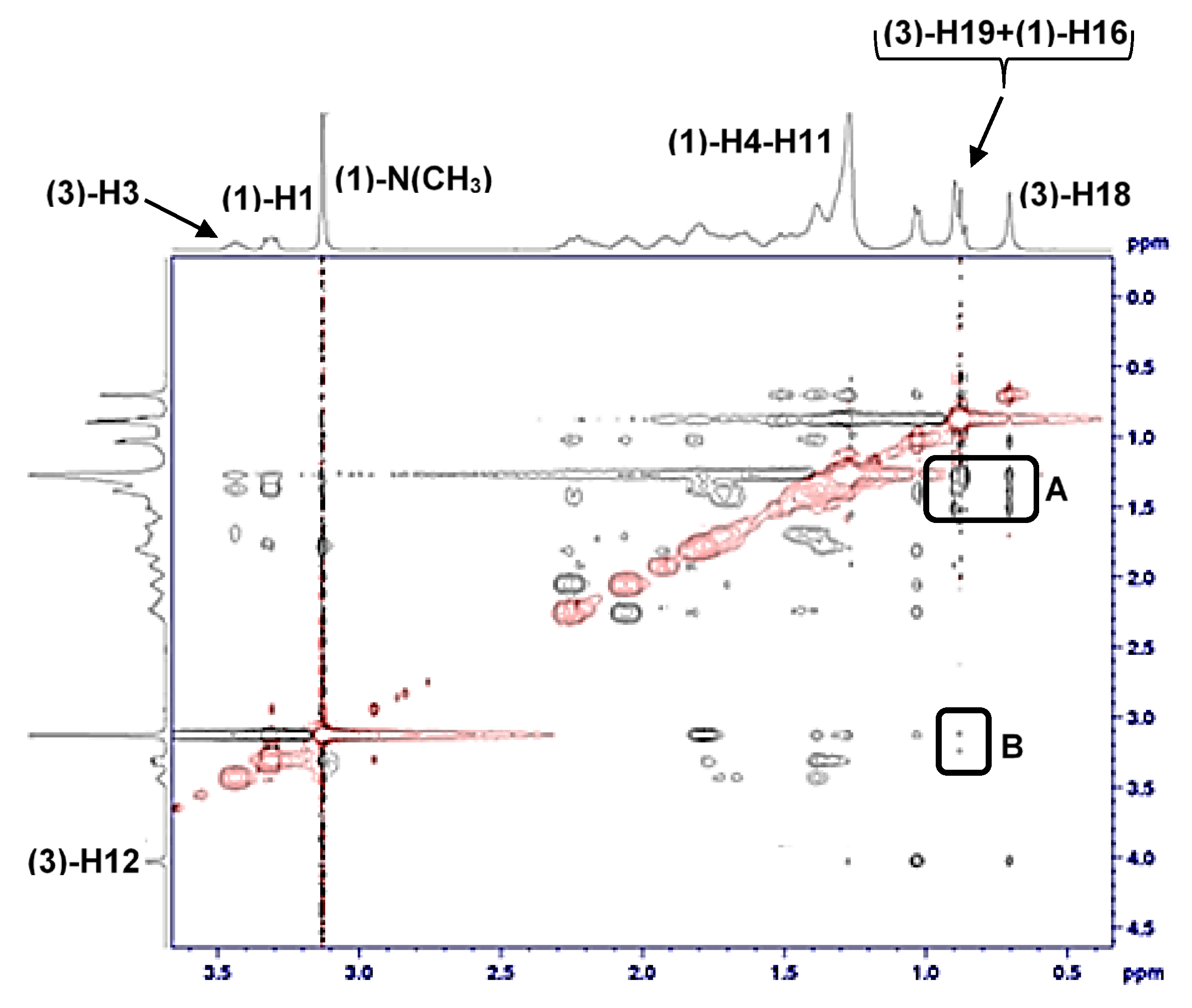
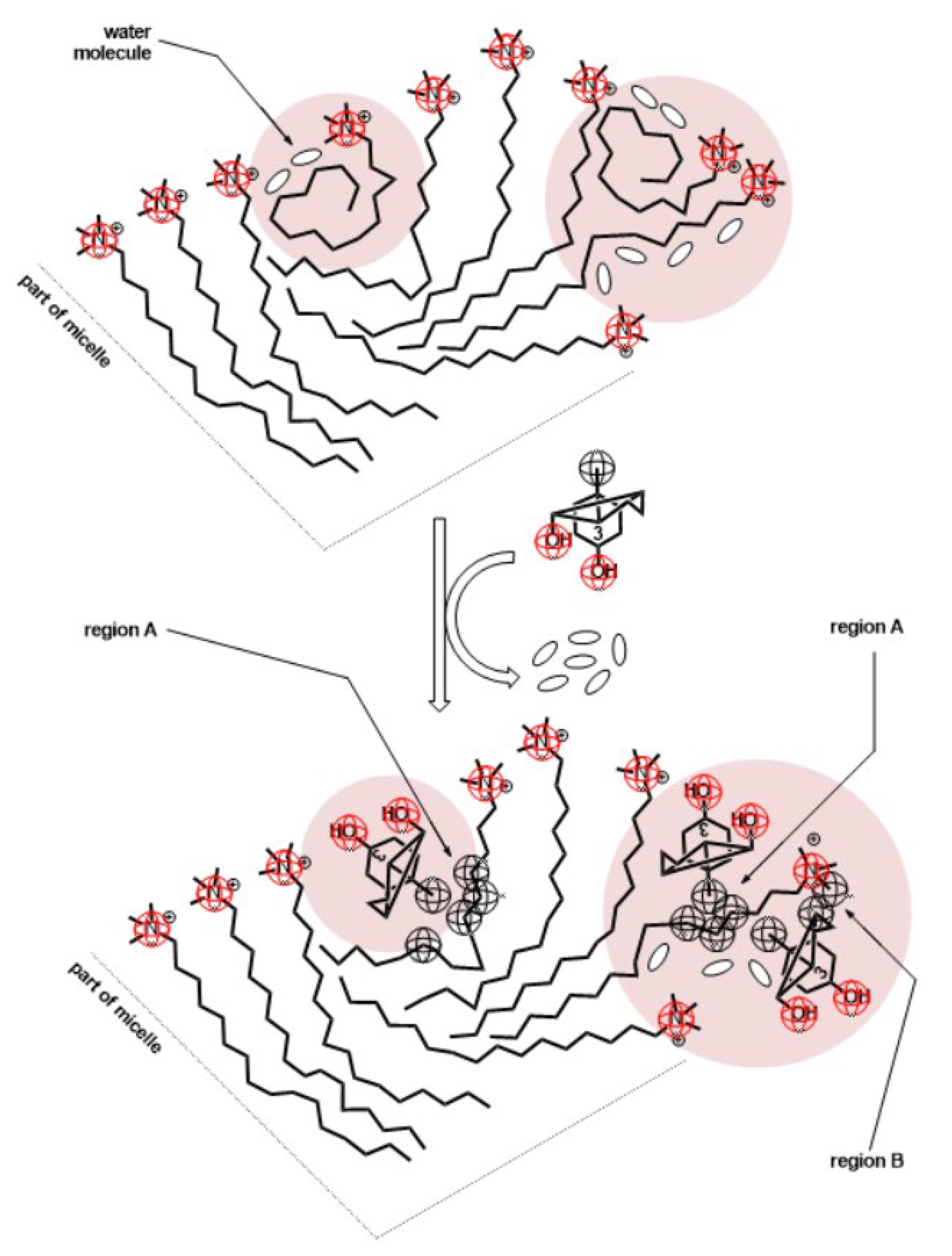
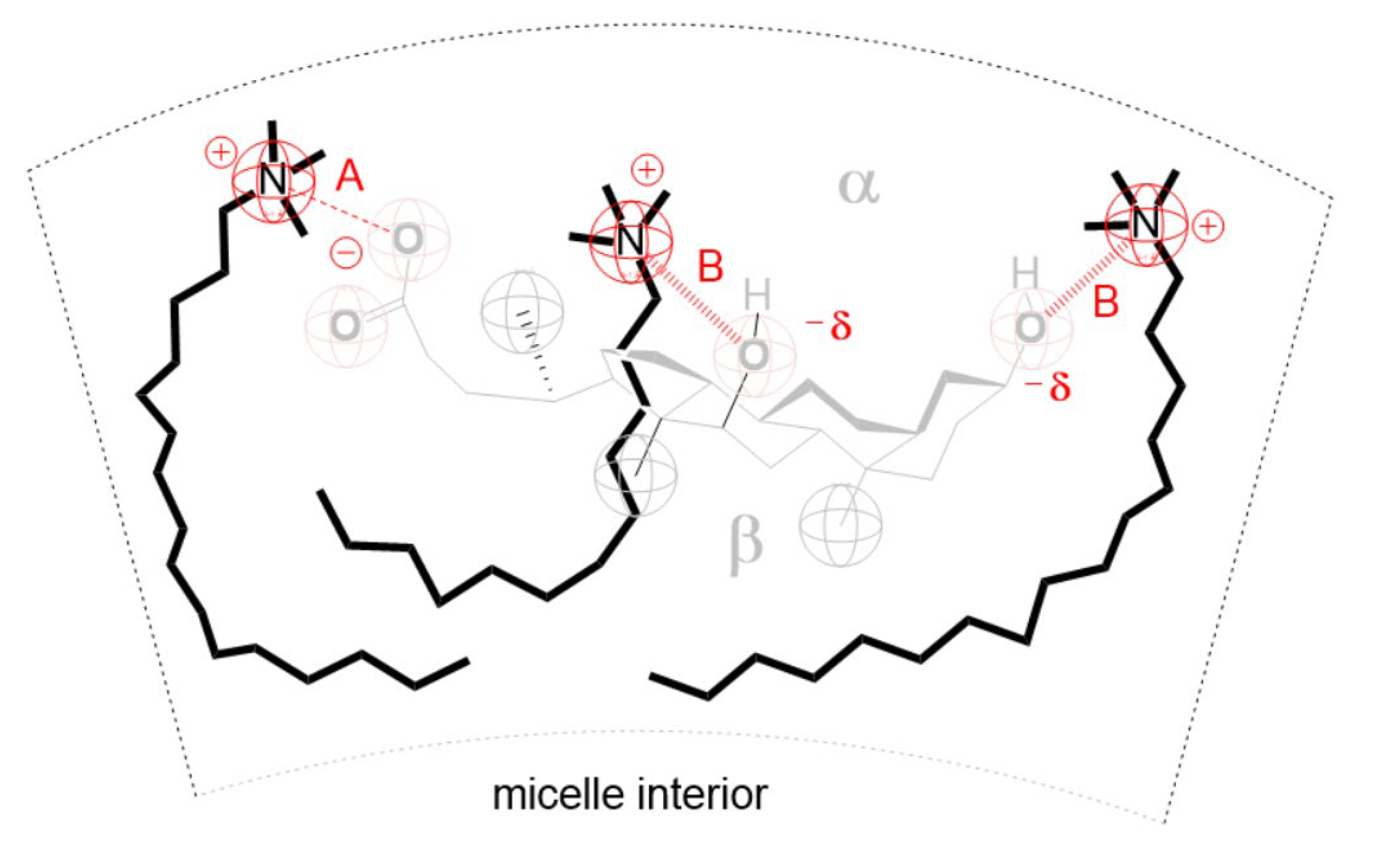
| T /K | CMC123 /mmolkg−1 | x1 | x2 | x3 | lnf1 | lnf2 | lnf3 | /kJmol−1 | (17)/kJmol−1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| α1 = 0.05; α2 = 0.35; α3 = 0.6 | ||||||||||
| 278.1 | 0.5128 | 0.33 | 0.28 | 0.39 | −2.64 | −2.56 | −2.85 | −6.25 | −17.52 | 0.35 |
| 283.1 | 0.5362 | 0.32 | 0.29 | 0.39 | −2.53 | −2.53 | −2.81 | −6.22 | −17.73 | 0.35 |
| 288.1 | 0.5471 | 0.31 | 0.29 | 0.39 | −2.55 | −2.56 | −2.76 | −6.31 | −17.99 | 0.35 |
| 293.1 | 0.5362 | 0.31 | 0.29 | 0.40 | −2.64 | −2.66 | −2.73 | −6.54 | −18.35 | 0.36 |
| 298.1 | 0.5595 | 0.30 | 0.31 | 0.39 | −2.58 | −2.74 | −2.81 | −6.74 | −18.56 | 0.36 |
| 303.1 | 0.5704 | 0.30 | 0.31 | 0.39 | −2.78 | −2.72 | −2.81 | −6.99 | −18.82 | 0.37 |
| 308.1 | 0.6156 | 0.31 | 0.29 | 0.39 | −2.78 | −2.85 | −2.82 | −7.22 | −18.94 | 0.38 |
| 313.1 | 0.7307 | 0.32 | 0.31 | 0.38 | −2.62 | −2.86 | −3.03 | −7.41 | −18.80 | 0.39 |
| α1 = 0.1; α2 = 0.3; α3 = 0.6 | ||||||||||
| 278.1 | 0.2251 | 0.33 | 0.15 | 0.52 | −2.93 | −3.08 | −1.72 | −5.36 | −19.42 | 0.27 |
| 283.1 | 0.2392 | 0.30 | 0.17 | 0.53 | −2.73 | −3.06 | −1.51 | −5.02 | −19.63 | 0.26 |
| 288.1 | 0.2607 | 0.29 | 0.18 | 0.53 | −2.63 | −3.06 | −1.49 | −5.03 | −19.76 | 0.25 |
| 293.1 | 0.2885 | 0.20 | 0.25 | 0.56 | −1.90 | −3.30 | −1.31 | −4.69 | −19.86 | 0.23 |
| 298.1 | 0.3856 | 0.21 | 0.27 | 0.52 | −1.80 | −3.10 | −1.56 | −5.02 | −19.48 | 0.26 |
| 303.1 | 0.4296 | 0.22 | 0.27 | 0.51 | −1.95 | −2.99 | −1.59 | −5.16 | −19.54 | 0.26 |
| 308.1 | 0.5107 | 0.22 | 0.29 | 0.49 | −1.72 | −3.10 | −1.93 | −5.68 | −19.42 | 0.29 |
| 313.1 | 0.5881 | 0.23 | 0.29 | 0.48 | −1.68 | −3.06 | −2.00 | −5.82 | −19.36 | 0.30 |
| α1 = 0.2; α2 = 0.2; α3 = 0.6 | ||||||||||
| 278.1 | 0.1811 | 0.58 | 0.11 | 0.31 | −1.71 | −1.57 | −4.58 | −5.96 | −19.92 | 0.30 |
| 283.1 | 0.1425 | 0.57 | 0.14 | 0.29 | −1.59 | −1.45 | −4.75 | −5.84 | −20.84 | 0.25 |
| 288.1 | 0.1858 | 0.57 | 0.11 | 0.33 | −1.83 | −1.66 | −4.32 | −6.28 | −20.58 | 0.31 |
| 293.1 | 0.2129 | 0.51 | 0.02 | 0.46 | −2.82 | −2.65 | −2.86 | −6.91 | −20.60 | 0.34 |
| 298.1 | 0.2455 | 0.49 | 0.01 | 0.50 | −3.24 | −3.06 | −2.51 | −7.14 | −20.60 | 0.35 |
| 303.1 | 0.2843 | 0.46 | 0.05 | 0.49 | −3.26 | −2.99 | −2.49 | −7.22 | −20.57 | 0.35 |
| 308.1 | 0.3225 | 0.39 | 0.12 | 0.48 | −2.66 | −3.13 | −2.24 | −6.44 | −20.59 | 0.31 |
| 313.1 | 0.3772 | 0.35 | 0.14 | 0.51 | −2.23 | −3.15 | −1.83 | −5.61 | −20.52 | 0.27 |
| α1 = 0.3; α2 = 0.1; α3 = 0.6 | ||||||||||
| 278.1 | 0.2208 | 0.35 | 0.16 | 0.48 | −3.33 | −2.35 | −2.92 | −6.88 | −19.46 | 0.35 |
| 283.1 | 0.2312 | 0.35 | 0.16 | 0.49 | −3.53 | −2.32 | −2.95 | −7.18 | −19.71 | 0.36 |
| 288.1 | 0.2444 | 0.32 | 0.19 | 0.48 | −3.42 | −2.30 | −2.88 | −7.04 | −19.92 | 0.35 |
| 293.1 | 0.2607 | n.d. | n.d. | n.d. | n.d. | n.d. | n.d. | n.d. | −20.11 | n.d. |
| 298.1 | 0.2739 | 0.39 | 0.11 | 0.50 | −3.34 | −2.49 | −2.87 | −7.47 | −20.33 | 0.37 |
| 303.1 | 0.2587 | 0.39 | 0.12 | 0.49 | −3.15 | −2.60 | −2.68 | −7.19 | −20.81 | 0.35 |
| 308.1 | 0.4113 | n.d. | n.d. | n.d. | n.d. | n.d. | n.d. | n.d. | −19.97 | n.d. |
| 313.1 | 0.4757 | 0.31 | 0.23 | 0.46 | −2.31 | −2.22 | −2.97 | −6.75 | −19.92 | 0.34 |
| α1 = 0.35; α2 = 0.05; α3 = 0.6 | ||||||||||
| 278.1 | 0.2272 | 0.55 | 0.09 | 0.35 | −3.45 | −3.10 | −4.76 | −8.98 | −19.39 | 0.46 |
| 283.1 | 0.1991 | 0.55 | 0.03 | 0.42 | −2.95 | −2.55 | −3.93 | −7.88 | −20.06 | 0.39 |
| 288.1 | 0.2149 | 0.60 | 0.02 | 0.38 | −3.14 | −2.80 | −4.63 | −8.86 | −20.23 | 0.44 |
| 293.1 | 0.2557 | 0.61 | 0.02 | 0.37 | −2.99 | −2.72 | −4.67 | −8.79 | −20.15 | 0.44 |
| 298.1 | 0.2594 | 0.59 | 0.03 | 0.38 | −2.80 | −2.63 | −4.24 | −8.30 | −20.46 | 0.41 |
| 303.1 | 0.2865 | 0.50 | 0.11 | 0.39 | −3.36 | −3.07 | −3.73 | −8.75 | −20.56 | 0.43 |
| 308.1 | 0.2737 | 0.54 | 0.03 | 0.43 | −2.99 | −3.01 | −3.28 | −7.98 | −21.01 | 0.38 |
| 313.1 | 0.3805 | 0.54 | 0.01 | 0.45 | −3.03 | −2.57 | −3.08 | −7.93 | −20.49 | 0.39 |
| Compound | Origin | CAS Number | Purity |
|---|---|---|---|
| Hexadecyltrimethylammonium bromide | Alfa Aesar | 57-09-0 | >0.980 |
| Dodecyltrimethylammonium bromide | Alfa Aesar | 1119-94-4 | >0.980 |
| Sodium Deoxycholate | Alfa Aesar | 302-95-4 | >0.980 |
| Pyrene | Aldrich | 129-00-0 | >0.980 |
| Ternary Mixture 1:2:3 | Corresponding Binary Mixtures | ||
|---|---|---|---|
| 1:2 | 1:3 | 2:3 | |
| 0.5:3.5:0.6 | 0.125:0.875 | 0.077:0.923 | 0.368:0.632 |
| 1:3:6 | 0.25:0.75 | 0.143:0.857 | 0.33:0.67 |
| 2:2:6 | 0.5:0.5 | 0.25:0.75 | 0.25:0.75 |
| 3:1:6 | 0.75:0.25 | 0.33:0.67 | 0.25:0.75 |
| 3.5:0.5:6 | 0.875:0.125 | 0.368:0.632 | 0.125:0.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilipović, A.; Vapa, I.; Tepavčević, V.; Puača, G.; Poša, M. Ternary Mixed Micelle Hexadecyltrimethylammonium Bromide—Dodecyltrimethylammonium Bromide—Sodium Deoxycholate: Gibbs Free Energy of Mixing and Excess Gibbs Energy of Mixing. Molecules 2023, 28, 6722. https://doi.org/10.3390/molecules28186722
Pilipović A, Vapa I, Tepavčević V, Puača G, Poša M. Ternary Mixed Micelle Hexadecyltrimethylammonium Bromide—Dodecyltrimethylammonium Bromide—Sodium Deoxycholate: Gibbs Free Energy of Mixing and Excess Gibbs Energy of Mixing. Molecules. 2023; 28(18):6722. https://doi.org/10.3390/molecules28186722
Chicago/Turabian StylePilipović, Ana, Ivana Vapa, Vesna Tepavčević, Gorana Puača, and Mihalj Poša. 2023. "Ternary Mixed Micelle Hexadecyltrimethylammonium Bromide—Dodecyltrimethylammonium Bromide—Sodium Deoxycholate: Gibbs Free Energy of Mixing and Excess Gibbs Energy of Mixing" Molecules 28, no. 18: 6722. https://doi.org/10.3390/molecules28186722
APA StylePilipović, A., Vapa, I., Tepavčević, V., Puača, G., & Poša, M. (2023). Ternary Mixed Micelle Hexadecyltrimethylammonium Bromide—Dodecyltrimethylammonium Bromide—Sodium Deoxycholate: Gibbs Free Energy of Mixing and Excess Gibbs Energy of Mixing. Molecules, 28(18), 6722. https://doi.org/10.3390/molecules28186722







