Computational Studies on Diverse Characterizations of Molecular Descriptors for Graphyne Nanoribbon Structures
Abstract
:1. Introduction
2. Basic Aspects of Molecular Descriptors
3. Molecular Descriptors of -Graphyne Nanoribbon Structures
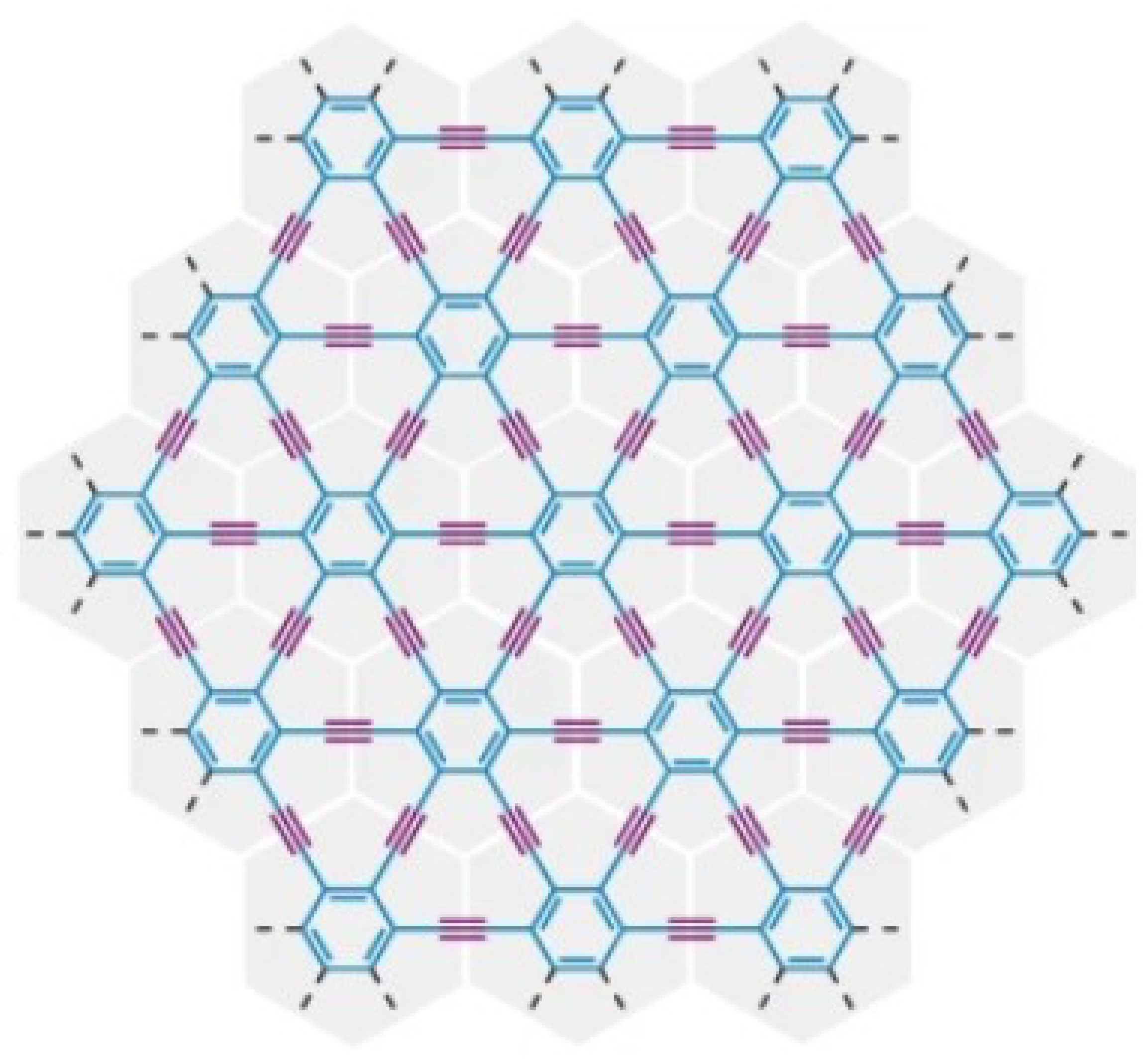
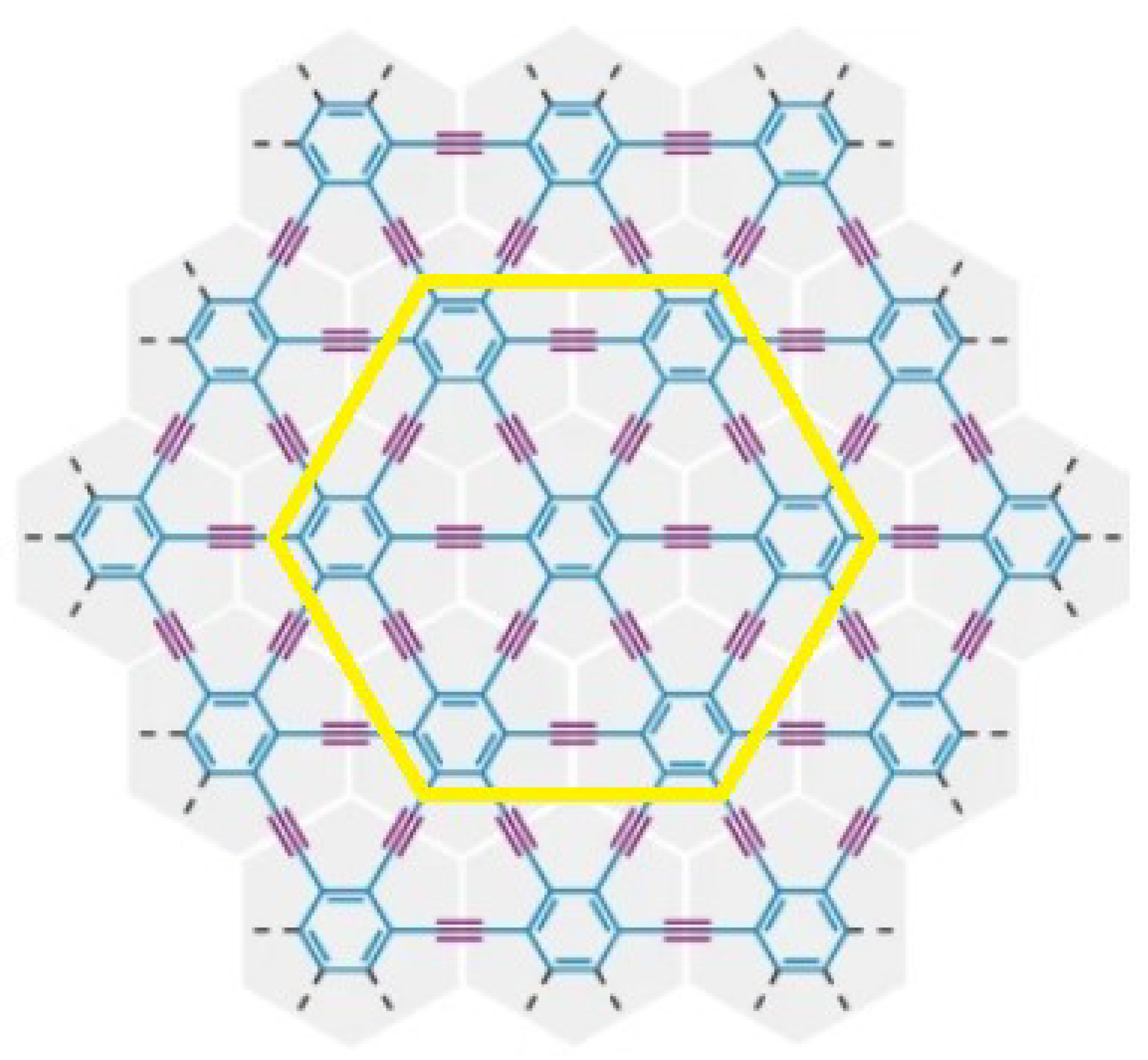
3.1. γ-Graphyne
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- First Leap Zagreb Index
- (ii)
- Second Leap Zagreb Index
- (iii)
- First Hyper Leap Zagreb Index
- (iv)
- Second Hyper Leap Zagreb Index
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
- (i)
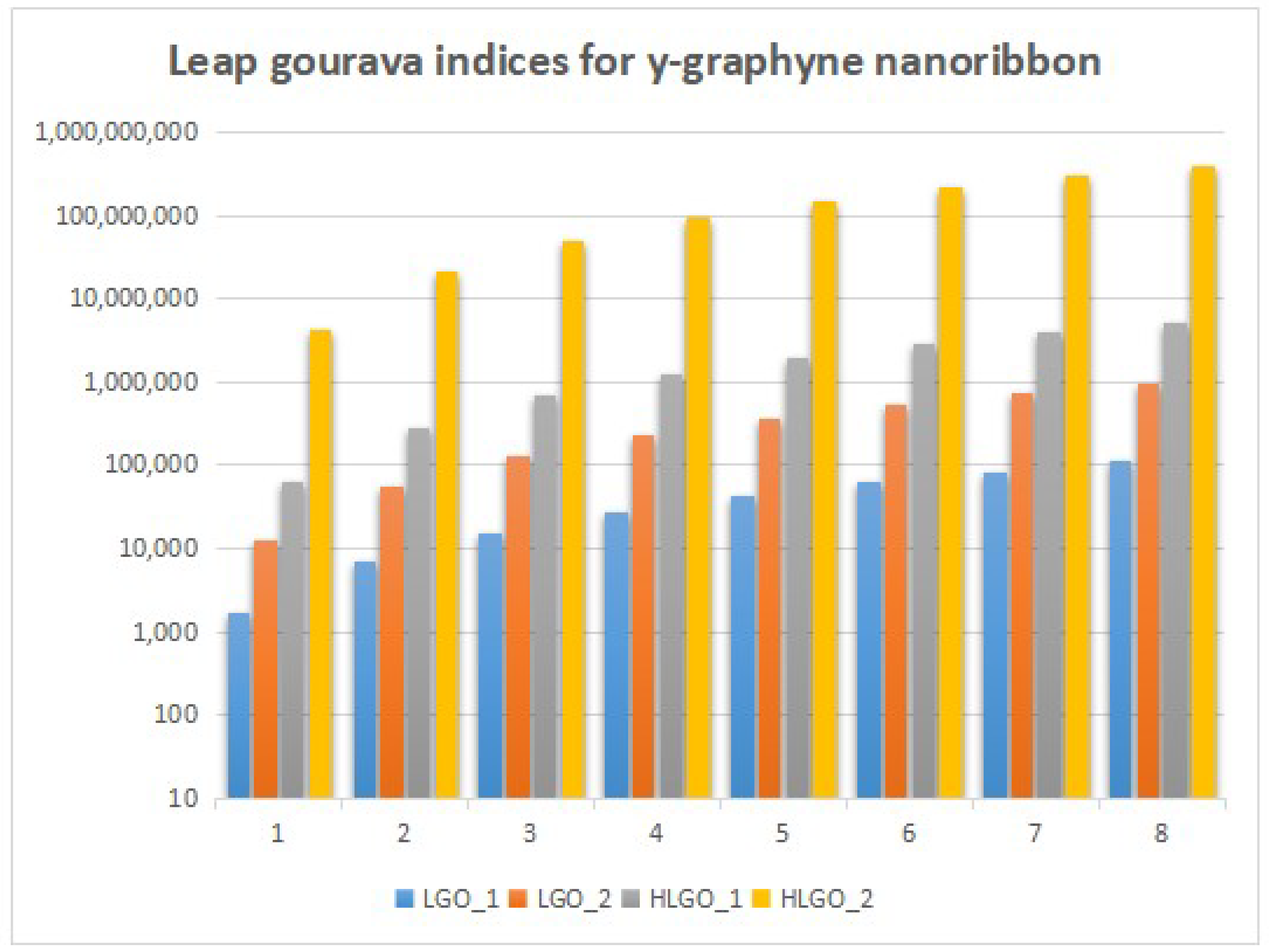
- First Leap Gourava Index
- (ii)
- Second Leap Gourava Index
- (iii)
- First Hyper Leap Gourava Index
- (iv)
- Second Hyper Leap Gourava Index
- (v)
- Sum Connectivity Leap Gourava Index
- (vi)
- Product Connectivity Leap Gourava Index
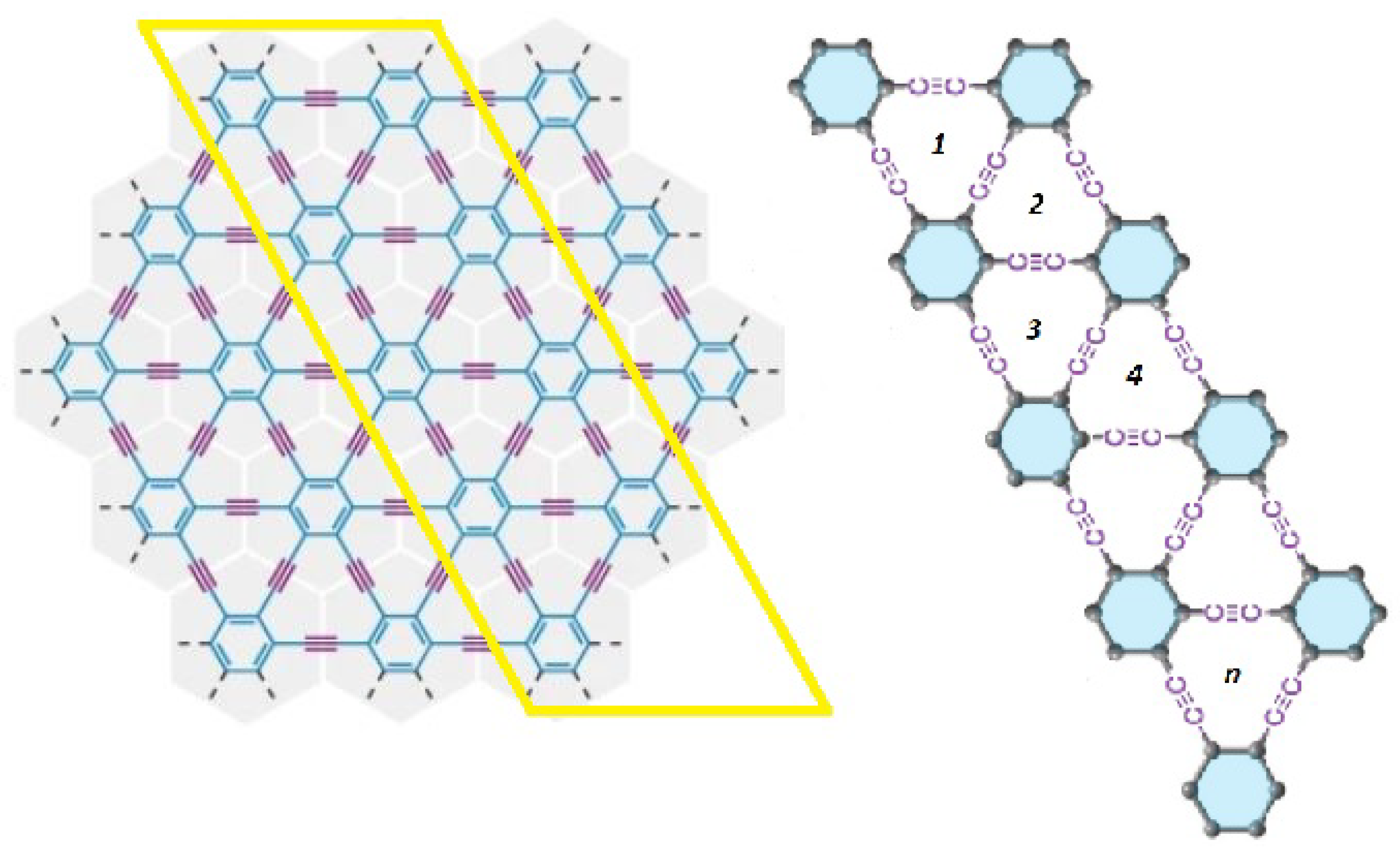
3.2. Zigzag -Graphyne Nanoribbon
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- First Leap Zagreb Index
- (ii)
- Second Leap Zagreb Index
- (iii)
- First Hyper Leap Zagreb Index
- (iv)
- Second Hyper Leap Zagreb Index
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
- (i)
- First Leap Gourava Index
- (ii)
- Second Leap Gourava Index
- (iii)
- First Hyper Leap Gourava Index
- (iv)
- Second Hyper Leap Gourava Index
- (v)
- Sum Connectivity Leap Gourava Index
- (vi)
- Product Connectivity Leap Gourava Index
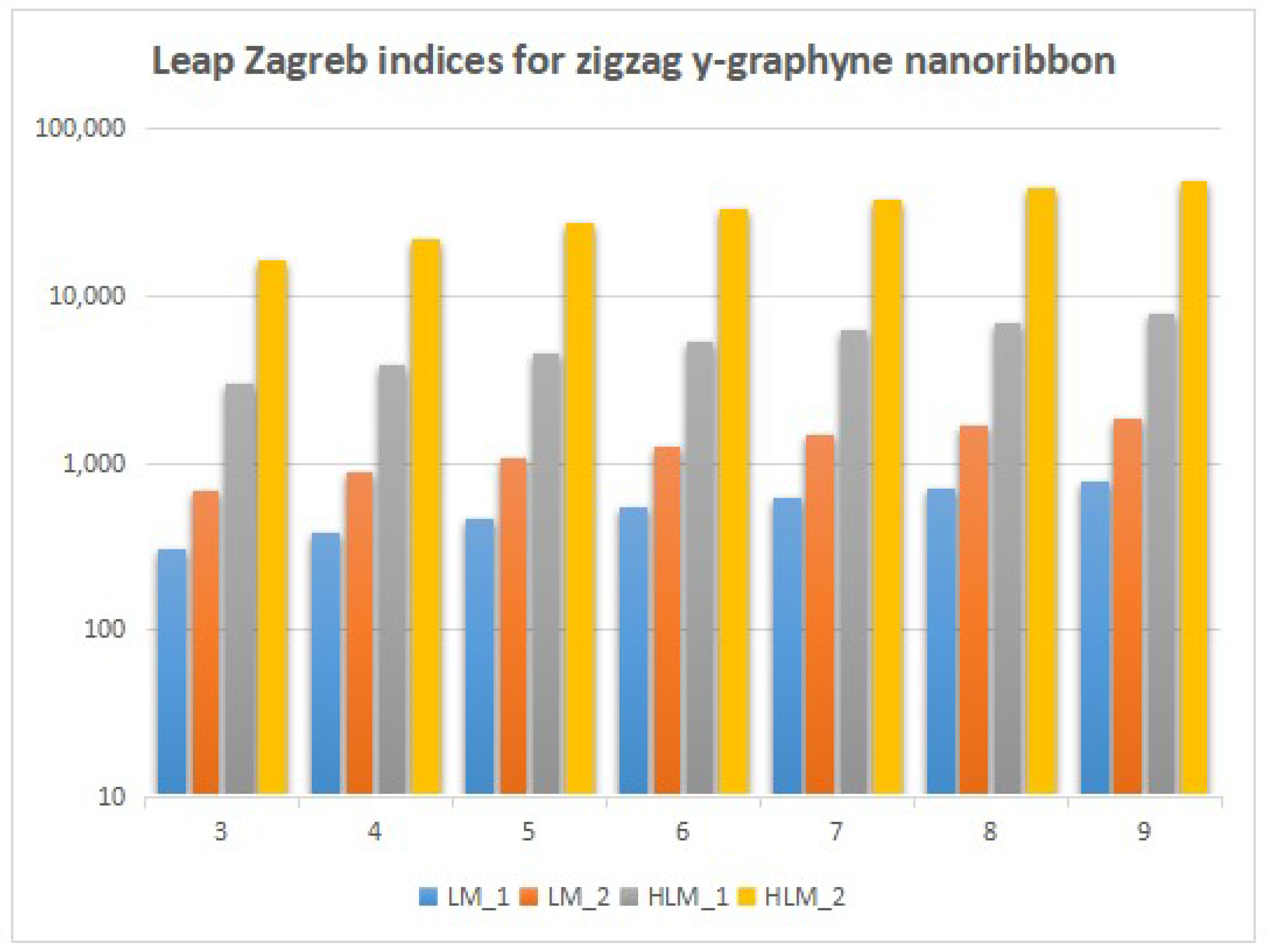
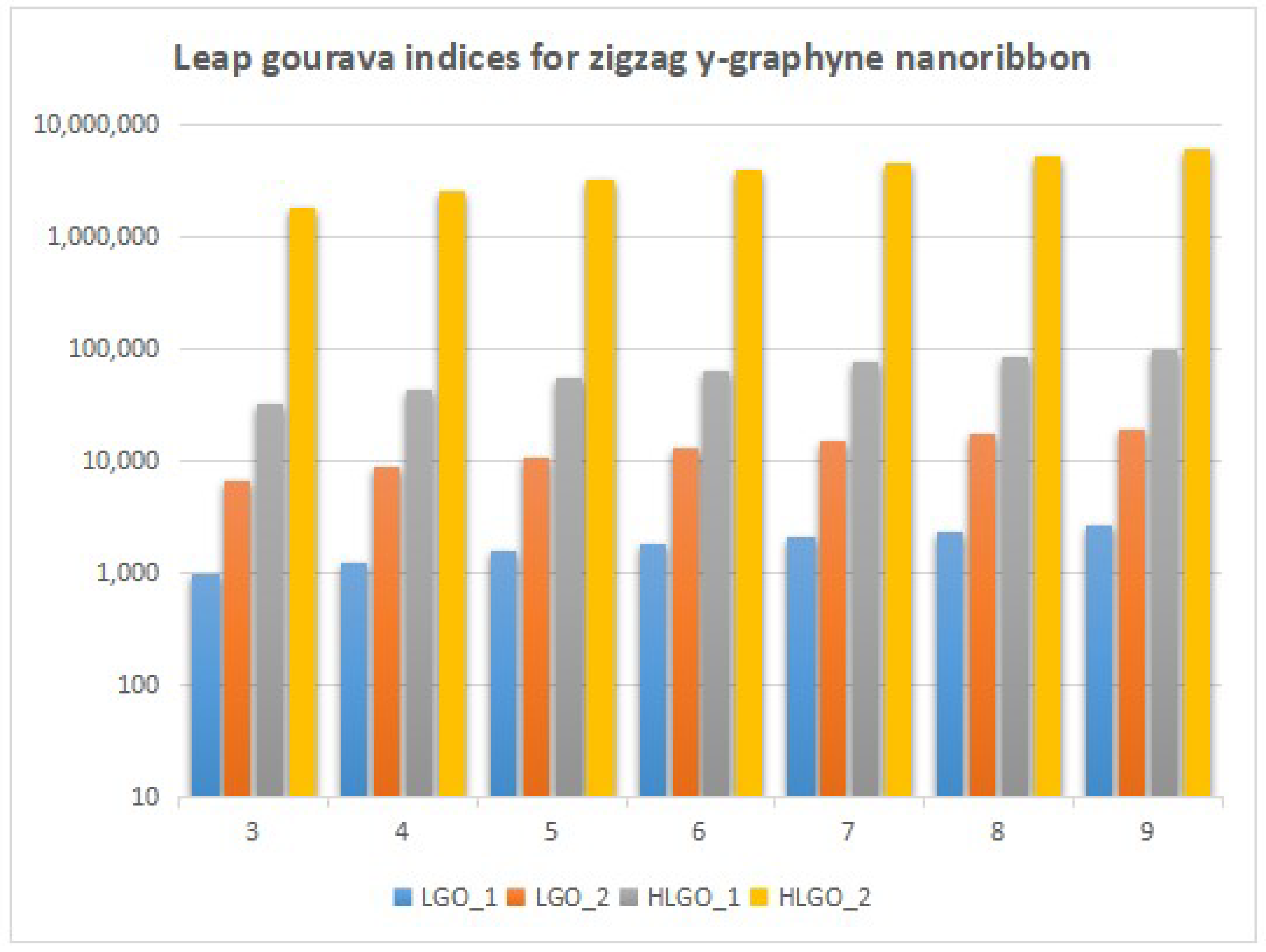
4. Numerical Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Hirsch, A. The era of carbon allotropes. Nat. Mater. 2010, 10, 868–871. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Helical Microtubules of Graphitic Carbon. Nature 2008, 363, 56–58. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, F.; Shen, B.; Zhang, R.J.; Zheng, Y.X.; Chen, L.Y.; Wang, S.Y.; Wang, C.Z.; Ho, K.M.; Fan, Y.J.; et al. Electronic and optical properties of novel carbon allotropes. Carbon 2016, 101, 77–85. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene network: A nonbenzenoid carbon allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef]
- Kaiser, K.; Scriven, L.M.; Schulz, F.; Gawel, P.; Gross, L.; Anderson, H.L. An sp-hybridized molecular carbon allotrope, cyclo[18]carbon. Science 2019, 365, 1299–1301. [Google Scholar] [CrossRef]
- Worsley, M.A.; Pauzauskie, P.J.; Olson, T.Y.; Biener, J.; Satcher, J.H.; Baumann, T.F. Synthesis of graphene aerogel with high electrical conductivity. J. Am. Chem. Soc. 2010, 132, 14067–14069. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, N.; Cui, Y.; Gao, W.; Zhao, Q.; Gao, C.; Bai, H.; Xie, T. Biomimetic architectured graphene aerogel with exceptional strength and resilience. ACS Nano 2017, 11, 6817–6824. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.; Pan, Q.; Jin, Y.; Lyu, R.; Martinez, V.; Huang, S.; Wu, J.; Wayment, L.J.; Clark, N.A.; et al. Synthesis of γ-graphyne using dynamic covalent chemistry. Nat. Synth. 2022, 1, 449–454. [Google Scholar] [CrossRef]
- Wei, X.; Guo, G.; Ouyang, T.; Xiao, H. Tuning thermal conductance in the twisted graphene and gamma graphyne nanoribbons. J. Appl. Phys. 2014, 115, 154313. [Google Scholar] [CrossRef]
- Costa, P.C.; Evangelista, J.S.; Leal, I.; Miranda, P.C. Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR. Mathematics 2020, 9, 60. [Google Scholar] [CrossRef]
- Estrada, E.; Molina, E. Novel local (fragment-based) topological molecular descriptors for QSPR/QSAR and molecular design. J. Mol. Graph. Model. 2001, 20, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Trinajstić, N. Total ϕ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Rafiullah, M.; Siddiqui, H.M.A.; Siddiqui, M.K.; Dhlamini, M. On Degree-Based Topological Indices for Strong Double Graphs. J. Chem. 2021, 2021, 4852459. [Google Scholar] [CrossRef]
- Wiener, H. Structural Determination of Paraffin Boiling Points. J. Chem. Phys. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Platt, J.R. Influence of neighbor bonds on additive bond properties in paraffins. J. Chem. Phys. 1947, 15, 419–420. [Google Scholar] [CrossRef]
- Gutman, I.; Ruscic, B.; Trinajstić, N.; Wilcox, C.F. Graph Theory and Molecular Orbitals. XII. Acyclic Polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Awais, M.; Ahmed, Z.; Khalid, W.; Bonyah, E. Analysis of Zigzag and Rhombic Benzenoid Systems via Irregularity Indices. J. Math. 2023, 2023, 4833683. [Google Scholar] [CrossRef]
- Idrees, N.; Naeem, M.N.; Hussain, F.; Sadiq, A.; Siddiqui, M.K. Molecular descriptors of benzenoid systems. Quim. Nova 2017, 40, 143–145. [Google Scholar] [CrossRef]
- Gao, W.; Farahani, M.R.; Siddiqui, M.K.; Jamil, M.K. On the first and second zagreb and first and second hyper-zagreb indices of carbon nanocones CNCk[n]. J. Comput. Theor. Nanosci. 2016, 13, 7475–7482. [Google Scholar] [CrossRef]
- Ghani, M.U.; Campena, F.J.H.; Ali, S.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Galal, A.M. Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices. Symmetry 2023, 15, 143. [Google Scholar] [CrossRef]
- Shi, J.; Yu, W.; Hu, C.; Duan, H.; Ji, J.; Kang, Y.; Cai, K. Effects of Tearing Conditions on the Crack Propagation in a Monolayer Graphene Sheet. Int. J. Mol. Sci. 2022, 23, 6471. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem. 2021, 86, 11–16. [Google Scholar]
- Alrowaili, D.A.; Farid, F.; Javaid, M. Gutman Connection Index of Graphs under Operations. Symmetry 2023, 15, 21. [Google Scholar] [CrossRef]
- Das, K.C.; Çevik, A.S.; Cangul, I.N.; Shang, Y. On Sombor index. Symmetry 2021, 13, 140. [Google Scholar] [CrossRef]
- Redzepovic, I. Chemical applicability of Sombor indices. J. Serb. Chem. Soc. 2021, 10, 2298. [Google Scholar] [CrossRef]
- Maji, D.; Ghorai, G.; Mahmood, M.K.; Alam, M.A. On the Inverse Problem for Some Topological Indices. J. Math. 2021, 2021, 9411696. [Google Scholar] [CrossRef]
- Naji, A.M.; Soner, N.D. The k-distance degree index of a graph. Palest. J. Math. 2018, 7, 690–701. [Google Scholar]
- Gutman, I.; Naji, A.M.; Soner, N.D. On leap Zagreb indices of graphs. Commun. Comb. Optim. 2017, 2, 99–117. [Google Scholar]
- Naji, A.M.; Davvaz, B.; Mahde, S.S.; Soner, N.D. A study on some properties of leap graphs. Commun. Comb. Optim. 2020, 5, 9–17. [Google Scholar]
- Shiladhar, P.; Naji, A.M.; Soner, N.D. Leap Zagreb indices of some wheel related graphs. J. Comput. Math. Sci. 2018, 9, 221–231. [Google Scholar]
- Lal, S.; Sharma, K.; Bhat, V.K. On k-distance degree based topological indices of benzenoid systems. arXiv 2022, arXiv:2212.04200. [Google Scholar]
- Hakeem, A.; Ullah, A.; Zaman, S. Computation of some important degree-based topological indices for γ-graphyne and Zigzag graphyne nanoribbon. Mol. Phys. 2023, 121, e2211403. [Google Scholar] [CrossRef]
- Kulli, V.R. Leap hyper-Zagreb indices and their polynomials of certain graphs. Int. J. Curr. Life Sci. 2018, 7, 2783–2791. [Google Scholar]
- Kulli, V.R. Leap Gourava indices certain windmill graphs. Int. J. Math. Arch. 2019, 10, 7–14. [Google Scholar]

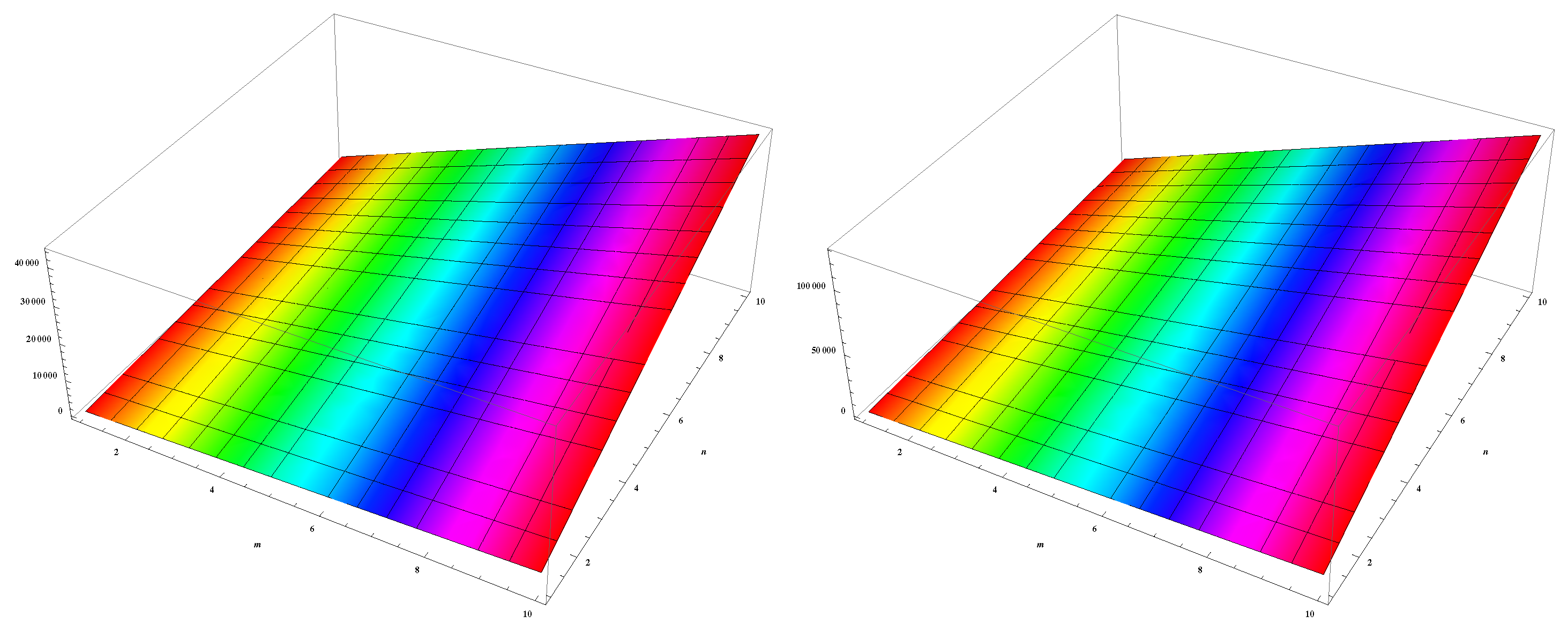
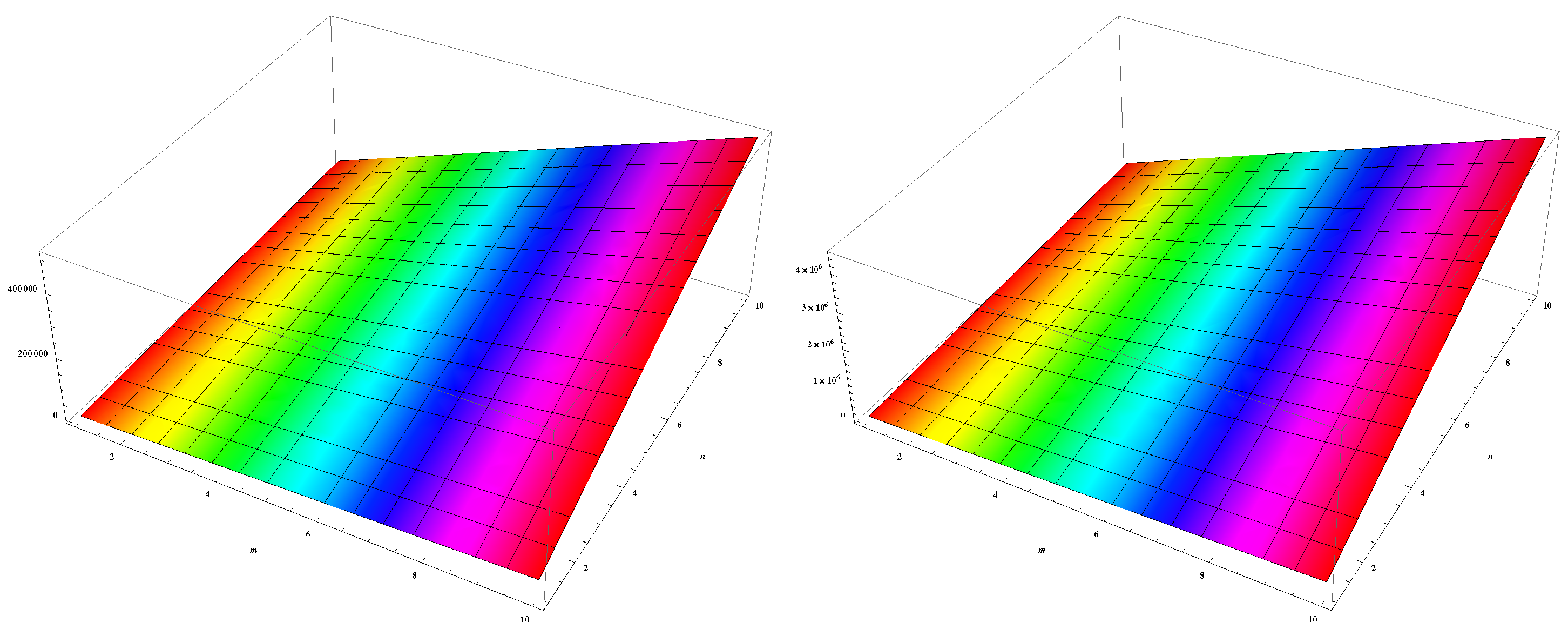
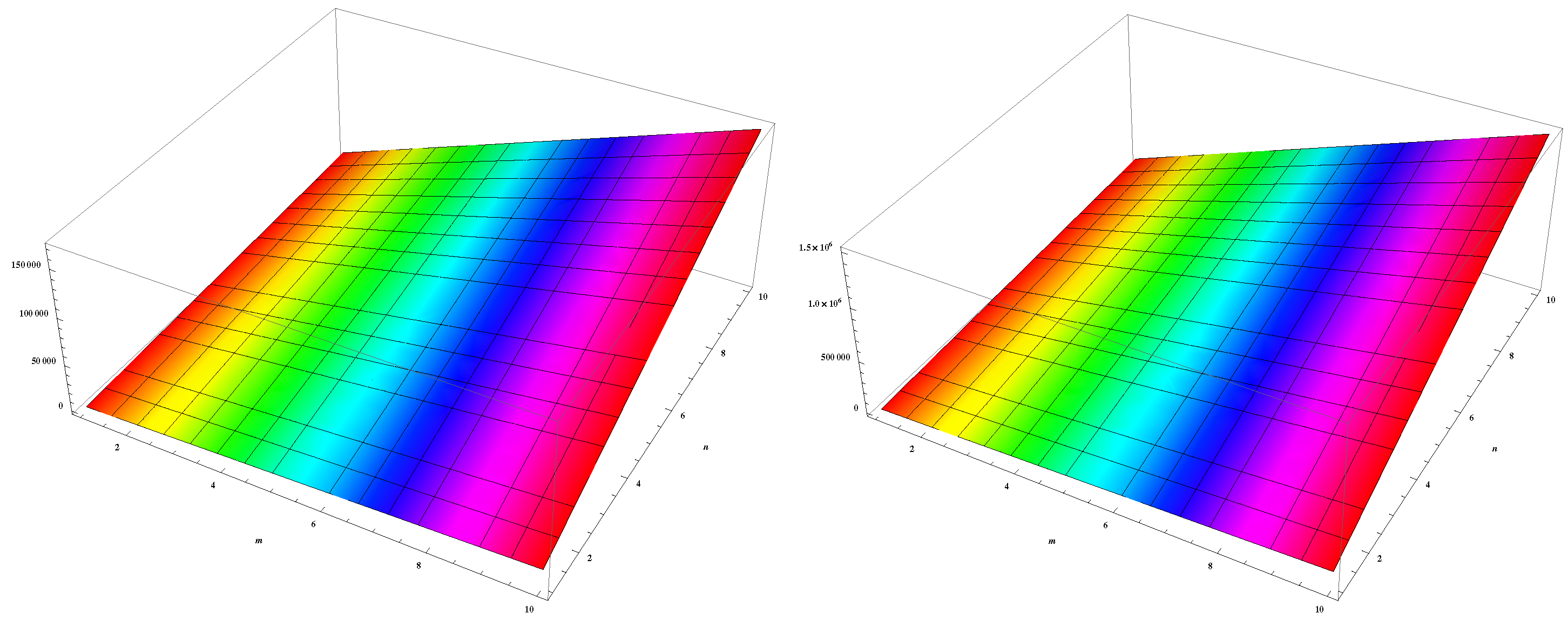
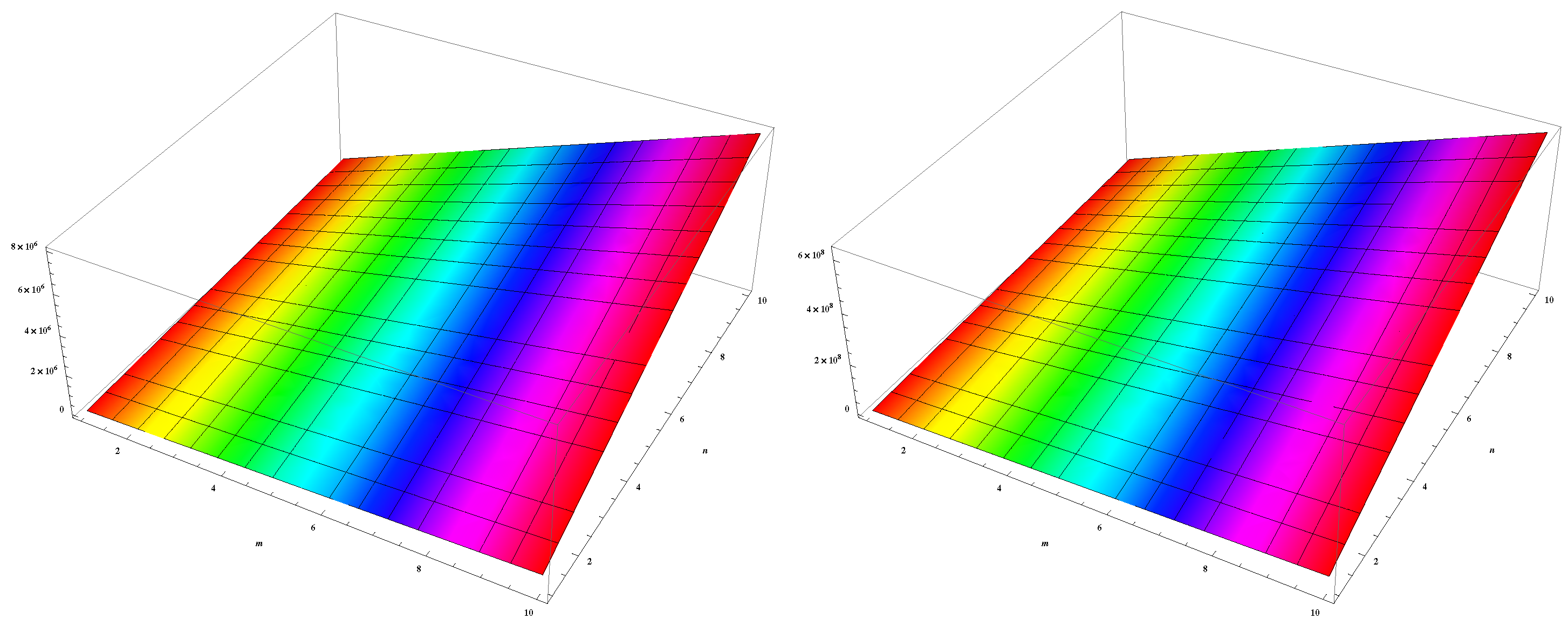

| (m,n) | ||||
|---|---|---|---|---|
| 492 | 1194 | 4848 | ||
| 1868 | 4942 | |||
| 4108 | ||||
| 7212 | ||||
| (m,n) | ||||
|---|---|---|---|---|
| 1686 | ||||
| 6810 | ||||
| [n] | ||||
|---|---|---|---|---|
| 3 | 306 | 678 | 3022 | |
| 4 | 384 | 874 | 3816 | |
| 5 | 462 | 1070 | 4610 | |
| 6 | 540 | 1266 | 5404 | |
| 7 | 618 | 1462 | 6198 | |
| 8 | 696 | 1658 | 6992 | |
| 9 | 774 | 1854 | 7786 |
| [n] | ||||
|---|---|---|---|---|
| 3 | 978 | 6540 | ||
| 4 | 1250 | 8604 | ||
| 5 | 1522 | |||
| 6 | 1794 | |||
| 7 | 2066 | |||
| 8 | 2338 | |||
| 9 | 2610 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, M.A.; Mahmood, M.K.; Imran, M.; Tchier, F.; Ahmad, D.; Masood, M.K. Computational Studies on Diverse Characterizations of Molecular Descriptors for Graphyne Nanoribbon Structures. Molecules 2023, 28, 6597. https://doi.org/10.3390/molecules28186597
Raza MA, Mahmood MK, Imran M, Tchier F, Ahmad D, Masood MK. Computational Studies on Diverse Characterizations of Molecular Descriptors for Graphyne Nanoribbon Structures. Molecules. 2023; 28(18):6597. https://doi.org/10.3390/molecules28186597
Chicago/Turabian StyleRaza, Muhammad Awais, Muhammad Khalid Mahmood, Muhammad Imran, Fairouz Tchier, Daud Ahmad, and Muhammad Kashif Masood. 2023. "Computational Studies on Diverse Characterizations of Molecular Descriptors for Graphyne Nanoribbon Structures" Molecules 28, no. 18: 6597. https://doi.org/10.3390/molecules28186597
APA StyleRaza, M. A., Mahmood, M. K., Imran, M., Tchier, F., Ahmad, D., & Masood, M. K. (2023). Computational Studies on Diverse Characterizations of Molecular Descriptors for Graphyne Nanoribbon Structures. Molecules, 28(18), 6597. https://doi.org/10.3390/molecules28186597







