First Principles Study of the Photoelectric Properties of Alkaline Earth Metal (Be/Mg/Ca/Sr/Ba)-Doped Monolayers of MoS2
Abstract
:1. Introduction
2. Results
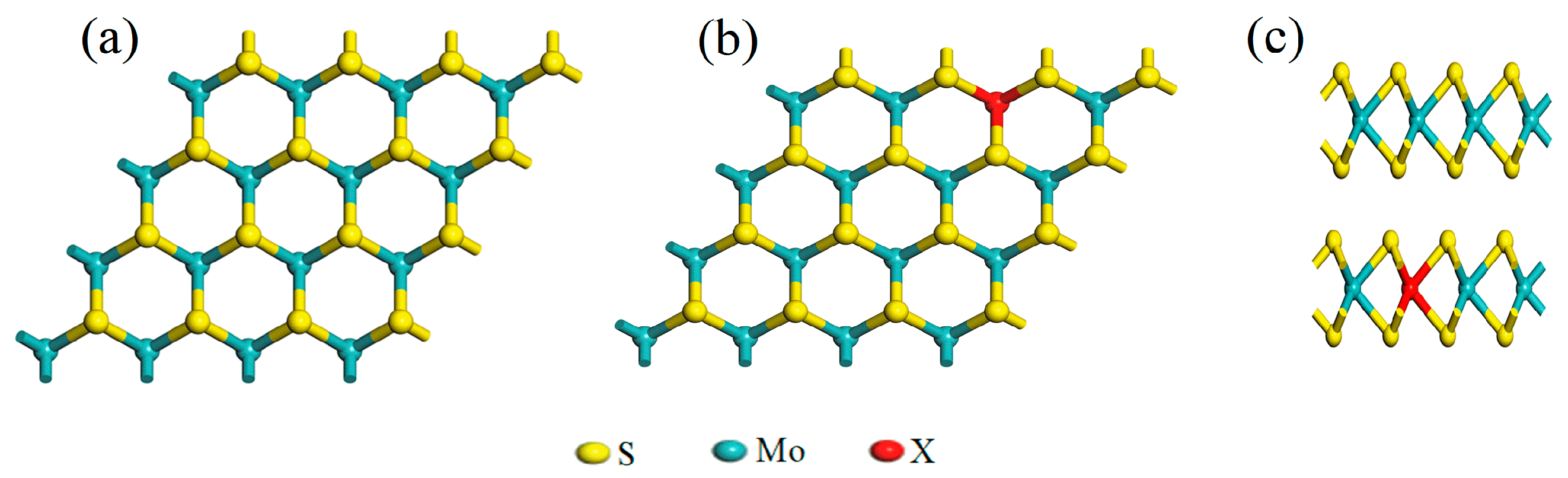
2.1. Analysis of Lattice Constants and Bond Population
2.2. Band Structures
2.3. Density of States
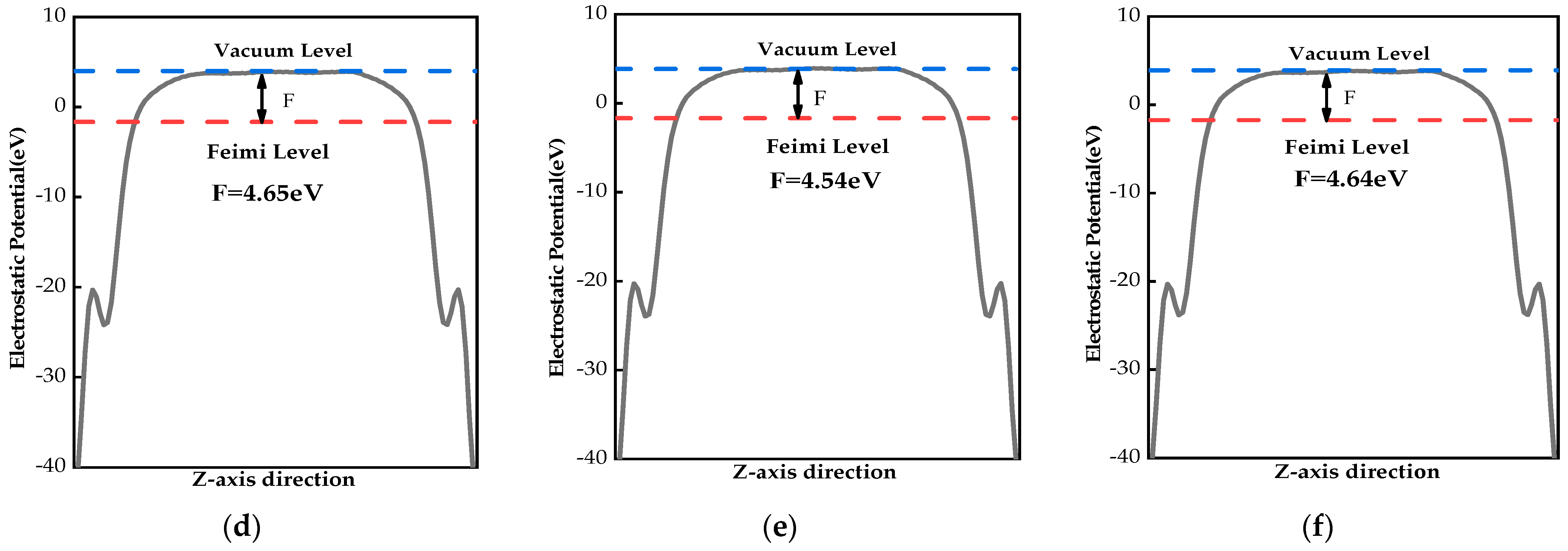
2.4. Work Functions
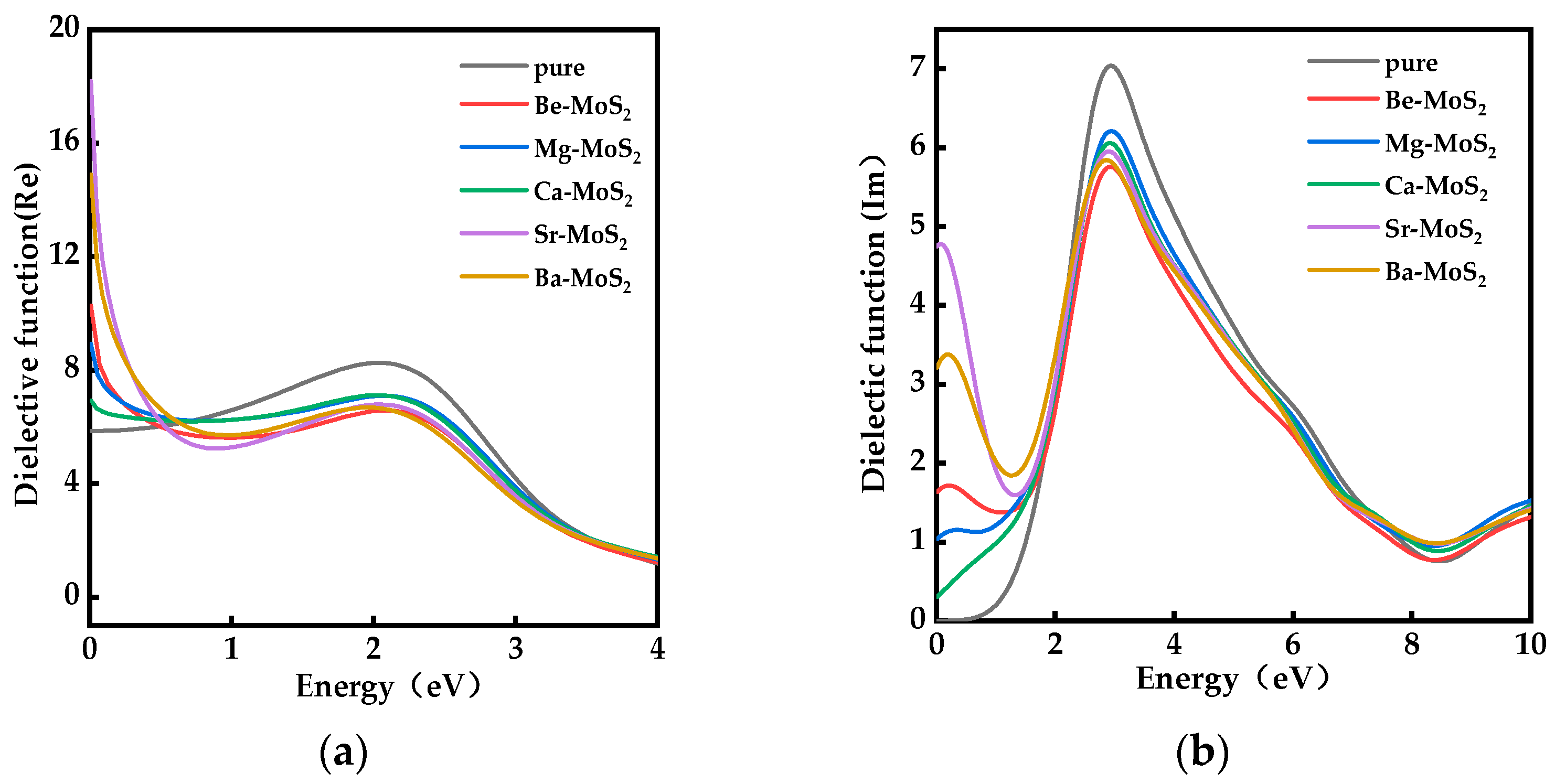
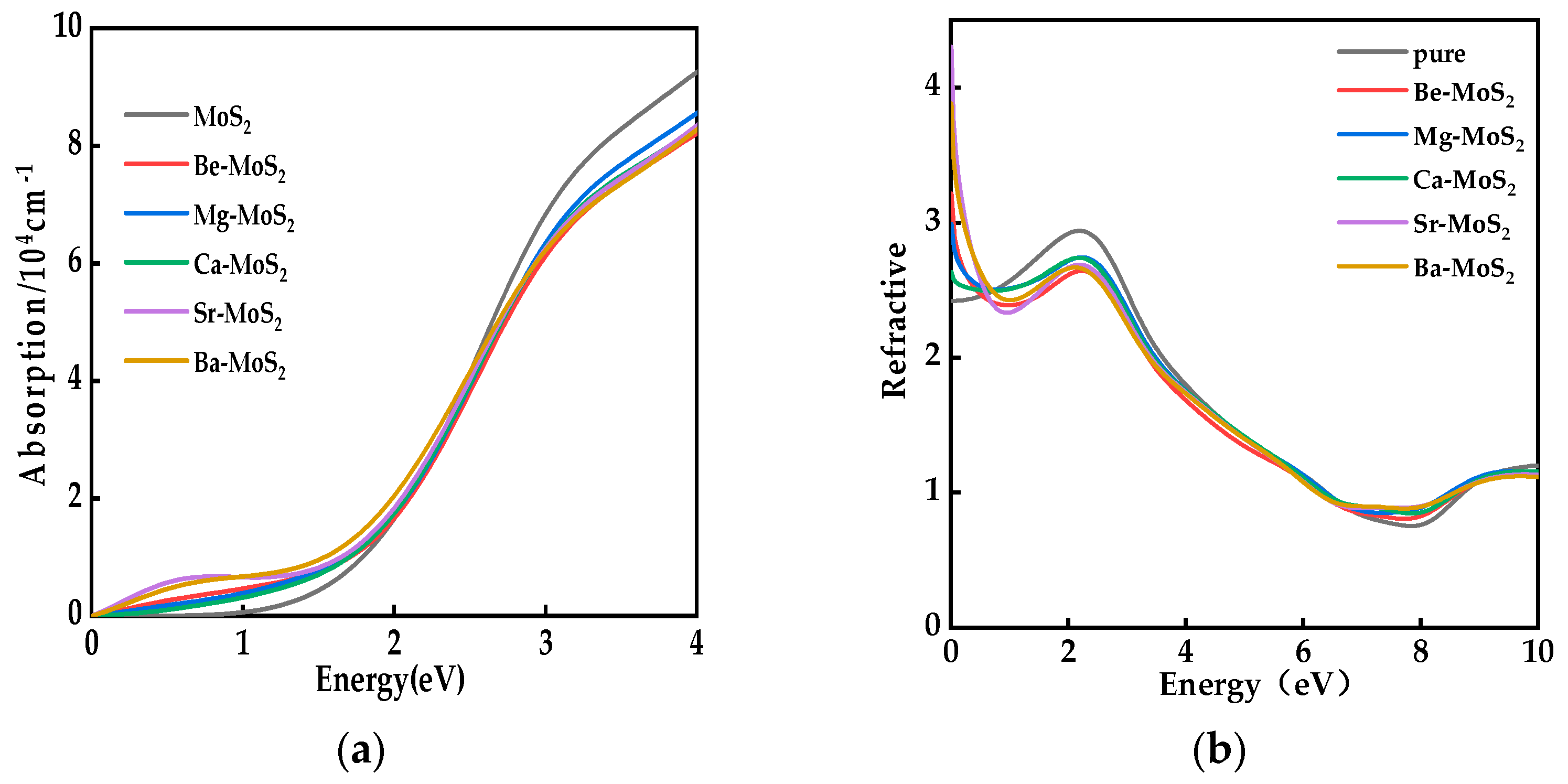
2.5. Optical Properties
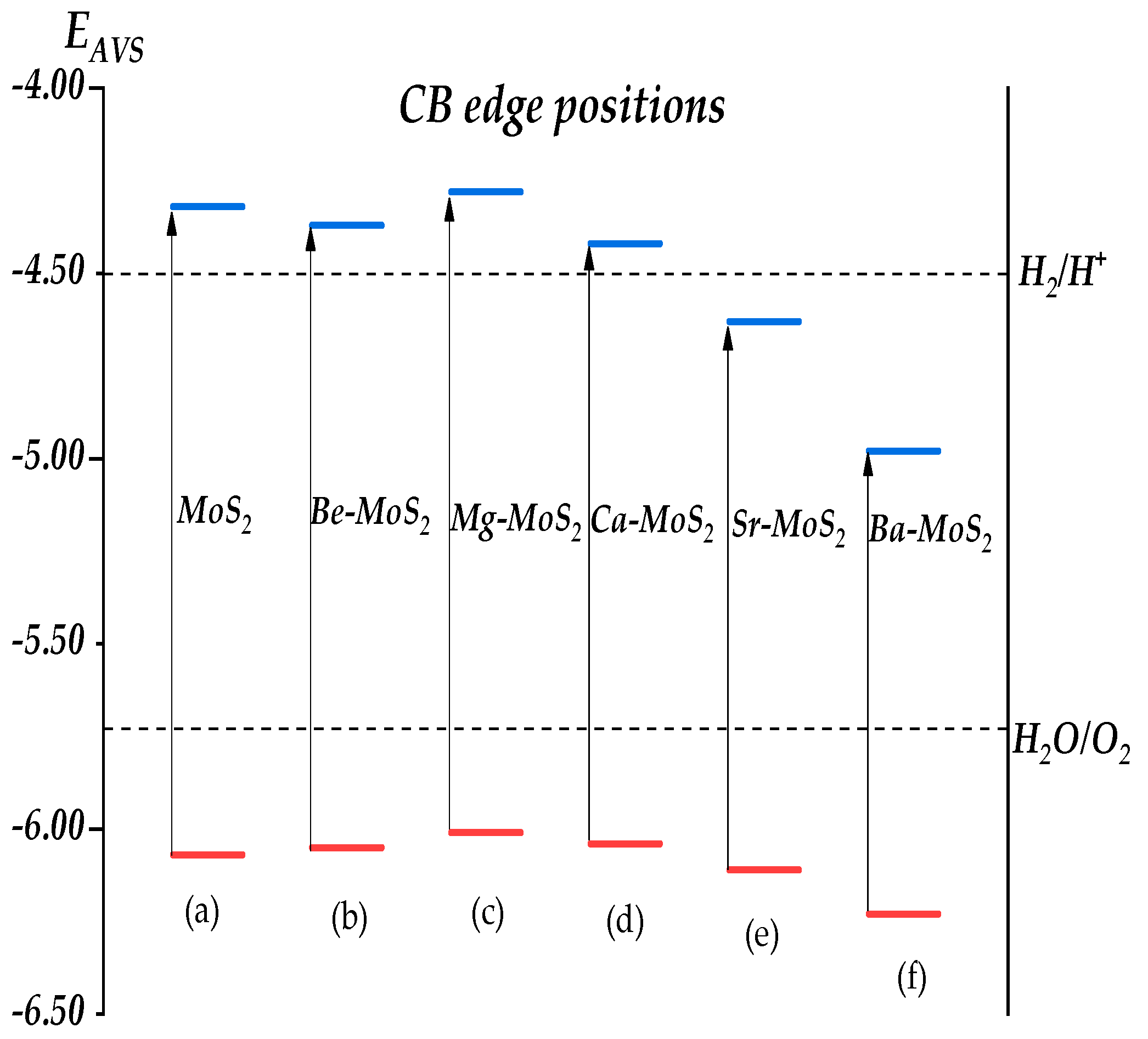
2.6. Band Alignment
3. Experimental Section
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Xia, Y.; Cheng, B.; Fan, J.J.; Yu, J.G.; Liu, G. Near-infrared absorbing 2D/3D ZnIn2S4/N-doped graphene photocatalyst for highly efficient CO2 capture and photocatalytic reduction. Sci. China Mater. 2020, 63, 552–565. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Zhang, S.J.; Xu, S.S.; Wu, X.G.; Chang, J.C.; He, Z.L. Hexagonal boron nitride composite photocatalysts for hydrogen production. J. Alloys Compd. 2021, 864, 158153. [Google Scholar] [CrossRef]
- Li, M.R.; Zheng, K.T.; Zhang, J.J.; Li, X.M.; Xu, C.J. Design and construction of 2D/2D sheet-on-sheet transition metal sulfide/phosphide heterostructure for efficient oxygen evolution reaction. Appl. Surf. Sci. 2021, 565, 150510. [Google Scholar] [CrossRef]
- Ao, K.L.; Shao, Y.F.; Chan, I.N.; Shi, X.Q.; Kawazoe, Y.; Yang, M.; Ng, K.W.; Pan, H. Design of novel pentagonal 2d transitional-metal sulphide monolayers for hydrogen evolution reaction. Int. J. Hydrogen Energy 2020, 45, 16201–16209. [Google Scholar] [CrossRef]
- Dongxu, W.; Juan, C.; Xin, G.; Yanhui, A.; Peifang, W. Maximizing the utilization of photo-generated electrons and holes of g-C3N4 photocatalyst for harmful algae inactivation. Chem. Eng. J. 2022, 431, 134105. [Google Scholar]
- Liu, D.Q.; Barbar, A.; Najam, T.; Javed, M.S.; Shen, J.; Tsiakaras, P.; Cai, X.K. Single noble metal atoms doped 2D materials for catalysis. Appl. Catal. B Environ. 2021, 297, 120389. [Google Scholar] [CrossRef]
- Chang, C.; Chen, W.; Chen, Y.; Chen, Y.; Chen, Y.; Ding, F.; Fan, C.; Fan, H.; Fan, Z.; Gong, C.; et al. Recent progress on two-dimensional materials. Acta Phys. Chem. Sin. 2021, 37, 2108017. [Google Scholar] [CrossRef]
- Liu, C.; Kong, C.; Zhang, F.J.; Kai, C.M.; Cai, W.Q.; Sun, X.Y.; Oh, W.C. Research progress of defective MoS2 for photocatalytic hydrogen evolution. J. Korean Ceram. Soc. 2021, 58, 135–147. [Google Scholar] [CrossRef]
- Xia, Z.H.; Tao, Y.Q.; Pan, Z.G.; Shen, X.D. Enhanced photocatalytic performance and stability of 1T MoS2 transformed from 2H MoS2 via li intercalation. Results Phys. 2019, 12, 2218–2224. [Google Scholar] [CrossRef]
- Zhao, Y.; Tu, J.; Zhang, Y.; Hu, X.; Xu, Y.; He, L. Improved photocatalytic property of monolayer MoS2 by B and F co-doping: First principles study. J. Catal. 2020, 382, 280–285. [Google Scholar] [CrossRef]
- Le, O.K.; Chihaia, V.; Pham-Ho, M.; Son, D.N. Electronic and optical properties of monolayer MoS2 under the influence of polyethyleneimine adsorption and pressure. RSC Adv. 2020, 10, 4201–4210. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Zhang, Q.; Zhao, B.; Marken, F.; Gao, Q.; Lu, H.; Guan, L.; Wang, H.; Shao, G.; Xu, H.; et al. Novel hierarchical structure of MoS2/TiO2/Ti3C2Tx composites for dramatically enhanced electromagnetic absorbing properties. J. Adv. Ceram. 2021, 10, 1042–1051. [Google Scholar] [CrossRef]
- Kuc, A.; Zibouche, N.; Heine, T. Influence of quantum confinement on the electronic structure of the transition metal sulfide TMS2. Phys. Rev. B 2011, 83, 245213. [Google Scholar] [CrossRef]
- Yoffe, A.D. Low-dimensional systems: Quantum size effects and electronic properties of semiconductor microcrystallites (zero-dimensional systems) and some quasi-two-dimensional systems. Adv. Phys. 2010, 51, 799–890. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, K.; Zhao, Q.; Huang, M.; Ouyang, X. Electrocatalytic and photocatalytic performance of noble metal doped monolayer MoS2 in the hydrogen evolution reaction: A first principles study. Nano Mater. Sci. 2021, 3, 89–94. [Google Scholar] [CrossRef]
- Loh, L.; Zhang, Z.; Bosman, M.; Eda, G. Substitutional doping in 2D transition metal dichalcogenides. Nano Res. 2020, 14, 1668–1681. [Google Scholar] [CrossRef]
- Yeonwoong, J.; Yu, Z.; Cha, J.J. Intercalation in two-dimensional transition metal chalcogenides. Inorg. Chem. Front. 2016, 3, 452–463. [Google Scholar]
- Zhang, K.; Bersch, B.M.; Joshi, J.; Addou, R.; Cormier, C.R.; Zhang, C.; Ke, X.; Briggs, N.C.; Ke, W.; Subramanian, S. Tuning the electronic and photonic properties of monolayer MoS2 via in situ rhenium substitutional doping. Adv. Funct. Mater. 2018, 28, 1706950. [Google Scholar] [CrossRef]
- Xu, Z.; Luo, B.; Chen, M.; Xie, W.; Xiao, X. Enhanced photogalvanic effects in the two-dimensional WTe2 monolayer by vacancy- and substitution-doping. Appl. Surf. Sci. 2021, 548, 148751. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Zhu, Z.Y.; Mi, W.B.; Guo, Z.B.; Schwingenschlögl, U. Prediction of two-dimensional diluted magnetic semiconductors: Doped monolayer MoS2 systems. Phys. Rev. B 2013, 87, 1214–1222. [Google Scholar] [CrossRef]
- Zhou, J.; Lin, J.; Sims, H.; Jiang, C.; Cong, C.; Brehm, J.A.; Zhang, Z.; Niu, L.; Chen, Y.; Zhou, Y. Synthesis of co-doped MoS2 monolayers with enhanced valley splitting. Adv. Mater. 2020, 32, 1906536. [Google Scholar] [CrossRef] [PubMed]
- Burman, D.; Raha, H.; Manna, B.; Pramanik, P.; Guha, P. Substitutional doping of MoS2 for superior gas-sensing applications: A proof of concept. ACS Sens. 2021, 6, 3398–3408. [Google Scholar] [CrossRef] [PubMed]
- Suh, J.; Park, T.E.; Lin, D.Y.; Fu, D.; Park, J.; Jung, H.J.; Chen, Y.; Ko, C.; Jang, C.; Sun, Y. Doping against the native propensity of MoS2: Degenerate hole doping by cation substitution. Nano Lett. 2014, 14, 6976–6982. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; Zhang, X.; Wang, P.; Chen, H.S.; Yang, P. Formation of Ni-doped MoS2 nanosheets on N-doped carbon nanotubes towards superior hydrogen evolution. Electrochim. Acta 2020, 338, 135885. [Google Scholar] [CrossRef]
- Zhang, K.; Jia, Y.; Wang, Z.; Wang, L.; Hu, X. Awakening solar hydrogen evolution of MoS2 in alkalescent electrolyte via doping of Co. ChemSusChem 2019, 12, 3336–3342. [Google Scholar]
- Sanakousar, F.M.; Vidyasagar, C.C.; Jiménez-Pérez, V.M.; Prakash, K. Recent progress on visible-light-driven metal and non-metal doped ZnO nanostructures for photocatalytic degradation of organic pollutants. Mat. Sci. Semicon. Proc. 2022, 140, 106390. [Google Scholar] [CrossRef]
- Ullah, S.; Hussain, A.; Waqaradil, S.; Muhammad Saqlain, A.; Idrees, A.; Ortwin, L.; Altaf, K. Band-gap tuning of graphene by be doping and Be, B co-doping: A DFT study. RSC Adv. 2015, 5, 55762–55773. [Google Scholar] [CrossRef]
- Tayyab, M.; Hussain, A.; Asif, Q.U.A.; Adil, W. Band-gap tuning of graphene by Mg doping and adsorption of Br and Be on impurity: A DFT study. Comput. Condens. Matter 2020, 23, e00469. [Google Scholar] [CrossRef]
- Kumar, G.M.; Cho, H.D.; Ilanchezhiyan, P.; Siva, C.; Ganesh, V.; Yuldashev, S.; Kumar, A.M.; Kang, T.W. Evidencing enhanced charge-transfer with superior photocatalytic degradation and photoelectrochemical water splitting in Mg modified few-layered SnS2. J. Colloid Interface Sci. 2019, 540, 476–485. [Google Scholar] [CrossRef]
- Inamdar, A.N.; Som, N.N.; Pratap, A.; Jha, P.K. Hydrogen evolution and oxygen evolution reactions of pristine and alkali metal doped SnSe2 monolayer. Int. J. Hydrogen Energy 2020, 45, 18657–18665. [Google Scholar] [CrossRef]
- Moss, B.S.A.J. Anisotropic mean-square displacements (msd) in single-crystals of 2H-and 3R-MoS2. Acta Crystallogr. B 1983, 39, 404–407. [Google Scholar]
- Hu, J.S.; Duan, W.; He, H.; Lv, H.; Ma, X. A promising strategy to tune the schottky barrier of a MoS2(1-x)Se2x/graphene heterostructure by asymmetric Se doping. J. Mater. Chem. C 2019, 7, 7798–7805. [Google Scholar] [CrossRef]
- Zhu, J.; Vasilopoulou, M.; Davazoglou, D. Intrinsic defects and h doping in WO3. Sci. Rep. 2017, 7, 40882. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Lin, S.; Yang, L.; Liao, J.; Chen, Y.; Wang, C.Z. First-principles investigation of metal-doped cubic BaTiO3. Mater. Res. Bull. 2017, 96, 372–378. [Google Scholar] [CrossRef]
- Wang, S.; Fan, X.; An, Y. Room-temperature ferromagnetism in alkaline-earth-metal doped alp: First-principle calculations. Comput. Mater. Sci. 2018, 142, 338–345. [Google Scholar] [CrossRef]
- Ruan, L.W.; Zhu, Y.J.; Qiu, L.G.; Lu, Y.X. Mechanical properties of doped g-C3N4-a first-principle study. Vacuum 2014, 106, 79–85. [Google Scholar] [CrossRef]
- Wang, Y.R.; Li, S.; Yi, J.B. Transition metal-doped tin monoxide monolayer: A first-principles study. J. Phys. Chem. C 2018, 122, 4651–4661. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Mo, Y.; Peyerimhoff, S.D. Theoretical analysis of electronic delocalization. J. Chem. Phys. 1998, 109, 1687–1697. [Google Scholar] [CrossRef]
- Li, G.; Chen, M.Q.; Zhao, S.X.; Li, P.W.; Hu, J.; Sang, S.B.; Hou, J.J. Effect of Se doping on the electronic band structure and optical absorption properties of single layer MoS2. Acta Phys.-Chim. Sin. 2016, 32, 2905–2912. [Google Scholar] [CrossRef]
- Pan, F.C.; Lin, X.L.; Cao, Z.J.; Li, X.F. Electronic structures and optical properties of Fe, Co, and Ni doped GaSb. Acta Phys. Sin. 2019, 68, 184202. [Google Scholar] [CrossRef]
- Ma, J.; Shang, S.L.; Kim, H.; Liu, Z.K. An ab initio molecular dynamics exploration of associates in Ba-Bi liquid with strong ordering trends. Acta Mater. 2020, 190, 81–92. [Google Scholar] [CrossRef]
- Guo, X.; Gu, J.; Lin, S.; Zhang, S.; Huang, S. Tackling the activity and selectivity challenges of electrocatalysts towards nitrogen reduction reaction via atomically dispersed Bi-atom catalysts. J. Am. Chem. Soc. 2020, 124, 5709–5712. [Google Scholar] [CrossRef]
- Lv, L.; Shen, Y.; Liu, J.; Meng, X.; Gao, X.; Zhou, M.; Zhang, Y.; Gong, D.; Zheng, Y.; Zhou, Z. Computational screening of high activity and selectivity Tm/g-G3N4 single-atom catalysts for electrocatalytic reduction of nitrates to ammonia. J. Phys. Chem. Lett. 2021, 12, 11143–11150. [Google Scholar] [CrossRef]
- Kam, K.K.; Parkinson, B.A. Detailed photocurrent spectroscopy of the semiconducting group vib transition metal dichalcogenides. J. Phys. Chem. 1982, 86, 463–467. [Google Scholar] [CrossRef]
- Lebgue, S.; Eriksson, O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 2009, 79, 115409. [Google Scholar] [CrossRef]
- Pereira, F.; Xiao, K.; Latino, D.A.; Wu, C.; Zhang, Q.; Aires-De-Sousa, J. Machine learning methods to predict density functional theory B3LYP energies of HOMO and LUMO orbitals. J. Chem. Inf. Model. 2017, 57, 11–21. [Google Scholar] [CrossRef]
- Obeid, M.M.; Stampfl, C.; Bafekry, A.; Guan, Z.; Jappor, H.R.; Nguyen, C.V.; Naseri, M.; Hoat, D.M.; Hieu, N.N.; Krauklis, A.E. First-principles investigation of nonmetal doped single-layer BiOBr as a potential photocatalyst with a low recombination rate. Phys. Chem. Chem. Phys. 2020, 22, 15354–15364. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Ma, X.G.; Zhu, L.; He, H.; Huang, C.Y. Interfacial cohesive interaction and band modulation of two-dimensional MoS2/graphene heterostructure. Acta Phys. Sin. 2017, 66, 87101. [Google Scholar]
- Zhang, L.L.; Xia, T.; Liu, G.A.; Lei, B.C.; Zhao, X.C.; Wang, S.X.; Huang, Y.N. Electronic and optical properties of N-Pr co-doped anatase TiO2 from first-principles. Acta Phys. Sin.-Cn. Ed. 2019, 68, 17401. [Google Scholar] [CrossRef]
- Lang, Q.Z.; Huang, Y.B.; Wei, J.M.; Wang, Y.; Ding, Z. The magnetic, optical and electronic properties of Mn-X(X = O, Se, Te, Po) co-doped MoS2 monolayers via first principle calculation. Mater. Res. Express 2020, 7, 116301. [Google Scholar] [CrossRef]
- Liping, Z.; Mietek, J. Toward designing semiconductor-semiconductor heterojunctions for photocatalytic applications. Appl. Surf. Sci. 2018, 430, 2–17. [Google Scholar]
- Ma, L.; Li, M.N.; Zhang, L.L. Electronic and optical properties of GaN/MoSe2 and its vacancy heterojunctions studied by first-principles. J. Appl. Phys. 2023, 133, 45307. [Google Scholar] [CrossRef]
- Pang, Y.; Feng, Q.; Kou, Z.; Xu, G.; Gao, F.; Wang, B.; Pan, Z.; Lv, J.; Zhang, Y.; Wu, Y. A surface precleaning strategy intensifies the interface coupling of the Bi2O3/TiO2 heterostructure for enhanced photoelectrochemical detection properties. Mat. Chem. Front. 2020, 4, 638–644. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Robertson, J. Chemical bonding and band alignment at X2O3/GaN (X = Al, Sc) interfaces. Appl. Phys. Lett. 2019, 114, 161601. [Google Scholar] [CrossRef]
- Fawadkhan, I.M.; Nguyen, C.; Iftikharahmad, B. A first-principles study of electronic structure and photocatalytic performance of GaN-MX2 (M = Mo, W. X = S, Se) van der Waals heterostructures. RSC Adv. 2020, 10, 24683–24690. [Google Scholar]
- Jia, G.; Liu, Y.; Gong, J.Y.; Lei, D.; Wang, D.L.; Huang, Z.X. Excitonic quantum confinement modified optical conductivity of monolayer and few-layered MoS2. J. Mater. Chem. C 2016, 37, 4. [Google Scholar] [CrossRef]
- Wang, X.; Kim, S.Y.; Wallace, R.M. Interface chemistry and band alignment study of Ni and Ag contacts on MoS2. ACS Appl. Mater. Interfaces 2021, 13, 15802–15810. [Google Scholar] [CrossRef]
- McDonell, S.; Azcatl, A.; Addou, R.; Gong, C.; Battaglia, C.; Chuang, S.; Cho, K.; Javey, A.; Wallace, R.M. Hole contacts on transition metal dichalcogenides: Interface chemistry and band alignments. ACS Nano 2014, 8, 6265–6272. [Google Scholar] [CrossRef]
- Gong, C.; Huang, C.; Miller, J.; Cheng, L.; Hao, Y.; Cobden, D.; Kim, J.; Ruoff, R.S.; Wallace, R.M.; Cho, K. Metal contacts on physical vapor deposited monolayer MoS2. ACS Nano 2013, 7, 11350–11357. [Google Scholar] [CrossRef]
- Li, S.S.; Sun, J.R.; Guan, J.Q. Strategies to improve electrocatalytic and photocatalytic performance of two-dimensional materials for hydrogen evolution reaction. Chin. J. Catal. 2021, 42, 511–556. [Google Scholar] [CrossRef]
- Lin, L.; Guo, Y.; He, C.; Tao, H.; Huang, J.; Yu, W.; Chen, R.; Lou, M.; Yan, L. First-principles study of magnetism of 3d transition metals and nitrogen co-doped monolayer MoS2. Chin. Phys. B 2020, 29, 517–524. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the castep code. J. Phys. Condens. Mat. 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using castep: Zeitschrift für kristallographie-crystalline materials. Z. Krist. 2005, 220, 567–570. [Google Scholar]
- Sun, J.; Leng, J.; Zhang, G. Theoretically exploring the possible configurations, the electronic and transport properties of MoS2 -OH bilayer. Phys. Lett. A 2020, 384, 126575. [Google Scholar] [CrossRef]
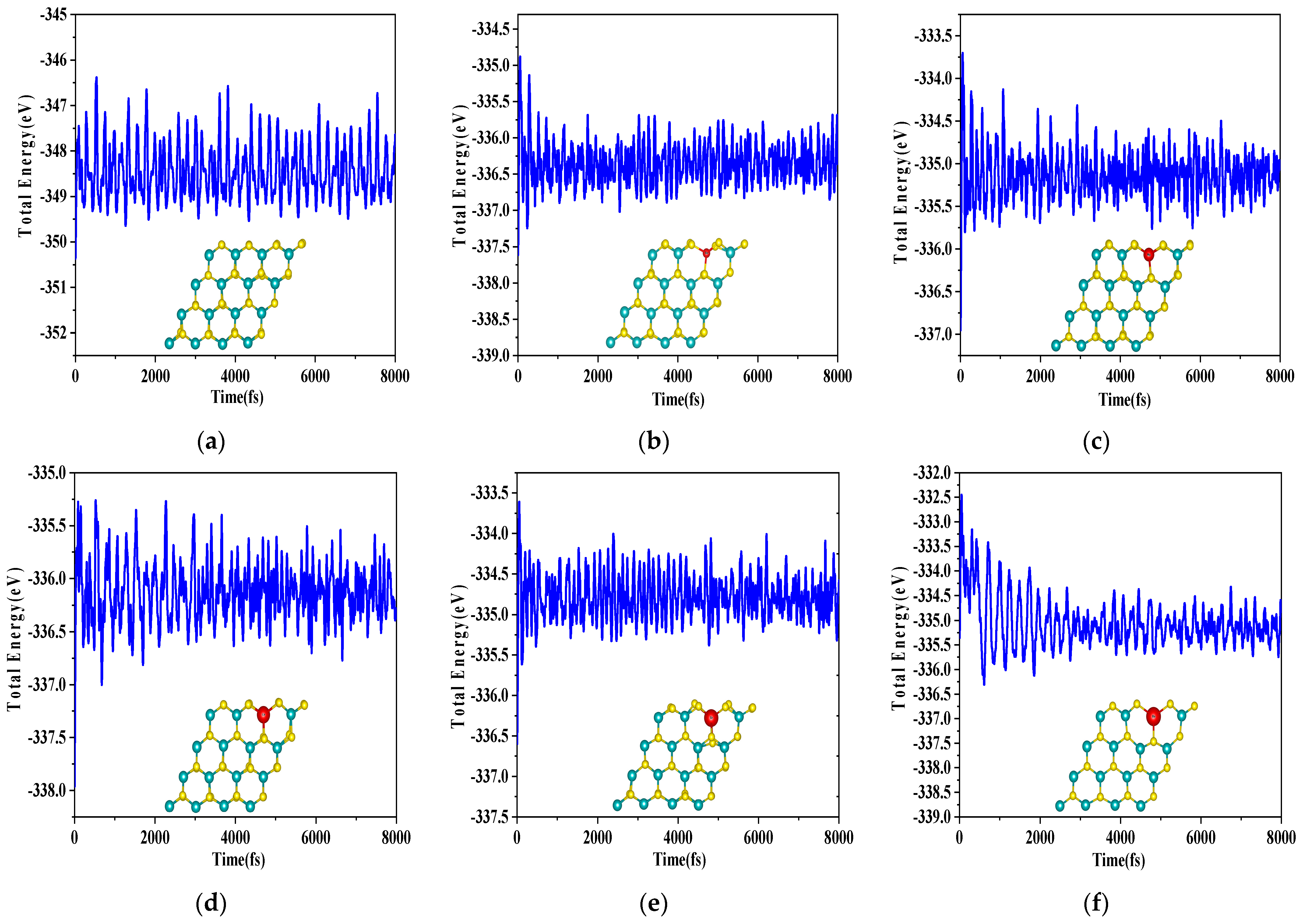



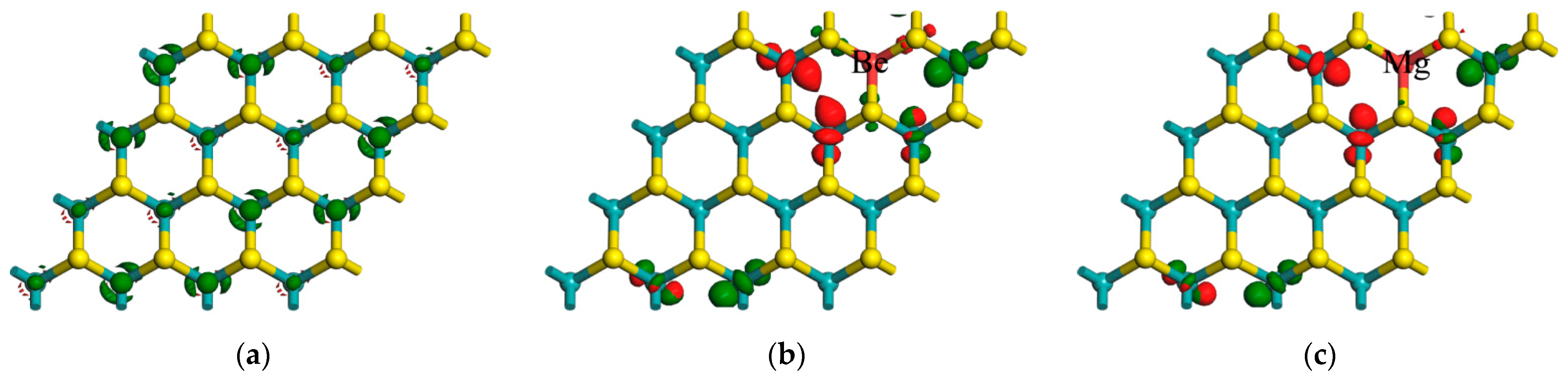
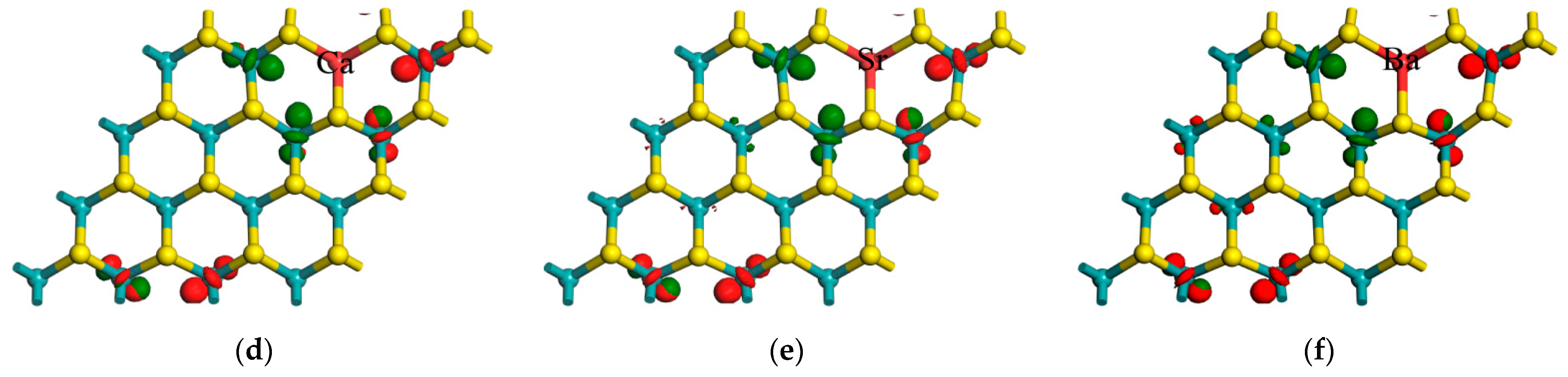
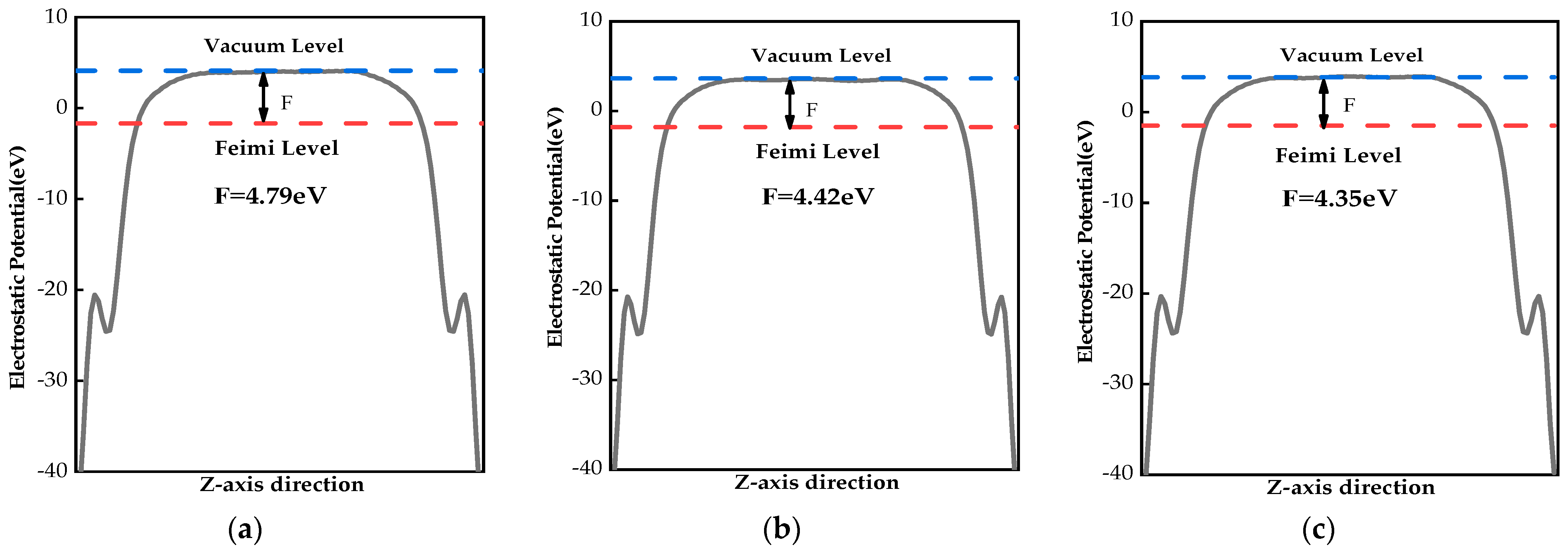
| Formation Energy/eV | Bond Population of Mo–S (Max) | Bond Population of Mo–S (Min) | Bond Length of Mo–S/Å (Min) | Bond Length of Mo–S/Å (Min) | 1 Δγ/Å | |
|---|---|---|---|---|---|---|
| MoS2 | / | 0.37 | 0.37 | 2.4083 | 2.4077 | 0.0006 |
| Be-MoS2 | 10.92 | 0.52 | 0.34 | 2.4274 | 2.3369 | 0.0905 |
| Mg-MoS2 | 7.27 | 0.47 | 0.36 | 2.4291 | 2.3960 | 0.0331 |
| Ca-MoS2 | 12.17 | 0.50 | 0.34 | 2.4461 | 2.3901 | 0.0560 |
| Sr-MoS2 | 13.45 | 0.49 | 0.35 | 2.4593 | 2.3841 | 0.0752 |
| Ba-MoS2 | 14.60 | 0.47 | 0.34 | 2.4750 | 2.3775 | 0.0975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.-Z.; Yu, X.-S.; Wang, S.-X.; Zhang, L.-L.; Zhao, X.-C.; Lei, B.-C.; Yin, H.-M.; Huang, Y.-N. First Principles Study of the Photoelectric Properties of Alkaline Earth Metal (Be/Mg/Ca/Sr/Ba)-Doped Monolayers of MoS2. Molecules 2023, 28, 6122. https://doi.org/10.3390/molecules28166122
Liu L-Z, Yu X-S, Wang S-X, Zhang L-L, Zhao X-C, Lei B-C, Yin H-M, Huang Y-N. First Principles Study of the Photoelectric Properties of Alkaline Earth Metal (Be/Mg/Ca/Sr/Ba)-Doped Monolayers of MoS2. Molecules. 2023; 28(16):6122. https://doi.org/10.3390/molecules28166122
Chicago/Turabian StyleLiu, Li-Zhi, Xian-Sheng Yu, Shao-Xia Wang, Li-Li Zhang, Xu-Cai Zhao, Bo-Cheng Lei, Hong-Mei Yin, and Yi-Neng Huang. 2023. "First Principles Study of the Photoelectric Properties of Alkaline Earth Metal (Be/Mg/Ca/Sr/Ba)-Doped Monolayers of MoS2" Molecules 28, no. 16: 6122. https://doi.org/10.3390/molecules28166122
APA StyleLiu, L.-Z., Yu, X.-S., Wang, S.-X., Zhang, L.-L., Zhao, X.-C., Lei, B.-C., Yin, H.-M., & Huang, Y.-N. (2023). First Principles Study of the Photoelectric Properties of Alkaline Earth Metal (Be/Mg/Ca/Sr/Ba)-Doped Monolayers of MoS2. Molecules, 28(16), 6122. https://doi.org/10.3390/molecules28166122







