Simple Rate Expression for Catalyzed Ammonia Decomposition for Fuel Cells
Abstract
1. Background
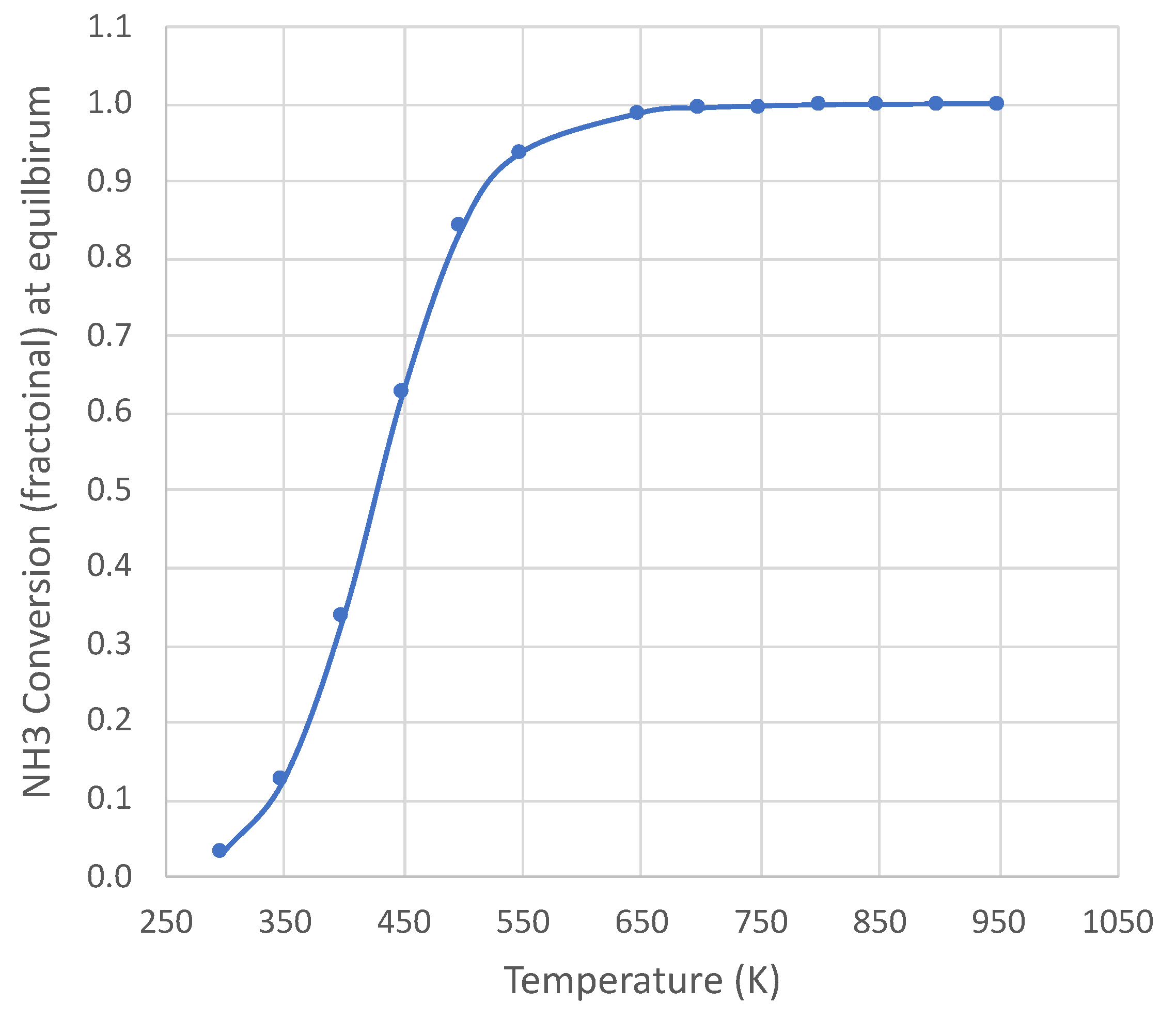
2. Equilibrium
3. Kinetics and Mechanism
4. Simplified Overall Rate Expression
4.1. Derivation by Langmuir–Hinshelwood Algorithm
4.2. Preparation for Calibration of Overall Rate Expression
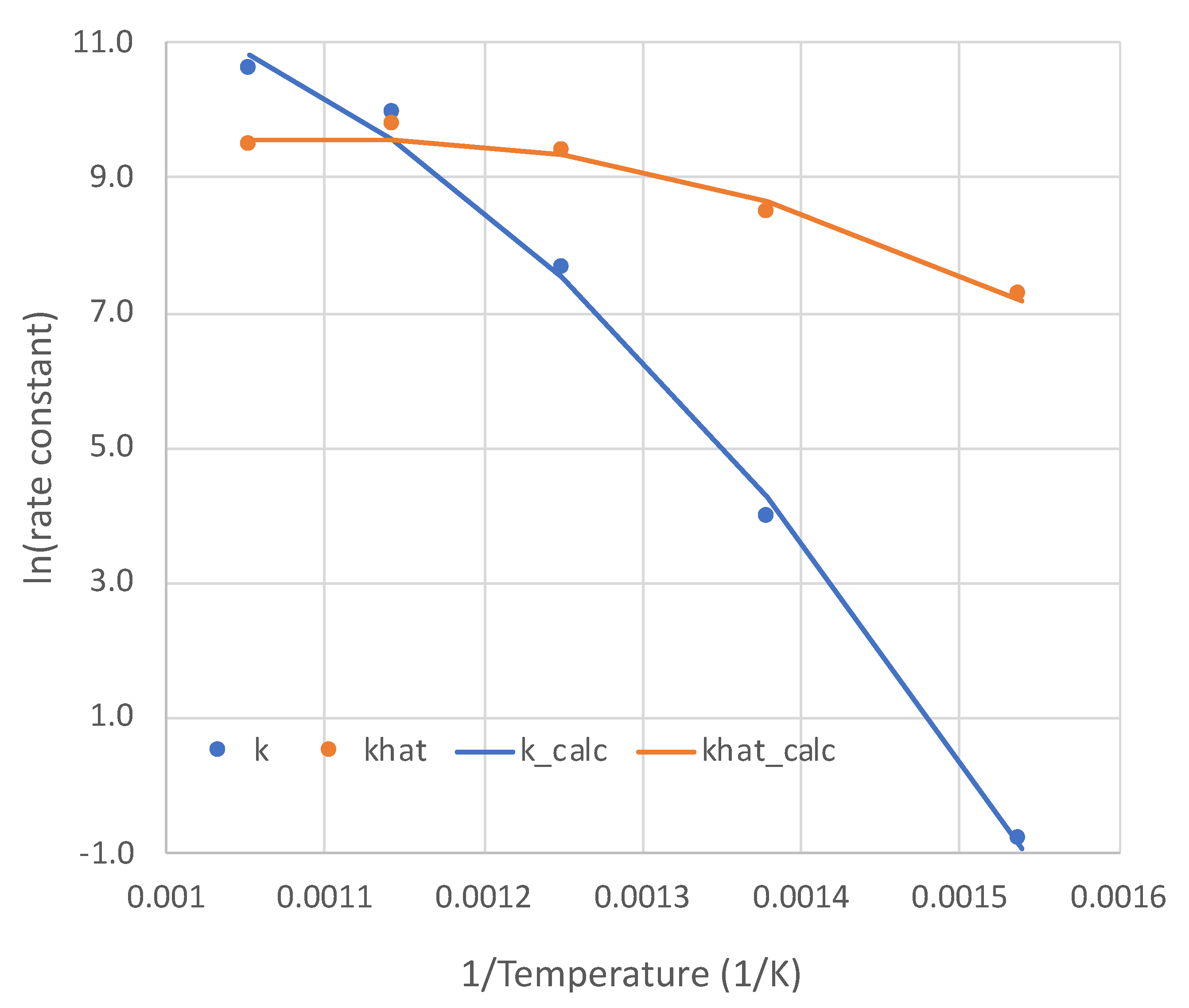
5. Calibration of the Simplified Overall Rate Expression
5.1. Calibration Results
6. PBR Species and Energy Balances Used with Overall Rate Expression
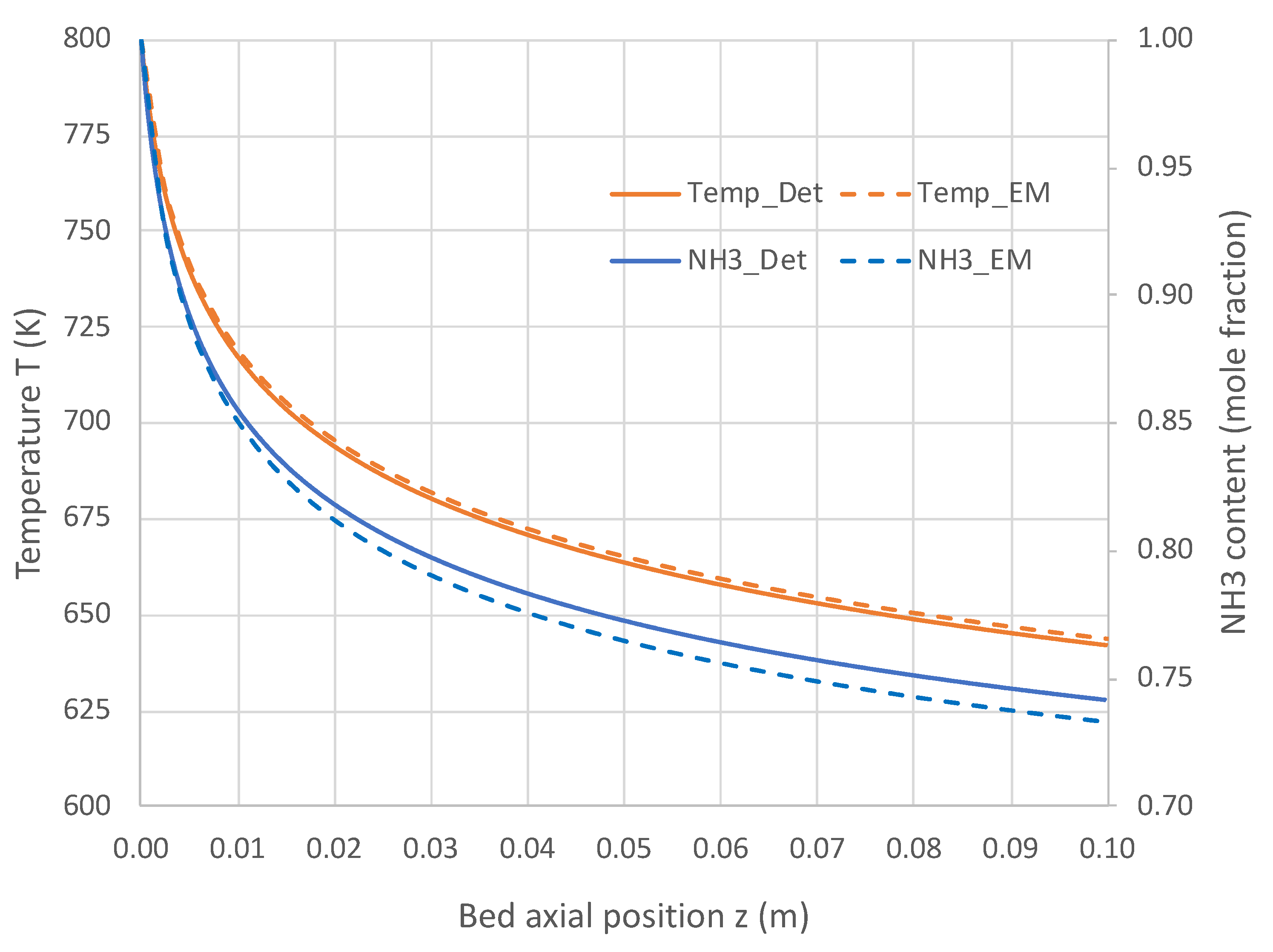
6.1. Packed Bed Reactor Simulations
| Bed radius: 5 × 10−3 m | Bed length: 0.1 m |
| Catalyst area/bed volume: 2.19 × 105 m−1 | Total catalyst area: 0.172 m2 |
| Bed porosity: 0.38 | Particle diameter: 2 × 10−5 m |
| Feed: pure NH3 | Total feed rates: 1 × 10−5, 1 × 10−4 mole/s |
| Pressure: 1 × 105 Pa (constant) | Feed temperature range: 650–950 K |
| Diffusion coefficient kc (Equation (5)): 5 × 10−7 mol/s-m-Pa | (used for Figure 7, Figure 8, Figure 9 and Figure 10 only) |
| Heat transfer factor f (Equation (7)): 0.12 | (used for Figure 7, Figure 8, Figure 9 and Figure 10 only) |
6.2. Extended PBR Simulations

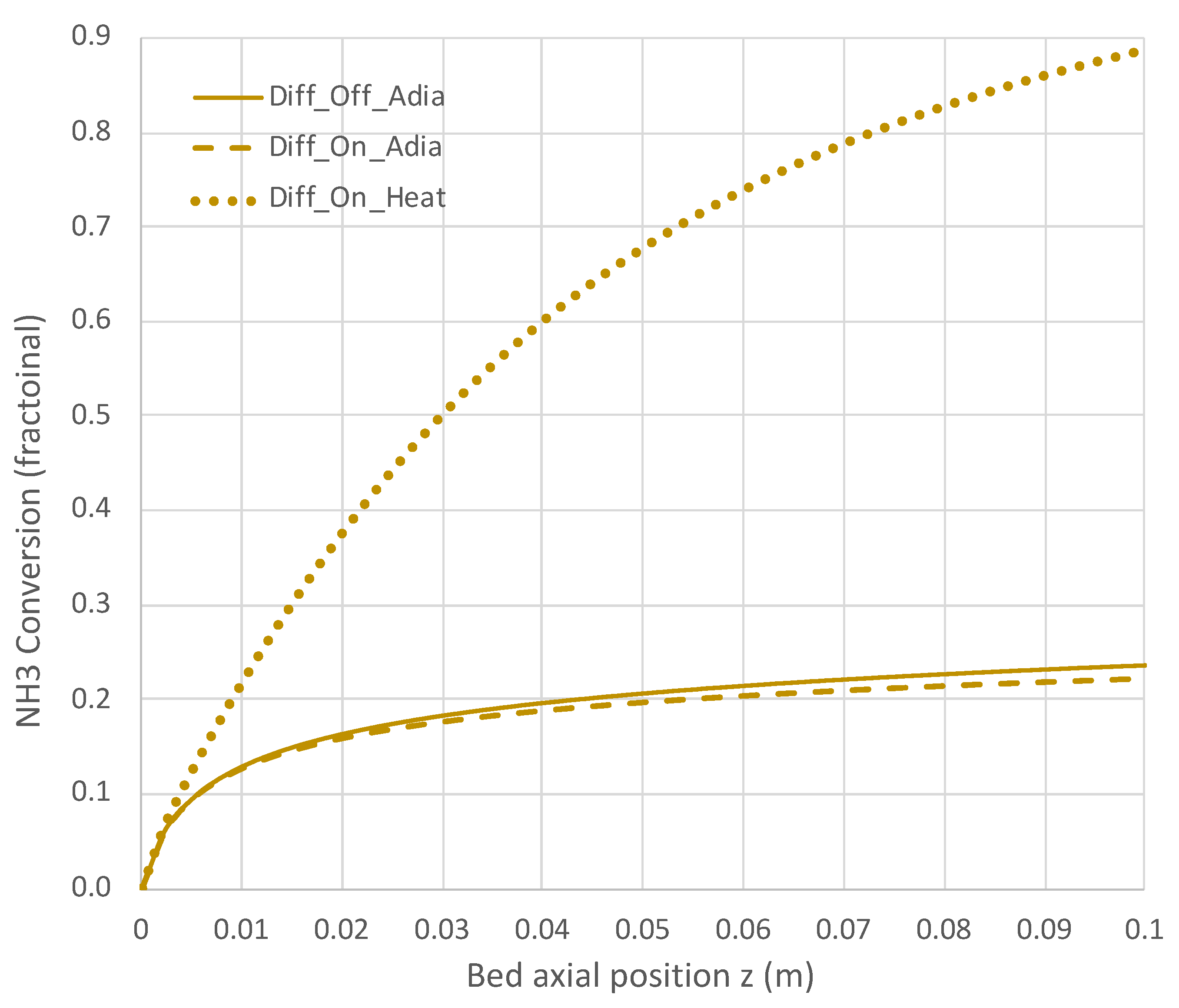
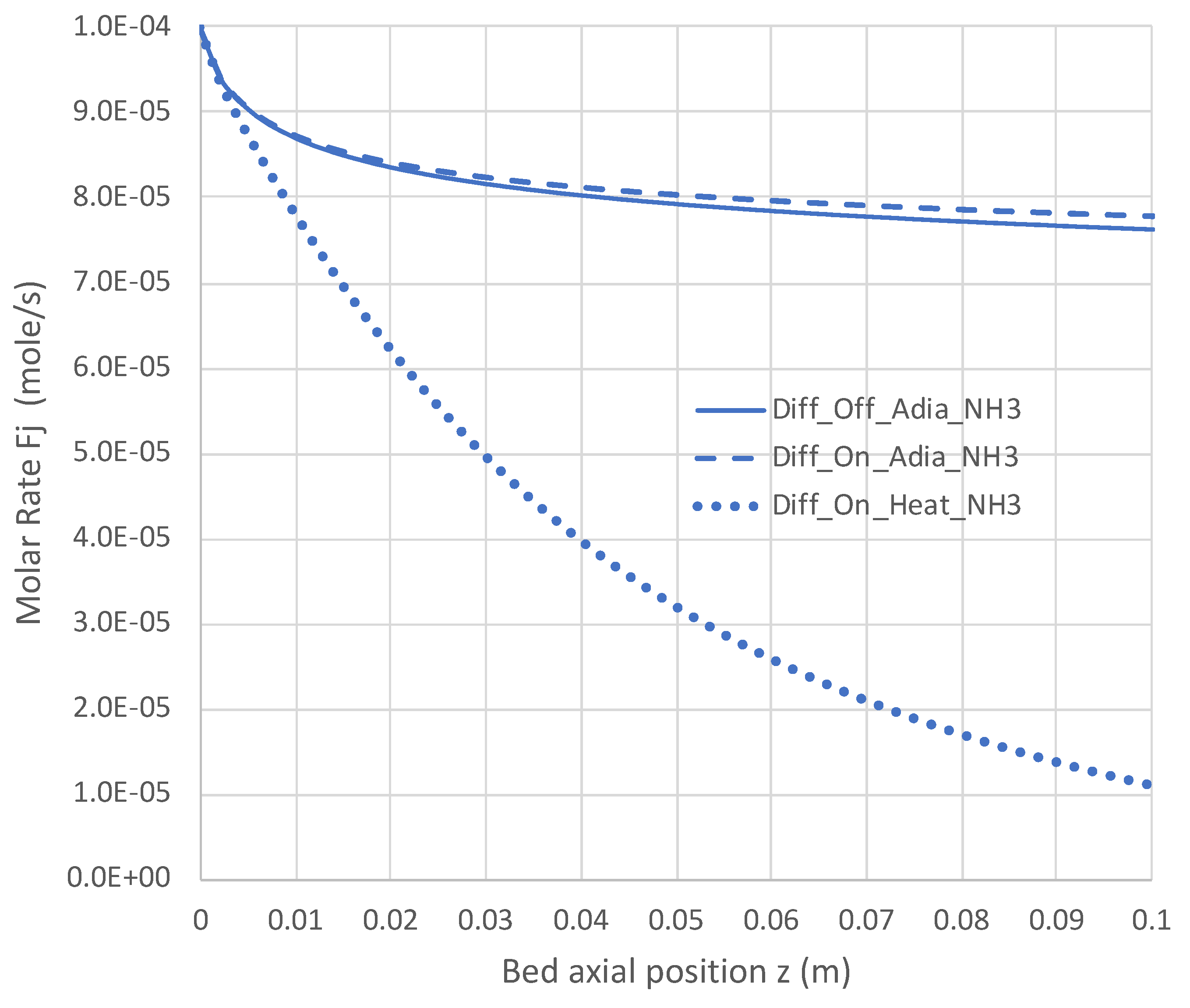

7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | first of three fitted parameters for lumped kinetic constants (Equation (12) |
| Ac | packed bed reactor cross section (m2) |
| ACSTR | catalytic surface area for CSTR (m2) |
| av | catalytic surface area/packed bed volume (m2/m3) |
| b | second of three fitted parameters for lumped kinetic constants (Equation (12) |
| c | last of three fitted parameters for lumped kinetic constants (Equation (12) |
| surface concentration of adsorbed species j (mol/m2) | |
| cp,j | heat capacity of species j (J/mol-K) |
| CS | concentration of vacant surface sites (mole/m2) |
| CT | total concentration of surface sites (mole/m2) |
| f | assumed fraction of H2 oxidation heat transferring from cathode to anode |
| , Fjo, FT | molar rate of species j (mol/s) - subscript “o” for feed, “T” for total |
| k | lumped constant (mol-Pa/s-m2) |
| lumped constants (Pa0.5) | |
| ki,-i | rate constants (forward/reverse) for reaction “i” in decomposition mechanism |
| Ki | equilibrium constant for reaction “i” in decomposition mechanism |
| kc | mass transfer coefficient for H2 diffusion across cell membrane (mol/s-m-Pa) |
| partial pressure of species j (Pa) - subscript “o” indicates feed | |
| local external heat transfer rate in packed bed reactor (J/s-m) | |
| catalytic surface-based reaction rate of species j (mol/s-m2) | |
| T | temperature (K) - subscript “o” indicates feed |
| fractional conversion of NH3 | |
| yj | gaseous species j mole fraction |
| z | packed bed reactor axial length (m) |
| net change in moles per mole of key reactant (NH3) as per reaction stoichiometry | |
| heat of reaction (J/mol of j) | |
| product of feed mole fraction of key reactant and net change in moles by reaction | |
| ratio of feed flow rate of species j to feed rate of key reactant (NH3) | |
| stoichiometric coefficient (+/−) assuming key reactant coefficient (NH3) is unity |
Appendix A
| cp,j (J/mol-K) | |
| H2 | 29.66 |
| N2 | 31.42 |
| NH3 | 0.02815 T + 28.64 |
| (J/mol) | |
| NH3 = 0.5N2 + 1.5H2 | 45,900. (per mol NH3) at 298 K * |
| H2 + 0.5O2 = H2O | −241,830. (per mol H2O) |
References
- Service, R.F. Ammonia—A renewable fuel made from sun, air, and water—Could power the globe without carbon. Science, 12 July 2018. Available online: https://www.science.org/content/article/ammonia-renewable-fuel-made-sun-air-and-water-could-power-globe-without-carbon (accessed on 1 March 2023).
- Cha, J.; Jo, Y.S.; Jeong, H.; Han, J.; Nam, S.W.; Song, K.H.; Yoon, C.W. Ammonia as an efficient COx-free hydrogen carrier: Fundamentals and feasibility analyses for fuel cell applications. Appl. Energy 2018, 224, 194–204. [Google Scholar] [CrossRef]
- Lucentini, I.; Garcia, X.; Vendrell, X.; Llorca, J. Review of the Decomposition of Ammonia to Generate Hydrogen. Ind. Eng. Chem. Res. 2021, 60, 18560–18611. [Google Scholar] [CrossRef]
- Appari, S.; Janardhanan, V.M.; Jayanti, S.; Maier, L.; Tischer, S.; Deutschmann, O. Micro-kinetic modeling of NH3 decomposition on Ni and its application to solid oxide fuel cells. Chem. Eng. Sci. 2011, 66, 5184–5191. [Google Scholar] [CrossRef]
- Afif, A.; Radenahmad, N.; Cheok, Q.; Shams, S.; Kim, J.H.; Azad, A.K. Ammonia-fed fuel cells: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 60, 822–835. [Google Scholar] [CrossRef]
- Amogy. Amogy Presents World’s First Ammonia-Powered, Zero-Emission Semi Truck. 2023. Available online: https://amogy.co/amogy-presents-worlds-first-ammonia-powered-zero-emission-semi-truck/ (accessed on 1 March 2023).
- Stephens, B. Canadian Pacific’s hydrogen-powered locomotive makes first revenue run. Trains, 15 November 2022. [Google Scholar]
- Okura, K.; Miyazaki, K.; Muroyama, H.; Matsui, T.; Eguchi, K. Ammonia decomposition over Ni catalysts supported on perovskite-type oxides for the on-site generation of hydrogen. RSC Adv. 2018, 8, 32102–32110. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Karakaya, C.; Kee, R.J. Modeling ammonia-fueled co-flow dual-channel protonic-ceramic fuel cells. Int. J. Green Energy 2022, 19, 1568–1582. [Google Scholar] [CrossRef]
- NASA. Available online: https://www.grc.nasa.gov/www/CEAWeb/ceaHome.htm (accessed on 1 March 2023).
- NIST. Available online: https://webbook.nist.gov/chemistry/ (accessed on 1 March 2023).
- Karakaya, C.; Zhu, H.; Zohour, B.; Senkan, S. Detailed Reaction Mechanisms for the Oxidative Coupling of Methane over La2O3/CeO2 Nanofiber Fabric Catalysts. ChemCatChem 2017, 9, 4538–4551. [Google Scholar] [CrossRef]
- Deutschmann, O.; Tischer, S.; Correa, C.; Chatterjee, D.; Kleditzsch, S.; Janardhanan, V.M.; Mladenov, N.; Minh, H.D.; Karadeniz, H.; Hettel, M. DETCHEM Software Package, v. 2.5; DETCHEM: Karlsruhe, Germany, 2014; Available online: www.detchem.com (accessed on 11 January 2022).
- Fogler, H.S. Elements of Chemical Reaction Engineering, 6th ed.; Pearson: London, UK, 2020. [Google Scholar]
- Bell, T.E.; Torrente-Murciano, L. H2 Production via Ammonia Decomposition Using Non-Noble Metal Catalysts: A Review. Top. Cat. 2016, 59, 1438–1457. [Google Scholar] [CrossRef]
- Chacko, R.; Keller, K.; Tischer, S.; Shirsath, A.B.; Lott, P.; Angeli, S.; Deutschmann, O. Automating the Optimization of Catalytic Reaction Mechanism Parameters Using Basin-Hopping: A Proof of Concept. J. Phys. Chem. C 2023, 127, 7628–7639. [Google Scholar] [CrossRef]
- Lott, P.; Mokashi, M.; Muller, H.; Heitlinger, D.J.; Lichtenberg, S.; Shirsath, A.B.; Janzer, C.; Tischer, S.; Maier, L.; Deutschmann, O. Hydrogen Production and Carbon Capture by Gas-Phase Methane Pyrolysis: A Feasibility Study. ChemSusChem 2022, 16, e202300300. [Google Scholar]
- Rivera, S.; Molla, A.; Pera, P.; Landaverde, M.; Barat, R. Reactor engineering calculations with a detailed reaction mechanism for the oxidative coupling of methane. Int. J. Chem. React. Eng. 2020, 18, 20200138. [Google Scholar] [CrossRef]
- Polymath®. Available online: https://polymathplus.org/# (accessed on 1 March 2023).



| Feed Rate (mol/s) | ||
|---|---|---|
| Temperature (K) | Lowest | Highest |
| 650 | 1 × 10−11 | 1 × 10−7 |
| 725 | 1 × 10−10 | 1 × 10−5 |
| 800 | 1 × 10−8 | 1 × 10−4 |
| 875 | 1 × 10−7 | 1 × 10−3 |
| 950 | 1 × 10−6 | 1 × 10−4 |
| For k (mol-Pa/s-m2) | ||
|---|---|---|
| a | −5.996 | −6.181 |
| b | 4.344 × 104 | 2.849 × 104 |
| c | −2.610 × 107 | −1.287 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barat, R.B. Simple Rate Expression for Catalyzed Ammonia Decomposition for Fuel Cells. Molecules 2023, 28, 6006. https://doi.org/10.3390/molecules28166006
Barat RB. Simple Rate Expression for Catalyzed Ammonia Decomposition for Fuel Cells. Molecules. 2023; 28(16):6006. https://doi.org/10.3390/molecules28166006
Chicago/Turabian StyleBarat, Robert B. 2023. "Simple Rate Expression for Catalyzed Ammonia Decomposition for Fuel Cells" Molecules 28, no. 16: 6006. https://doi.org/10.3390/molecules28166006
APA StyleBarat, R. B. (2023). Simple Rate Expression for Catalyzed Ammonia Decomposition for Fuel Cells. Molecules, 28(16), 6006. https://doi.org/10.3390/molecules28166006






