Heat Capacity and Thermodynamic Functions of Titanium-Manganites of Lanthanum, Lithium and Sodium of LaLi2TiMnO6 and LaNa2TiMnO6
Abstract
:1. Introduction
2. Results and Discussion
1.5ΔfH°(298.15)Me2O + 3ΔfH°(298.15)MeO + 2ΔfH°(298.15)Mn2O3.
= ΔfH°(298.15) LaMeI2TiMnO6/ΔokH°(298.15) LaMeI2TiMnO6,
3. Experimental Part
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Tumarkin, A.V.; Al’myashev, V.I.; Razumov, S.V.; Gaidukov, M.M.; Gagarin, A.G.; Altynnikov, A.G.; Kozyrev, A.B. Structural properties of barium strontium titanate films grown under different technological conditions. Phys. Solid State 2015, 57, 553–557. [Google Scholar] [CrossRef]
- Volkov, N.B. Spintronics: Manganite-based magnetic tunnel structures. Physics-Uspekhi 2012, 55, 250–269. [Google Scholar] [CrossRef]
- Seliverstova, Y.V.; Ibraev, N.K.; Zhumabekov, A.Z. The Effect of Silver Nanoparticles on the Photodetecting Properties of the TiO2/Graphene Oxide Nanocomposite. Opt. Spectrosc. 2020, 128, 1449–1457. (In Russian) [Google Scholar] [CrossRef]
- Tretyakov, Y.D.; Brylev, O.A. New generations of inorganic functional materials. J. Russ. Chem. Soc. 2000, 45, 10–16. (In Russian) [Google Scholar]
- Protasov, N.M. Structural Modeling of Complex Oxides with a Perovskite Structure in a Partially Covalent Approximation; Publishing House of Moscow State University: Moscow, Russia, 2011; 51p. (In Russian) [Google Scholar]
- Aksenova, T.V.; Gavrilova, L.Y.; Cherepanov, V.A. Crystal structure and physicochemical properties of doped lanthanum manganites. Russ. J. Phys. Chem. A 2012, 86, 1862–1868. [Google Scholar] [CrossRef]
- Yanchevskii, O.Z.; V’yunov, O.I.; Belous, A.G.; Tovstolytkin, A.I.; Kravchik, V.P. Synthesis and Characterization of La0,7Sr0,3Mn1-xTixO3. Phys. Solid State 2006, 48, 709–716. [Google Scholar] [CrossRef]
- Ivanov, A.I.; Agarkov, D.A.; Burmistrov, I.N.; Kudrenko, E.A.; Bredikhin, S.I.; Kharton, V.V. Synthesis and Properties of Fuel Cell Anodes Based on (La0,5+xSr0,5–x)1–yMn0,5Ti0,5O3–δ (x = 0–0.25, y = 0–0.03). Russ. J. Electrochem. 2014, 50, 730–736. [Google Scholar] [CrossRef]
- Qasim, I.; Blanchard, E.R.; Kennedy, J.B.; Ling, D.C.; Ling-Yun, J.; Kamiyama, T.; Miao, P.; Torii, S. Soft ferromagnetism in mixed valence Sr1-xLaxTi0.5Mn0.5O3 perovskites. Dalton Trans. 2014, 18, 6909–6918. [Google Scholar] [CrossRef] [PubMed]
- Mesilov, V.V.; Galakhov, V.R.; Yermakov, A.Y.; Uimin, M.A.; Gubkin, A.F.; Sherstobitova, E.A.; Udintseva, M.S.; Zakharova, G.S.; Smirnov, D.A. Soft X-ray absorption spectroscopy of titanium dioxide nanopowders with cobalt impurities. J. Exp. Theor. Phys. 2017, 124, 908–913. [Google Scholar] [CrossRef]
- Barfoot, J. Introduction to the Physics of Ferroelectric Phenomena; Mir: Moscow, Russia, 1970; 352p. (In Russian) [Google Scholar]
- Yao, Z.; Zhu, K.; Zhang, J.; Li, J.; Li, X.; Wang, J.; Yan, K.; Liu, J. LiF-Assisted Synthesis of Perovskite-Type Li0.35La0.55TiO3 Solid Electrolyte for Rechargeable Lithium-Metal Batteries. J. Electron. Mater. 2022, 51, 736–744. [Google Scholar] [CrossRef]
- Denissova, L.T.; Molokeyev, M.S.; Galiakhmetova, N.A.; Denissov, V.M.; Vassilev, G.V. Synthesis, crystal structure and thermophysical properties of substituted titanates Bi2Pr2Ti3O12 and Bi2Nd2Ti3O12. Solid State Phys. 2021, 63, 1056–1061. (In Russian) [Google Scholar]
- Sankovich, A.M.; Markin, A.V.; Smirnova, N.N.; Zvereva, I.A. Heat capacity and thermodynamic properties of layered perovskite-like oxides of K2La2Ti3O10 and K2Nd2Ti3O10. J. Phys. Chem. 2019, 93, 407–416. (In Russian) [Google Scholar] [CrossRef]
- Denissova, L.T.; Molokeyev, M.S.; Ryabov, V.V.; Kargin, Y.F.; Chumalina, L.G.; Denissov, V.M. Crystal structure and thermodynamic properties of titanium, structure and thermodynamic properties of titanium ErGaTi2O7. J. Inorg. Chem. 2021, 66, 492–497. (In Russian) [Google Scholar]
- Denissova, L.T.; Molokeyev, M.S.; Kargin, Y.F.; Ryabov, V.V.; Chumalina, L.G.; Beloussova, N.V.; Denissov, V.M. Structure and thermodynamic properties of titanates of DyGaTi2O7 and EuGaTi2O7. Inorg. Mater. 2021, 57, 768–775. (In Russian) [Google Scholar] [CrossRef]
- Kasenov, B.K.; Kasenova, S.B.; Sagintaeva, Z.I.; Yermagambet, B.T.; Bekturganov, N.S.; Oskembekov, I.M. Double and Triple Manganites, Ferrites and Chromites of Alkaline, Alkaline Earth and Rare Earth Metals; Nauchnyi Mir: Moscow, Russia, 2017; 416p. (In Russian) [Google Scholar]
- Fedorov, V.A.; Kuznetsov, N.T. Analysis and Study of Semiconductor Materials; Samara State University: Samara, Russia, 2008; 84p. (In Russian) [Google Scholar]
- Reznitsky, L.A. Calorimetry of a Solid; Publishing House of Moscow State University: Moscow, Russia, 1981; 184p. (In Russian) [Google Scholar]
- Morris, M.C.; McMurdie, H.F.; Evans, E.H.; Paretzkin, B.; Parker, H.S.; Pyrros, N.P.; Hubbard, C.R. Standard X-ray Diffraction Powder Patterns; National Bureau of Standards: Washington, DC, USA, 1984; 158p, Available online: https://archive.org/details/standardxraydiff2520morr/page/8/mode/2up (accessed on 13 March 2023).
- Kubascewski, O.; Alcock, C.B. Metallurgical Thermochemistry; Pergamon Press: Oxford, UK, 1982; 390p. [Google Scholar]
- Kumok, V.N. Problem of Harmonization of Methods to Estimate Thermodynamic Characteristics. In Direct and Inverse Problems of Chemical Thermodynamics; Nauka: Moscow, Russia, 1987; p. 108. (In Russian) [Google Scholar]
- Wells, A.F. Structural Inorganic Chemistry; Oxford University Press: Oxford, UK, 1987; Volume 2, 69p. [Google Scholar]
- Bui, M.T. Investigation of Temperature Dependences of Electrophysical Properties of Ferroelectric Materials; Dissertation for Degree of Candidate of Physical and Mathematical Sciences; St. Petersburg National Research University: St. Petersburg, Russia, 2019; 143p. (In Russian) [Google Scholar]
- Gerasimov, Y.I.; Krestovnikov, A.N.; Shakhov, A.S. Chemical Thermodynamics in Non–Ferrous Metallurgy; Metallurgy: Moscow, Russia, 1960; Volume 1, 230p. (In Russian) [Google Scholar]
- Morachevsky, A.S.; Sladkov, I.B. Thermodynamic Calculations in Metallurgy: Handbook; Metallurgy: Moscow, Russia, 1985; 137p. (In Russian) [Google Scholar]
- Okazaki, K. Technology of Ceramic Dielectrics; Energy: Moscow, Russia, 1976; 327p. (In Russian) [Google Scholar]
- User Manual. RLC Meter (LCR-781). M.: CJSC “PriST”. 2012, p. 3. Available online: https://saprd.ru/grsi/53914-13/2013-53914-13.pdf (accessed on 13 March 2023).
- Kasenov, B.K.; Kasenova, S.B.; Sagintaeva, Z.I.; Kuanyshbekov, E.E.; Mukhtar, A.A. Thermodynamic and Electrophysics of New LaCaCuZnMnO6 Copper—Zinc Manganite of Lanthanum and Calcium. High Temp. 2022, 60, 474–478. (In Russian) [Google Scholar] [CrossRef]
- Fessenko, Y.G. Perovskite Family and Ferroelectricity; Atomizdat: Moscow, Russia, 1972; 248p. (In Russian) [Google Scholar]
- Venevtsev, Y.N.; Politova, Y.D.; Ivanov, S.A. Ferro- and Anti-Ferroelectrics of the Barium Titanate Family; Chemistry: Moscow, Russia, 1985; 256p. (In Russian) [Google Scholar]
- Lines, M.; Glass, A. Ferroelectrics and Their Related Materials; Mir: Moscow, Russia, 1981; 736p. (In Russian) [Google Scholar]
- Kasenov, B.K.; Edilbaeva, S.T.; Mustafin, E.S.; Zhumadilov, E.K. Evaluation of thermodynamic functions of ternary oxides LnMeMn2O5 (Ln—rare earth metal, Me—alkali metal). J. Phys. Chem. 1999, 73, 1116–1118. (In Russian) [Google Scholar]
- Kasenov, B.K.; Kasenova, S.B.; Sagintayeva, Z.I.; Kuanyshbekov, E.E.; Mukhtar, A.A.; Kakenov, K.S.; Esenbayeva, G.A. Evaluation of thermodynamic characteristics of nickel (cobalt)-cuprate-manganites LaMeI2Ni(Co)CuMnO6 and LaMeIINi(Co)CuMnO6 (MeI—Li, Na, K.; MeII—Mg, Ca, Sr, Ba). Chem. J. Kazakhstan 2019, 1, 149–156. (In Russian) [Google Scholar]
- Glushko, V.P. (Ed.) Thermal Constants of Substances/Handbook; Issue X, part 1; Nauka: Moscow, Russia, 1981; 300p. (In Russian) [Google Scholar]
- Glushko, V.P. (Ed.) Thermal Constants of Substances/Handbook; Issue XIII, part 1; Nauka: Moscow, Russia, 1978; 536p. (In Russian) [Google Scholar]
- Glushko, V.P. (Ed.) Thermal Constants of Substances/Handbook; Issue VII, part 1; Nauka: Moscow, Russia, 1974; 344p. (In Russian) [Google Scholar]
- Kasenov, B.K.; Kasenova, S.B.; Sagintaeva, Z.I.; Baisanov, S.O.; Lu, N.Y.; Kuanyshbekov, E.E.; Turtubaeva, M.O. Novel Titanium-Manganites of Lanthanum and Alkali Metals. Bull. Karaganda Univ.–Chem. 2022, 108, 136–141. [Google Scholar] [CrossRef]
- Kivilis, S.S. Technique of Measuring the Density of Liquids and Solids; Standardgiz: Moscow, Russia, 1959; 191p. (In Russian) [Google Scholar]
- Portnoi, K.I.; Timofeyeva, N.I. Oxygen Compounds of Rare Earth Elements. Guide; Metallurgy: Moscow, Russia, 1986; 480p. (In Russian) [Google Scholar]
- Kostrominka, N.A.; Kumok, V.N.; Skorik, N.A. Chemistry of Coordination Compounds; Higher school: Moscow, Russia, 1990; 432p. (In Russian) [Google Scholar]
- Platunov, Y.S.; Buravoi, S.Y.; Kurepin, V.V.; Petrov, G.S. Thermophysical Measurements and Devices; Mashinostroenie: Moscow, Russia, 1986; 256p. (In Russian) [Google Scholar]
- Specification and Operating Instructions of IT-C-400. Aktobe. Aktobe Plant “Etalon”. 1986. 48p. (In Russian). Available online: https://nd-gsi.ru/grsi/060xx/06000-77.pdf (accessed on 13 March 2023).
- Bodryakov, V.Y.; Bykov, A.A. Correlation Characteristics of the Volumetric Thermal Expansion Coefficient and Specific Heat of Corundum. Glass Ceram. 2015, 72, 67–70. [Google Scholar] [CrossRef]
 —experimental data, ●—calculated data.
—experimental data, ●—calculated data.
 —experimental data, ●—calculated data.
—experimental data, ●—calculated data.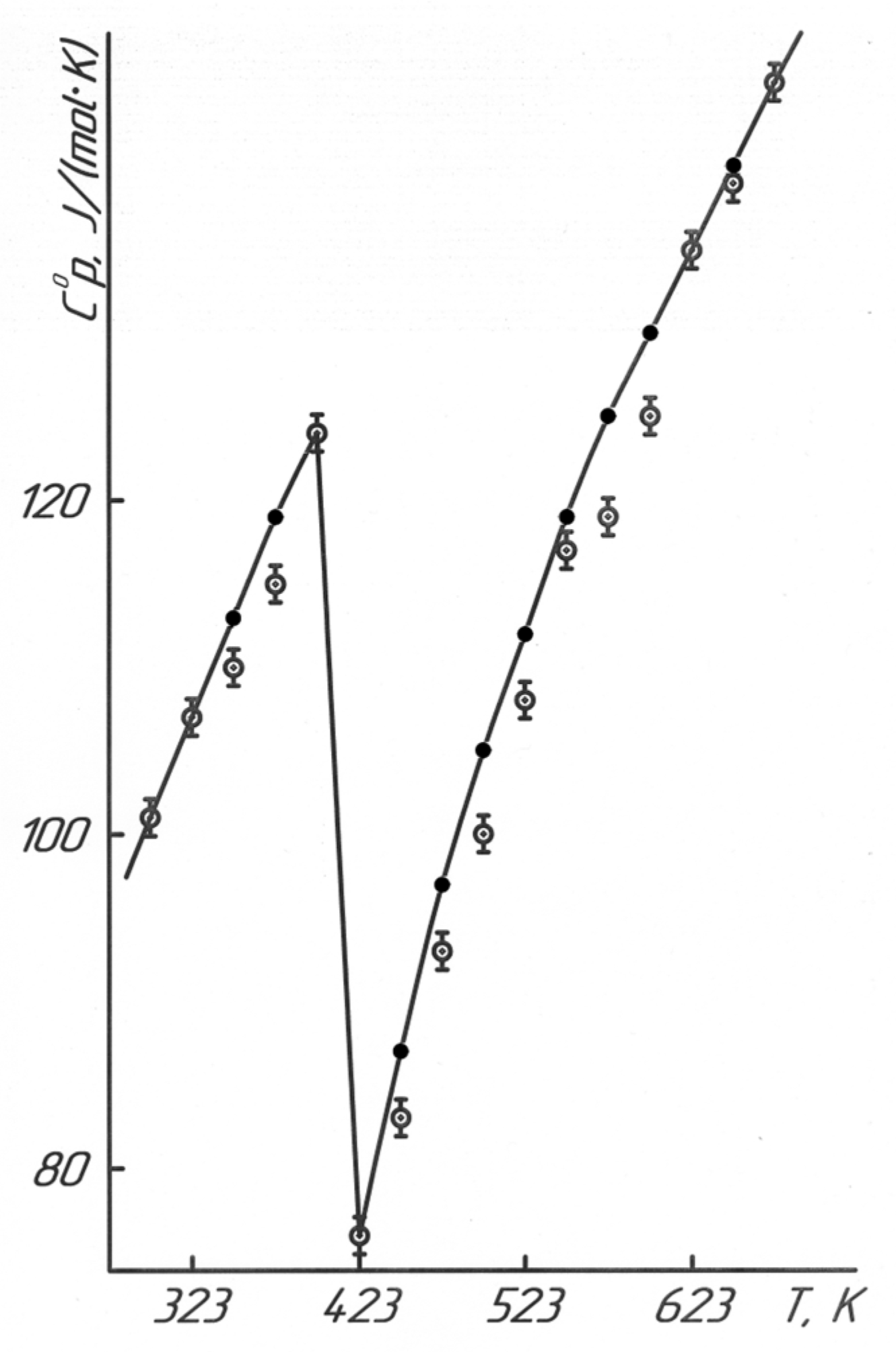
 —experimental data.
—experimental data.
 —experimental data.
—experimental data.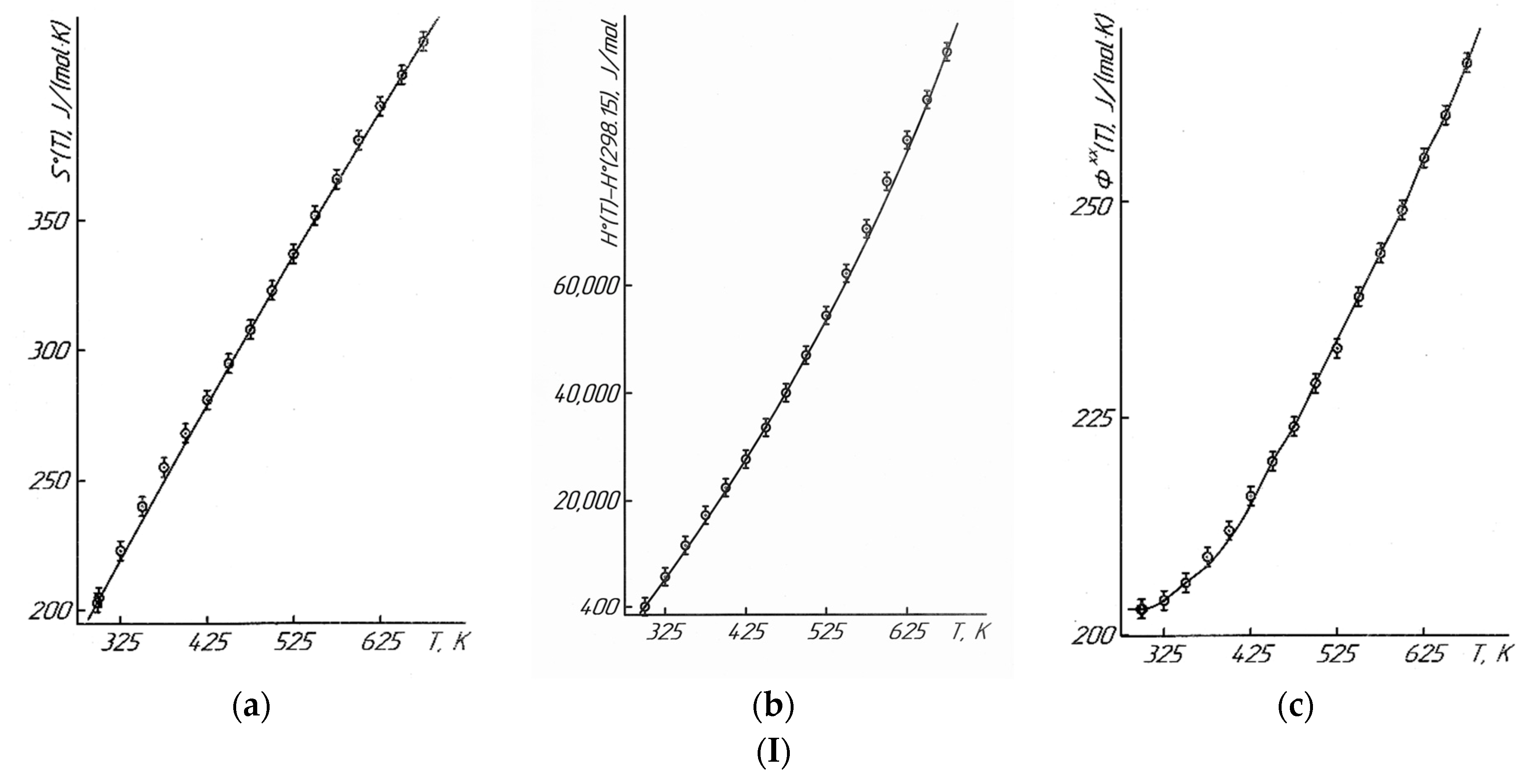
 —experimental data.
—experimental data.
 —experimental data.
—experimental data.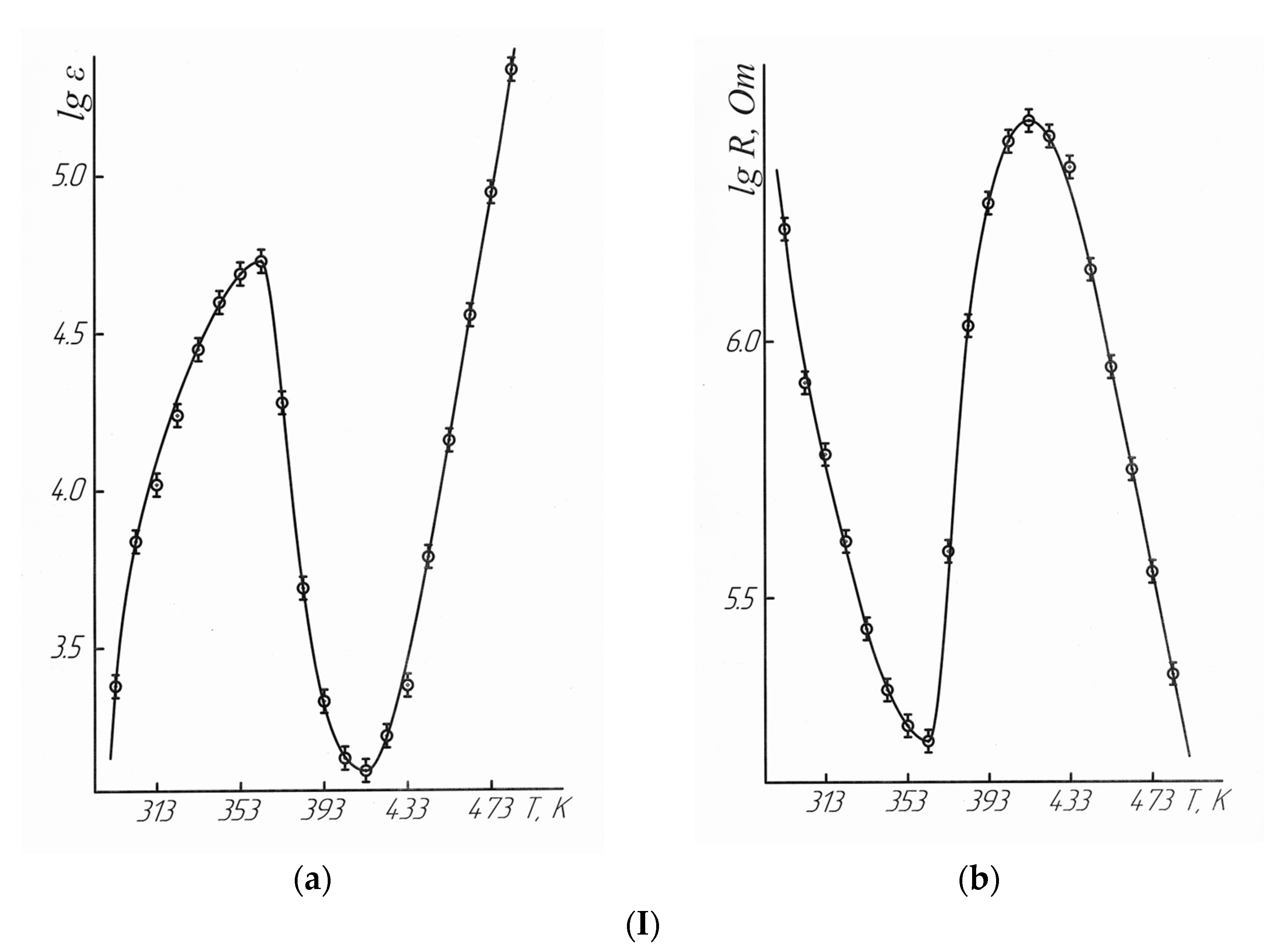
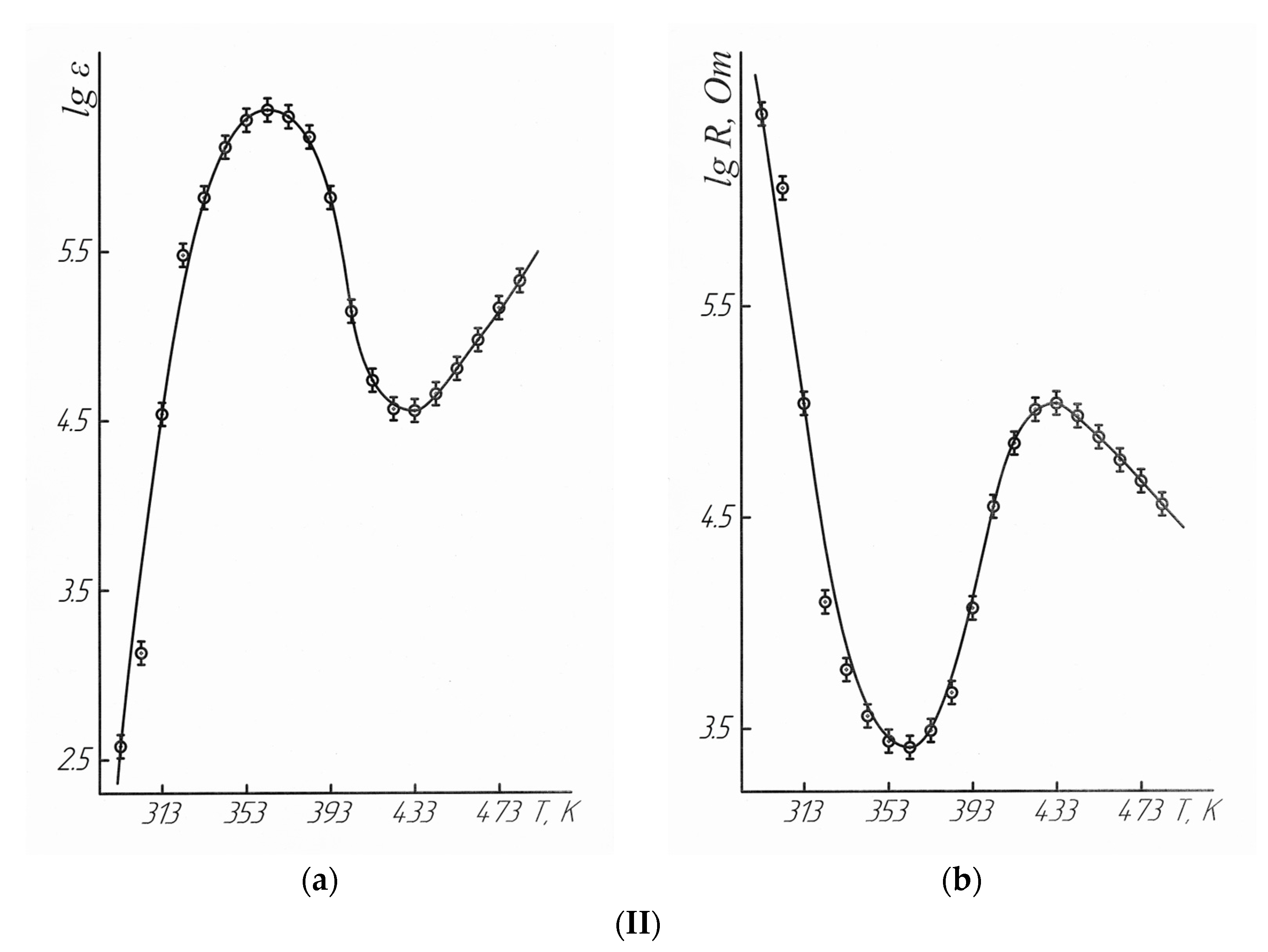
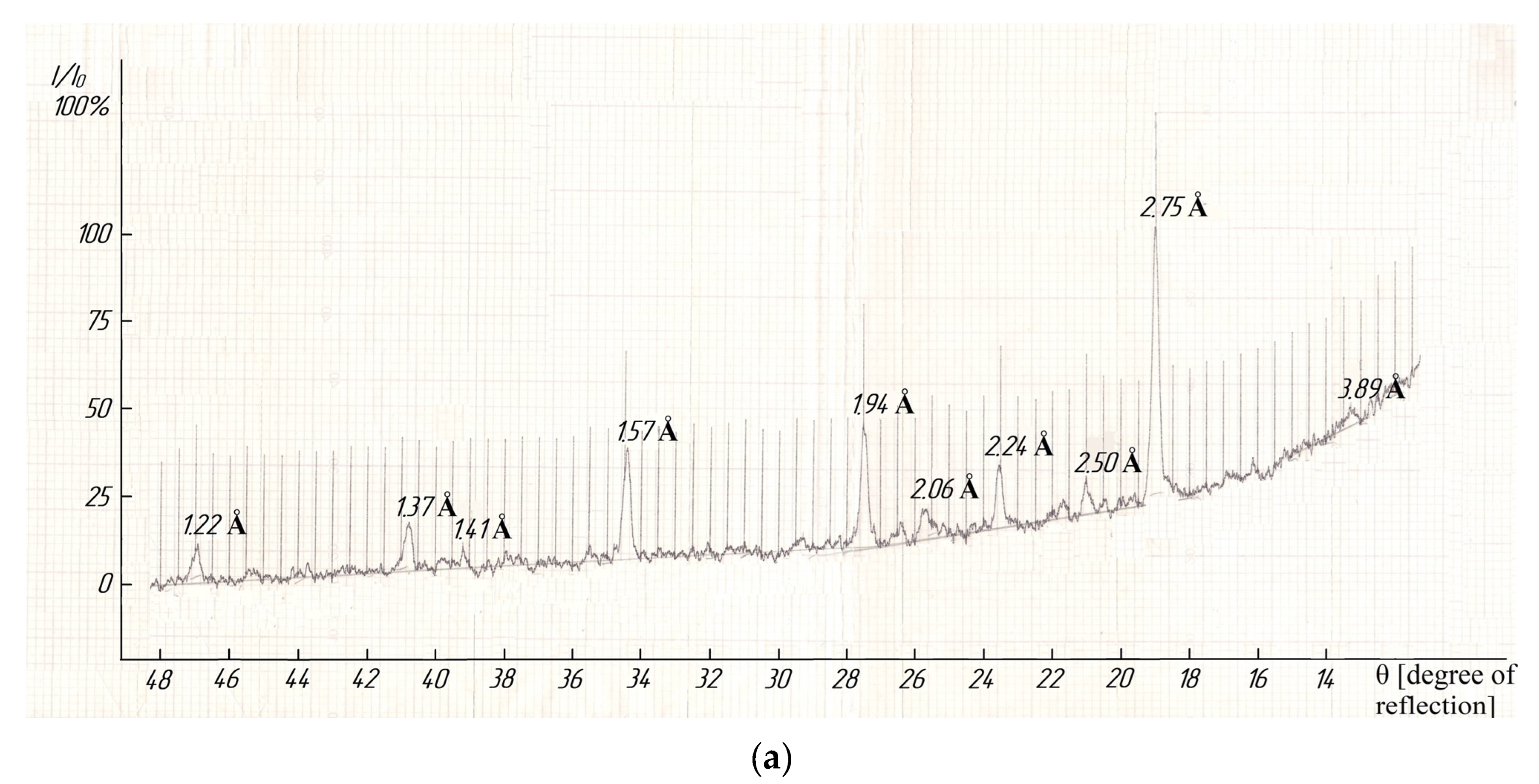
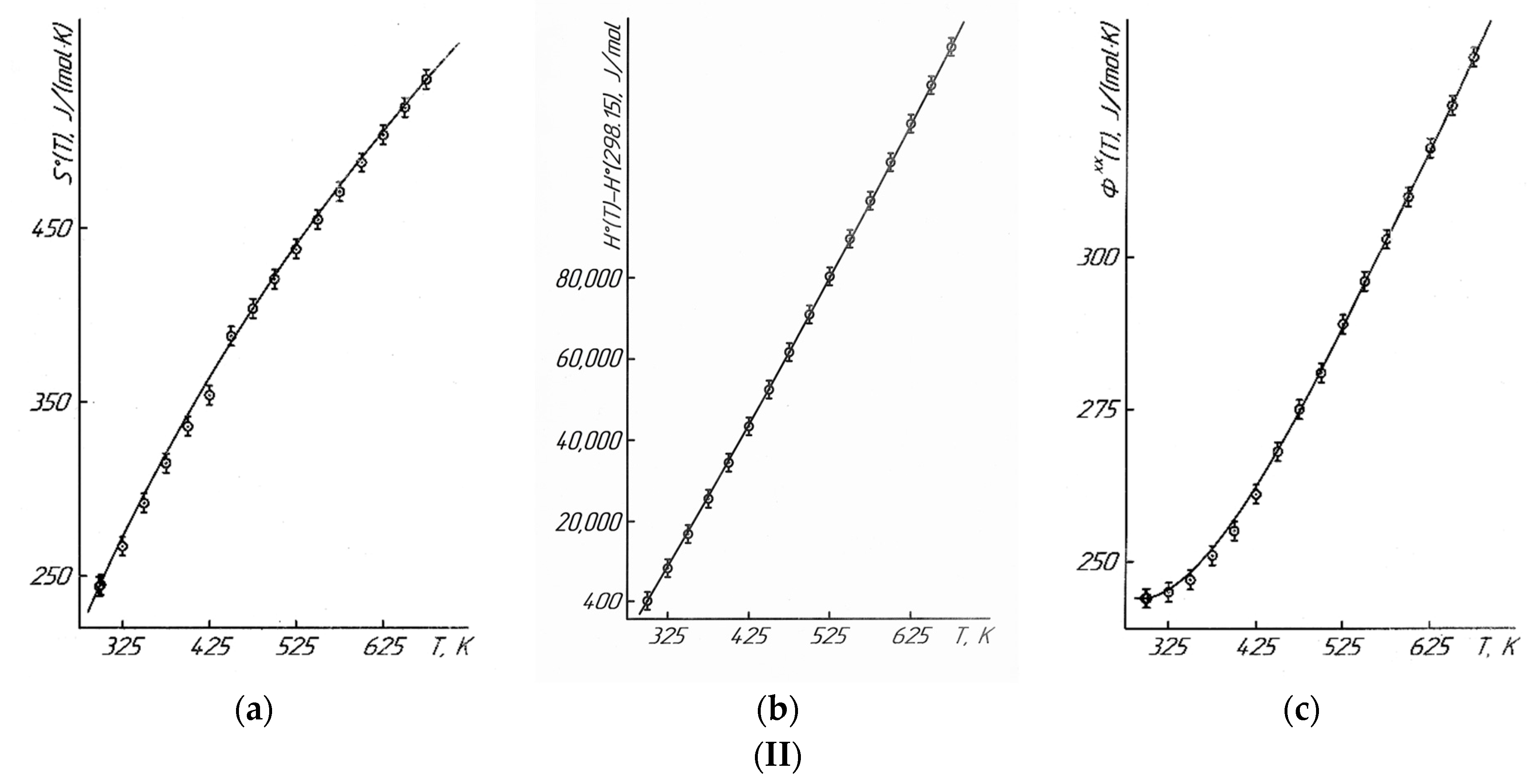
 —experimental data, ●—calculated data.
—experimental data, ●—calculated data.
 —experimental data, ●—calculated data.
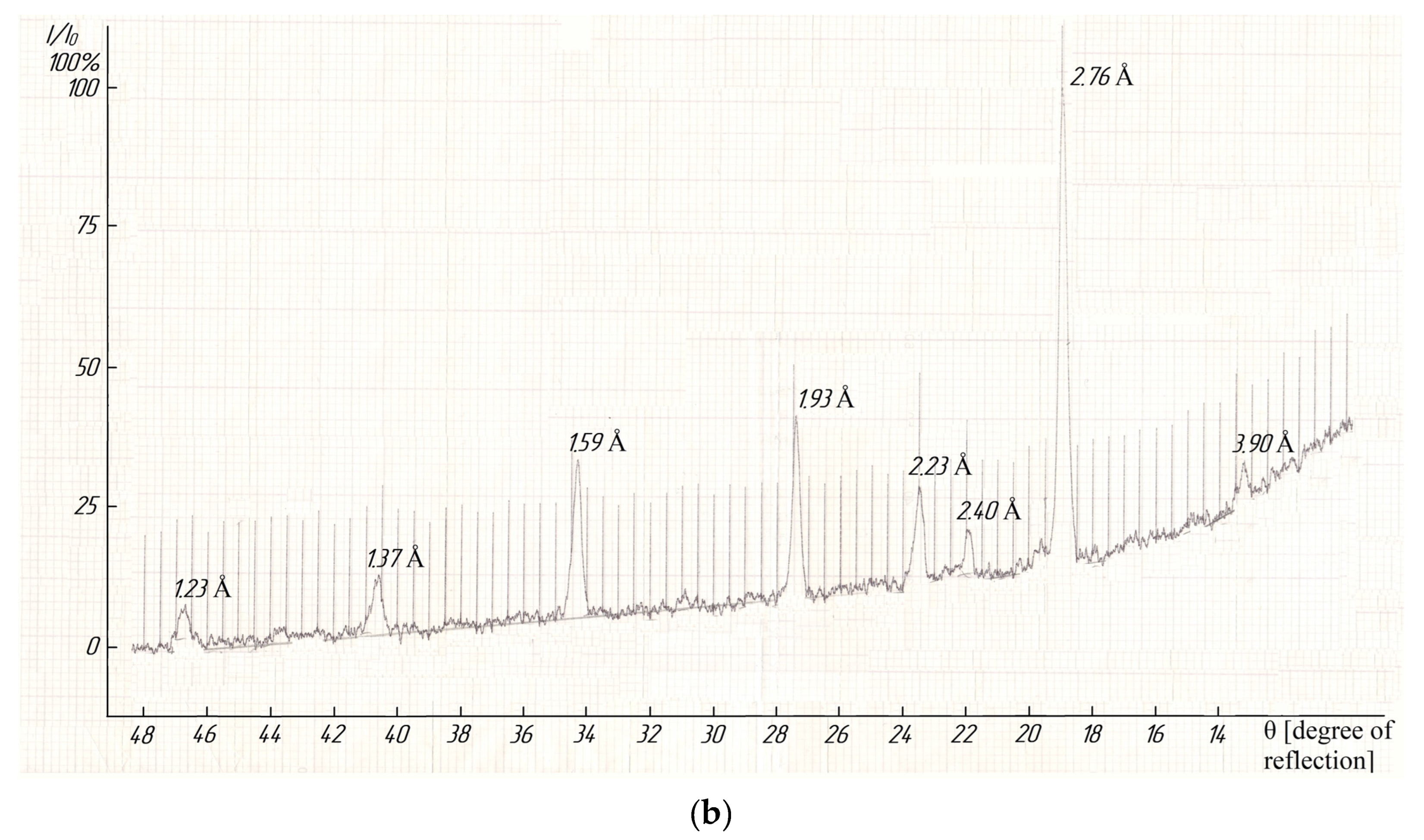
—experimental data, ●—calculated data.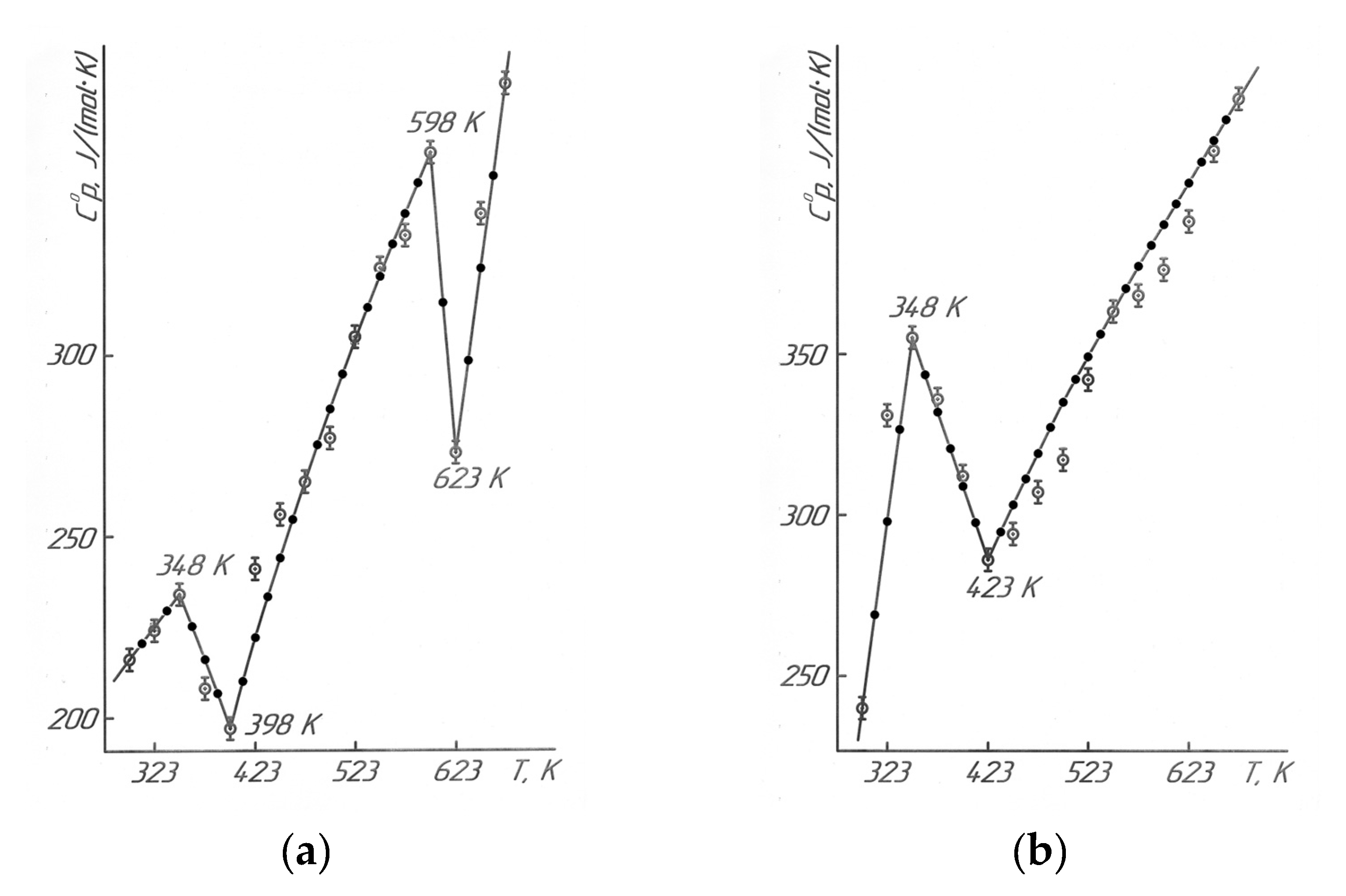
| Compound | Coefficients of Equation C°p = a + b⋅T + c⋅T−2, J/(mol·K) | ∆T, K | ||
|---|---|---|---|---|
| a | b⋅10−3 | c⋅105 | ||
| LaLi2TiMnO6 | 107 ± 5 | 365.8 ± 17.0 | - | 298–348 |
| 491 ± 23 | −(737.3 ± 34.4) | - | 348–398 | |
| 101 ± 5 | 502.4 ± 23.4 | −(578.8 ± 7.7) | 398–598 | |
| 2325 ± 108 | −(3292.4 ± 153.4) | - | 598–623 | |
| −(988 ± 46) | 2025.4 ± 94.4 | 623–673 | ||
| LaNa2TiMnO6 | −(444 ± 21) | 2297.2 ± 106.1 | - | 298–348 |
| 674 ± 31 | −(916.9 ± 42.4) | - | 348–423 | |
| 161 ± 7.45 | 431.0 ± 19.9 | −(102.2 ± 4.7) | 423–673 | |
| T, K | T, K | ||||
|---|---|---|---|---|---|
| 298 | 0.4319 ± 0.0114 | 101 ± 7 | 498 | 0.4331 ± 0.0036 | 101 ± 3 |
| 323 | 0.4583 ± 0.0120 | 107 ± 8 | 523 | 0.4669 ± 0.1229 | 109 ± 4 |
| 348 | 0.47083 ± 0.0105 | 110 ± 7 | 548 | 0.5041 ± 0.0087 | 118 ± 8 |
| 373 | 0.49223 ± 0.0102 | 115 ± 7 | 573 | 0.5110 ± 0.0069 | 119 ± 9 |
| 398 | 0.5330 ± 0.0049 | 124 ± 3 | 598 | 0.5382 ± 0.0107 | 126 ± 7 |
| 423 | 0.3279 ± 0.0083 | 76 ± 5 | 623 | 0.5801 ± 0.0112 | 135 ± 8 |
| 448 | 0.3563 ± 0.0084 | 83 ± 5 | 648 | 0.6000 ± 0.0134 | 140 ± 7 |
| 473 | 0.3992 ± 0.0084 | 93 ± 4 | 673 | 0.6210 ± 0.0095 | 145 ± 6 |
| T, K | J/(mol·K) | J/(mol·K) | J/mol | J/(mol·K) |
|---|---|---|---|---|
| LaLi2TiMnO6 | ||||
| 298.15 | 216 ± 10 | 203 ± 6 | - | 203 ± 15 |
| 300 | 217 ± 10 | 205 ± 16 | 433 ± 20 | 203 ± 15 |
| 325 | 226 ± 11 | 223 ± 17 | 5960 ± 280 | 204 ± 16 |
| 350 | 235 ± 11 | 240 ± 18 | 11,720 ± 5160 | 206 ± 16 |
| 375 | 214 ± 10 | 255 ± 20 | 17,310 ± 800 | 209 ± 16 |
| 400 | 196 ± 9 | 268 ± 21 | 22,440 ± 1050 | 212 ± 16 |
| 425 | 224 ± 10 | 281 ± 22 | 27,730 ± 1290 | 216 ± 17 |
| 450 | 246 ± 11 | 295 ± 23 | 33,610 ± 1570 | 220 ± 17 |
| 475 | 267 ± 12 | 308 ± 24 | 40,030 ± 1860 | 224 ± 17 |
| 500 | 287 ± 13 | 323 ± 25 | 46,950 ± 2190 | 229 ± 18 |
| 525 | 305 ± 14 | 337 ± 26 | 54,350 ± 2530 | 233 ± 18 |
| 550 | 323 ± 15 | 352 ± 27 | 62,210 ± 2900 | 239 ± 19 |
| 575 | 340 ± 16 | 366 ± 28 | 70,510 ± 3290 | 244 ± 19 |
| 600 | 357 ± 17 | 381 ± 29 | 79,230 ± 3690 | 249 ± 19 |
| 625 | 267 ± 12 | 394 ± 30 | 86,930 ± 4050 | 255 ± 20 |
| 650 | 328 ± 15 | 406 ± 31 | 94,500 ± 4400 | 260 ± 20 |
| 675 | 379 ± 18 | 419 ± 32 | 103,340 ± 4820 | 266 ± 20 |
| LaNa2TiMnO6 | ||||
| 298.15 | 240 ± 11 | 244 ± 7 | - | 244 ± 19 |
| 300 | 245 ± 11 | 245 ± 19 | 480 ± 20 | 244 ± 19 |
| 325 | 302 ± 14 | 267 ± 20 | 7320 ± 340 | 245 ± 19 |
| 350 | 360 ± 17 | 292 ± 22 | 15,600 ± 720 | 247 ± 19 |
| 375 | 330 ± 15 | 315 ± 24 | 24,140 ± 1110 | 251 ± 19 |
| 400 | 307 ± 14 | 336 ± 26 | 32,120 ± 1480 | 255 ± 19 |
| 425 | 285 ± 13 | 354 ± 27 | 39,520 ± 1830 | 261 ± 20 |
| 450 | 305 ± 14 | 388 ± 30 | 53,900 ± 2490 | 268 ± 20 |
| 475 | 321 ± 15 | 404 ± 31 | 61,710 ± 2850 | 275 ± 21 |
| 500 | 336 ± 16 | 421 ± 32 | 69,920 ± 3230 | 281 ± 21 |
| 525 | 350 ± 16 | 438 ± 33 | 78,500 ± 3500 | 289 ± 22 |
| 550 | 364 ± 17 | 455 ± 35 | 87,430 ± 4040 | 296 ± 23 |
| 575 | 378 ± 17 | 471 ± 36 | 96,710 ± 4470 | 303 ± 23 |
| 600 | 391 ± 18 | 488 ± 37 | 106,330 ± 4910 | 310 ± 24 |
| 625 | 404 ± 19 | 504 ± 38 | 116,280 ± 5370 | 318 ± 24 |
| 650 | 417 ± 19 | 520 ± 40 | 126,550 ± 5850 | 325 ± 25 |
| 675 | 430 ± 20 | 536 ± 41 | 137,130 ± 6340 | 333 ± 25 |
| T, K | R, Om | ε | lgε | lgR | R, Om | ε | lgε | lgR |
|---|---|---|---|---|---|---|---|---|
| LaLi2TiMnO6 | LaNa2TiMnO6 | |||||||
| 293 | 1,643,000 | 2381 | 3.38 | 6.22 | 2,549,000 | 379 | 2.58 | 6.41 |
| 303 | 832,700 | 6869 | 3.84 | 5.92 | 1,142,000 | 1351 | 3.13 | 6.06 |
| 313 | 604,400 | 10,571 | 4.02 | 5.78 | 109,000 | 34,515 | 4.54 | 5.04 |
| 323 | 404,300 | 17,528 | 4.24 | 5.61 | 12,560 | 305,305 | 5.48 | 4.10 |
| 333 | 272,600 | 28,456 | 4.45 | 5.44 | 6040 | 665,659 | 5.82 | 3.78 |
| 343 | 209,400 | 39,654 | 4.60 | 5.32 | 3636 | 1,308,086 | 6.12 | 3.56 |
| 353 | 177,400 | 48,911 | 4.69 | 5.25 | 2741 | 1,896,966 | 6.28 | 3.44 |
| 363 | 165,500 | 53,224 | 4.73 | 5.22 | 2580 | 2,182,878 | 6.34 | 3.41 |
| 373 | 392,800 | 19,155 | 4.28 | 5.59 | 3075 | 1,972,968 | 6.30 | 3.49 |
| 383 | 1,079,000 | 4849 | 3.69 | 6.03 | 4673 | 1,507,719 | 6.18 | 3.67 |
| 393 | 1,867,000 | 2119 | 3.33 | 6.27 | 11,750 | 653,784 | 5.82 | 4.07 |
| 403 | 2,428,000 | 1404 | 3.15 | 6.39 | 35,800 | 141,285 | 5.15 | 4.55 |
| 413 | 2,690,000 | 1294 | 3.11 | 6.43 | 70,030 | 55,338 | 4.74 | 4.85 |
| 423 | 2,510,000 | 1649 | 3.22 | 6.40 | 101,900 | 36,877 | 4.57 | 5.01 |
| 433 | 2,200,000 | 2379 | 3.38 | 6.34 | 109,100 | 36,200 | 4.56 | 5.04 |
| 443 | 1,371,000 | 6162 | 3.79 | 6.14 | 95,920 | 45,756 | 4.66 | 4.98 |
| 453 | 883,800 | 14,420 | 4.16 | 5.95 | 76,300 | 64,238 | 4.81 | 4.88 |
| 463 | 557,400 | 36,387 | 4.56 | 5.75 | 59,120 | 94,570 | 4.98 | 4.77 |
| 473 | 351,100 | 89,319 | 4.95 | 5.55 | 46,470 | 148,444 | 5.17 | 4.67 |
| 483 | 225,400 | 218,458 | 5.34 | 5.35 | 36,220 | 216,081 | 5.33 | 4.56 |
| Compounds | −ΔokH°(298.15)/ kJ/mol | −ΔfH°(298.15)/ kJ/mol | References | |
|---|---|---|---|---|
| LaLi3Mg3Mn4O12 | 5514.4 | 1.2375 | 6824.1 | [17] |
| LaNa3Ca3Mn4O12 | 5340.5 | 1.3084 | 6987.5 | -//- |
| Li2O | 593.94 | [35] | ||
| Na2O | 414.84 | [35] | ||
| La2O3 | 1794.94 | [36] | ||
| Mn2O3 | 957.72 | [37] | ||
| TiO2 | 944.5 | [37] |
| T, K | C°p (T), J/(mol·K) | |
|---|---|---|
| Our Data | Data in [44] | |
| 180 | 44.50 | 43.83 |
| 230 | 64.86 | 61.18 |
| 250 | 70.37 | 67.08 |
| 280 | 77.07 | 74.82 |
| 300 | 76.31 | 79.41 |
| 350 | 86.49 | 88.86 |
| 400 | 94.12 | 95.21 |
| 450 | 100.26 | 101.8 |
| 500 | 105.47 | 106.1 |
| 550 | 110.09 | 109.7 |
| 600 | 114.29 | 112.5 |
| 650 | 118.20 | 114.9 |
| T, K | , J/(g·K) | , J/(mol·K) | , J/(g·K) | , J/(mol·K) |
|---|---|---|---|---|
| LaLi2TiMnO6 | LaNa2TiMnO6 | |||
| 298.15 | 0.6142 ± 0.0147 | 216 ± 14 | 0.6262 ± 0.0089 | 240 ± 11 |
| 323 | 0.6374 ± 0.0083 | 224 ± 8 | 0.8620 ± 0.0188 | 331 ± 15 |
| 348 | 0.6662 ± 0.0100 | 234 ± 10 | 0.9255 ± 0.0183 | 355 ± 16 |
| 373 | 0.5910 ± 0.0123 | 208 ± 12 | 0.8763 ± 0.0153 | 336 ± 16 |
| 398 | 0.5613 ± 0.0100 | 197 ± 10 | 0.8140 ± 0.0147 | 312 ± 14 |
| 423 | 0.6857 ± 0.0115 | 241 ± 11 | 0.7463 ± 0.0129 | 286 ± 13 |
| 448 | 0.7275 ± 0.0124 | 256 ± 12 | 0.7676 ± 0.0072 | 294 ± 14 |
| 473 | 0.7548 ± 0.0155 | 265 ± 15 | 0.8005 ± 0.0127 | 307 ± 14 |
| 498 | 0.7891 ± 0.0126 | 277 ± 12 | 0.8261 ± 0.0171 | 317 ± 15 |
| 523 | 0.8688 ± 0.0181 | 305 ± 18 | 0.8919 ± 0.0151 | 342 ± 16 |
| 548 | 0.9214 ± 0.0113 | 324 ± 11 | 0.9468 ± 0.0190 | 363 ± 17 |
| 573 | 0.9458 ± 0.0157 | 333 ± 15 | 0.9588 ± 0.0147 | 368 ± 17 |
| 598 | 1.0118 ± 0.0128 | 356 ± 13 | 0.9805 ± 0.0158 | 376 ± 17 |
| 623 | 0.7777 ± 0.0095 | 273 ± 9 | 1.0192 ± 0.0174 | 391 ± 18 |
| 648 | 0.9653 ± 0.0179 | 339 ± 17 | 1.0777 ± 0.0128 | 413 ± 19 |
| 673 | 1.0657 ± 0.0150 | 375 ± 15 | 1.1171 ± 0.0151 | 429 ± 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasenov, B.K.; Kasenova, S.B.; Sagintaeva, Z.I.; Baisanov, S.; Lu, N.Y.; Nukhuly, A.; Kuanyshbekov, E.E. Heat Capacity and Thermodynamic Functions of Titanium-Manganites of Lanthanum, Lithium and Sodium of LaLi2TiMnO6 and LaNa2TiMnO6. Molecules 2023, 28, 5194. https://doi.org/10.3390/molecules28135194
Kasenov BK, Kasenova SB, Sagintaeva ZI, Baisanov S, Lu NY, Nukhuly A, Kuanyshbekov EE. Heat Capacity and Thermodynamic Functions of Titanium-Manganites of Lanthanum, Lithium and Sodium of LaLi2TiMnO6 and LaNa2TiMnO6. Molecules. 2023; 28(13):5194. https://doi.org/10.3390/molecules28135194
Chicago/Turabian StyleKasenov, Bulat Kunurovich, Shuga Bulatovna Kasenova, Zhenisgul Imangalievna Sagintaeva, Sailaubai Baisanov, Natalya Yulievna Lu, Altynbek Nukhuly, and Erbolat Ermekovich Kuanyshbekov. 2023. "Heat Capacity and Thermodynamic Functions of Titanium-Manganites of Lanthanum, Lithium and Sodium of LaLi2TiMnO6 and LaNa2TiMnO6" Molecules 28, no. 13: 5194. https://doi.org/10.3390/molecules28135194
APA StyleKasenov, B. K., Kasenova, S. B., Sagintaeva, Z. I., Baisanov, S., Lu, N. Y., Nukhuly, A., & Kuanyshbekov, E. E. (2023). Heat Capacity and Thermodynamic Functions of Titanium-Manganites of Lanthanum, Lithium and Sodium of LaLi2TiMnO6 and LaNa2TiMnO6. Molecules, 28(13), 5194. https://doi.org/10.3390/molecules28135194







