Abstract
The growth behavior, stability, electronic and magnetic properties of the Gd2Sin− (n = 3–12) clusters are reported, which are investigated using density functional theory calculations combined with the Saunders ‘Kick’ and the Artificial Bee Colony algorithm. The lowest-lying structures of Gd2Sin− (n = 3–12) are all exohedral structures with two Gd atoms face-capping the Sin frameworks. Results show that the pentagonal bipyramid (PB) shape is the basic framework for the nascent growth process of the present clusters, and forming the PB structure begins with n = 5. The Gd2Si5− is the potential magic cluster due to significantly higher average binding energies and second order difference energies, which can also be further verified by localized orbital locator and adaptive natural density partitioning methods. Moreover, the localized f-electron can be observed by natural atomic orbital analysis, implying that these electrons are not affected by the pure silicon atoms and scarcely participate in bonding. Hence, the implantation of these elements into a silicon substrate could present a potential alternative strategy for designing and synthesizing rare earth magnetic silicon-based materials.
1. Introduction
The developments of nanoclusters not only exhibit size-independent properties but also provide a rational tool to “design” the tailored physical and chemical properties. Hence, the research on this aspect has achieved great success in the past few decades [1,2,3,4,5,6]. As the foundation of modern industry, Si plays an important role in electronic materials, nanomaterials and self-assembled materials. In particular, small silicon clusters are promising for the blocks of nanometric materials; consequently, silicon-based clusters have drawn wide attention and have been investigated extensively between experiment [7,8,9,10] and theory [11,12,13,14]. Unfortunately, the presence of dangling bonds on the clusters makes the pure silicon clusters unstable [15,16], which is unsuitable for building blocks. Unlike carbon atoms, silicon atoms prefer the sp3 hybridization to sp2 [17] because the π bonding in silicon is much weaker than in carbon. Although both C and Si have diamond crystal structures, there is no silicon solid in the graphite phase, and the hollow cage structures in silicon clusters are usually unstable. Therefore, silicon-based clusters are both unstable and unsuitable as a unit for modern nanomaterials.
Since the discovery that the “impurity” could shed light on silicon-based clusters with particular properties and enhanced stability, especially for metal-doped silicon clusters, many investigations on doped silicon clusters have been reported [18,19,20,21,22,23,24]. In pioneering studies in 1987 [25] and 1989 [26], Beck carried out experiments on metal-doped silicon clusters, especially with the addition of transition metal™, and found that the structure of closed shell usually brings higher stability. Kumar et al. [11] reported the three new classes of metal-encapsulated M@Sin clusters with high stability and large HOMO-LUMO gaps; a large gap was observed for Ti@Si16 Frank-Kasper polyhedron. Combined mass spectra with photoelectron spectra, Koyasu et al. [10] determined the formation of metal atom encapsulated in a Si cage MSi16 (M = Sc, Ti and V); it was found that the magnitude HOMO-LUMO gap for TiSi16 is the largest among those measured for single metal-atom-doped silicon clusters. A Frank–Kasper polyhedron was also predicted by their calculations. However, magnetic moments tend to quench in metal-atom-doped silicon-based clusters owing to the strong hybridization between metal-3d and Si-3p orbital [27,28,29,30].
In contrast to 3d TM atoms, 4f-orbital electrons are well preserved and localized at both lanthanide atoms. Thus, intensive research on lanthanide-atom-doped silicon clusters has been carried out in recent years on silicon clusters [31,32,33]. Grubisic et al. [34] published the photoelectron spectra of EuSin cluster anions, and EuSi12 was measured to be the smallest fully endohedral europium-silicon cluster. Nguyen and co-workers investigated the magnetic properties and geometric and electronic structures of Si7M0/−1 with M = Pr, Gd, Ho [35], and the limited f-electrons of the lanthanide metal atoms were observed by density functional theory (DFT). As a consequence, high magnetic moments were induced in doped clusters. Motivated by these, we set out to systematically probe the structural, spectral, electronic and bonding properties of Gd2Sin− (n = 3–12), expanding the investigation of Gd-diatom doped silicon systems. The aim of this work is (1) to obtain the various global minimum structures of Gd2Sin− (n = 3–12); (2) to pursue the growth behavior of Gd2Sin− (n = 3–12); (3) to understand the effect of the doping of two Gd atoms on the electronic properties; and (4) to explore the interaction mechanism between Gd and pure silicon atoms. We hope that the present work will greatly deepen understanding of these diatomic lanthanide systems, and as promising building blocks in developing cluster-assembled materials.
2. Results and Discussion
The top several optimized lowest-lying isomers of Sin+2− and Gd2Sin− (n = 3–12) clusters are depicted in Figure 1 and Figure 2, and more information on isomeric structures is depicted in Figures S2 and S3 (see Supplementary Materials). The Cartesian coordinates of the top four isomeric structures are summarized in Table S2 of the Supplementary Material. The detailed descriptions of the geometric structures are shown below.
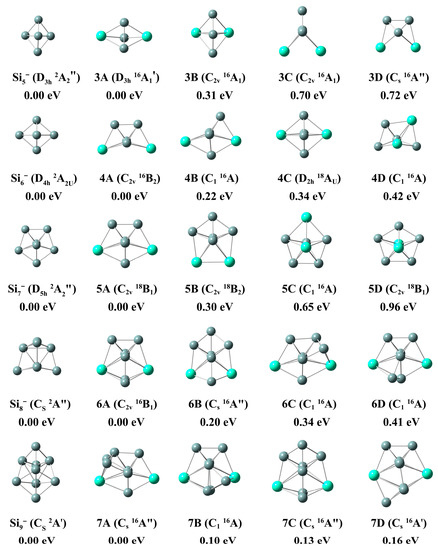
Figure 1.
The global minimum and low-energy isomers of Gd2Sin− and Sin+2− (n = 3–7) with relative energy, symmetry and electron state at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. The gray and light green balls represent silicon and gadolinium atoms, respectively.
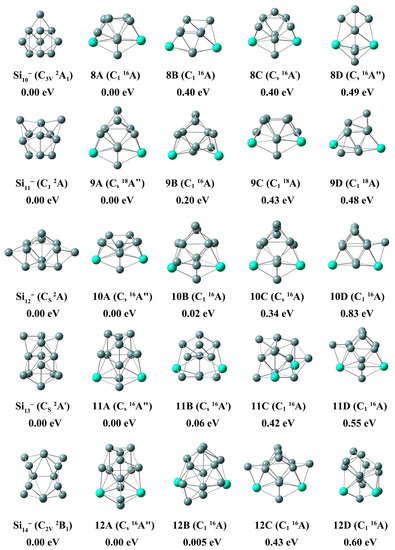
Figure 2.
The global minimum and low-energy isomers of Gd2Sin− and Sin+2− (n = 8–12) with relative energy, symmetry and electron state at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. The gray and light green balls represent silicon and gadolinium atoms, respectively.
2.1. Geometric Structures
In this section, we discuss the structural details of some low-lying isomers of Gd2Sin− clusters. Here, in order to discuss the effects of doped bimetallic Gd atoms on pure silicon clusters, the structures of silicon clusters are also plotted in Figure 1 and Figure 2 for comparison, and are consistent with previous work [36,37,38]. The detailed spin multiplicity (SM), the symmetry (Sym), the relative energy (∆E), the first adiabatic detachment energy (ADE) and the first vertical detachment energy (VDE) for the low-lying isomers of Gd2Sin− (n = 3–12) clusters are shown in Table S3.
2.1.1. Si5-8− and Gd2Si3-6−
Compared to trigonal bipyramid-shaped Si5−, as for Gd2Si3−, the lowest-lying isomer 3A (D3h, 16A1′) can be obtained by the two Gd atoms substituting two Si atoms located at the vertex of top and bottom sides. The first ADE and VDE for 3A are 1.20 and 1.37 eV, respectively. Si6− is predicted to be a square bipyramid-shaped structure with D4h symmetry. Isomer 4A can be regarded as adding a Si atom to the vertex of 3A, forming a distorted tetragonal bipyramid pattern structure with C1 point group symmetry and 16A electron state. The computed first ADE and VDE are 1.01 and 1.09 eV, respectively. The pentagonal bipyramid-shaped structure of Si7− with a more symmetric configuration (D5h) is presented in Figure 1. Meanwhile, analogous to pure Si7−, the most stable isomer of Gd2Si5− was also found to be a pentagonal bipyramid (PB) with C2v symmetry and 18B1 electron state. Substituting two Si atoms on the D5h planar of the decahedron with two Gd atoms, the first ADE and VDE values of 5A (0.78 and 0.84 eV) were obtained at the same level of calculation. In contrast to pure crown-shaped Si8− (Cs, 2A″), the most stable Gd2-doped 6A can be obtained by adding a Si atom to face-cap the bottom of 5A coupled with C2v symmetry and 16B1 electron state; the first ADE and VDE are 1.95 and 2.09 eV, respectively.
2.1.2. Si9-14− and Gd2Si7-12−
With respect to Gd2Si7−, the top-four isomers (7A, 7B, 7C and 7D, relative energy within ~0.20 eV) all emerged as the candidates, as shown in Figure 1 at PBE0/Gd/ECP28 MWB//Si/6-311+G(d) level. The ground state structure of isomer 7A can be described as putting two Si atoms on the top left side of PB (5A) with Cs point group symmetry and 16A″, and it also can be seen as attaching a Si atom to the top left of 6C. Both the computed ADE and VDE (2.16 eV for ADE and 2.20 eV for VDE) of 7A are measured in this work, suggesting that the anionic structure is essentially unchanged by the loss of an electron. Si10− is of C3v symmetry with a fruit basket-shaped structure. It was found that 8A is based on the 5A and three Si which connect to PB, with C1 symmetry and 16A electron state, and the ADE and VDE values of 8A are 1.77 and 2.19 eV, respectively. Comparing the low symmetric structure of Si11−, the lowest-lying stable geometrical structure of 9A is of Cs symmetry with 18A″ electron state, which can be generated based on 8C. Appending an excess Si atom to the apex of 8C, eleven atoms were separated into two parts (one of which was a PB and the other was a triangular pyramid). The computed ADE and VDE values of 9A are 1.75 and 1.86 eV. Si12− is predicted to be a teapot-shaped geometry with Cs symmetry. With respect to Gd2Si10− cluster, isomer 10A was generated when capping the five-atom pentagon on the top of 5A, with Cs point group symmetry and 16A electron state. The theoretical ADE and VDE values of 10A are 2.26 and 2.31 eV. As far as the Gd2Si11− clusters are concerned, the lowest-lying stable geometry was generated when two additional Si capped the top side of 9A, which can also be depicted as the combination between a Si6 with a pentagonal bipyramid-shaped Gd2Si5. Its computed ADE and VDE values are 2.31 and 2.54 eV, respectively. Compared to pure Si14− (C2V, 2A) cluster, the lowest-lying structure 12A can be considered as appending an additional Si atom at the bottom of 11A, and also can be seen capping seven Si atoms on the framework of PB. The values of ADE and VDE for ground state Gd2Si12− are 2.53 and 2.85 eV.
2.2. The Growth Behavior of Gd2Sin−
It is interesting to probe the structural evolution, and it can be found that the lowest-lying structures of Gd2Sin−, with n = 5–12, are all exohedral structures. The optimized structures show that the ground states of clusters favor high spin state. It is strongly worth mentioning that the PB is the basic framework for the growing size of Gd2Sin− (n = 3–12), as presented in Figure S4. Gd2Sin− still can be regarded as replacing two Si atoms with two Gd atoms, the basic framework of PB initially formed in n = 5. For n = 6–12, all clusters can be viewed as absorbing one to seven Si atoms on the different positions of PB; each of the ground-state structures retained the motif and grew on it. However, they cannot simply be seen as occupying the original silicon-based clusters. Compared to previous investigations of T2Sin−1/0 (T = Fe, Co and Ni, 1 ≤ n ≤ 8) [39], T2Sin (T = Cr, Mn, 1 ≤ n ≤ 8) [40], Au2Sin−1/0 (n = 1–7) [41], Nb2Sin (n = 2–12) [42], Mo2Sin (n = 9–16) [43] and Fe2Sin (n = 1–12)+/0/− [44], the two TMs tend to form a strong metal–metal bond, which is different from the weak interaction between Gd-Gd, implying the bonding properties of two Gd-atom-doped silicon clusters are different from those silicon clusters doped with other TMs. On the one hand, the early formation of half-endohedral geometric structures appears at n ≥ 9; one of the metal atoms is embedded in the cage while the other metal atom tends to adsorb on the surface. It is interesting to compare the growth behaviors with the corresponding bimetal-doped Si clusters counterparts; both of the Gd atoms always adsorb on the surface of Si-based clusters. The reason for this is probably because Gd atoms have a larger atomic radius and are more difficult to embed into the silicon cage. On the other hand, the infrequent interaction between dual Gd reveals that they are inclined to adsorb the surface instead of being embedded in a Si cage.
2.3. Simulated Photoelectron Spectrum
In order to provide theoretical guidance for further experiments, we have generated simulated photoelectron spectra (PESs) for the lowest-lying isomers of Gd2Sin− (n = 3–12), as illustrated in Figure 3. The simulated PESs were fitted by adding the energy of the occupied orbital to the VDE, based on the generalized Koopman’s theorem (GKT) [45], with a full width at half maximum (FWHM) value of 0.20 eV. Additionally, more simulated PESs of low-lying isomers can be obtained in Figure S5.
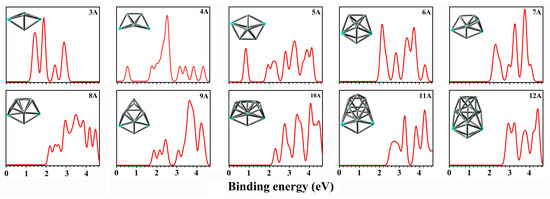
Figure 3.
The simulated photoelectron spectra of lowest energy isomers of Gd2Sin− (n = 3–12) at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. The simulated photoelectron spectra exhibit a full width at half maximum (FWHM) of 0.20 eV.
In Figure 3, the PESs of Gd2Sin− (n = 3–12) reveal unique features. The first peak of the spectrum of Gd2Si3− is denoted as the first VDE, centered at 1.44 eV, and followed by three distinct features at 1.87, 2.44 and 2.89 eV, respectively. Similarly, Gd2Si4− shows a small peak at 1.91 eV, followed by four spectrum features located at 1.36, 2.30, 2.96 and 3.49 eV, respectively. As for the spectrum of Gd2Si5−, it shows a very broad feature extending from approximated 0.8–4.2 eV, furthermore, six sharp peaks can be observed at 0.84, 1.95, 2.83, 3.27, 3.89 and 4.13 eV, respectively. There are five obvious peaks centered at 2.14, 2.83, 3.37, 3.72 and 4.27 eV that can be detected in the spectrum of Gd2Si6−. The spectrum of Gd2Si7− displays three prominent peaks located at 2.30, 3.26 and 3.75 eV, along with two small peaks centered at 2.96 and 4.04 eV. The spectrum of Gd2Si8− shows six sharp peaks centered at 2.19, 2.96, 3.48, 3.85 and 4.17 eV, followed by two small peaks located at 2.45 and 2.62 eV, respectively. There are six distinguishable features at 1.86, 2.15, 2.44, 3.08, 3.64 and 4.21 eV that can be detected in the spectrum of Gd2Si9−. The spectrum of Gd2Si10−, displays five obvious features at 2.31, 2.78, 3.39, 4.07 and 4.48 eV. Three peaks can be observed at higher electron binding energy regions centered at 3.26, 3.82 and 4.25 eV, which are distinguishable in the spectrum of Gd2Si11−. Finally, the spectrum of Gd2Si12− shows four distinct peaks located at 2.94, 3.24, 3.77 and 4.39 eV.
2.4. Relative Stability
To measure the relative stability of bimetallic Gd doped silicon clusters, the average binding energy and second order difference energy of the lowest energy structures for Gd2Sin− are calculated at PBE0/Si/6-311+G(d)//Gd/ECP28MWB level for Gd2Sin− and the PBE0/Si/6-311+G(d) level for Sin+2. The results of average binding energy are shown in Figure S6.
The average binding energy and second order difference energy are defined by the following formulas:
where the E(Gd2Sin+1−), E(Gd2Sin−), E(Gd2Sin-1−), E(Sin+3−), E(Sin+2−), E(Sin+1−) represent the total energy of Gd2Sin+1−, Gd2Sin−, Gd2Sin-1−, Sin+3−, Sin+2−, Sin+1− in ground state, respectively. E(Si−), E(Si) and E(Gd) correspond to the single-point energies of Gd and Si atoms.
Eb (Gd2Sin−) = [(n − 1) E(Si) + E(Si−) + 2 E(Gd) − E(Gd2Sin−)]/n + 2
Eb (Sin+2−) = [(n + 1) E(Si) + E(Si−) − E(Sin+2−)]/n + 2
∆2E(Gd2Sin−) = E(Gd2Sin+1−) + E(Gd2Sin-1−) − 2E(Gd2Sin−)
∆2E(Sin+2−) = E(Sin+3−) + E(Sin+1−) − 2E(Sin+2−)
2.4.1. Average Binding Energy
Figure S6 shows the average binding energy of ground-state structures of Gd2Sin− (n = 3–12) at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. There are several observations worth noting from Figure S6.
- (1)
- The binding energy of pure Sin+2− and mixed Gd2Sin− clusters both rise monotonically with increasing dimensions of growing size; however, the binding energy per atom for Sin+2− is slightly higher than Gd2Sin−, suggesting that the stability of two Gd atoms doping is smaller than Sin+2−.
- (2)
- It is interesting to find that Gd2Si5− and Gd2Si8− have a relatively steep upward trend along with increasing dimensions of growing size, signifying that Gd2Si5− and Gd2Si8− are the most stable clusters in the range researched here.
2.4.2. Second Order Difference Energy
The second order difference energy ∆2E for Sin+2− and Gd2Sin− is presented in Figure 4. As a sensitive indicator to measure the relative stability of clusters in comparison with their smaller and larger neighbors, ∆2E gives the evidence to identify the most stable clusters by the maximum values. The primary features are concluded below:
- (1)
- The second difference energy of Sin+2− and Gd2Sin− as a function of the cluster size exhibits a pronounced even–odd alternation phenomenon.
- (2)
- The relative stabilities of Gd2Si5− and Gd2Si8− are quite strong among all the clusters in terms of second order difference energy.
- (3)
- We could easily screen out the magic clusters (Gd2Si5−) with the help of results of second order difference energy.
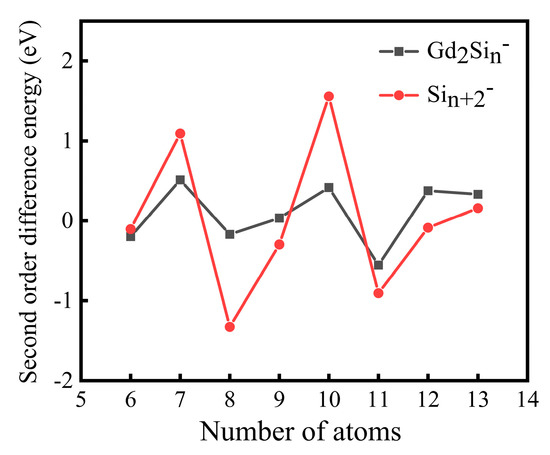
Figure 4.
The second order difference energies of Gd2Sin− (n = 4–11) and Sin+2− at PBE0 /Gd/ECP28MWB//Si/6-311+G(d) level.
2.5. Magnetic Properties and Natural Atomic Orbital
In order to comprehend the interaction between Gd atoms and silicon-based clusters, we performed natural atomic orbital (NAO) for the lowest-energy structures of Gd2Sin− cluster using PBE0 functional. The natural population analysis (NPA) charges of the lowest-energy structures of Gd2Sin− (n = 3–12) are given in Table S4. As shown in Table S4, charges always transfer from the two Gd atoms to Si atoms in the system of increasing size. This indicates that the two Gd atoms act as donors while the Si atoms act as receptors, reflecting the bonding process. This is further supported by the valence electron configurations and magnetic moments given in Table S5. It is well known that the valence electron configuration of a free Gd atom is [Xe]4f75d16s2. Based on the data in Table S5, two conclusions can be drawn. Firstly, both Gd atoms still possess half-filled 4f electrons, which is quite different from dual TMs doping [39,40,44], suggesting the hard participation in bonding between Si atoms; therefore, it has a very good prospect in the application of Si-based cluster-assembled materials. Secondly, the transferred 6s and 5d electrons reveal that the interaction among 6s and 5d orbitals can be proposed. This conclusion is discussed in detail below.
Gd-4f electrons to a large extent appear not to interact significantly with their neighboring Si atoms, as demonstrated by the distribution of single spin electron population of Gd2Sin− (n = 3–12) in Figure S7. Obviously, the excess electrons are mainly distributed around the Gd atoms, as indicated by the red region, which confirm that the high magnetic moments are derived from the two Gd atoms, visually. Additionally, the red dense isosurface can be inferred mainly to distribute a bunch of 4f electrons with the help of NAO analysis, and then the results of spin density isosurface more strongly confirm the distribution of bimetallic Gd among the mixed system.
2.6. Bonding Analysis
In order to shed some light on the origins of the high stability of Gd2Si5−, the compositions of their molecular orbitals (MOs) in the vicinity of the frontier MOs of the Gd2Si5− are plotted in Figure 5 to research stability mechanisms. The frontier orbital energy gaps can be regarded as a distinguishing feature of kinetic stability of chemical compounds. In addition, high reluctance of compounds for chemical reactions also can be elaborated by a large gap. It can be seen that the identical frontier molecular orbitals (α-HOMO, α-LUMO, β-HOMO, and β-LUMO) are mainly derived from Si-3p and Gd-6s 6p 5d. In particular, the 5d orbital of Gd atom can be seen as the main participant in α-HOMO, α-LUMO, β-HOMO, and β-LUMO orbitals; that is, the distinctive p-d hybridization makes Gd2Si5− possess high stability. Furthermore, the higher HOMO-LUMO gap also can be observed in Figure 5. The large gaps at both alpha (1.07 eV) and beta (2.37 eV) orbitals can be expected to give rise to the stability of Gd2Si5−, which gives further support for this enhanced stability.
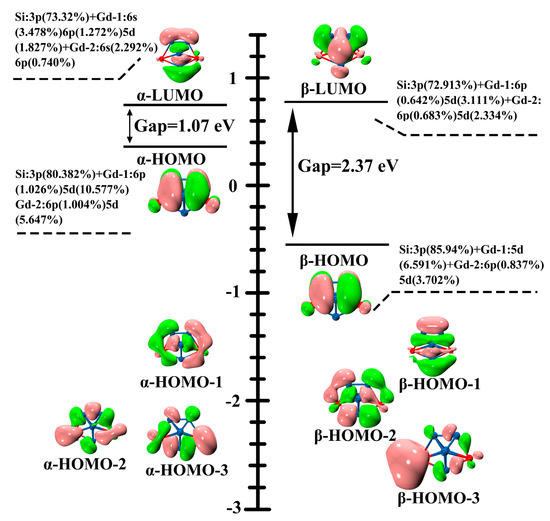
Figure 5.
Valence MOs and the corresponding energy levels of Gd2Si5−, in conjunction with molecular orbital composition and SOMO-LUMO gap is indicated (in black).
With the purpose to characterize the Si-Gd and Si-Si bond, the localized orbital locator (LOL) is adopted for double Gd-atom-doped silicon clusters, which is plotted in Figure 6a. As a tool for classification of chemical bonding, atomic shell structure and electronic structure, LOL has been widely applied for organic or inorganic small molecules, atomic crystals, clusters and coordination compounds, which helps us better understand the strength of the interaction between atoms. It is significant to gain deep insight into the bonding property of Gd2Si5−. The mean electronic population is distinguished by different colors. The regions with high LOL values indicate more localized electrons and are of great interest in chemical bonding. As can be seen from Figure 6a, the high LOL values are determined between Si1, Si4 and Si3, suggesting that the Si-Si covalent interaction can be intuitively identified based on the red region and the electrons are remarkably limited between the Si atoms. Furthermore, it is worth mentioning that the distinct red region can be observed at Figure 6a, indicating that the localized Si-Gd bonding is accountable for the interaction between double Gd dopant and Si moiety. This can be validated by bond length and fuzzy bond order, as shown in Figure 6b,c, and it is found that both high values of fuzzy bond for Si-Si and Si-Gd can be intuitively visualized and indeed this case can be supported by bond length. To summarize, the high stability of Gd2Si5− is attributed to the interaction between Si atoms in the host silicon cluster. Furthermore, the enhanced stability of the Gd-doped silicon cluster is derived from the strong interaction between Si atoms and the Gd dopant.
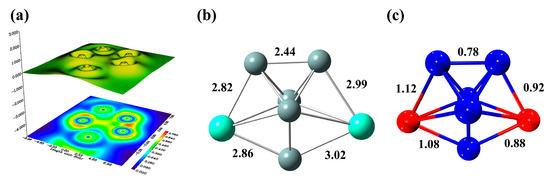
Figure 6.
The color-filled map of LOL (a), bond length (b) and fuzzy bond order (c) of global minimum structure of Gd2Si5− at PBE0/Gd/ECP28MWB//Si/6-311+G(d) level.
The analysis of AdNDP results also gives insight into the multicenter bond (nc-2e) and delocalization of Gd2Si5− (as shown in Figure 7). Moreover, the AdNDP results provide compelling evidence to support the conclusion regarding the stability of Gd2Si5−. The effect of mixing two Gd atoms on the chemical bonding could be further elaborated in current work. AdNDP is based on natural atomic orbital (NAO), which is defined as the diagonalization of the density matrix of the n-atomic sub-block of N-atomic molecular system. The three (1c-2e) lone pairs are responsible for the impact on the geometric structure, where localized electrons are concentrated on three Si atoms that surround the plane of the pentagonal bipyramid of the ground-state structure for Gd2Si5−. It should be noted that five 2c-2e Si-Si σ bonds could be observed in Figure 7 while these 2c-2e σ bonds all concentrated on Si atoms with ON = 1.85–1.89|e|, indicating the strong covalent bonding could be observed among Si atoms. This observation is consistent with the LOL analysis, bond length and fuzzy bond order analysis (see Figure 6), mentioned above, which provides a good illustration of the existence of covalent bonds with high LOL values. Furthermore, the shorter bond length on Gd-Si incorporated with a high value of fuzzy bond order also confirms the strong Gd-Si interaction. The remaining delocalized π bonds can be characterized on twelve 3c-2e AdNDP orbitals (1.76–1.89|e|). Most interestingly, both two Gd atoms can almost be seen in delocalized bonds, which explains the strong stability of Gd2Si5−.
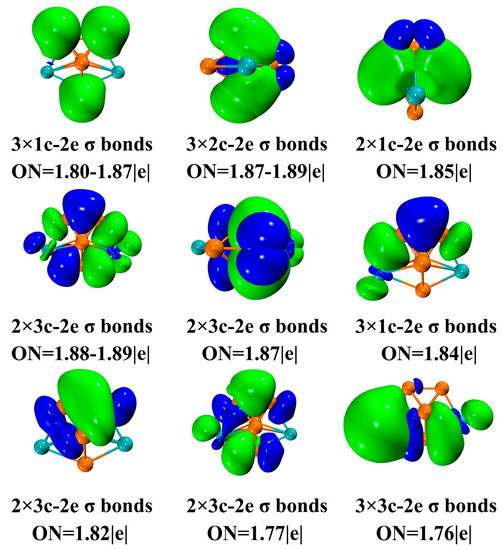
Figure 7.
Analysis of the AdNDP chemical bonds for Gd2Si5−.
3. Computational Methods
All the calculations of equilibrium geometries of Gd2Sin− (n = 3–12) are carried out by DFT with PBE0 functional [46], as implemented in GAUSSIAN 09 program package [47]. They are all optimized until the harmonic vibration analysis gives no imaginary frequency. The introduction of the two Gd atoms makes the search even more difficult; for small clusters, this problem can be solved by using the Saunders “Kick” (SK) global search technique [48]. However, as the size increases, the number of local minimal isomers increases exponentially; how to search the initial structures quickly and comprehensively is a difficult problem. In addition to the SK stochastic method, we also employed the Artificial Bee Colony cluster (ABC) [49] algorithm to search global minimum and low-lying structures for larger clusters. Two global optimization schemes (SK and ABC) complement each other to obtain the real global optimal structure. Our group has successfully performed the investigations of binary clusters by these methods [50,51,52,53,54,55].
During the pre-optimization, about 300–600 isomeric structures for Gd2Sin− (number of atoms less than 8) and 600–1000 structures for Gd2Sin− (number of atoms more than 8) were generated with unbiased search and optimized at PBE0 functional with the 6-31G basis set for Si atoms. Due to significant relativistic effects on lanthanide elements, the larger scalar Stuttgart relativistic effective core potential basis set (ECP54MWB) [56] was chosen for Gd atoms. Furthermore, we carried out substitution and adsorption of the two Gd atoms on the basis of Sin+2− and GdSin+1−, respectively. Subsequently, the obtained low-lying isomers from the result of random kicking and unbiased search were reoptimized at the PBE0 level with the 6-311+G(d) [57] basis set for Si atoms and the ECP28MWB [58] basis set for Gd atoms (PBE0/Gd/ECP28MWB//Si/6-311+G(d)). Additionally, there are several points worth noting: (1) a sequence of probable spin multiplicities must be taken into consideration during the process of obtaining global minimum structures; (2) self-consistent calculations were performed with a convergence criterion of 10−6 Hartree on the total energy and corresponding neutral counterpart; (3) the zero-point energy (ZPE) was not considered in this work, because the ZPE correction of a specific cluster was small and almost the same and was not expected to affect the relative energy ordering.
To test the reliability of the present computational method, we performed the calculation of GdSi4− with five different exchange-correlation functionals (PBE0 [46], B3LYP [59], PBE [60], TPSSh [61], and BPW91 [62]) with the same basis set. The choice of functionals has a significant impact on the results of the ADE calculation and the simulation of the photoelectron spectrum. It is worth noting that the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level of theory has good consistency with experimental results (Table S1 and Figure S1), and, therefore, the same level has been selected as the method of choice for Gd2Sin−. Furthermore, all kinds of wavefunction analyses, containing natural atomic orbital (NAO) [63], spin density, localized orbital locator (LOL) [64] and adaptive natural density partitioning (AdNDP) [65] theory, are conducted by multifunctional wavefunction analyzer (Multiwfn) program [66,67] and visualized by Visual Molecular Dynamics (VMD) software [68].
4. Conclusions
In summary, the growth behavior, stability, electronic and magnetic properties of Gd2Si− (n = 3–12) clusters were investigated with the aid of DFT calculations. Extensive searches of the lowest-energy structures were performed by considering a number of isomeric structures. The ground-state structures of Gd2Sin− were inclined to form three-dimensional exohedral structures. All of the results can be summarized as follows:
- (1)
- The doped double Gd atoms do not play an important role in geometric structures in small clusters Sin− (n ≤ 6), but they contribute largely to the equilibrium structures from n = 7 to n = 12. More interestingly, the PB can be observed in the basic framework for the growth process of Gd2Sin− (n = 5–12).
- (2)
- The result of NAO reveals that the induction of bimetallic Gd2 atoms provides great magnetic moments, which suggests that it may assemble magnetic semiconductor materials by using double Gd-atom-doped Si-based clusters as building blocks.
- (3)
- According to the energetic stability, Gd2Si5− is determined to the most stable cluster among the size n = 3–12. The frontier molecular orbitals also illustrate the high stability.
- (4)
- The LOL and AdNDP reveal that the stabilization mechanism of Gd2Si5− is due to strong covalent bonding interactions between Gd and Si atoms.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28135071/s1, Table S1: Comparison of ADEs and VDEs using different methods for GdSi4− Table S2: Cartesian coordinates for the top low-lying isomers of Gd2Sin− (n = 3–12) at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. Table S3: Various structures with type the spin multiplicity (SM), the symmetry (Sym), the relative energy (∆E), the first adiabatic detachment energy (ADE) and first vertical detachment energy (VDE) for the low-lying isomers of Gd2Sin− (n = 3–12) at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. All energies are in eV. Table S4: The NPA charges (e) on the parent Si atoms, double-Gd atoms and total charges for the most stable isomers. Table S5: The valence electron configuration of each one of the two Gd atoms, magnetic moments (μB) of the Gd-4f orbital, total magnetic moments of the two Gd atoms and total magnetic moments for the most stable isomers. Figure S1: (a) Photoelectron spectrum of GdSi4− measured at 266 nm (4.66 eV), the spectrum is taken from Ref. [20]. (b) Simulated photoelectron spectra (PES) from the lowest-energy structures for GdSi4− clusters at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level, together with B3LYP, PBE, TPSSh and BPW91 functionals for comparison. Each VDE was fitted with a full width at half-maximum (FWHM) of 0.20 eV to yield the simulated PES spectra. Figure S2: The various geometrical structures of Gd2Sin− (n = 3–7) with relative energy, symmetry and electron state at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. The gray and light green balls represent silicon and gadolinium atoms, respectively. Figure S3: The various geometrical structures of Gd2Sin− (n = 8–12) with relative energy, symmetry and electron state at the PBE0/Gd/ECP28MWB//Si/6-311+G(d) level. The gray and light green balls represent silicon and gadolinium atoms, respectively. Figure S4. The growth behavior of Gd2Sin− (n = 5–12) clusters. Figure S5: The simulated photoelectron spectra (PESs) for the assigned major clusters within 0.3 eV at the PBE0/Gd/ ECP28MWB//Si/6-311+G(d) level. The simulated PESs exhibit a full width at half maximum (FWHM) of 0.20 eV. Figure S6: The average binding energies of Gd2Sin− (n = 3–12) and Sin+2− at PBE0/Gd/ECP 28MWB//Si/6-311+G(d) level. Figure S7: The spin-density (ρalpha–ρbeta) isosurfaces of lowest-lying isomers of Gd2Sin− (n = 3–12). The isosurface is set to ±0.02. The red and blue isosurfaces show that the spin density has positive and negative values, respectively.
Author Contributions
Conceptualization, B.X., H.-Q.W. and H.-F.L.; methodology, H.-Q.W.; software, H.-Q.W.; validation, B.X., H.-Q.W., H.-F.L. and X.-J.M.; formal analysis, H.-Q.W. and J.-M.Z.; investigation, B.X. and H.-Q.W.; resources, H.-Q.W.; data curation, B.X. and L.-X.Q.; writing—original draft preparation, B.X.; writing—review and editing, B.X., H.-Q.W., H.-F.L., J.-M.Z., J.-K.Z., X.-J.M., Y.-H.Z. and H.Z.; visualization, B.X.; supervision, H.-Q.W.; project administration, H.-Q.W.; funding acquisition, H.-Q.W. and H.-F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Fujian Province of China, grant numbers 2023J01141 and 2017J01001, the Science and Technology Plan of Quanzhou grant numbers 2018C077R and 2018C078R and the New Century Excellent Talents in Fujian Province University grant number 2014FJ-NCET-ZR07.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article and its Supplementary Material.
Acknowledgments
The authors warmly thank Yi-Wei Fan for fruitful discussions.
Conflicts of Interest
The authors have no conflict to disclose.
Sample Availability
Not applicable.
References
- Uchiyama, T.; Nakamura, T.; Hiyama, M.; Kudo, T. Theoretical study of Si/C equally mixed dodecahedrane analogues. Molecules 2023, 28, 2769. [Google Scholar] [CrossRef] [PubMed]
- Khanna, V.; McGrady, J.E. Mn-2 dimers encapsulated in silicon cages: A complex challenge to MC-SCF theory. Molecules 2022, 27, 7544. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.F.F.; Burggraf, L.W.; Huang, L.Y. Searching for stable SinCn clusters: Combination of stochastic potential surface search and pseudopotential Plane-Wave Car-Parinello simulated annealing simulations. Molecules 2013, 18, 8591–8606. [Google Scholar] [CrossRef]
- Lu, C.; Kuang, X.Y.; Lu, Z.W.; Mao, A.J.; Ma, Y.M. Determination of structures, stabilities, and electronic properties for bimetallic cesium-doped gold clusters. J. Phys. Chem. A 2011, 115, 9273–9281. [Google Scholar]
- Chen, Y.; Deng, J.-J.; Yao, W.-W.; Gurti, J.I.; Li, W.; Wang, W.-J.; Yao, J.-X.; Ding, X.-L. Non-stoichiometric molybdenum sulfide clusters and their reactions with the hydrogen molecule. Phys. Chem. Chem. Phys. 2021, 23, 347–355. [Google Scholar] [CrossRef]
- Farooq, U.; Naz, S.; Xu, H.G.; Yang, B.; Xu, X.L.; Zheng, W.J. Recent progress in theoretical and experimental studies of metal-doped silicon clusters: Trend among elements of periodic table. Coord. Chem. Rev. 2020, 403, 213095. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Tanigaki, K.; Yasukawa, M. Silicon clathrate with an f-electron system. Phys. Rev. Lett. 2000, 85, 3189–3192. [Google Scholar] [CrossRef]
- Ohara, M.; Miyajima, K.; Pramann, A.; Nakajima, A.; Kaya, K. Geometric and electronic structures of terbium-silicon mixed clusters (TbSin; 6 ≤ n ≤ 16). J. Phys. Chem. A 2002, 106, 3702–3705. [Google Scholar] [CrossRef]
- Ohara, M.; Koyasu, K.; Nakajima, A.; Kaya, K. Geometric and electronic structures of metal (M)-doped silicon clusters (M = Ti, Hf, Mo and W). Chem. Phys. Lett. 2003, 371, 490–497. [Google Scholar] [CrossRef]
- Koyasu, K.; Atobe, J.; Furuse, S.; Nakajima, A. Anion photoelectron spectroscopy of transition metal- and lanthanide metal-silicon clusters: MSin− (n = 6–20). J. Chem. Phys. 2008, 129, 214301. [Google Scholar] [CrossRef]
- Kumar, V.; Kawazoe, Y. Metal-encapsulated fullerenelike and cubic caged clusters of silicon. Phys. Rev. Lett. 2001, 87, 045503. [Google Scholar] [CrossRef]
- Kumar, V. Predictions of novel nanostructures of silicon by metal encapsulation. Comput. Mater. Sci. 2004, 30, 260–268. [Google Scholar] [CrossRef]
- Kumar, V. Alchemy at the nanoscale: Magic heteroatom clusters and assemblies. Comput. Mater. Sci. 2006, 36, 1–11. [Google Scholar] [CrossRef]
- Zheng, W.J.; Nilles, J.M.; Radisic, D.; Bowen, K.H. Photoelectron spectroscopy of chromium-doped silicon cluster anions. J. Chem. Phys. 2005, 122, 71101. [Google Scholar] [CrossRef]
- Hiura, H.; Miyazaki, T.; Kanayama, T. Formation of metal-encapsulating Si cage clusters. Phys. Rev. Lett. 2001, 86, 1733–1736. [Google Scholar] [CrossRef]
- Ishimaru, M. Molecular-dynamics study on atomistic structures of amorphous silicon. J. Phys. Condens. Matter 2001, 13, 4181–4189. [Google Scholar] [CrossRef]
- De Padova, P.; Quaresima, C.; Olivieri, B.; Perfetti, P.; Le, L.G. sp2-like hybridization of silicon valence orbitals in silicene nanoribbons. Appl. Phys. Lett. 2011, 98, 081909. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Yang, J.C.; Dong, C.X. Structural and electronic properties of nanosize semiconductor CeSin0/− (n = 4–20) material: A double-hybrid density functional theory investigation. Comput. Theor. Chem. 2019, 1170, 112635. [Google Scholar] [CrossRef]
- Grubisic, A.; Ko, Y.J.; Wang, H.; Bowen, K.H. Photoelectron spectroscopy of lanthanide-silicon cluster anions LnSin− (3 ≤ n ≤13; Ln = Ho, Gd, Pr, Sm, Eu, Yb): Prospect for magnetic silicon-based clusters. J. Am. Chem. Soc. 2009, 131, 10783–10790. [Google Scholar] [CrossRef]
- Janssens, E.; Gruene, P.; Meijer, G.; Woste, L.; Lievens, P.; Fielicke, A. Argon physisorption as structural probe for endohedrally doped silicon clusters. Phys. Rev. Lett. 2007, 99, 063401. [Google Scholar] [CrossRef]
- Zhao, J.; Du, Q.; Zhou, S.; Kumar, V. Endohedrally doped cage clusters. Chem. Rev. 2020, 120, 9021–9163. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yang, J.C.; Cheng, L. Structural stability and evolution of scandium-doped silicon clusters: Evolution of linked to encapsulated structures and its influence on the prediction of electron affinities for ScSin (n = 4–16) clusters. Inorg. Chem. 2018, 57, 12934–12940. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wu, J.H.; Cui, J.W.; Lu, C.; Zhou, P.P.; Lu, Z.W.; Li, G.Q. Geometries, Stabilities and electronic properties of beryllium-silicon Be2Sin clusters. J. Mol. Model. 2014, 20, 2242. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.J.; Cao, G.J.; Xu, X.L.; Xu, H.G.; Zheng, W.J. The structural and electronic properties of NbSin−/0 (n = 3–12) clusters: Anion photoelectron spectroscopy and ab initio calculations. Nanoscale 2016, 8, 19769–19778. [Google Scholar] [CrossRef] [PubMed]
- Beck, S.M. Studies of silicon cluster–metal atom compound formation in a supersonic molecular beam. J. Chem. Phys. 1987, 87, 4233–4234. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the rare earth elements. J. Chem. Phys. 1989, 90, 1730–1734. [Google Scholar] [CrossRef]
- Gu, M.; Tang, T.B.; Feng, D. C60 with complete pentagon orientational ordering: A dielectric and 13C NMR study of solid C60 charged with NO. Phys. Rev. B 2002, 66, 073404. [Google Scholar] [CrossRef]
- Huang, X.M.; Xu, H.G.; Lu, S.J.; Su, Y.; King, R.B.; Zhao, J.J.; Zheng, W.J. Discovery of a silicon-based ferrimagnetic wheel structure in VxSi12− (x = 1–3) clusters: Photoelectron spectroscopy and density functional theory investigation. Nanoscale 2014, 6, 14617–14621. [Google Scholar] [CrossRef]
- Li, Y.J.; Tam, N.M.; Claes, P.; Woodham, A.P.; Lyon, J.T.; Ngan, V.T.; Nguyen, M.T.; Lievens, P.; Fielicke, A.; Janssens, E. Structure assignment, electronic properties, and magnetism quenching of endohedrally doped neutral silicon clusters, SinCo (n = 10–12). J. Phys. Chem. A 2014, 118, 8198–8203. [Google Scholar] [CrossRef]
- Yang, B.; Xu, X.L.; Xu, H.G.; Farooq, U.; Zheng, W.J. Structural evolution and electronic properties of CoSin− (n = 3–12) clusters: Mass-selected anion photoelectron spectroscopy and quantum chemistry calculations. Phys. Chem. Chem. Phys. 2019, 21, 6207–6215. [Google Scholar] [CrossRef]
- Zwijnenburg, M.A.; Bromley, S.T.; van Alsenoy, C.; Maschmeyer, T. Factors affecting ionicity in all-silica materials: A density functional cluster study. J. Phys. Chem. A 2002, 106, 12376–12385. [Google Scholar] [CrossRef]
- Yang, J.C.; Feng, Y.; Xie, X.; Wu, H.; Liu, Y. Gadolinium-doped silicon clusters GdSin (n = 2–9) and their anions: Structures, thermochemistry, electron affinities, and magnetic moments. Theor. Chem. Acc. 2016, 135, 204. [Google Scholar] [CrossRef]
- Peng, Q.; Shen, J. Growth behavior of La@Sin (n = 1–21) metal-encapsulated clusters. J. Chem. Phys. 2008, 128, 084711. [Google Scholar] [CrossRef]
- Grubisic, A.; Wang, H.; Ko, Y.J.; Bowen, K.H. Photoelectron spectroscopy of europium-silicon cluster anions, EuSin− (3≤ n ≤17). J. Chem. Phys. 2008, 129, 054302. [Google Scholar] [CrossRef]
- Hang, D.; Hung, M.; Nguyen, M.T. Structural assignment, and electronic and magnetic properties of lanthanide metal doped silicon heptamers Si7M0/− with M = Pr, Gd and Ho. Phys. Chem. Chem. Phys. 2016, 18, 31054–31063. [Google Scholar] [CrossRef]
- Raghavachari, K.; Rohlfing, C.M. Bonding and stabilities of small silicon clusters: A theoretical study of Si7–Si1. J. Chem. Phys. 1988, 89, 2219–2234. [Google Scholar] [CrossRef]
- Lyon, J.T.; Gruene, P.; Fielicke, A.; Meijer, G.; Janssens, E.; Claes, P.; Lievens, P. Structures of silicon cluster cations in the gas phase. J. Am. Chem. Soc. 2009, 131, 1115–1121. [Google Scholar] [CrossRef]
- Zhao, L.Z.; Lu, W.C.; Qin, W.; Zang, Q.J.; Ho, K.M.; Wang, C.Z. Theoretical prediction of Si2–Si33 absorption spectra. J. Phys. Chem. A 2017, 121, 6388–6397. [Google Scholar] [CrossRef]
- Robles, R.; Khanna, S.N. Stable T2Sin (T = Fe, Co, Ni, 1 ≤ n ≤ 8) cluster motifs. J. Chem. Phys. 2009, 130, 164313. [Google Scholar] [CrossRef]
- Robles, R.; Khanna, S.N.; Castleman, A.W. Stability and magnetic properties of T2Sin (T = Cr, Mn, 1 ≤ n ≤ 8) clusters. Phys. Rev. B 2008, 77, 235441. [Google Scholar] [CrossRef]
- Lu, S.J.; Xu, X.L.; Xu, H.G.; Zheng, W.J. Structural evolution and bonding properties of Au2Sin−/0 (n = 1–7) clusters: Anion photoelectron spectroscopy and theoretical calculations. J. Chem. Phys. 2018, 148, 244306. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.J.; Xu, H.G.; Xu, X.L.; Zheng, W.J. Anion photoelectron spectroscopy and theoretical investigation on Nb2Sin−/0 (n = 2–12) clusters. J. Phys. Chem. C 2017, 121, 11851–11861. [Google Scholar] [CrossRef]
- Han, J.G.; Zhao, R.N.; Duan, Y.H. Geometries, stabilities, and growth patterns of the bimetal Mo2-doped Sin (n = 9–16) clusters: A density functional investigation. J. Phys. Chem. A 2007, 111, 2148–2155. [Google Scholar] [CrossRef]
- Bista, D.; Reber, A.C.; Chauhan, V.; Khanna, S.N. Electronic and magnetic properties of Fe2Sin (1 ≤ n ≤ 12)+/0/− clusters. Chem. Phys. Lett. 2018, 706, 113–119. [Google Scholar] [CrossRef]
- Tozer, D.J.; Handy, N.C. Improving virtual Kohn–Sham orbitals and eigenvalues: Application to excitation energies and static polarizabilities. J. Chem. Phys. 1998, 109, 10180–10189. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Saunders, M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
- Wang, H.Q.; Li, H.F. Probing the structural and electronic properties of al-doped small niobium clusters. Chem. Phys. Lett. 2012, 554, 231–235. [Google Scholar] [CrossRef]
- Zhang, J.; Dolg, M. Abcluster: The artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 2015, 17, 24173–24181. [Google Scholar] [CrossRef]
- Li, H.F.; Wang, H.Q. Stabilization of golden cages by encapsulation of a single transition metal atom. R. Soc. Open Sci. 2018, 5, 171019. [Google Scholar] [CrossRef]
- Fan, Y.W.; Wang, H.Q.; Li, H.F. Probing the structural and electronic properties of anionic europium-doped silicon clusters by density functional theory and comparison of experimental photoelectron spectroscopy. Chem. Phys. 2020, 538, 110918. [Google Scholar] [CrossRef]
- Fan, Y.W.; Wang, H.Q.; Li, H.F. Structural and electronic properties of exohedrally doped neutral silicon clusters LnSin (n = 5, 10; Ln = Sm, Eu, Yb). Phys. Chem. Chem. Phys. 2020, 22, 20545–20552. [Google Scholar] [CrossRef]
- Fan, Y.W.; Kong, X.Y.; Zhao, L.J.; Wang, H.Q.; Li, H.F.; Zhan, Q.; Xie, B.; Xu, H.G.; Zheng, W.J. A joint experimental and theoretical study on structural, electronic, and magnetic properties of MnGen− (n = 3–14) clusters. J. Chem. Phys. 2021, 154, 204302. [Google Scholar] [CrossRef]
- Xie, B.; Wang, H.Q.; Li, H.F.; Zeng, J.K. Structural and electronic properties of Ln2Si6q: (Sm, Eu, Yb; q = 0, −1) clusters. Chem. Phys. 2023, 566, 111782. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. [Google Scholar] [CrossRef]
- McLean, A.; Chandler, G. Contracted gaussian basis sets for molecular calculations. I. Second row atoms, z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Cao, X.; Dolg, M. Segmented contraction scheme for small-core lanthanide pseudopotential basis sets. J. Molec. Struct. Theochem. 2002, 581, 139–147. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy into a function of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Erratum: Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2004, 121, 11507. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A Gen. Phys. 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, D. Architectures, electronic structures, and stabilities of Cu-doped Gen clusters: Density functional modeling. J. Mol. Model. 2012, 18, 3887–3902. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Chemical content of the kinetic energy density. J. Mol. Struct. THEOCHEM 2000, 527, 51–61. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F.W. Comparison of computational methods for atomic charges. Acta Phys. Chim. Sin. 2012, 28, 1–18. [Google Scholar]
- Lu, T.; Chen, F.W. Meaning and Functional Form of the Electron Localization Function. Acta Phys. Chim. Sin. 2011, 27, 2786–2792. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).