Vibronic and Cationic Features of 2-Fluorobenzonitrile and 3-Fluorobenzonitrile Studied by REMPI and MATI Spectroscopy and Franck–Condon Simulations
Abstract
1. Introduction
2. Results
2.1. Vibronic Features of 2-Fluorobenzonitrile in the S1 State
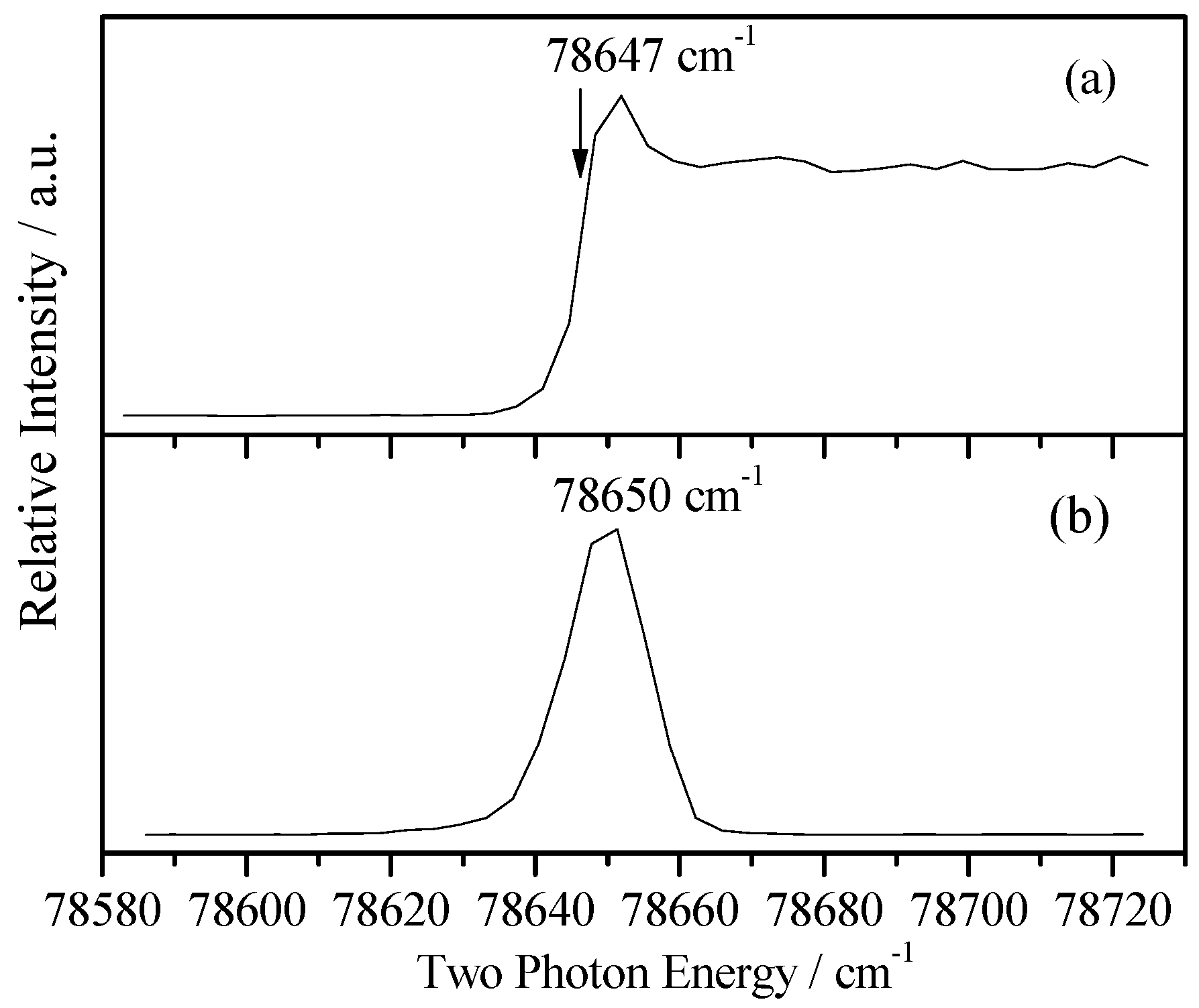
2.2. Photoionization Efficiency (PIE) Spectra of 2FBN
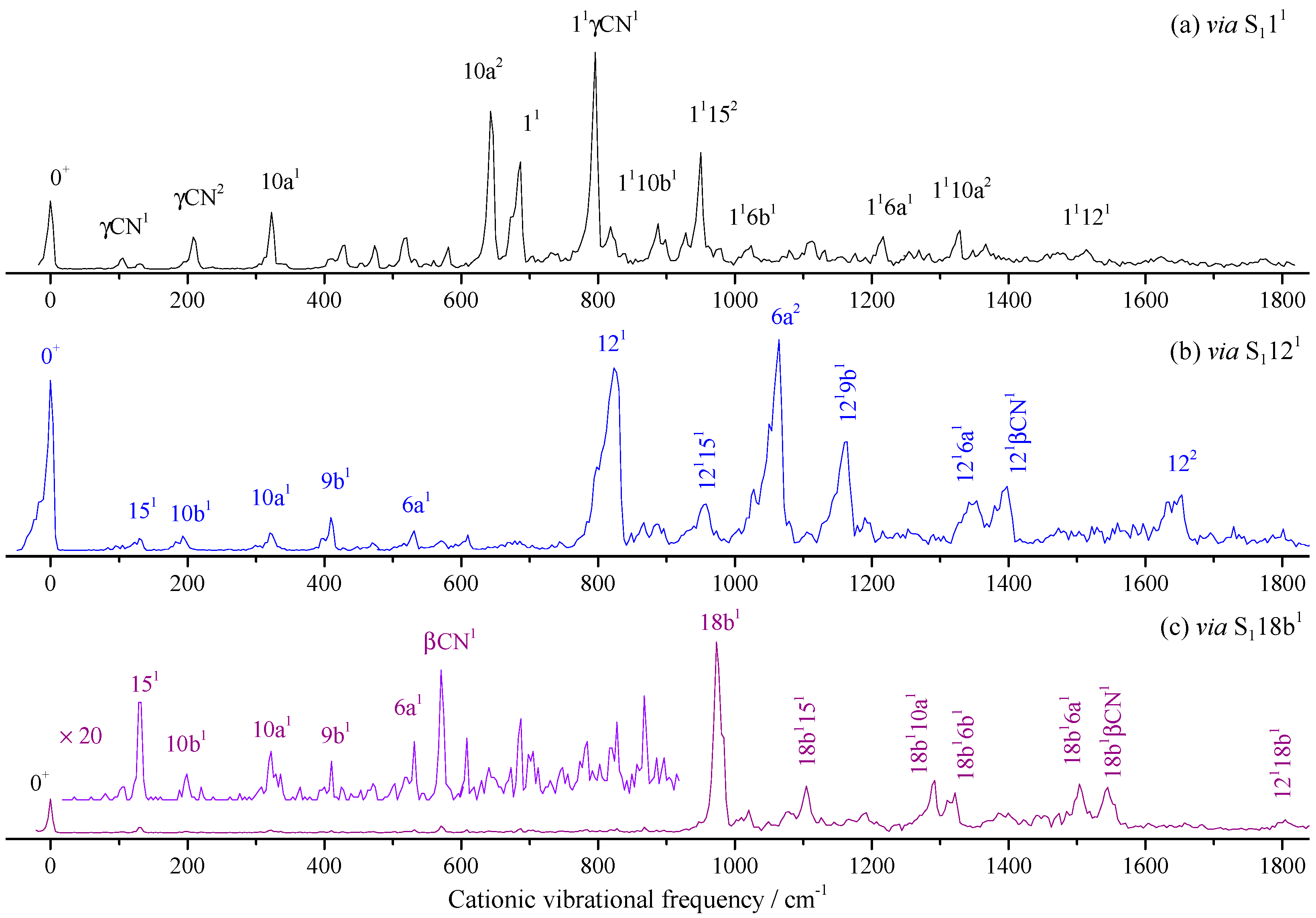
2.3. Cationic Spectra of 2FBN
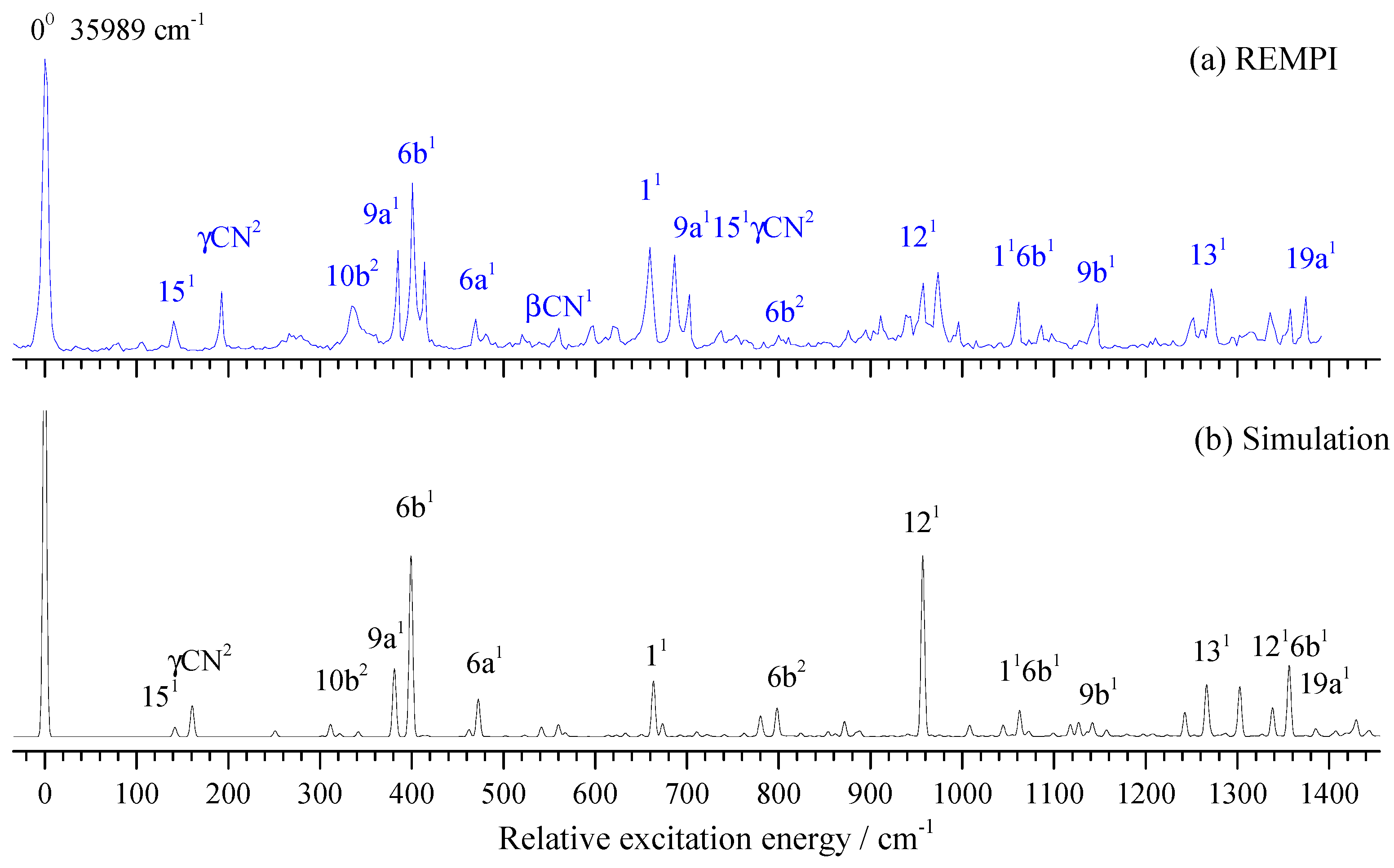
2.4. Vibronic Features of 3-Fluorobenznitrile in the S1 State
2.5. PIE Spectra of 3FBN
2.6. MATI Spectra of 3FBN
3. Discussion
3.1. Breathing Vibrational Band of 2FBN
3.2. Molecular Structure in S0, S1, and D0 States and Vibrational Frequencies
3.3. Substitution Effect on Ionization Energy
4. Materials and Methods
4.1. Experimental Methods
4.2. Theoretical Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Berger, R.; Resnati, G.; Metrangolo, P.; Weber, E.; Hulliger, J. ChemInform Abstract: Organic Fluorine Compounds: A Great Opportunity for Enhanced Materials Properties. ChemInform 2011, 42, 3496–3508. [Google Scholar] [CrossRef]
- Ametamey, S.M.; Honer, M.; Schubiger, P.A. Molecular imaging with PET. Chem. Rev. 2008, 108, 1501–1516. [Google Scholar] [CrossRef]
- Müller, K.; Faeh, C.; Diederich, F. Fluorine in pharmaceuticals: Looking beyond intuition. Science 2007, 317, 1881–1886. [Google Scholar] [CrossRef]
- Jeschke, P. The unique role of fluorine in the design of active ingredients for modern crop protection. Chembiochem 2004, 5, 571–589. [Google Scholar] [CrossRef]
- Krüger, S.; Witte, F.; Helfrich, J.; Grotemeyer, J. Mass-analyzed-threshold-ionization (MATI) spectroscopy of 1,2,3-substituted halogenated benzenes via different intermediate vibrational states in the S1 state. RSC Adv. 2015, 5, 937–948. [Google Scholar] [CrossRef]
- Ling, F.; Li, S.; Song, X.; Tang, Y.; Wang, Y.; Zhang, B. Visualization of coherent nuclear motion between different geometries in photoexcited 2,4-difluorophenol. Phys. Rev. A 2017, 95, 043421. [Google Scholar] [CrossRef]
- Ling, F.; Wang, Y.; Li, S.; Wei, J.; Tang, Y.; Zhang, B. Imaging Reversible and Irreversible Structural Evolution in Photoexcited 2,4-Difluoroaniline. J. Phys. Chem. Lett. 2018, 9, 5468–5473. [Google Scholar] [CrossRef]
- Sun, W.; Lozada, I.B.; van Wijngaarden, J. Fourier Transform Microwave Spectroscopic and ab Initio Study of the Rotamers of 2-Fluorobenzaldehyde and 3-Fluorobenzaldehyde. J. Phys. Chem. A 2018, 122, 2060–2068. [Google Scholar] [CrossRef]
- Sun, W.; van Wijngaarden, J. Structural elucidation of 2-fluorothiophenol from Fourier transform microwave spectra and ab initio calculations. J. Mol. Struct. 2017, 1144, 496–501. [Google Scholar] [CrossRef]
- Kamaee, M.; Sun, M.; Luong, H.; van Wijngaarden, J. Investigation of Structural Trends in Mono-, Di-, and Pentafluorobenzonitriles Using Fourier Transform Microwave Spectroscopy. J. Phys. Chem. A 2015, 119, 10279–10292. [Google Scholar] [CrossRef]
- Zhang, B.; Li, C.; Su, H.; Lin, J.L.; Tzeng, W.B. Mass analyzed threshold ionization spectroscopy of p-fluorophenol cation and the p-fluoro substitution effect. Chem. Phys. Lett. 2004, 390, 65–70. [Google Scholar] [CrossRef]
- Huang, J.; Huang, K.; Liu, S.; Luo, Q.; Tzeng, W. Vibrational spectra and theoretical calculations of p-chlorophenol in the electronically excited S1 and ionic ground D0 states. J. Photochem. Photobiol. A Chem. 2008, 193, 245–253. [Google Scholar] [CrossRef]
- Ratzer, C.; Nispel, M.; Schmitt, M. Structure of 4-fluorophenol and barrier to internal –OH rotation in the S1-state. Phys. Chem. Chem. Phys. 2003, 5, 812–819. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, S.; Cheng, M.; Du, Y.; Zhu, Q. Vibrational Spectra and Theoretical Calculations of cis- and trans-3-Fluoro-N-methylaniline in the Neutral (S0) and Cationic (D0) Ground States. J. Phys. Chem. A 2016, 120, 81–94. [Google Scholar] [CrossRef]
- Arivazhagan, M.; Meenakshi, R.; Prabhakaran, S. Vibrational spectroscopic investigations, first hyperpolarizability, HOMO-LUMO and NMR analyzes of p-fluorobenzonitrile. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2013, 102, 59–65. [Google Scholar] [CrossRef]
- Da Ribeiro Silva, M.A.V.; Monte, M.J.S.; Rocha, I.M.; Cimas, A. Energetic study applied to the knowledge of the structural and electronic properties of monofluorobenzonitriles. J. Org. Chem. 2012, 77, 4312–4322. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Jaman, A.I. Centrifugal distortion analysis of the millimeter-wave spectrum of 2-fluorobenzonitrile and ab initio DFT calculations. J. Mol. Spectrosc. 2006, 236, 70–74. [Google Scholar] [CrossRef]
- Kumar, A.P.; Rao, G.R. Vibrational analysis of substituted benzonitriles. I. Vibrational spectra, normal coordinate analysis and transferability of force constants of monohalogenated benzonitriles. Spectrochim. Acta A Mol. Biomol. Spectrosc. 1997, 53A, 2023–2032. [Google Scholar] [CrossRef]
- Palmer, M.H.; Moyes, W.; Spiers, M. The electronic structure of substituted benzenes: Ab initio calculations and photoelectron spectra for benzonitrile, the tolunitriles, fluorobenzonitriles, dicyanobenzenes and ethynylbenzene. J. Mol. Struct. 1980, 62, 165–187. [Google Scholar] [CrossRef]
- Jiang, S.; Levy, D.H. Supersonic Jet Studies on the Photophysics of Substituted Benzenes and Naphthalenes. J. Phys. Chem. A 2002, 106, 8590–8598. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, Y.; Hao, J.; Yang, Y.; Li, C.; Jia, S. Resonance enhanced multiphoton ionization and mass analyzed threshold ionization spectroscopy of 4-fluorobenzonitrile. Chem. Phys. Lett. 2018, 711, 127–131. [Google Scholar] [CrossRef]
- Eom, S.Y.; Lee, Y.R.; Kwon, C.H. Accurate conformational stability and cationic structure of piperidine determined by conformer-specific VUV-MATI spectroscopy. Phys. Chem. Chem. Phys. 2020, 22, 22823–22832. [Google Scholar] [CrossRef] [PubMed]
- Park, S.M.; Lee, Y.R.; Kwon, C.H. Conformational Structures of Neutral and Cationic Pivaldehyde Revealed by IR-Resonant VUV-MATI Mass Spectroscopy. Int. J. Mol. Sci. 2022, 23, 14777. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.R.; Kwon, C.H. Valence molecular orbitals and cationic structures of 2-fluoropyridine by high-resolution ion spectroscopy and Franck-Condon fitting. J. Chem. Phys. 2022, 157, 154306. [Google Scholar] [CrossRef]
- Lee, Y.R.; Kwon, C.H. Innovative mass spectrometer for high-resolution ion spectroscopy. J. Chem. Phys. 2021, 155, 164203. [Google Scholar] [CrossRef]
- Eom, S.Y.; Lee, Y.R.; Park, S.M.; Kwon, C.H. Determination of the highest occupied molecular orbital and conformational structures of morpholine based on its conformer-specific photoionization dynamics. Phys. Chem. Chem. Phys. 2022, 24, 28477–28485. [Google Scholar] [CrossRef]
- Eom, S.Y.; Kang, D.W.; Kwon, C.H. Conformational structure of cationic tetrahydropyran by one-photon vacuum ultraviolet mass-analyzed threshold ionization spectroscopy. Phys. Chem. Chem. Phys. 2021, 23, 1414–1423. [Google Scholar] [CrossRef]
- Lee, Y.R.; Kim, H.L.; Kwon, C.H. Determination of the cationic conformational structure of tetrahydrothiophene by one-photon MATI spectroscopy and Franck-Condon fitting. Phys. Chem. Chem. Phys. 2020, 22, 6184–6191. [Google Scholar] [CrossRef]
- Kang, D.W.; Yoon, D.K.; Kwon, C.H. Conformational potential energy surfaces and cationic structure of 3,4-dihydro-2H-pyran by VUV-MATI spectroscopy and Franck-Condon fitting. Phys. Chem. Chem. Phys. 2020, 22, 27673–27680. [Google Scholar] [CrossRef]
- Ketkov, S.Y.; Tzeng, S.-Y.; Rychagova, E.A.; Markin, G.V.; Makarov, S.G.; Tzeng, W.-B. Laser spectroscopic and computational insights into unexpected structural behaviours of sandwich complexes upon ionization. Dalton Trans. 2021, 50, 10729–10736. [Google Scholar] [CrossRef]
- Ketkov, S.; Tzeng, S.-Y.; Rychagova, E.; Tzeng, W.-B. Ionization of Decamethylmanganocene: Insights from the DFT-Assisted Laser Spectroscopy. Molecules 2022, 27, 6226. [Google Scholar] [CrossRef] [PubMed]
- Ketkov, S.Y.; Tzeng, S.Y.; Rychagova, E.A.; Kalakutskaya, L.V.; Fuss, M.; Braunschweig, H.; Tzeng, W.-B. Rydberg state mediated multiphoton ionization of (η7-C7H7)(η5-C5H5)Cr: DFT-supported experimental insights into the molecular and electronic structures of excited sandwich complexes. Phys. Chem. Chem. Phys. 2019, 21, 9665–9671. [Google Scholar] [CrossRef] [PubMed]
- Ketkov, S.Y.; Rychagova, E.A.; Tzeng, S.-Y.; Tzeng, W.-B. TD DFT insights into unusual properties of excited sandwich complexes: Structural transformations and vibronic interactions in Rydberg-state bis(η6-benzene)chromium. Phys. Chem. Chem. Phys. 2018, 20, 23988–23997. [Google Scholar] [CrossRef] [PubMed]
- Ketkov, S.Y.; Tzeng, S.-Y.; Wu, P.-Y.; Markin, G.V.; Tzeng, W.-B. DFT-Supported Threshold Ionization Study of Chromium Biphenyl Complexes: Unveiling the Mechanisms of Substituent Influence on Redox Properties of Sandwich Compounds. Chemistry 2017, 23, 13669–13675. [Google Scholar] [CrossRef] [PubMed]
- Ketkov, S.Y.; Markin, G.V.; Tzeng, S.Y.; Tzeng, W.B. Fine Substituent Effects in Sandwich Complexes: A Threshold Ionization Study of Monosubstituted Chromium Bisarene Compounds. Chemistry 2016, 22, 4690–4694. [Google Scholar] [CrossRef]
- Tzeng, S.Y.; Takahashi, K.; Tzeng, W.B. Two-Color Resonant Two-Photon Mass-Analyzed Threshold Ionization of 2,4-Difluoroanisole and the Additivity Relation of Ionization Energy. J. Phys. Chem. A 2020, 124, 10517–10526. [Google Scholar] [CrossRef]
- Kemp, D.J.; Whalley, L.E.; Tuttle, W.D.; Gardner, A.M.; Speake, B.T.; Wright, T.G. Vibrations of the p-chlorofluorobenzene cation. Phys. Chem. Chem. Phys. 2018, 20, 12503–12516. [Google Scholar] [CrossRef]
- Davies, A.R.; Kemp, D.J.; Wright, T.G. Electronic, vibrational, and torsional couplings in N-methylpyrrole: Ground, first excited, and cation states. J. Chem. Phys. 2021, 154, 224305. [Google Scholar] [CrossRef]
- Kemp, D.J.; Gardner, A.M.; Tuttle, W.D.; Midgley, J.; Reid, K.L.; Wright, T.G. Identifying complex Fermi resonances in p-difluorobenzene using zero-electron-kinetic-energy (ZEKE) spectroscopy. J. Chem. Phys. 2018, 149, 094301. [Google Scholar] [CrossRef]
- Davies, A.R.; Kemp, D.J.; Wright, T.G. Comment on “Electronic, vibrational and torsional couplings in N-methylpyrrole: Ground, first excited and cation states” [J. Chem. Phys. 154, 224305 (2021)]. J. Chem. Phys. 2021, 155, 117101. [Google Scholar] [CrossRef]
- Kemp, D.J.; Fryer, E.F.; Davies, A.R.; Wright, T.G. Vibration-modified torsional potentials and vibration-torsion (“vibtor”) levels in the m-fluorotoluene cation. J. Chem. Phys. 2019, 151, 084311. [Google Scholar] [CrossRef] [PubMed]
- Davies, A.R.; Kemp, D.J.; Warner, L.G.; Fryer, E.F.; Rees, A.; Wright, T.G. Variations in Duschinsky rotations in m-fluorotoluene and m-chlorotoluene during excitation and ionization. J. Chem. Phys. 2020, 152, 214303. [Google Scholar] [CrossRef] [PubMed]
- Varsányi, G. Assignments for Vibrational Spectra of Seven Hundred Benzene Derivatives; Adam Hilger: London, UK, 1974; ISBN 0852742835. [Google Scholar]
- Wilson, E.B. The Normal Modes and Frequencies of Vibration of the Regular Plane Hexagon Model of the Benzene Molecule. Phys. Rev. 1934, 45, 706–714. [Google Scholar] [CrossRef]
- Asmis, K.R.; Yang, Y.; Santambrogio, G.; Brümmer, M.; Roscioli, J.R.; McCunn, L.R.; Johnson, M.A.; Kühn, O. Gas-phase infrared spectroscopy and multidimensional quantum calculations of the protonated ammonia dimer N2H7+. Angew. Chem. Int. Ed. Engl. 2007, 46, 8691–8694. [Google Scholar] [CrossRef]
- Yang, Y.; Kuhn, O. A concise method for kinetic energy quantisation. Mol. Phys. 2008, 106, 2445–2457. [Google Scholar] [CrossRef]
- Davies, A.R.; Kemp, D.J.; Wright, T.G. Unpicking vibration-vibration and vibration-torsion interactions in m-fluorotoluene. J. Mol. Spectrosc. 2021, 381, 111522. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, D.; Dong, C.; Cheng, M.; Hu, L.; Zhou, Z.; Du, Y.; Zhu, Q.; Zhang, C. Rotamers and isotopomers of 3-chloro-5-fluoroanisole studied by resonant two-photon ionization spectroscopy and theoretical calculations. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2013, 104, 235–242. [Google Scholar] [CrossRef]
- Xu, Y.; Tzeng, S.Y.; Shivatare, V.; Takahashi, K.; Zhang, B.; Tzeng, W.B. Identification of four rotamers of m-methoxystyrene by resonant two-photon ionization and mass analyzed threshold ionization spectroscopy. J. Chem. Phys. 2015, 142, 124314. [Google Scholar] [CrossRef]
- Xu, Y.; Tzeng, S.Y.; Zhang, B.; Tzeng, W.B. Rotamers of 3,4-difluoroanisole studied by two-color resonant two-photon mass-analyzed threshold ionization spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2013, 102, 365–370. [Google Scholar] [CrossRef]
- Huang, W.C.; Huang, P.S.; Hu, C.H.; Tzeng, W.B. Vibronic and cation spectroscopy of 2,4-difluoroaniline. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2012, 93, 176–179. [Google Scholar] [CrossRef]
- Shivatare, V.S.; Kundu, A.; Patwari, G.N.; Tzeng, W.B. Studies of structural isomers o-, m-, and p-fluorophenylacetylene by two-color resonant two-photon mass-analyzed threshold ionization spectroscopy. J. Phys. Chem. A 2014, 118, 8277–8286. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lin, J.L.; Tzeng, W.B. Mass-analyzed threshold ionization spectroscopy of the rotamers of p-n-propylphenol cations and configuration effect. J. Chem. Phys. 2005, 122, 44311. [Google Scholar] [CrossRef] [PubMed]
- Neuhauser, R.G.; Siglow, K.; Neusser, H.J. High n Rydberg spectroscopy of benzene: Dynamics, ionization energy and rotational constants of the cation. J. Chem. Phys. 1997, 106, 896–907. [Google Scholar] [CrossRef]
- Lembach, G.; Brutschy, B. Fragmentation energetics and dynamics of fluorobenzene⋅Arn (n = 1–3) clusters studied by mass analyzed threshold ionization spectroscopy. J. Chem. Phys. 1997, 107, 6156–6165. [Google Scholar] [CrossRef]
- Araki, M.; Sato, S.; Kimura, K. Two-Color Zero Kinetic Energy Photoelectron Spectra of Benzonitrile and Its van der Waals Complexes with Argon. Adiabatic Ionization Potentials and Cation Vibrational Frequencies. J. Phys. Chem. 1996, 100, 10542–10546. [Google Scholar] [CrossRef]
- Dopfer, O.; Müller-Dethlefs, K. S1 excitation and zero kinetic energy spectra of partly deuterated 1:1 phenol–water complexes. J. Chem. Phys. 1994, 101, 8508–8516. [Google Scholar] [CrossRef]
- Yuan, L.; Li, C.; Lin, J.L.; Yang, S.C.; Tzeng, W.B. Mass analyzed threshold ionization spectroscopy of o-fluorophenol and o-methoxyphenol cations and influence of the nature and relative location of substituents. Chem. Phys. 2006, 323, 429–438. [Google Scholar] [CrossRef]
- Oikawa, A.; Abe, H.; Mikami, N.; Ito, M. Electronic spectra and ionization potentials of rotational isomers of several disubstituted benzenes. Chem. Phys. Lett. 1985, 116, 50–54. [Google Scholar] [CrossRef]
- Yosida, K.; Suzuki, K.; Ishiuchi, S.; Sakai, M.; Fujii, M.; Dessent, C.E.H.; Müller-Dethlefs, K. The PFI-ZEKE photoelectron spectrum of m-fluorophenol and its aqueous complexes: Comparing intermolecular vibrations in rotational isomers. Phys. Chem. Chem. Phys. 2002, 4, 2534–2538. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, Y.; Hao, J.; Yang, Y.; Wang, L.; Li, C.; Jia, S. Rotamers of p-isopropylphenol studied by hole-burning resonantly enhanced multiphoton ionization and mass analyzed threshold ionization spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2019, 207, 328–336. [Google Scholar] [CrossRef]
- Li, N.; Li, S.; Wang, L.; Wang, H.; Zhao, J.; Li, C. Vibrational spectra of 2-cyanophenol cation studied by the mass analyzed threshold ionization technique. Chem. Phys. Lett. 2022, 792, 139402. [Google Scholar] [CrossRef]
- Hao, J.; Duan, C.; Yang, Y.; Li, C.; Jia, S. Resonance enhanced two-photon ionization and mass analyzed threshold ionization spectroscopy of 4-ethylanisole. J. Mol. Spectrosc. 2020, 369, 111258. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Baiardi, A.; Bloino, J.; Barone, V. General Time Dependent Approach to Vibronic Spectroscopy Including Franck-Condon, Herzberg-Teller, and Duschinsky Effects. J. Chem. Theory Comput. 2013, 9, 4097–4115. [Google Scholar] [CrossRef] [PubMed]

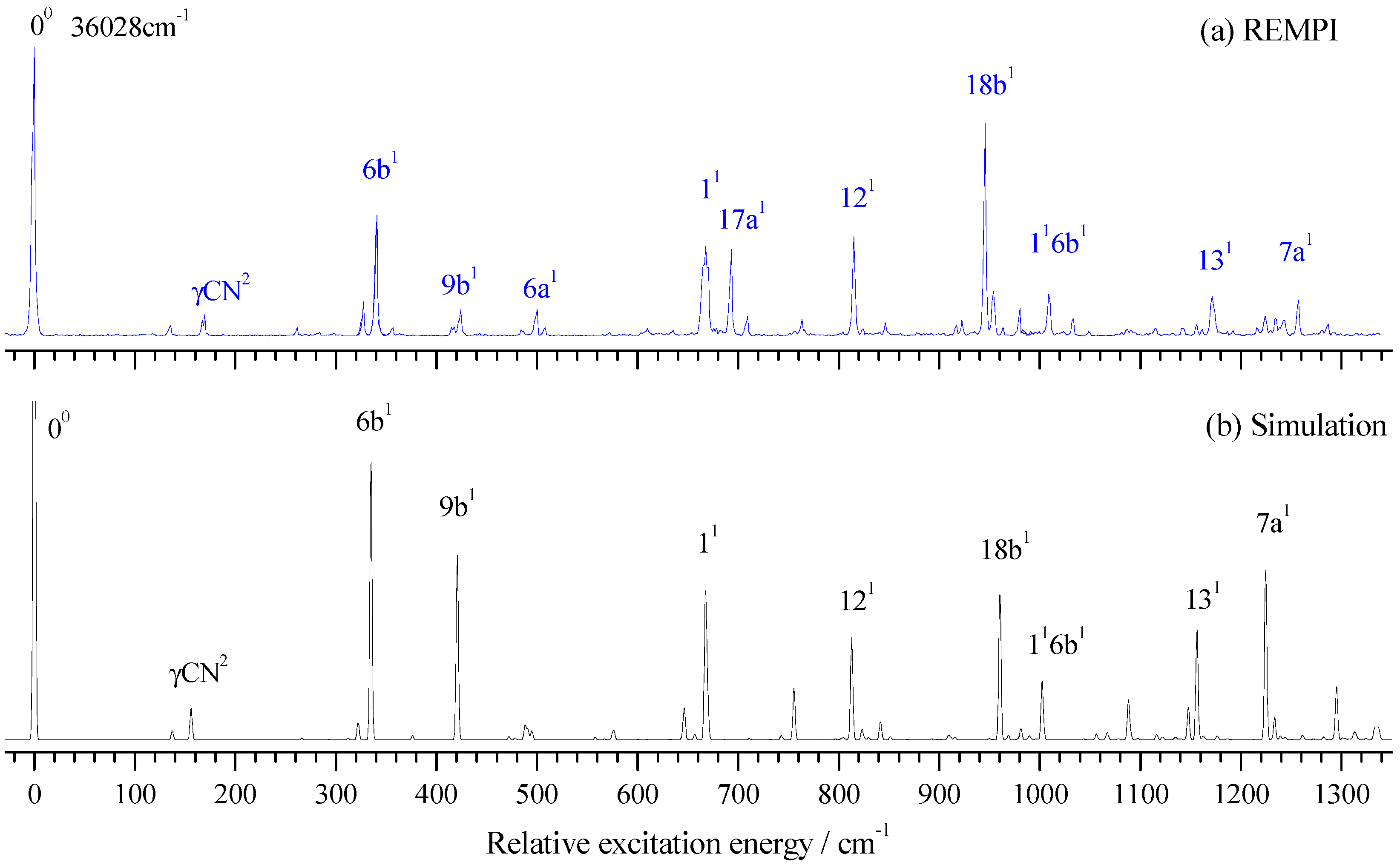


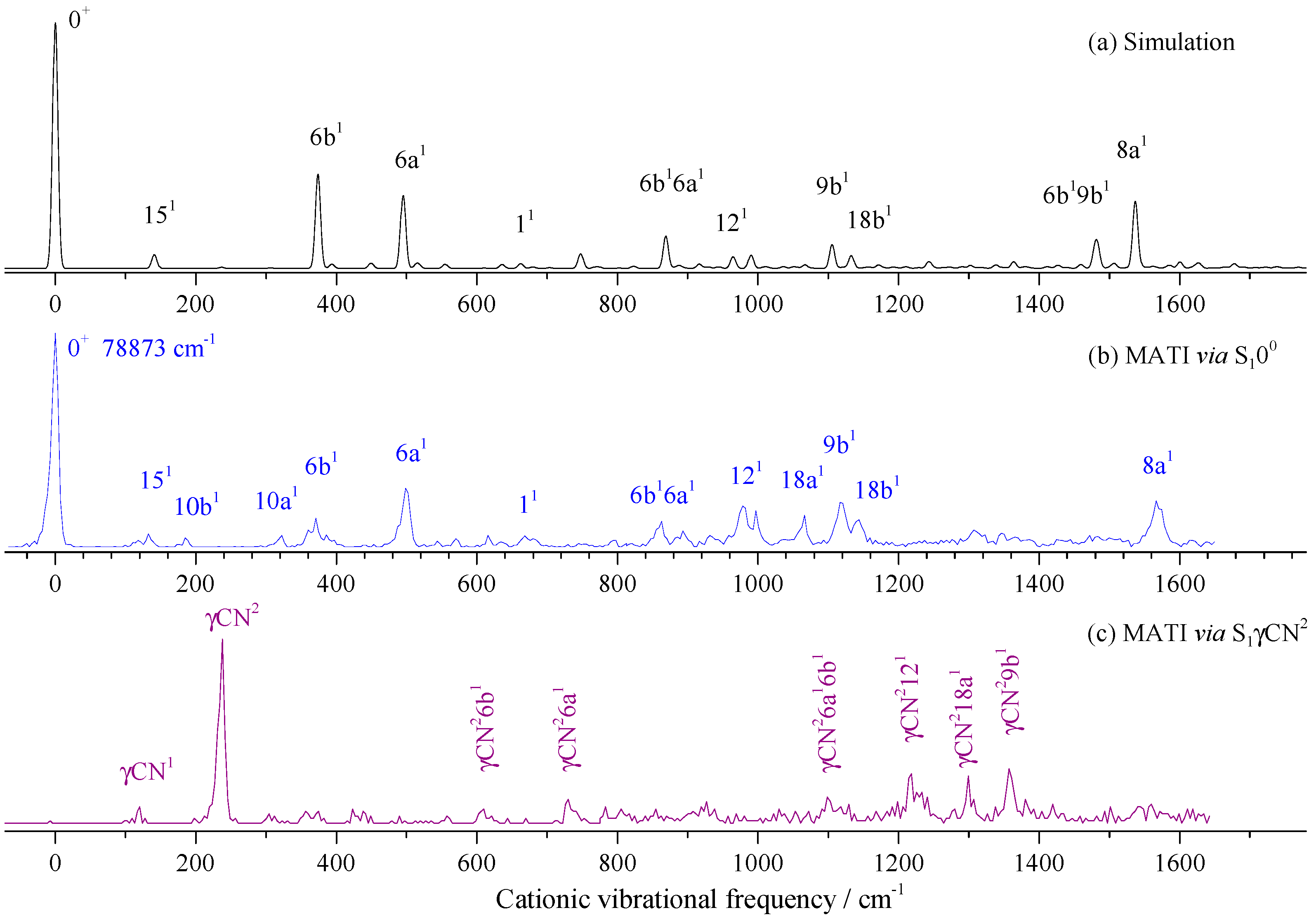
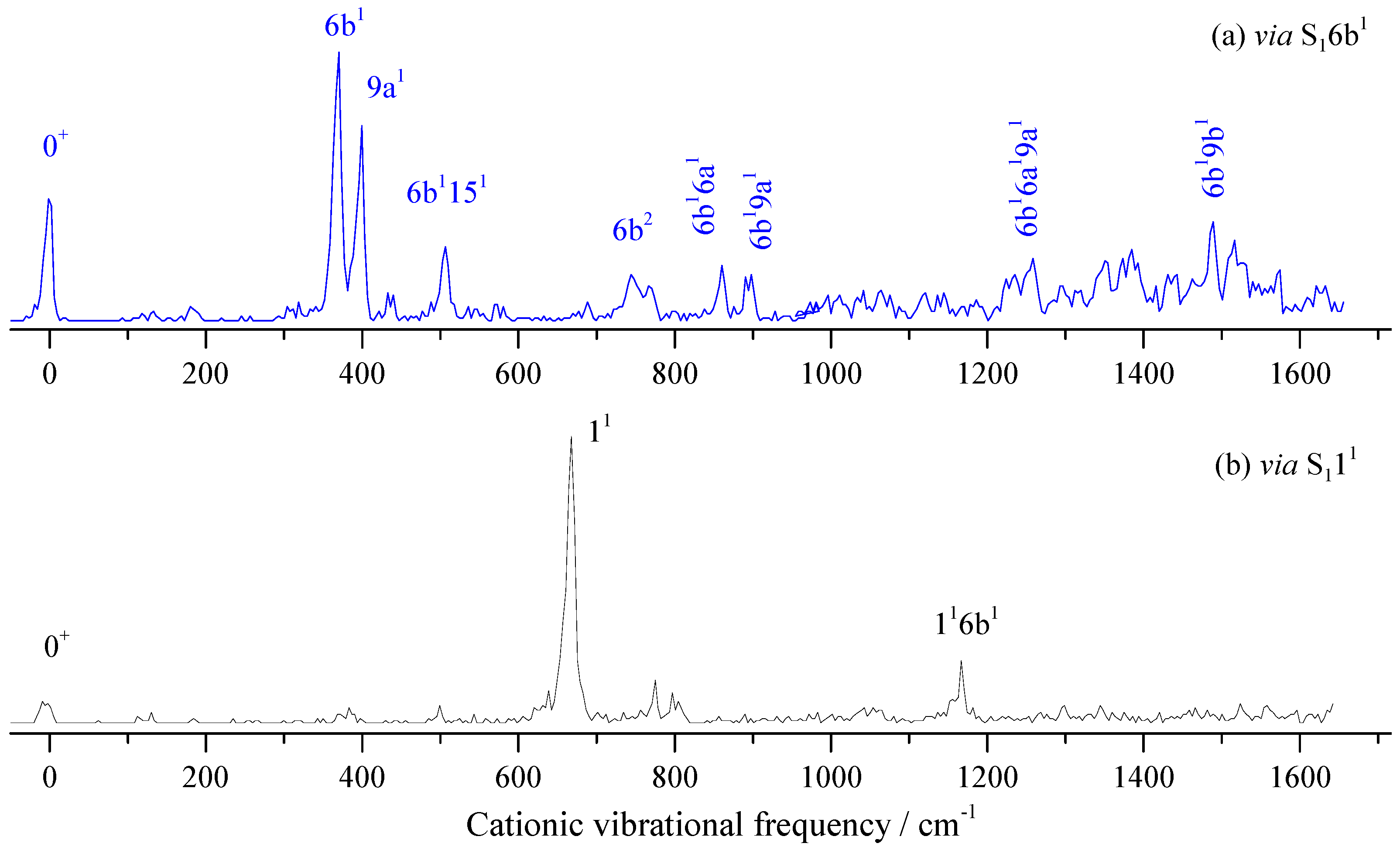
| Transition Energy (cm−1) | Relative Intensity | Shift (cm−1) | Calc. (cm−1) | Assignment b |
|---|---|---|---|---|
| 36,028 | 100 | 0 | 0 | 00 |
| 36,164 | 4 | 136 | 137 | 151 |
| 36,198 | 7 | 170 | 156 | γCN2 |
| 36,290 | 3 | 262 | 10b1γCN1 | |
| 36,356 | 12 | 328 | 10a1γCN1 | |
| 36,369 | 42 | 341 | 335 | 6b1 |
| 36,452 | 9 | 424 | 421 | 9b1 |
| 36,528 | 9 | 500 | 495 | 6a1 |
| 36,638 | 3 | 610 | 16a110b1 | |
| 36,663 | 31 | 635 | 646 | 16b2 |
| 36,696 | 30 | 668 | 668 | 11 |
| 36,721 | 30 | 693 | 698 | 17a1 |
| 36,738 | 7 | 710 | 711 | 6b110b2 |
| 36,792 | 6 | 764 | 755 | 9b16b1 |
| 36,843 | 34 | 815 | 813 | 121 |
| 36,874 | 2 | 846 | 841 | 9b2 |
| 36,945 | 4 | 917 | 910 | βCN16b1 |
| 36,950 | 5 | 922 | 916 | 6a19b1 |
| 36,974 | 74 | 946 | 960 | 18b1 |
| 36,982 | 15 | 954 | 969 | 121γCN2 |
| 37,008 | 10 | 980 | 981 | 6b116b2 |
| 37,037 | 14 | 1009 | 1003 | 116b1 |
| 37,062 | 6 | 1034 | 1022 | 16b210b2 |
| 37,199 | 14 | 1171 | 1156 | 131 |
| 37,285 | 12 | 1257 | 1224 | 7a1 |
| 37,315 | 4 | 1287 | 1295 | 18b16b1 |
| Intermediate Levels in the S1 State | Calc. | Assignment b | ||||
|---|---|---|---|---|---|---|
| 00 | 6b1 | 11 | 121 | 18b1 | ||
| 106 | 106 | 104 | γCN1 | |||
| 131 | 130 | 132 | 139 | 151 | ||
| 197 | 193 | 199 | 205 | 10b1 | ||
| 209 | γCN2 | |||||
| 323 | 321 | 322 | 335 | 10a1 | ||
| 333 | 335 | 341 | 6b1 | |||
| 407 | 408 | 409 | 410 | 410 | 9b1 | |
| 430 | 6b1γCN1 | |||||
| 466 | 6b1151 | |||||
| 474 | 473 | 152γCN2 | ||||
| 520 | 10a110b1 | |||||
| 530 | 531 | 532 | 547 | 6a1 | ||
| 532 | 6b110b1 | |||||
| 582 | 6b1151γCN1 | |||||
| 643 | 10a2 | |||||
| 571 | 570 | 571 | 584 | βCN1 | ||
| 672 | 672 | 6b2 | ||||
| 683 | 687 | 687 | 696 | 11 | ||
| 698 | 16a110b1 | |||||
| 746 | 6b19b1 | |||||
| 796 | 11γCN1 | |||||
| 818 | 11151 | |||||
| 826 | 823 | 826 | 121 | |||
| 865 | 6b16a1 | |||||
| 888 | 1110b1 | |||||
| 906 | 6b1βCN1 | |||||
| 950 | 11152 | |||||
| 955 | 121151 | |||||
| 972 | 973 | 976 | 18b1 | |||
| 1023 | 116b1 | |||||
| 1036 | 6b3 | |||||
| 1059 | 1064 | 6a2 | ||||
| 1104 | 18b1151 | |||||
| 1164 | 1160 | 6b1121 | ||||
| 1217 | 116a1 | |||||
| 1268 | 1271 | 7a1 | ||||
| 1292 | 18b110a1 | |||||
| 1316 | 1321 | 6b118b1 | ||||
| 1329 | 1110a2 | |||||
| 1349 | 1216a1 | |||||
| 1394 | 121βCN1 | |||||
| 1396 | 1410 | 121βCN1 | ||||
| 1466 | 1466 | 19b1 | ||||
| 1503 | 18b16a1 | |||||
| 1513 | 11121 | |||||
| 1545 | 18b1βCN1 | |||||
| 1555 | 1551 | 8b1 | ||||
| 1607 | 6b17a1 | |||||
| 1646 | 122 | |||||
| Transition Energy | Exp. | Relative Intensity | Calc. a | Assignment b |
|---|---|---|---|---|
| 35,989 | 0 | 100 | 00, band origin | |
| 36,129 | 140 | 11 | 142 | 151 |
| 36,182 | 193 | 21 | 171 | γ(CN)2 |
| 36,255 | 266 | 7 | 251 | 10b1γ(CN)1 |
| 36,324 | 335 | 16 | 342 | 10b2 |
| 36,374 | 385 | 35 | 381 | 9a1, β(C-F) |
| 36,390 | 401 | 58 | 399 | 6b1, β(CCC) |
| 36,403 | 414 | 31 | 417 | 10b1γ(CN)3 |
| 36,459 | 470 | 11 | 473 | 6a1, β(CCC) |
| 36,469 | 480 | 6 | 484 | 10b2151 |
| 36,509 | 520 | 6 | 523 | 9a1151 |
| 36,549 | 560 | 9 | 567 | βCN |
| 36,584 | 595 | 9 | 593 | 10b3γ(CN)1 |
| 36,611 | 622 | 9 | 623 | 10a2γ(CN)2 |
| 36,649 | 660 | 36 | 663 | 11, breather |
| 36,675 | 686 | 33 | 684 | 9a1151γ(CN)2 |
| 36,692 | 703 | 20 | 709 | 151β(CN)1 |
| 36,727 | 738 | 8 | 741 | 6b110b2 |
| 36,789 | 800 | 6 | 798 | 6b2 |
| 36,864 | 875 | 8 | 872 | 6a16b1 |
| 36,900 | 911 | 13 | 915 | 1110b1γ(CN)1 |
| 36,927 | 938 | 13 | 940 | 6b2151 |
| 36,947 | 958 | 24 | 957 | 121 |
| 36,963 | 974 | 27 | 975 | 1110a1γ(CN)1 |
| 36,985 | 996 | 11 | 996 | 6a19a1151 |
| 37,051 | 1062 | 17 | 1063 | 116b1 |
| 37,075 | 1086 | 9 | 1087 | 416a1γ(CN)1 |
| 37,136 | 1147 | 17 | 1142 | 9b1 |
| 37,241 | 1252 | 12 | 1253 | 6a16b19a1 |
| 37,260 | 1271 | 22 | 1266 | 131 |
| 37,304 | 1315 | 7 | 1314 | 1116b116b1 |
| 37,324 | 1335 | 14 | 1338 | 1219a1 |
| 37,347 | 1358 | 15 | 1356 | 1216b1 |
| 37,363 | 1374 | 19 | 1385 | 19a1 |
| Intermediate Levels in the S1 State | Calc. | Assignment b | |||
|---|---|---|---|---|---|
| 00 | γ(CN)2 | 6b1 | 11 | ||
| 120 | 118 | γ(CN)1 | |||
| 133 | 141 | 151 | |||
| 238 | 237 | γ(CN)2 | |||
| 185 | 188 | 10b1 | |||
| 322 | 331 | 10a1 | |||
| 371 | 370 | 374 | 6b1, β(CCC) | ||
| 399 | 394 | 9a1 | |||
| 498 | 495 | 6a1, β(CCC) | |||
| 506 | 6b1151 | ||||
| 609 | γ(CN)26b1 | ||||
| 615 | 605 | 16a1 | |||
| 668 | 668 | 679 | 11, breathing | ||
| 688 | 6b110b1151 | ||||
| 730 | γ(CN)26a1 | ||||
| 744 | 6b2 | ||||
| 775 | 4110b1 | ||||
| 803 | 11151 | ||||
| 863 | 860 | 6b16a1 | |||
| 893 | 894 | 6a19a1 | |||
| 978 | 965 | 121, β(CCC) | |||
| 997 | 990 | 6a2 | |||
| 1066 | 1067 | 18a1, β(CH) | |||
| 1098 | γ(CN)26a16b1 | ||||
| 1117 | 1105 | 9b1, β(CH) | |||
| 1144 | 1133 | 18b1, β(CH) | |||
| 1166 | 116b1 | ||||
| 1218 | γ(CN)2121 | ||||
| 1235 | 6b26a1 | ||||
| 1258 | 6b16a19a1 | ||||
| 1299 | γ(CN)218a1 | ||||
| 1307 | 1302 | 131, β(CH) | |||
| 1350 | 6b1121 | ||||
| 1357 | γ(CN)29b1 | ||||
| 1374 | 6b16a2 | ||||
| 1385 | 1382 | 19a1 | |||
| 1489 | 6b19b1 | ||||
| 1566 | 1537 | 8a1, ν(CC) | |||
| 1516 | 6b118b1 | ||||
| 1574 | 6b118a1151 | ||||
| S0 | S1 | D0 | Δ(S1 − S0) | Δ(D0 − S1) | Δ(D0 − S0) | |
|---|---|---|---|---|---|---|
| Bond length (Å) | ||||||
| C1−C2 | 1.396 | 1.436 | 1.455 | 0.040 | 0.019 | 0.059 |
| C2−C3 | 1.381 | 1.406 | 1.393 | 0.025 | −0.013 | 0.012 |
| C3−C4 | 1.389 | 1.409 | 1.372 | 0.020 | −0.037 | −0.017 |
| C4−C5 | 1.392 | 1.408 | 1.434 | 0.016 | 0.026 | 0.042 |
| C5−C6 | 1.385 | 1.421 | 1.386 | 0.036 | −0.035 | 0.001 |
| C6−C1 | 1.401 | 1.424 | 1.391 | 0.023 | −0.033 | −0.010 |
| C1−C11 | 1.427 | 1.395 | 1.407 | −0.032 | 0.012 | −0.020 |
| C11−N12 | 1.152 | 1.165 | 1.158 | 0.013 | −0.007 | 0.006 |
| C2−F13 | 1.341 | 1.324 | 1.296 | −0.017 | −0.028 | −0.045 |
| Bond angle (°) | ||||||
| C1−C2−C3 | 122.0 | 124.7 | 122.5 | 2.7 | −2.2 | 0.5 |
| C2−C3−C4 | 118.8 | 119.0 | 117.5 | 0.2 | −1.5 | −1.3 |
| C3−C4−C5 | 120.5 | 118.1 | 121.1 | −2.4 | 3.0 | 0.6 |
| C4−C5−C6 | 120.0 | 122.7 | 121.4 | 2.7 | −1.3 | 1.4 |
| C5−C6−C1 | 120.4 | 120.6 | 119.0 | 0.2 | −1.6 | −1.4 |
| C6−C1−C2 | 118.3 | 114.9 | 118.4 | −3.4 | 3.5 | 0.1 |
| S0 | S1 | D0 | Δ(S1 − S0) | Δ(D0 − S1) | Δ(D0 − S0) | |
|---|---|---|---|---|---|---|
| Bond length (Å) | ||||||
| C1−C2 | 1.398 | 1.425 | 1.380 | 0.026 | −0.045 | −0.018 |
| C2−C3 | 1.380 | 1.413 | 1.393 | 0.033 | −0.019 | 0.013 |
| C3−C4 | 1.384 | 1.406 | 1.433 | 0.022 | 0.027 | 0.049 |
| C4−C5 | 1.390 | 1.404 | 1.374 | 0.014 | −0.029 | −0.016 |
| C5−C6 | 1.387 | 1.411 | 1.395 | 0.024 | −0.016 | 0.008 |
| C6−C1 | 1.398 | 1.438 | 1.449 | 0.039 | 0.010 | 0.051 |
| C1−C11 | 1.430 | 1.397 | 1.415 | −0.033 | 0.017 | −0.015 |
| C11−N12 | 1.152 | 1.165 | 1.155 | 0.013 | −0.009 | 0.003 |
| C2−F13 | 1.346 | 1.330 | 1.300 | −0.016 | −0.030 | −0.046 |
| Bond angle (°) | ||||||
| C1−C2−C3 | 118.2 | 118.4 | 116.9 | 0.2 | −1.4 | −1.3 |
| C2−C3−C4 | 122.5 | 125.2 | 123.4 | 2.7 | −1.7 | 0.9 |
| C3−C4−C5 | 118.5 | 115.9 | 118.8 | −2.6 | 2.9 | 0.3 |
| C4−C5−C6 | 120.6 | 121.1 | 119.2 | 0.4 | −1.9 | −1.4 |
| C5−C6−C1 | 119.6 | 122.2 | 120.9 | 2.6 | −1.3 | 1.3 |
| C6−C1−C2 | 120.4 | 116.9 | 120.5 | −3.4 | 3.5 | 0.1 |
| Molecule | IE | ΔIE | Molecule | IE | ΔIE |
|---|---|---|---|---|---|
| Benzene a | 74,557 | 0 | Benzonitrile c | 78,490 | 0 |
| Fluorobenzene b | 74,227 | −330 | 2-Fluorobenzonitrile d | 78,650 | 160 |
| Benzonitrile c | 78,490 | 3933 | 3-Fluorobenzonitrile d | 78,873 | 383 |
| 4-Fluorobenzonitrile e | 78,000 | −490 | |||
| Phenol f | 68,625 | 0 | |||
| 2-Fluorophenol g | 70,006 | 1381 | Fluorobenzene b | 74,227 | 0 |
| 3-Fluorophenol, cis h,i | 70,188 | 1563 | 2-Fluorobenzonitrile d | 78,650 | 4423 |
| 3-Fluorophenol, trans h,i | 70,449 | 1824 | 3-Fluorobenzonitrile d | 78,873 | 4646 |
| 4-Fluorophenol j | 68,577 | −48 | 4-Fluorobenzonitrile e | 78,000 | 3773 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhao, Y.; Jiao, Y.; Zhao, J.; Li, C.; Jia, S. Vibronic and Cationic Features of 2-Fluorobenzonitrile and 3-Fluorobenzonitrile Studied by REMPI and MATI Spectroscopy and Franck–Condon Simulations. Molecules 2023, 28, 4702. https://doi.org/10.3390/molecules28124702
Li S, Zhao Y, Jiao Y, Zhao J, Li C, Jia S. Vibronic and Cationic Features of 2-Fluorobenzonitrile and 3-Fluorobenzonitrile Studied by REMPI and MATI Spectroscopy and Franck–Condon Simulations. Molecules. 2023; 28(12):4702. https://doi.org/10.3390/molecules28124702
Chicago/Turabian StyleLi, Shuxian, Yan Zhao, Yuechun Jiao, Jianming Zhao, Changyong Li, and Suotang Jia. 2023. "Vibronic and Cationic Features of 2-Fluorobenzonitrile and 3-Fluorobenzonitrile Studied by REMPI and MATI Spectroscopy and Franck–Condon Simulations" Molecules 28, no. 12: 4702. https://doi.org/10.3390/molecules28124702
APA StyleLi, S., Zhao, Y., Jiao, Y., Zhao, J., Li, C., & Jia, S. (2023). Vibronic and Cationic Features of 2-Fluorobenzonitrile and 3-Fluorobenzonitrile Studied by REMPI and MATI Spectroscopy and Franck–Condon Simulations. Molecules, 28(12), 4702. https://doi.org/10.3390/molecules28124702







