Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions
Abstract
1. Introduction
2. Results
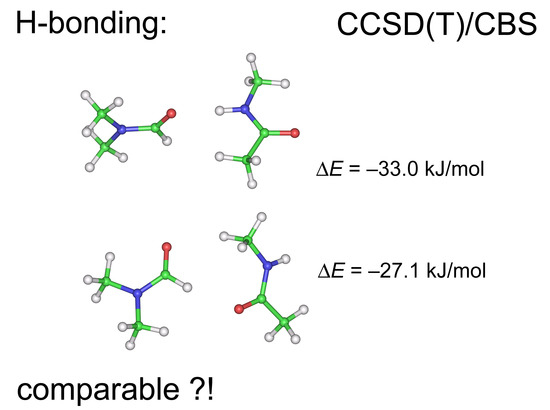
2.1. Interaction Energies
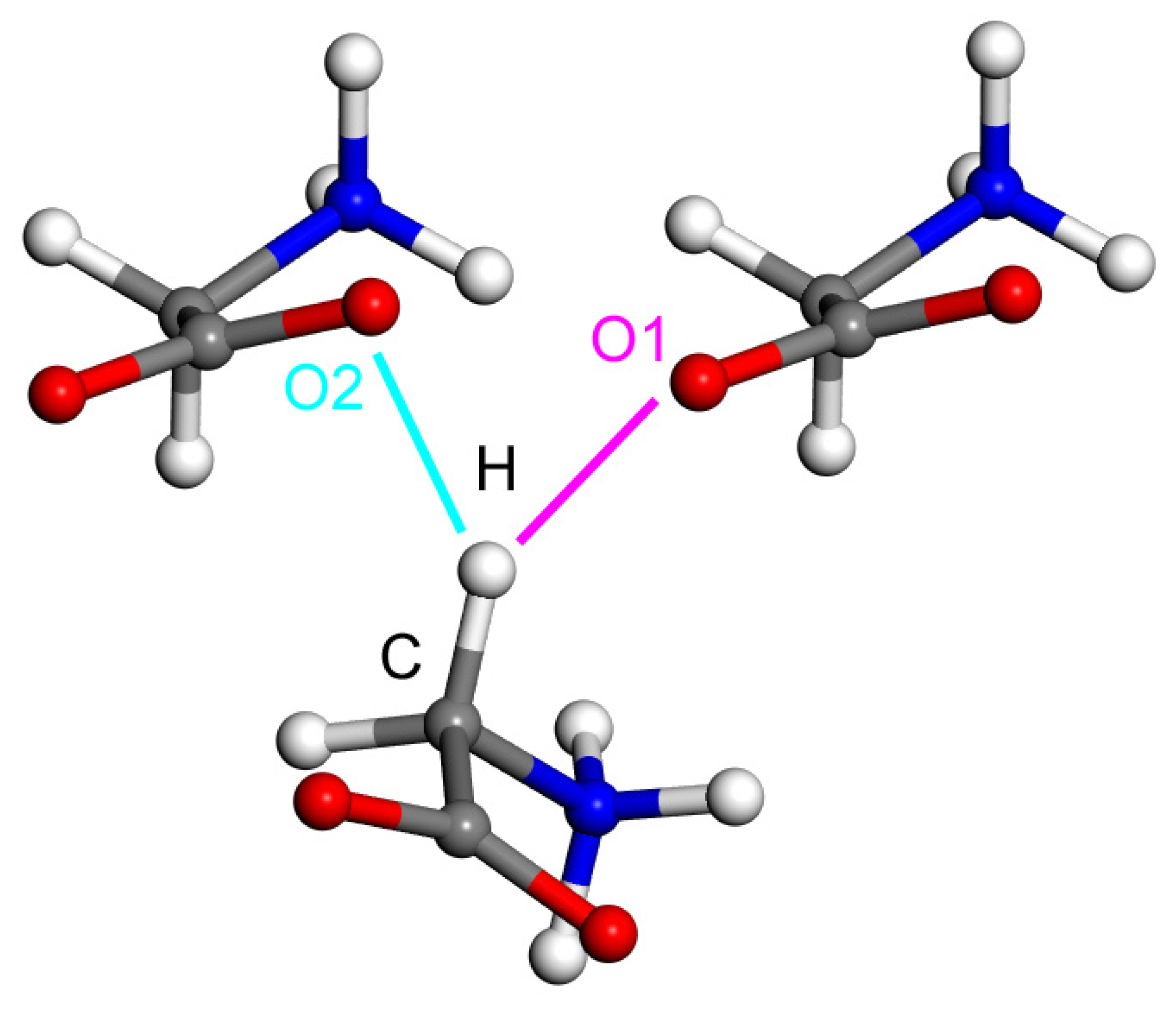
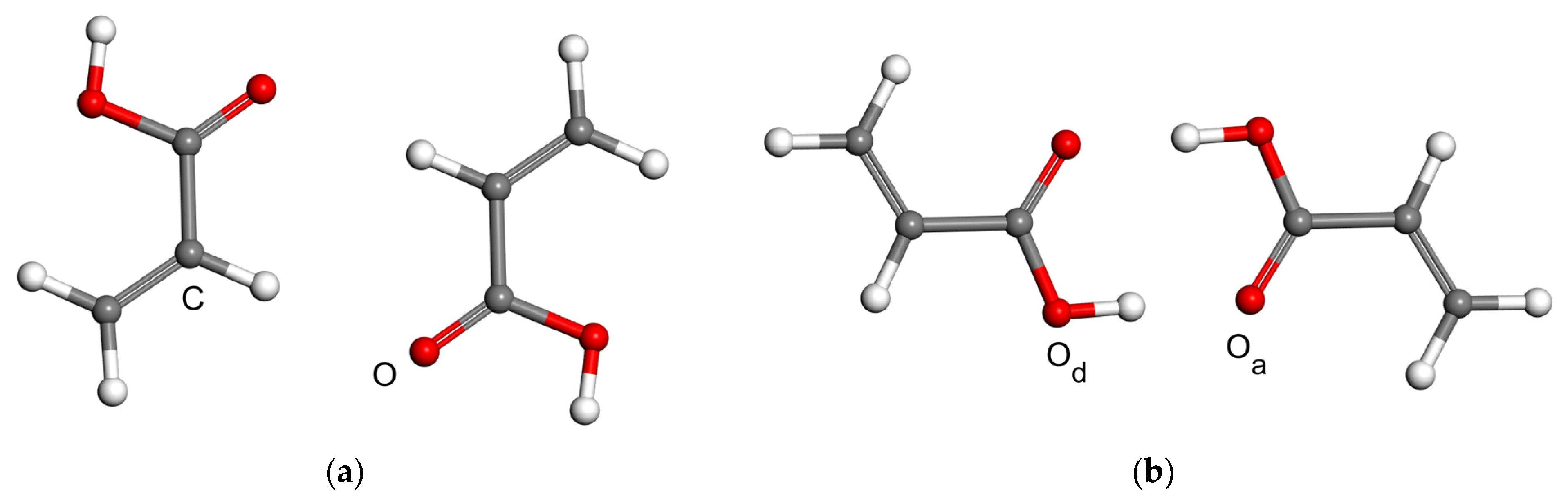
2.2. Model Geometries
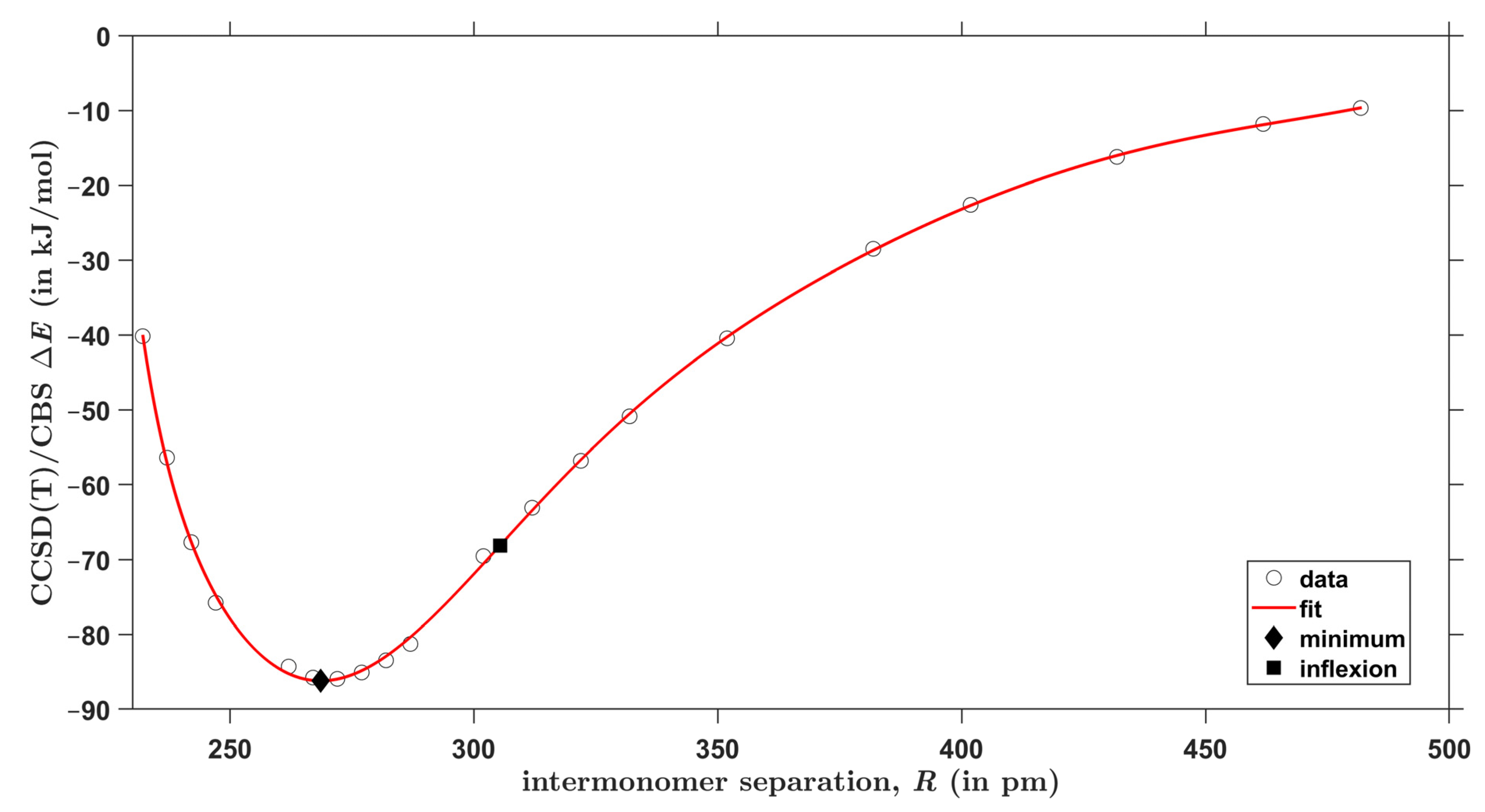
2.3. The Interaction Energy Curves
2.4. SAPT-DFT Partitioning of the Interaction Energy
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond. Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Schneider, H.J. Noncovalent interactions: A brief account of a long history. J. Phys. Org. Chem. 2022, 35, e4340. [Google Scholar] [CrossRef]
- Vennelakanti, V.; Qi, H.W.; Mehmood, R.; Kulik, H.J. When are two hydrogen bonds better than one? Accurate first-principles models explain the balance of hydrogen bond donors and acceptors found in proteins. Chem. Sci. 2021, 12, 1147–1162. [Google Scholar] [CrossRef]
- Jabłoński, M. Hydrogen Bonds. Molecules 2023, 28, 1616. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.; Jemmis, E.D. Red-, Blue- or No-Shift in Hydrogen Bonds: A Unified Explanation. J. Am. Chem. Soc. 2007, 129, 4620–4632. [Google Scholar] [CrossRef]
- Taylor, R. Identifying intermolecular atom⋯atom interactions that are not just bonding but also competitive. CrystEngComm 2020, 22, 7145–7151. [Google Scholar] [CrossRef]
- Newberry, R.W.; Raines, R.T. Secondary Forces in Protein Folding. ACS Chem. Biol. 2019, 14, 1677–1686. [Google Scholar] [CrossRef]
- Galle Kankanamge, S.R.; Ma, J.; Mackin, R.T.; Leonik, F.M.; Taylor, C.M.; Rubtsov, I.V.; Kuroda, D.G. Proving and Probing the Presence of the Elusive C−H⋯O Hydrogen Bond in Liquid Solutions at Room Temperature. Angew. Chem. 2020, 59, 17012–17017. [Google Scholar] [CrossRef]
- Mineva, T.; Dib, E.; Gaje, A.; Petitjean, H.; Bantignies, J.L.; Alonso, B. Zeolite Structure Direction: Identification, Strength and Involvement of Weak CH⋯O Hydrogen Bonds. ChemPhysChem 2020, 21, 149–153. [Google Scholar] [CrossRef]
- Pullanchery, S.; Kulik, S.; Rehl, B.; Hassanali, A.; Roke, S. Charge transfer across C–H⋯O hydrogen bonds stabilizes oil droplets in water. Science 2021, 374, 1366–1370. [Google Scholar] [CrossRef]
- Itoh, Y.; Nakashima, Y.; Tsukamoto, S.; Kurohara, T.; Suzuki, M.; Sakae, Y.; Oda, M.; Okamoto, Y.; Suzuki, T. N+–C–H⋯O Hydrogen bonds in protein-ligand complexes. Sci. Rep. 2019, 9, 767. [Google Scholar] [CrossRef] [PubMed]
- Brus, J.; Urbanova, M.; Czernek, J.; Pavelkova, M.; Kubova, K.; Vyslouzil, J.; Abbrent, S.; Konefal, R.; Horsky, J.; Vetchy, D.; et al. Structure and Dynamics of Alginate Gels Cross-Linked by Polyvalent Ions Probed via Solid State NMR Spectroscopy. Biomacromolecules 2017, 18, 2478–2488. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Wang, H.; Zeng, H.; Hong, X.; Huang, F. A [15]paracyclophenone and its fluorenone-containing derivatives: Syntheses and binding to nerve agents mimics via aryl-CH hydrogen bonding interactions. Org. Chem. Front. 2021, 8, 25–31. [Google Scholar] [CrossRef]
- Gu, Y.; Kar, T.; Scheiner, S. Fundamental Properties of the CH⋯O Interaction: Is It a True Hydrogen Bond? J. Am. Chem. Soc. 1999, 121, 9411–9422. [Google Scholar] [CrossRef]
- Kar, T.; Scheiner, S. Comparison of Cooperativity in CH⋯O and OH⋯O Hydrogen Bonds. J. Phys. Chem. A 2004, 108, 9161–9168. [Google Scholar] [CrossRef]
- Moore, K.B.; Sadeghian, K.; Sherrill, C.D.; Ochsenfeld, C.; Schaefer, H.F. C–H⋯O Hydrogen Bonding. The Prototypical Methane-Formaldehyde System: A Critical Assessment. J. Chem. Theory Comput. 2017, 13, 5379–5395. [Google Scholar] [CrossRef]
- Mao, Y.; Head-Gordon, M. Probing Blue-Shifting Hydrogen Bonds with Adiabatic Energy Decomposition Analysis. J. Phys. Chem. Lett. 2019, 10, 3899–3905. [Google Scholar] [CrossRef]
- Yates, J.R.; Pham, T.N.; Pickard, C.J.; Mauri, F.; Amado, A.M.; Gil, A.M.; Brown, S.P. An Investigation of Weak CH⋯O Hydrogen Bonds in Maltose Anomers by a Combination of Calculation and Experimental Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2005, 127, 10216–10220. [Google Scholar] [CrossRef]
- Moggach, S.A.; Marshall, W.G.; Rogers, D.M.; Parsons, S. How focussing on hydrogen bonding interactions in amino acids can miss the bigger picture: A high pressure neutron powder diffraction study of ε-glycine. CrystEngComm 2015, 17, 5315–5328. [Google Scholar] [CrossRef]
- Calvin, J.A.; Peng, C.; Rishi, V.; Kumar, A.; Valeev, E.F. Many-Body Quantum Chemistry on Massively Parallel Computers. Chem. Rev. 2021, 121, 1203–1231. [Google Scholar] [CrossRef]
- Patkowski, K. Recent developments in symmetry-adapted perturbation theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1452. [Google Scholar] [CrossRef]
- Shahbaz, M.; Szalewicz, K. Evaluation of methods for obtaining dispersion energies used in density functional calculations of intermolecular interactions. Theor. Chem. Acc. 2019, 138, 25. [Google Scholar] [CrossRef]
- Bartalucci, E.; Malär, A.A.; Mehnert, A.; Büning, J.B.K.; Günzel, L.; Icker, M.; Börner, M.; Wiebeler, C.; Meier, B.H.; Grimme, S.; et al. Probing a Hydrogen-π Interaction Involving a Trapped Water Molecule in the Solid State. Angew. Chem. Int. Ed. 2023, 62, e2022117725. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J.; Czerneková, V. A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes. Int. J. Mol. Sci. 2022, 23, 15773. [Google Scholar] [CrossRef] [PubMed]
- Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Marshall, M.S.; Burns, L.A.; Sherrill, C.D. Basis set convergence of the coupled-cluster correction: Best practices for benchmarking non-covalent interactions and the attendant revision of the S22, NBC10, HBC6, and HSG databases. J. Chem. Phys. 2011, 135, 194102. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Spada, L.; Alessandrini, S.; Zheng, Y.; Lengsfeld, K.G.; Grabow, J.-U.; Feng, G.; Puzzarini, C.; Barone, V. Stacked but not Stuck: Unveiling the Role of π→π* Interactions with the Help of the Benzofuran–Formaldehyde Complex. Angew. Chem. Int. Ed. 2022, 61, 264–270. [Google Scholar] [CrossRef] [PubMed]
- Souza de, G.L.C.; Peterson, K.A. Probing the ionization potentials of the formaldehyde dimer. J. Chem. Phys. 2020, 152, 194305. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796. [Google Scholar] [CrossRef]
- Alessandrini, S.; Barone, V.; Puzzarini, C. Extension of the “Cheap” Composite Approach to Noncovalent Interactions: The jun-ChS Scheme. J. Chem. Theory Comput. 2020, 16, 988–1006. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef] [PubMed]
- Czernek, J.; Brus, J.; Czerneková, V. A computational inspection of the dissociation energy of mid-sized organic dimers. J. Chem. Phys. 2022, 156, 204303. [Google Scholar] [CrossRef]
- Dornshuld, E.V.; Holy, C.M.; Tschumper, G.S. Homogeneous and Heterogeneous Noncovalent Dimers of Formaldehyde and Thioformaldehyde: Structures, Energetics, and Vibrational Frequencies. J. Phys. Chem. A 2014, 118, 3376–3385. [Google Scholar] [CrossRef]
- Andersen, J.; Voute, A.; Mihrin, D.; Heimdal, J.; Berg, R.W.; Torsson, M.; Larsen Wugt, R. Probing the global potential energy minimum of (CH2O)2: THz absorption spectrum of (CH2O)2 in solid neon and para-hydrogen. J. Chem. Phys. 2017, 146, 244311. [Google Scholar] [CrossRef]
- Gavezzotti, A. Molecular Aggregation: Structure Analysis and Molecular Simulation of Crystals and Liquids, 1st ed.; Oxford University Press: Oxford, UK, 2007; pp. 304–329. [Google Scholar]
- Jabłoński, M.; Monaco, G. Different Zeroes of Interaction Energies As the Cause of Opposite Results on the Stabilizing Nature of C−H⋯O Intramolecular Interactions. J. Chem. Inf. Model. 2013, 53, 1661–1675. [Google Scholar] [CrossRef]
- Jabłoński, M. A Critical Overview of Current Theoretical Methods of Estimating the Energy of Intramolecular Interactions. Molecules 2020, 25, 5512. [Google Scholar] [CrossRef]
- Becucci, M.; Melandri, S. High-Resolution Spectroscopic Studies of Complexes Formed by Medium-Size Organic Molecules. Chem. Rev. 2016, 116, 5014–5037. [Google Scholar] [CrossRef] [PubMed]
- Feng, G.; Favero, L.B.; Maris, A.; Vigorito, A.; Caminati, W.; Meyer, R. Proton Transfer in Homodimers of Carboxylic Acids: The Rotational Spectrum of the Dimer of Acrylic Acid. J. Am. Chem. Soc. 2012, 134, 19281–19286. [Google Scholar] [CrossRef] [PubMed]
- Boese, R.; Bläser, D.; Steller, I.; Latz, R.; Bäumen, A. Redetermination of 2-propenoic acid at 125K. Acta Crystallogr. Sect. C 1999, 55, IUC9900006. [Google Scholar] [CrossRef]
- Das, A.K.; Urban, L.; Leven, I.; Loipersberger, M.; Aldossary, A.; Head-Gordon, M.; Head-Gordon, T. Development of an Advanced Force Field for Water Using Variational Energy Decomposition Analysis. J. Chem. Theory Comput. 2019, 15, 5001–5013. [Google Scholar] [CrossRef] [PubMed]
- Carter-Fenk, C.; Lao, K.U.; Herbert, J.M. Predicting and Understanding Non-Covalent Interactions Using Novel Forms of Symmetry-Adapted Perturbation Theory. Acc. Chem. Res. 2021, 54, 3679–3690. [Google Scholar] [CrossRef]
- Hopffgarten, M.v.; Frenking, G. Energy Decomposition Analysis. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
- Mo, Y.; Bao, P.; Gao, J. Energy Decomposition Analysis Based on a Block-Localized Wavefunction and Multistate Density Functional Theory. Phys. Chem. Chem. Phys. 2011, 13, 6760–6775. [Google Scholar] [CrossRef]
- Chen, X.; Gao, J. Fragment Exchange Potential for Realizing Pauli Deformation of Inter-Fragment Interactions. J. Phys. Chem. Lett. 2020, 11, 4008–4016. [Google Scholar] [CrossRef]
- Stone, A.J. The Theory of Intermolecular Forces, 1st ed.; Clarendon Press: Oxford, UK, 2002; pp. 79–102. [Google Scholar]
- Heßelmann, A.; Jansen, G.; Schütz, M. Interaction Energy Contributions of H-Bonded and Stacked Structures of the AT and GC DNA Base Pairs from the Combined Density Functional Theory and Intermolecular Perturbation Theory Approach. J. Am. Chem. Soc. 2006, 128, 11730–11731. [Google Scholar] [CrossRef]
- Moszynski, R.; Heijmen, T.G.A.; Jeziorski, B. Symmetry-adapted perturbation theory for the calculation of Hartree–Fock interaction energies. Mol. Phys. 1996, 88, 741–758. [Google Scholar] [CrossRef]
- Řezáč, J.; Hobza, P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef] [PubMed]
- AMS 2023.1, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 26 May 2023).
- Bickelhaupt, F.M.; Baerends, E.J. Kohn–Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry, 1st ed.; Lipkowitz, K.B., Boyd, D.B., Eds.; Wiley: Hoboken, NJ, USA, 2009; Volume 15, pp. 1–86. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Lenthe van, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- Fiedler, J.; Berland, K.; Borchert, J.W.; Corkery, R.W.; Eisfeld, A.; Gelbwaser-Klimovsky, D.; Greve, M.M.; Holst, B.; Jacobs, K.; Krüger, M.; et al. Perspectives on weak interactions in complex materials at different length scales. Phys. Chem. Chem. Phys. 2023, 25, 2671–2705. [Google Scholar] [CrossRef]
- Southern, S.A.; Bryce, D.L. To what extent do bond length and angle govern the 13C and 1H NMR response to weak CH⋯O hydrogen bonds? A case study of caffeine and theophylline cocrystals. Solid State Nucl. Magn. Reson. 2022, 119, 101796. [Google Scholar] [CrossRef]
- Lo Presti, L.; Soave, R.; Destro, R. On the interplay between CH⋯O and OH⋯O interactions in determining crystal packing and molecular conformation: An experimental and theoretical charge density study of the fungal secondary metabolite austdiol (C12H12O5). J. Phys. Chem. B 2006, 110, 640–6414. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. Polymorphic Forms of Valinomycin Investigated by NMR Crystallography. Int. J. Mol. Sci. 2020, 21, 4907. [Google Scholar] [CrossRef]
- Cuellar, J.; Parada-Díaz, L.; Garza, J.; Mejía, S.M. A Theoretical Analysis of Interaction Energies and Intermolecular Interactions between Amphotericin B and Potential Bioconjugates Used in the Modification of Nanocarriers for Drug Delivery. Molecules 2023, 28, 2674. [Google Scholar] [CrossRef] [PubMed]
- Gress, M.E.; Jeffrey, G.A. A Neutron Diffraction Refinement of the Crystal Structure of β-Maltose Monohydrate. Acta Cryst. B 1977, 33, 2490–2495. [Google Scholar] [CrossRef]
- Verbist, J.J.; Lehman, M.S.; Koetzle, T.F.; Hamilton, W.C. Precision neutron diffraction structure determination of protein and nucleic acid components. VI. The crystal and molecular structure of the amino acid l-asparagine monohydrate. Acta Cryst. B 1972, 28, 3006–3013. [Google Scholar] [CrossRef]
- Frish, M.J.; Trucks, J.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Weigend, F.; Häser, M. RI-MP2: First derivatives and global consistency. Theor. Chem. Acc. 1997, 97, 331–340. [Google Scholar] [CrossRef]
- Weigend, F.; Häser, M.; Patzelt, H.; Ahlrichs, R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143–152. [Google Scholar] [CrossRef]
- Balasubramani, S.G.; Chen, G.P.; Coriani, S.; Diedenhofen, M.; Frank, M.S.; Franzke, Y.J.; Furche, F.; Grotjahn, R.; Harding, M.E.; Hättig, C.; et al. TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations. J. Chem. Phys. 2020, 152, 184107. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Hesselmann, A.; Kats, D.; Kohn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef]
- Heßelmann, A.; Jansen, G. First-order intermolecular interaction energies from Kohn–Sham orbitals. Chem. Phys. Lett. 2002, 357, 464–470. [Google Scholar] [CrossRef]
- Heßelmann, A.; Jansen, G. Intermolecular dispersion energies from time-dependent density functional theory. Chem. Phys. Lett. 2003, 367, 778–784. [Google Scholar] [CrossRef]
- Heßelmann, A.; Jansen, G. Intermolecular induction and exchange-induction energies from coupled-perturbed Kohn–Sham density functional theory. Chem. Phys. Lett. 2002, 362, 319–325. [Google Scholar] [CrossRef]
- Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Koch, H.; Olsen, J.; Wilson, A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Pinski, P.; Becker, U.; Valeev, E.F.; Neese, F. Sparse maps–A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. [Google Scholar] [CrossRef] [PubMed]
- Pinski, P.; Riplinger, C.; Valeev, E.F.; Neese, F. Sparse maps–A systematic infrastructure for reduced-scaling electronic structure methods. I. An efficient and simple linear scaling local MP2 method that uses an intermediate basis of pair natural orbitals. J. Chem. Phys. 2015, 143, 034108. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system–Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Scheiner, S.; Kar, T.; Gu, Y. Strength of the CαH··O Hydrogen Bond of Amino Acid Residues. J. Biol. Chem. 2001, 276, 9832–9837. [Google Scholar] [CrossRef]
- Puzzarini, C.; Spada, L.; Alessandrini, S.; Barone, V. The challenge of non-covalent interactions: Theory meets experiment for reconciling accuracy and interpretation. J. Phys. Condens. Matter. 2020, 32, 343002. [Google Scholar] [CrossRef]
- Civiš, S.; Lamanec, M.; Špirko, V.; Kubišta, J.; Špeťko, M.; Hobza, P. Hydrogen Bonding with Hydridic Hydrogen–Experimental Low-Temperature IR and Computational Study: Is a Revised Definition of Hydrogen Bonding Appropriate? J. Am. Chem. Soc. 2023, 145, 8550–8559. [Google Scholar] [CrossRef]

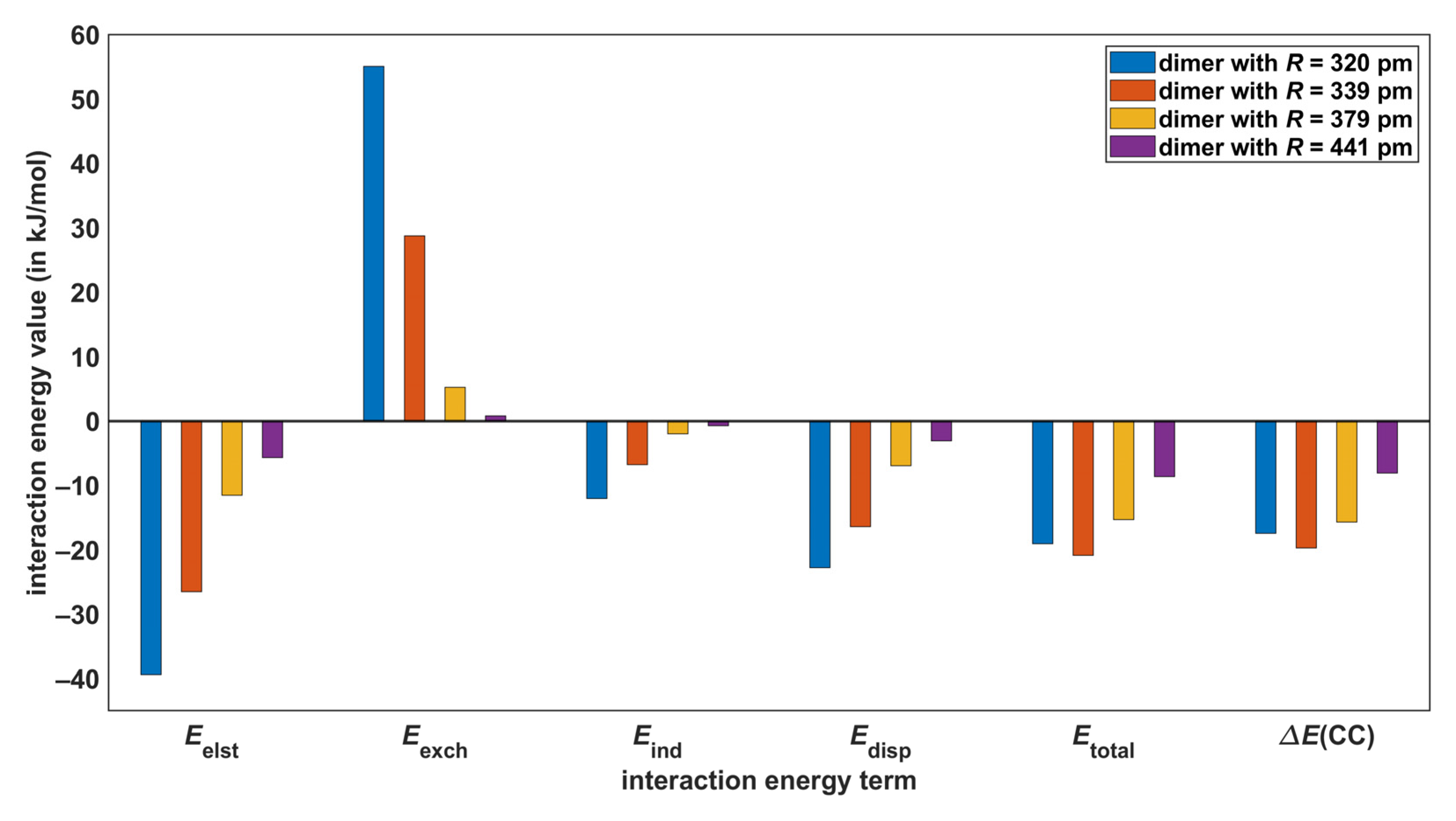
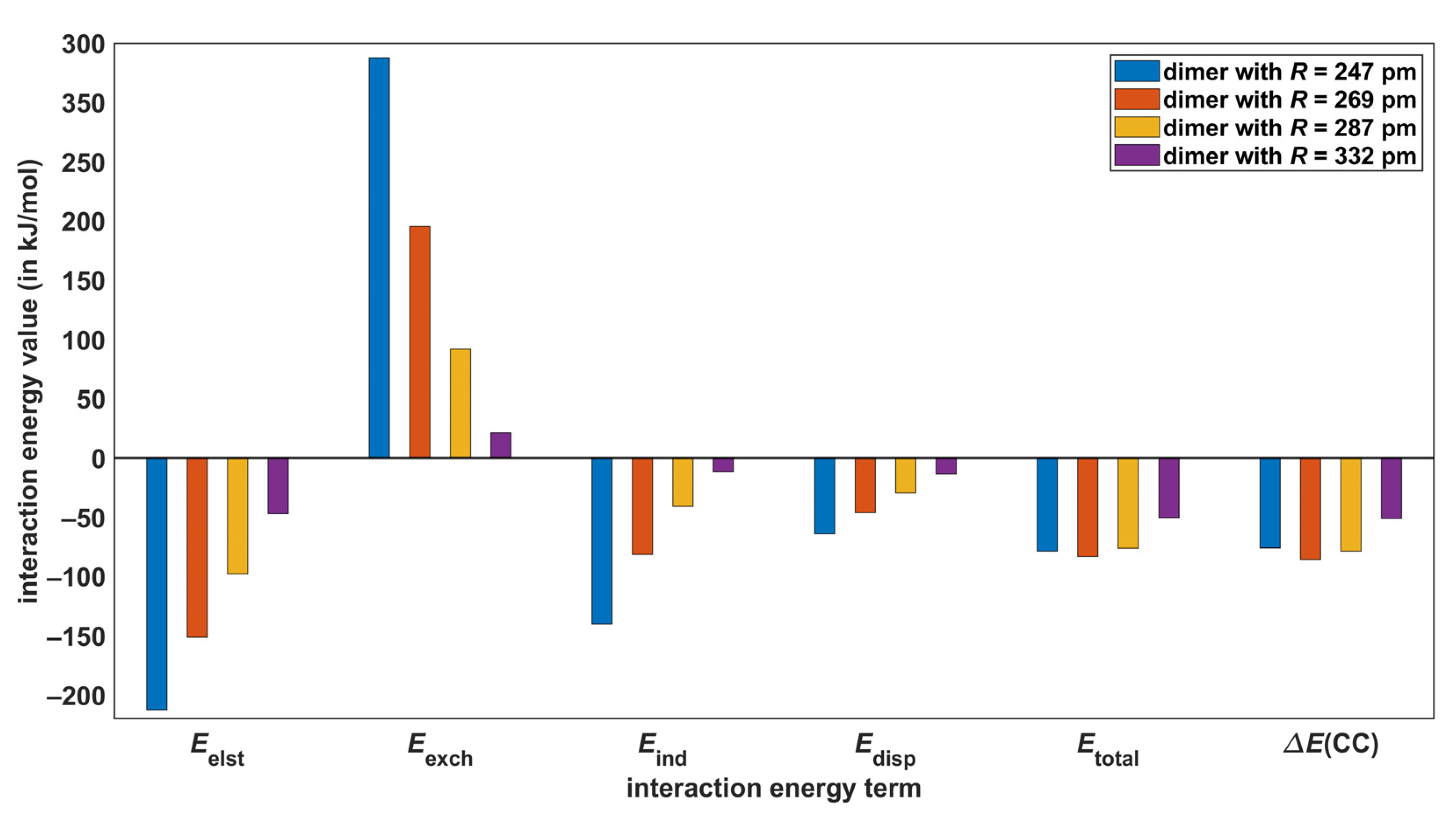
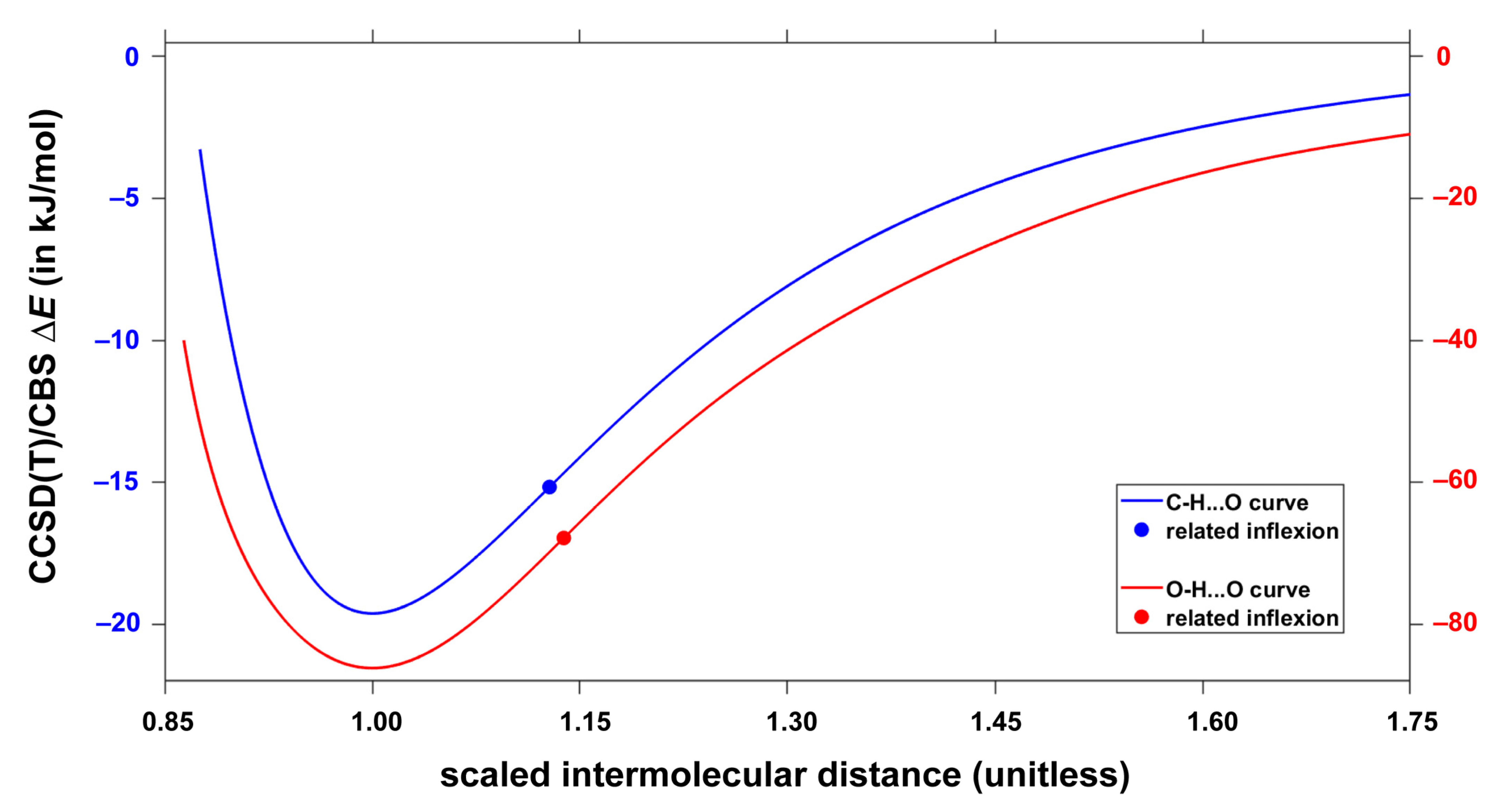
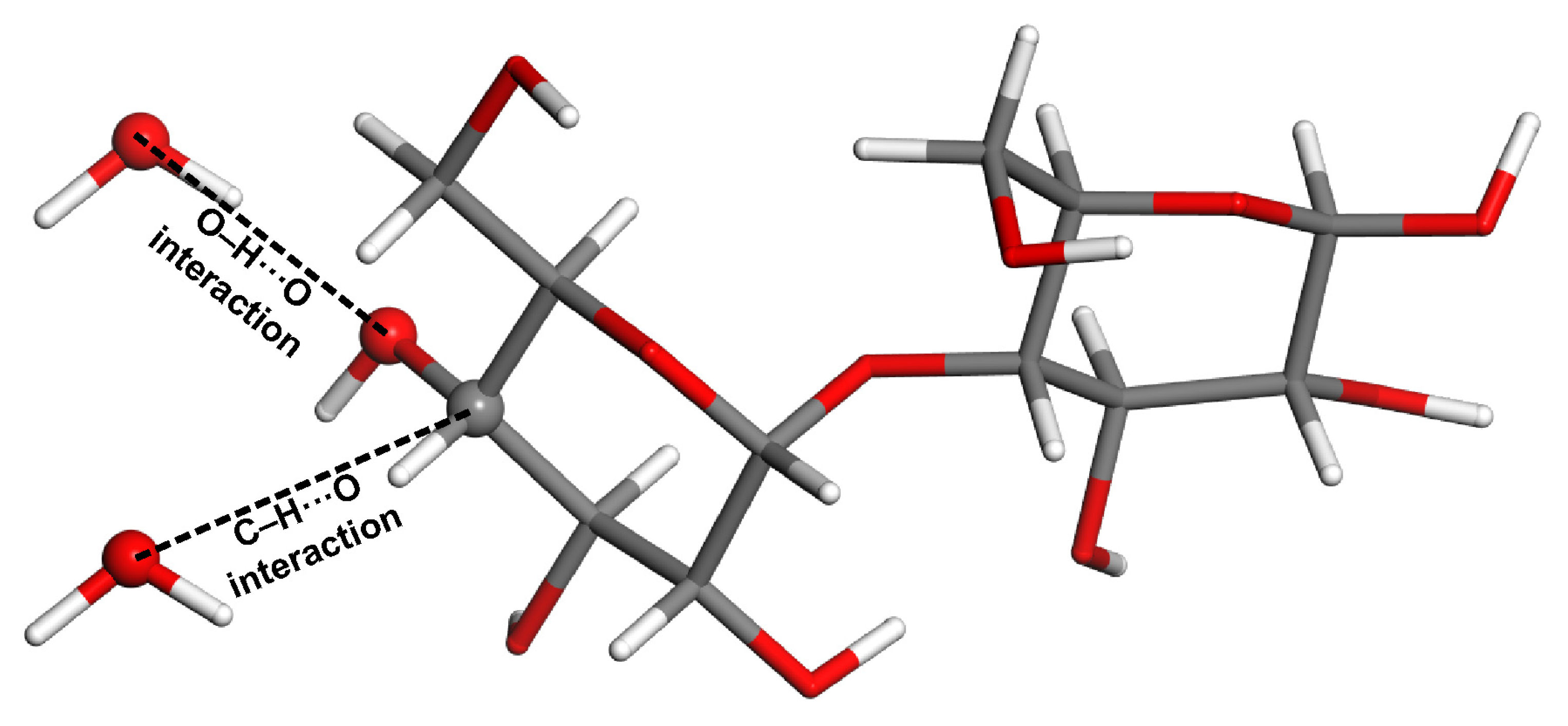

| Structure | Rotational Constants/MHz | |||||
|---|---|---|---|---|---|---|
| A | B | C | ||||
| optimized by MP2/aTZ | 1235 | 1174 | 841.7 | −15.28 | −14.64 | −14.73 |
| semi-experimental 1 | 1180 | 1103 | 789.0 | −15.58 (−16.15) 2 | −15.36 | −15.08 |
| Parameter | Optimized Structure | ||
|---|---|---|---|
| MP2/aTZ (This Work) | MP2/haTZ (Ref. [37]) | MP2/aQZ (Ref. [38]) | |
| −19.1 1 (−16.0) 1 | −18.7 2 (−15.5) 2 | −19.2 3 | |
| 7.1 1 (4.3) 1 | 6.9 4 (4.1) 4 | — | |
| 6.2 1 (3.7) 1 | — | 5.5 5 | |
| −12.0 1 (−11.7) 1 | −11.8 (−11.4) | — | |
| −12.9 1 (−12.3) 1 | — | −13.7 | |
| Interaction | ||||
|---|---|---|---|---|
| C–H⋯O | 320 | −17.5 | −19.1 | 0.580 |
| 329 1 | −19.7 | −20.9 | 0.620 | |
| 379 | −15.7 | −15.3 | 0.599 | |
| 441 | −8.1 | −8.7 | 0.543 | |
| O–H⋯O | 247 | −75.8 | −78.6 | 0.302 |
| 269 2 | −85.6 | −83.1 | 0.304 | |
| 287 | −78.7 | −76.1 | 0.303 | |
| 332 | −50.9 | −50.3 | 0.284 |
| Hydrogen Bonding Type | |||
|---|---|---|---|
| C–H⋯O | −13.12 | −12.91 | −12.34 |
| O–H⋯O | −49.09 | −48.88 | −48.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, J.; Brus, J.; Czerneková, V.; Kobera, L. Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions. Molecules 2023, 28, 4478. https://doi.org/10.3390/molecules28114478
Czernek J, Brus J, Czerneková V, Kobera L. Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions. Molecules. 2023; 28(11):4478. https://doi.org/10.3390/molecules28114478
Chicago/Turabian StyleCzernek, Jiří, Jiří Brus, Vladimíra Czerneková, and Libor Kobera. 2023. "Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions" Molecules 28, no. 11: 4478. https://doi.org/10.3390/molecules28114478
APA StyleCzernek, J., Brus, J., Czerneková, V., & Kobera, L. (2023). Quantifying the Intrinsic Strength of C–H⋯O Intermolecular Interactions. Molecules, 28(11), 4478. https://doi.org/10.3390/molecules28114478