Review on the QM/MM Methodologies and Their Application to Metalloproteins
Abstract
1. Introduction
2. Methodologies
2.1. Density Functional Theory
2.2. Semiempirical Methods
2.3. Molecular Mechanics (MM)
2.4. Molecular Dynamics Simulations
2.5. QM/MM and QM/MM/MD Approaches
2.6. Computational Times of Methodologies
3. Metalloproteins
3.1. Reactions of Metalloproteins
3.2. Nitrogenase and FeMo Cofactor
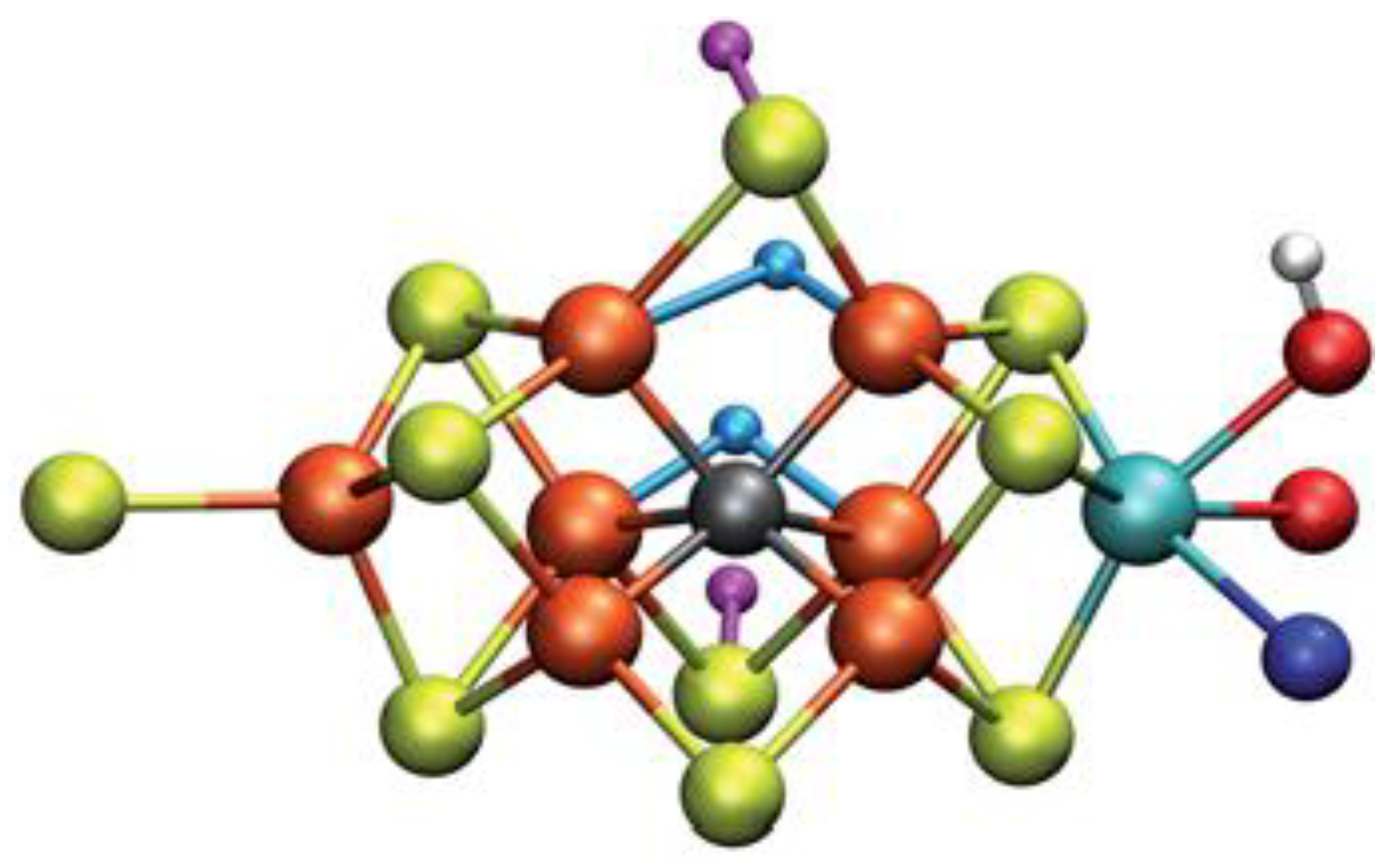
3.2.1. General about Nitrogenase—Structure

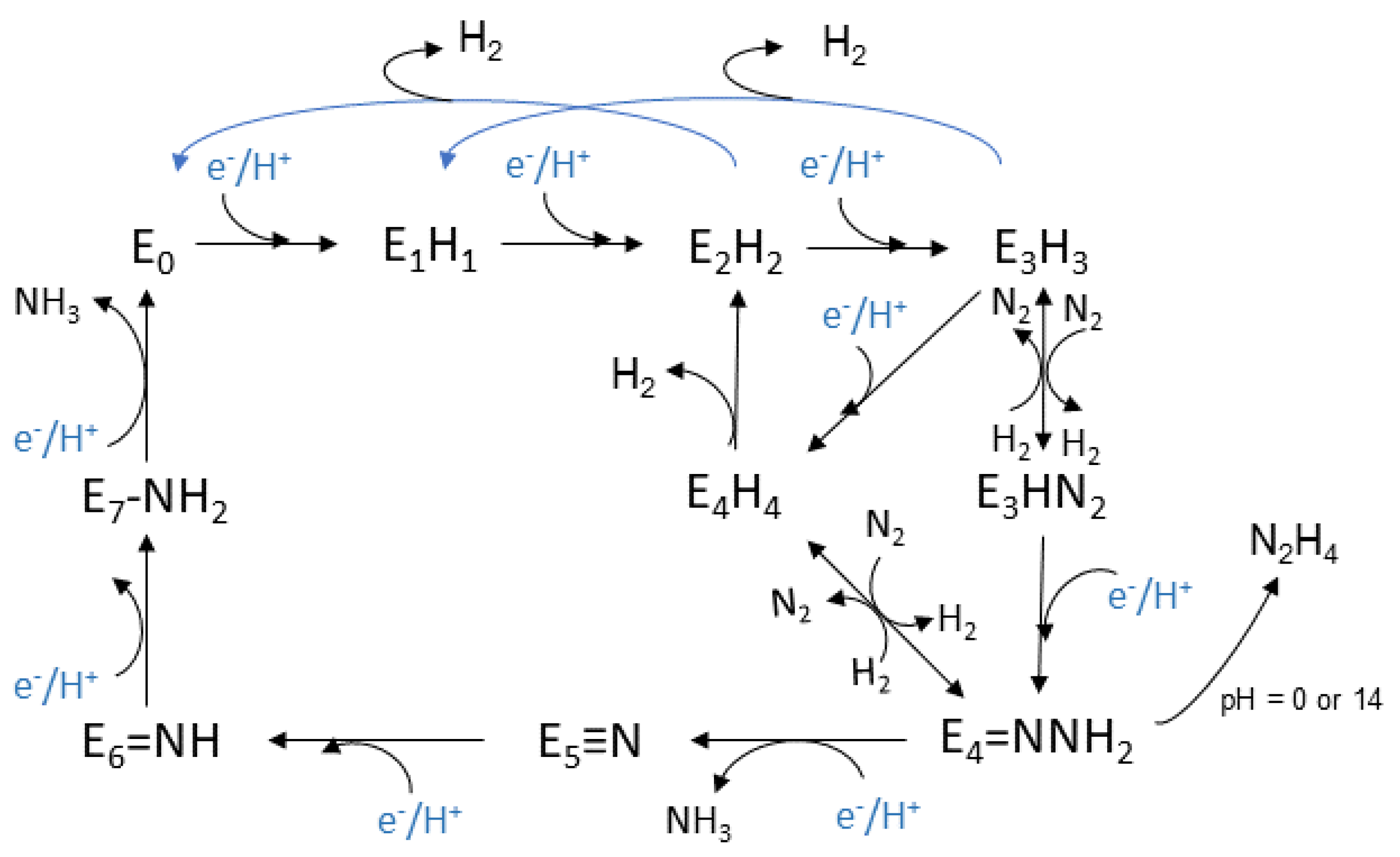
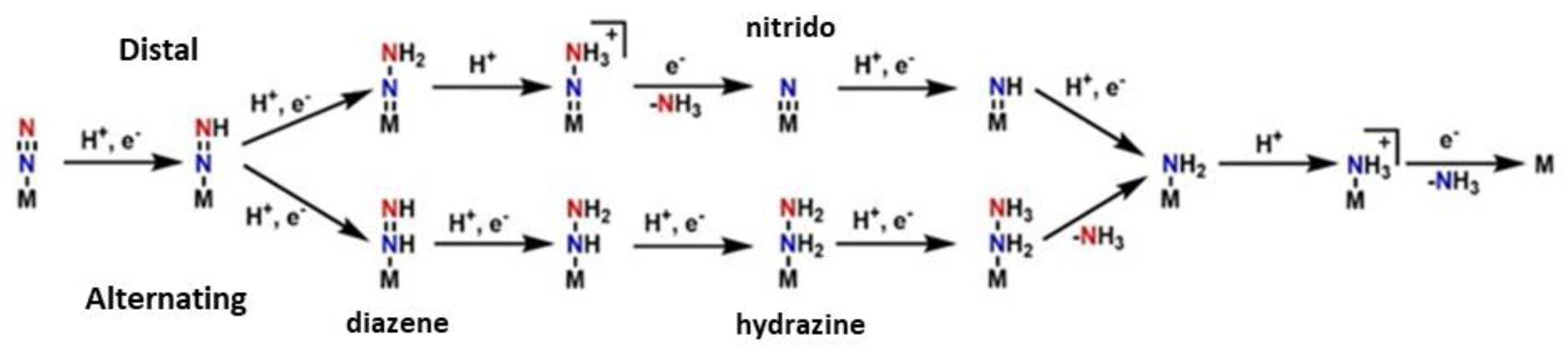
3.2.2. General Mechanism
3.2.3. Calculations
4. Discussion and Conclusions
5. Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. Engl. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- Noorden, R.V. Modellers react to chemistry award. Nature. 2013, 502, 280. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kristyán, S.; Csonka, G.I. New development in RECEP (rapid estimation of correlation energy from partial charges) method. Chem. Phys. Lett. 1999, 307, 469–478. [Google Scholar] [CrossRef]
- Kristyán, S. Immediate estimation of correlation energy for molecular systems from the partial charges on atoms in the molecule. Chem. Phys. 1997, 224, 33–51. [Google Scholar] [CrossRef]
- Kristyán, S. Theory of variational calculation with a scaling correct moment functional to solve the electronic schrödinger equation directly for ground state one-electron density and electronic energy. Int. J. Quantum Chem. 2013, 113, 1479–1492. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Grimme, S.; Neese, F. Double-hybrid density functional theory for excited electronic states of molecules. J. Chem. Phys. 2007, 127, 154116. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef]
- Skone, J.H.; Govoni, M.; Galli, G. Nonempirical range-separated hybrid functionals for solids and molecules. Phys. Rev. B 2016, 93, 235106. [Google Scholar] [CrossRef]
- Paier, J.; Janesko, B.G.; Henderson, T.M.; Scuseria, G.E.; Grüneis, A.; Kresse, G. Hybrid functionals including random phase approximation correlation and second-order screened exchange. J. Chem. Phys. 2010, 132, 094103. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, Y.; Gong, X.; Ying, F.; Su, P.; Wu, W. Hamiltonian Matrix Correction Based Density Functional Valence Bond Method. J. Chem. Theory Comput. 2017, 13, 627–634. [Google Scholar] [CrossRef]
- Te Vrugt, M.; Löwen, H.; Wittkowski, R. Classical dynamical density functional theory: From fundamentals to applications. Adv. Phys. 2020, 69, 121–247. [Google Scholar] [CrossRef]
- Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can short-range hybrids describe long-range-dependent properties? J. Chem. Phys. 2009, 131, 044108. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Elliott, P.; Furche, F.; Burke, K. Excited States from Time-Dependent Density Functional Theory. Rev. Comp. Chem. 2008, 26, 91–165. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Lingwood, M.; Hammond, J.R.; Hrovat, D.A.; Mayer, J.M.; Thatcher Borden, W. MPW1K Performs Much Better than B3LYP in DFT Calculations on Reactions that Proceed by Proton-Coupled Electron Transfer (PCET). J. Chem. Theory Comput. 2006, 2, 740–745. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into Current Limitations of Density Functional Theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef]
- Carpentieri, M.; Porro, L.; Del Re, G. Numerical studies for a theoretical analysis of semiempirical LCAO–CI methods. Int. J. Quantum Chem. 1968, 2, 807–824. [Google Scholar] [CrossRef]
- Thiel, W. Semiempirical quantum–chemical methods. WIREs Comput. Mol. Sci. 2014, 4, 145–157. [Google Scholar] [CrossRef]
- Hückel, E. Quantum contributions to the benzene problem. Z Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hoffmann, R. An extended Hückel theory. I. Hydrocarbons. J. Chem. Phys. 1963, 39, 1397–1412. [Google Scholar] [CrossRef]
- Pariser, R.; Parr, R.G. A semi-empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. J. Chem. Phys. 1953, 21, 466–471. [Google Scholar] [CrossRef]
- Pople, J.A. Electron interaction in unsaturated hydrocarbons. Trans. Farad. Soc. 1953, 49, 1375–1385. [Google Scholar] [CrossRef]
- Pople, J.A.; Santry, D.P.; Segal, G.A. Approximate Self-Consistent Molecular Orbital Theory. I. Invariant procedures. J. Chem. Phys. 1965, 43, S129–S135. [Google Scholar] [CrossRef]
- Bingham, R.C.; Dewar, M.J.S.; Lo, D.H. Ground states of molecules. XXV. MINDO/3. Improved version of the MINDO semiempirical SCF-MO method. J. Am. Chem. Soc. 1975, 97, 1285–1293. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 1977, 99, 4899–4907. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Thiel, W. Ground states of molecules. 39. MNDO results for molecules containing hydrogen, carbon, nitrogen and oxygen. J. Am. Chem. Soc. 1977, 99, 4907–4917. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods I. Method. J. Comput. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods II. Applications. J. Comput. Chem. 1989, 10, 221–264. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef]
- Weber, W.; Thiel, W. Orthogonalization corrections for semiempirical methods. Theor. Chem. Acc. 2000, 103, 495–506. [Google Scholar] [CrossRef]
- Thiel, W. Semiempirical methods: Current status and perspectives. Tetrahedron 1988, 44, 7393–7408. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Semiempirical Molecular orbital methods. Rev. Comput. Chem. 1990, 1, 45–81. [Google Scholar] [CrossRef]
- Stewart, J.J.P. MOPAC: A semiempirical molecular orbital program. J. Comp-Aided Mol. Des. 1990, 4, 1–103. [Google Scholar] [CrossRef]
- Thiel, W. Perspectives on semiempirical molecular orbital theory. Adv. Chem. Phys. 1996, 93, 703–757. [Google Scholar] [CrossRef]
- Clark, T. Quo vadis semiempirical MO theory. J. Mol. Struct. (THEOCHEM) 2000, 530, 1–10. [Google Scholar] [CrossRef]
- Thiel, W. Semiempirical methods. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; John von Neumann Institute for Computing: Jülich, Germany, 2000; Volume 3, pp. 261–283. ISBN 3-00-005834-6. [Google Scholar]
- Bredow, T.; Jug, K. Theory and range of modern semiempirical molecular orbital methods. Theor. Chem. Acc. 2005, 113, 1–14. [Google Scholar] [CrossRef]
- Thiel, W. Semiempirical quantum-chemical methods in computational chemistry. In Theory and Applications of Computational Chemistry: The First 40 Years; Dykstra, C.E., Kim, K.S., Frenking, G., Scuseria, G.E., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2005; pp. 559–580. ISBN 9780080456249. [Google Scholar]
- Leach, A.R. Molecular Modelling: Principles and Applications; Pearson Education: London, UK, 2001; ISBN 0-582-38210-6. [Google Scholar]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; Wiley: Louisville, KY, USA, 2013; ISBN 978-0-470-09182-1. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry, 3rd ed.; John Wiley & Sons: Louisville, KY, USA, 2006; ISBN 978-1-118-82599-0. [Google Scholar]
- Jones, J.E.; Chapman, S. On the determination of molecular fields. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. A 1924, 106, 441–462. [Google Scholar] [CrossRef]
- Hospital, A.; Goñi, J.R.; Orozco, M.; Gelpí, J.L. Molecular dynamics simulations: Advances and applications. Adv. Appl. Bioinform Chem. 2015, 8, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Han, Y.; Jin, J.; Wagner, J.W.; Voth, G.A. Quantum theory of multiscale coarse-graining. J. Chem. Phys. 2018, 148, 102335. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Batoulis, J.; Bürger, T.; Hahn, O. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61–74. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624. [Google Scholar] [CrossRef]
- Murtola, T.; Falck, E.; Patra, M.; Karttunen, M.; Vattulainen, I. Coarse-grained model for phospholipid/cholesterol bilayer. J. Chem. Phys. 2004, 121, 9156–9165. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. A Multiscale Coarse-Graining Method for Biomolecular Systems. J. Phys. Chem. B 2005, 109, 2469–2473. [Google Scholar] [CrossRef] [PubMed]
- Comba, P.; Remenyi, R. Inorganic and bioinorganic molecular mechanics modeling—The problem of the force field parameterization. Coord. Chem. Rev. 2003, 238–239, 9–20. [Google Scholar] [CrossRef]
- Rueda, M.; Ferrer-Costa, C.; Meyer, T.; Pérez, A.; Camps, J.; Hospital, A.; Gelpí, J.L.; Orozco, M. A consensus view of protein dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 796–801. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.; Lankas, F.; Luque, F.J.; Orozco, M. Towards a molecular dynamics consensus view of B-DNA flexibility. Nucleic Acids Res. 2008, 36, 2379–2394. [Google Scholar] [CrossRef]
- Tian, C. Improving the Accuracy of Amber Force Field for Biomolecular Simulation. Ph.D Thesis, Stony Brook University, New York, NY, USA, November 2019. [Google Scholar]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard III, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Warshel, A.; Weiss, R.M. An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes. J. Am. Chem. Soc. 1980, 102, 6218–6226. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E.I.; Simmerling, C.; Wang, J. AMBER 12; University of California: San Francisco, CA, USA, 2012. [Google Scholar]
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D.; Nilsson, I., Jr.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S. CHARMM: The biomolecular simulation program. J Comput Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Nelson, M.T.; Humphrey, W.; Gursoy, A.; Dalke, A.; Kalé, L.V.; Skeel, R.D.; Schulten, K. NAMD: A parallel, object-oriented molecular dynamics program. Int. J. Supercomput. Appl. High Perform. Comput. 1996, 10, 251–268. [Google Scholar] [CrossRef]
- Larsson, P.; Hess, B.; Lindahl, E. Algorithm improvements for molecular dynamics simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 93–108. [Google Scholar] [CrossRef]
- Harvey, M.J.; Giupponi, G.; De Fabritiis, G. ACEMD: Accelerating biomolecular dynamics in the microsecond time scale. J. Chem. Theory Comput. 2009, 5, 1632–1639. [Google Scholar] [CrossRef] [PubMed]
- Blomberg, M.R.A.; Borowski, T.; Himo, F.; Liao, R.-Z.; Siegbahn, P.E.M. Quantum chemical studies of mechanisms for metalloenzymes. Chem. Rev. 2014, 114, 3601–3658. [Google Scholar] [CrossRef] [PubMed]
- Georgieva, P.; Himo, F. Quantum chemical modeling of enzymatic reactions: The case of histone lysine methyltransferase. J. Comput. Chem. 2010, 31, 1707–1714. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, P.E.M.; Himo, F. The quantum chemical cluster approach for modeling enzyme reactions. WIREs Comput. Mol. Sci. 2011, 1, 323–336. [Google Scholar] [CrossRef]
- Ramos, M.J.; Fernandes, P.A. Computational Enzymatic Catalysis. Acc. Chem. Res. 2008, 41, 689–698. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.; Barrios Herrera, L.; Chehelamirani, M.; Hostaš, J.; Jalife, S.; Salahub, D.R. Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: A tutorial review. Int. J. Quantum Chem. 2018, 118, e25558. [Google Scholar] [CrossRef]
- Tzeli, D.; Tsoungas, P.G.; Petsalakis, I.D.; Kozielewicz, P.; Zloh, M. Intramolecular Cyclization of β-Nitroso-o-Quinone Methides. A Theoretical Endoscopy of a Potentially Useful Innate “Reclusive” Reaction. Tetrahedron 2015, 71, 359–369. [Google Scholar] [CrossRef]
- Dapprich, S.; Komaromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. 1999, 461, 1–21. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K. Chapter 3: Hybrid methods: ONIOM(QM:MM) and QM/MM. Annu. Rep. Comput. Chem. 2006, 2, 35–51. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K.; Farkas, Ö.; Schlegel, H.B.; Frisch, M.J. Geometry optimization with QM/MM, ONIOM, and other combined methods. I. Microiterations and constraints. J. Comput. Chem. 2003, 24, 760–769. [Google Scholar] [CrossRef]
- Tzeli, D.; Theodorakopoulos, G.; Petsalakis, I.D.; Ajami, D.; Rebek, J. Theoretical study of hydrogen bonding in homodimers and heterodimers of amide, boronic acid and carboxylic acid, free and in encapsulation complexes. J. Am. Chem. Soc. 2011, 133, 16977. [Google Scholar] [CrossRef] [PubMed]
- Tzeli, D.; Theodorakopoulos, G.; Petsalakis, I.D.; Ajami, D.; Rebek Jr, J. Conformations and Fluorescence of Encapsulated Stilbene. J. Am. Chem. Soc. 2012, 134, 4346–4354. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411. [Google Scholar] [CrossRef]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates, Inc.: Oxford, UK, 2001; ISBN 0-87893-334-4. [Google Scholar]
- Koehl, P.; Levitt, M. A brighter future for protein structure prediction. Nat. Struct. Biol. 1999, 6, 108–111. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Li, Y.; Zhang, Y. Born–Oppenheimer Ab Initio QM/MM Molecular Dynamics Simulations of Enzyme Reactions. Methods Enzymol. 2016, 577, 105–118. [Google Scholar] [CrossRef]
- Zuckerman, D.M. Equilibrium Sampling in Biomolecular Simulations. Annu. Rev. Biophys. 2011, 40, 41–62. [Google Scholar] [CrossRef]
- Watanabe, H.C.; Cui, Q. Quantitative Analysis of QM/MM Boundary Artifacts and Correction in Adaptive QM/MM Simulations. J. Chem. Theory Comput. 2019, 15, 3917–3928. [Google Scholar] [CrossRef]
- Shiga, M.; Masia, M. Boundary based on exchange symmetry theory for multilevel simulations. I. Basic theory. J. Chem. Phys. 2013, 139, 044120. [Google Scholar] [CrossRef]
- Takahashi, H.; Kambe, H.; Morita, A. A simple and effective solution to the constrained QM/MM simulations. J. Chem. Phys. 2018, 148, 134119. [Google Scholar] [CrossRef]
- Rowley, C.N.; Roux, B. The Solvation Structure of Na+ and K+ in Liquid Water Determined from High Level ab Initio Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8, 3526–3535. [Google Scholar] [CrossRef]
- Heyden, A.; Lin, H.; Truhlar, D.G. Adaptive partitioning in combined quantum mechanical and molecular mechanical calculations of potential energy functions for multiscale simulations. J. Phys. Chem. B 2007, 111, 2231–2241. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, N.; Kitamura, Y.; Koyano, Y.; Nagaoka, M. The number-adaptive multiscale QM/MM molecular dynamics simulation: Application to liquid water. Chem. Phys. Lett. 2012, 524, 56–61. [Google Scholar] [CrossRef]
- Watanabe, H.C.; Kubar, T.; Elstner, M. Size-Consistent Multipartitioning QM/MM: A Stable and Efficient Adaptive QM/MM Method. J. Chem. Theory Comput. 2014, 10, 4242–4252. [Google Scholar] [CrossRef]
- Bernstein, N.; Varnai, C.; Solt, I.; Winfield, S.A.; Payne, M.C.; Simon, I.; Fuxreiter, M.; Csanyi, G. QM/MM simulation of liquid water with an adaptive quantum region. Phys. Chem. Chem. Phys. 2012, 14, 646–656. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Lev, B.; Cuervo, J.E.; Noskov, S.Y.; Salahub, D.R. A guide to QM/MM methodology and applications. Adv. Quantum Chem. 2010, 59, 353–400. [Google Scholar] [CrossRef]
- Cerqueira, N.M.F.S.A.; Moorthy, H.; Fernandes, P.A.; Ramos, M.J. The mechanism of the Ser-(cis)Ser-Lys catalytic triad of peptide amidases. Phys. Chem. Chem. Phys. 2017, 19, 12343–12354. [Google Scholar] [CrossRef]
- Zhang, Y. Pseudobond ab initio QM/MM approach and its applications to enzyme reactions. Theor. Chem. Acc. 2006, 116, 43–50. [Google Scholar] [CrossRef]
- Groenhof, G. Introduction to QM/MM Simulations. Methods Mol. Biol. 2013, 924, 43–46. [Google Scholar] [CrossRef]
- Chung, L.W.; Hirao, H.; Li, X.; Morokuma, K. The ONIOM method: Its foundation and applications to metalloenzymes and photobiology. WIREs Comput. Mol. Sci. 2012, 2, 327–350. [Google Scholar] [CrossRef]
- Villalobos, R.; Garcia, E.; Quintanar, D.; Young, P. Drug release from inert spherical matrix systems using Monte Carlo simulations. Curr. Drug Deliv. 2017, 14, 65–72. [Google Scholar] [CrossRef]
- Ryde, U. QM/MM Calculations on Proteins. Methods Enzymol. 2016, 577, 119–158. [Google Scholar] [CrossRef] [PubMed]
- Lopes, D.; Jakobtorweihen, S.; Nunes, C.; Sarmento, B.; Reis, S. Shedding light on the puzzle of drugmembrane interactions: Experimental techniques and molecular dynamics simulations. Prog. Lipid Res. 2017, 65, 24–44. [Google Scholar] [CrossRef] [PubMed]
- Albano, J.M.R.; de Paula, E.; Pickholz, M. Molecular dynamics simulations to study drug delivery systems. In Molecular Dynamics; Vakhrushev, A., Ed.; IntechOpen: London, UK, 2018; p. 73. [Google Scholar] [CrossRef]
- Sousa, S.F.; Ribeiro, A.J.M.; Neves, R.P.P.; Brás, N.F.; Cerqueira, N.M.F.S.A.; Fernandes, P.A.; Ramos, M.J. Application of quantum mechanics/molecular mechanics methods in the study of enzymatic reaction mechanisms. WIREs Comput. Mol. Sci. 2017, 7, e1281. [Google Scholar] [CrossRef]
- Difley, S.; Wang, L.-P.; Yeganeh, S.; Yost, S.R.; Van Voorhis, T. Electronic Properties of Disordered Organic Semiconductors via QM/MM Simulations. Acc. Chem. Res. 2010, 43, 995–1004. [Google Scholar] [CrossRef]
- Shen, L.; Yang, W. Molecular Dynamics Simulations with Quantum Mechanics/Molecular Mechanics and Adaptive Neural Networks. J. Chem. Theory Comput. 2018, 14, 1442–1455. [Google Scholar] [CrossRef]
- Pokorná, P.; Kruse, H.; Krepl, M.; Šponer, J. QM/MM Calculations on Protein-RNA Complexes: Understanding Limitations of Classical MD Simulations and Search for Reliable Cost-Effective QM Methods. J. Chem. Theory Comput. 2018, 14, 5419–5433. [Google Scholar] [CrossRef]
- Altoè, P.; · Stenta, M.; · Bottoni, A.; Garavelli, M. A tunable QM/MM approach to chemical reactivity, structure and physico-chemical properties prediction. Theor. Chem. Acc. 2007, 118, 219–240. [Google Scholar] [CrossRef]
- Small, D.W. Remarkable Accuracy of an O(N6) Perturbative Correction to Opposite-Spin CCSD: Are Triples Necessary for Chemical Accuracy in Coupled Cluster? J. Chem. Theory Comput. 2020, 16, 4014–4020. [Google Scholar] [CrossRef]
- Banci, L.; Sigel, A.; Sigel, H.; Sigel, R.K. (Eds.) Metallomics and the Cell; Metal Ions in Life Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 12, pp. 1–13. ISBN 978-94-007-5561-1. [Google Scholar] [CrossRef]
- Thomson, A.J.; Gray, H.B. Bioinorganic chemistry. Curr. Opin. Chem. Biol. 1998, 2, 155–158. [Google Scholar] [CrossRef]
- Waldron, K.J.; Robinson, N.J. How do bacterial cells ensure that metalloproteins get the correct metal? Nat. Rev. Microbiol. 2009, 7, 25–35. [Google Scholar] [CrossRef]
- Carver, P.L. Metal Ions and Infectious Diseases. An Overview from the Clinic. In Interrelations between Essential Metal Ions and Human Diseases; Sigel, A., Sigel, H., Sigel, R.K., Eds.; Metal Ions in Life Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 13, pp. 1–28. ISBN 978-94-007-7499-5. [Google Scholar] [CrossRef]
- Maret, W. Metalloproteomics, metalloproteomes, and the annotation of metalloproteins. Metallomics. 2010, 2, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, J. Metalloproteins. Nature 2009, 460, 813. [Google Scholar] [CrossRef] [PubMed]
- Sparta, M.; Shirvanyants, D.; Ding, F.; Dokholyan, N.V.; Alexandrova, A.N. Hybrid Dynamics Simulation Engine for Metalloproteins. Biophys. J. 2012, 103, 767–776. [Google Scholar] [CrossRef] [PubMed]
- Rulíšek, L.; Havlas, Z. Using DFT Methods for the Prediction of the Structure and Energetics of Metal-Binding Sites in Metalloproteins. Int. J. Quantum Chem. 2003, 91, 504–510. [Google Scholar] [CrossRef]
- Ling, Y.; Zhang, Y. Deciphering Structural Fingerprints for Metalloproteins with Quantum Chemical Calculations. Annu. Rep. Comput. Chem. 2010, 6, 65–77. [Google Scholar] [CrossRef]
- Shirvanyants, D.; Ding, F.; Tsao, D.; Ramachandran, S.; Dokholyan, N.V. Discrete molecular dynamics: An efficient and versatile simulation method for fine protein characterization. J. Phys. Chem. B 2012, 116, 8375–8382. [Google Scholar] [CrossRef]
- Nechay, M.R.; Valdez, C.E.; Alexandrova, A.N. Computational Treatment of Metalloproteins. J. Phys. Chem. B 2015, 119, 5945–5956. [Google Scholar] [CrossRef]
- Xu, M.; He, X.; Zhu, T.; Zhang, J.Z.H. A Fragment Quantum Mechanical Method for Metalloproteins. J. Chem. Theory Comput. 2019, 15, 1430–1439. [Google Scholar] [CrossRef]
- Yan, Z.; Li, X.; Chung, L.W. Multiscale Quantum Refinement Approaches for Metalloproteins. J. Chem. Theory Comput. 2021, 17, 3783–3796. [Google Scholar] [CrossRef]
- Nikolova, V.; Angelova, S.E.; Markova, N.; Dudev, T. Gallium as a Therapeutic Agent: A Thermodynamic Evaluation of the Competition between Ga3+ and Fe3+ Ions in Metalloproteins. J. Phys. Chem. B 2016, 120, 2241–2248. [Google Scholar] [CrossRef]
- Prytkova, T.R.; Kurnikov, I.V.; Beratan, D.N. Ab Initio Based Calculations of Electron-Transfer Rates in Metalloproteins. J. Phys. Chem. B 2005, 109, 1618–1625. [Google Scholar] [CrossRef] [PubMed]
- Zheng, P.; Arantes, G.M.; Field, M.J.; Li, H. Force-induced chemical reactions on the metal centre in a single metalloprotein molecule. Nat. Commun. 2015, 6, 7569. [Google Scholar] [CrossRef] [PubMed]
- Khandelwal, A.; Lukacova, V.; Comez, D.; Kroll, D.M.; Raha, S.; Balaz, S. A Combination of Docking, QM/MM Methods, and MD Simulation for Binding Affinity Estimation of Metalloprotein Ligands. J. Med. Chem. 2005, 48, 5437–5447. [Google Scholar] [CrossRef]
- Banci, L. Molecular dynamics simulations of metalloproteins. Curr. Opin. Chem. Biol. 2003, 7, 143–149. [Google Scholar] [CrossRef]
- Sinnecker, S.; Neese, F. QM/MM calculations with DFT for taking into account protein effects on the EPR and optical spectra of metalloproteins. Plastocyanin as a case study. J. Comput. Chem. 2006, 27, 1463–1475. [Google Scholar] [CrossRef] [PubMed]
- Gleeson, D.; Gleeson, M.P. Application of QM/MM and QM methods to investigate histone deacetylase 8. MedChemComm 2015, 6, 477–485. [Google Scholar] [CrossRef]
- Srnec, M.; Ryde, U.; Rulíšek, L. Reductive cleavage of the O–O bond in multicopper oxidases: A QM/MM and QM study. Faraday Discuss. 2011, 148, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM studies of enzymes. Curr. Opin. Chem. Biol. 2007, 11, 182–187. [Google Scholar] [CrossRef] [PubMed]
- Bowman, A.L.; Ridder, L.; Rietjens, I.M.C.M.; Vervoort, J.; Mulholland, A.J. Molecular Determinants of Xenobiotic Metabolism: QM/MM Simulation of the Conversion of 1-Chloro-2,4-dinitrobenzene Catalyzed by M1-1 Glutathione S-Transferase. Biochemistry 2007, 46, 6353–6363. [Google Scholar] [CrossRef]
- Khandelwal, A.; Balaz, S. QM/MM linear response method distinguishes ligand affinities for closely related metalloproteins. Proteins: Struct. Funct. Bioinform. 2007, 69, 326–339. [Google Scholar] [CrossRef]
- Cho, K.-B.; Derat, E.; Shaik, S. Compound I of Nitric Oxide Synthase: The Active Site Protonation State. J. Am. Chem. Soc. 2007, 129, 3182–3188. [Google Scholar] [CrossRef] [PubMed]
- Robertazzi, A.; Platts, J.A. Gas-Phase DNA Oligonucleotide Structures. A QM/MM and Atoms in Molecules Study. J. Phys. Chem. A 2006, 110, 3992–4000. [Google Scholar] [CrossRef] [PubMed]
- Sala, D.; Giachetti, A.; Rosato, A. Molecular dynamics simulations of metalloproteins: A folding study of rubredoxin from Pyrococcus furiosus. AIMS Biophys. 2018, 5, 77–96. [Google Scholar] [CrossRef]
- Kim, J.; Rees, D.C. Nitrogenase and Biological Nitrogen Fixation. Biochemistry 1994, 33, 389–397. [Google Scholar] [CrossRef]
- Hoffman, B.M.; Lukoyanov, D.; Yang, Z.Y.; Dean, D.R.; Seefeldt, L.C. Mechanism of nitrogen fixation by nitrogenase: The next stage. Chem. Rev. 2014, 114, 4041–4062. [Google Scholar] [CrossRef] [PubMed]
- Burges, B.K.; Lowe, D.J. Mechanism of Molybdenum Nitrogenase. Chem. Rev. 1996, 96, 2983–3011. [Google Scholar] [CrossRef]
- Lawson, D.M.; Smith, B.E. Molybdenum nitrogenases: A crystallographic and mechanistic view. In Metals Ions in Biological System; Sigel, A., Sigel, H., Eds.; CRC Press: Boca Raton, FL, USA, 2002; Volume 39, pp. 75–119. [Google Scholar]
- Brigle, K.E.; Newton, W.E.; Dean, D.R. Complete nucleotide sequence of the Azotobacter vinelandii nitrogenase structural gene cluster. Gene 1985, 37, 37–44. [Google Scholar] [CrossRef]
- Bjornsson, R.; Delgado-Jaime, M.U.; Lima, F.A.; Sippel, D.; Schlesier, J.; Weyhermüller, T.; Einsle, O.; Neese, F.; DeBeer, S. Molybdenum L-Edge XAS Spectra of MoFe Nitrogenase. Z. Anorg. Allg. Chem. 2015, 641, 65–71. [Google Scholar] [CrossRef]
- Hales, B.J. Vanadium Nitrogenase. Catalysts for Nitrogen Fixation: Nitrogenases, Relevant Chemical Models and Commercial Processes; Springer: Berlin/Heidelberg, Germany, 2004; pp. 255–279. ISBN 978-1-4020-3611-8. [Google Scholar] [CrossRef]
- Schneider, K.; Mueller, A. Iron-Only Nitrogenase: Exceptional Catalytic, Structural and Spectroscopic Features. Catalysts for Nitrogen Fixation: Nitrogenases, Relevant Chemical Models and Commercial Processes; Springer: Berlin/Heidelberg, Germany, 2004; pp. 281–307. ISBN 978-1-4020-3611-8. [Google Scholar] [CrossRef]
- Igarashi, R.Y.; Seefeldt, L.C. Nitrogen Fixation: The Mechanism of the Mo-Dependent Nitrogenase. Cr. Rev. Biochem. Mol. Biol. 2003, 38, 351–384. [Google Scholar] [CrossRef]
- Modak, J.M. Haber Process for Ammonia Synthesis. Resonance 2002, 7, 69–77. [Google Scholar] [CrossRef]
- Burgess, B.K. Molybdenum Enzymes (Metal Ions in Biology Series); Spiro, T.G., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 1985; ISBN 978-0471885429. [Google Scholar]
- Simpson, F.B.; Burris, R.H. A nitrogen pressure of 50 atmospheres does not prevent evolution of hydrogen by nitrogenase. Science 1984, 224, 1095–1097. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.Y.; Danyal, K.; Seefeldt, L.C. Mechanism of Mo-Dependent Nitrogenase. Nitrogen Fixation. In Methods in Molecular Biology (Methods and Protocols); Ribbe, M., Ed.; Humana Press: Totowa, NJ, USA, 2011; Volume 766. [Google Scholar] [CrossRef]
- Barney, B.M.; Lee, H.I.; Dos Santos, P.C.; Hoffman, B.M.; Dean, D.R.; Seefeldt, L.C. Breaking the N2 triple bond: Insights into the nitrogenase mechanism. DalT Trans. 2006, 19, 2277–2284. [Google Scholar] [CrossRef]
- Neese, F. The Yandulov/Schrock cycle and the nitrogenase reaction: Pathways of nitrogen fixation studied by density functional theory. Ang. Chem. 2005, 45, 196–199. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Ryde, U. Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase. Int. J. Quant. Chem. 2018, 118, e25627. [Google Scholar] [CrossRef]
- Benediktsson, B.; Bjornsson, R. QM/MM Study of the Nitrogenase MoFe Protein Resting State: Broken-Symmetry States, Protonation States, and QM Region Convergence in the FeMoco Active Site. Inorg. Chem. 2017, 56, 13417–13429. [Google Scholar] [CrossRef]
- Spatzal, T.; Aksoyoglu, M.; Zhang, L.; Andrade, S.L.A.; Schleicher, E.; Weber, S.; Rees, D.C.; Einsle, O. Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor. Science 2011, 334, 940. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Van Stappen, C.; Thorhallsson, A.T.; Decamps, L.; Bjornsson, R.; DeBeer, S. Resolving the structure of the E1 state of Mo nitrogenase through Mo and Fe K-edge EXAFS and QM/MM calculations. Chem. Sci. 2019, 10, 9807–9821. [Google Scholar] [CrossRef]
- Thorhallsson, A.T.; Benediktsson, B.; Bjornsson, R. A model for dinitrogen binding in the E4 state of nitrogenase. Chem. Sci. 2019, 10, 11110–11124. [Google Scholar] [CrossRef]
- Cao, L.; Caldararu, O.; Ryde, U. Protonation and Reduction of the FeMo Cluster in Nitrogenase Studied by Quantum Mechanics/Molecular Mechanics (QM/MM) Calculations. J. Chem. Theory Comput. 2018, 14, 6653–6678. [Google Scholar] [CrossRef] [PubMed]
- Lukoyanov, D.A.; Yang, Z.-Y.; Dean, D.R.; Seefeldt, L.C.; Raugei, S.; Hoffman, B.M. Electron Redistribution within the Nitrogenase Active Site FeMo- Cofactor During Reductive Elimination of H2 to Achieve N≡N Triple-Bond Activation. J. Am. Chem. Soc. 2020, 142, 21679–21690. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Ryde, U. N2H2 binding to the nitrogenase FeMo cluster studied by QM/MM methods. J. Biol. Inorg. Chem. 2020, 25, 521–540. [Google Scholar] [CrossRef] [PubMed]
- Seefeldt, L.C.; Yang, Z.-Y.; Lukoyanov, D.A.; Harris, D.F.; Dean, D.R.; Raugei, S.; Hoffman, B.M. Reduction of Substrates by Nitrogenases. Chem. Rev. 2020, 120, 5082–5106. [Google Scholar] [CrossRef]
- Hoffman, B.M.; Lukoyanov, D.; Dean, D.R.; Seefeldt, L.C. Nitrogenase: A draft mechanism. Acc. Chem. Res. 2013, 46, 587–595. [Google Scholar] [CrossRef]
- Sgrignani, J.; Franco, D.; Magistrato, A. Theoretical Studies of Homogeneous Catalysts Mimicking Nitrogenase. Molecules 2011, 16, 442–465. [Google Scholar] [CrossRef]
- Lukoyanov, D.; Khadka, N.; Yang, Z.Y.; Dean, D.R.; Seefeldt, L.C.; Hoffman, B.M. Reversible Photoinduced Reductive Elimination of H2 from the Nitrogenase Dihydride State, the E4(4H) Janus Intermediate. J. Am. Chem. Soc. 2016, 138, 1320–1327. [Google Scholar] [CrossRef]
- Lukoyanov, D.A.; Krzyaniak, M.D.; Dean, D.R.; Wasielewski, M.R.; Seefeldt, L.C.; Hoffman, B.M. Time-Resolved EPR Study of H2 Reductive Elimination from the Photoexcited Nitrogenase Janus E4(4H) Intermediate. J. Phys. Chem. B 2019, 123, 8823–8828. [Google Scholar] [CrossRef]
- Lukoyanov, D.; Khadka, N.; Dean, D.R.; Raugei, S.; Seefeldt, L.C.; Hoffman, B.M. Photoinduced Reductive Elimination of H2 from the Nitrogenase Dihydride (Janus) State Involves a FeMo-cofactor-H2 Intermediate. Inorg. Chem. 2017, 56, 2233–2240. [Google Scholar] [CrossRef]
- Raugei, S.; Seefeldt, L.C.; Hoffman, B.M. Critical computational analysis illuminates the reductive-elimination mechanism that activates nitrogenase for N2 reduction. Proc. Natl. Acad. Sci. USA 2018, 115, E10521. [Google Scholar] [CrossRef]
- Tzeli, D.; Raugei, S.; Xantheas, S.S. Quantitative Account of the Bonding Properties of a Rubredoxin Model Complex [Fe(SCH3)4]q, q = −2, −1, +2, +3. J. Chem. Theory Comput. 2021, 17, 6080–6091. [Google Scholar] [CrossRef] [PubMed]
- Mejuto-Zaera, C.; Tzeli, D.; Williams-Young, D.; Tubman, N.M.; Matoušek, M.; Brabec, J.; Veis, L.; Xantheas, S.S.; de Jong, W.A. The Effect of Geometry, Spin and Orbital Optimization in Achieving Accurate, Correlated Results for Iron-Sulfur Cubanes. J. Chem. Theory Comput. 2022. accepted. [Google Scholar] [CrossRef] [PubMed]
- Elghobashi-Meinhardt, N.; Tombolelli, D.; Mroginski, M.A. Electronic and Structural Properties of the Double Cubane Iron-Sulfur Cluster. Catalysts 2021, 11, 245. [Google Scholar] [CrossRef]
- Bartlett, R.J. Adventures in DFT by a wavefunction theorist. J. Chem. Phys. 2019, 151, 160901. [Google Scholar] [CrossRef]
- Church, J.R.; Olsen, J.M.H.; Schapiro, I. The Impact of Retinal Configuration on the Protein–Chromophore Interactions in Bistable Jumping Spider Rhodopsin-1. Molecules 2022, 27, 71. [Google Scholar] [CrossRef]
- Chontzopoulou, E.; Papaemmanouil, C.; Chatziathanasiadou, M.V.; Kolokouris, D.; Kiriakidi, S.; Konstantinidi, A.; Gerogianni, I.; Tselios, T.; Kostakis, I.K.; Chrysina, E.D.; et al. Artificial and natural sweeteners as potential anti-inflammatory agents. J. Biomol. Struct. Dyn. 2021, 9, 1–13. [Google Scholar] [CrossRef]
- Tolbatov, I.; Marrone, A.; Coletti, C.; Re, N. Computational Studies of Au(I) and Au(III) Anticancer MetalLodrugs: A Survey. Molecules 2021, 26, 7600. [Google Scholar] [CrossRef]
- Skoko, S.; Ambrosetti, M.; Giovannini, T.; Cappelli, C. Simulating Absorption Spectra of Flavonoids in Aqueous Solution: A Polarizable QM/MM Study. Molecules 2020, 25, 5853. [Google Scholar] [CrossRef]
- Spinello, A.; Ritacco, I.; Magistrato, A. The Catalytic Mechanism of Steroidogenic Cytochromes P450 from All-Atom Simulations: Entwinement with Membrane Environment, Redox Partners, and Post-Transcriptional Regulation. Catalysts 2019, 9, 81. [Google Scholar] [CrossRef]
- Krivitskaya, A.V.; Khrenova, M.G.; Nemukhin, A.V. Two Sides of Quantum-Based Modeling of Enzyme-Catalyzed Reactions: Mechanistic and Electronic Structure Aspects of the Hydrolysis by Glutamate Carboxypeptidase. Molecules 2021, 26, 6280. [Google Scholar] [CrossRef]
- Yu, Μ.; Liu, Υ. A QM/MM Study on the Initiation Reaction of Firefly Bioluminescence- Enzymatic Oxidation of Luciferin. Molecules 2021, 26, 4222. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, N.; Gouleni, N.; Chontzopoulou, E.; Skoufas, G.S.; Gkionis, A.; Tzeli, D.; Vassiliou, S.; Mavromoustakos, T. Structure assignment, conformational properties and discovery of potential targets of the Ugi cinnamic adduct NGI25. J. Biomol. Struct. Dyn. 2021. [Google Scholar] [CrossRef] [PubMed]
- Zlobin, A.; Diankin, I.; Pushkarev, S.; Golovin, A. Probing the Suitability of Different Ca2+ Parameters for Long Simulations of Diisopropyl Fluorophosphatase. Molecules 2021, 26, 5839. [Google Scholar] [CrossRef] [PubMed]
- Landi, A.; Capobianco, A.; Peluso, A. The Time Scale of Electronic Resonance in Oxidized DNA as Modulated by Solvent Response: An MD/QM-MM Study. Molecules 2021, 26, 5497. [Google Scholar] [CrossRef] [PubMed]
- Bouback, T.A.; Pokhrel, S.; Albeshri, A.; Aljohani, A.M.; Samad, A.; Alam, R.; Hossen, M.S.; Al-Ghamdi, K.; Talukder, M.E.K.; Ahammad, F.; et al. Pharmacophore-Based Virtual Screening, Quantum Mechanics Calculations, and Molecular Dynamics Simulation Approaches Identified Potential Natural Antiviral Drug Candidates against MERS-CoV S1-NTD. Molecules 2021, 26, 4961. [Google Scholar] [CrossRef]
- Breijyeh, Z.; Karaman, R. Enzyme Models-From Catalysis to Prodrugs. Molecules 2021, 26, 3248. [Google Scholar] [CrossRef]
- Khrenova, M.G.; Bulavko, E.S.; Mulashkin, F.D.; Nemukhin, A.V. Mechanism of Guanosine Triphosphate Hydrolysis by the Visual Proteins Arl3-RP2: Free Energy Reaction Profiles Computed with Ab Initio Type QM/MM Potentials. Molecules 2021, 26, 3998. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzeliou, C.E.; Mermigki, M.A.; Tzeli, D. Review on the QM/MM Methodologies and Their Application to Metalloproteins. Molecules 2022, 27, 2660. https://doi.org/10.3390/molecules27092660
Tzeliou CE, Mermigki MA, Tzeli D. Review on the QM/MM Methodologies and Their Application to Metalloproteins. Molecules. 2022; 27(9):2660. https://doi.org/10.3390/molecules27092660
Chicago/Turabian StyleTzeliou, Christina Eleftheria, Markella Aliki Mermigki, and Demeter Tzeli. 2022. "Review on the QM/MM Methodologies and Their Application to Metalloproteins" Molecules 27, no. 9: 2660. https://doi.org/10.3390/molecules27092660
APA StyleTzeliou, C. E., Mermigki, M. A., & Tzeli, D. (2022). Review on the QM/MM Methodologies and Their Application to Metalloproteins. Molecules, 27(9), 2660. https://doi.org/10.3390/molecules27092660








