Modeling the Dynamics of Protein–Protein Interfaces, How and Why?
Abstract
1. Introduction
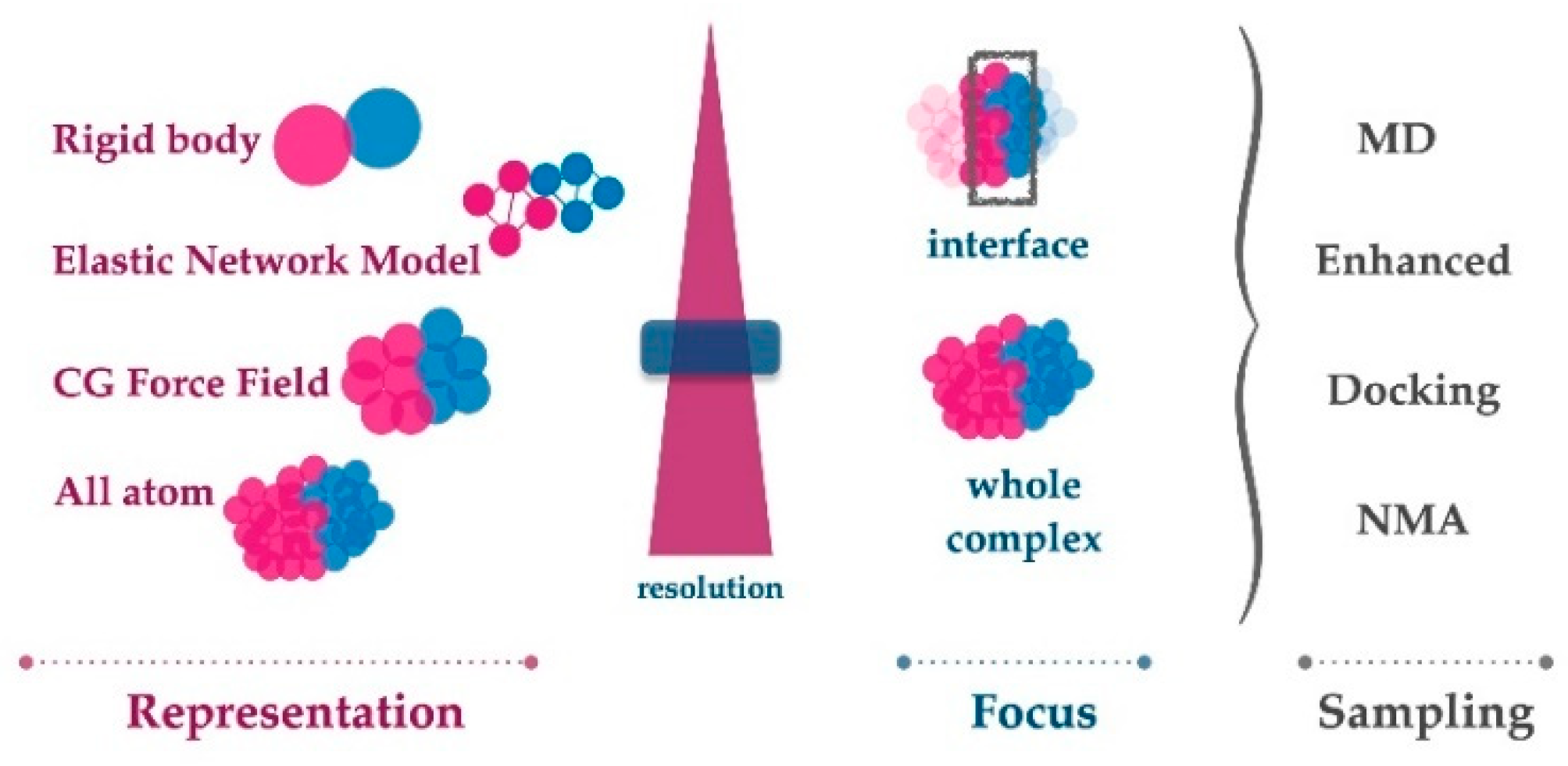
2. Tools for Calculating PPI Dynamics
2.1. Classical All-Atom Molecular Dynamics Simulations
2.2. All-Atom Enhanced Interface Sampling Approaches
2.3. Sampling the Protein Interface at the Coarse-Grain Level
2.4. Integrating Experimental Data Reporting on the Protein Interface Dynamics
2.5. Analysis of the Interface Dynamics
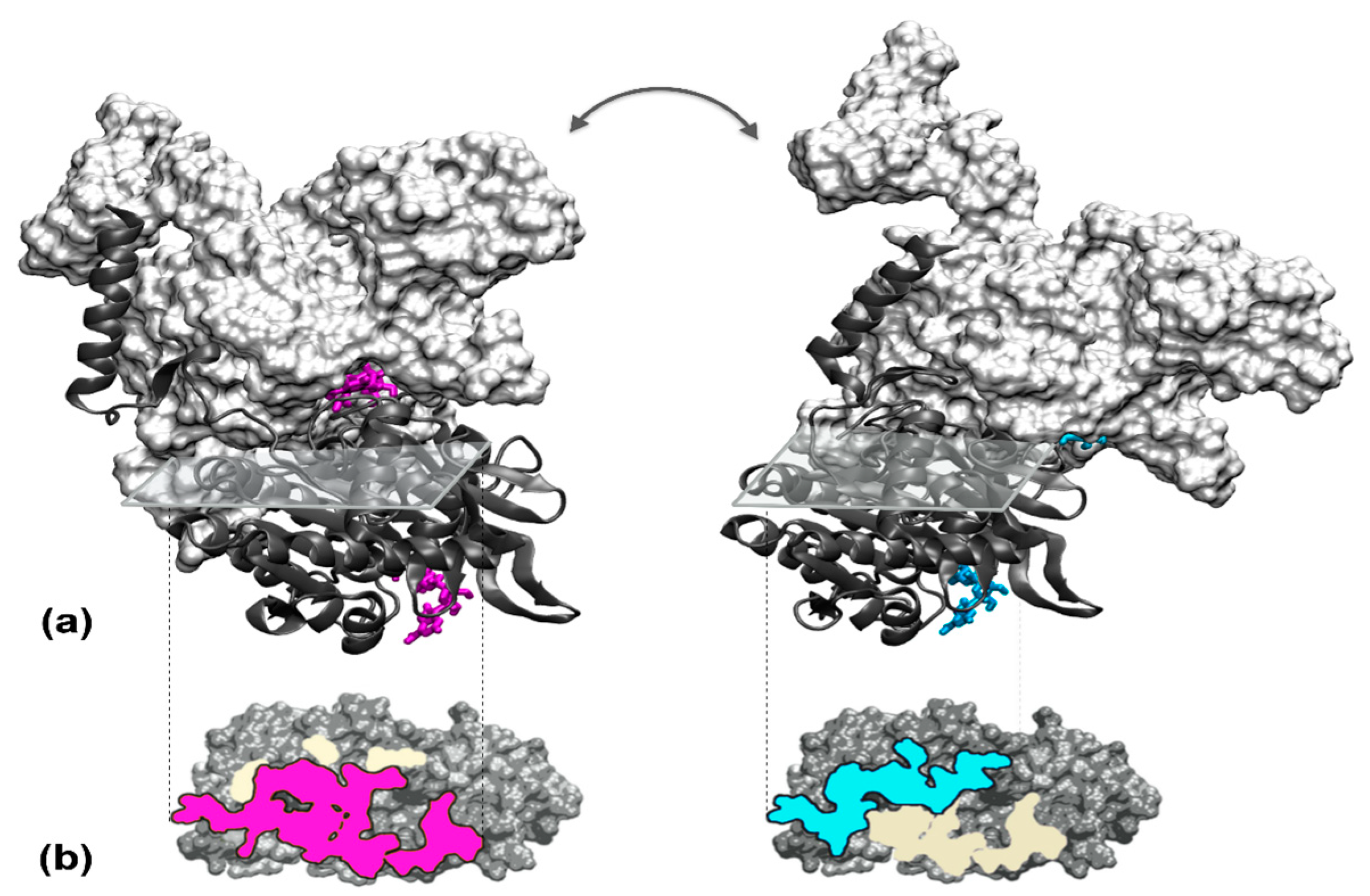
3. E Pur Si Muove! How Can We Relate Protein Function to Interfaces Dynamics?
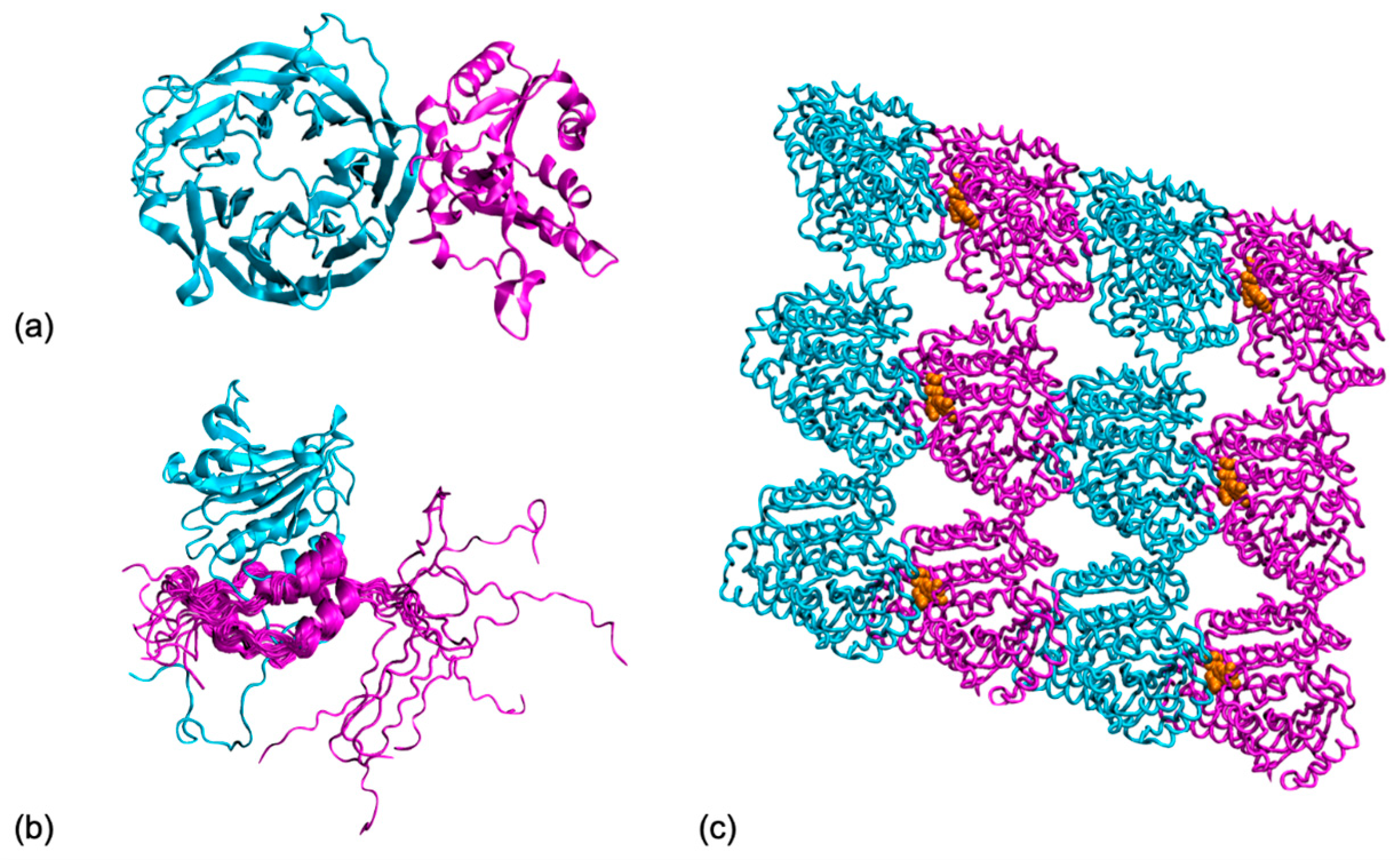
3.1. Interface Dynamics between Folded Partners
3.1.1. Dynamics of the Isolated Partners
3.1.2. Interface Dynamics within the Protein Complex
3.2. Interfaces Dynamics within Disordered Partners
3.3. Active Interfaces within Molecular Machines
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alberts, B. The cell as a collection of protein machines: Preparing the next generation of molecular biologists. Cell 1998, 92, 291–294. [Google Scholar] [CrossRef]
- Robinson, C.V.; Sali, A.; Baumeister, W. The molecular sociology of the cell. Nature 2007, 450, 973–982. [Google Scholar] [CrossRef]
- Braun, P.; Gingras, A.C. History of protein-protein interactions: From egg-white to complex networks. Proteomics 2012, 12, 1478–1498. [Google Scholar] [CrossRef] [PubMed]
- Ideker, T.; Sharan, R. Protein networks in disease. Genome Res 2008, 18, 644–652. [Google Scholar] [CrossRef] [PubMed]
- Nooren, I.M.A.; Thornton, J.M. Diversity of protein-protein interactions. EMBO J. 2003, 22, 3486–3492. [Google Scholar] [CrossRef] [PubMed]
- Marsh, J.A.; Teichmann, S.A. Structure, dynamics, assembly, and evolution of protein complexes. Annu. Rev. Biochem. 2015, 84, 551–575. [Google Scholar] [CrossRef]
- Pieters, B.J.; van Eldijk, M.B.; Nolte, R.J.; Mecinovic, J. Natural supramolecular protein assemblies. Chem. Soc. Rev. 2016, 45, 24–39. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Sit, A.; Christoffer, C.; Chen, S.; Kihara, D. A global map of the protein shape universe. PLoS Comput Biol 2019, 15, e1006969. [Google Scholar] [CrossRef]
- Zhao, G.; Perilla, J.R.; Yufenyuy, E.L.; Meng, X.; Chen, B.; Ning, J.; Ahn, J.; Gronenborn, A.M.; Schulten, K.; Aiken, C.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643–646. [Google Scholar] [CrossRef]
- Perkins, J.R.; Diboun, I.; Dessailly, B.H.; Lees, J.G.; Orengo, C. Transient Protein-Protein Interactions: Structural, Functional, and Network Properties. Structure 2010, 18, 1233–1243. [Google Scholar] [CrossRef]
- Shoemaker, B.A.; Panchenko, A.R. Deciphering protein-protein interactions. Part I. Experimental techniques and databases. PLoS Comput. Biol. 2007, 3, e42. [Google Scholar] [CrossRef]
- Hein, M.Y.; Hubner, N.C.; Poser, I.; Cox, J.; Nagaraj, N.; Toyoda, Y.; Gak, I.A.; Weisswange, I.; Mansfeld, J.; Buchholz, F.; et al. A human interactome in three quantitative dimensions organized by stoichiometries and abundances. Cell 2015, 163, 712–723. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Battistuz, T.; Bhat, T.N.; Bluhm, W.F.; Bourne, P.E.; Burkhardt, K.; Feng, Z.; Gilliland, G.L.; Iype, L.; Jain, S.; et al. The Protein Data Bank. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, 58, 899–907. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.C.; McMullan, G.; Scheres, S.H. How cryo-EM is revolutionizing structural biology. Trends Biochem. Sci. 2015, 40, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Glaeser, R.M.; Nogales, E. How Cryo-EM Became so Hot. Cell 2017, 171, 1229–1231. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Li, Q.; Wang, R. Current Experimental Methods for Characterizing Protein-Protein Interactions. ChemMedChem 2016, 11, 738–756. [Google Scholar] [CrossRef] [PubMed]
- Vamparys, L.; Laurent, B.; Carbone, A.; Sacquin-Mora, S. Great interactions: How binding incorrect partners can teach us about protein recognition and function. Proteins 2016, 84, 1408–1421. [Google Scholar] [CrossRef]
- Lagarde, N.; Carbone, A.; Sacquin-Mora, S. Hidden partners: Using cross-docking calculations to predict binding sites for proteins with multiple interactions. Proteins 2018, 86, 723–737. [Google Scholar] [CrossRef] [PubMed]
- Schweke, H.; Mucchielli, M.H.; Sacquin-Mora, S.; Bei, W.; Lopes, A. Protein Interaction Energy Landscapes are Shaped by Functional and also Non-functional Partners. J. Mol. Biol. 2020, 432, 1183–1198. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, B.A.; Panchenko, A.R. Deciphering protein-protein interactions. Part II. Computational methods to predict protein and domain interaction partners. PLoS Comput. Biol. 2007, 3, e43. [Google Scholar] [CrossRef]
- Kuzu, G.; Keskin, O.; Nussinov, R.; Gursoy, A. Modeling protein assemblies in the proteome. Mol Cell Proteomics 2014, 13, 887–896. [Google Scholar] [CrossRef] [PubMed]
- Vakser, I.A. Challenges in protein docking. Curr. Opin. Struct. Biol. 2020, 64, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Mendez, R.; Leplae, R.; De Maria, L.; Wodak, S.J. Assessment of blind predictions of protein-protein interactions: Current status of docking methods. Proteins 2003, 52, 51–67. [Google Scholar] [CrossRef] [PubMed]
- Lensink, M.F.; Nadzirin, N.; Velankar, S.; Wodak, S.J. Modeling protein-protein, protein-peptide, and protein-oligosaccharide complexes: CAPRI 7th edition. Proteins 2020, 88, 916–938. [Google Scholar] [CrossRef] [PubMed]
- Lensink, M.F.; Brysbaert, G.; Mauri, T.; Nadzirin, N.; Velankar, S.; Chaleil, R.A.G.; Clarence, T.; Bates, P.A.; Kong, R.; Liu, B.; et al. Prediction of protein assemblies, the next frontier: The CASP14-CAPRI experiment. Proteins 2021, 89, 1800–1823. [Google Scholar] [CrossRef]
- Lafita, A.; Bliven, S.; Kryshtafovych, A.; Bertoni, M.; Monastyrskyy, B.; Duarte, J.M.; Schwede, T.; Capitani, G. Assessment of protein assembly prediction in CASP12. Proteins 2018, 86 (Suppl. 1), 247–256. [Google Scholar] [CrossRef] [PubMed]
- Guzenko, D.; Lafita, A.; Monastyrskyy, B.; Kryshtafovych, A.; Duarte, J.M. Assessment of protein assembly prediction in CASP13. Proteins 2019, 87, 1190–1199. [Google Scholar] [CrossRef]
- Ozden, B.; Kryshtafovych, A.; Karaca, E. Assessment of the CASP14 assembly predictions. Proteins 2021, 89, 1787–1799. [Google Scholar] [CrossRef]
- Fong, J.H.; Shoemaker, B.A.; Garbuzynskiy, S.O.; Lobanov, M.Y.; Galzitskaya, O.V.; Panchenko, A.R. Intrinsic disorder in protein interactions: Insights from a comprehensive structural analysis. PLoS Comput Biol 2009, 5, e1000316. [Google Scholar] [CrossRef]
- Kuzu, G.; Gursoy, A.; Nussinov, R.; Keskin, O. Exploiting conformational ensembles in modeling protein-protein interactions on the proteome scale. J Proteome Res 2013, 12, 2641–2653. [Google Scholar] [CrossRef]
- Fuchs, J.E.; Huber, R.G.; Waldner, B.J.; Kahler, U.; von Grafenstein, S.; Kramer, C.; Liedl, K.R. Dynamics Govern Specificity of a Protein-Protein Interface: Substrate Recognition by Thrombin. PLoS ONE 2015, 10, e0140713. [Google Scholar] [CrossRef]
- Visscher, K.M.; Kastritis, P.L.; Bonvin, A.M. Non-interacting surface solvation and dynamics in protein-protein interactions. Proteins 2015, 83, 445–458. [Google Scholar] [CrossRef]
- Fuxreiter, M. Fuzziness in Protein Interactions-A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287. [Google Scholar] [CrossRef]
- Halakou, F.; Gursoy, A.; Keskin, O. Embedding Alternative Conformations of Proteins in Protein-Protein Interaction Networks. Methods Mol Biol 2020, 2074, 113–124. [Google Scholar] [CrossRef] [PubMed]
- van Wijk, S.J.; Melquiond, A.S.; de Vries, S.J.; Timmers, H.T.; Bonvin, A.M. Dynamic control of selectivity in the ubiquitination pathway revealed by an ASP to GLU substitution in an intra-molecular salt-bridge network. PLoS Comput. Biol. 2012, 8, e1002754. [Google Scholar] [CrossRef] [PubMed]
- Vishwanath, S.; Sukhwal, A.; Sowdhamini, R.; Srinivasan, N. Specificity and stability of transient protein-protein interactions. Curr. Opin. Struct. Biol. 2017, 44, 77–86. [Google Scholar] [CrossRef]
- Nicoludis, J.M.; Green, A.G.; Walujkar, S.; May, E.J.; Sotomayor, M.; Marks, D.S.; Gaudet, R. Interaction specificity of clustered protocadherins inferred from sequence covariation and structural analysis. Proc. Natl. Acad. Sci. USA 2019, 116, 17825–17830. [Google Scholar] [CrossRef]
- Ozdemir, E.S.; Nussinov, R.; Gursoy, A.; Keskin, O. Developments in integrative modeling with dynamical interfaces. Curr. Opin. Struct. Biol. 2019, 56, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Kharche, S.A.; Sengupta, D. Dynamic protein interfaces and conformational landscapes of membrane protein complexes. Curr. Opin. Struct. Biol. 2020, 61, 191–197. [Google Scholar] [CrossRef]
- Kurkcuoglu, Z.; Bonvin, A. Pre- and post-docking sampling of conformational changes using ClustENM and HADDOCK for protein-protein and protein-DNA systems. Proteins 2020, 88, 292–306. [Google Scholar] [CrossRef]
- Perilla, J.R.; Goh, B.C.; Cassidy, C.K.; Liu, B.; Bernardi, R.C.; Rudack, T.; Yu, H.; Wu, Z.; Schulten, K. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 2015, 31, 64–74. [Google Scholar] [CrossRef]
- Rakers, C.; Bermudez, M.; Keller, B.G.; Mortier, J.; Wolber, G. Computational close up on protein–protein interactions: How to unravel the invisible using molecular dynamics simulations? WIREs Comput. Mol. Sci. 2015, 5, 345–359. [Google Scholar] [CrossRef]
- Eyrisch, S.; Helms, V. Transient pockets on protein surfaces involved in protein-protein interaction. J. Med. Chem. 2007, 50, 3457–3464. [Google Scholar] [CrossRef]
- Eyrisch, S.; Medina-Franco, J.L.; Helms, V. Transient pockets on XIAP-BIR2: Toward the characterization of putative binding sites of small-molecule XIAP inhibitors. J. Mol. Model. 2012, 18, 2031–2042. [Google Scholar] [CrossRef]
- Jász, Á.; Rák, Á.; Ladjánszki, I.; Cserey, G. Classical molecular dynamics on graphics processing unit architectures. WIREs Comput. Mol. Sci. 2020, 10, e1444. [Google Scholar] [CrossRef]
- Bock, L.V.; Blau, C.; Schroder, G.F.; Davydov, I.I.; Fischer, N.; Stark, H.; Rodnina, M.V.; Vaiana, A.C.; Grubmuller, H. Energy barriers and driving forces in tRNA translocation through the ribosome. Nat. Struct. Mol. Biol. 2013, 20, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.H.; Hsin, J.; Sotomayor, M.; Comellas, G.; Schulten, K. Discovery Through the Computational Microscope. Structure 2009, 17, 1295–1306. [Google Scholar] [CrossRef]
- Pavadai, E.; Bhattarai, N.; Baral, P.; Stahelin, R.V.; Chapagain, P.P.; Gerstman, B.S. Conformational Flexibility of the Protein-Protein Interfaces of the Ebola Virus VP40 Structural Matrix Filament. J. Phys. Chem. B 2019, 123, 9045–9053. [Google Scholar] [CrossRef]
- Padhi, A.K.; Rath, S.L.; Tripathi, T. Accelerating COVID-19 Research Using Molecular Dynamics Simulation. J. Phys. Chem. B 2021, 125, 9078–9091. [Google Scholar] [CrossRef]
- Gong, X.; Zhang, Y.; Chen, J. Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions. Biomolecules 2021, 11, 1416. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffenberger, E.; Bates, P.A. Refinement of protein-protein complexes in contact map space with metadynamics simulations. Proteins 2019, 87, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Emperador, A.; Solernou, A.; Sfriso, P.; Pons, C.; Gelpi, J.L.; Fernandez-Recio, J.; Orozco, M. Efficient Relaxation of Protein-Protein Interfaces by Discrete Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 1222–1229. [Google Scholar] [CrossRef]
- Siebenmorgen, T.; Engelhard, M.; Zacharias, M. Prediction of protein-protein complexes using replica exchange with repulsive scaling. J. Comput. Chem. 2020, 41, 1436–1447. [Google Scholar] [CrossRef]
- Siebenmorgen, T.; Zacharias, M. Efficient Refinement and Free Energy Scoring of Predicted Protein-Protein Complexes Using Replica Exchange with Repulsive Scaling. J. Chem. Inf. Model. 2020, 60, 5552–5562. [Google Scholar] [CrossRef]
- Scafuri, N.; Soler, M.A.; Spitaleri, A.; Rocchia, W. Enhanced Molecular Dynamics Method to Efficiently Increase the Discrimination Capability of Computational Protein-Protein Docking. J. Chem. Theory Comput. 2021, 7, 7271–7280. [Google Scholar] [CrossRef]
- Dominguez, C.; Boelens, R.; Bonvin, A.M. HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 2003, 125, 1731–1737. [Google Scholar] [CrossRef]
- Mollica, L.; Decherchi, S.; Zia, S.R.; Gaspari, R.; Cavalli, A.; Rocchia, W. Kinetics of protein-ligand unbinding via smoothed potential molecular dynamics simulations. Sci. Rep. 2015, 5, 11539. [Google Scholar] [CrossRef]
- Harmalkar, A.; Gray, J.J. Advances to tackle backbone flexibility in protein docking. Curr. Opin. Struct. Biol. 2021, 67, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Pak, A.J.; Voth, G.A. Advances in coarse-grained modeling of macromolecular complexes. Curr. Opin. Struct. Biol. 2018, 52, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Kurcinski, M.; Kmiecik, S.; Zalewski, M.; Kolinski, A. Protein-Protein Docking with Large-Scale Backbone Flexibility Using Coarse-Grained Monte-Carlo Simulations. Int. J. Mol. Sci. 2021, 22, 7341. [Google Scholar] [CrossRef] [PubMed]
- Emperador, A.; Sfriso, P.; Villarreal, M.A.; Gelpi, J.L.; Orozco, M. PACSAB: Coarse-Grained Force Field for the Study of Protein-Protein Interactions and Conformational Sampling in Multiprotein Systems. J. Chem. Theory Comput. 2015, 11, 5929–5938. [Google Scholar] [CrossRef]
- Emperador, A.; Meyer, T.; Orozco, M. Protein flexibility from discrete molecular dynamics simulations using quasi-physical potentials. Proteins 2010, 78, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Grossfield, A. Recent progress in the study of G protein-coupled receptors with molecular dynamics computer simulations. Biochim. Biophys. Acta 2011, 1808, 1868–1878. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.; Zhao, X.; Liu, J.; Schneebeli, S.T.; Shelley, J.C.; Li, J. Capturing the multiscale dynamics of membrane protein complexes with all-atom, mixed-resolution, and coarse-grained models. Phys. Chem. Chem. Phys. PCCP 2017, 19, 9181–9188. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef]
- Tirion, M.M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Tozzini, V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 2005, 15, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Zen, A.; Micheletti, C.; Keskin, O.; Nussinov, R. Comparing interfacial dynamics in protein-protein complexes: An elastic network approach. BMC Struct. Biol. 2010, 10, 26. [Google Scholar] [CrossRef] [PubMed]
- Stadler, A.M.; Garvey, C.J.; Bocahut, A.; Sacquin-Mora, S.; Digel, I.; Schneider, G.J.; Natali, F.; Artmann, G.M.; Zaccai, G. Thermal fluctuations of haemoglobin from different species: Adaptation to temperature via conformational dynamics. J. R. Soc. Interface 2012, 9, 2845–2855. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Hu, J.; Yan, W.; Jiang, H.; Hu, G.; Luo, C. Deciphering the role of dimer interface in intrinsic dynamics and allosteric pathways underlying the functional transformation of DNMT3A. Biochim. Biophys. Acta Gen. Subj. 2018, 1862, 1667–1679. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, Y.; Kinoshita, K.; Endo, S.; Wako, H. Dynamic features of homodimer interfaces calculated by normal-mode analysis. Protein Sci. A Publ. Protein Soc. 2012, 21, 1503–1513. [Google Scholar] [CrossRef] [PubMed]
- Wako, H.; Endo, S. Normal mode analysis based on an elastic network model for biomolecules in the Protein Data Bank, which uses dihedral angles as independent variables. Comput. Biol. Chem. 2013, 44, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Dudas, E.F.; Palfy, G.; Menyhard, D.K.; Sebak, F.; Ecsedi, P.; Nyitray, L.; Bodor, A. Tumor-Suppressor p53TAD(1-60) Forms a Fuzzy Complex with Metastasis-Associated S100A4: Structural Insights and Dynamics by an NMR/MD Approach. ChemBioChem 2020, 21, 3087–3095. [Google Scholar] [CrossRef]
- Sprangers, R.; Velyvis, A.; Kay, L.E. Solution NMR of supramolecular complexes: Providing new insights into function. Nat. Methods 2007, 4, 697–703. [Google Scholar] [CrossRef]
- Spreitzer, E.; Usluer, S.; Madl, T. Probing Surfaces in Dynamic Protein Interactions. J. Mol. Biol. 2020, 432, 2949–2972. [Google Scholar] [CrossRef]
- Hennig, J.; de Vries, S.J.; Hennig, K.D.; Randles, L.; Walters, K.J.; Sunnerhagen, M.; Bonvin, A.M. MTMDAT-HADDOCK: High-throughput, protein complex structure modeling based on limited proteolysis and mass spectrometry. BMC Struct. Biol. 2012, 12, 29. [Google Scholar] [CrossRef]
- Rey, M.; Sarpe, V.; Burns, K.M.; Buse, J.; Baker, C.A.; van Dijk, M.; Wordeman, L.; Bonvin, A.M.; Schriemer, D.C. Mass spec studio for integrative structural biology. Structure 2014, 22, 1538–1548. [Google Scholar] [CrossRef]
- Graziadei, A.; Rappsilber, J. Leveraging crosslinking mass spectrometry in structural and cell biology. Structure 2022, 30, 37–54. [Google Scholar] [CrossRef]
- Schneidman-Duhovny, D.; Hammel, M. Modeling Structure and Dynamics of Protein Complexes with SAXS Profiles. Methods Mol. Biol. 2018, 1764, 449–473. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, C.; Macpherson, J.A.; Lau, A.M.; Tan, K.W.; Fraternali, F.; Politis, A. Surface Accessibility and Dynamics of Macromolecular Assemblies Probed by Covalent Labeling Mass Spectrometry and Integrative Modeling. Anal. Chem. 2017, 89, 1459–1468. [Google Scholar] [CrossRef]
- do Nascimento, N.M.; Juste-Dolz, A.; Bueno, P.R.; Monzó, I.; Tejero, R.; Lopez-Paz, J.L.; Maquieira, A.; Morais, S.; Gimenez-Romero, D. Mapping molecular binding by means of conformational dynamics measurements. RSC Adv 2018, 8, 867–876. [Google Scholar] [CrossRef]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. ROSETTA3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011, 487, 545–574. [Google Scholar] [CrossRef]
- Karaca, E.; Rodrigues, J.; Graziadei, A.; Bonvin, A.; Carlomagno, T. M3: An integrative framework for structure determination of molecular machines. Nat. Methods 2017, 14, 897–902. [Google Scholar] [CrossRef]
- Webb, B.; Viswanath, S.; Bonomi, M.; Pellarin, R.; Greenberg, C.H.; Saltzberg, D.; Sali, A. Integrative structure modeling with the Integrative Modeling Platform. Protein Sci. A Publ. Protein Soc. 2018, 27, 245–258. [Google Scholar] [CrossRef]
- Kharche, S.; Joshi, M.; Chattopadhyay, A.; Sengupta, D. Conformational plasticity and dynamic interactions of the N-terminal domain of the chemokine receptor CXCR1. PLoS Comput. Biol. 2021, 17, e1008593. [Google Scholar] [CrossRef]
- Morcos, F.; Onuchic, J.N. The role of coevolutionary signatures in protein interaction dynamics, complex inference, molecular recognition, and mutational landscapes. Curr. Opin. Struct. Biol. 2019, 56, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Weigt, M.; White, R.A.; Szurmant, H.; Hoch, J.A.; Hwa, T. Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. USA 2009, 106, 67–72. [Google Scholar] [CrossRef]
- Dago, A.E.; Schug, A.; Procaccini, A.; Hoch, J.A.; Weigt, M.; Szurmant, H. Structural basis of histidine kinase autophosphorylation deduced by integrating genomics, molecular dynamics, and mutagenesis. Proc. Natl. Acad. Sci. USA 2012, 109, E1733–E1742. [Google Scholar] [CrossRef]
- Szurmant, H.; Weigt, M. Inter-residue, inter-protein and inter-family coevolution: Bridging the scales. Curr. Opin. Struct. Biol. 2018, 50, 26–32. [Google Scholar] [CrossRef]
- Malinverni, D.; Jost Lopez, A.; De Los Rios, P.; Hummer, G.; Barducci, A. Modeling Hsp70/Hsp40 interaction by multi-scale molecular simulations and coevolutionary sequence analysis. eLife 2017, 6, e23471. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernandez, C.X.; Schwantes, C.R.; Wang, L.P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef]
- Bouysset, C.; Fiorucci, S. ProLIF: A library to encode molecular interactions as fingerprints. J. Cheminform. 2021, 13, 72. [Google Scholar] [CrossRef]
- Rodrigues, J.; Valentine, C.; Jimenez, B. Joaorodrigues/Interfacea: First Beta Version of the API. 2019. Available online: https://github.com/JoaoRodrigues/interfacea/tree/0.1-beta (accessed on 28 January 2022).
- Serçinoğlu, O.; Ozbek, P. gRINN: A tool for calculation of residue interaction energies and protein energy network analysis of molecular dynamics simulations. Nucleic Acids Res. 2018, 46, W554–W562. [Google Scholar] [CrossRef]
- Bakan, A.; Meireles, L.M.; Bahar, I. ProDy: Protein Dynamics Inferred from Theory and Experiments. Bioinformatics 2011, 27, 1575–1577. [Google Scholar] [CrossRef]
- Brown, D.K.; Penkler, D.L.; Sheik Amamuddy, O.; Ross, C.; Atilgan, A.R.; Atilgan, C.; Tastan Bishop, Ö. MD-TASK: A software suite for analyzing molecular dynamics trajectories. Bioinformatics 2017, 33, 2768–2771. [Google Scholar] [CrossRef] [PubMed]
- Agamennone, M.; Nicoli, A.; Bayer, S.; Weber, V.; Borro, L.; Gupta, S.; Fantacuzzi, M.; Di Pizio, A. Protein-protein interactions at a glance: Protocols for the visualization of biomolecular interactions. Methods Cell Biol 2021, 166, 271–307. [Google Scholar] [CrossRef] [PubMed]
- Bayarri, G.; Hospital, A.; Orozco, M. 3dRS, a Web-Based Tool to Share Interactive Representations of 3D Biomolecular Structures and Molecular Dynamics Trajectories. Front. Mol. Biosci. 2021, 8, 726232. [Google Scholar] [CrossRef]
- Nguyen, H.; Case, D.A.; Rose, A.S. NGLview–interactive molecular graphics for Jupyter notebooks. Bioinformatics 2017, 34, 1241–1242. [Google Scholar] [CrossRef] [PubMed]
- Tiemann, J.K.S.; Guixà-González, R.; Hildebrand, P.W.; Rose, A.S. MDsrv: Viewing and sharing molecular dynamics simulations on the web. Nat. Methods 2017, 14, 1123–1124. [Google Scholar] [CrossRef]
- Schreiber, G.; Haran, G.; Zhou, H.X. Fundamental aspects of protein-protein association kinetics. Chem. Rev. 2009, 109, 839–860. [Google Scholar] [CrossRef]
- Kastritis, P.L.; Rodrigues, J.P.; Folkers, G.E.; Boelens, R.; Bonvin, A.M. Proteins feel more than they see: Fine-tuning of binding affinity by properties of the non-interacting surface. J. Mol. Biol. 2014, 426, 2632–2652. [Google Scholar] [CrossRef]
- Kozakov, D.; Li, K.; Hall, D.R.; Beglov, D.; Zheng, J.; Vakili, P.; Schueler-Furman, O.; Paschalidis, I.; Clore, G.M.; Vajda, S. Encounter complexes and dimensionality reduction in protein-protein association. eLife 2014, 3, e01370. [Google Scholar] [CrossRef]
- Wang, L.; Stumm, B.; Helms, V. Graph-theoretical identification of dissociation pathways on free energy landscapes of biomolecular interaction. J. Comput. Chem. 2010, 31, 847–854. [Google Scholar] [CrossRef]
- Phillip, Y.; Harel, M.; Khait, R.; Qin, S.; Zhou, H.X.; Schreiber, G. Contrasting factors on the kinetic path to protein complex formation diminish the effects of crowding agents. Biophys. J. 2012, 103, 1011–1019. [Google Scholar] [CrossRef]
- Peri, C.; Morra, G.; Colombo, G. Surface energetics and protein-protein interactions: Analysis and mechanistic implications. Sci. Rep. 2016, 6, 24035. [Google Scholar] [CrossRef] [PubMed]
- Sakaizawa, H.; Watanabe, H.C.; Furuta, T.; Sakurai, M. Thermal fluctuations enable rapid protein–protein associations in aqueous solution by lowering the reaction barrier. Chem. Phys. Lett. 2016, 643, 114–118. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Zheng, W.; Balamurugan, D.; Schafer, N.P.; Kim, B.L.; Cheung, M.S.; Wolynes, P.G. Electrostatics, structure prediction, and the energy landscapes for protein folding and binding. Protein Sci. A Publ. Protein Soc. 2016, 25, 255–269. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, Y.N.; Yang, M.; Zhang, J.Z. Interaction entropy for protein-protein binding. J. Chem. Phys. 2017, 146, 124124. [Google Scholar] [CrossRef] [PubMed]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef]
- Kastritis, P.L.; Bonvin, A. Are scoring functions in protein-protein docking ready to predict interactomes? clues from a novel binding affinity benchmark. J. Proteome Res. 2010, 9, 2216–2225. [Google Scholar] [CrossRef]
- Lambert, N.A. GPCR dimers fall apart. Sci. Signal. 2010, 3, pe12. [Google Scholar] [CrossRef]
- Lensink, M.F.; Wodak, S.J. Score_set: A CAPRI benchmark for scoring protein complexes. Proteins 2014, 82, 3163–3169. [Google Scholar] [CrossRef]
- Kuttner, Y.Y.; Engel, S. Complementarity of stability patches at the interfaces of protein complexes: Implication for the structural organization of energetic hot spots. Proteins 2018, 86, 229–236. [Google Scholar] [CrossRef]
- Fornili, A.; Pandini, A.; Lu, H.C.; Fraternali, F. Specialized Dynamical Properties of Promiscuous Residues Revealed by Simulated Conformational Ensembles. J. Chem. Theory Comput. 2013, 9, 5127–5147. [Google Scholar] [CrossRef]
- Halakou, F.; Kilic, E.S.; Cukuroglu, E.; Keskin, O.; Gursoy, A. Enriching Traditional Protein-protein Interaction Networks with Alternative Conformations of Proteins. Sci. Rep. 2017, 7, 7180. [Google Scholar] [CrossRef]
- Moal, I.H.; Chaleil, R.A.G.; Bates, P.A. Flexible Protein-Protein Docking with SwarmDock. Methods Mol. Biol. 2018, 1764, 413–428. [Google Scholar] [CrossRef] [PubMed]
- Torchala, M.; Gerguri, T.; Chaleil, R.A.G.; Gordon, P.; Russell, F.; Keshani, M.; Bates, P.A. Enhanced sampling of protein conformational states for dynamic cross-docking within the protein-protein docking server SwarmDock. Proteins 2020, 88, 962–972. [Google Scholar] [CrossRef] [PubMed]
- Kozakov, D.; Hall, D.R.; Xia, B.; Porter, K.A.; Padhorny, D.; Yueh, C.; Beglov, D.; Vajda, S. The ClusPro web server for protein-protein docking. Nat. Protoc. 2017, 12, 255–278. [Google Scholar] [CrossRef] [PubMed]
- Lensink, M.F.; Brysbaert, G.; Nadzirin, N.; Velankar, S.; Chaleil, R.A.G.; Gerguri, T.; Bates, P.A.; Laine, E.; Carbone, A.; Grudinin, S.; et al. Blind prediction of homo- and hetero-protein complexes: The CASP13-CAPRI experiment. Proteins 2019, 87, 1200–1221. [Google Scholar] [CrossRef] [PubMed]
- Schneidman-Duhovny, D.; Inbar, Y.; Nussinov, R.; Wolfson, H.J. PatchDock and SymmDock: Servers for rigid and symmetric docking. Nucleic Acids Res. 2005, 33, W363–W367. [Google Scholar] [CrossRef]
- Tovchigrechko, A.; Vakser, I.A. GRAMM-X public web server for protein-protein docking. Nucleic Acids Res. 2006, 34, W310–W314. [Google Scholar] [CrossRef]
- Lyskov, S.; Gray, J.J. The RosettaDock server for local protein-protein docking. Nucleic Acids Res. 2008, 36, W233–W238. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zou, X. MDockPP: A hierarchical approach for protein-protein docking and its application to CAPRI rounds 15-19. Proteins 2010, 78, 3096–3103. [Google Scholar] [CrossRef]
- de Vries, S.J.; van Dijk, M.; Bonvin, A.M. The HADDOCK web server for data-driven biomolecular docking. Nat. Protoc. 2010, 5, 883–897. [Google Scholar] [CrossRef]
- Jimenez-Garcia, B.; Pons, C.; Fernandez-Recio, J. pyDockWEB: A web server for rigid-body protein-protein docking using electrostatics and desolvation scoring. Bioinformatics 2013, 29, 1698–1699. [Google Scholar] [CrossRef] [PubMed]
- Pierce, B.G.; Wiehe, K.; Hwang, H.; Kim, B.H.; Vreven, T.; Weng, Z. ZDOCK server: Interactive docking prediction of protein-protein complexes and symmetric multimers. Bioinformatics 2014, 30, 1771–1773. [Google Scholar] [CrossRef] [PubMed]
- Mirabello, C.; Wallner, B. InterPred: A pipeline to identify and model protein-protein interactions. Proteins 2017, 85, 1159–1170. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Zhang, D.; Zhou, P.; Li, B.; Huang, S.Y. HDOCK: A web server for protein-protein and protein-DNA/RNA docking based on a hybrid strategy. Nucleic Acids Res. 2017, 45, W365–W373. [Google Scholar] [CrossRef]
- Christoffer, C.; Chen, S.; Bharadwaj, V.; Aderinwale, T.; Kumar, V.; Hormati, M.; Kihara, D. LZerD webserver for pairwise and multiple protein-protein docking. Nucleic Acids Res. 2021, 49, W359–W365. [Google Scholar] [CrossRef] [PubMed]
- van Zundert, G.C.P.; Rodrigues, J.; Trellet, M.; Schmitz, C.; Kastritis, P.L.; Karaca, E.; Melquiond, A.S.J.; van Dijk, M.; de Vries, S.J.; Bonvin, A. The HADDOCK2.2 Web Server: User-Friendly Integrative Modeling of Biomolecular Complexes. J. Mol. Biol. 2016, 428, 720–725. [Google Scholar] [CrossRef]
- Radom, F.; Pluckthun, A.; Paci, E. Assessment of ab initio models of protein complexes by molecular dynamics. PLoS Comput. Biol. 2018, 14, e1006182. [Google Scholar] [CrossRef]
- Jandova, Z.; Vargiu, A.V.; Bonvin, A. Native or Non-Native Protein-Protein Docking Models? Molecular Dynamics to the Rescue. J. Chem. Theory Comput. 2021, 17, 5944–5954. [Google Scholar] [CrossRef]
- Prevost, C.; Sacquin-Mora, S. Moving pictures: Reassessing docking experiments with a dynamic view of protein interfaces. Proteins 2021, 89, 1315–1323. [Google Scholar] [CrossRef]
- Karakulak, T.; Rifaioglu, A.S.; Rodrigues, J.P.G.L.M.; Karaca, E. Predicting the Specificity- Determining Positions of Receptor Tyrosine Kinase Axl. Front. Mol. Biosci. 2021, 8, 658906. [Google Scholar] [CrossRef]
- Hou, Q.; Lensink, M.F.; Heringa, J.; Feenstra, K.A. CLUB-MARTINI: Selecting Favourable Interactions amongst Available Candidates, a Coarse-Grained Simulation Approach to Scoring Docking Decoys. PLoS ONE 2016, 11, e0155251. [Google Scholar] [CrossRef]
- Perthold, J.W.; Oostenbrink, C. GroScore: Accurate Scoring of Protein-Protein Binding Poses Using Explicit-Solvent Free-Energy Calculations. J. Chem. Inf. Model. 2019, 59, 5074–5085. [Google Scholar] [CrossRef] [PubMed]
- Schindler, C.E.; de Vries, S.J.; Zacharias, M. iATTRACT: Simultaneous global and local interface optimization for protein-protein docking refinement. Proteins 2015, 83, 248–258. [Google Scholar] [CrossRef] [PubMed]
- Frezza, E.; Lavery, R. Internal Coordinate Normal Mode Analysis: A Strategy To Predict Protein Conformational Transitions. J. Phys. Chem. B 2019, 123, 1294–1301. [Google Scholar] [CrossRef] [PubMed]
- Eren, M.; Tuncbag, N.; Jang, H.; Nussinov, R.; Gursoy, A.; Keskin, O. Normal Mode Analysis of KRas4B Reveals Partner Specific Dynamics. J. Phys. Chem. B 2021, 125, 5210–5221. [Google Scholar] [CrossRef]
- Paul, S.; Ainavarapu, S.R.K.; Venkatramani, R. Variance of Atomic Coordinates as a Dynamical Metric to Distinguish Proteins and Protein-Protein Interactions in Molecular Dynamics Simulations. J. Phys. Chem. B 2020, 124, 4247–4262. [Google Scholar] [CrossRef]
- Csizmok, V.; Follis, A.V.; Kriwacki, R.W.; Forman-Kay, J.D. Dynamic Protein Interaction Networks and New Structural Paradigms in Signaling. Chem. Rev. 2016, 116, 6424–6462. [Google Scholar] [CrossRef] [PubMed]
- Monzon, A.M.; Necci, M.; Quaglia, F.; Walsh, I.; Zanotti, G.; Piovesan, D.; Tosatto, S.C.E. Experimentally Determined Long Intrinsically Disordered Protein Regions Are Now Abundant in the Protein Data Bank. Int. J. Mol. Sci. 2020, 21, 4496. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Dunker, A.K. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef] [PubMed]
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell. Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Vacic, V.; Iakoucheva, L.M. Disease mutations in disordered regions--exception to the rule? Mol. Biosyst. 2012, 8, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M. Classifying the Binding Modes of Disordered Proteins. Int. J. Mol. Sci. 2020, 21, 8615. [Google Scholar] [CrossRef] [PubMed]
- Sacquin-Mora, S.; Prevost, C. When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes. Biomolecules 2021, 11, 1529. [Google Scholar] [CrossRef]
- Fuxreiter, M. Fold or not to fold upon binding—Does it really matter? Curr. Opin. Struct. Biol. 2019, 54, 19–25. [Google Scholar] [CrossRef]
- Chu, X.; Wang, J. Position-, disorder-, and salt-dependent diffusion in binding-coupled-folding of intrinsically disordered proteins. Phys. Chem. Chem. Phys. PCCP 2019, 21, 5634–5645. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, J.; Chen, J. Residual Structure Accelerates Binding of Intrinsically Disordered ACTR by Promoting Efficient Folding upon Encounter. J. Mol. Biol. 2019, 431, 422–432. [Google Scholar] [CrossRef]
- Guo, P.; Noji, H.; Yengo, C.M.; Zhao, Z.; Grainge, I. Biological Nanomotors with a Revolution, Linear, or Rotation Motion Mechanism. Microbiol. Mol. Biol. Rev. 2016, 80, 161–186. [Google Scholar] [CrossRef]
- Boyer, B.; Ezelin, J.; Poulain, P.; Saladin, A.; Zacharias, M.; Robert, C.H.; Prevost, C. An integrative approach to the study of filamentous oligomeric assemblies, with application to RecA. PLoS ONE 2015, 10, e0116414. [Google Scholar] [CrossRef] [PubMed]
- Boyer, B.; Danilowicz, C.; Prentiss, M.; Prevost, C. Weaving DNA strands: Structural insight on ATP hydrolysis in RecA-induced homologous recombination. Nucleic Acids Res. 2019, 47, 7798–7808. [Google Scholar] [CrossRef]
- Alushin, G.M.; Lander, G.C.; Kellogg, E.H.; Zhang, R.; Baker, D.; Nogales, E. High-resolution microtubule structures reveal the structural transitions in alphabeta-tubulin upon GTP hydrolysis. Cell 2014, 157, 1117–1129. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yu, X.; VanLoock, M.S.; Jezewska, M.J.; Bujalowski, W.; Egelman, E.H. Flexibility of the rings: Structural asymmetry in the DnaB hexameric helicase. J. Mol. Biol. 2002, 321, 839–849. [Google Scholar] [CrossRef]
- Liu, S.; Chistol, G.; Bustamante, C. Mechanical operation and intersubunit coordination of ring-shaped molecular motors: Insights from single-molecule studies. Biophys. J. 2014, 106, 1844–1858. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Schulten, K. Mechanism of substrate translocation by a ring-shaped ATPase motor at millisecond resolution. J. Am. Chem. Soc. 2015, 137, 3031–3040. [Google Scholar] [CrossRef] [PubMed]
- Uchihashi, T.; Watanabe, Y.H.; Nakazaki, Y.; Yamasaki, T.; Watanabe, H.; Maruno, T.; Ishii, K.; Uchiyama, S.; Song, C.; Murata, K.; et al. Dynamic structural states of ClpB involved in its disaggregation function. Nat. Commun. 2018, 9, 2147. [Google Scholar] [CrossRef]
- Hensen, U.; Meyer, T.; Haas, J.; Rex, R.; Vriend, G.; Grubmuller, H. Exploring protein dynamics space: The dynasome as the missing link between protein structure and function. PLoS ONE 2012, 7, e33931. [Google Scholar] [CrossRef]
- Meyer, T.; D’Abramo, M.; Hospital, A.; Rueda, M.; Ferrer-Costa, C.; Perez, A.; Carrillo, O.; Camps, J.; Fenollosa, C.; Repchevsky, D.; et al. MoDEL (Molecular Dynamics Extended Library): A database of atomistic molecular dynamics trajectories. Structure 2010, 18, 1399–1409. [Google Scholar] [CrossRef]
- Rodriguez-Espigares, I.; Torrens-Fontanals, M.; Tiemann, J.K.S.; Aranda-Garcia, D.; Ramirez-Anguita, J.M.; Stepniewski, T.M.; Worp, N.; Varela-Rial, A.; Morales-Pastor, A.; Medel-Lacruz, B.; et al. GPCRmd uncovers the dynamics of the 3D-GPCRome. Nat. Methods 2020, 17, 777–787. [Google Scholar] [CrossRef]
- Evans, R.; O’Neill, M.; Pritzel, A.; Antropova, N.; Senior, A.; Green, T.; Žídek, A.; Bates, R.; Blackwell, S.; Yim, J.; et al. Protein complex prediction with AlphaFold-Multimer. bioRxiv 2021, 2021.2010.2004.463034. [Google Scholar] [CrossRef]
- Capponi, S.; Wang, S.; Navarro, E.J.; Bianco, S. AI-driven prediction of SARS-CoV-2 variant binding trends from atomistic simulations. Eur. Phys. J. E Soft Matter 2021, 44, 123. [Google Scholar] [CrossRef]
- Pavlova, A.; Zhang, Z.; Acharya, A.; Lynch, D.L.; Pang, Y.T.; Mou, Z.; Parks, J.M.; Chipot, C.; Gumbart, J.C. Machine Learning Reveals the Critical Interactions for SARS-CoV-2 Spike Protein Binding to ACE2. J. Phys. Chem. Lett. 2021, 12, 5494–5502. [Google Scholar] [CrossRef]
| Tool Name | Related Link (All Sites Were Accessed on 28 January 2022) |
|---|---|
| GROMACS | https://manual.gromacs.org/documentation/2021/reference-manual/analysis.html |
| VMD | https://www.ks.uiuc.edu/Research/vmd/ |
| PYTRAJ/CPPTRAJ | https://amber-md.github.io/pytraj/latest/index.html |
| MDTraj | https://www.mdtraj.org/1.9.5/index.html |
| MDAnalysis | https://www.mdanalysis.org |
| ProLIF | https://github.com/chemosim-lab/ProLIF |
| interfacea | https://github.com/JoaoRodrigues/interfacea/tree/master |
| gRINN | grinn.readthedocs.io |
| ProDy | http://prody.csb.pitt.edu/ |
| MD-TASK | https://md-task.readthedocs.io/ |
| Server Name | Web Site (Accessed on 28 January 2022) | Conformational Ensemble Retrieval | Reference |
|---|---|---|---|
| ClusPro | https://cluspro.org/ | 10 most populated low energy clusters, irmsd > 9 Å | [125] |
| PatchDock | http://bioinfo3d.cs.tau.ac.il/PatchDock/ | Up to 100 top ranking candidates; clustering cutoff adjustable | [127] |
| GRAMM-X | http://vakser.compbio.ku.edu/resources/gramm/grammx/ | Up to 300 lowest energy conformations | [128] |
| RosettaDock | http://rosettadock.graylab.jhu.edu | 1000 decoys can be downloaded | [129] |
| MDockPP | https://zougrouptoolkit.missouri.edu/MDockPP/ | Up to 3000 generated geometries; clustering cutoff adjustable | [130] |
| HADDOCK | https://wenmr.science.uu.nl/haddock2.4/ | All generated geometries can be downloaded | [131] |
| pyDockWEB | http://life.bsc.es/servlet/pydock | Top 100 lowest energy conformations | [132] |
| ZDOCK | https://zdock.umassmed.edu/ | Top 10 lowest energy conformations; possibility to retrieve top 500 | [133] |
| InterPred | http://bioinfo.ifm.liu.se/inter/interpred/ | No conformational search (template-based) | [134] |
| HDOCK | http://hdock.phys.hust.edu.cn/ | Top 100 lowest energy clusters, lmrsd > 5 Å | [135] |
| LZerD | https://lzerd.kiharalab.org/ | Up to 50,000 generated geometries | [136] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaca, E.; Prévost, C.; Sacquin-Mora, S. Modeling the Dynamics of Protein–Protein Interfaces, How and Why? Molecules 2022, 27, 1841. https://doi.org/10.3390/molecules27061841
Karaca E, Prévost C, Sacquin-Mora S. Modeling the Dynamics of Protein–Protein Interfaces, How and Why? Molecules. 2022; 27(6):1841. https://doi.org/10.3390/molecules27061841
Chicago/Turabian StyleKaraca, Ezgi, Chantal Prévost, and Sophie Sacquin-Mora. 2022. "Modeling the Dynamics of Protein–Protein Interfaces, How and Why?" Molecules 27, no. 6: 1841. https://doi.org/10.3390/molecules27061841
APA StyleKaraca, E., Prévost, C., & Sacquin-Mora, S. (2022). Modeling the Dynamics of Protein–Protein Interfaces, How and Why? Molecules, 27(6), 1841. https://doi.org/10.3390/molecules27061841