A Mechanistic Study of Asymmetric Transfer Hydrogenation of Imines on a Chiral Phosphoric Acid Derived Indium Metal-Organic Framework
Abstract
1. Introduction
2. Results and Discussion
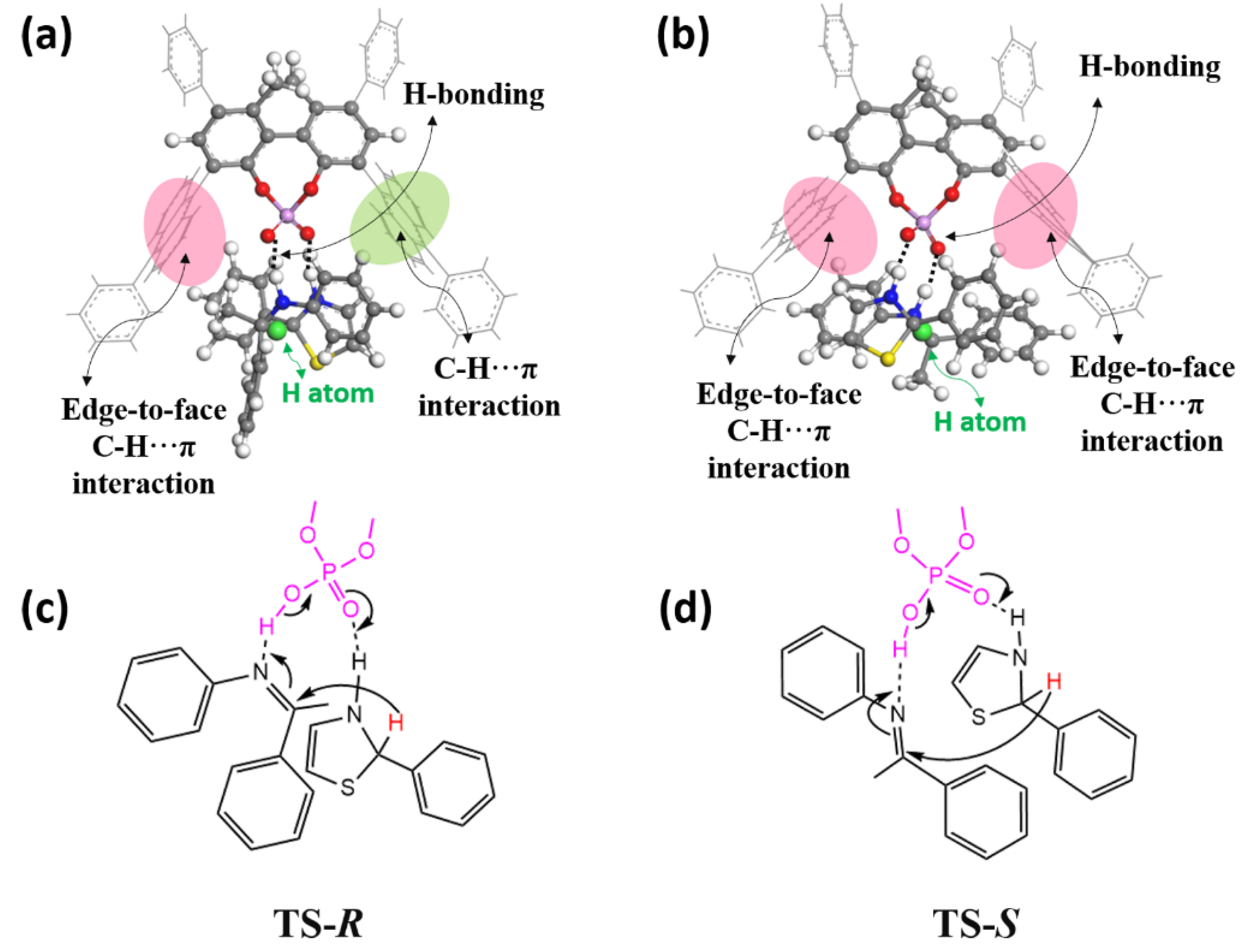
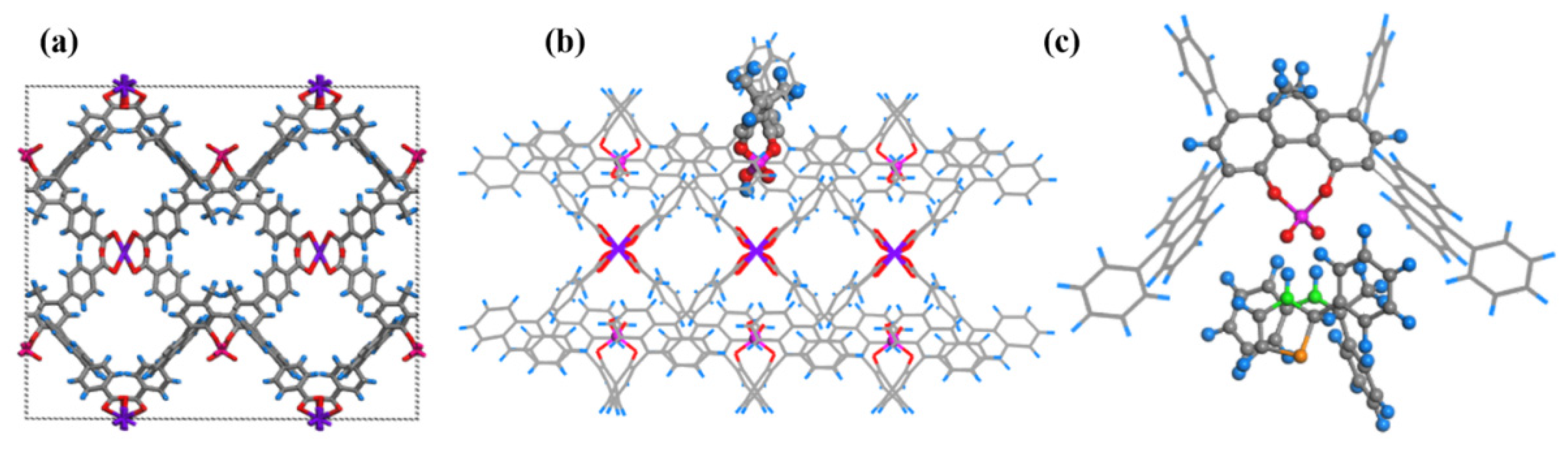
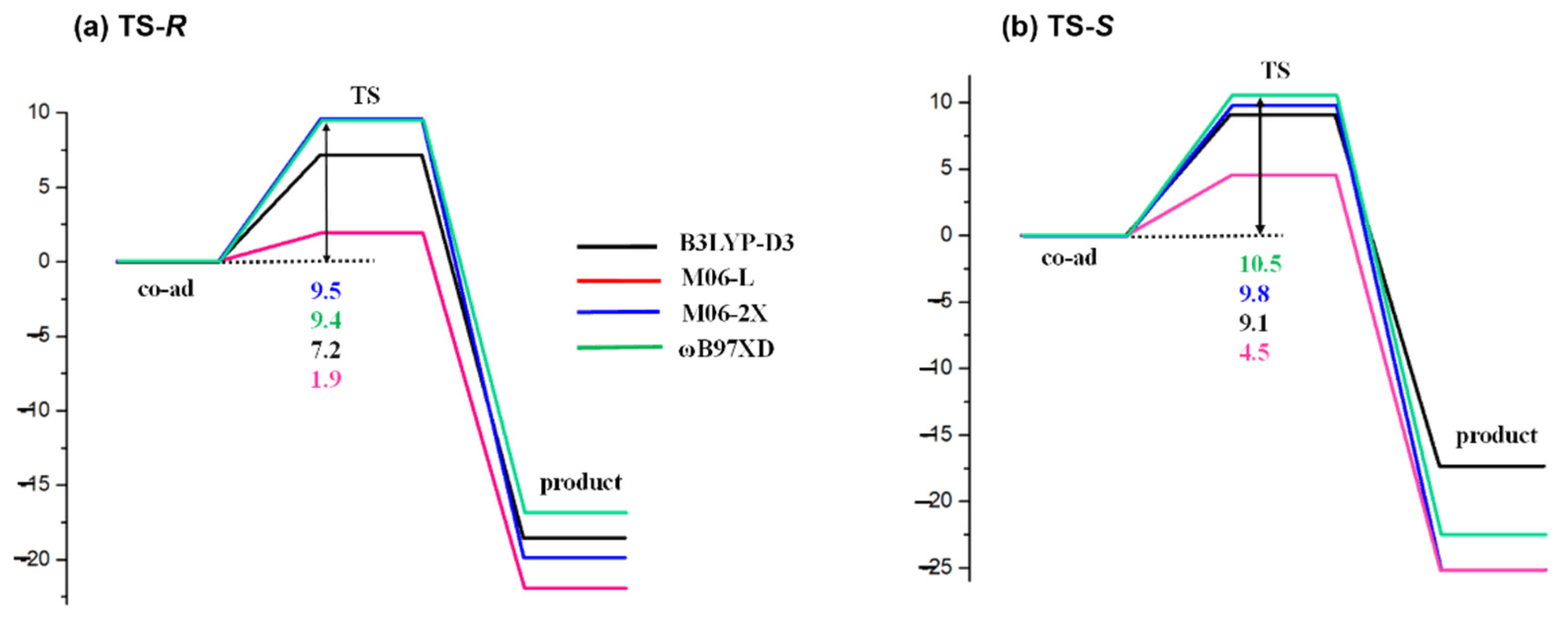
2.1. Mechanism
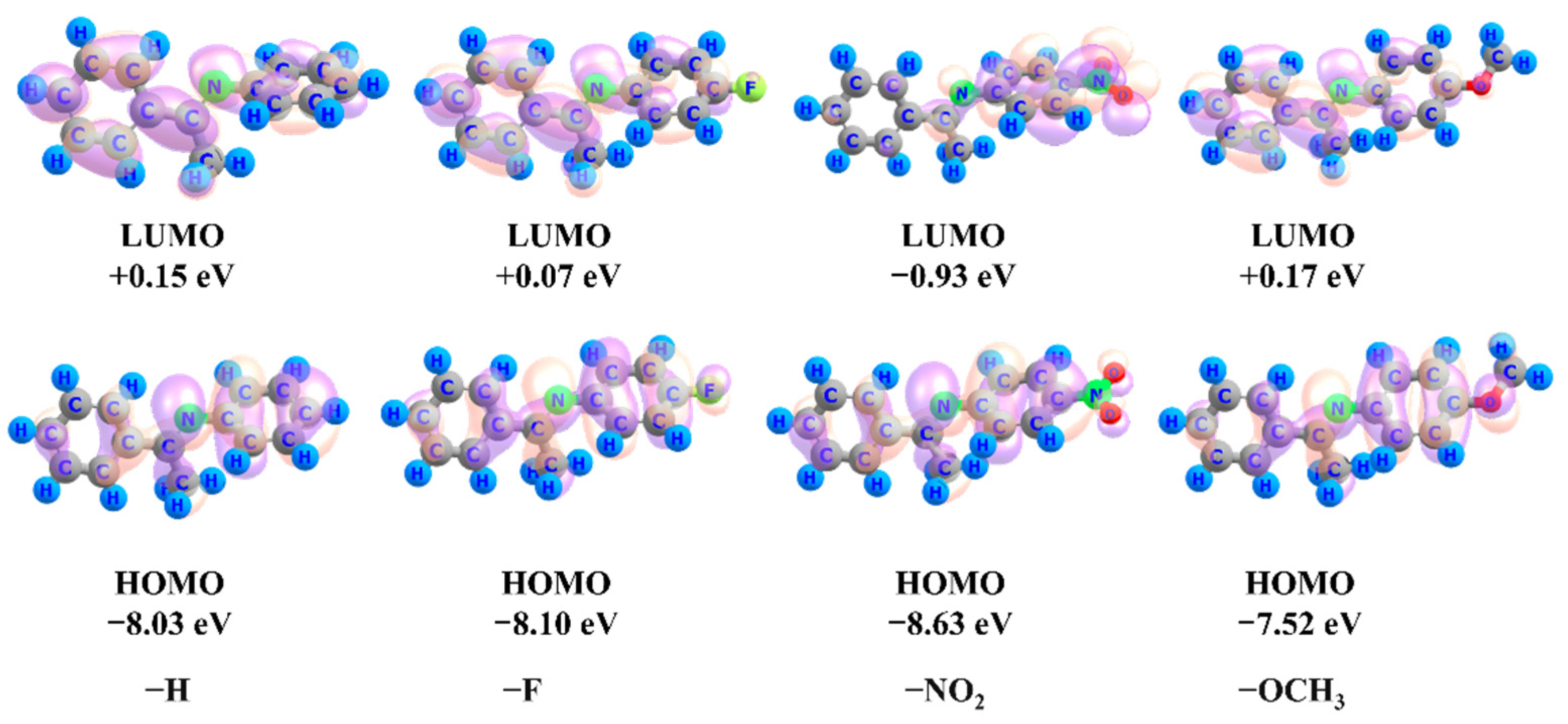
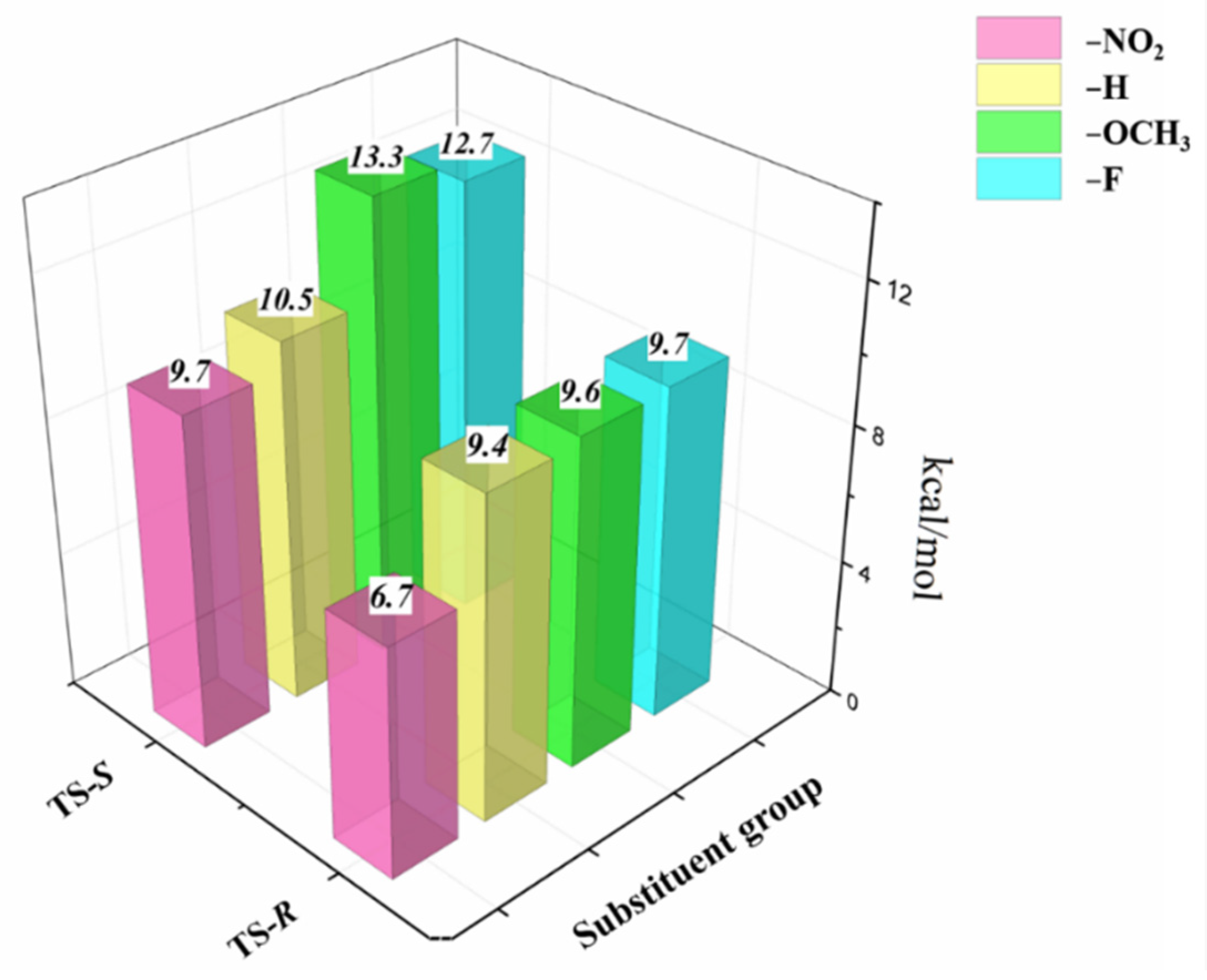
2.2. Substitution Effects
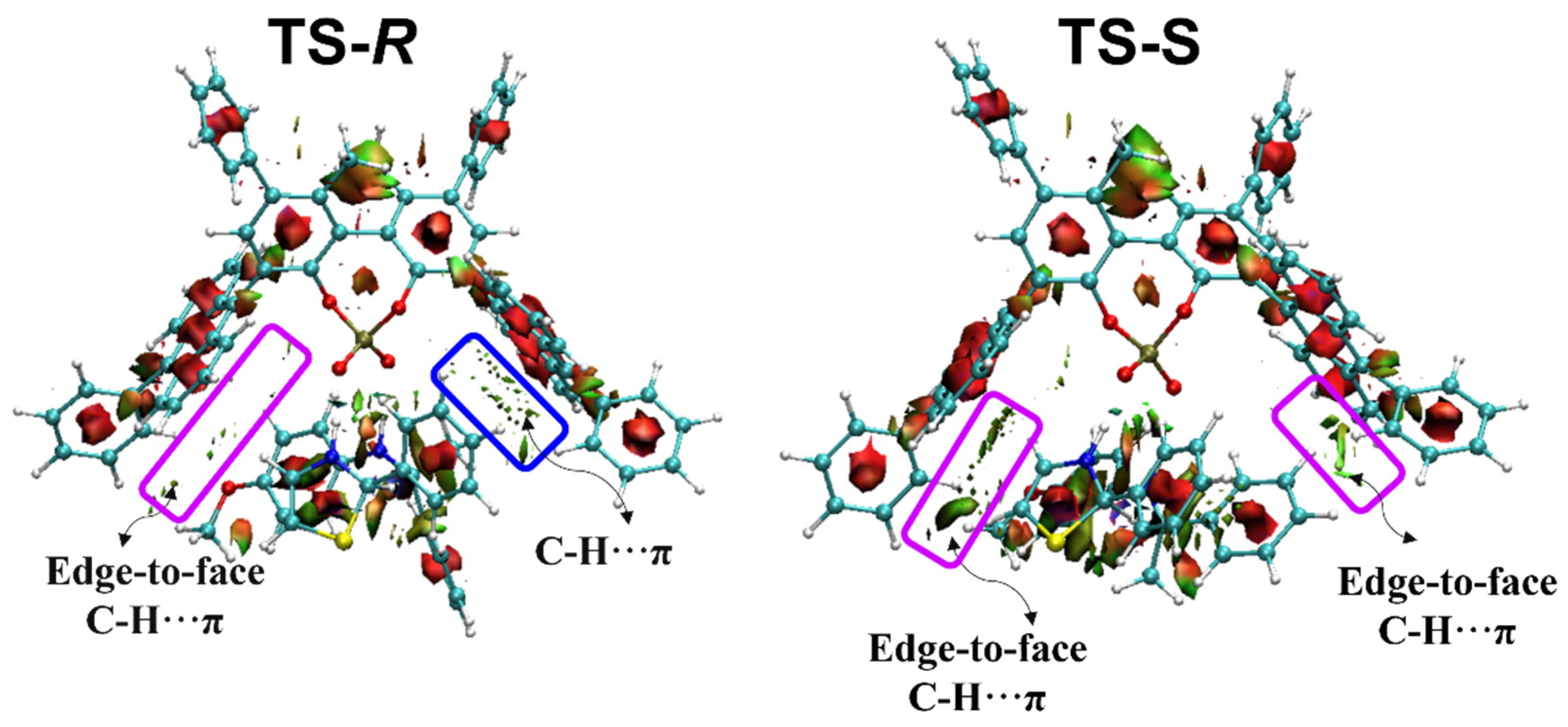
2.3. Original of Enantioselectivity
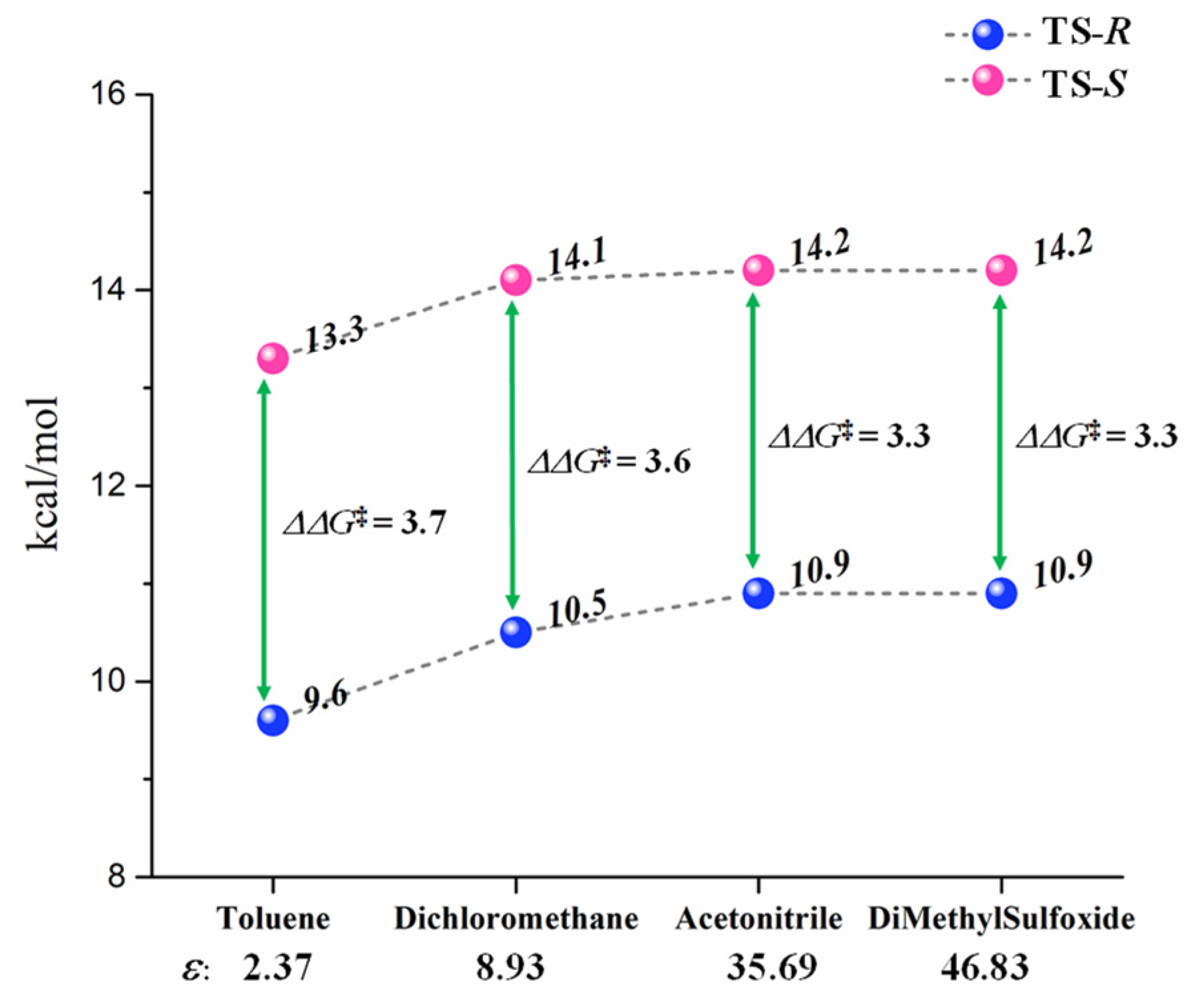
2.4. Solvent Effects
3. Computational Models and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef] [PubMed]
- Chughtai, A.H.; Ahmad, N.; Younus, H.A.; Laypkov, A.; Verpoort, F. Metal–Organic Frameworks: Versatile Heterogeneous Catalysts for Efficient Catalytic Organic Transformations. Chem. Soc. Rev. 2015, 44, 6804–6849. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Liu, X.Q.; Jiang, H.L.; Sun, L.B. Metal−Organic Frameworks for Heterogeneous Basic Catalysis. Chem. Rev. 2017, 117, 8129–8176. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Gates, B.C. Catalysis by Metal Organic Frameworks: Perspective and Suggestions for Future Research. ACS Catal. 2019, 9, 1779–1798. [Google Scholar] [CrossRef]
- Gu, Z.-G.; Zhan, C.; Zhang, J.; Bu, X. Chiral Chemistry of Metal–Camphorate Frameworks. Chem. Soc. Rev. 2016, 45, 3122–3144. [Google Scholar] [CrossRef]
- Ma, L.; Falkowski, J.M.; Abney, C.; Lin, W. A Series of Isoreticular Chiral Metal–Organic Frameworks as a Tunable Platform for Asymmetric Catalysis. Nat. Chem. 2010, 2, 838. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Liu, Y.; Wang, C.; Liu, S.; Lin, W. Cavity-Induced Enantioselectivity Reversal in a Chiral Metal–Organic Framework Brønsted Acid Catalyst. Chem. Sci. 2012, 3, 2623–2627. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, Y.R.; Wojtas, L.; Gao, W.-Y.; Ma, S.; Zaworotko, M.J.; Antilla, J.C. Two Homochiral Organocatalytic Metal Organic Materials with Nanoscopic Channels. Chem. Commun. 2013, 49, 7693–7695. [Google Scholar] [CrossRef]
- Xu, C.; Peng, Y.; Xing, H.; Liu, Y.; Cui, Y. Sixteen Isostructural Phosphonate Metal-Organic Frameworks with Controlled Lewis Acidity and Chemical Stability for Asymmetric Catalysis. Nature Commun. 2017, 8, 2171. [Google Scholar]
- Chen, X.; Jiang, H.; Li, X.; Hou, B.; Gong, W.; Wu, X.; Han, X.; Zheng, F.; Liu, Y.; Jiang, J.W.; et al. Chiral Phosphoric Acids in Metal-Organic Frameworks with Enhanced Acidity and Tunable Catalytic Selectivity. Angew. Chem. Int. Ed. 2019, 58, 14748–14757. [Google Scholar] [CrossRef]
- Reid, J.P.; Simón, L.; Goodman, J.M. A Practical Guide for Predicting the Stereochemistry of Bifunctional Phosphoric Acid Catalyzed Reactions of Imines. Acc. Chem. Res. 2016, 49, 1029–1041. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Duarte, F.; Paton, R.S. Computing Organic Stereoselectivity–from Concepts to Quantitative Calculations and Predictions. Chem. Soc. Rev. 2016, 45, 6093–6107. [Google Scholar] [CrossRef] [PubMed]
- Simón, L.; Goodman, J.M. Theoretical Study of the Mechanism of Hantzsch Ester Hydrogenation of Imines Catalyzed by Chiral Binol-Phosphoric Acids. J. Am. Chem. Soc. 2008, 130, 8741–8747. [Google Scholar] [CrossRef]
- Simón, L.; Goodman, J.M. A Model for the Enantioselectivity of Imine Reactions Catalyzed by Binol−Phosphoric Acid Catalysts. J. Org. Chem. 2011, 76, 1775–1788. [Google Scholar] [CrossRef]
- Reid, J.P.; Goodman, J.M. Goldilocks Catalysts: Computational Insights into the Role of the 3,3′ Substituents on the Selectivity of Binol-Derived Phosphoric Acid Catalysts. J. Am. Chem. Soc. 2016, 138, 7910–7917. [Google Scholar] [CrossRef]
- Shibata, Y.; Yamanaka, M. Dft Study of the Mechanism and Origin of Enantioselectivity in Chiral Binol-Phosphoric Acid Catalyzed Transfer Hydrogenation of Ketimine and A-Imino Ester Using Benzothiazoline. J. Org. Chem. 2013, 78, 3731–3736. [Google Scholar] [CrossRef]
- Pan, H.J.; Zhang, Y.; Shan, C.; Yu, Z.; Lan, Y.; Zhao, Y. Asymmetric Transfer Hydrogenation of Imines Using Alcohol: Efficiency and Selectivity Are Influenced by the Hydrogen Donor. Angew. Chem. Int. Ed. 2016, 55, 9615–9619. [Google Scholar] [CrossRef]
- Chen, Q.-A.; Ye, Z.-S.; Duan, Y.; Zhou, Y.-G. Homogeneous Palladium-Catalyzed Asymmetric Hydrogenation. Chem. Soc. Rev. 2013, 42, 497–511. [Google Scholar] [CrossRef] [PubMed]
- Bickelhaupt, F.M. Understanding reactivity with Kohn–Sham molecular orbital theory: E2–SN2 mechanistic spectrum and other concepts. J. Comput. Chem. 1999, 20, 114–128. [Google Scholar] [CrossRef]
- van Zeist, W.-J.; Bickelhaupt, F.M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef]
- Rueping, M.; Sugiono, E.; Azap, C.; Theissmann, T.; Bolte, M. Enantioselective Brønsted Acid Catalyzed Transfer Hydrogenation: Organocatalytic Reduction of Imines. Org. Lett. 2005, 7, 3781–3783. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Sameera, W.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F. The Oniom Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.W. Molecular Design of Chiral Metal-Organic Frameworks for Asymmetric Transfer Hydrogenation of Imines. Catal. Sci. Technol. 2019, 9, 4888–4897. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (Cam-B3lyp). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.; Goddard Iii, W.; Skiff, W. Uff, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions-the Irc Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of Ab Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Yadnum, S.; Choomwattana, S.; Khongpracha, P.; Sirijaraensre, J.; Limtrakul, J. Comparison of Cu-Zsm-5 Zeolites and Cu-Mof-505 as Heterogeneous Catalysts for the Mukaiyama Aldol Reaction: A DFT Mechanistic Study. ChemPhysChem 2013, 14, 923–928. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Liao, P.; Mendonca, M.L.; Snurr, R.Q. Insights into Catalytic Hydrolysis of Organophosphate Warfare Agents by Metal-Organic Framework NU-1000. J. Phys. Chem. C 2018, 122, 12362–12368. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.W. Methanol-to-Olefin Conversion in Abc-6 Zeolite Cavities: Unravelling the Role of Cavity Shape and Size from Density Functional Theory Calculations. Phys. Chem. Chem. Phys. 2018, 20, 14322–14330. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Lesthaeghe, D.; De Sterck, B.; Van Speybroeck, V.; Marin, G.B.; Waroquier, M. Zeolite Shape-Selectivity in the Gem-Methylation of Aromatic Hydrocarbons. Angew. Chem. Int. Ed. 2007, 46, 1311–1314. [Google Scholar] [CrossRef]
- Van Speybroeck, V.; Van der Mynsbrugge, J.; Vandichel, M.; Hemelsoet, K.; Lesthaeghe, D.; Ghysels, A.; Marin, G.B.; Waroquier, M. First Principle Kinetic Studies of Zeolite-Catalyzed Methylation Reactions. J. Am. Chem. Soc. 2010, 133, 888–899. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2014. [Google Scholar]
- Eyring, H. The Activated Complex and the Absolute Rate of Chemical Reactions. Chem. Rev. 1935, 17, 65–77. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Ess, D.H.; Houk, K.N. Distortion/interaction energy control of 1, 3-dipolar cycloaddition reactivity. J. Am. Chem. Soc. 2007, 129, 10646–10647. [Google Scholar] [CrossRef] [PubMed]
- Ess, D.H.; Houk, K.N. Theory of 1,3-dipolar cycloadditions: Distortion/interaction and frontier molecular orbital models. J. Am. Chem. Soc. 2008, 130, 10187–10198. [Google Scholar] [CrossRef] [PubMed]

| −H | −OCH3 | −F | −NO2 | ||||
|---|---|---|---|---|---|---|---|
| TS-R | TS-S | TS-R | TS-S | TS-R | TS-S | TS-R | TS-S |
| 3.185 | 2.866 | 3.204 | 2.754 | 3.167 | 2.896 | 2.795 | 2.753 |
| 3.258 | 2.894 | 3.241 | 2.915 | 3.207 | 2.989 | 3.188 | 2.769 |
| 3.335 | 3.211 | 3.348 | 3.215 | 3.450 | 3.225 | 3.360 | 3.260 |
| 3.281 | 3.278 | 3.235 | 3.481 | ||||
| Substituent R | ΔG‡ (kcal/mol) | ΔΔG‡ | ee% | |
|---|---|---|---|---|
| TS-R | TS-S | |||
| Exp. (−H) a | 99.0 | |||
| −H | 9.4 | 10.5 | 1.1 | 68.1 |
| −F | 9.7 | 12.7 | 3.0 | 97.9 |
| −NO2 | 6.7 | 9.7 | 3.0 | 97.9 |
| −OCH3 | 9.6 | 13.3 | 3.7 | 99.3 |
| Substituent R | ΔΔE | ΔΔEdist | ΔΔEint | ΔΔEdist-orien | ΔΔEdist-conf |
|---|---|---|---|---|---|
| −H | 1.1 | −1.8 | 2.9 | −4.7 | 2.9 |
| −F | 6.2 | 5.9 | 0.3 | 2.3 | 3.6 |
| −NO2 | 4.3 | −1.4 | 5.7 | −1.3 | −0.1 |
| −OCH3 | 5.5 | 7.3 | −1.8 | 5.6 | 1.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fan, T.; Wang, Q.; Shi, T. A Mechanistic Study of Asymmetric Transfer Hydrogenation of Imines on a Chiral Phosphoric Acid Derived Indium Metal-Organic Framework. Molecules 2022, 27, 8244. https://doi.org/10.3390/molecules27238244
Li X, Fan T, Wang Q, Shi T. A Mechanistic Study of Asymmetric Transfer Hydrogenation of Imines on a Chiral Phosphoric Acid Derived Indium Metal-Organic Framework. Molecules. 2022; 27(23):8244. https://doi.org/10.3390/molecules27238244
Chicago/Turabian StyleLi, Xu, Ting Fan, Qingji Wang, and Tongfei Shi. 2022. "A Mechanistic Study of Asymmetric Transfer Hydrogenation of Imines on a Chiral Phosphoric Acid Derived Indium Metal-Organic Framework" Molecules 27, no. 23: 8244. https://doi.org/10.3390/molecules27238244
APA StyleLi, X., Fan, T., Wang, Q., & Shi, T. (2022). A Mechanistic Study of Asymmetric Transfer Hydrogenation of Imines on a Chiral Phosphoric Acid Derived Indium Metal-Organic Framework. Molecules, 27(23), 8244. https://doi.org/10.3390/molecules27238244






