Abstract
The four new complexes, [Cu(HL1)(L2)Cl] (1), [Cu(HL1)(L1)]∙Cl∙2H2O (2), [Co(L1)2]∙Cl (3) and [Cd(HL1)I2]∙dmso (4), have been prepared by one-pot reactions of the respective chloride or iodide metal salt with a non-aqueous solution of the polydentate Schiff base, HL1, resulted from in situ condensation of benzhydrazide and 2-pyridinecarboxaldehyde, while a ligand HL2, in case of 1, has been formed due to the oxidation of 2-pyridinecarboxaldehyde under reaction conditions. The crystallographic analysis revealed that the molecular building units in 1–4 are linked together into complex structures by hydrogen bonding, resulting in 1D, 2D and 3D supramolecular architectures for 1, 2 and 4, respectively, and the supramolecular trimer for 3. The electronic structures of 1–4 were investigated by the DFT theoretical calculations. The non-covalent interactions in the crystal structures of 1–4 were studied by means of the Hirshfeld surface analysis and the QTAIM theory with a special focus on the C–H⋯Cl bonding. From the DFT/DLPNO-CCSD(T) calculations, using a series of charged model {R3C–H}0⋯Cl− assemblies, we propose linear regressions for assessment of the interaction enthalpy (ΔH, kcal mol−1) and the binding energy (BE, kcal mol−1) between {R3C–H}0 and Cl− sites starting from the electron density at the bond critical point (ρ(rBCP), a.u.): ΔH = −678 × ρ(r) + 3 and BE = −726 × ρ(r) + 4. It was also has been found that compounds 1, 3 and 4 during in vitro screening showed an antibacterial activity toward the nine bacteria species, comprising both Gram-positive and Gram-negative, with MIC values ranging from 156.2 to 625 mg/L. The best results have been obtained against Acinetobacter baumannii MβL.
1. Introduction
The Schiff bases are recognized as an important class of organic ligands for the design and construction of the polymeric and polynuclear coordination compounds since they can be easily formed as novel ligand systems using the simple in situ condensation of a large and variable library of readily available aldehydes and amines [1,2]. Such complexes present many applications in catalysis, magnetochemistry, oxygen storage devices and show antitumoral and antiviral and antibacterial activity [1,3,4,5]. The creation of effective antimicrobial agents is currently one of the most important challenges for medicinal chemistry. Due to the non-terminating development of the resistance of microorganisms (bacteria, fungi, viruses and parasites) to antimicrobial drugs, the search for new antimicrobial drugs still remains an essential and highly demanded task [6].
Nowadays, special attention is paid to the weak non-covalent interactions that often have predetermining role in the formation of supramolecular structures [7] as well as conformational changes in materials and bioactive molecules [8]. The molecular Schiff base complexes represent a good example for studying such types of intra- and intermolecular weak bonding due to the great diversity of Schiff base ligands [2]. The DFT theoretical calculation of the electron density and the extraction of its descriptors by means of quantum theory of atoms in molecules (QTAIM) provides a basis for the analysis of a weak interaction [9]. The search for the reliable correlation between the electron density at the bond critical points ρ(rBCP) and the bond energy is an open question. Emamian and Lu described simple linear regressions that allow an easy estimation of the binding energy from ρ(rBCP) for charged and neutral {X–H⋯Y} assemblies [10]. However, it is known that weak interactions (e.g., halogen bonding) are better described by regressions fitted to a specific data set rather than a broad one [11]. The C–H⋯Cl bonding is a case of particular interest because the respective contacts between chlorine-containing drugs and biological targets have a strong influence on the drug affinity and, therefore, the bioactivity [12,13,14]. Moreover, the interaction of a halide anion with C–H groups is the basis of many anion-selective receptors [12,15,16].
Earlier, we described the Schiff-based [Fe(HL3)Cl2(dmf)]Cl∙dmf (HL3 is formed from salicylic aldehyde and aminoethylpiperazine), [Cu(HL4)(NO3)(dmf)](NO3)∙H2O, [Cu(HL4)Cl2]∙0.5dmso (HL4 is formed from salicylaldehyde and 1-(2-aminoethyl)piperazine) and [CuCl2L5]·dmf (HL5 is formed from 2-pyridinecarbaldehyde and aminoguanidine) complexes which revealed the prominent catalytic activity in the cyclohexane oxidation with H2O2 in the presence of an acid promoter [17,18,19]. Moreover, it was found that homo-[CoL63]·dmf and heterometallic [CoCdL63Cl2]·0.5H2O and [CoZnL63Cl2]·CH3OH (HL6 is formed from o-vanillin and methylamine) complexes demonstrate a profound catalytic activity in the stereoselective oxidation of cis-1,2-dimethylcyclohexane with m-chloroperbenzoic acid under mild conditions in the presence of promoters of different acidity [20,21]. Further, the heterometallic polynuclear [Co4Fe2O(L7)8]∙4dmf∙H2O complex (H2L7 is formed from salicylaldehyde and ethanolamine) shows exceptionally high activity in both catalytic systems mentioned above [22,23]. Apart from the catalytic studies, we previously described magneto-structural ones for the number of Schiff-based transition metal compounds, including [Fe4(µ4-O)4Mn4(L8)8(dmf)4]∙2dmf (H2L8 is formed from salicylaldehyde and hydroxylamine hydrochloride), [Cu2Fe2(HL9)2(H2L9)2]·10dmso, [Cu2Fe2(HL10)2(H2L10)2]·2dmf (H2L9 and H2L10 are formed from salicylaldehyde or 5-bromo-salicylaldehyde and tris(hydroxymethyl)aminomethane), [Cu3Mn(L7)4(CH3OH)3]I3, [Cu3Mn(L7)4(CH3OH)3(H2O)]NCS∙H2O, [Cu3Mn(L7)4(CH3OH)(H2O)2.55]Br∙0.45H2O, [Cu3Mn(L7)4(H2O)3.4]BF4∙0.6H2O, [Co2Fe2(L11)6]∙4dmf (H2L11 is formed from 5-bromo-salicylaldehyde and 2-aminobenzyl alcohol) and [Co4Fe4(HL12)8(dmso)2]∙18dmso (H4L12 is formed from 5-nitro-salicylaldehyde and tris(hydroxymethyl)aminomethane) complexes, revealed an antiferromagnetic coupling among the magnetic centers [24,25,26,27].
Continuing our research aiming at the synthesis and investigation of novel mono- and polynuclear transition metal complexes based on polydentate O,N-donor ligands [3,21,28,29,30,31,32,33], we have now synthesized four new complexes [CuII(HL1)(L2)Cl] (1), [CuII(HL1)(L1)]∙Cl∙2H2O (2), [CoIII(L1)2]∙Cl (3) and [CdII(HL1)I2]∙dmso (4) where HL1 is a product of in situ condensations of benzhydrazide and 2-pyridinecarboxaldehyde, HL2 is the 2-pyridinecarboxylic acid, studied their structural features, and tested the antibacterial activity toward the number of Gram-positive and Gram-negative bacteria species. Furthermore, we have investigated the electronic structures of the complexes 1–4 and have proposed new coefficients of linear regressions that allow the estimation of interaction enthalpies and binding energies for {C–H}0⋯Cl− hydrogen bonds.
2. Results
2.1. Synthesis
The complexes 1–4 (Scheme S1) were obtained using the two steps synthetic approach within the same reaction vessel: (1) in situ formations of a Schiff base ligand by condensation of benzhydrazide and 2-pyridinecarboxaldehyde and (2) reaction of the prepared Schiff base ligand (HL1, Scheme 1) with a metal precursor. The choosing strategy receives a broad application in the synthesis of Schiff base-containing coordination compounds and allows to use of the Schiff base ligand immediately after its formation. The interaction of metal chlorides (1–3) or iodide (4) with a non-aqueous (CH3OH for 1–3 and dmso for 4) solutions of HL1 using a molar ratio of MX2:HL1 = 1:2, resulted in green (1–2), brown (3) or yellow-orange (4) solutions obtained at the end of the reactions. All reactions were initiated and brought to completion by stirring and heating in the open air. Microcrystals 1 and 3 were formed in two days from the resulting solution, while microcrystals 2 were obtained from the filtrate of 1 in ca. one month. Microcrystals of 4 were obtained in two weeks after the addition of iPrOH into the resulting solution. Unexpectedly, in addition to the presence of desired HL1 Schiff base ligand in 1, the single crystal X-ray analysis disclosed a presence of HL2, 2-pyridinecarboxylic acid (Scheme 1) as well. The formation of HL2 can be understood by assuming aerobic oxidation of 2-pyridinecarboxaldehyde under reaction conditions since this process is known for aldehyde chemistry [34]. The IR spectra of 1–4 and the ligand HL1 are depicted in Figures S1–S5.
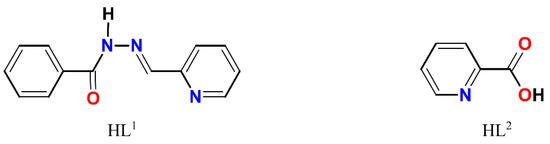
Scheme 1.
Structural formulae of HL1 and HL2.
2.2. Crystal Structures
The crystal structure of 1 consists of discrete mononuclear molecules [Cu(HL1)(L2)Cl] (Figure 1), which are jointed into supramolecular chains by means of hydrogen bonds (Figure 2). Complex 1 features two different ligands: the Schiff base ligand (HL1) showing tridentate N,N,O-donor coordination mode and the 2-pyridinecarboxylate (L2) coordinated in the N,O-donor fashion. The coordination polyhedron around the Cu(II) atom adopts O2N3Cl distorted elongated octahedral geometry formed by the O and N donor atoms of both organic ligands and coordinated chloride anion as well. The basal Cu–X (X = O, N, Cl) bond lengths in 1 vary from 1.9766(19) to 2.2591(7) Å, while the apical ones are 2.500(2) Å (Cu1–O3) and 2.378(2) Å (Cu1–N4) (Table S1). The X–Cu–Ntrans angles range from 144.84(7) to 173.00(6)°.
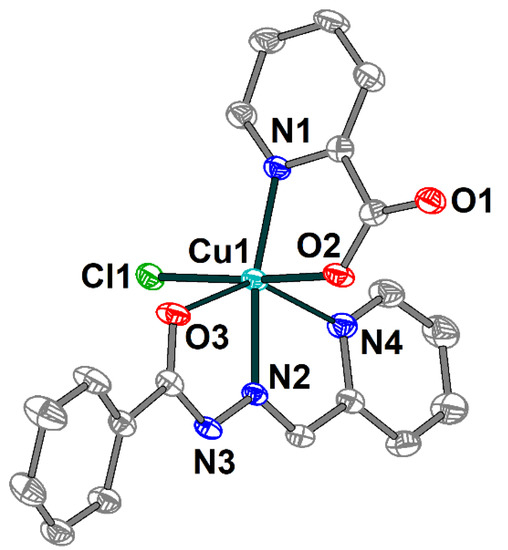
Figure 1.
Molecular structure of 1 with the atom numbering scheme. H atoms are omitted for clarity. The atoms are shown with 50% probability displacement ellipsoids. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green.
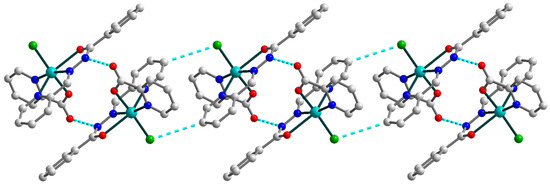
Figure 2.
Representation of the supramolecular chain in 1. H atoms are omitted for clarity. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green.
In the crystal lattice, the two closest neighboring molecules are strongly linked by hydrogen bonding between the oxygen atoms of the pyridine-carboxylates and the nitrogen atoms of Schiff base ligands (Figure 2) [N3–H3⋯O1a (a = 1 − x, 1 − y, 1 − z), D–A = 2.884(3) Å, D–H⋯A = 150.1°]. Moreover, the hydrogen bonds formed with the participation of the Schiff base ligands and coordinated chloride anions [C8–H8⋯Cl1b (b = 1 − x, 1 − y, −z), D–A = 3.734(3) Å, D–H⋯A = 153.9°] tie together abovementioned supramolecular dimers into one-dimensional chains. The nearest Cu⋯Cu distance within the supramolecular chain in 1 are 6.1899(10) and 8.1024(10) Å.
The single crystal X-ray analysis shows that 2 includes a [Cu(HL1)(L1)]+ cation (Figure 3), one Cl− anion and two uncoordinated water molecules joined into supramolecular two-dimensional layers assisted by hydrogen bonds. The Schiff base ligands in 2 are present in both deprotonated and non-deprotonated forms and reveal the tridentate-chelating (N,N,O) coordination mode. Similarly to 1, the Cu(II) atom has a distorted elongated octahedral environment but with an O2N4 donor set formed by the Schiff bases. The Cu–X (X = O, N) bond lengths in the equatorial plain are in the range 1.931(2)–2.069(2) Å, and the apical Cu1–O2 and Cu1–N6 distances are 2.582(2) and 2.254(3) Å, respectively (Table S2). The O(N)–Cu–Ntrans bond angles vary from 144.32(8) to 175.14(10)°.
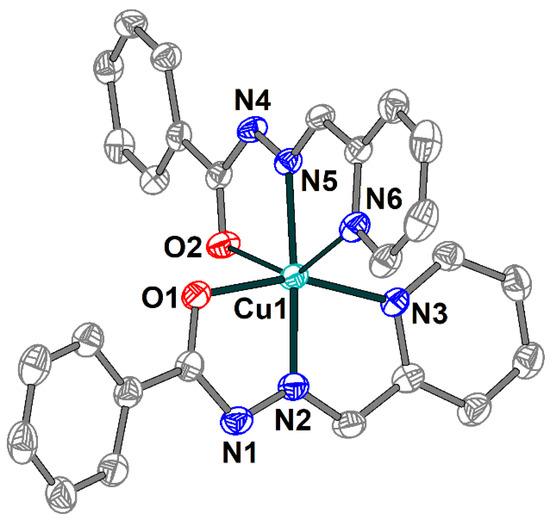
Figure 3.
Structure of [Cu(HL1)(L1)]+ cation in 2 with the atom numbering scheme. H atoms, uncoordinated water molecules and chloride anion are omitted for clarity. The atoms are shown with 50% probability displacement ellipsoids. Color scheme: Cu, cyan; O, red; N, blue; C, grey.
Due to the strong and multiple hydrogen bonds between uncoordinated chloride anions and donor atoms of Schiff base ligands [N4–H4⋯Cl1b (b = 1 − x, 1 − y, −z), D–A = 3.245(3) Å, D–H⋯A = 160(4)°; C13–H13⋯Cl1, D–A = 3.675(3) Å, D–H⋯A = 165.5°; C20–H20⋯Cl1b, D–A = 3.645(3) Å, D–H⋯A = 173.5°; C21–H21⋯Cl1b, D–A = 3.457(3) Å, D–H⋯A = 140.0°], the formation of the supramolecular dimers in 2 can be identified (Figure 4). The non-bonded Cu⋯Cu separation within this dimer is 10.0391(9) Å.
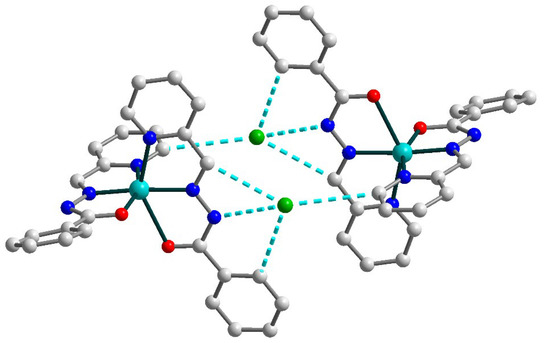
Figure 4.
Supramolecular dimer in 2. H atoms are omitted for clarity. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green.
Furthermore, the uncoordinated water molecules join the supramolecular dimers in 2, forming two-dimensional layers by means of strong O–H⋯O and O–H⋯Cl hydrogen bonding between dimers and chloride anions (Figure 5) [O4A–H4AA⋯O3b (b = 1 − x, 1 − y, −z), D–A = 2.721(9) Å, D–H⋯A = 150.3°; O4A–H4AB⋯Cl1, D–A = 3.288(8) Å, D–H⋯A = 151.5°; O3–H3A⋯Cl1, D–A = 3.315(3) Å, D–H⋯A = 166(6)°; O3–H3C⋯O3c (c = –x, –y, –z), D–A = 2.795(7) Å, D–H⋯A = 166.38(11)°].
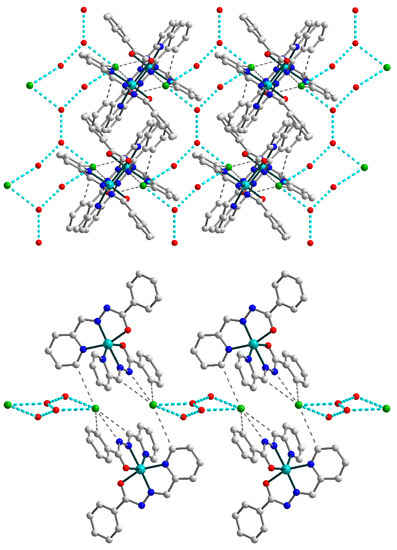
Figure 5.
(Top) supramolecular 2D layer in 2, showing supramolecular chains built by connected {OH2O⋯OH2O⋯Cl}2 synthons (highlighted by cyan dash lines). (Bottom) supramolecular layer in 2, viewed down the crystallographic a axis. The hydrogen atoms are omitted for clarity. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green.
The chains formed by uncoordinated H2O molecules and Cl anions within the overall 2D structure of 2 can be considered as an independent supramolecular motif. They are built by {OH2O⋯OH2O⋯Cl}2 synthons which are connected through O–H⋯O bridges (Figure 5, top). Further increase of the dimensionality of the supramolecular 2D polymer is not observed due to steric factors: the bulky Schiff base ligands on the outer positions of the layer (Figure 5, bottom) prevent the formation of hydrogen bonds between neighboring sheets.
Complex 3 is built of [Co(L1)2]+ cations (Figure 6) and chloride anions, which are joined together by strong hydrogen bonding forming supramolecular trimers (Figure 7). The cobalt(III) atom in 3 has an octahedral coordination environment with an O2N4 donor set formed by two deprotonated Schiff base ligands. The Co–O and Co–N bond lengths are in the ranges 1.8927(13)–1.9099(14) and 1.8564(15)–1.9253(16) Å, respectively. The trans angles at the metal atom vary from 165.19(6) to 175.36(7), while the cis angles are equal to 82.35(6)–100.84(7)° (Table S3).
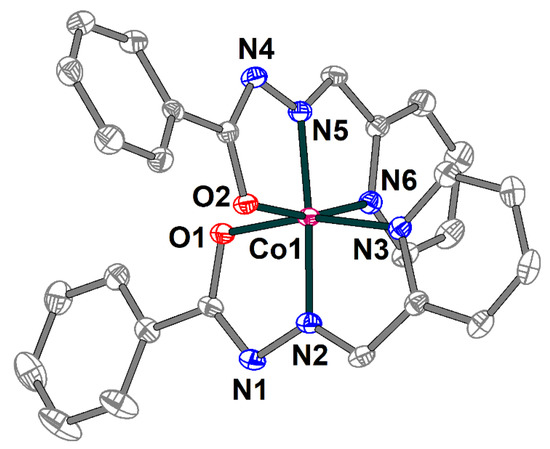
Figure 6.
Structure of [Co(L1)2]+ cation in 3 with the atom numbering scheme. H atoms and chloride anion are omitted for clarity. The atoms are shown with 50% probability displacement ellipsoids. Color scheme: Co, dark pink; O, red; N, blue; C, grey.
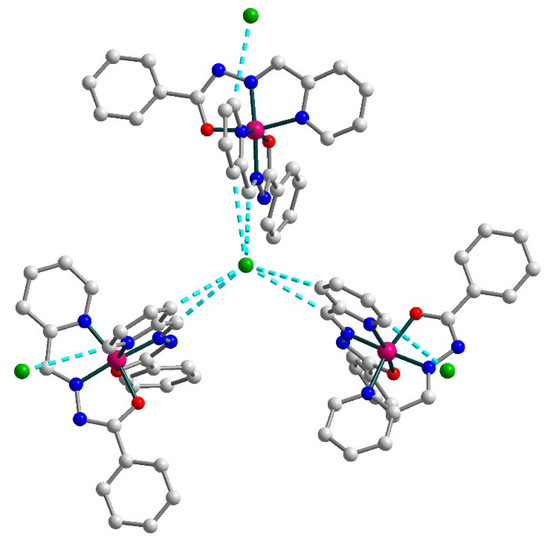
Figure 7.
Supramolecular trimer in 3. H atoms are omitted for clarity. Color scheme: Co, dark pink; O, red; N, blue; C, grey; Cl, green.
In the solid state, the [Co(L1)2]+ cations with uncoordinated Cl anions form supramolecular trimers by means of C–H⋯Cl bonding (Figure 7) [C21–H21⋯Cl1, D–A = 3.622(2) Å, D–H⋯A = 141.6°; C23–H23⋯Cl1, D–A = 3.571(2) Å, D–H⋯A = 150.8°]. Additionally, one more chlorine anion is connected by C–H⋯Cl contacts to each cobalt(III) moiety of this trimer [C26–H26⋯Cl2A, D–A = 3.480(4) Å, D–H⋯A = 154.6°]. The observed Co⋯Co intermolecular separation within the supramolecular trimer is 10.397 Å.
The crystal structure of the 4 is formed of discrete neutral [Cd(HL1)I2] molecules (Figure 8) and dmso molecules of crystallization, joined by strong hydrogen bonding with the formation of an extended supramolecular 3D structure (Figure 9). The Schiff base ligand in 4 is in a neutral form and shows the tridentate-chelating (N,N,O) coordination fashion, similar to 1–3. The Cd(II) atom is five-coordinated and has an ON2I2 donor set. The Cd–X (X = O, N, I) bond lengths fall in the range of 2.314(3)–2.7209(4) Å (Table S4), while the angles at the Cd atoms vary from 66.86(9) to 135.73(9)°.
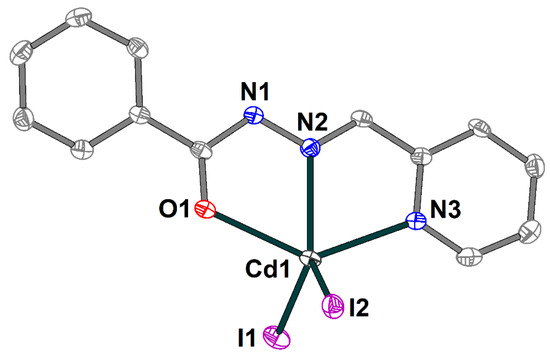
Figure 8.
Molecular structure of 4 with the atom numbering scheme. H atoms and solvate dmso molecules are omitted for clarity. The atoms are shown with 50% probability displacement ellipsoids. Color scheme: Cd, medium grey; O, red; N, blue; C, grey; I, violet.
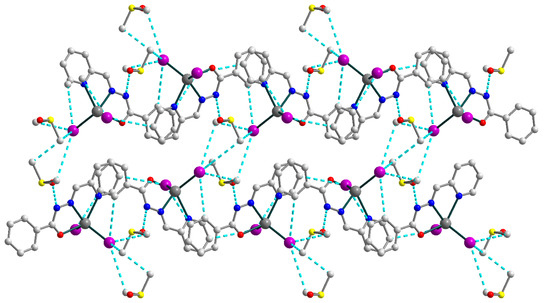
Figure 9.
Supramolecular 3D structure in 4, viewed down the crystallographic a axis. The hydrogen atoms are omitted for clarity. Color scheme: Cd, medium grey; O, red; N, blue; C, grey; I, violet; S, yellow.
The strong N–H⋯O and C–H⋯I hydrogen bonds [N1–H1⋯O2, D–A = 2.717(4) Å, D–H⋯A = 147.0°; C3–H3⋯I1d (d = x, 0.5 − y, −0.5 + z), D–A = 4.142(4) Å, D–H⋯A = 152.3°; C4–H4⋯I2e (e = −1 + x, 0.5 − y, −0.5 + z), D–A = 4.004(2) Å, D–H⋯A = 159.4°; C12–H12⋯I2d, D–A = 3.964(4) Å, D–H⋯A = 148.6°; C14–H14B⋯I1e, D–A = 4.283(4) Å, D–H⋯A = 154.8°; C14–H14C⋯I1f (f = 1 − x, −0.5 + y, 1.5 − z), D–A = 4.180(4) Å, D–H⋯A = 147.7°; C15–H15A⋯I1f, D–A = 4.112(4) Å, D–H⋯A = 160.8°; C15–H15B⋯I1e, D–A = 4.139(4) Å, D–H⋯A = 158.2°], involving nitrogen atoms from imine moieties of Schiff base ligands, oxygen atoms from uncoordinated dmso molecules, carbon atoms from Schiff bases and dmso molecules and coordinated I− anions, are responsible for the formation of the extended supramolecular three-dimensional framework (Figure 9). The closest Cd⋯Cd intermolecular separation within the framework exceeds 7.48 Å.
2.3. Theoretical Calculations
The mononuclear complex 1 represents a “classical” Cu(II) coordination compound with the S = 1/2 ground state and unpaired electron localized at the copper center (spin population of 0.710, according to the Löwdin population analysis of the quasi-restricted molecular orbitals). The HOMO orbital has large contributions from pz (30.1%) and px (19.0%) orbitals of the oxygen atom and pz (17.4%) of the chlorine one (Figure 10). The LUMO orbital is strongly delocalized over the atoms of the ligands.
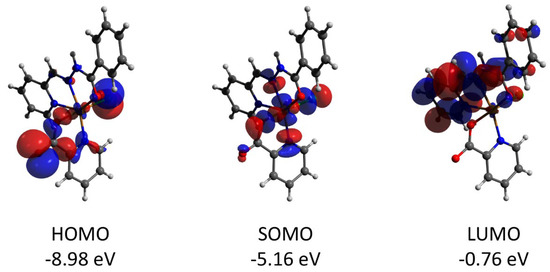
Figure 10.
Plots and energies of the frontier quasi-restricted molecular orbitals (shown at 0.01 a.u. isosurface) of 1, calculated at the ωB97X-D4/ma-def2-TZVP level and based on crystallographic atom coordinates. Colour scheme: Cu, orange; O, red; N, blue; C, grey; Cl, green.
In the supramolecular structure of 1 (Figure 2), one can select strongly bridged dimers, strengthened by the N–H⋯O and C–H⋯O hydrogen bonds as well as the π–π stacking. Analysis of the electron density ρ(r) and the bond critical points (BCPs) reveals two symmetrically equivalent sets of critical points (Figure 11), both formed by the oxygen atom O1 and Ha atoms from N3a, C12a and C19a ones (where the symmetry operation a is 1 − x, 1 − y, 1 − z). The sum electron density ρ(r) in these six BCPs is 7.1 × 10−2 a.u. According to the model developed by Emamian and Lu [10], this value corresponds to the binding energy of −15.1 kcal mol−1, which can be considered a strong H-bonded coupling.
Figure 11.
Structure of the supramolecular dimer in 2 showing the bond critical points (BPCs, dark-green dots) for the set of six strong hydrogen bonds. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green; H, white.
The additional contribution to the binding energy of −1 kcal mol−1 comes from the interaction of phenyl and pyridine rings of the Schiff base ligands (Figure 12). The aromatic rings interact in the distorted parallel offset mode [35] with the angle of 25.4° and ρ(rBCP) = 3.9 × 10−3 a.u. for the closest contacts. Optimization of the geometry of the dimer of 1 reveals that the parallel offset mode persists (Figure S6), while the angle between planes formed by the aromatic rings becomes much smaller (10.0°). This suggests that rotation of the aromatic rings in the solid state is induced by the intermolecular interactions, not accounted for in the molecular geometry optimization.
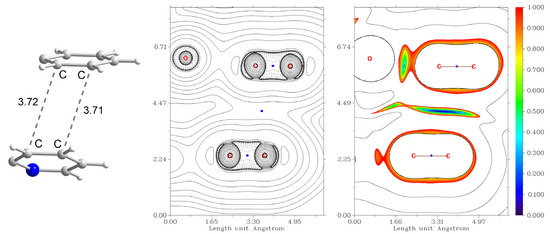
Figure 12.
Non-covalent interaction between the phenyl and pyridine rings of the Schiff base ligands in the supramolecular dimer of 1. (Left) the fragment of the structure showing the C⋯C distances. (Centre): plot of the Laplacian of electron density ∇2ρ(r), where BCPs are shown as blue dots. (Right) plot of the reduced density gradient (RDG) [36] isosurfaces showing attraction (blue), van der Waals (green) and repulsion (red) interactions. Color scheme: N, blue; C, grey; H, white.
The broken symmetry calculations revealed the very small singlet-triplet splitting of −0.05 and −0.12 cm−1 (using B3LYP and ωB97X-D4 functionals, respectively, H = JS1S2 notation and J = 2(EHS − EBS)/(SA + SB)2 formalism [37,38,39]). The calculated overlap between the magnetic orbitals (according to the analysis of unrestricted corresponding orbitals), containing unpaired electrons located on the copper atoms, constitutes 0.004 and 0.001 for B3LYP and ωB97X-D4 functionals, respectively. These values are ca. one order smaller than those expected for spin-coupled orbitals [40]. Thus, one can conclude that Cu(II) centers in 1 are almost magnetically isolated, but the existence of a small ferromagnetic coupling cannot be excluded.
Complex 2 features the HOMO and LUMO quasi-restricted molecular orbitals strongly delocalized over the ligands’ atoms (Figure 13). The spin population (S = 1/2 ground state) of the copper center is similar (0.727) to that found for complex 1. The HOMO orbital of the diamagnetic complex 3 is totally located on one of the ligands, while the LUMO orbital is delocalized over two ligand moieties (Figure 14). Both HOMO and LUMO molecular orbitals in the cation of 3 have negligible (less than 1%) contributions to the atomic orbitals of the cobalt atom. The same as for 3, the HOMO molecular orbital of the diamagnetic complex 4 is located at the halogen atoms and does not involve the cadmium center (Figure 15). Both iodine atoms have a high contribution, namely 39.1% of px orbital of I(1) and 22.8% pz and 22.1% of pz and py, respectively, of I(2).
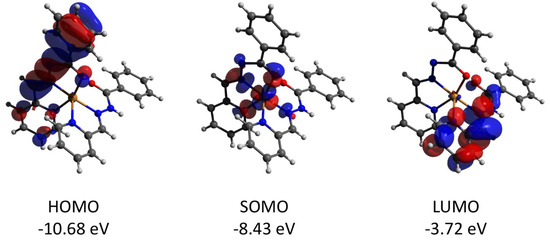
Figure 13.
Plots and energies of the frontier quasi-restricted molecular orbitals (shown at 0.01 a.u. isosurface) of the cation of 2, calculated at the ωB97X-D4/ma-def2-TZVP level and based on crystallographic atom coordinates. Color scheme: Cu, orange; O, red; N, blue; C, grey.
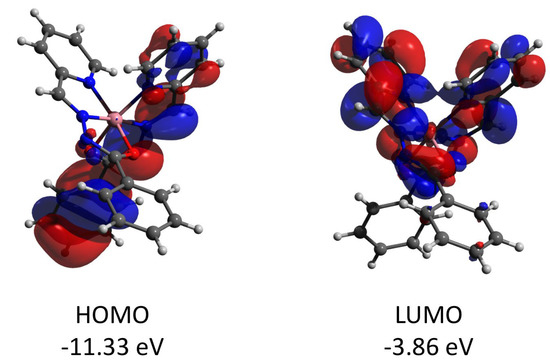
Figure 14.
Plots and energies of the frontier molecular orbitals (shown at 0.03 a.u. isosurface) of the cation of 3, calculated at the ωB97X-D4/ma-def2-TZVP level and based on crystallographic atom coordinates. Color scheme: Co, pink; O, red; N, blue; C, grey.
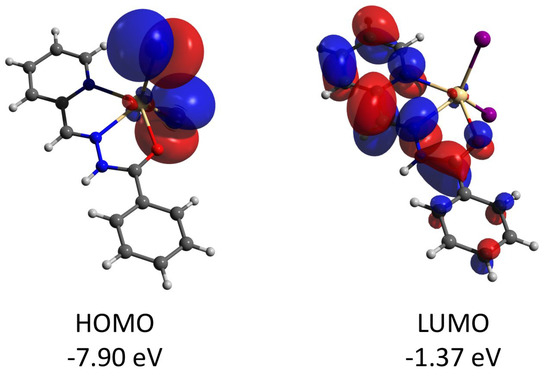
Figure 15.
Plots and energies of the frontier molecular orbitals (shown at 0.03 a.u. isosurface) of 4, calculated at the ωB97X-D4/ma-def2-TZVP level and based on crystallographic atom coordinates. Color scheme: Cd, pale yellow; O, red; N, blue; C, grey; I, violet.
The supramolecular structures of the complexes 1–3 reveal numerous C–H⋯Cl contacts of various strengths, where coordinated (1) or free (2 and 3) chloride anions are surrounded by the hydrogen atoms from the ligands. The Hirshfeld surface analysis [41] and the fingerprint plots disclose that the Cl⋯H contacts constitute the largest contribution to the intramolecular Cl⋯X interactions, being 100% for 3 (Figure 16). The non-deprotonated form of the ligand (HL1) is an excellent receptor for the anions due to the presence of three C–H groups directed approximately to a single point. Geometry optimization of the {HL1·Cl}− assembly using the coordinates from structure 2 as the starting point shows that the chlorine atom is in the ligand’s plane, forming three strong hydrogen bonds (Figure 17). The enthalpy of the interaction between HL and Cl− was found to be −32.1 kcal mol−1 (ωB97X-D4/ma-def2-TZVP level).
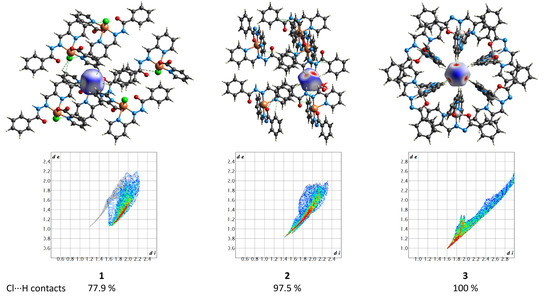
Figure 16.
(Top) the Hirshfeld surfaces of chloride anions in 1–3. The colored map corresponds to a normalized contact distance (dnorm). (Bottom) the respective fingerprint plots (de vs. di, Å). Color scheme: Cu, orange; Co, light grey; O, red; N, blue; C, grey; Cl, green.
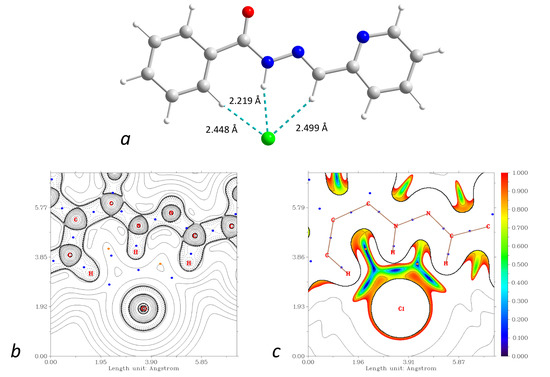
Figure 17.
(a): DFT-optimized structure of the {HL1·Cl}− assembly. (b): plot of the Laplacian of electron density ∇2ρ(r) highlighting the Cl⋯H interactions (BCPs are shown as blue dots). (c): plot of the reduced density gradient (RDG) at the same plane. Color scheme: Cu, cyan; O, red; N, blue; C, grey; Cl, green; H, green.
It is known that the energies of weak interactions (including hydrogen bonds) can be approximately estimated through the evaluation of the electron density ρ(r) at the respective bond critical points (BCPs). This approach allows for the extraction of the energies of intramolecular interactions for which the individual energies of donor and acceptor sites cannot be calculated due to the inseparability of the whole molecule. While the BE vs. ρ(r) linear regressions (where BE is the binding energy) proposed by Emamian and Lu can be applied to a broad range of hydrogen bonds [10], re-examination of the BE vs. ρ(r) reference data for a certain X–H⋯Y pair may result in more precise coefficients of regression.
The choice of a calculation method for precise estimation of interaction energies in weakly bonded supramolecular assemblies is a topic of broad discussion, where the computational resources required to perform calculations at high levels are a crucial factor [42]. We selected several examples from the S66 dataset of the Benchmark Energy & Geometry Database (BEGDB) [43], where small molecules (such as water and methanol) form weak hydrogen bonds with other fragments. The original binding energies reported by Hobza et al. [43] were reconsidered several times [44,45]. Herein we used the BEs reported by Martin et al. [45] as a reference, where energies were calculated using a few sets of explicitly correlated methods with the basis sets near the limit along with counterpoise (CP) and other corrections. Since the accurate geometries and interaction energies in S66 were accurately determined [43,45], we tested several routine methods against the models 01, 03, 04, 09 and 18 of the S66 dataset. The geometries re-optimized at the ωB97X-D4/ma-def2-TZVP level showed only a slight difference from those reported in S66 (Table S8). The lowest deviation was found for the model 01 (HOH⋯OH2 water dimer), while the highest one for the model 09 (interaction of methanol with methylamine). For these re-optimized geometries, we calculated the binding energies using the DLPNO-CCSD(T) scheme involving def2-TZVPPD and aug-cc-pV{D,T}Z, aug-ano-pV{D,T}Z and aug-ano-pV{T,Q}Z basis sets [46,47,48] with or without counterpoise correction [49] (Table S8). The extrapolated aug-ano-pV{T,Q}Z CP-corrected basis set gave excellent (<0.08 kcal mol−1) agreement with the reference data for 01 and 03 models (RMS = 0.09). However, this method is computationally demanding, and its use for heavier models was not justified under our conditions. Surprisingly, the second method of high accuracy was def2-TZVPPD without CP correction, which showed an RMS of 0.125 and the highest deviation of 0.21 kcal mol−1 (Table S8). A similar level of accuracy was observed for extrapolated aug-cc-pV{D,T}Z and aug-ano-pV{D,T}Z basis sets involving CP-correction (RMS = 0.161 and 0.182, respectively), while all extrapolated methods showed considerably higher RMS in the absence of counterpoise correction. Remarkably, the application of counterpoise correction along with the def2-TZVPPD basis set resulted in the highest RMS of 0.66 and BE deviation of almost 1 kcal mol−1. It is known that, in certain cases, the errors of smaller basis sets may compensate for basis set superposition error (BSSE) and other systematic errors. For example, Antony and Grimme recommended SCS-MP2 with the triple-ζ basis sets (TZVPP and cc-pVTZ) without CP correction as the methods give reasonable results for large systems involving weak interactions [50]. In some cases, the half-counterpoise correction [10,51] or extrapolation to the basis set limit was found to better describe the reference data [52,53]. Although the BSSE largely affects the small (double-ζ) basis sets [54,55], the DFT scheme used herein for geometry optimizations (ωB97X-D4/ma-def2-TZVP) may suffer from the BSSE when calculating binding energies [54], also because estimation of the absolute electronic energy is a known weak point of the DFT. However, the geometrical parameters of the S66 models calculated at the DFT level are close to those obtained at the ab initio level (Table S8), while the DLPNO-CCSD(T) correction of the final energy allows approaching the reference BE values.
We checked how the H⋯Cl separation in the {CH4⋯Cl}− model assembly is influenced by the calculation level (Table S9). The ωB97X-D4/ma-def2-TZVP method affords d(H⋯Cl) = 2.689 Å. The application of the geometrical semi-empirical counterpoise correction (gCP) [56] along with the def2-TZVP basis set shortens the d(H⋯Cl) distance down to 2.591 Å (the pure def2-TZVP calculation gives d(H⋯Cl) = 2.575 Å), indicating that diffuse functions are essential for the present case of anion assembly. The increase of the basis set up to def2-QZVPPD, which is large enough to minimize BSSE until negligible level [57,58], results in H⋯Cl separation of 2.672 Å, which is slightly shorter than that for ma-def2-TZVP. A very similar distance of 2.673 Å was obtained for a very large aug-cc-pV6Z basis set (Table S9). While the ωB97M-V [59] and M06-2X [60] functionals showed similar tendencies, the SCS-MP2 method [61] gave much shorter d(H⋯Cl) = 2.603 Å for aug-cc-pV6Z, while for def2-QZVPPD the elongated distance of 2.713 Å was obtained. Finally, we optimized the {CH4⋯Cl}− geometry at the DLPNO-CCSD(T)/def2-QZVPPD level, which gave d(H⋯Cl) = 2.651 Å (Table S9). Thus, the geometry exhibited by the ωB97X-D4/ma-def2-TZVP method fits into the spread of d(H⋯Cl) distances. Considering this, as well as the success in the description of the selected S66 models (Table S8), we assume the precision of this DFT method to be sufficient for the present study.
We considered a series of model complexes {R3C–H}0⋯Cl−, including radical forms (Tables S5 and S6, Figures S8–S10), for which BE vs. ρ(r) and ΔH vs. ρ(r) dependences were studied. Both binding energy and enthalpy data can be fitted to linear equations with R2 of 0.92 and 0.91 and the RMS values of 1.60 and 1.55, respectively (Figure 18).
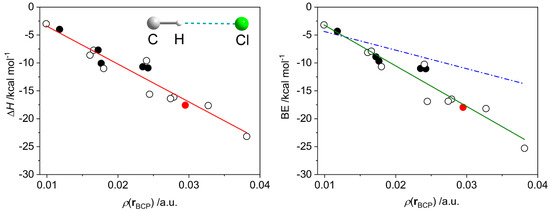
Figure 18.
Dependences of the dissociation enthalpy (ΔH, left) and the binding energy (BE, right) on the electron density ρ(r) at the H⋯Cl bond critical point in the set of model compounds featuring one (empty and black filled circles) or two (red filled circle) {R3C–H}0⋯Cl− hydrogen bonds (Figure S8), where Cl is an isolated atom. The black-filled circles correspond to the radical species (triplet state); all others are in the singlet state. Solid red and green lines correspond to the least-squares linear fits: ΔH = −678 × ρ(r) + 3 and BE = −726 × ρ(r) + 4. Dash dot blue line (right) was calculated using the parameters reported by Emamian and Lu [10].
The slope of the fitted line obtained for the BE vs. ρ(r) data (−726) significantly differs from that proposed by Emamian et al. for charged complexes (−332.34) [10]. Moreover, the latter equation is not able to describe the data in the region of strong interactions (Figure 18, right). To ensure that this discrepancy is not a result of differences in calculation methodology, we reproduced the geometries, electron densities and binding energies of several H-bonded assemblies used in [10]. We found that under our conditions, the energies of the assemblies and the slope of the BE vs. ρ(r) linear fit are almost identical to those reported by Emamian et al. [10] (Figure S11). Therefore, one can conclude that the case of {R3C–H}0⋯Cl− interactions is better described by the linear regression proposed herein. Further, we did not find a notable change in enthalpies when using larger basis sets (ma-def2-QZVPP and aug-cc-pVQZ) for DLPNO-CCSD(T) correction (Figure S12). The pure DFT calculations (without the DLPNO-CCSD(T) correction) give the binding energies only slightly different from those for CCSD-corrected DFT data, maintaining the overall statistical distribution (Figure S13).
From the proposed regressions, the interaction enthalpy of the {HL1·Cl}− assembly (Figure 17) is expected to be –37.6 kcal mol−1, which is rather close to the value found from the vibrational energies at the DFT level (−32.1 kcal mol−1). As the {HL1·Cl}− constitutes two C–H⋯Cl and one N–H⋯Cl bonds, we checked the applicability of the proposed model for {N–H}0⋯Cl− contacts: the DFT and regression model predicted ΔH for {CH3NH2⋯Cl}− equal to −9.8 and −9.7 kcal mol−1, respectively. For the protonated ligand {H2L1}+ interacting with the chloride anion, the regression predicts ΔH = −58.6 kcal mol−1, while the DFT calculations give twice higher value ΔH of −112.8 kcal mol−1. Such a strong interaction is illustrated by significant shortening of the N–H⋯Cl contact from 2.219 to 1.857 Å for {HL1·Cl}− and {H2L1·Cl}0, respectively (Figure 17 and Figure S7), where the Löwdin charges at the respective H atoms in the free ligands are 0.219 and 0.241, respectively. Therefore, the linear regressions proposed herein should be used with care for the assessment of the stability of supramolecular assemblies with charges other than {R3C–H}0⋯Cl−.
2.4. Antibacterial Activity Studies
Complexes 1, 3 and 4 were screened for antibacterial activity with a following evaluation of the minimal inhibitory concentration (MIC) (Table 1) toward the panel of reference microorganisms from the American Type Culture Collection (ATCC), including Gram-negative bacteria (Escherichia coli ATCC 25922, Pseudomonas aeruginosa ATCC 27853, Klebsiella pneumoniae ATCC 700603, Acinetobacter baumannii ATCC BAA 747, Pseudomonas aeruginosa HUI PAMβL) and Gram-positive bacteria (Staphylococcus aureus ATCC 25923, Staphylococcus aureus HUI MRSA, Staphylococcus aureus ATCC MR 43300, Staphylococcus haemolyticus HUI MRCNS).

Table 1.
Antibacterial activity of complexes 1, 3 and 4.
The MIC values ranged between 156.25 and 312.5 mg/L for compounds 1 and 4 and varied in the range of 156.2–625 mg/L for compound 3. Among the strains of Gram-negative bacteria, the best results were obtained in the case of Acinetobacter baumannii ATCC BAA 747, where all three studied compounds show the lowest observed MIC value of 156.25 mg/L. The other tests involving Gram-negative bacteria mostly show the moderate antibacterial activity of 1, 3 and 4 with MIC of 312.5 mg/L, while the lowest activity was documented in the case of 3 toward Pseudomonas aeruginosa HUI PAMβL (625 mg/L). The most active compound in the experiments with a group of Gram-positive bacteria was complex 4, showing the MIC value of 156.25 mg/L in the case of three out of four studied strains. Compounds 1 and 3 reveal moderate activity toward Gram-positive bacteria with an MIC value of 312.5 mg/L, except for tests including Staphylococcus aureus ATCC 25923 and compound 3, which shows MIC equal to 156.25 mg/L. The obtained results indicate that all studied compounds show a broad spectrum of activity against the tested microorganisms and reveal relatively better activity against Gram-positive than Gram-negative bacteria, and the best activity was observed against Acinetobacter baumannii ATCC BAA 747.
Comparing the results obtained for 1 with those reported previously for Cu(II) complexes, one can observe that in the case of Gram-positive bacteria Staphylococcus aureus ATCC 25923 the complex 1 showed lower antibacterial activity (MIC of 312.5 mg/L) than the compound [Cu(ClNBz)(o-PDA)]Cl (where ClNBz is 4-chloro-3-nitrobenzoate and o-PDA is o-phenylenediamine) [62] revealing a MIC of 39 mg/L. However, in the case of Gram-negative bacteria Pseudomonas aeruginosa ATCC 27853, compound 1 performed much better, showing a MIC value of 312.5 mg/L in comparison with a MIC of 625 mg/L of [Cu(ClNBz)(o-PDA)]Cl [62]. The Cu(II) complexes CuL1A and CuL2A (where HL1A and HL2A are asymmetrical Schiff base ligands) [63] have the same MIC value of 128 mg/L against the tested Gram-positive (Staphylococcus aureus ATCC 25923) and Gram-negative (Escherichia coli ATCC 25922 and Pseudomonas aeruginosa ATCC 27853) bacteria, while 1 showed MIC = 312.5 mg/L in all similar tests. The CuCl2 is known to have the same as 1 antibacterial activity toward Staphylococcus aureus ATCC 25923 (MIC of 312 mg/L) and higher than 1 activity toward Pseudomonas aeruginosa ATCC 27853 (MIC of 156 mg/L) [62]. The MIC value of 272 mg/L was determined during the antibacterial study of the Co(II) complex [Co(H2BPClNOL)Cl2] (where H2BPClNOL is N-(2-hydroxybenzyl)-N-(2-pyridylmethyl)[(3-chloro)(2-hydroxy)]propylamine) [64] against the Gram-positive bacteria Staphylococcus aureus ATCC 25923. This value is higher than the respective MIC value of 3 (156.25 mg/L) and indicates a lower activity of [Co(H2BPClNOL)Cl2] in such a test. Similarly to 1, 3 and 4, the Ni(II) complex, [Ni3(C10H11NO2S)3]·C3H7NO [65], showed the highest activity with the lowest minimum inhibitory concentration value of 156.2 mg/L against Gram-negative bacteria Acinetobacter baumannii ATCC BAA 747.
3. Experimental
All chemicals were of reagent grade and used as received. All chemical experiments were carried out in air. Elemental analyses for CHN were provided by the Microanalytical Service of the Taras Shevchenko National University of Kyiv. Infrared spectra (4000–400 cm−1) were recorded in KBr pellets using a PerkinElmer 1600 FT-IR (PerkinElmer Inc., Waltham, MA, USA) instrument.
3.1. Syntheses of [Cu(HL1)(L2)Cl] (1) and [Cu(HL1)(L1)]∙Cl∙2H2O (2)
Benzhydrazide (0.27 g, 2 mmol) and 2-pyridinecarboxaldehyde (0.19 mL, 2 mmol) were dissolved in CH3OH (20 mL), forming a light-yellow solution which was magnetically stirred at 50–60 °C (30 min). Then, CuCl2·2H2O (0.17 g, 1 mmol) was added, and the resulting mixture was stirred for 1 h. The brown precipitate, which was immediately formed after cooling the obtained solution, was filtered, and the resulting solution was kept at r.t. Dark green crystals of 1, suitable for the X-ray crystallographic study, were formed in two days. Yield: 0.1 g. Anal. calc. for C19H15ClCuN4O3 (M = 446.34): C, 51.13; H, 3.39; N, 12.65%. Found: C, 51.4; H, 3.4; N, 12.6%. Further, the obtained filtrate was kept at r.t., and dark green crystals of 2 suitable for X-ray crystallographic study were formed in one month. Yield: 0.06 g (the total yield of 1 and 2 is 33%). Anal. calc. for C26H25ClCuN6O4 (M = 584.51): C, 53.42; H, 4.31; N, 14.38%. Found: C, 53.4; H, 4.0; N, 14.7%.
3.2. Synthesis of [Co(L1)2]∙Cl (3)
Benzhydrazide (0.27 g, 2 mmol) and 2-pyridinecarboxaldehyde (0.19 mL, 2 mmol) were dissolved in CH3OH (20 mL), forming a light-yellow solution which was magnetically stirred at 50–60 °C (30 min). Then, CoCl2·6H2O (0.24 g, 1 mmol) was added, and the resulting mixture was stirred for 1 h. Dark red crystals of 3, suitable for the X-ray crystallographic study, were formed in two days. Yield: 0.33 g, 60%. Anal. calc. for C26H20ClCoN6O2 (M = 542.86): C, 57.52; H, 3,71; N, 15.48%. Found: C, 57.6; H, 3.9; N, 15.2%.
3.3. Synthesis of [Cd(HL1)I2]∙dmso (4)
Benzhydrazide (0.27 g, 2 mmol) and 2-pyridinecarboxaldehyde (0.19 mL, 2 mmol) were dissolved in dmso (20 mL), forming a light-yellow solution which was magnetically stirred at 50–60 °C (30 min). Then, CdI2 (0.37 g, 1 mmol) was added, and the resulting mixture was stirred for 2 h. Yellow-orange crystals of 4, suitable for X-ray crystallographic study, were formed two weeks after the addition of 4 mL of iPrOH. Yield: 0.14 g, 21%. Anal. calc. for C15H17CdI2N3O2S (M = 669.58): C, 26.91; H, 2.56; N, 6.28%. Found: C, 26.7; H, 2.3; N, 5.9%.
3.4. Crystallography
Single-crystal X-ray data for all compounds were collected on a Gemini A diffractometer (Agilent Technologies Inc., Santa Clara, CA, USA) equipped with an Atlas CCD detector, using graphite monochromated MoKα radiation. The data were treated using the CrysAlisPro software suite program package [66]. Analytical absorption corrections were applied to all data sets. All structures were solved using the dual-space algorithm of the SHELXT [67] program implemented in the Olex2 (version 1.5) crystallographic software [68]. Structure refinement was performed with SHELXL-2014 software [69]. The atom O4 in 2 was found to be disordered over two positions, O4A and O4B, with occupancies of 0.74(2) and 0.26(2), respectively. Details of the data collection and processing, structure solution and refinement are summarized in Table 2.

Table 2.
Crystal data and structure refinement for 1–4.
Crystallographic data for the structures reported can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif quoting the deposition numbers CCDC 2209507 (1), 2209509 (2), 2209508 (3), and 2209510 (4).
3.5. Theoretical Calculations
The ORCA 5.0.3 package was used for all calculations [70,71,72]. Unless stated otherwise, the calculations were performed using ωB97X-D4 functional [73] with the minimally augmented ma-def2-TZVP basis sets [74,75]. The effective core potentials (ECP) included in the ma-def2-TZVP basis set were used to describe the core electrons of Cd and I atoms. Grimme’s atom-pairwise dispersion correction was employed [76]. The SCF and optimization convergence criteria were settled with VeryTightSCF and TightOPT keywords, respectively. Integration grids of high density (Defgrid3 keyword) were used. The CCSD calculations were performed through the DLPNO-CCSD(T) scheme [77] using the def2-TZVPPD basis set [46,75] and the TightPNO keyword. For calculations of singlet molecules, the “UseFullLMP2Guess false” command was applied to adjust the energies of closed-shell and open-shell calculations. AutoAux keyword [78] was used to generate auxiliary basis sets in all cases. To obtain the binding energy (BE) of the X⋯Y assembly, the whole geometry was optimized at the DFT level, and individual electronic energies EXY, EX and EY were calculated at the DLPNO-CCSD(T) level with no structural relaxation of the X and Y components. The final BE was calculated according to the equation BEXY = EXY − EX − EY. The counterpoise (CP) correction [49] was not applied unless stated otherwise. The interaction enthalpy ΔH was obtained from the vibrational energies calculated on the DFT-optimized structures of dimers and relaxed monomers, where the electronic energies were corrected at the DLPNO-CCSD(T) level for relaxed geometries of the monomers. The root mean square deviation (RMS) was defined as , where Ecalcd. and Efit. are energies or enthalpies obtained from DFT/DLPNO-CCSD(T) calculations and linear regression, respectively. Visualization of molecular orbitals was made using Avogadro 1.2 program [79]. Analysis of bond critical points and non-covalent interactions indexes [36] was performed using Multiwfn 3.8 program [80]. Hirshfeld analysis and surface visualization were made using the CrystalExplorer 17.5 program [81]. Cartesian coordinates of the DFT-optimized structures are given in Listing S1.
3.6. Strains Culturing Conditions and Antibacterial Assay
Gram-negative bacteria (Escherichia coli ATCC 25922, Pseudomonas aeruginosa ATCC 27853, Klebsiella pneumoniae ATCC 700603, Acinetobacter baumannii ATCC BAA 747, Pseudomonas aeruginosa HUI PAMβL) and Gram-positive bacteria (Staphylococcus aureus ATCC 25923, Staphylococcus aureus HUI MRSA, Staphylococcus aureus ATCC MR 43300, Staphylococcus haemolyticus HUI MRCNS). All strains were stored as frozen stocks in 25 (v/v)% glycerol at −80 °C. Pseudomonas aeruginosa HUI PAMβL, Staphylococcus aureus HUI MRSA, Staphylococcus haemolyticus HUI MRCNS were obtained from Ukrainian hospitals. The Kirby–Bauer disc-diffusion assay was used to determine the antimicrobial susceptibility as the diameter (mm) of inhibition or minimum inhibitory concentration (MIC) value after incubation for two days and interpreted according to the European Committee on Antimicrobial Susceptibility Testing (EUCAST) guidelines [82]. Antibiotic susceptibilities of the studied strains are listed in Tables S10 and S11.
Antibacterial activity of 1, 3 and 4 was studied by the MICs method using the broth microdilution approach. The compounds were dissolved in dmso:H2O = 1:1 mixture under heating in a water bath for 1 h to achieve a stock concentration of 1.25 µg/mL. Further, the resulting solutions were incubated at 37 °C for 12 h. Separately, the control of the growth in the experiments with sterile distilled water or solvent mixture without the addition of coordination compounds was carried out. If the solutions with high concentrations of dmso (50% and 25%) showed antibacterial activity, such an effect was not associated with the activity of the studied complexes and was neglected.
All bacteria were cultured in Cation-adjusted Mueller–Hinton broth (CAMHB) at 37 °C overnight. Then a sample of each culture was then diluted 40-fold in fresh broth and incubated at 37 °C for 1.5–3 h. The resultant mid-log phase cultures were diluted (CFU/mL measured by OD600) and added to each of the compound-containing plates, giving a cell density of 5 × 105 CFU/mL and a total volume of 50 µL. All the plates were covered and incubated at 37 °C for 18 h without shaking. Growth inhibition of all bacteria was determined by measuring absorbance at 600 nm (OD600) using a Tecan M1000 Pro (Tecan Austria GmbH, Grödig, Austria) monochromator plate reader. The percentage of growth inhibition was calculated for each well using the negative control (media only) and positive control (bacteria without inhibitors) on the same plate as the references. The growth rates for bacteria had a variation of ±10%, which is within the reported normal distribution of bacterial growth.
The MIC was determined as the lowest concentration at which the growth was fully inhibited, defined by an inhibition ≥ 80%. In addition, the maximal percentage of growth inhibition is reported as DMax, indicating any compounds with partial activity.
4. Conclusions
Using the one-pot synthetic approach, we have prepared four new complexes, [Cu(HL1)(L2)Cl] (1), [Cu(HL1)(L1)]∙Cl∙2H2O (2), [Co(L1)2]∙Cl (3) and [Cd(HL1)I2]∙dmso (4) based on Schiff base ligand HL1 prepared in situ by condensation of benzhydrazide and 2-pyridinecarboxaldehyde. For 1, under the experimental conditions, the oxidation of 2-pyridinecarboxaldehyde led to the formation of ligand HL2. According to the single crystal X-ray diffraction data, the crystal structures of 1–4 show broad supramolecular diversity of the complex architectures, including 1D polymeric chains in 1, 2D polymeric layers in 2, supramolecular trimers in 3 and 3D framework in 4.
We evaluated the non-covalent interactions in structures 1–3 with special attention to the C–H⋯Cl contacts. After DFT and QTAIM analysis of a series of model {R3C–H}0⋯Cl− assemblies, we propose the linear regressions ΔH = −678 × ρ(rBCP) + 3 and BE = −726 × ρ(rBCP) + 4 which coefficients differ from those proposed earlier for charged X–H⋯Y hydrogen bonds [10]. Although the R2 and MAD values of the present regression demonstrate that the dispersion of the data is not negligible, we believe these regressions will help in the assessment of energies of charged {C–H⋯Cl}− contacts.
Complexes 1, 3 and 4 were screened against some bacteria strains and were found to be active against nine Gram-negative and Gram-Positive bacteria. The MIC obtained for these compounds showed that the best activity was observed against Acinetobacter baumannii MβL, and 4 was the most effective against all the tested organisms.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules27238233/s1, Scheme S1: Schematic representation of the coordination compounds 1–4. Figure S1: IR spectrum of 1; Figure S2: IR spectrum of 2; Figure S3: IR spectrum of 3; Figure S4: IR spectrum of 4; Figure S5: IR spectrum of HL1; Figure S6: Dimeric structure of 1 optimized at the DFT level, Figure S7: DFT-optimized structure of the {H2L1·Cl}0 assembly, the plot of Laplacian of electron density, reduced density gradient plot; Figure S8: DFT-optimized model assemblies 1m–16m; Figure S9: plot of Laplacian of electron density and reduced density gradient plot for 1m; Figure S10: plot of Laplacian of electron density and reduced density gradient plot for 16m; Figure S11: Plot of the BE vs. ρ(rBCP) dependence obtained for three reference assemblies from [10]; Figure S12: Plot of the ΔH vs. ρ(rBCP) data obtained using different basis sets; Figure S13: Plot of the ΔH vs. ρ(rBCP) data with and without DLPNO-CCSD(T) correction of the electronic energy; Table S1. Selected geometrical parameters for 1; Table S2. Selected geometrical parameters for 2; Table S3. Selected geometrical parameters for 3; Table S4. Selected geometrical parameters for 4; Table S5. DFT and DLPNO-CCSD(T)-corrected total energies and enthalpies of the model assemblies 1m–16m; Table S6. Thermodynamic parameters of the model assemblies 1m–16m and electron densities at the H⋯Cl bond critical points; Table S7. Binding energies of the model assemblies 1m–16m calculated using different basis sets; Table S8. Geometry and binding energies of the selected model H-bonded assemblies from the S66 dataset calculated at different theory levels; Table S9. Selected properties of the {CH4⋯Cl}− assembly optimized at various levels of theory. Table S10. The susceptibility of studied gram-positive strains to some known antibiotics. Table S11. The susceptibility of studied gram-negative strains to some known antibiotics. Listing S1. Cartesian coordinates (Å) of the monomers and dimers of the {R3C-H⋯Cl}− and selected S66 model assemblies optimized at the ωB97X-D4/ma-def2-TZVP level.
Author Contributions
Conceptualization, O.V.N. and E.A.B.; methodology, O.V.N., D.S.N. and S.R.P.; investigation, O.V.N., D.S.N., E.A.B., E.A.G. and H.V.V.; writing—original draft preparation, review and editing O.V.N. and D.S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Fundação para a Ciência e Tecnologia (FCT), Portugal (projects UIDB/00100/2020, UIDP/00100/2020, and LA/P/0056/2020 of Centro de Química Estrutural, contracts IST-ID/086/2018 and IST-ID/117/2018), and by the Ministry of Education and Science of Ukraine (Project no. 22BP037-13). E.G. acknowledge the financial support from the Slovenian Research Agency (research core funding No. P1–0045; Inorganic Chemistry and Technology).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Crystallographic data for the structures reported can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif quoting the deposition numbers CCDC 2209507 (1), 2209509 (2), 2209508 (3), and 2209510 (4).
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Samples of the compounds are not available from the authors.
References
- Gupta, K.C.; Sutar, A.K. Catalytic activities of Schiff base transition metal complexes. Coord. Chem. Rev. 2008, 252, 1420–1450. [Google Scholar] [CrossRef]
- Liu, X.; Hamon, J.R. Recent developments in penta-, hexa- and heptadentate Schiff base ligands and their metal complexes. Coord. Chem. Rev. 2019, 389, 94–118. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Nesterova, O.V.; Pombeiro, A.J.L. Homo- and heterometallic polynuclear transition metal catalysts for alkane C-H bonds oxidative functionalization: Recent advances. Coord. Chem. Rev. 2018, 355, 199–222. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, L.L.; Wong, W.Y. Energy materials based on metal Schiff base complexes. Coord. Chem. Rev. 2018, 355, 180–198. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Nesterov, D.S. Polynuclear Cobalt Complexes as Catalysts for Light-DrivenWater Oxidation: A Review of Recent Advances. Catalysts 2018, 8, 602. [Google Scholar] [CrossRef]
- Berendonk, T.U.; Manaia, C.M.; Merlin, C.; Fatta-Kassinos, D.; Cytryn, E.; Walsh, F.; Burgmann, H.; Sorum, H.; Norstrom, M.; Pons, M.N.; et al. Tackling antibiotic resistance: The environmental framework. Nat. Rev. Microbiol. 2015, 13, 310–317. [Google Scholar] [CrossRef]
- Desiraju, G.R. A Bond by Any Other Name. Angew. Chem. Int. Ed. 2011, 50, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Webber, M.J.; Appel, E.A.; Meijer, E.W.; Langer, R. Supramolecular biomaterials. Nat. Mater. 2016, 15, 13–26. [Google Scholar] [CrossRef]
- Saleh, G.; Gatti, C.; Lo Presti, L.; Contreras-Garcia, J. Revealing Non-covalent Interactions in Molecular Crystals through Their Experimental Electron Densities. Chem. Eur. J. 2012, 18, 15523–15536. [Google Scholar] [CrossRef]
- Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef]
- Kuznetsov, M.L. Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)(n)Z-Y center dot center dot center dot X- (X, Y = F, Cl, Br) interactions. Int. J. Quant. Chem. 2019, 119, e25869. [Google Scholar] [CrossRef]
- Petelski, A.N.; Marquez, J.; Pamies, S.C.; Sosa, G.L.; Peruchena, N.M. Understanding the Chloride Affinity of Barbiturates for Anion Receptor Design. ChemPhysChem 2021, 22, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Aakeroy, C.B.; Evans, T.A.; Seddon, K.R.; Palinko, I. The C-H center dot center dot center dot Cl hydrogen bond: Does it exist? New J. Chem. 1999, 23, 145–152. [Google Scholar] [CrossRef]
- Maia, E.H.B.; Assis, L.C.; de Oliveira, T.A.; da Silva, A.M.; Taranto, A.G. Structure-Based Virtual Screening: From Classical to Artificial Intelligence. Front. Chem. 2020, 8, 343. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, W.; Chen, C.H.; Flood, A.H. Chloride capture using a C-H hydrogen-bonding cage. Science 2019, 365, 159. [Google Scholar] [CrossRef] [PubMed]
- Molina, P.; Zapata, F.; Caballero, A. Anion Recognition Strategies Based on Combined Noncovalent Interactions. Chem. Rev. 2017, 117, 9907–9972. [Google Scholar] [CrossRef] [PubMed]
- Nesterova, O.V.; Vassilyeva, O.Y.; Skelton, B.W.; Benko, A.; Pombeiro, A.J.L.; Nesterov, D.S. A novel o-vanillin Fe(III) complex catalytically active in C-H oxidation: Exploring the magnetic exchange interactions and spectroscopic properties with different DFT functionals. Dalton Trans. 2021, 50, 14782–14796. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Nesterov, D.S.; Krogul-Sobczak, A.; da Silva, M.F.C.G.; Pombeiro, A.J.L. Synthesis, crystal structures and catalytic activity of Cu(II) and Mn(III) Schiff base complexes: Influence of additives on the oxidation catalysis of cyclohexane and 1-phenylehanol. J. Mol. Catal. A 2017, 426, 506–515. [Google Scholar] [CrossRef]
- Buvaylo, E.A.; Kokozay, V.N.; Vassilyeva, O.Y.; Skelton, B.W.; Nesterova, O.V.; Pombeiro, A.J.L. Copper(II) complex of the 2-pyridinecarbaldehyde aminoguanidine Schiff base: Crystal structure and catalytic behaviour in mild oxidation of alkanes. Inorg. Chem. Commun. 2017, 78, 85–90. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Kasyanova, K.V.; Makhankova, V.G.; Kokozay, V.N.; Vassilyeva, O.Y.; Skelton, B.W.; Nesterov, D.S.; Pombeiro, A.J.L. Stereospecific sp3 C-H oxidation with m-CPBA: A CoIII Schiff base complex as pre-catalyst vs. its CoIIICdII heterometallic derivative. Appl. Catal. A 2018, 560, 171–184. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Kasyanova, K.V.; Buvaylo, E.A.; Vassilyeva, O.Y.; Skelton, B.W.; Nesterov, D.S.; Pombeiro, A.J.L. Heterometallic CoIIIZnII Schiff Base Catalyst for Mild Hydroxylation of C(sp3)-H Bonds of Unactivated Alkanes: Evidence for Dual Mechanism Controlled by the Promoter. Catalysts 2019, 9, 209. [Google Scholar] [CrossRef]
- Nesterova, O.V.; Kuznetsov, M.L.; Pombeiro, A.J.L.; Shul’pin, G.B.; Nesterov, D.S. Homogeneous oxidation of C-H bonds with m-CPBA catalysed by a Co/Fe system: Mechanistic insights from the point of view of the oxidant. Catal. Sci. Technol. 2022, 12, 282–299. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Chygorin, E.N.; Kokozay, V.N.; Bon, V.V.; Boca, R.; Kozlov, Y.N.; Shul’pina, L.S.; Jezierska, J.; Ozarowski, A.; Pombeiro, A.J.L.; et al. Heterometallic CoIII4FeIII2 Schiff Base Complex: Structure, Electron Paramagnetic Resonance, and Alkane Oxidation Catalytic Activity. Inorg. Chem. 2012, 51, 9110–9122. [Google Scholar] [CrossRef] [PubMed]
- Nesterova, O.V.; Chygorin, E.N.; Kokozay, V.N.; Omelchenko, I.V.; Shishkin, O.V.; Boca, R.; Pombeiro, A.J.L. A self-assembled octanuclear complex bearing the uncommon close-packed {Fe4Mn4(µ4-O)4(µ-O)4} molecular core. Dalton Trans. 2015, 44, 14918–14924. [Google Scholar] [CrossRef] [PubMed]
- Nesterova, O.V.; Chygorin, E.N.; Kokozay, V.N.; Bon, V.V.; Omelchenko, I.V.; Shishkin, O.V.; Titis, J.; Boca, R.; Pombeiro, A.J.L.; Ozarowski, A. Magnetic, high-field EPR studies and catalytic activity of Schiff base tetranuclear CuII2FeIII2 complexes obtained by direct synthesis. Dalton Trans. 2013, 42, 16909–16919. [Google Scholar] [CrossRef] [PubMed]
- Stetsiuk, O.; Nesterova, O.V.; Kokozay, V.N.; Domasevitch, K.V.; Omelchenko, I.V.; Shishkin, O.V.; Vranovicova, B.; Boca, R.; Pombeiro, A.J.L.; Petrusenko, S.R. Details make the difference: A family of tetranuclear CuIIMnIII complexes with cube-like and double open cube-like cores. Dalton Trans. 2017, 46, 7480–7494. [Google Scholar] [CrossRef] [PubMed]
- Chygorin, E.N.; Nesterova, O.V.; Rusanoya, J.A.; Kokozay, V.N.; Bon, V.V.; Boca, R.; Ozarowski, A. Novel Heterometallic Schiff Base Complexes Featuring Unusual Tetranuclear {CoIII2FeIII2(µ-O)6} and Octanuclear {CoIII4FeIII4(µ-O)14} Cores: Direct Synthesis, Crystal Structures, and Magnetic Properties. Inorg. Chem. 2012, 51, 386–396. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Nesterova, O.V.; Kokozay, V.N.; Pombeiro, A.J.L. Polynuclear Heterometallic Complexes from Metal Powders: The “Direct Synthesis” Approach. Eur. J. Inorg. Chem. 2014, 2014, 4496–4517. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Jezierska, J.; Nesterova, O.V.; Pombeiro, A.J.L.; Ozarowski, A. An unprecedented octanuclear copper core with C3i symmetry and a paramagnetic ground state. Chem. Commun. 2014, 50, 3431–3434. [Google Scholar] [CrossRef] [PubMed]
- Nesterov, D.S.; Kokozay, V.N.; Skelton, B.W. A Pentanuclear Cu/Co/Ni Complex with 2-(Dimethylamino)ethanol-Observation of a Rare Molecular Structure Type and Its Place in General Structural Types: An Analysis of the Cambridge Structural Database. Eur. J. Inorg. Chem. 2009, 2009, 5469–5473. [Google Scholar] [CrossRef]
- Semenaka, V.V.; Nesterova, O.V.; Kokozay, V.N.; Zybatyuk, R.I.; Shishkin, O.V.; Boca, R.; Gomez-Garcia, C.J.; Clemente-Juan, J.M.; Jezierska, J. Structural and magnetic studies of tetranuclear heterometallic M/Cr (M = Co, Mn) complexes self-assembled from zerovalent cobalt or manganese, Reineckes salt and diethanolamine. Polyhedron 2010, 29, 1326–1336. [Google Scholar] [CrossRef]
- Pryma, O.V.; Petrusenko, S.R.; Kokozay, V.N.; Shishkin, O.V.; Zhigalko, M.V. Novel heterometallic Cu/Cd complex containing a unique polymeric ladder-like anion [Cd2(O2CMe)6]2−n derived from elemental copper and cadmium oxide. Inorg. Chem. Commun. 2003, 6, 896–899. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Makhankova, V.G.; Kokozay, V.N.; Skelton, B.W. Direct synthesis and crystal structures of new heteropolynuclear complexes containing aminoalcohol ligands: From heterobi- (Co/Zn) to heterotrimetallic (Cu/Co/Zn) compounds. Inorg. Chim. Acta 2005, 358, 4519–4526. [Google Scholar] [CrossRef]
- Sankar, M.; Nowicka, E.; Carter, E.; Murphy, D.M.; Knight, D.W.; Bethell, D.; Hutchings, G.J. The benzaldehyde oxidation paradox explained by the interception of peroxy radical by benzyl alcohol. Nat. Commun. 2014, 5, 3332. [Google Scholar] [CrossRef] [PubMed]
- Martinez, C.R.; Iverson, B.L. Rethinking the term “pi-stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-Garcia, J.; Cohen, A.J.; Yang, W.T. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Noodleman, L.; Davidson, E.R. Ligand spin polarization and antiferromagnetic coupling in transition-metal dimers. Chem. Phys. 1986, 109, 131–143. [Google Scholar] [CrossRef]
- Noodleman, L. Valence bond description of anti-ferromagnetic coupling in transition-metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Ginsberg, A.P. Magnetic exchange in transition-metal complexes. 12. Calculation of cluster exchange coupling-constants with the x-alpha-scattered wave method. J. Am. Chem. Soc. 1980, 102, 111–117. [Google Scholar] [CrossRef]
- Ye, S.F.; Geng, C.Y.; Shaik, S.; Neese, F. Electronic structure analysis of multistate reactivity in transition metal catalyzed reactions: The case of C-H bond activation by non-heme iron(IV)-oxo cores. Phys. Chem. Chem. Phys. 2013, 15, 8017–8030. [Google Scholar] [CrossRef] [PubMed]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Rezac, J.; Hobza, P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. [Google Scholar] [CrossRef] [PubMed]
- Rezac, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theor. Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef] [PubMed]
- Rezac, J.; Riley, K.E.; Hobza, P. Extensions of the S66 Data Set: More Accurate Interaction Energies and Angular-Displaced Nonequilibrium Geometries. J. Chem. Theor. Comput. 2011, 7, 3466–3470. [Google Scholar] [CrossRef]
- Kesharwani, M.K.; Karton, A.; Sylvetsky, N.; Martin, J.M.L. The S66 Non-Covalent Interactions Benchmark Reconsidered Using Explicitly Correlated Methods Near the Basis Set Limit. Aust. J. Chem. 2018, 71, 238–248. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef] [PubMed]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron-affinities of the 1st-row atoms revisited-systematic basis-sets and wave-functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations. 4. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Is spin-component scaled second-order moller-plesset perturbation theory an appropriate method for the study of noncovalent interactions in molecules? J. Phys. Chem. A 2007, 111, 4862–4868. [Google Scholar] [CrossRef]
- Burns, L.A.; Marshall, M.S.; Sherrill, C.D. Comparing Counterpoise-Corrected, Uncorrected, and Averaged Binding Energies for Benchmarking Noncovalent Interactions. J. Chem. Theor. Comput. 2014, 10, 49–57. [Google Scholar] [CrossRef]
- Minenkov, Y.; Chermak, E.; Cavallo, L. Accuracy of DLPNO-CCSD(T) Method for Noncovalent Bond Dissociation Enthalpies from Coinage Metal Cation Complexes. J. Chem. Theor. Comput. 2015, 11, 4664–4676. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Idaboy, J.R.; Galano, A. Counterpoise corrected interaction energies are not systematically better than uncorrected ones: Comparison with CCSD(T) CBS extrapolated values. Theor. Chem. Acc. 2010, 126, 75–85. [Google Scholar] [CrossRef]
- Gray, M.; Bowling, P.E.; Herbert, J.M. Systematic Evaluation of Counterpoise Correction in Density Functional Theory. J. Chem. Theor. Comput. 2022, 18, 6742. [Google Scholar] [CrossRef] [PubMed]
- Plumley, J.A.; Dannenberg, J.J. A Comparison of the Behavior of Functional/Basis Set Combinations for Hydrogen-Bonding in the Water Dimer with Emphasis on Basis Set Superposition Error. J. Comput. Chem. 2011, 32, 1519–1527. [Google Scholar] [CrossRef] [PubMed]
- Kruse, H.; Grimme, S. A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems. J. Chem. Phys. 2012, 136, 154101. [Google Scholar] [CrossRef]
- Schmitz, G.; Elm, J. Assessment of the DLPNO Binding Energies of Strongly Noncovalent Bonded Atmospheric Molecular Clusters. ACS Omega 2020, 5, 7601–7612. [Google Scholar] [CrossRef]
- Brauer, B.; Kesharwani, M.K.; Kozuch, S.; Martin, J.M.L. The S66x8 benchmark for noncovalent interactions revisited: Explicitly correlated ab initio methods and density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 20905–20925. [Google Scholar] [CrossRef] [PubMed]
- Mardirossian, N.; Head-Gordon, M. omega B97M-V: A combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation. J. Chem. Phys. 2016, 144, 214110. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Moller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Kabbani, A.T.; Hammud, H.H.; Ghannoum, A.M. Preparation and antibacterial activity of copper and cobalt complexes of 4-chloro-3-nitrobenzoate with a nitrogen donor ligand. Chem. Pharm. Bull. 2007, 55, 446–450. [Google Scholar] [CrossRef]
- Sahin, M.; Kocak, N.; Erdenay, D.; Arslan, U. Zn(II), Ni(II), Cu(II) and Pb(II) complexes of tridentate asymmetrical Schiff base ligands: Synthesis, characterization, properties and biological activity. Spectrochim. Acta A Mol. Biomol. Spectr. 2013, 103, 400–408. [Google Scholar] [CrossRef]
- Fernandes, C.; Horn, A.; Vieira-da-Motta, O.; de Assis, V.M.; Rocha, M.R.; Mathias, L.D.; Bull, E.S.; Bortoluzzi, A.J.; Guimaraes, E.V.; Almeida, J.C.A.; et al. Synthesis, characterization and antibacterial activity of FeIII, CoII, CuII and ZnII complexes probed by transmission electron microscopy. J. Inorg. Biochem. 2010, 104, 1214–1223. [Google Scholar] [CrossRef]
- Rusanova, J.A.; Kokozay, V.N.; Pokas, O.V. Tris(mu(2)-2-methoxy-6-{ (2-sulfidoethyl)imino -methyl}phenolato)trinick el(II) dimethylformamide monosolvate: Crystal structure, spectroscopic characterization and antibacterial activity. Acta Crystallogr. E 2019, 75, 616. [Google Scholar] [CrossRef]
- CrysAlisPro, Version 1.171.37.31; Release 14 January 2014 CrysAlis171.NET; Software That Was Supplied with the Equipment “Gemini A Diffractometer”. Agilent Technologies: Santa Clara, CA, USA, 2014.
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 18. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wil. Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wil. Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Zheng, J.J.; Xu, X.F.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theor. Comput. 2017, 13, 554–562. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Wolff, S.K.; Grimwood, D.J.; McKinnon, J.J.; Turner, M.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer (Version 17.5); University of Western Australia: Perth, Australia, 2020. [Google Scholar]
- EUCAST Guidelines for Detection of Resistance Mechanisms and Specific Resistances of Clinical and/or Epidemiological Importance, Version 1.0, December 2013. Available online: www.eucast.org/resistance_mechanisms (accessed on 1 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).