Next Article in Journal
Effect of Solvothermal Temperature on Morphology and Supercapacitor Performance of Ni-MOF
Next Article in Special Issue
Revealing the Reasons for Degeneration of Resonance-Assisted Hydrogen Bond on the Aromatic Platform: Calculations of Ortho-, Meta-, Para-Disubstituted Benzenes, and (Z)-(E)-Olefins
Previous Article in Journal
Chemical Composition, Phytotoxic and Antibiofilm Activity of Seven Eucalyptus Species from Tunisia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 27
Issue 23
10.3390/molecules27238225
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Long-Range Proton Transfer in 7-Hydroxy-Quinoline-Based Azomethine Dyes: A Hidden Reason for the Low Efficiency

by
Michał F. Rode
1,*,
Daniela Nedeltcheva-Antonova
2,3 and
Liudmil Antonov
2,*
1
Institute of Physics, Polish Academy of Sciences, Aleja Lotników 32/46, 02-668 Warsaw, Poland
2
Institute of Electronics, Bulgarian Academy of Sciences, 72 Tzarigradsko Chaussee blvd., 1784 Sofia, Bulgaria
3
Institute of Organic Chemistry with Centre of Phytochemistry, Bulgarian Academy of Sciences, Acad. G.Bonchev Str., bl. 9, 1113 Sofia, Bulgaria
*
Authors to whom correspondence should be addressed.
Molecules 2022, 27(23), 8225; https://doi.org/10.3390/molecules27238225
Submission received: 18 October 2022 / Revised: 16 November 2022 / Accepted: 18 November 2022 / Published: 25 November 2022
(This article belongs to the Special Issue Computational and Theoretical Studies on Isomeric Organic Compounds)
Browse Figures
Versions Notes

Abstract

:
In the tautomeric Schiff bases, derived from 7-hydroxyquinoline, two competitive channels are possible upon excitation of the enol tautomer, namely proton transfer (PT) through intramolecular hydrogen bonding to the corresponding keto form and trans–cis isomerization around the azomethine double bond. The former leads to switching, based on twist-assisted excited state intramolecular PT, where the long-range proton transfer can occur as a targeted process. The latter, determined by the flexibility of the crane part, reduces the efficiency of the main targeted process. In previously studied molecular switches based on the 7-hydroxyquinoline skeleton, only the intramolecular PT photo-process undergoing from the excited enol form towards the keto tautomer, which is in most cases barrierless, has been discussed. Therefore, in the current study, the ground state PT properties and isomerization of (E)-8-((phenylimino)methyl)quinolin-7-ol and (E)-8-(((pentafluorophenyl)imino)methyl)quinolin-7-ol are investigated in depth using the MP2 methodology, while the excited state energy profiles are calculated with the ADC(2) method. The obtained results are discussed in light of the existing experimental data.

1. Introduction

Photo switching systems, based on the proton craning mechanism, are the molecules where a proton is transferred intramolecularly over a long distance within the same molecule. Called proton cranes, they contain in general a tautomeric unit (frame) with clearly defined, spatially separated, proton donor and proton acceptor sites, which exchange, under external stimuli, the tautomeric (or pseudo tautomeric) proton, using a crane unit as a proton delivery system [1,2,3,4,5,6].
7-hydroxyquinoline (7HQ) is one of the most frequently studied examples of long-range proton transfer (PT) [7,8,9,10,11,12,13,14,15,16,17], where the proton donating OH group and the proton accepting N atom are far apart to provide conditions for truly intramolecular proton exchange. The enol tautomer is substantially more stable, while the NH tautomer has been experimentally observed only in protic organic solvents or in the presence of water and results from the intermolecular, solvent-assisted PT mechanism [17,18]. Previous computational studies of the potential energy profiles along the relevant internal coordinates, such as the O–H and N–H bond stretching distances, suggested that forward and backward PT process could be observed for a series of molecules containing 7HQ, as a general tautomeric frame for the location of the O and N atoms in the space, and oxazine [5,19], other six-membered ring heterocycles [19], pyridines [19], carbaldehyde groups [18], and CO-BF2 [20,21] as proton cranes. Among them, the smallest in size, the carbaldehyde moiety, seemed to be a reasonably good choice allowing for fast rotation even when protonated [18,22].
Recently, we have reported several classes of proton craning switches, based on 7HQ, where the azomethine group plays a role of a crane unit, providing, in some cases, truly intramolecular long-range PT upon irradiation [23,24,25]. It was shown (Scheme 1) that the proton is transferred from the 7HQ oxygen atom to the basic nitrogen through series of short-range PT steps, accompanied by intramolecular rotation around the axle binding the tautomeric and crane units. The process is initiated by photoexcitation of the E-tautomer, followed by excited-state intramolecular PT (ESIPT) to KE*, consecutive intramolecular rotation and relaxation to the ground state intermediate tautomers (KE and KK) through a conical intersection (CI) [5], leading a priori to relatively low yield of formation of the terminal form K. The efficiency could be additionally worsened by the potential possibility of a competitive process originating from the flexibility of the crane unit, namely trans–cis isomerization around the azomethine bond [26,27], as shown in Scheme 2. Therefore, in the current study, we investigate in depth, by using advanced theoretical calculations, the ground and excited state PT properties and isomerization of compounds 1 and 2 (Scheme 3), which are based on 7HQ. Compound 3, where long-range PT to K is impossible, is taken as a reference compound of 1. The theoretical results will be compared with the existing experimental data in order to define simple tips allowing to distinguish between the long-range PT and the C=N trans–cis isomerization in proton cranes with a flexible crane part.

2. Results and Discussion

The studied 1 and 2, belong to the class of photo switchable molecules, which photo switching mechanism is based on the twist-assisted ESIPT process [5,19]. Each of them consists of the two units in conjugation: the proton donating 7HQ frame and the proton accepting crane (C=N) being attached to position eight of the 7HQ tautomeric frame. As a result of photoexcitation of the enol form, (E), 7HQ is able to donate the proton to the crane, while its own proton acceptor site (quinoline N atom) is far away. The proton crane is able to accept the proton in the excited state (S1), rotate, and dissipate photoexcitation energy to the ground state due to the internal conversion process undergoing in the vicinity of the CI(S1/S0) geometry. The CI geometry corresponds to a structure with both the crane and tautomeric frame units being perpendicular to each other, and thus both states (S0 and S1) are prone to meet leading to nonadiabatic transition S1→S0. This may result in the population of either the initial enol form, (E), or, the generation of a new keto form, (K). An experiment conveyed in a low-temperature Ar-matrix isolation proved that such a photo switching mechanism, based on single twist-assisted ESIPT, can be a reversible process gaining from enol to keto, E→K, and back, from keto to enol, K→ E with UV light excitation at a proper wavelength or thermally [22].
The reversibility of the switching process is based on the different stability of the two terminal forms, E and K. Of course, the real picture also depends on the relative stability of the intermediate tautomers KE and KK (Scheme 1). Although the aim is to have clean switching from E to K, depending on the particular molecular structure and relative stability of all four possible tautomers, the switching process can start from a mixture of tautomers and end in another tautomeric equilibrium, as it happens in 1 [24].
In most of the photo switchable molecules based on 7HQ, studied so far [5,19,20,21], the ESIPT process from the initially photoexcited enol form towards the nitrogen atom in the proton crane to form proton-transferred KE(S1) tautomer was considered as a dominating channel. However, the presence of the double C=N bond in the azomethine craning group gives a possibility of an additional geometrical transformation in the molecule, namely trans–cis photoisomerization. Both are activated in the excited state just after photoexcitation of the E(S0) form (to be punctual, E is actually Etrans, but for simplicity, only E will be used in the discussion below). Thus, these two excited-state processes seem to be coupled and their competition is visualized in Figure 1, where two-dimensional potential energy surfaces (PES) of the first (S1) exited states of 1 and 3 are shown. Each point at the PES is obtained by optimization of the geometry of the corresponding molecule imposing two constraints for driving coordinates: R(OH) stretching and θ dihedral angle (as defined in Scheme 2), separately in a given electronic state. The ESIPT process in such constructed S1-PES can be visualized along the direction parallel to the R(OH)-axis. The isomerization process, however, can be observed along the direction parallel to the θ-axis. The excited state potential energy surface of the next steps of the twist-assisted ESIPT process (according to Scheme 1) is shown in Figure 2.

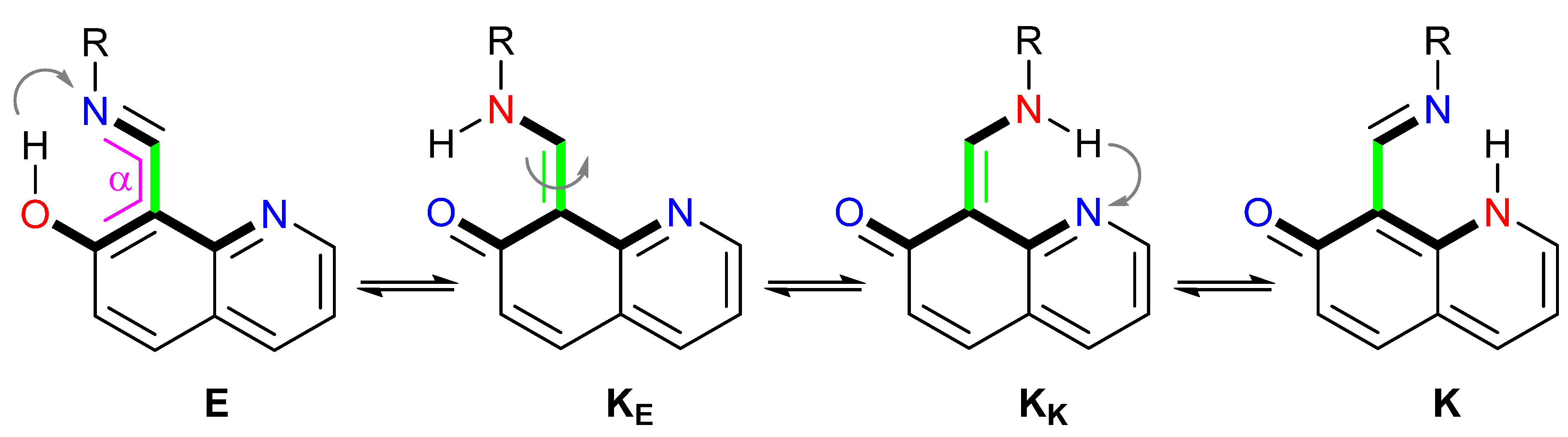
2.1. Ground State Tautomerization and Isomerization

The relative stability of the ground state tautomers of 1 and 3 are summarized in Table 1 and Table 2, respectively. The same information for 2 is given in the Supplementary Materials part Table S1.
As seen in Table 1, the enol form, 1E, constitutes the ground state global minimum (μg = 3.2 D) of the compound in the gas phase. The intramolecular hydrogen bond OH…N ensures planarity of the 7HQ ring along the C7HQ-C=N-CPh backbone, while the phenyl ring attached to the azomethine N atom is tilted out of the plane of the 7HQ skeleton. The second-in-energy, 1KE tautomer lying 0.203 eV (Table 1) above the 1E global minimum is separated from it by a very low energy barrier of 0.048 eV (details are given in the Supplementary Materials part Table S2). Both isomers seem to be present in thermal equilibrium. The third-in-energy keto tautomer 1KK (Ea=0.274 eV) can be obtained by rotating the proton transferred 1KE minimum by ~ 180o, about the α dihedral angle (as defined in Scheme 1). The barrier separating those two intermediate keto tautomers in the S0 state is huge, at ~1.6 eV, which precludes their direct S0-state isomerization. Putative 1K form related to its 1KK tautomer by proton transfer between the azomethine N and quinoline nitrogen atom is lying much higher in energy, by 0.535 eV, and is separated from the KK(S0) tautomer with an energy barrier of 0.060 eV. This is why the K(S0) tautomer is rather not likely to be populated both thermally due to the photo process. Contrary to 1KE, the relatively high-in-energy 1Ecis(S0) isomer (see Table 1) lying 0.531 eV above the global minimum cannot be populated thermally due to the large S0-state energy barrier of 1.35 eV separating it from the 1E(S0) isomer, but it can be photo populated in the reversible photoisomerization process. The S0-state energy barrier for the back Ecis(S0) → E(S0) isomerization is also large, at +0.8 eV, assuming a slow thermal depopulation of Ecis(S0). As seen in Table S1 (see see Supplementary Materials part), the fluorine substitution in 2, leads to reduced basicity of the azomethine nitrogen atom and, hence, to a lower stability of the intermediate tautomers. The terminal tautomer 2K is slightly stabilized, but remains higher in energy compared to 2KK, which makes its population improbable.
The theoretical data for model compound 3 (Table 2), and the existing experimental data for the ground state tautomerism of 1 [24] and 3 [28], allow us to validate the current theoretical findings. Comparing the data from Table 1 and Table 2, and bearing in mind that results for the gas phase are shown, it seems that in both compounds the stability of the E and KE tautomers should be similar in solution. From one side, the 3KE tautomer is slightly less stable compared to 1KE, but at the same time, the former is more polar compared to the corresponding enol, so the increased polarity of the solvent should compensate for this difference. The experimental results show that the ΔG value at room temperature in cyclohexane for 3 is around 1.4 kcal/mol [28], indicating a more stable E tautomer, as suggested by the theoretical calculations. In the case of 1 in toluene, all three (E, KE, and KK) tautomers are presented, again with the enol form being dominant [24]. The increased solvent polarity by using acetonitrile as a solvent shift the equilibrium towards the more polar KE in 3 and the more polar KK in 1 [24]. In 2, the E form predominance and the existence of traces of KE only, are evident from the absorption and NMR spectra in agreement with the data collected in Table S1 (see Supplementary Materials part). Therefore, we can assume that the used level of theory correctly predicts the tendencies in the ground state energy landscape, bearing in mind that the MP2 theory overestimates the stability of the enol tautomer, as previously observed [28].

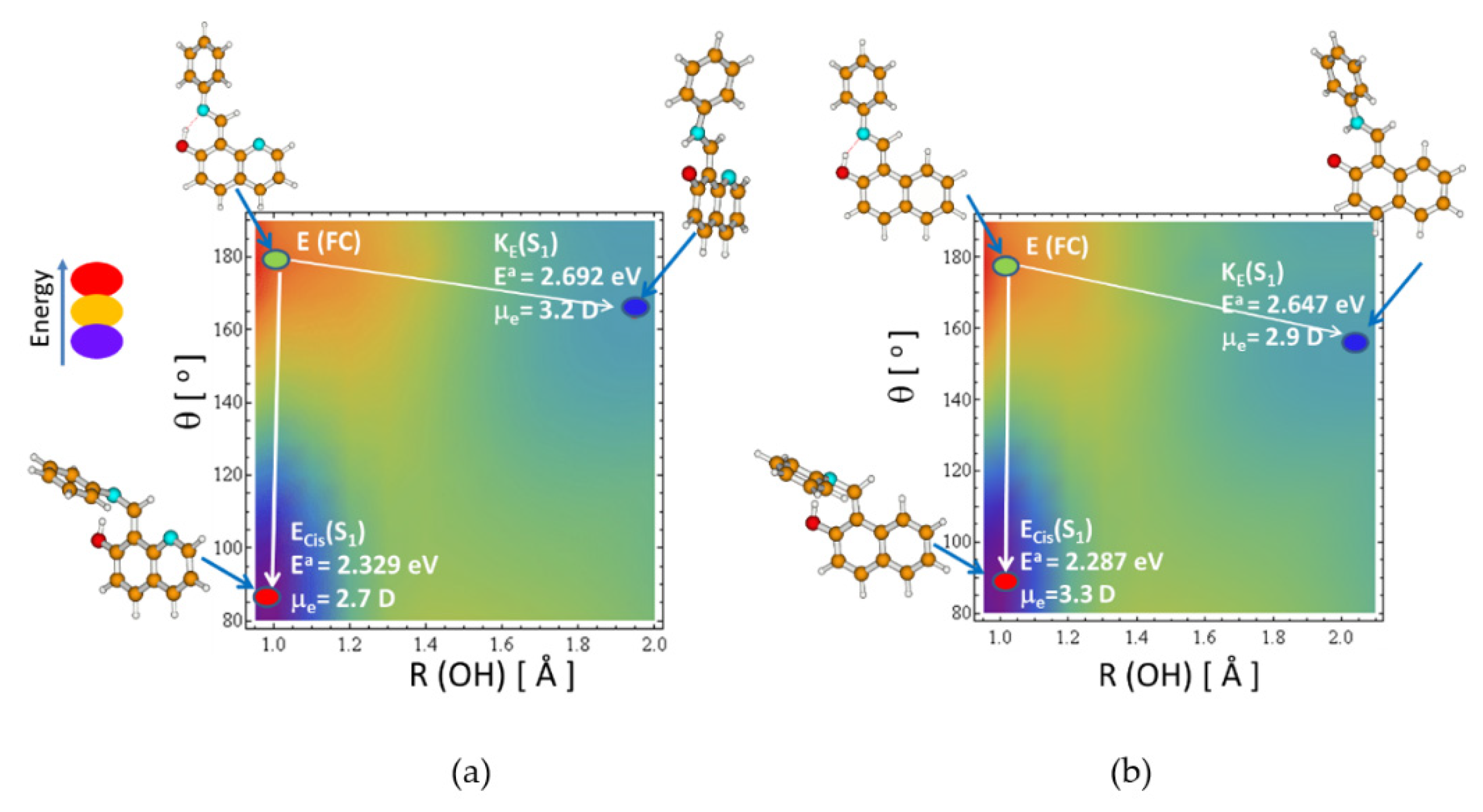
2.2. ESIPT vs. Trans–cis Isomerization in S1

In the calculated absorption spectrum of the global minimum, E(S0), there are three lowest strongly absorbing states: S0→S1,2,3 of meaningful oscillator strength (see Table 1 and Table 2, and Figure 3). S0→S1 is the most intense transition for all three compounds with a maximum absorption slightly blue-shifted for 3 vs. 1 and 2. Since the photo physics of 1 and 2 seems to be similar (see Figure 2a and Figure S1 (see Supplementary Materials part)), below we will discuss only 1 in comparison with 3.
The vertical excitation energy, ΔEVE, of the lowest S0→S1 electronic transition calculated for E(S0) is 3.70 eV (335 nm, CC2/aug-cc-pVDZ). The photoexcitation of 1E(S0) of one of those ππ* excited states populates eventually the lowest excited state (S1) at the Franck–Condon region what is indicated by a green dot in Figure 1a. Since ΔEVE for 1E is lying above the potential energy profiles describing both processes, the trans–cis photoisomerization competes with the ESIPT process, leading toward the 1KE tautomer (both indicated by the white arrow in Figure 1a). Both processes represent, in fact, a ballistic wave packet motion [29] along a given coordinate (either θ or R(OH), while α is practically not affected) without significant barriers and both can be easily activated upon photoexcitation of E(S0), since the adiabatic energies of their S1-state energy profiles are lying much below the vertical excitation energies, ΔEVE, of the absorbing ππ* states (compare Table 1, Table 2 and Table S1).
As seen in Figure 1, a diagonal rim is representing the excited state barrier separating two deep S1-state minima. The proton-transferred KE(S1) form is at the upper-right corner (blue dot) and the Ecis(S1) isomer is localized at the bottom-left corner (red dot). While the arrow, illustrating E to Ecis isomerization, is almost parallel to the θ-axis, the arrow indicating the ESIPT process is tilted away from horizontal movement indicating the mixing of both the R(OH) and θ coordinates along the process. It is also evident that the trans–cis isomerization is a more exoergic process than the ESIPT one and should be a more preferred channel. It ends up at the CI(S1/S0) region for θ close to 90o. In the CI geometry, the internal conversion takes place, where the S1-state is depopulated to the ground state and the molecule can either populate the new Ecis(S0) minimum or repopulate back the E(S0) isomer.
If the molecule undergoes the ESIPT process, leading towards the KE(S1) minimum (Ea = 2.692 eV), the obtained KE(S1) form may emit Efl = 1.4 eV or may further photoisomerize to the KK tautomer (see Figure 2). In a such photoisomerization reaction, the rotation of the protonated crane vs. the 7HQ frame about the α dihedral angle is needed. A relatively low excited-state energy barrier should be overpassed (see the solid blue line in Figure 2a, left panel, for compound 1, and in Figure 2b, for compound 3) to reach the conical intersection region CI(S1/S0). This excited-state barrier is much lower than the S0-state barrier, where the rotation is around a double bond since the same double bond becomes nominally a single bond being elongated in the excited state. Along this excited-state process, related to the twist of the protonated crane vs. molecular 7HQ frame, the molecule meets the conical intersection region CI(S1/S0) for the geometry, where the protonated crane and the frame are almost perpendicular to each other. The CI(S1/S0) geometry becomes a bifurcation point of the reaction, where depopulation to the ground state may favor either a return to the initial enol E form or a generation of a new KK tautomer.
The shape of the excited-state energy profile along the N1H coordinate in 1 (Figure 2a, right panel) indicates the presence of both the ground and the excited-state energy barrier for the proton transfer from KK(S1) to K(S1), so these barriers also preclude direct population of the K form.
Comparing compounds 1 vs. 3, one may notice that the S1-state minimum potential energy surfaces are also similar, indicating competition between two barrierless downhill processes: ESIPT and trans–cis photoisomerization. The excited-state proton-transferred minimum for 3 is a little more stable, Ea=2.647 eV (see Figure 1b, details are given in the Supplementary Materials part Table S3), than that for 1 of Ea=2.692 eV, and the OH distance in the excited state KE form is more elongate, being 2.040 A, for 3, vs. 1.947 A, for 1.
Bearing in mind that Figure 1 and Figure 2 originate from the gas phase calculational results, the transfer to the solution could change the relative stabilities of the excited-state species, making one or another pathway more favorable. In this respect, two points should be taken into account: the dipole moments of KE and Ecis in S1, and the overstabilization of the keto tautomers by MP2-based calculations, as discussed above. A definite answer can be given by the experiment, but first, we should discuss what could be expected as a result of each of the competitive processes.

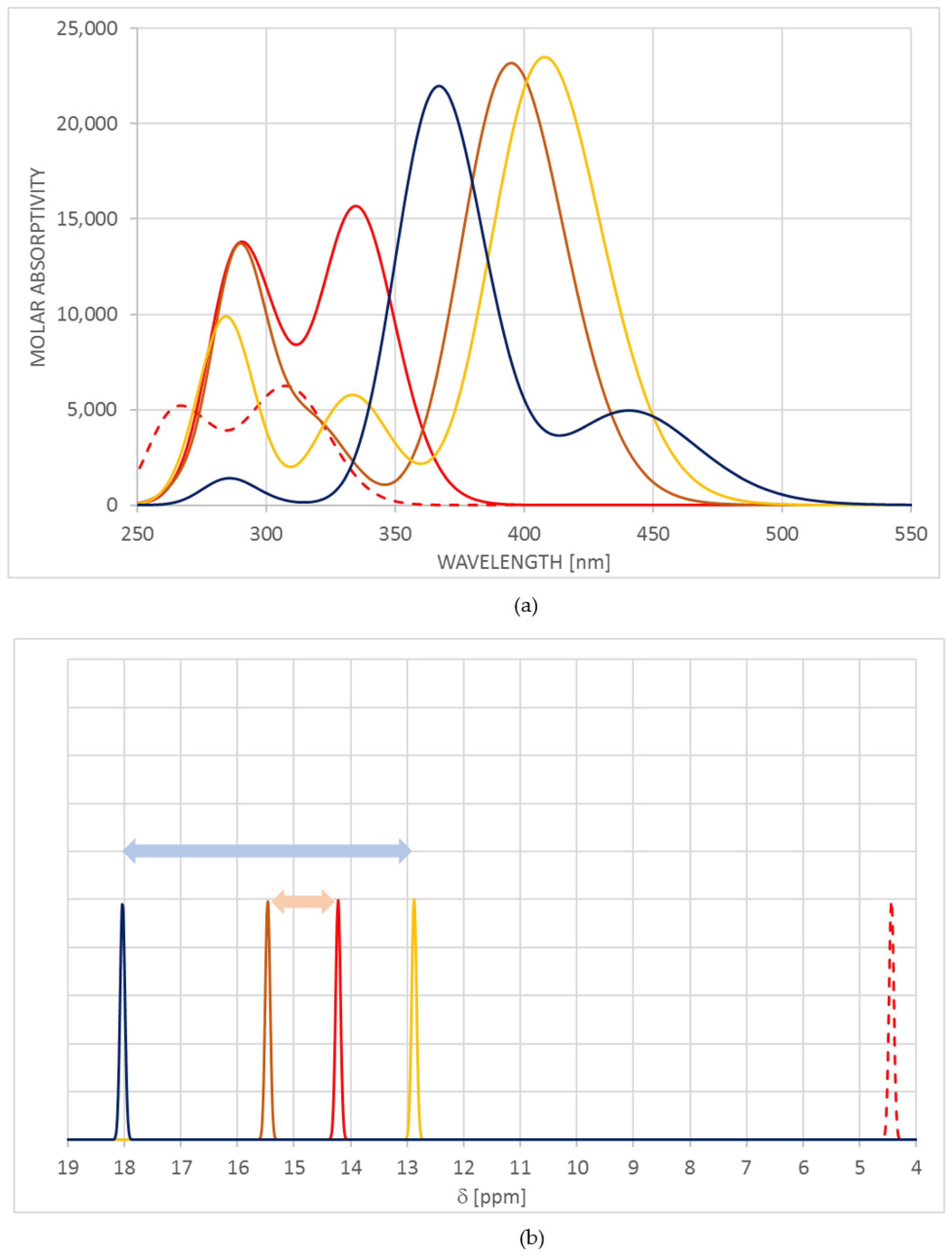
2.3. Long-Range PT and Trans–cis Isomerization in Terms of Spectral Changes to Be Experimentally Detected

The results in Table 1, Table 2 and Table S3 clearly suggest which kind of spectral changes could be expected upon ESIPT switching. The predicted absorption spectra of 1 are simulated in Figure 3a. It should be noted, that method-determined deviations from the experimental data exist in the absolute values, but in the discussion, the relative changes are of importance to show the expected tendencies [30]. According to the theoretically predicted absorption band positions, the appearance of the intermediate keto tautomers should cause a slight red shift in the absorption, while the appearance of the terminal K form leads to substantial bathochromic and hypochromic effects. As seen from the chemical structures of 1 and 2, the intermediate keto tautomers (KE and KK) contain the same conjugated motif and their absorption spectra should be similar, which makes their detection practically impossible by using the optical spectra. More or less the same could be stated for 3, but the steric hindrance in KK leads to lower oscillator strength, which could be used as a kind of proof if it appears. Actually, a very slight red shift in both absorption and emission was observed in the case of 1, experimentally upon irradiation [24], leading to the conclusion that the KK form, but not K, is populated in agreement with the theoretical predictions. In the case of 3, the irradiation does not cause any spectral changes [24] due to the instability of KK in the ground state, which leads to a reduced KK→KE barrier (~1.2 eV, see Table S2 in the Supplementary Materials part), and to the very fast thermal restoration of the equilibrium between E and KE, being separated by a very low barrier of +0.025 eV in respect of KE.
As seen from the data in Table 1 and Figure 3a, the appearance of the cis enol (Ecis) form could lead to hypochromic and hypochromic effects in the absorption spectra. In the case of a pure trans–cis transition, such an effect could be noticed as a reduction of the initial enol absorption, because the populated Ecis should return relatively slowly to E. As a pure effect, it was not observed in 1 experimentally [24], but in general, blue shifts in the spectra are not easy to detect, especially if the content of the cis form is low and additional processes occur. More precisely this can be seen in 3. The photoinitiated ESIPT, leading to a population only of KE in the ground state, cannot be detected by absorption spectroscopy, because the back relaxation to the existing thermal equilibrium is extremely fast. The trans–cis process should be detected, if occurring due to the significant barrier of the Ecis→E process (see Table S2 in the Supplementary Materials part). The absorption spectra of 3 under irradiation do not change, which proves the appearance only of the tautomeric process.
Here is the moment to discuss the use of NMR for monitoring the long-range PT process. Due to the very low ground state energy barriers, the proton transfer between E and KE, and between KK and K, is too fast in the NMR time scale [31]. For this reason, averaged signals of the pair E/KE and KK/K could be only detected. At the same time, the participation of the tautomeric proton in strong intramolecular hydrogen bonding in any of four possible tautomeric forms leads to a down-fielded 1H chemical shift, much above 10 ppm. The observed chemical shifts depend on the population of the particular tautomer in the pair and its individual chemical shift [32]. As it is sketched in Figure 3b the ranges of signals of the pairs E/KE and KK/K are given in pink and light blue, correspondingly. Comparing only the terminal E and K tautomers, in general, the NH chemical shift of the K form should be substantially down-fielded in comparison with the OH shift of the enol (Figure 3b). In the case of 1, the existence of two NH signals is detected in CD3CN, a strong intensive at 15.47 and a weak one at 14.25 ppm. The former is a result of the co-existence of the tautomers in the pair E/KE, while the latter is attributed to KK and can be used for monitoring the switching process upon irradiation. The 1K tautomer, which NH chemical shift should be measured > 17 ppm, is impossible to appear due to the low stability as discussed above, which is the reason for the up-field (from 15.47 to 14.25) of the signal following the internal rotation around the axle.
The tautomeric behavior of 2 is substantially easier to interpret. The fluorine substitution, compared to 1, leads to reduced basicity of the azomethine nitrogen atom and, hence, to the lower stability of the intermediate tautomer. The predominance of E and the existence of traces only on KE only is evident from the absorption and NMR spectra in full agreement with the data, collected in Table S1 (See Supplementary Materials Part). According to the photochemical experiments, the irradiation leads to a slight red shift in both absorption and emission spectra, indicating populating of the KK tautomer as a result. As it happens in 1, no direct evidence for the trans–cis process is found, but the difficulties in detecting the blue-shifted Ecis should be taken into account in this respect.
In all studied compounds, the yield of the aimed ESIPT process is reduced, even if Ecis is not directly populated, as a result of the trans–cis isomerization in the excited state, i.e., the relaxation through CI leads only back to E. This might be an explanation for the observed low efficiency of ESIPT in the Schiff bases [24,33].

3. Theoretical Methodology

Theoretical calculations were performed in vacuo without imposing any symmetry constraints. The ground state (S0) of the molecules is modeled with the MP2 method [34] with the use of the correlation-consistent valence double zeta basis set with polarization functions on all atoms (cc-pVDZ) [35]. The MP2/cc-pVDZ energy of the enol form E is the reference energy for other isomers of the molecules, both in the ground and in the excited state. The same method was used to estimate the potential energy barriers separating the isomers in their ground state. The effect of using aug-cc-pVDZ and cc-pVTZ basis sets, shown in Table S4 (see Supplementary Materials part), indicates that the change of the basis set does not lead to a dramatic change in the overall PES and relative stabilities of the tautomers, proving the use of the less computationally demanding cc-pVDZ.
The UV spectrum was theoretically simulated with aid of the CC2 [36,37] method with the aug-cc-pVDZ basis set [35] and with the ADC(2) method [38,39,40,41] for comparison. ADC(2) is a computationally efficient single-reference propagator method, which yields similar excitation energies as the simplified second-order coupled-cluster (CC2) method [36]. Additionally, the ADC(2) energy for the ground state is equal to the MP2 energy (MP2 energy is a reference for the ADC(2) method). The accuracy of CC2 and ADC(2) for excitation energies of organic molecules has been extensively benchmarked in comparison with more accurate methods, such as CC3 and EOM-CCSD [42,43,44].
Certain problems were experienced with the choice of the proper method for excited-state optimization. The CC2/cc-pVDZ method gives barrierless ESIPT from the photoexcited S0-state E global minimum in its Franck–Condon region toward the proton-transferred KE tautomer, while the optimization with the ADC(2)/cc-pVDZ method shows barrierless evolution of the same E form toward the Ecis isomer of the molecule. However, optimization of the ADC(2) and CC2 methods with larger basis sets aug-cc-pVDZ and cc-pVTZ finally converged to the Ecis isomer. Such results give the idea that the processes photoinitiated at the E form (ESIPT and trans-cis photoisomerization), are competitive with each other and the best choice would be to present this competition in a form of the relaxed PES spanned over two coordinates: R(O-H) stretching and θ (C=N) torsion angle. For this purpose, the excited-state (S1) equilibrium geometries were determined with the second-order algebraic diagrammatic construction ADC(2) method [38,39,41], since this method seemed to be faster for relaxed energy surface calculations. The same method was used to estimate the S1-state energy barriers along the proton transfer: OH and NH stretching coordinates as well as for the torsion angles α and θ in a single parameter-relaxed potential energy scan calculation. All calculations were performed using the TURBOMOLE program package [45].
The absorption spectra were visualized in Figure 3a by using the Gauss shape [46] of the individual bands with a half-band width of 3000 cm−1 and molar absorptivity extracted from the predicted oscillator strength [47]. The NMR chemical shieldings of the tautomeric forms of the studied compounds were calculated using the GIAO approximation [48] using MP2/ cc-pVDZ. The calculated absolute shieldings were transformed to chemical shifts using the reference compound tetramethylsilane, Si(CH3)4, for the hydrogen atoms.

4. Conclusions

In the proton cranes, being Schiff bases derived from 7-hydroxyquinoline, two competitive channels are possible upon photoexcitation, namely proton transfer and trans–cis isomerization around the azomethine double bond in the enol tautomer. The former leads to switching, based on twist-assisted ESIPT, where the long-range proton transfer can occur as a targeted process. The latter, determined by the flexibility of the crane part, reduces the efficiency of the switching process. Both ESIPT and trans–cis photoisomerization are barrierless processes initiated from the E(S0) Franck–Condon region. Which of these two channels dominate depends on the chemical structure and the chemical environment, but the experimental spectral data allow us to recognize it. The tautomeric proton transfer leads to a red shift in the absorption spectra, while the trans–cis isomerization causes a hypochromic and hypochromic effect, originating from the reduced conjugation.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules27238225/s1, Figure S1: Potential energy profiles of 2 in the S0 state (circles), determined at the MP2/cc-pVDZ theory level, in the S1 state (blue squares), determined at the ADC(2)/cc-pVDZ theory level along the minimum-energy path for N-phenyl crane torsion (KE to KK), and for hydrogen transfer from the intermediate form KK, toward proton-transferred form, K. S0(S1) denotes the energy of the S0 state, calculated along the minimum energy path of the S1 excited state (red dashed curves); Table S1: Vertical excitation energy, ΔEVE (in eV), oscillator strength, f, and dipole moment, μe (in Debye), of the lowest excited singlet states calculated with the CC2/aug-cc-pVDZ method for the ground state equilibrium forms of 2, optimized at the MP2/cc-pVDZ theory level; Table S2: Relative S0-state adiabatic energies, Ea, (in eV), of the stable tautomers and S0-state energy barriers separating the ground-state minima of the studied compounds 1, 2 and 3; Table S3: Adiabatic energy, Ea, and fluorescence energy, Efl, in eV, excited-state dipole moment, μe, in Debye, and OH distance for different excited-state minima of compounds 1, 2 and 3; Table S4: Ground-state S0 energy minima (relative energy in eV) and energy barriers of compound 1 optimized with the MP2 method using three different basis sets: cc-pVDZ, cc-pVTZ and aug-cc-pVDZ.

Author Contributions

Conceptualization, L.A. and M.F.R.; methodology, M.F.R.; validation, L.A., D.N.-A. and M.F.R.; investigation, M.F.R. and D.N.-A.; resources, M.F.R.; writing—original draft preparation, L.A., D.N.-A. and M.F.R.; writing—review and editing, L.A., D.N.-A. and M.F.R.; visualization, M.F.R. and D.N.-A.; supervision, L.A.; project administration, L.A.; All authors have read and agreed to the published version of the manuscript.

Funding

Bulgarian National Science Fund within the National Science Program VIHREN by project T-Motors (contracted as KP-06-DV-9/2019).

Data Availability Statement

The data presented in this study are available in this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jalink, C.J.; van Ingen, W.M.; Huizer, A.H.; Varma, C.A.G.O. Prospects for Using Photoinduced Intramolecular Proton Transfer to Study the Dynamics of Conformational Changes in Flexible Molecular Chains. J. Chem. Soc. Faraday Trans. 1991, 87, 1103. [Google Scholar] [CrossRef]
  2. Jalink, C.J.; Huizer, A.H.; Varma, C.A.G.O. Rate-Limiting Action of a Proton Crane in Long-Range Intramolecular Proton Transfer. J. Chem. Soc. Faraday Trans. 1992, 88, 2655. [Google Scholar] [CrossRef]
  3. de Bekker, E.J.A.; Geerlings, J.D.; Varma, C.A.G.O. Mechanism of a Photoinduced Solvent-Assisted Transfer of a Proton to a Specified Remote Target. J. Phys. Chem. A 2000, 104, 5916–5927. [Google Scholar] [CrossRef]
  4. de Bekker, E.J.A.; Pugzlys, A.; Varma, C.A.G.O. Elementary Processes in Photoinduced Proton Transfers in 2-Hydroxy-1-(N-Morpholinomethyl)Naphthalene and 7-Hydroxy-8-(N-Morpholinomethyl)Quinoline in Liquid Solutions. J. Phys. Chem. A 2001, 105, 399–409. [Google Scholar] [CrossRef]
  5. Sobolewski, A.L. Reversible Molecular Switch Driven by Excited-State Hydrogen Transfer. Phys. Chem. Chem. Phys. 2008, 10, 1243. [Google Scholar] [CrossRef]
  6. van der Loop, T.H.; Ruesink, F.; Amirjalayer, S.; Sanders, H.J.; Buma, W.J.; Woutersen, S. Unraveling the Mechanism of a Reversible Photoactivated Molecular Proton Crane. J. Phys. Chem. B 2014, 118, 12965–12971. [Google Scholar] [CrossRef]
  7. Ewing, G.W.; Steck, E.A. Absorption Spectra of Heterocyclic Compounds. I. Quinolinols and Isoquinolinols 1. J. Am. Chem. Soc. 1946, 68, 2181–2187. [Google Scholar] [CrossRef]
  8. Mason, S.F. The Tautomerism of N-Heteroaromatic Hydroxy-Compounds. Part I. Infrared Spectra. J. Chem. Soc. Resumed 1957, 980, 4874–4880. [Google Scholar] [CrossRef]
  9. Mason, S.F. The Tautomerism of N-Heteroaromatic Hydroxy-Compounds. Part II. Ultraviolet Spectra. J. Chem. Soc. Resumed 1957, 1002, 5010–5017. [Google Scholar] [CrossRef]
  10. Mason, S.F.; Philp, J.; Smith, B.E. Prototropic Equilibria of Electronically Excited Molecules. Part II. 3-, 6-, and 7-Hydroxyquinoline. J. Chem. Soc. Inorg. Phys. Theor. 1968, 3051–3056. [Google Scholar] [CrossRef]
  11. Lee, S.-I.; Jang, D.-J. Proton Transfers of Aqueous 7-Hydroxyquinoline in the First Excited Singlet, Lowest Triplet, and Ground States. J. Phys. Chem. 1995, 99, 7537–7541. [Google Scholar] [CrossRef]
  12. García-Ochoa, I.; Bisht, P.B.; Sánchez, F.; Martinez-Atáz, E.; Santos, L.; Tripathi, H.B.; Douhal, A. Experimental and Theoretical Studies of the Proton-Hopping Reaction of 7-Hydroxyquinoline in Viscous Hydroxylic Media. J. Phys. Chem. A 1998, 102, 8871–8880. [Google Scholar] [CrossRef]
  13. Chou, P.-T.; Wei, C.-Y.; Chris Wang, C.-R.; Hung, F.-T.; Chang, C.-P. Proton-Transfer Tautomerism of 7-Hydroxyquinolines Mediated by Hydrogen-Bonded Complexes. J. Phys. Chem. A 1999, 103, 1939–1949. [Google Scholar] [CrossRef]
  14. Kwon, O.-H.; Lee, Y.-S.; Yoo, B.K.; Jang, D.-J. Excited-State Triple Proton Transfer of 7-Hydroxyquinoline along a Hydrogen-Bonded Alcohol Chain: Vibrationally Assisted Proton Tunneling. Angew. Chem. Int. Ed. 2006, 45, 415–419. [Google Scholar] [CrossRef] [PubMed]
  15. Park, S.-Y.; Lee, Y.-S.; Kwon, O.-H.; Jang, D.-J. Proton Transport of Water in Acid–Base Reactions of 7-Hydroxyquinoline. Chem. Commun. 2009, 8, 926. [Google Scholar] [CrossRef]
  16. Park, S.-Y.; Jang, D.-J. Excited-State Hydrogen Relay along a Blended-Alcohol Chain as a Model System of a Proton Wire: Deuterium Effect on the Reaction Dynamics. Phys. Chem. Chem. Phys. 2012, 14, 8885. [Google Scholar] [CrossRef]
  17. Kumpulainen, T.; Lang, B.; Rosspeintner, A.; Vauthey, E. Ultrafast Elementary Photochemical Processes of Organic Molecules in Liquid Solution. Chem. Rev. 2017, 117, 10826–10939. [Google Scholar] [CrossRef]
  18. Vetokhina, V.; Nowacki, J.; Pietrzak, M.; Rode, M.F.; Sobolewski, A.L.; Waluk, J.; Herbich, J. 7-Hydroxyquinoline-8-Carbaldehydes. 1. Ground- and Excited-State Long-Range Prototropic Tautomerization. J. Phys. Chem. A 2013, 117, 9127–9146. [Google Scholar] [CrossRef]
  19. Rode, M.F.; Sobolewski, A.L. Effect of Chemical Substituents on the Energetical Landscape of a Molecular Photoswitch: An Ab Initio Study. J. Phys. Chem. A 2010, 114, 11879–11889. [Google Scholar] [CrossRef]
  20. Csehi, A.; Illés, L.; Halász, G.J.; Vibók, Á. The Effect of Chemical Substituents on the Functionality of a Molecular Switch System: A Theoretical Study of Several Quinoline Compounds. Phys. Chem. Chem. Phys. 2013, 15, 18048. [Google Scholar] [CrossRef]
  21. Csehi, A.; Halász, G.J.; Vibók, Á. Molecular Switch Properties of 7-Hydroxyquinoline Compounds. Int. J. Quantum Chem. 2014, 114, 1135–1145. [Google Scholar] [CrossRef]
  22. Lapinski, L.; Nowak, M.J.; Nowacki, J.; Rode, M.F.; Sobolewski, A.L. A Bistable Molecular Switch Driven by Photoinduced Hydrogen-Atom Transfer. ChemPhysChem 2009, 10, 2290–2295. [Google Scholar] [CrossRef] [PubMed]
  23. Nakashima, K.; Petek, A.; Hori, Y.; Georgiev, A.; Hirashima, S.; Matsushima, Y.; Yordanov, D.; Miura, T.; Antonov, L. Acylhydrazone Subunits as a Proton Cargo Delivery System in 7-Hydroxyquinoline. Chem.-Eur. J. 2021, 27, 11559–11566. [Google Scholar] [CrossRef] [PubMed]
  24. Georgiev, A.; Yordanov, D.; Ivanova, N.; Deneva, V.; Vassilev, N.; Kamounah, F.S.; Pittelkow, M.; Crochet, A.; Fromm, K.M.; Antonov, L. 7-OH Quinoline Schiff Bases: Are They the Long Awaited Tautomeric Bistable Switches? Dyes Pigment. 2021, 195, 109739. [Google Scholar] [CrossRef]
  25. Nakashima, K.; Georgiev, A.; Yordanov, D.; Matsushima, Y.; Hirashima, S.; Miura, T.; Antonov, L. Solvent-Triggered Long-Range Proton Transport in 7-Hydroxyquinoline Using a Sulfonamide Transporter Group. J. Org. Chem. 2022, 87, 6794–6806. [Google Scholar] [CrossRef]
  26. Jankowska, J.; Rode, M.F.; Sadlej, J.; Sobolewski, A.L. Excited-State Intramolecular Proton Transfer: Photoswitching in Salicylidene Methylamine Derivatives. ChemPhysChem 2014, 15, 1643–1652. [Google Scholar] [CrossRef]
  27. Spörkel, L.; Jankowska, J.; Thiel, W. Photoswitching of Salicylidene Methylamine: A Theoretical Photodynamics Study. J. Phys. Chem. B 2015, 119, 2702–2710. [Google Scholar] [CrossRef]
  28. Antonov, L. Tautomerism in Azo and Azomethyne Dyes: When and If Theory Meets Experiment. Molecules 2019, 24, 2252. [Google Scholar] [CrossRef]
  29. Lochbrunner, S.; Schriever, C.; Riedle, E. Direct Observation of Nuclear Motion during Ultrafast Intramolecular Proton Transfer. In Hydrogen-Transfer Reactions; Hynes, J.T., Klinman, J.P., Limbach, H.-H., Schowen, R.L., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; pp. 349–375. ISBN 978-3-527-30777-7. [Google Scholar]
  30. Adamo, C.; Jacquemin, D. The calculations of excited-state properties with Time-Dependent DensityFunctional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [Google Scholar] [CrossRef]
  31. Kleinpeter, E. NMR Spectroscopic Study of Tautomerism in Solution and in the Solid State. In Tautomerism: Methods and Theories; Antonov, L., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 103–143. ISBN 978-3-527-65882-4. [Google Scholar]
  32. Nedeltcheva, D.; Antonov, L.; Lycka, A.; Damyanova, B.; Popov, S. Chemometric Models for Quantitative Analysis of Tautomeric Schiff Bases and Azo Dyes. Curr. Org. Chem. 2009, 13, 217–240. [Google Scholar] [CrossRef]
  33. Joshi, H.; Kamounah, F.S.; Gooijer, C.; van der Zwan, G.; Antonov, L. Excited State Intramolecular Proton Transfer in Some Tautomeric Azo Dyes and Schiff Bases Containing an Intramolecular Hydrogen Bond. J. Photochem. Photobiol. Chem. 2002, 152, 183–191. [Google Scholar] [CrossRef]
  34. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
  35. Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  36. Christiansen, O.; Koch, H.; Jørgensen, P. The second-order approximate coupled cluster singles and doubles model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar] [CrossRef]
  37. Hättig, C.; Weigend, F. CC2 excitation energy calculations on large molecules using the resolution of the identity approximation. J. Chem. Phys. 2000, 113, 5154–5161. [Google Scholar] [CrossRef]
  38. Schirmer, J. Beyond the Random-Phase Approximation: A New Approximation Scheme for the Polarization Propagator. Phys. Rev. A At. Mol. Opt. Phys. 1982, 26, 2395–2416. [Google Scholar] [CrossRef]
  39. Trofimov, A.B.; Schirmer, J. An Efficient Polarization Propagator Approach to Valence Electron Excitation Spectra. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 2299–2324. [Google Scholar] [CrossRef]
  40. Trofimov, A.B.; Stelter, G.; Schirmer, J. A Consistent Third-Order Propagator Method for Electronic Excitation. J. Chem. Phys. 1999, 111, 9982–9999. [Google Scholar] [CrossRef]
  41. Hättig, C. Structure Optimizations for Excited States with Correlated Second-Order Methods: CC2 and ADC(2). Adv. Quantum Chem. 2005, 50, 37–60. [Google Scholar]
  42. Dreuw, A.; Wormit, M. The Algebraic Diagrammatic Construction Scheme for the Polarization Propagator for the Calculation of Excited States. WIREs Comput. Mol. Sci. 2015, 5, 82–95. [Google Scholar] [CrossRef]
  43. Jacquemin, D.; Duchemin, I.; Blase, X. 0–0 Energies Using Hybrid Schemes: Benchmarks of TD-DFT, CIS(D), ADC(2), CC2, and BSE/GW Formalisms for 80 Real-Life Compounds. J. Chem. Theory Comput. 2015, 11, 5340–5359. [Google Scholar] [CrossRef] [PubMed]
  44. Loos, P.-F.; Lipparini, F.; Boggio-Pasqua, M.; Scemama, A.; Jacquemin, D. A Mountaineering Strategy to Excited States: Highly Accurate Energies and Benchmarks for Medium Sized Molecules. J. Chem. Theory Comput. 2020, 16, 1711–1741. [Google Scholar] [CrossRef] [PubMed]
  45. Turbomole V7.1 2016. A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, Turbomole GmbH, Since 2007. Available online: https://Www.Turbomole.Org (accessed on 19 November 2022).
  46. Antonov, L. Drawbacks of the Present Standards for Processing Absorption Spectra Recorded Linearly as a Function of Wavelength. TrAC Trends Anal. Chem. 1997, 16, 536–543. [Google Scholar] [CrossRef]
  47. Antonov, L.; Stoyanov, S. Analysis of the Overlapping Bands in UV-Vis Absorption Spectroscopy. Appl. Spectrosc. 1993, 47, 1030–1035. [Google Scholar] [CrossRef]
  48. Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
Molecules 27 08225 sch001 550
Scheme 1. Long-range PT reaction of the proton cranes based on 7HQ as a tautomeric sub-unit and C=N group as a crane sub-unit. The proton donor and proton acceptor sites are given in red and blue, respectively. The axle of intramolecular rotation is given in green. The twisting angle α is given in magenta.
Scheme 1. Long-range PT reaction of the proton cranes based on 7HQ as a tautomeric sub-unit and C=N group as a crane sub-unit. The proton donor and proton acceptor sites are given in red and blue, respectively. The axle of intramolecular rotation is given in green. The twisting angle α is given in magenta.
Molecules 27 08225 sch001
Molecules 27 08225 sch002 550
Scheme 2. Trans–cis isomerization around the C=N bond. The twisting angle θ is given in magenta.
Scheme 2. Trans–cis isomerization around the C=N bond. The twisting angle θ is given in magenta.
Molecules 27 08225 sch002
Molecules 27 08225 sch003 550
Scheme 3. Compounds, investigated in the current study, presented in their enol tautomeric forms.
Scheme 3. Compounds, investigated in the current study, presented in their enol tautomeric forms.
Molecules 27 08225 sch003
Molecules 27 08225 g001 550
Figure 1. Relaxed potential energy surface of the lowest excited electronic state, S1, of 1 (a) and 3 (b), as a function of R(OH) stretching and θ (C = N) torsion angle coordinates, showing competition between the two processes: E→ KE ESIPT and E→Ecis photoisomerization after photoexcitation of the S0-state E global minimum in the Franck-Condon region. The green circle represents the Franck–Condon region of the ground-state E global minimum initially populated after photoexcitation (E(FC)), the blue circle represents the excited-state KE(S1) proton-transferred minimum, and the red circle represents the Ecis(S1) excited-state minimum. The results were obtained with the aid of the ADC(2)/cc-pVDZ method. S1-state dipole moment, μe, in Debye. Adiabatic energy, Ea, in eV.
Figure 1. Relaxed potential energy surface of the lowest excited electronic state, S1, of 1 (a) and 3 (b), as a function of R(OH) stretching and θ (C = N) torsion angle coordinates, showing competition between the two processes: E→ KE ESIPT and E→Ecis photoisomerization after photoexcitation of the S0-state E global minimum in the Franck-Condon region. The green circle represents the Franck–Condon region of the ground-state E global minimum initially populated after photoexcitation (E(FC)), the blue circle represents the excited-state KE(S1) proton-transferred minimum, and the red circle represents the Ecis(S1) excited-state minimum. The results were obtained with the aid of the ADC(2)/cc-pVDZ method. S1-state dipole moment, μe, in Debye. Adiabatic energy, Ea, in eV.
Molecules 27 08225 g001
Molecules 27 08225 g002 550
Figure 2. Relaxed potential energy scans of 1 (a) and 3 (b) in the S0 state (circles), determined at the MP2/cc-pVDZ theory level in the S1 state (blue squares), determined at the ADC(2)/cc-pVDZ theory level along the minimum potential energy path for N-phenyl crane torsion (KE to KK, α coordinate), and for hydrogen transfer from the intermediate form KK, toward terminal form K (N1H coordinate). S0(S1) denotes the energy of the S0 state, calculated at the geometry of the S1 excited state (red dashed curves). Adiabatic energies (in blue), Ea, in eV.
Figure 2. Relaxed potential energy scans of 1 (a) and 3 (b) in the S0 state (circles), determined at the MP2/cc-pVDZ theory level in the S1 state (blue squares), determined at the ADC(2)/cc-pVDZ theory level along the minimum potential energy path for N-phenyl crane torsion (KE to KK, α coordinate), and for hydrogen transfer from the intermediate form KK, toward terminal form K (N1H coordinate). S0(S1) denotes the energy of the S0 state, calculated at the geometry of the S1 excited state (red dashed curves). Adiabatic energies (in blue), Ea, in eV.
Molecules 27 08225 g002
Molecules 27 08225 g003 550
Figure 3. (a, top) Simulated absorption spectra of 1, using the data from Table 1; (b, down). Simulated 1H NMR chemical shifts of the tautomeric proton. The tautomeric form is given as follows: E—red solid line, KE—brown solid line, KK—yellow solid line, K—blue solid line, and Ecis—red dashes.
Figure 3. (a, top) Simulated absorption spectra of 1, using the data from Table 1; (b, down). Simulated 1H NMR chemical shifts of the tautomeric proton. The tautomeric form is given as follows: E—red solid line, KE—brown solid line, KK—yellow solid line, K—blue solid line, and Ecis—red dashes.
Molecules 27 08225 g003
Table
Table 1. Vertical excitation energy, ΔEVE (in eV), oscillator strength, f, and dipole moment, μe (in Debye), of the lowest excited singlet states calculated with the CC2/aug-cc-pVDZ method for the ground state equilibrium forms of 1, optimized at the MP2/cc-pVDZ theory level. The dipole moment of the ground-state, μg (in Debye, MP2/cc-pVDZ).
Table 1. Vertical excitation energy, ΔEVE (in eV), oscillator strength, f, and dipole moment, μe (in Debye), of the lowest excited singlet states calculated with the CC2/aug-cc-pVDZ method for the ground state equilibrium forms of 1, optimized at the MP2/cc-pVDZ theory level. The dipole moment of the ground-state, μg (in Debye, MP2/cc-pVDZ).
Tautomer ΔEVEfμe
1E
Molecules 27 08225 i001		S00.00 μg = 3.2
S0→S1(ππ*)3.700.3440.7
S0→S2(ππ*)4.110.1292.7
S0→S3(ππ*)4.320.2352.1
S0→S4(nπ*)4.400.0041.2
S0→S5(ππ*)4.580.0201.8
S0→S6(nπ*)4.750.0001.9
1KE
Molecules 27 08225 i002		S00.203 a μg = 2.5
S0→S1(ππ*)3.140.5152.4
S0→S2(nπ*)3.400.0001.7
S0→S3(ππ*)3.890.0905.3
S0→S4(ππ*)4.280.2984.7
S0→S5(nπ*)4.470.0007.6
S0→S6(ππ*)4.610.0222.9
1KK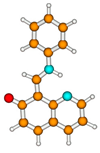
Molecules 27 08225 i003		S00.274 a μg = 4.7
S0→S1(ππ*)3.040.5215.6
S0→S2(nπ*)3.150.0010.9
S0→S3(ππ*)3.720.1285.1
S0→S4(ππ*)4.350.2076.1
S0→S5(ππ*)4.560.0295.3
S0→S6(nπ*)4.570.0008.2
1K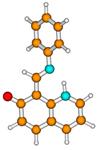
Molecules 27 08225 i004		S00.535 a μg = 7.3
S0→S1(ππ*)2.810.1095.4
S0→S2(nπ*)3.090.0011.9
S0→S3(ππ*)3.380.4886.1
S0→S4(nπ*)3.840.0013.8
S0→S5(ππ*)4.330.0287.0
S0→S6(nπ*)4.430.0045.6
1Ecis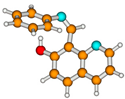
Molecules 27 08225 i005		S00.531 a μg = 3.9
S0→S1(ππ*)3.930.0862.8
S0→S2(ππ*)4.130.0813.4
S0→S3(ππ*)4.420.0382.2
S0→S4(nπ*)4.550.0243.2
S0→S5(ππ*)4.660.0524.1
S0→S6(nπ*)4.800.0484.0
a—Ea, relative to the 1E form optimized at the MP2/cc-pVDZ theory level.
Table
Table 2. Vertical excitation energy, ΔEVE (in eV), oscillator strength, f, and dipole moment, μe (in Debye), of the lowest excited singlet states calculated with the CC2/aug-cc-pVDZ method for the ground state equilibrium forms of 3, optimized at the MP2/cc-pVDZ theory level. The dipole moment of the ground-state, μg (in Debye, MP2/cc-pVDZ).
Table 2. Vertical excitation energy, ΔEVE (in eV), oscillator strength, f, and dipole moment, μe (in Debye), of the lowest excited singlet states calculated with the CC2/aug-cc-pVDZ method for the ground state equilibrium forms of 3, optimized at the MP2/cc-pVDZ theory level. The dipole moment of the ground-state, μg (in Debye, MP2/cc-pVDZ).
Tautomers ΔEVEfμe
3E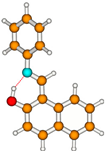
Molecules 27 08225 i006		S00.00 μg = 2.4
S0→S1(ππ*)3.560.3733.0
S0→S2(ππ*)4.130.2142.8
S0→S3(nπ*)4.360.0033.0
S0→S4(nπ*)4.460.0010.9
S0→S5(nπ*)4.740.0012.6
S0→S6(ππ*)4.950.0980.3
3KE
Molecules 27 08225 i007		S00.240 a μg = 3.0
S0→S1(ππ*)3.050.4873.5
S0→S2(nπ*)3.370.0011.6
S0→S3(ππ*)3.940.0274.2
S0→S4(ππ*)4.150.2533.3
S0→S5(nπ*)4.560.0183.5
S0→S6(nπ*)4.660.0017.1
3KK
Molecules 27 08225 i008		S00.611 a μg = 4.6
S0→S1(ππ*)3.070.2694.6
S0→S2(nπ*)3.210.1853.4
S0→S3(ππ*)3.980.0053.7
S0→S4(ππ*)4.290.3194.9
S0→S5(ππ*)4.530.0174.6
S0→S6(nπ*)4.580.0254.4
3Ecis
Molecules 27 08225 i009		S00.450 a μg = 2.0
S0→S1(ππ*)3.820.1072.8
S0→S2(ππ*)4.160.0923.4
S0→S3(ππ*)4.390.0334.2
S0→S4(nπ*)4.620.0212.6
S0→S5(ππ*)4.740.0011.5
S0→S6(nπ*)5.140.1755.6
a—Ea, relative to the 3E form optimized at the MP2/cc-pVDZ theory level.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Rode, M.F.; Nedeltcheva-Antonova, D.; Antonov, L. Long-Range Proton Transfer in 7-Hydroxy-Quinoline-Based Azomethine Dyes: A Hidden Reason for the Low Efficiency. Molecules 2022, 27, 8225. https://doi.org/10.3390/molecules27238225

AMA Style

Rode MF, Nedeltcheva-Antonova D, Antonov L. Long-Range Proton Transfer in 7-Hydroxy-Quinoline-Based Azomethine Dyes: A Hidden Reason for the Low Efficiency. Molecules. 2022; 27(23):8225. https://doi.org/10.3390/molecules27238225

Chicago/Turabian Style

Rode, Michał F., Daniela Nedeltcheva-Antonova, and Liudmil Antonov. 2022. "Long-Range Proton Transfer in 7-Hydroxy-Quinoline-Based Azomethine Dyes: A Hidden Reason for the Low Efficiency" Molecules 27, no. 23: 8225. https://doi.org/10.3390/molecules27238225

APA Style

Rode, M. F., Nedeltcheva-Antonova, D., & Antonov, L. (2022). Long-Range Proton Transfer in 7-Hydroxy-Quinoline-Based Azomethine Dyes: A Hidden Reason for the Low Efficiency. Molecules, 27(23), 8225. https://doi.org/10.3390/molecules27238225

Article Metrics

Back to TopTop