Cascade Forest-Based Model for Prediction of RNA Velocity
Abstract
1. Introduction
2. Result
2.1. Data Set
2.2. Data Preprocessing
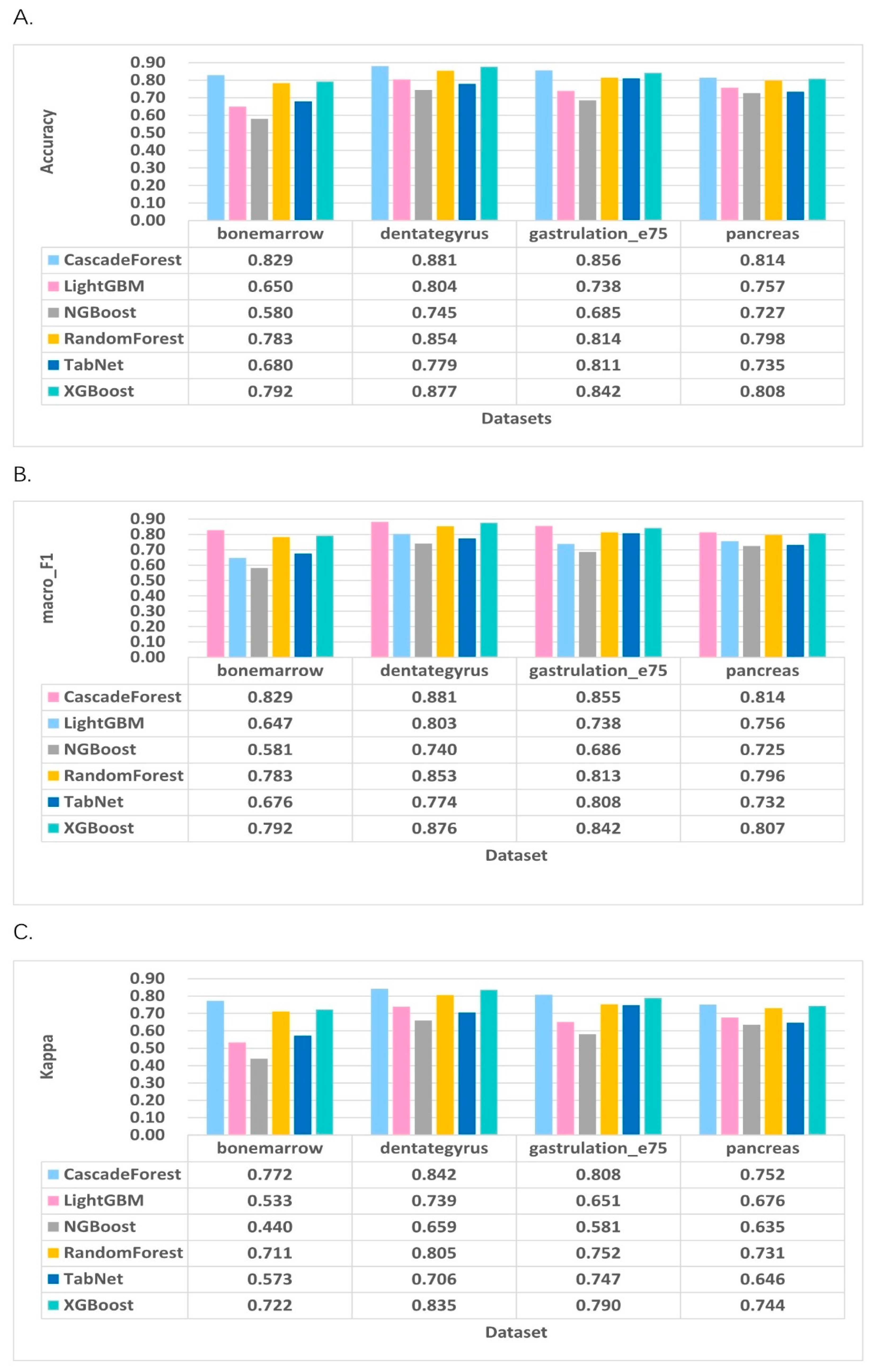
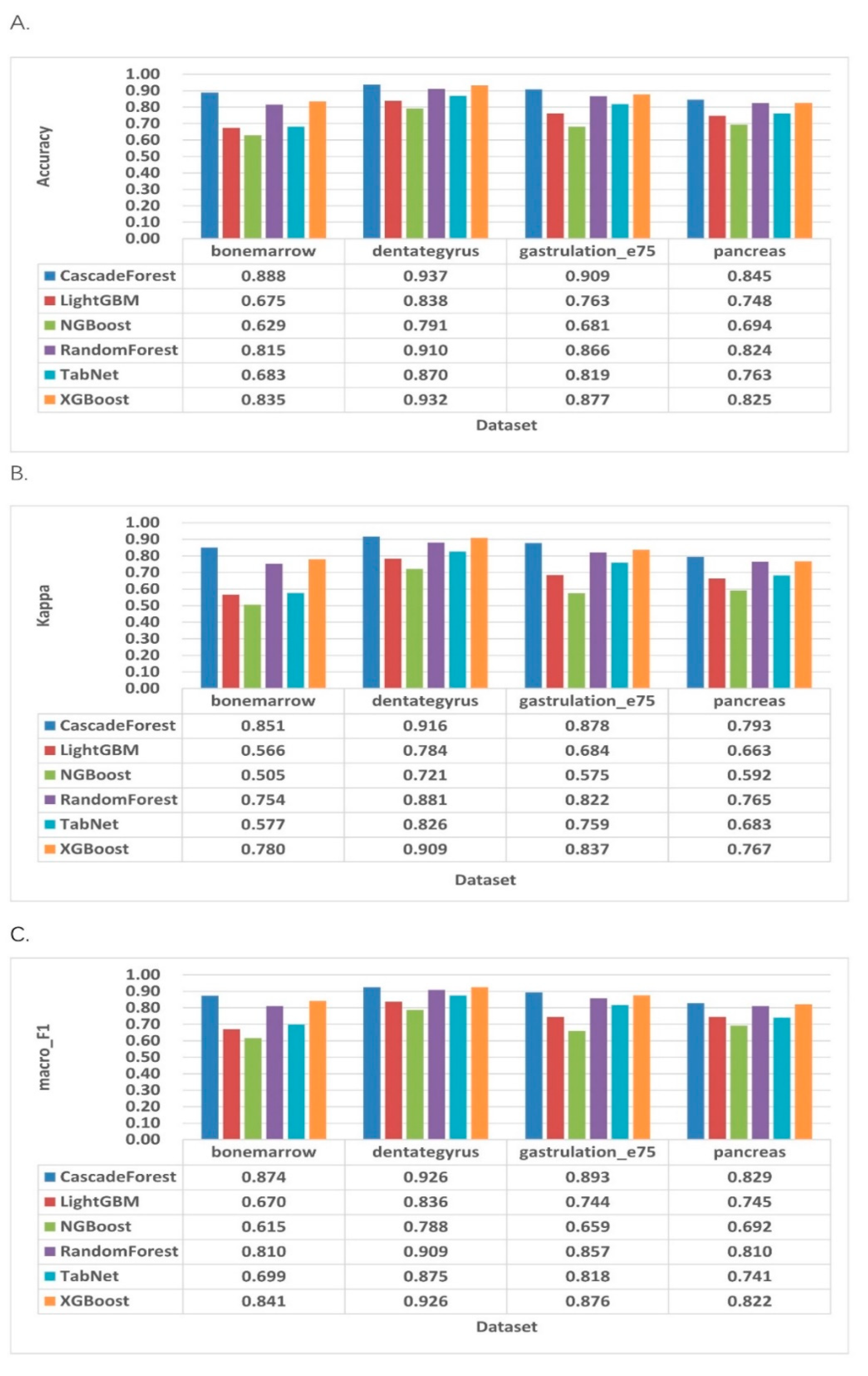
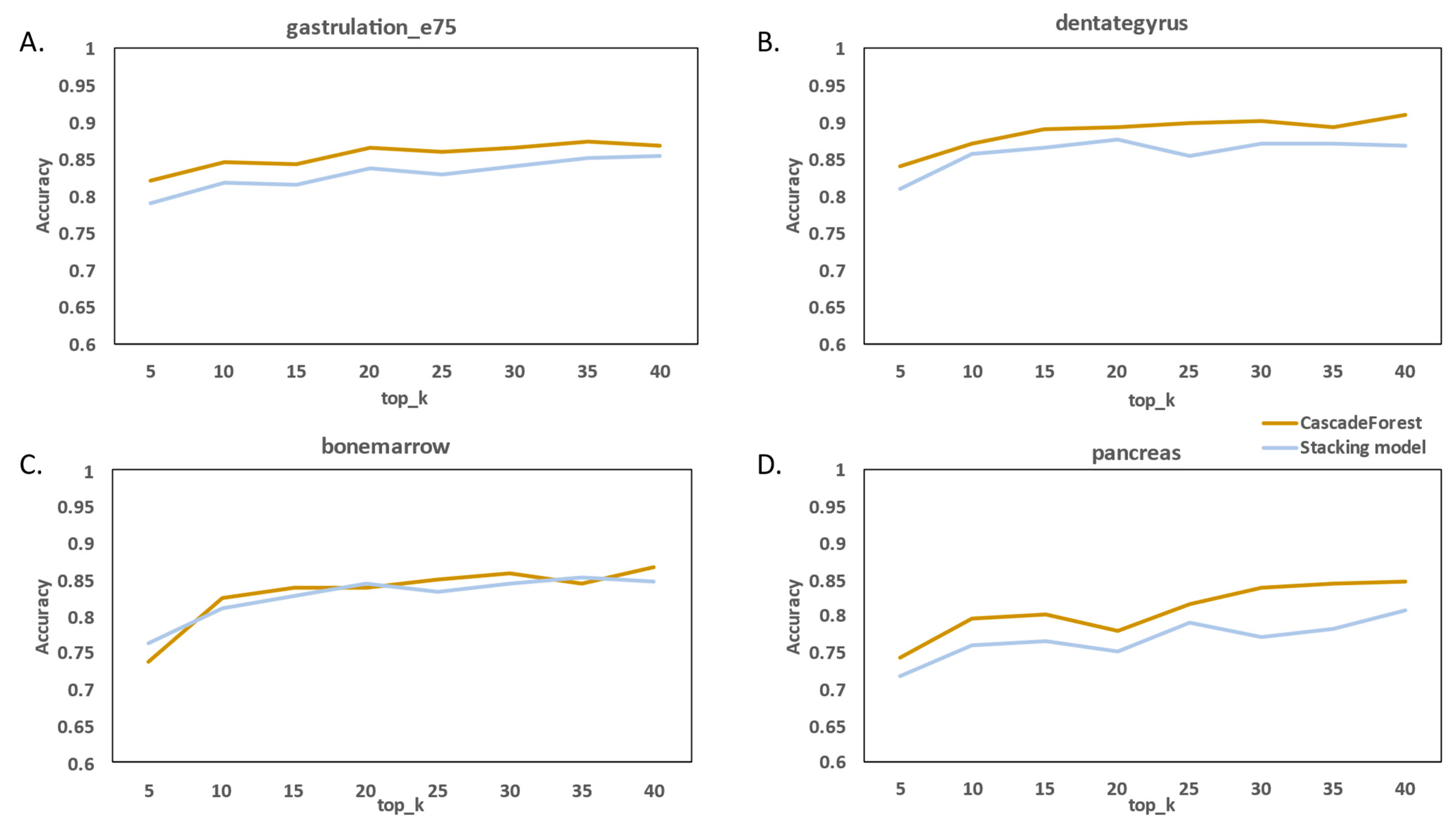
2.3. Performance Evaluation
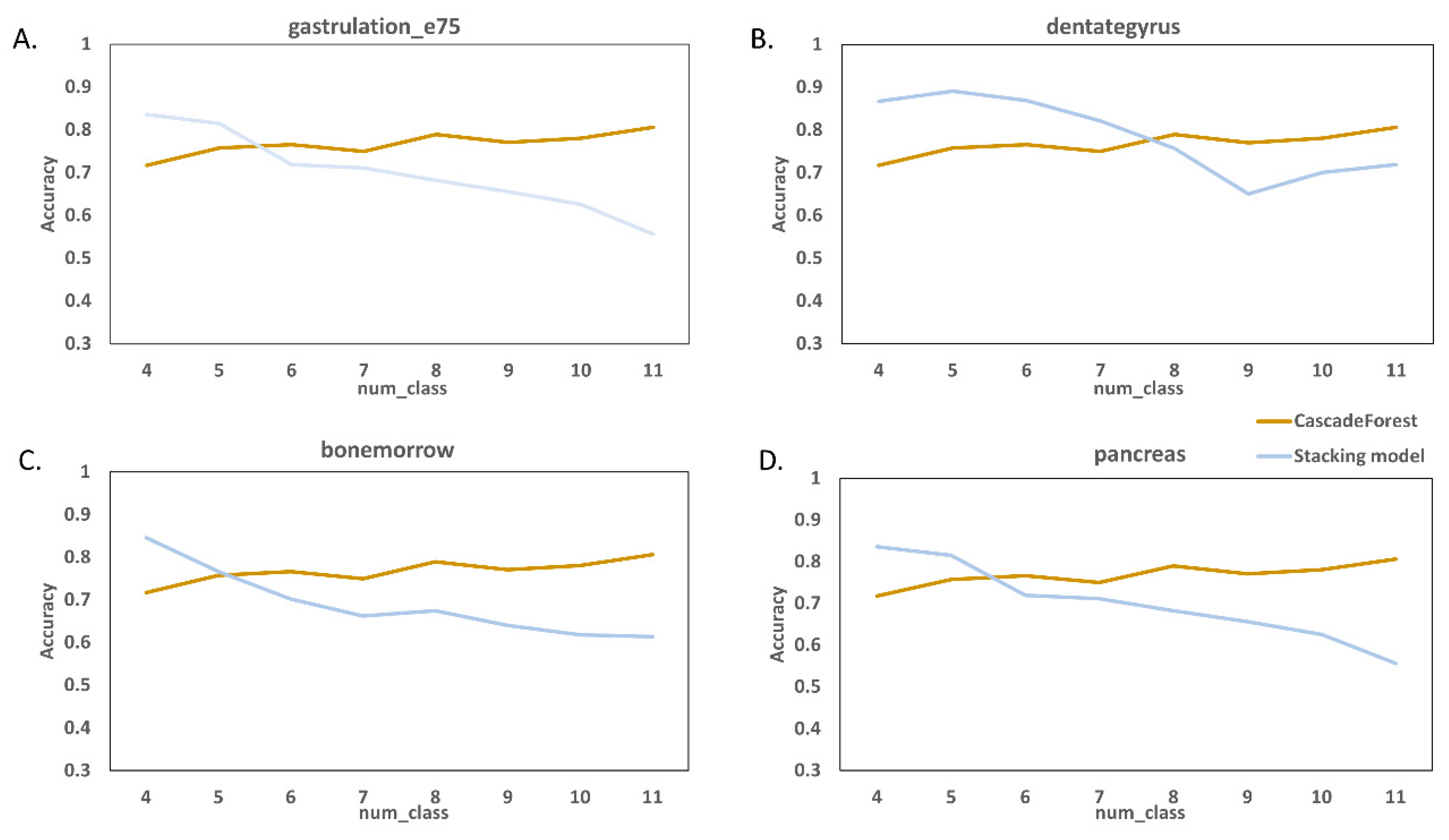
2.4. Comparison with Existing RNA Velocity Prediction Classification Methods
3. Discussion
4. Materials and Methods
4.1. RNA Velocity Estimation
4.2. Steady-State Model
4.3. Dynamic Model
4.4. Performance Metrics
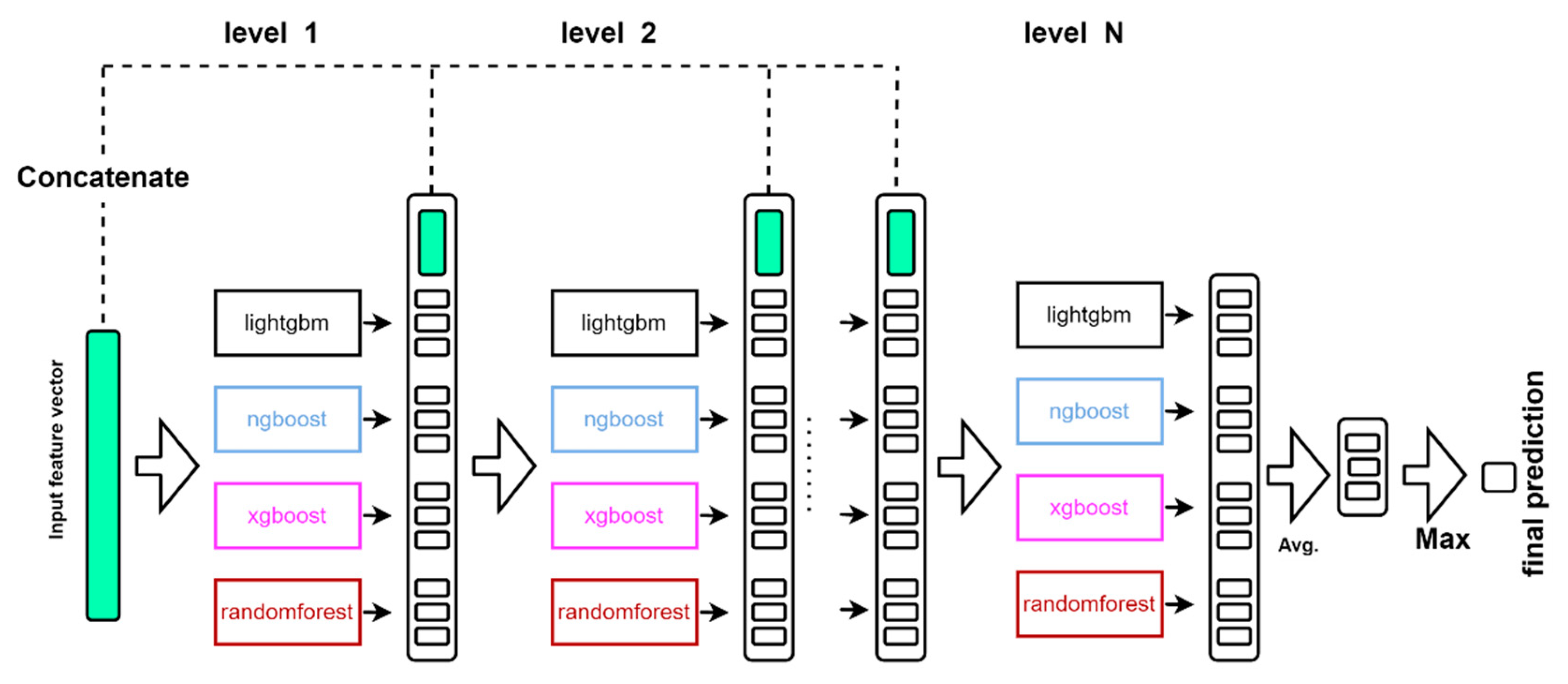
4.5. Classification Tool
4.6. Availability of Data and Materials
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Gierahn, T.M.; Wadsworth, M.H.; Hughes, T.K.; Bryson, B.D.; Butler, A.; Satija, R.; Fortune, S.; Love, J.C.; Shalek, A.K. Seq-Well: Portable, low-cost RNA sequencing of single cells at high throughput. Nat. Methods 2017, 14, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.M.; Mazutis, L.; Akartuna, I.; Tallapragada, N.; Veres, A.; Li, V.; Peshkin, L.; Weitz, D.A.; Kirschner, M.W. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 2015, 161, 1187–1201. [Google Scholar] [CrossRef] [PubMed]
- Macosko, E.Z.; Basu, A.; Satija, R.; Nemesh, J.; Shekhar, K.; Goldman, M.; Tirosh, I.; Bialas, A.R.; Kamitaki, N.; Martersteck, E.M. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 2015, 161, 1202–1214. [Google Scholar] [CrossRef] [PubMed]
- Picelli, S.; Björklund, Å.K.; Faridani, O.R.; Sagasser, S.; Winberg, G.; Sandberg, R. Smart-seq2 for sensitive full-length transcriptome profiling in single cells. Nat. Methods 2013, 10, 1096–1098. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.X.; Terry, J.M.; Belgrader, P.; Ryvkin, P.; Bent, Z.W.; Wilson, R.; Ziraldo, S.B.; Wheeler, T.D.; McDermott, G.P.; Zhu, J. Massively parallel digital transcriptional profiling of single cells. Nat. Commun. 2017, 8, 14049. [Google Scholar] [CrossRef]
- Han, X.; Wang, R.; Zhou, Y.; Fei, L.; Sun, H.; Lai, S.; Saadatpour, A.; Zhou, Z.; Chen, H.; Ye, F. Mapping the mouse cell atlas by microwell-seq. Cell 2018, 172, 1091–1107.e17. [Google Scholar] [CrossRef]
- Fan, H.C.; Fu, G.K.; Fodor, S.P. Combinatorial labeling of single cells for gene expression cytometry. Science 2015, 347, 1258367. [Google Scholar] [CrossRef]
- Guo, F.; Yin, Z.; Zhou, K.; Li, J. PLncWX: A Machine-Learning Algorithm for Plant lncRNA Identification Based on WOA-XGBoost. J. Chem. 2021, 2021, 6256021. [Google Scholar] [CrossRef]
- Haghverdi, L.; Büttner, M.; Wolf, F.A.; Buettner, F.; Theis, F.J. Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods 2016, 13, 845–848. [Google Scholar] [CrossRef]
- Setty, M.; Tadmor, M.D.; Reich-Zeliger, S.; Angel, O.; Salame, T.M.; Kathail, P.; Choi, K.; Bendall, S.; Friedman, N.; Pe’er, D. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotechnol. 2016, 34, 637–645. [Google Scholar] [CrossRef]
- Trapnell, C.; Cacchiarelli, D.; Grimsby, J.; Pokharel, P.; Li, S.; Morse, M.; Lennon, N.J.; Livak, K.J.; Mikkelsen, T.S.; Rinn, J.L. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014, 32, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Cannoodt, R.; Saelens, W.; Saeys, Y. Computational methods for trajectory inference from single-cell transcriptomics. Eur. J. Immunol. 2016, 46, 2496–2506. [Google Scholar] [CrossRef] [PubMed]
- Wolf, F.A.; Hamey, F.K.; Plass, M.; Solana, J.; Dahlin, J.S.; Göttgens, B.; Rajewsky, N.; Simon, L.; Theis, F.J. PAGA: Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 2019, 20, 59. [Google Scholar] [CrossRef] [PubMed]
- Saelens, W.; Cannoodt, R.; Todorov, H.; Saeys, Y. A comparison of single-cell trajectory inference methods. Nat. Biotechnol. 2019, 37, 547–554. [Google Scholar] [CrossRef]
- Zhou, K.; Yin, Z.; Guo, F.; Li, J. Application of Combined Prediction Model Based on Core and Coritivity Theory in Continuous Blood Pressure Prediction. Comb. Chem. High Throughput Screen. 2022, 25, 579–585. [Google Scholar] [CrossRef]
- Ji, Z.; Ji, H. TSCAN: Pseudo-time reconstruction and evaluation in single-cell RNA-seq analysis. Nucleic Acids Res. 2016, 44, e117. [Google Scholar] [CrossRef]
- Bendall, S.C.; Davis, K.L.; Amir, E.-a.D.; Tadmor, M.D.; Simonds, E.F.; Chen, T.J.; Shenfeld, D.K.; Nolan, G.P.; Pe’er, D. Single-cell trajectory detection uncovers progression and regulatory coordination in human B cell development. Cell 2014, 157, 714–725. [Google Scholar] [CrossRef]
- Welch, J.D.; Hartemink, A.J.; Prins, J.F. SLICER: Inferring branched, nonlinear cellular trajectories from single cell RNA-seq data. Genome Biol. 2016, 17, 106. [Google Scholar] [CrossRef]
- Wang, S.; MacLean, A.L.; Nie, Q. SoptSC: Similarity matrix optimization for clustering, lineage, and signaling inference. bioRxiv 2018, 168922. [Google Scholar] [CrossRef]
- La Manno, G.; Soldatov, R.; Zeisel, A.; Braun, E.; Hochgerner, H.; Petukhov, V.; Lidschreiber, K.; Kastriti, M.E.; Lönnerberg, P.; Furlan, A. RNA velocity of single cells. Nature 2018, 560, 494–498. [Google Scholar] [CrossRef]
- Bergen, V.; Lange, M.; Peidli, S.; Wolf, F.A.; Theis, F.J. Generalizing RNA velocity to transient cell states through dynamical modeling. Nat. Biotechnol. 2020, 38, 1408–1414. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zheng, J. Velo-Predictor: An ensemble learning pipeline for RNA velocity prediction. BMC Bioinform. 2021, 22, 419. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting; R Package Version 0.71. 2.; Grin Verlag: München, Germnay, 2018. [Google Scholar]
- Rumpf, H. The characteristics of systems and their changes of state disperse. In Particle Technology, Chapman and Hall; Springer: Berlin/Heidelberg, Germany, 1990; pp. 8–54. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Duan, T.; Anand, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.; Schuler, A. Ngboost: Natural gradient boosting for probabilistic prediction. In Proceedings of the International Conference on Machine Learning (PMLR), Virtual Event, 13–18 July 2020; pp. 2690–2700. [Google Scholar]
- Arik, S.Ö.; Pfister, T. Tabnet: Attentive interpretable tabular learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; pp. 6679–6687. [Google Scholar]
- Zhou, Z.-H.; Feng, J. Deep forest. Natl. Sci. Rev. 2019, 6, 74–86. [Google Scholar] [CrossRef]
- Pijuan-Sala, B.; Griffiths, J.A.; Guibentif, C.; Hiscock, T.W.; Jawaid, W.; Calero-Nieto, F.J.; Mulas, C.; Ibarra-Soria, X.; Tyser, R.C.; Ho, D.L.L. A single-cell molecular map of mouse gastrulation and early organogenesis. Nature 2019, 566, 490–495. [Google Scholar] [CrossRef] [PubMed]
- Bastidas-Ponce, A.; Tritschler, S.; Dony, L.; Scheibner, K.; Tarquis-Medina, M.; Salinno, C.; Schirge, S.; Burtscher, I.; Böttcher, A.; Theis, F.J. Comprehensive single cell mRNA profiling reveals a detailed roadmap for pancreatic endocrinogenesis. Development 2019, 146, dev173849. [Google Scholar] [CrossRef] [PubMed]
- Hochgerner, H.; Zeisel, A.; Lönnerberg, P.; Linnarsson, S. Conserved properties of dentate gyrus neurogenesis across postnatal development revealed by single-cell RNA sequencing. Nat. Neurosci. 2018, 21, 290–299. [Google Scholar] [CrossRef] [PubMed]
- Goel, G.; Maguire, L.; Li, Y.; McLoone, S. Evaluation of sampling methods for learning from imbalanced data. In Proceedings of the International Conference on Intelligent Computing, Nanning, China, 28–31 July 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 392–401. [Google Scholar]
- Slyper, M.; Porter, C.; Ashenberg, O.; Waldman, J.; Drokhlyansky, E.; Wakiro, I.; Smillie, C.; Smith-Rosario, G.; Wu, J.; Dionne, D. A single-cell and single-nucleus RNA-Seq toolbox for fresh and frozen human tumors. Nat. Med. 2020, 26, 792–802. [Google Scholar] [CrossRef]
- Gorin, G.; Fang, M.; Chari, T.; Pachter, L. RNA velocity unraveled. bioRxiv 2022. [Google Scholar] [CrossRef]
- Melsted, P.; Booeshaghi, A.; Liu, L.; Gao, F.; Lu, L.; Min, K.H.J.; da Veiga Beltrame, E.; Hjörleifsson, K.E.; Gehring, J.; Pachter, L. Modular, efficient and constant-memory single-cell RNA-seq preprocessing. Nat. Biotechnol. 2021, 39, 813–818. [Google Scholar] [CrossRef]
- Srivastava, A.; Malik, L.; Smith, T.; Sudbery, I.; Patro, R. Alevin efficiently estimates accurate gene abundances from dscRNA-seq data. Genome Biol. 2019, 20, 65. [Google Scholar] [CrossRef]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]
- Vieira, S.M.; Kaymak, U.; Sousa, J.M. Cohen’s kappa coefficient as a performance measure for feature selection. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway Township, NJ, USA, 2010; pp. 1–8. [Google Scholar]
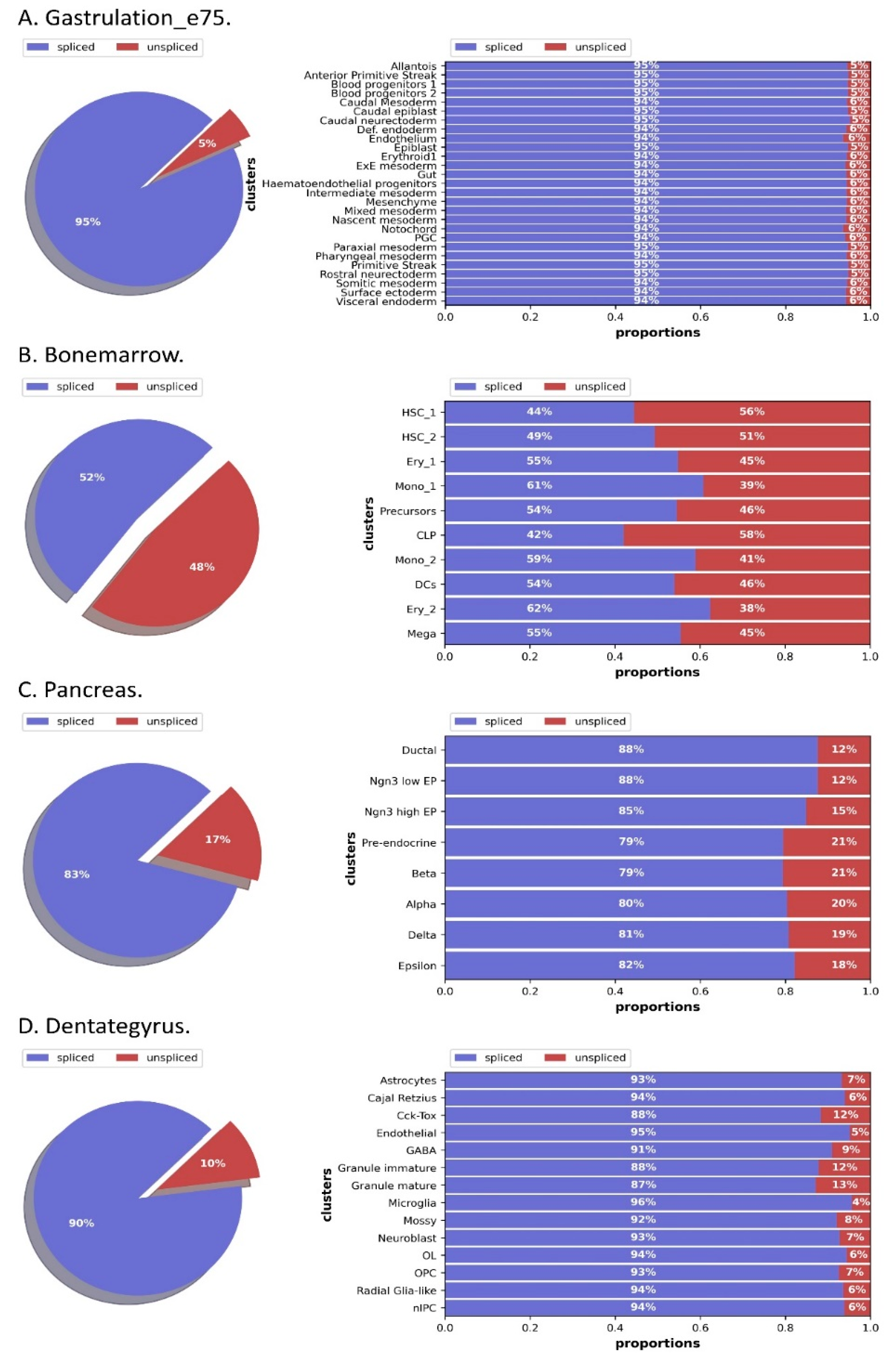
| Datasets | Cell Number | Gene Number | Highly Variable Genes | Feature Numbers (k = 20) |
|---|---|---|---|---|
| gastrulation_e75 | 7202 | 53,801 | 3000 | 291 |
| bonemarrow | 5780 | 14,319 | 2500 | 141 |
| pancreas | 3696 | 27,998 | 2500 | 143 |
| dantategrus | 2930 | 13,913 | 2000 | 151 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Zhao, S.; Peng, Y.; Hu, X.; Yin, Z. Cascade Forest-Based Model for Prediction of RNA Velocity. Molecules 2022, 27, 7873. https://doi.org/10.3390/molecules27227873
Zeng Z, Zhao S, Peng Y, Hu X, Yin Z. Cascade Forest-Based Model for Prediction of RNA Velocity. Molecules. 2022; 27(22):7873. https://doi.org/10.3390/molecules27227873
Chicago/Turabian StyleZeng, Zhiliang, Shouwei Zhao, Yu Peng, Xiang Hu, and Zhixiang Yin. 2022. "Cascade Forest-Based Model for Prediction of RNA Velocity" Molecules 27, no. 22: 7873. https://doi.org/10.3390/molecules27227873
APA StyleZeng, Z., Zhao, S., Peng, Y., Hu, X., & Yin, Z. (2022). Cascade Forest-Based Model for Prediction of RNA Velocity. Molecules, 27(22), 7873. https://doi.org/10.3390/molecules27227873






