Next Article in Journal
Preparation of Chiral Enantioenriched Densely Substituted Cyclopropyl Azoles, Amines, and Ethers via Formal SN2′ Substitution of Bromocylopropanes
Previous Article in Journal
Synthesis of Trifluoromethylated Monoterpene Amino Alcohols
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 27
Issue 20
10.3390/molecules27207070
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

GGA and GGA + U Study of ThMn2Si2 and ThMn2Ge2 Compounds in a Body-Centered Tetragonal Ferromagnetic Phase

by
Abdul Ahad Khan
1,
Zeshan Zada
2,
Ali H. Reshak
3,4,5,*,
Muhammad Ishaq
6,
Sabeen Zada
7,
Muhammad Saqib
8,
Muhammad Ismail
7,
Muhammad Fazal-ur-Rehman
9,
Ghulam Murtaza
10,
Shafqat Zada
11 and
Muhammad M. Ramli
4
1
Department of Physics, University of Peshawar, Peshawar 25120, Pakistan
2
Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
3
Physics Department, College of Science, University of Basrah, Basrah 61004, Iraq
4
Center of Excellence Geopolymer and Green Technology (CEGeoGTech), University Malaysia Perlis, Kangar 01007, Perlis, Malaysia
5
Department of Instrumentation and Control Engineering, Faculty of Mechanical Engineering, CTU in Prague, Technicka 4, 616607 Prague, Czech Republic
6
Electrical Engineering Department, COMSATS University Islamabad, Islamabad 45550, Pakistan
7
Department of Chemistry, Women University Swabi, Swabi 23430, Pakistan
8
Department of Electrical and Computer Engineering, Abbottabad Campus, COMSATS University Islamabad, Abbottabad 22060, Pakistan
9
Department of Chemistry, Lahore Garrison University, Lahore 54000, Pakistan
10
Materials Modeling Lab, Department of Physics, Islamia College University, Peshawar 25120, Pakistan
11
Department of BioChemistry, Quaid azam University, Islamabad 45320, Pakistan
 
add Show full affiliation list
 
remove Hide full affiliation list
*
Author to whom correspondence should be addressed.
Molecules 2022, 27(20), 7070; https://doi.org/10.3390/molecules27207070
Submission received: 5 September 2022 / Revised: 30 September 2022 / Accepted: 14 October 2022 / Published: 20 October 2022
(This article belongs to the Section Organometallic Chemistry)
Browse Figures
Versions Notes

Abstract

:
Our study used the full-potential linearized augmented plane waves (FP-LAPW) method to conduct a first-principles evaluation of the structural, electronic, and magnetic properties of ThMn2X2 (X = Si and Ge) compounds. To establish theoretical dependability with the currently available experimental results, computations for the structural findings of ternary intermetallic thorium (Th)-based compounds were achieved using the generalized gradient approximation in the scheme of Perdew–Burke–Ernzerhof (PBE–GGA) potential, while the generalized gradient approximation plus the Hubbard U (GGA + U) approach was employed to improve the electrical and magnetic properties. In contrast with both the paramagnetic (PM) and antiferromagnetic (AFM) phases, the ThMn2X2 compounds were optimized in a stable ferromagnetic (FM) phase, which was more suited for studying and analyzing magnetic properties. The electronic band structures (BS) and the density of state (DOS) were computed using the two PBE–GGA and GGA + U approximations. The thorium (Th)-based ThMn2X2 compound has full metallic character, due to the crossing and overlapping of bands across the Fermi level of energy, as well as the absence of a gap through both spin (up and down) channels. There was a significant hybridization between (Mn-d and (X = Si and Ge)-p states of conduction band with Th-f states in the valence band. The total magnetic moment of ThMn2Si2 in the ferromagnetic phase was 7.94534 μB, while for ThMn2Ge2 it was 8.73824 μB with a major contribution from the Mn atom. In addition, the ThMn2Ge2 compound’s total magnetic moment confirmed that it exhibits higher ferromagnetism than does the ThMn2Si2 compound.

1. Introduction

Interest in the search for intermetallic phase materials has been rising over the last few decades because of their mysterious features and the diverse range of sensible and modern applications, such as the computer readings by shape memory alloys (SMAs) in the jewelry and dentistry industries [1,2], as well as the rapid utilization of intermetallic materials for polishing various attractive and intriguing giant magneto resistive (GMR) and colossal magneto resistive (CMR) materials. Magnetoresistance inside metallic thin films varies and regulates resistivity, due to the presence of an external magnetic field to progress the technology [3]. To date, the achieved applications of GMR materials have been uses as spin valves, as spin filters collectively with magnetic field dependent sensors [4,5] (in which the most significant and critical part is the GMR material that is further used to deal with read heads in modern hard disk drives), in several biosensors, and in advanced micro-electro mechanical (MEMS) systems. These intermetallic materials have a distinct electronic structure and deserve special attention; if further investigated, they could lead to a variety of novel quantum characteristic features.
Normally, intermetallic phases with the formula AM2X2 (where A belongs to rare/alkaline earth metals), M belongs to d-block metals), and X represents Group 13–15 elements) are typically found in various structural types, such as the body-centered tetragonal of space groups ThCr2Si2 and CeAl2Ge2 (14/mmm) and CaAl2Si2 (P 3 ¯ m1), respectively. In numerous works, the latter group, in particular, was utilized to investigate various physical aspects of intermetallic ternary compounds [6,7,8,9,10].
The discovery of several isostructural thorium-based ThM2X2, (M = Cr, Mn, Fe, Co, Ni, and Cu; X = Si or Ge) ternary intermetallic silicide and germanide compounds that crystallize in the tetragonal CeAl2Ge2-type structure at temperatures ranging from 100 K to 570 K by means of the Faraday method [11,12] was reported early in 1971, wherein all three components can be replaced while maintaining the same structure. Furthermore, all of these compounds have ordered BaA14-type crystal structures. In contrast to the pure elements, the transition metal atoms in the crystal structure are spaced much farther apart by X-Th-X sandwiches, implying that metamagnetic activity is expected [13]. Depending on the atomic number of the attached transition metal atoms, the thorium containing silicide and germanide compounds were found to be ferromagnetic or antiferromagnetic.
Omejec and Ban [13] were the first to study the magnetic properties of these compounds experimentally. They discovered a maximum of magnetic susceptibility of approximately 500 K in ThMn2Si2, but a small saturation magnetization below 400 K in ThMn2Ge2. They claimed that by comparing inverse susceptibility curves of ThM2X2 compounds with Curie–Weiss law curves for magnetic susceptibility measurement, they were able to determine “a complete magnetic parameter, numeric values for Neel and Curie temperatures, along with the effective magnetization per atom of transition metal”. They further noted the ferromagnetic ordering at positive Curie temperatures in the thorium compound ThMn2X2 [13]. Because thorium (Th) has no magnetic dipole moment, the ordering is caused by 3d-transition elements.
Magnetic studies on Mn-containing compounds were carried out to see how changing the Mn–Mn distance affects magnetic ordering, Curie temperature, and anisotropy [11,12]. The first-principles approach and XPS studies was used to examine the magnetic structures and magnetic phase transitions in intermetallic-layered RMn2Si2 compounds [14,15]. In accordance with experimental results, it was discovered that the distances between the Mn ions in the ab plane, as opposed to the interplane distances, influence the type of ordering of Mn magnetic moments along the c-axis [14].
Over a wide temperature range (4.2 K to 1200 K)., the magnetic properties of RMn2Ge2 and RMn2Si2 compounds were examined. The Curie temperatures were found to be above 300 K when rare earth (R) was replaced with La, Ce, Pr, and Nd, and the easiest direction of magnetization was discovered to be along the c-axis [16]. When R was replaced with a heavy rare earth, an antiferromagnetic coupling between the R and manganese moments was observed at about 4.2 K, whereas a ferromagnetic coupling was observed when R was replaced with a light rare earth. At 4.2 K, YMn2Si2, ThMn2Si2, and ThMn2Ge2 all had a small moment at less than 0.2 µB [16]. Furthermore, by using the self-consistent Korringa–Kohn–Rostoker approach, the electronic structure of the tetragonal RMn2Ge2 (R = Ca, Y, La, and Ba) antiferromagnets was reported by a few researchers. All of the reported Mn-based compounds had computed magnetic moments that were in good accord with the neutron data. All systems were metallic, according to antiferromagnetic density of states, although ΒaΜn2Ge2 was discovered to be close to the semi-metallic limit [17].
The magnetic properties of the RMn2Ge2 compounds have been studied were between the temperature range 4.2 and 500 K. Only R = La, Ce, Pr, and Nd are ferromagnetic, with Curie temperatures of 306, 316, 334, and 334 K, respectively [18]. Until very low temperatures are reached, the heavier rare-earth compounds do not arrange ferromagnetically. In both magnetization and resistivity-vs-temperature measurements, GdMn2Ge2 exhibits an abrupt magnetic transition at 97 K. It is hypothesized that the Mn moments in this compound order antiferromagnetically among themselves above 97 K, whereas the Gd moments are disordered. Mn moments pair ferromagnetically with each other below 97 K, but they oppose the ordered Gd sublattice [18]. An antiferromagnetic interaction between Mn and rare-earth spins can explain the magnetic moment reported at 4.2 K for all of the investigated compounds. McCall et al. [19] studied the RC02Ge2 compounds for the first time and determined that cobalt has no moment in these Ge rare-earth-based compounds. It is important to select a transition metal with a less fully filled d band in order for M (transition metal) atoms to have a moment. According to Gyorgy et al. [20], the Sm-based SmMn2Ge2 compound is ferromagnetic below a Curie temperature of T c = 350 K. Further cooling causes an antiferromagnetic phase, T = 150 K, to form, which is almost stable until T = 100 K is reached, when it transitions to a ferromagnetic phase.
In line with the preceding discussion, several researchers have tried to physically explore the physical structure and magnetic properties of ThMn2X2 (X = Si, Ge) compounds to some extent, although theoretical evidence is still lacking. Because of their attracting physical properties, some research has already been done on members of the same class of materials [21,22,23,24,25,26]. The current study was prompted in part by a knowledge gap in the fundamental structural, electronic, and magnetic properties of ternary intermetallic ThMn2Si2 and ThMn2Ge2 compounds, which were not well known or improved, in comparison with their counterparts.

2. Computational Details

Our investigations for ThMn2X2 (X = Si and Ge) compounds were performed using the full-potential linearized augmented plane wave (FPLAPW) method and the Wien2 k algorithm [27]. Muffin-tin sphere radii (RMT) were chosen, so that the atoms did not overlap at values of 2.5 atom units (a.u.) for thorium (Th), 2.41 and 2.08 a.u. for manganese (Mn), and 1.78 and 1.98 a.u. for silicon (Si) and germanium (Ge), respectively. The Muffin-tin minimum radius (RMT) and the greatest possible reciprocal lattice constant, Kmax, were utilized to determine the cut-off parameter for the basis set’s convergence. RMT*Kmax = 7 illustrates the separation among various valence and core states. This tactic relies on the partitioning of the entire crystal into the non-overlapping muffin-tin (Mu-T) spheres that are parted from one another by an interstitial zone. This is where spherical harmonic functions within MT spheres are supported by a simple basic set function that is chosen and extended, and basic plane waves are also used in the interstitial area. The biggest vector (Gmax) in the charge density’s Fourier expansion has a magnitude of 12 atom units (a.u.)−1 [28,29,30,31]. We employed energy convergence with the value 0.0001 Ry and charge convergence with the value 0.001 e for the self-consistency cycle. We did not factor in the impact of spin orbit coupling in our estimates. The tetrahedron approach [32], with special 195 k-points (together with 10 × 10 × 10 k-points in the complete BZ) in the irreducible wedge, was taken into consideration to determine the charge density in every self-consistency step for the integration of the Brillouin zone (BZ). Furthermore, with both the exchange and the correlation (GGA + U/GGA–PBE/LDA) potentials [33,34,35,36] that are implemented in Wien-2 k code, the structural characteristics of the compound ThMn2X2 (X = Si and Ge) were determined. According to previously published research [37], the value employed in this study for both compounds is U = 6 eV, which is a fairly excellent approximation for handling d-states of Mn atoms. GGA–PBE and GGA + U potentials were used to find the electronic and magnetic characteristics of ThMn2X2 (X = Si and Ge) compounds.

3. Results and Discussion

3.1. Structural Properties

The thorium (Th)-based isostructural ternary intermetallic silicide and germanide systems, along with general formula ThMn2X2 (X = Si and Ge), has crystallized in the body-centered tetragonal lattice structure with the space group (14/mmm #139). The site positions for thorium (Th) atoms are the Wyckoff position 2(a) [38]; for manganese (Mn) atom, it is 4(d); for (X = Si and Ge) silicon and germanium atoms, it is 4(e). As a result, atoms of the same element are stacked in the sequence Th-X-Mn-X-Th on alternating layers that are stacked along the c-axis, as shown in Figure 1.
The structural morphology of the compounds is determined by computing both the lattice atomic positions and cell dimensions. The ferromagnetic phase is the most suited and stable phase for ThMn2X2 (X = Si, Ge), based on optimization. In addition, available experimental results, up to our literature review, concluded that the most appropriate phase for these materials is the ferromagnetic phase [13,16].
We estimated the total energy for dissimilar volumes in the vicinity of the calculated experimental volume to optimize the unit cell and to obtain the ground state energy. To derive the compound’s ground state parameters, we reported its total energy and plotted it versus volume, fitting it to the known empirical Murnaghan’s equation of state (EOS) [39]. Figure 2 depicts the computed total energy of the state as a function of volume in the paramagnetic (PM), ferromagnetic (FM), and antiferromagnetic (AFM) phases for compounds ThMn2Si2 and ThMn2Ge2.
Only PM phase energy is provided for both of these reported compounds; the remaining parameters were calculated by PBE–GGA potentials and derived in the FM phase, as in a prior study [31]. Furthermore, in the FM phase, both compounds were stabilized. Table 1 shows the computed values of the lattice parameters, the ground state energy, the unit cell volume, the bulk modulus, and the derivative of the bulk modulus for both compounds, based on structural optimization.
When the Si anion was replaced by Ge, the lattice constants (ɑ and c(Å)) and unit cell volume ( V 0 ) increased as the PM and FM phases were computed. This improvement was due to an increase in the atomic sizes of the anions as they move from the Si to the Ge element. Finally, the B(GPa), which describes the natural compressibility of materials, showed a definite declining trend in the computed values from Si to Ge, making the ThMn2Ge2 compound more squeezable or compressible than the ThMn2Si2 compound.

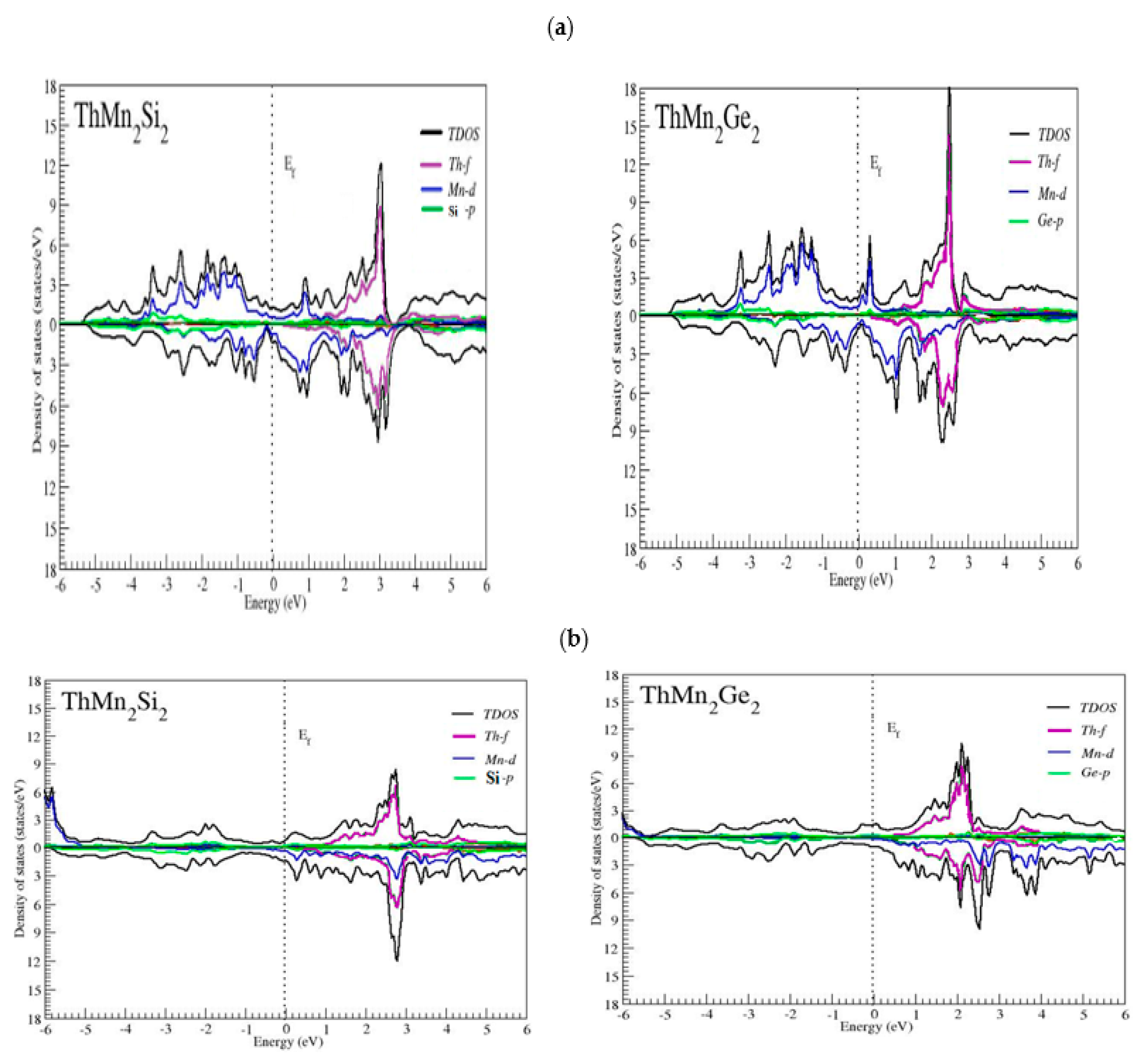
3.2. Electronic Properties

Band Structures and Density of States

Electronic band structure and density of state are important factors in determining crystal structure [40,41,42,43]. The evaluations of the total density of states (TDOS) and partial density of states (PDOS) are particularly important for a full understanding of a compound’s bonding character. In the energy range between −6 eV and 6 eV, we estimated the TDOS and the PDOS using two distinct (exchange and correlation) known approximations, PBE–GGA and GGA + U. For spins both up and down the channels, Figure 3a,b depicts the DOS plots of the thorium (Th)-based ThMn2Si2 and ThMn2Ge2 compounds.
Both compounds have a full metallic character, as the total and partial (p, d, f) states appear to cross the Fermi energy level in both spin states. As a result, we concluded, as shown in Figure 3a,b, that the contribution of orbitals in both compounds is relatively similar. Furthermore, it was obvious from the TDOS that the active progress at (EF) was primarily because of the Mn-d state. Moreover, in the region of valence band, there was a substantial hybridization between the Mn-d and X = Si and Ge-p states, with the Th-f state in the region of the conduction band. These states bore complete responsibility for the materials with metallic characteristics.
The Mn-d state’s primary appearance and contribution were placed at the Fermi level, as well as the leading spread ranging from high to low energy with values and approximations (−0.2 to −4 eV through (GGA–PBE) and −4.9 to −6 eV through (GGA + U)) for ThMn2Si2 while (0 to −3.4 eV through (GGA–PBE) and −5 to −6 eV through (GGA + U)) for ThMn2Ge2 in the region of valence band is clearly observed. This change toward a lower energy range of d-state for ThMn2X2 was due to the application of (GGA + U), which handled the Mn atom-localized d-shell electrons. Furthermore, the elimination of the Mn-d state from both channels at lower energies when employing (GGA–PBE) and the shift towards higher energies of the identical Mn-d state by down spin when using (GGA + U) are visible in the DOS plots of Figure 3 a,b. In addition, the Th-d state with a straight line emerges throughout the full energy range of the valence band area, with a minor contribution from the (X = Si and Ge)-p state in the region of the valence band and over the whole energy range in ThMn2X2, through both approximations. The value employed in this study for both compounds was U = 6 eV, which is a fair estimate for dealing with Mn atom d-states, as stated in a previous study [37].
Furthermore, in the conduction band region across both spin states, the Th-f state showed pointedly toward with values that were higher in the energy range: 0.8 eV to 3.4 eV through both potentials for ThMn2Si2 and 0.6 eV to 3 eV (GGA–PBE) and 0.4 eV to 2.8 eV (GGA + U) for the ThMn2Ge2 compound. Furthermore, the Mn-d state placed at the Fermi level made a minor contribution in the different spin states of ThMn2X2 toward lower energy by GGA–PBE and toward higher energy by GGA + U approximation. To conclude the extremely symmetrical or balanced appearance of ThMn2X2, various states’ spectra (Th-f, Mn-d and X-p) through both spin states resided in bands of both the valence and the conduction region, indicating that Stoner’s argument was frequently fulfilled [44,45].
To further understand the electronic characteristics of ThMn2X2 (X = Si, Ge), the electronic band structure is displayed in Figure 4a,b for both spin states, using two distinct approximations, PBE–GGA and GGA + U. The Fermi level of energy was set to origin as a reference point in these plotted figures, and the analyzed band structures in the Brillouin zone (BZ) are displayed in Figure 4b, while the calculated Fermi surface of ThMn2Ge2 as a prototype (shown in Figure 4c) along the Γ, H, N, and (Γ, P) high symmetry directions are also shown. Furthermore, the minima of CB were more dominant because of Mn-d and Th-f, while the VB maxima were mostly due to p characters from the Si/Ge in both spin channels. However, because more continuing d orbitals arise in compounds various channels, the overlap between the p (Si and Ge) and f (Th) with d (Mn) orbitals twists to the stronger side. As a result, the overlaps between these bands in the compounds under study were sufficient for metallicity.
It is easy to notice the valence band maximum’s considerable dispersion at the high-symmetry (H) point. By utilizing PBE–GGA and GGA + U approximations with small adjustments in the features, the bands with dominant shoulders appeared on both sides while crossing the Fermi energy level and remained in the region of the conduction band, especially in the up-spin states of ThMn2X2. This was similar to the disappearance of the same single band at the H point in the spin-down channel of the ThMn2Si2 compound and the minor appearance of a single narrow band dispersion among the high symmetry (Γ and H, Γ and N, Γ and P) basal points in the compound ThMn2Ge2 spin-down state. In addition, the conduction band minimum for the ThMn2X2 compounds exhibited the same pattern of dispersion of a few bands between the high symmetry points (Γ and H, Γ and N, Γ and P) from both spin states, indicating that the conduction bands held additional electrons and were fully filled, as well as meeting and overlapping the mechanisms with the available valence bands by both (PBE–GGA and GGA + U) approximations.
The bands clearly split when the GGA + U approximation was computed; however, both thorium compounds continued to show their metallic nature. The CB traveled up and the VB traveled down at high symmetry (Γ point) by bounding d-states and computing the approximation GGA + U. Furthermore, the calculation using the GGA + U resulted in peculiar behavior, such as the absence of gaps in the ThMn2X2 compounds where the valence and conduction bands met at both high Γ symmetry points in up-spin channels while shifting the same meeting bands back to their original locations in spin-down channels.
In addition, there was no energy (absent) gap at the Femi level of energy, expressing the pure metallic nature, although the spin-up channel states were significantly closer to one another than the spin-down channels that were nearby the Fermi level. Even the closer states allowed for simple electron mobility, which over time affected the materials’ conductivity. Moreover, the compounds adopted the tetragonal ThCr2Si2-type structure with three-dimensional electron and hole-like multiband Fermi surfaces (FSs), as appeared in the majority of the same types [46,47] and other types [41,48,49] of compounds that were related to the phonon-mediated types that were currently under electron-phonon mediated superconductivity, according to a few other research studies that calculated Fermi surfaces (FSs). Due to the crossing and overlapping of bands across the Fermi level of energy, as well as the absence of a gap in both spin states when utilizing two separate (PBE–GGA and GGA + U) approximations, the thorium compound ThMn2X2 band structures generally described the full metallic nature.

3.3. Magnetic Properties

The spin polarization calculations using the PBE–GGA and GGA + U potentials were computed to explore the magnetic characteristics of the ThMn2Si2 and ThMn2Ge2 compounds. Table 2 summarizes the overall mc magnetic moment (MM) of each cell, interstitial and local (Th, Mn, Si, and Ge) individual (MM) magnetic moments of the materials under study. According to the noted data, the active and most contributing atom in the total cell magnetic moment (MM) of ThMn2X2 (X = Si and Ge) is the Mn, contributing high values of a parallel ferromagnetic nature, in contrast to other atoms such as those at the interstitial and individual Th, Si and Ge atoms that were participating with negative anti-parallel values by both PBE–GGA and GGA + U approximations.
The fundamental source of magnetization in these thorium (Th) ternary intermetallic materials predominantly originates from unoccupied or empty Th-f and Mn-d orbitals. However, except for the leading manganese site, the remaining sites had a tendency to lower the ferromagnetic nature of the materials under study. These thorium ternary intermetallic compounds’ fundamental source of magnetism, in particular, derived from unoccupied or empty Th-f and Mn-d orbitals. As a result, with the exception of the dominating manganese site, the remaining spots tended to reduce the overall ferromagnetic character of the aforementioned compounds.
The stable or steady magnetic ground state, as shown in optimization plots in Figure 2, was ferromagnetic, as previously reported in experimental works [13,16]. This is supported by the non-negative or positive values of the net magnetic moments (MM) of the ThMn2Si2 and ThMn2Ge2 compounds by both the PBE–GGA and GGA + U approximations. Due to the compounds’ ferromagnetic nature, both in this study and in earlier research [13,16,21,22,28,30,31], the parallel magnetic moment was the primary focus of our work. Furthermore, the calculation due to the GGA + U approximation provided a value with a higher scale or magnitude, compared with other currently known potentials, as it frequently dealt with d-shell-localized electrons of the Mn atom and raised its MM to some level in comparison with the PBE–GGA approximation. In addition, the calculation due to the GGA + U yielded a value with a larger magnitude, compared with other approximations that were previously identified, because it primarily dealt with d-shell-localized electrons of the Mn atom and raised its MM to a greater extent than the PBE–GGA.
In addition, the computed values of ThMn2X2 (MM) by both approximations, precisely at interstitial and individual Th, Si, and Ge atoms, opposed the net magnetic moment, whereas Mn supported it due to the dominant appearance of the Mn-d state over the entire range of energy in both spin states, as previously mentioned, whereas investigating by both approximations, as shown in the DOS plots Figure 3a,b, supported this claim. The antiferromagnetic (AFM) interaction between the electrons in the valence band (VB) was seen by the opposing sign appearing in the magnetic moments of the Inst, Th, Si/Ge, total cell, and Mn element. Due to Mn being oriented in the direction of the compounds’ net magnetic moment, ThMn2Ge2 exhibited higher ferromagnetism. As seen in Table 2, the value of MMn changed from 2.17623 to 4.42327 when the d states of the Mn atom were bound through the GGA + U potential. Finally, the total magnetic moments aligned in parallel by both the PBE–GGA and GGA + U potentials, indicating that the thorium (Th)-based ThMn2Ge2 metallic compound exhibited stronger FM behavior than the ThMn2Si2 compound, due to a difference of electro negativity between available Ge (2.01) and Si (1.90) atoms in a prior study [23,24,25]. As a result, the greater the electronegativity difference, the greater the magnetic moment demonstrated by the ThMn2Ge2, confirming stronger ferromagnetism.

4. Conclusions

We used the full-potential linearized augmented plane wave (FPLAPW) method through DFT within the generalized gradient approximation (GGA), as applied in the Wien2 k code, to investigate the various physical properties of tetragonal structure thorium (Th)-based ThMn2X2 (X = Si and Ge) compounds. When the silicon (Si) anion was replaced by germanium (Ge), the lattice constants (ɑ and c(Å)) and unit cell volume ( V 0 ) increased due to the increase in the atomic sizes of the anions as the PM and FM phases were computed. Furthermore, the B(GPa), which describes the natural compressibility of materials, showed a definite declining trend in computed values from Si to Ge, making the ThMn2Ge2 compound more squeezable or compressible than ThMn2Si2. While we employed the GGA + U approach to enhance the electrical and magnetic properties, the computations for the structural findings of ternary thorium intermetallic were produced using the PBE–GGA potential to establish theoretical reliability with the currently existing experimental works. The ThMn2X2 were optimized in a ferromagnetic stable phase, which was better suited than paramagnetic and antiferromagnetic phases for studying a compound’s magnetic properties. The plotted crossing and overlapping electronic band structures (BS) (with absent gap) and the density of state (DOS) plots by both spin states indicated that the ThMn2X2 compound had full metallic character, due to the presence of significant hybridization between (Mn-d and (X = Si and Ge)-p states with Th-f states. The total magnetic moment of ThMn2Si2 in the ferromagnetic phase was 7.94534 μB, while the total magnetic moment for ThMn2Ge2 was 8.73824 μB (exhibiting higher ferromagnetism), with a major contribution from the Mn atom via the GGA + U approach. Additionally, the achieved ferromagnetism in the examined compounds was revealed by the acquired total magnetic moments (MM), which were aligned in parallel to the overall ferromagnetic direction.

Author Contributions

Conceptualization, Formal analysis, Software, Investigation, Methodology, Writing original draft, Editing, and proofreading, A.A.K.; Investigation, Conceptualization, Software, Methodology, Resources, Z.Z.; Conceptualization, Formal analysis, Project administration, Supervision, editing, funding and proofreading, A.H.R.; Formal analysis, Resources, Investigation, Writing-original draft, editing, M.I. (Muhammad Ishaq); Data curation, Investigation, Methodology, Writing-original draft, G.M., Data curation, Investigation, Methodology, editing, M.S.; Formal analysis, Software, Investigation-Supporting, S.Z. (Sabeen Zada) and S.Z. (Shafqat Zada); Investigation, Methodology, Resources, Writing-review, M.I. (Muhammad Ismail); Data curation, Investigation, Methodology. M.F.-u.-R. and M.M.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by (Ali H. Reshak).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Masumoto, K.; McGahan, W.A. Electromagnetic applications of intermetallic compounds. MRS Bull. 1996, 21, 44–49. [Google Scholar] [CrossRef]
  2. Schetky, L.M. Miscellaneous applications of intermetallic compounds. MRS Bull. 1996, 21, 50–55. [Google Scholar] [CrossRef]
  3. Zada, Z.; Laref, A.; Murtaza, G.; Zeb, A.; Yar, A. First-principles calculations of electronic and magnetic properties of XMn2Y2 (X = Ca, Sr; Y = Sb, Bi) compounds. Int. J. Mod. Phys. B 2019, 33, 1950199. [Google Scholar] [CrossRef]
  4. Katsnelson, M.I.; Irkhin, V.Y.; Chioncel, L.; Lichtenstein, A.I.; de Groot, R.A. Half-metallic ferromagnets: From band structure to many-body effects. Rev. Mod. Phys. 2008, 80, 315. [Google Scholar] [CrossRef] [Green Version]
  5. Hirohata, A.; Takanashi, K. Future perspectives for spintronic devices. J. Phys. D Appl. Phys. 2014, 47, 193001. [Google Scholar] [CrossRef]
  6. Khan, A.A.; Yaseen, M.; Laref, A.; Murtaza, G. Impact of anion replacement on the optoelectronic and thermoelectric properties of CaMg2X2, X = (N, P, As, Sb, Bi) compounds. Phys. B Condens. Matter 2018, 541, 24–31. [Google Scholar] [CrossRef]
  7. Pearson, P.; Calvert, L. Pearson’s Handbook of Crystallographics Data for Intermetallic Phases, 2nd ed.; ASM International: Geauga, OH, USA, 1991. [Google Scholar]
  8. Khan, A.A.; Hasil, R.; Laref, A.; Ullah, N.; Sajjad, M.; Zeb, A.; Murtaza, G. DFT prediction of the structural, electronic, thermoelectric and optical properties of ternary pnictides MgBe2X2 (X= N, P, As, Sb, Bi): A novel analysis of beryllium with 2A-and 5B-Elements of the structure type CaAl2Si2. Solid State Commun. 2019, 300, 113667. [Google Scholar] [CrossRef]
  9. Murtaza, G.; Khan, A.A.; Yaseen, M.; Laref, A.; Ullah, N.; ur Rahman, I. The effect of replacing pnictogen elements on the physical properties SrMg2 (, P, As, Sb, Bi) Zintl compounds. Chin. Phys. B 2018, 27, 047102. [Google Scholar] [CrossRef]
  10. Khan, A.A.; Rehman, A.U.; Laref, A.; Yousaf, M.; Murtaza, G. Structural, optoelectronic and thermoelectric properties of ternary CaBe2X2 (X= N, P, As, Sb, Bi) compounds. Z. Für Nat. A 2018, 73, 965–973. [Google Scholar] [CrossRef]
  11. Sikirica, M.; Ban, Z. Thorium Transition Metals Ternary Germanides. Croat. Chem. Acta 1964, 36, 151–158. [Google Scholar]
  12. Ban, Z.; Sikirica, M. The crystal structure of ternary silicides ThM2Si2 (M= Cr, Mn, Fe, Co, Ni and Cu). Acta Crystallogr. 1965, 18, 594–599. [Google Scholar] [CrossRef]
  13. Omejec, L.; Ban, Z. Magnetic Susceptibilities of ThM2X2 Compounds (M= Cr, Mn, Fe, Co, Ni and Cu; X= Si and Ge). Z. Für Anorg. Und Allg. Chem. 1971, 380, 111–117. [Google Scholar] [CrossRef]
  14. Korotin, D.M.; Finkelstein, L.D.; Streltsov, S.V.; Gerasimov, E.G.; Kurmaev, E.Z.; Mushnikov, N.V. Origin of magnetic phase transition in RMn2Si2 (R= rare-earth ion or Y) intermetallics. Comput. Mater. Sci. 2020, 184, 109901. [Google Scholar] [CrossRef]
  15. Korotin, D.M.; Rosenfeld, E.V.; Mushnikov, N.V.; Gerasimov, E.G.; Zhidkov, I.S.; Kukharenko, A.I.; Finkelstein, L.D.; Cholakh, S.O.; Kurmaev, E.Z. Electronic structure of RMn2Si2 (R= Y, La) intermetallics: DFT and XPS studies. J. Alloys Compd. 2017, 695, 1663–1671. [Google Scholar] [CrossRef]
  16. Narasimhan, K.S.V.L.; Rao, V.U.S.; Wallace, W.E.; Pop, I. Magnetic properties of RMn2X2 compounds (R= Rare earth, Y or Th and X= Ge, Si). In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 1976; Volume 29, pp. 594–595. [Google Scholar] [CrossRef]
  17. Venturini, G. The Electronic Structure of the RΜn2Ge2 (R= Ca, Y, La, Ba) Antiferromagnets. Acta Phys. Pol. Ser. A 2000, 97, 761–765. [Google Scholar] [CrossRef]
  18. Narasimhan, K.S.V.L.; Rao, V.U.S.; Bergner, R.L.; Wallace, W.E. Magnetic properties of R Mn2Ge2 compounds (R= La, Ce, Pr, Nd, Cd, Tb, Dy, Ho, Er, and Th). J. Appl. Phys. 1975, 46, 4957–4960. [Google Scholar] [CrossRef]
  19. McCall, W.M.; Narasimhan, K.S.V.L.; Butera, R.A. Magnetic properties of R Co2 Ge2 compounds (R= La, Ce, Pr, Nd, Sm, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, and Y). J. Appl. Phys. 1973, 44, 4724–4726. [Google Scholar] [CrossRef]
  20. Gyorgy, E.M.; Batlogg, B.; Remeika, J.P.; Van Dover, R.B.; Fleming, R.M.; Bair, H.E.; Espinosa, G.P.; Cooper, A.S.; Maines, R.G. The P-T magnetic phase diagram of SmMn2Ge2. J. Appl. Phys. 1987, 61, 4237–4239. [Google Scholar] [CrossRef]
  21. Bibi, R.; Zada, Z.; Khan, A.A.; Azam, S.; Irfan, M.; Haq, B.U.; Ahmad, M.; Khan, S.A. First-principles calculations of structural, electronic, magnetic, thermoelectric, and thermodynamic properties of BaMn2P2 in the Anti and ferromagnetic phase. J. Solid State Chem. 2021, 302, 122388. [Google Scholar] [CrossRef]
  22. Khan, A.A.; Saqib, M.; Zada, Z.; Chahed, F.; Ismail, M.; Ishaq, M.; Khan, Q.; Faizan, M. Electronic structure, magnetic, and thermoelectric properties of BaMn2As2 compound: A first-principles study. Phys. Scr. 2022, 97, 065810. [Google Scholar] [CrossRef]
  23. Khan, A.A.; Zada, Z.; Reshak, A.H.; Akbar, J.; Saqib, M.; Naeem, M.A.; Ismail, M.; Zada, S.; Murtaza, G.; Laref, A.; et al. Effects of anion-ligands replacement on the structural, electronic and magnetic properties of ThCo2X2 (X= Si, Ge). Chin. J. Phys. 2022, 77, 956–964. [Google Scholar] [CrossRef]
  24. Zada, Z.; Khan, A.A.; Zada, R.; Reshak, A.H.; Murtaza, G.; Saqib, M.; Ramli, M.M.; Bila, J. First-principles calculations to investigate variation of cationic-ligand LmAl2Ge2 (Lm= Ca, Y, La and Ce). Indian J. Phys. 2022, 96, 3151–3159. [Google Scholar] [CrossRef]
  25. Khan, A.A.; Reshak, A.H.; Zada, Z.; Saqib, M.; Abbas, Z.; Ismail, M.; Zada, S.; Murtaza, G.; Ali, S.; Laref, A. Thermoelectric, structural, electronic, magnetic, and thermodynamic properties of CaZn2Ge2 compound. Eur. Phys. J. Plus 2022, 137, 351. [Google Scholar] [CrossRef]
  26. Zada, Z.; Zada, R.; Khan, A.A.; Saqib, M.; Rehman, M.F.U.; Ismail, M.; Kulhari, N.; Sharma, K.S.; Shen, X.; Faizan, M. Investigation of electronic structure, magnetic stability, spin coupling, and thermodynamic properties of novel antiferromagnets XMn2Y2 (X= Ca, Sr; Y= P, As). J. Mol. Struct. 2022, 1268, 133698. [Google Scholar] [CrossRef]
  27. Blaha, P.; Schwarz, K.; Madsen, G.K.; Kvasnicka, D.; Luitz, J. Wien2k, An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties; Schwarz, Vienna University of Technology: Vienna, Austria, 2001; ISBN 3-9501031-1-2. [Google Scholar]
  28. Zada, Z.; Khan, A.A.; Reshak, A.H.; Ismail, M.; Zada, S.; Murtaza, G.; Saqib, M.; Ramli, M.M.; Bila, J. Cationic variation for LnAl2Si2 (Ln= Y, Sm, Tb, Dy, Yb) compounds by density functional theory. J. Mol. Struct. 2022, 1252, 132136. [Google Scholar] [CrossRef]
  29. Zada, Z.; Ullah, H.; Zada, R.; Khan, A.A.; Mahmood, A.; Ramay, S.M. Electronic band profiles, magnetic stability, antiferromagnetic spins ordering and thermodynamics properties of novel antiferromagnet CaCr2Sb2. Eur. Phys. J. Plus 2021, 136, 371. [Google Scholar] [CrossRef]
  30. Zada, Z.; Ullah, H.; Zada, R.; Zada, S.; Laref, A.; Azam, S.; Khan, A.A.; Irfan, M. Structure stability, half metallic ferromagnetism, magneto-electronic and thermoelectric properties of new zintl XCr2Bi2 (X= Ca, Sr) compounds for spintronic and renewable energy applications. Phys. B Condens. Matter 2021, 607, 412866. [Google Scholar] [CrossRef]
  31. Zada, Z.; Ullah, H.; Bibi, R.; Zada, S.; Mahmood, A. Electronic band profiles and magneto-electronic properties of ternary XCu2P2 (X= Ca, Sr) compounds: Insight from ab initio calculations. Z. Für Nat. A 2020, 75, 543–549. [Google Scholar] [CrossRef]
  32. Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
  33. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  34. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef] [PubMed]
  35. Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef] [Green Version]
  36. Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Wu, S.Q.; Zhu, Z.Z.; Yang, Y.; Hou, Z.F. Structural stabilities, electronic structures and lithium deintercalation in LixMSiO4 (M= Mn, Fe, Co, Ni): A GGA and GGA+ U study. Comput. Mater. Sci. 2009, 44, 1243–1251. [Google Scholar] [CrossRef]
  38. Rossi, D.; Marazza, R.; Mazzone, D.; Ferro, R. Lattice parameters of RMn2Si2 and RMn2Ge2 compounds. J. Less Common Met. 1978, 59, 79–83. [Google Scholar] [CrossRef]
  39. Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Naseri, M.; Jalilian, J.; Reshak, A.H. Electronic and optical properties of pentagonal-B2C monolayer: A first-principles calculation. Int. J. Mod. Phys. B 2017, 31, 1750044. [Google Scholar] [CrossRef]
  41. Khan, A.A.; Khan, W.; Khan, A.; Laref, A.; Zeb, A.; Murtaza, G. Investigation of the structural, electrical, optical and magnetic properties of XMg4Mn6O15 (X= K, Rb, and Cs) compounds. Mater. Res. Express 2019, 6, 066102. [Google Scholar] [CrossRef]
  42. Rahim, I.; Azam, S.; Gul, B.; Khan, A.A.; Yousaf, N.; Zada, Z.; Saqib, M.; Subhan, F.; Ismail, M.; Khan, A.; et al. Advances in tuning band gap of graphene by potential doping using DFT: A review. Dig. J. Nanomater. Biostruct. (DJNB) 2021, 16, 975–988. [Google Scholar]
  43. Murtaza, G.; Khan, A.A.; AL-Anazy, M.M.; Laref, A.; Mahmood, Q.; Zada, Z.; Aman, M. Anionic variations for BaMg2X2 (X= N to Bi) compounds by density functional theory. Eur. Phys. J. Plus 2021, 136, 136. [Google Scholar] [CrossRef]
  44. Sahnoun, M.; Daul, C.; Haas, O.; Wokaun, A. Investigation of the electronic structure in La1−xCaxCoO3 (x = 0, 0.5) using full potential calculations. J. Phys. Condens. Matter 2005, 17, 7995. [Google Scholar] [CrossRef]
  45. Siddique, M.; Iqbal, A.; Rahman, A.U.; Azam, S.; Zada, Z.; Talat, N. Mechanical and thermodynamic stability, structural, electronics and magnetic properties of new ternary thorium-phosphide silicides ThSixP1-x: First-principles investigation and prospects for clean nuclear energy applications. Nucl. Eng. Technol. 2021, 53, 592–602. [Google Scholar] [CrossRef]
  46. Sinaga, G.S.; Utimula, K.; Nakano, K.; Hongo, K.; Maezono, R. First Principles Calculations of Superconducting Critical Temperature of ThCr2 Si2-Type Structure 2019. arXiv 2019, arXiv:1911.10716. [Google Scholar]
  47. Ciesielski, K.; Chajewski, G.; Samsel–Czekała, M.; Hackemer, A.; Obstarczyk, P.; Pikul, A.P.; Kaczorowski, D. Electronic properties of LaTE2Ge2 (TE= Fe, Co, Ni, Cu and Ru). Solid State Commun. 2018, 280, 13–17. [Google Scholar] [CrossRef]
  48. Khan, Z.; Murtaza, G.; Khan, A.A.; Laref, A.; Kattan, N.A.; Haneef, M. Different physical properties of bi-alkali pnictogen compounds using density functional theory. Int. J. Energy Res. 2021, 45, 7703–7718. [Google Scholar] [CrossRef]
  49. Khan, A.A.; Reshak, A.H.; Noor, Z.; Murtaza, G.; Al-Anazy, M.M.; Althib, H.; Flemban, T.H.; Laref, A.; Bakri, A.M.A.; Bila, J. First-principles calculations of structural, electronic, optical, and thermoelectric properties of ternary d-metal sulfides Sc2CdS4 and Y2CdS4 compounds. Int. J. Energy Res. 2021, 45, 13657–13667. [Google Scholar] [CrossRef]
Molecules 27 07070 g001 550
Figure 1. Relaxed crystal structure of ThMn2Si2 compound.
Figure 1. Relaxed crystal structure of ThMn2Si2 compound.
Molecules 27 07070 g001
Molecules 27 07070 g002 550
Figure 2. Optimized plots of ThMn2Si2 and ThMn2Ge2 compounds.
Figure 2. Optimized plots of ThMn2Si2 and ThMn2Ge2 compounds.
Molecules 27 07070 g002
Molecules 27 07070 g003 550
Figure 3. (a) Plotted DOS of ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase, using GGA in both orientations; (b) plotted DOS of ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase, using GGA + U in both orientations.
Figure 3. (a) Plotted DOS of ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase, using GGA in both orientations; (b) plotted DOS of ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase, using GGA + U in both orientations.
Molecules 27 07070 g003
Molecules 27 07070 g004a 550Molecules 27 07070 g004b 550
Figure 4. (a) Band structures of the ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase while using GGA–PBE in both spin states; (b) band structures of the ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase while using GGA + U in both spin states; (c) Fermi surface sheet of ThMn2Ge2 as a prototype of ThMn2X2, in the body-centered tetragonal Brillouin zone boundaries. The character of Fermi surfaces are primarily constituted by the Th f, Mn d, and X p states.
Figure 4. (a) Band structures of the ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase while using GGA–PBE in both spin states; (b) band structures of the ThMn2Si2 and ThMn2Ge2 compounds in body-centered tetragonal ferromagnetic phase while using GGA + U in both spin states; (c) Fermi surface sheet of ThMn2Ge2 as a prototype of ThMn2X2, in the body-centered tetragonal Brillouin zone boundaries. The character of Fermi surfaces are primarily constituted by the Th f, Mn d, and X p states.
Molecules 27 07070 g004aMolecules 27 07070 g004b
Table
Table 1. Noted unit cell parameters of ThMn2Si2 and ThMn2Ge2 compounds, together with available experimental studies.
Table 1. Noted unit cell parameters of ThMn2Si2 and ThMn2Ge2 compounds, together with available experimental studies.
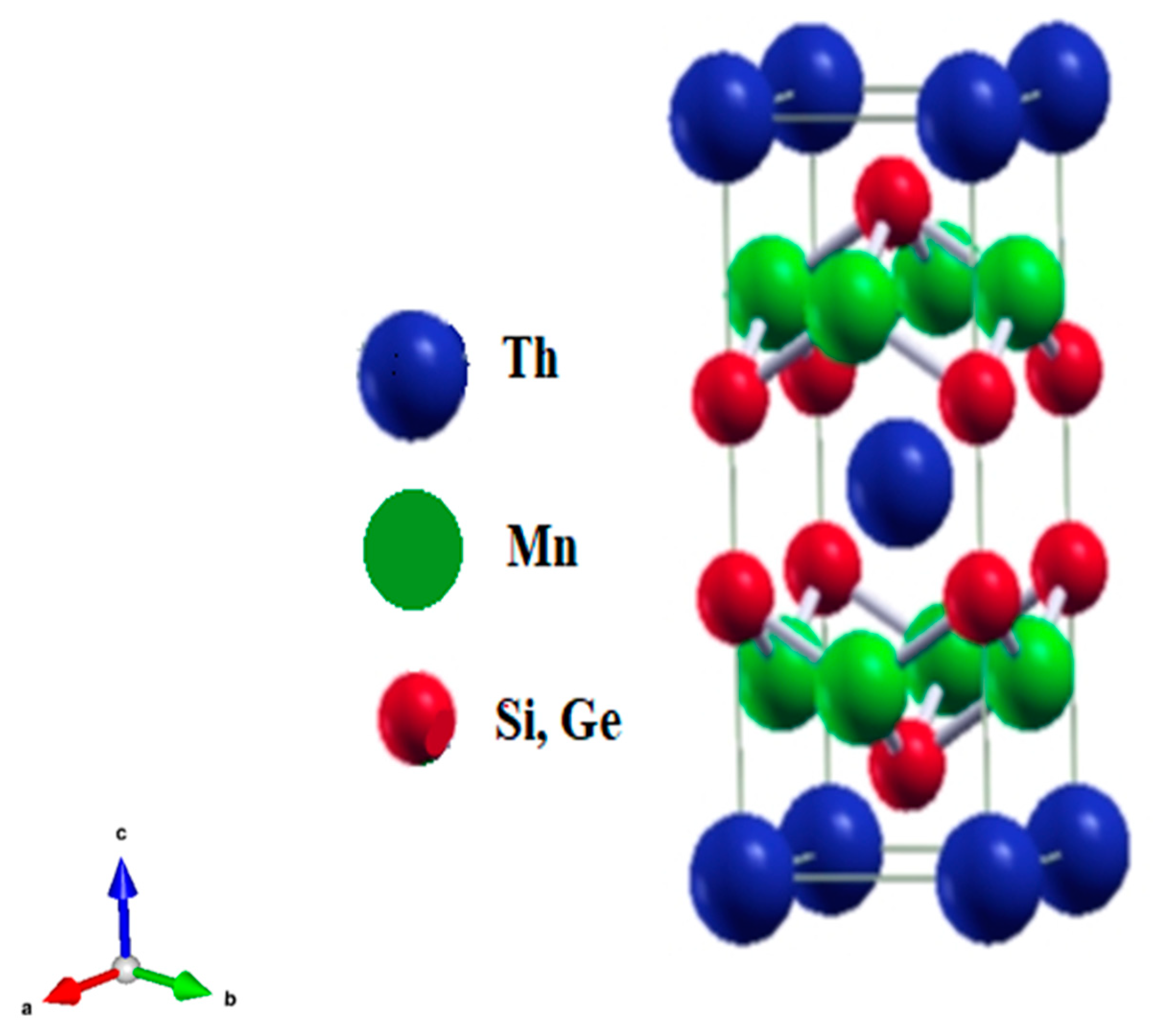
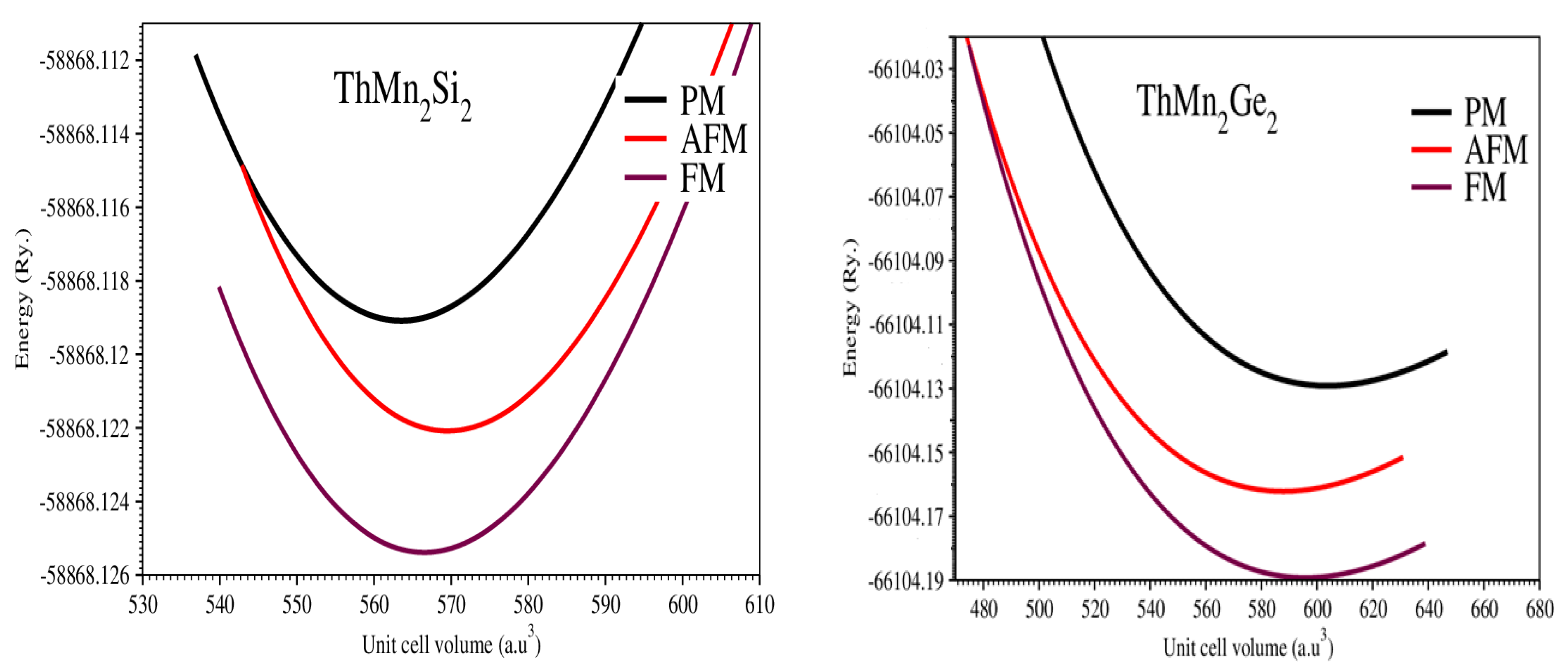
CompoundsLattice Constant (A)0V0 (a.u)3B (GPa)BpE0 (Ry)
acFMPMAFM
ThMn2Si2
Exp b		4.015
4.019 b		10.480
10.483 b		563.5188152.95765.0−58,868.125−58,868.119−58,868.122
ThMn2Ge2
Expa,b,c		4.088
4.084 a, 4.090 b, 4.690 c		10.904
10.930 a,
10.907 b,
10.907 c		595.9810118.42295.44−66,104.19−66,104.13−66,104.16
a Ref. [11], b Ref. [16], c Ref. [18].
Table
Table 2. Magnetic moments of the interstitial region (minte), single atoms (MTh/Mn/Si/Ge), and overall cell for the ThMn2Si2 and ThMn2Ge2 compounds computing both schemes (Bohr magnetrons μB).
Table 2. Magnetic moments of the interstitial region (minte), single atoms (MTh/Mn/Si/Ge), and overall cell for the ThMn2Si2 and ThMn2Ge2 compounds computing both schemes (Bohr magnetrons μB).
CompoundsminteMThMMnMSi/GemcellΔ = mcell − MMn
ThMn2Si2(PBE-GGA)−0.04156−0.003001.90730−0.041943.686151.77885
GGA + U−0.15905−0.081264.18022−0.087407.945343.76512
Exp.----------------------2.98 a---------------------------------
Other calc.------------------------------------------------------------------
ThMn2Ge2(PBE-GGA)−0.17642−0.058452.17623−0.038844.039921.86369
GGA + U0.01043−0.027844.42327−0.045448.738244.31497
Exp.----------------------1.57 a, 0.10 b---------------------------------
Other calc.------------------------------------------------------------------
a Ref. [13], b Ref. [16].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Khan, A.A.; Zada, Z.; Reshak, A.H.; Ishaq, M.; Zada, S.; Saqib, M.; Ismail, M.; Fazal-ur-Rehman, M.; Murtaza, G.; Zada, S.; et al. GGA and GGA + U Study of ThMn2Si2 and ThMn2Ge2 Compounds in a Body-Centered Tetragonal Ferromagnetic Phase. Molecules 2022, 27, 7070. https://doi.org/10.3390/molecules27207070

AMA Style

Khan AA, Zada Z, Reshak AH, Ishaq M, Zada S, Saqib M, Ismail M, Fazal-ur-Rehman M, Murtaza G, Zada S, et al. GGA and GGA + U Study of ThMn2Si2 and ThMn2Ge2 Compounds in a Body-Centered Tetragonal Ferromagnetic Phase. Molecules. 2022; 27(20):7070. https://doi.org/10.3390/molecules27207070

Chicago/Turabian Style

Khan, Abdul Ahad, Zeshan Zada, Ali H. Reshak, Muhammad Ishaq, Sabeen Zada, Muhammad Saqib, Muhammad Ismail, Muhammad Fazal-ur-Rehman, Ghulam Murtaza, Shafqat Zada, and et al. 2022. "GGA and GGA + U Study of ThMn2Si2 and ThMn2Ge2 Compounds in a Body-Centered Tetragonal Ferromagnetic Phase" Molecules 27, no. 20: 7070. https://doi.org/10.3390/molecules27207070

Article Metrics

Back to TopTop