The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains
Abstract
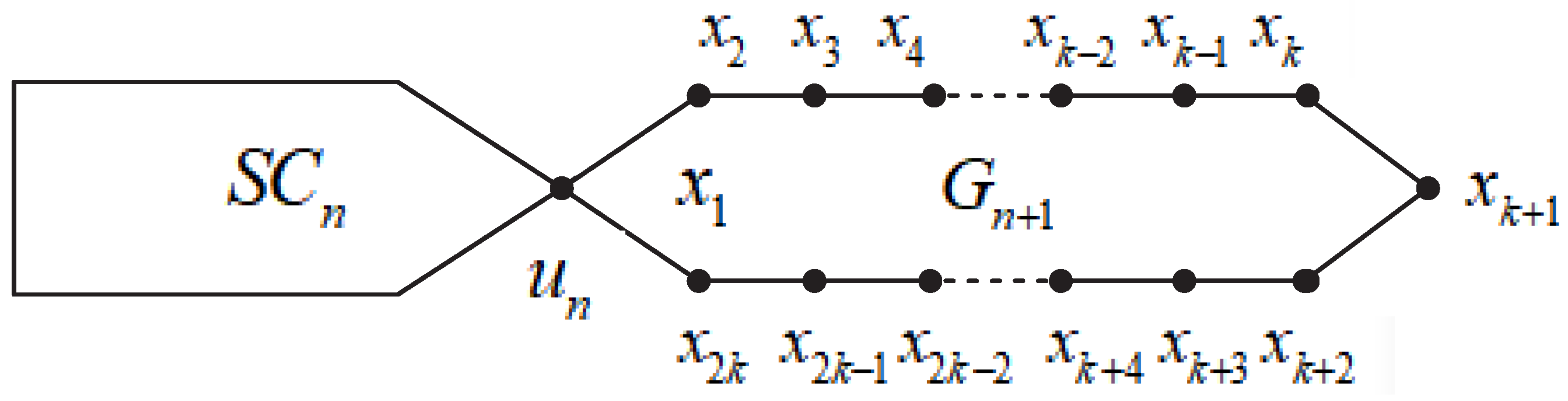
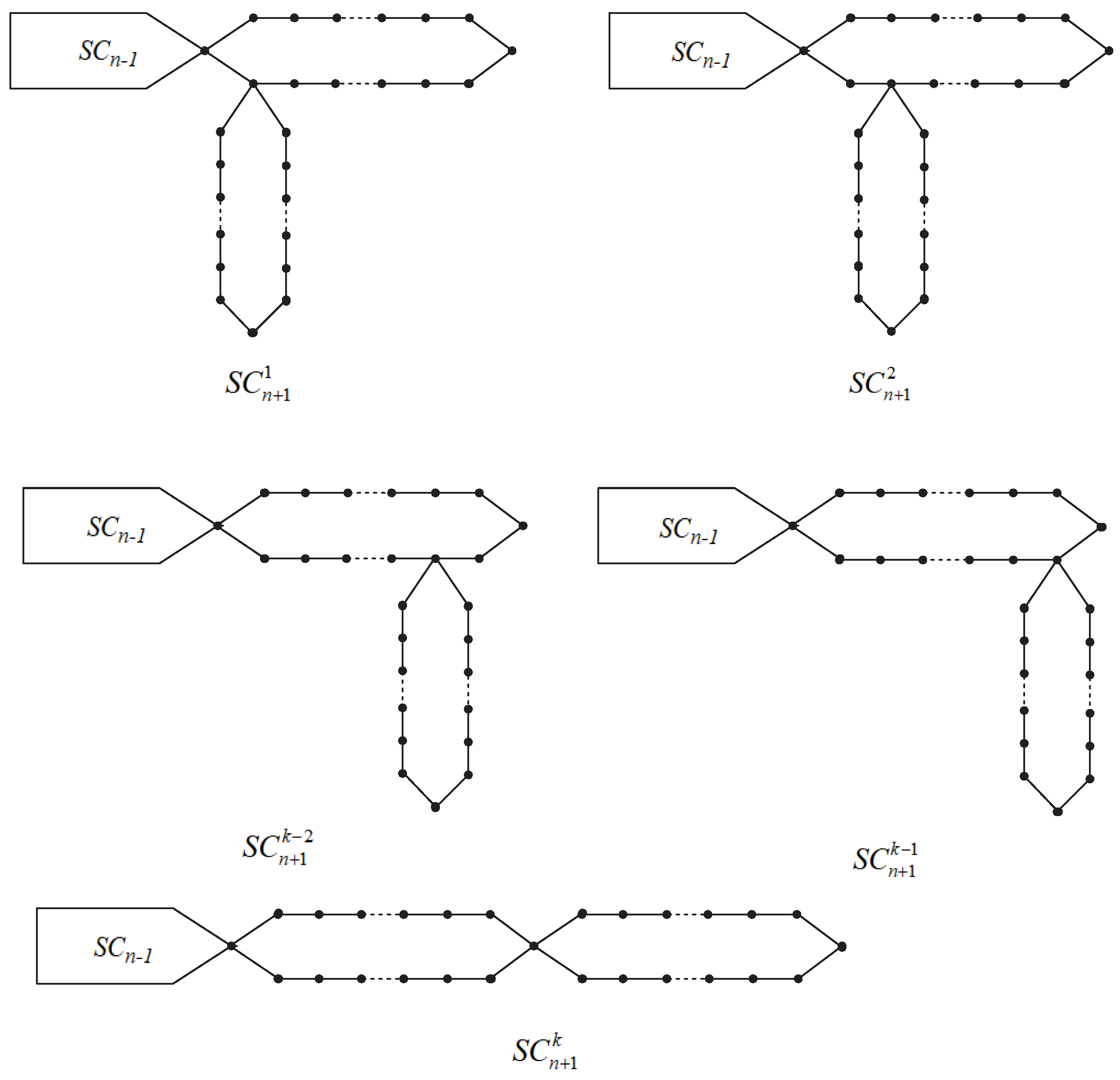
1. Introduction
- with probability ,
- with probability ,
- with probability ,
- with probability ,
2. The Gutman Index of the Random Regular Polygonal Chain
3. The Schultz Index of the Random Regular Polygonal Chain
4. Average Values of the Indices
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Estrada, E.; Bonchev, D. Chemical Graph Theory. In Handbook of Graph Theory; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2013; pp. 1538–1558. [Google Scholar]
- Flower, D.R. On the properties of bit string-based measures of chemical similarity. J. Chem. Inf. Comput. Sci. 1998, 38, 379–386. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Evans, W.C.; Evans, D. Hydrocarbons and derivatives. In Trease and Evans’ Pharmacognosy, 16th ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 173–193. [Google Scholar]
- Bai, Y.; Zhao, B.; Zhao, P. Extremal Merrifield-Simmons index and Hosoya index of polyphenyl chains. MATCH Commun. Math. Comput. Chem. 2009, 62, 649–656. [Google Scholar]
- Chen, X.; Zhao, B.; Zhao, P. Six-membered ring spiro chains with extremal Merrifild-Simmons index and Hosoya index. MATCH Commun. Math. Comput. Chem. 2009, 62, 657–665. [Google Scholar]
- Diudea, M.V.; Gutman, I.; Jäntsci, L. Molecular Topology; Nova, Huntington: New York, NY, USA, 2001. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: New York, NY, USA, 2008. [Google Scholar]
- Wiener, H. Structrual determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Deng, H. Wiener indices of spiro and polyphenyl hexagonal chains. Math. Comput. Model. 2013, 55, 634–644. [Google Scholar] [CrossRef]
- Ma, L.; Bian, H.; Liu, B.J.; Yu, H.Z. The expected values of the Wiener indices in the random phenylene and spiro chains. Ars Combin. 2017, 130, 267–274. [Google Scholar]
- Wei, S.; Shiu, W. Enumeration of Wiener indices in random polygonal chains. J. Math. Anal. Appl. 2019, 469, 537–548. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, F. Wiener index in random polyphenyl chains. MATCH Commun. Math. Comput. Chem. 2012, 68, 371–376. [Google Scholar]
- Zhou, Q.N.; Wang, L.G.; Lu, Y. Wiener index and Harary index on Hamilton-connected graphs with large minimum degree. Discrete Appl. Math. 2018, 247, 180–185. [Google Scholar] [CrossRef]
- Buckley, F.; Harary, F. Distance in Graphs; Addison-Wesley: Reading, UK, 1989. [Google Scholar]
- Chen, H.; Zhang, F. Resistance distance and the normalized Laplacian spectrum. Discrete Appl. Math. 2017, 155, 654–661. [Google Scholar] [CrossRef]
- Entringer, R.C.; Jackson, D.E.; Snyder, D.A. Distance in graphs. Czechoslovak Math. J. 1976, 26, 283–296. [Google Scholar] [CrossRef]
- Gutman, I.; Feng, L.; Yu, G. Degree resistance distance of unicyclic graphs. Trans. Combin. 2012, 1, 27–40. [Google Scholar]
- Mukwembi, S.; Munyira, S. MunyiraDegree distance and minimum degree. Bull. Aust. Math. Soc. 2013, 87, 255–271. [Google Scholar] [CrossRef]
- Gutman, I. Selected properties of the Schultz molecular topological index. J. Chem. Inf. Comput. Sci. 1994, 34, 1087–1089. [Google Scholar] [CrossRef]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR; Gordon and Breach: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Farahani, M.R. Hosoya, Schultz, modified Schultz polynomials and their topological indices of benzene molecules: First members of polycyclic aromatic hydrocarbons (PAHs). Int. J. Theor. Chem. 2013, 1, 9–16. [Google Scholar]
- Huang, G.H.; Kuang, M.J.; Deng, H.Y. The expected values of Kirchhoff indices in the random polyphenyl and spiro chains. Ars Math. Contemp. 2015, 9, 197–207. [Google Scholar] [CrossRef]
- Qi, J.F.; Fang, M.L.; Geng, X.Y. The expected value for the wiener index in the random spiro chain. Polycycl. Aromat. Compd. 2022. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.; Li, S.; Zhang, M. The expected values for the Schultz index, Gutman index, multiplicative degree-Kirchhoff index and addtive degree-Kirchhoff index of a random polyphenylene chain. Discrete Appl. Math. 2020, 282, 243–356. [Google Scholar] [CrossRef]
- Deng, H.; Tang, Z. Kirchhoff indices of spiro and polyphenyl hexagonal chains. Util. Math. 2014, 95, 113–128. [Google Scholar]
- Xiao, Q.; Zeng, M.; Tang, Z.; Hua, H.; Deng, H. The hexagonal chains with the first three maximal Mostar indices. Discrete Appl. Math. 2021, 288, 180–191. [Google Scholar] [CrossRef]
- Zhao, P.; Zhao, B.; Chen, X.; Bai, Y. Two classes of chains with maximal and minimal total π-electron energy. MATCH Commun. Math. Comput. Chem. 2009, 62, 525–536. [Google Scholar]
- Liu, H.C.; Zeng, M.Y.; Deng, H.Y.; Tang, Z.K. Some indices in the random spiro chains. Iranian J. Math. Chem. 2020, 11, 255–270. [Google Scholar]
- Liu, J.B.; Zhang, T.; Wang, Y.K.; Lin, W.S. The Kirchhoff index and spanning trees of Mobius/cylinder octagonal chain. Discrete Appl. Math. 2022, 307, 22–31. [Google Scholar] [CrossRef]
- Liu, J.B.; Gu, J.J.; Wang, K. The expected values for the Gutman index, Schultz index, and some Sombor indices of a random cyclooctane chain. Int. J. Quantum Chem. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhan, Q. The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains. Molecules 2022, 27, 6838. https://doi.org/10.3390/molecules27206838
Liu X, Zhan Q. The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains. Molecules. 2022; 27(20):6838. https://doi.org/10.3390/molecules27206838
Chicago/Turabian StyleLiu, Xinmei, and Qian Zhan. 2022. "The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains" Molecules 27, no. 20: 6838. https://doi.org/10.3390/molecules27206838
APA StyleLiu, X., & Zhan, Q. (2022). The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains. Molecules, 27(20), 6838. https://doi.org/10.3390/molecules27206838





