A Computational Study of the S2 State in the Oxygen-Evolving Complex of Photosystem II by Electron Paramagnetic Resonance Spectroscopy
Abstract
1. Introduction
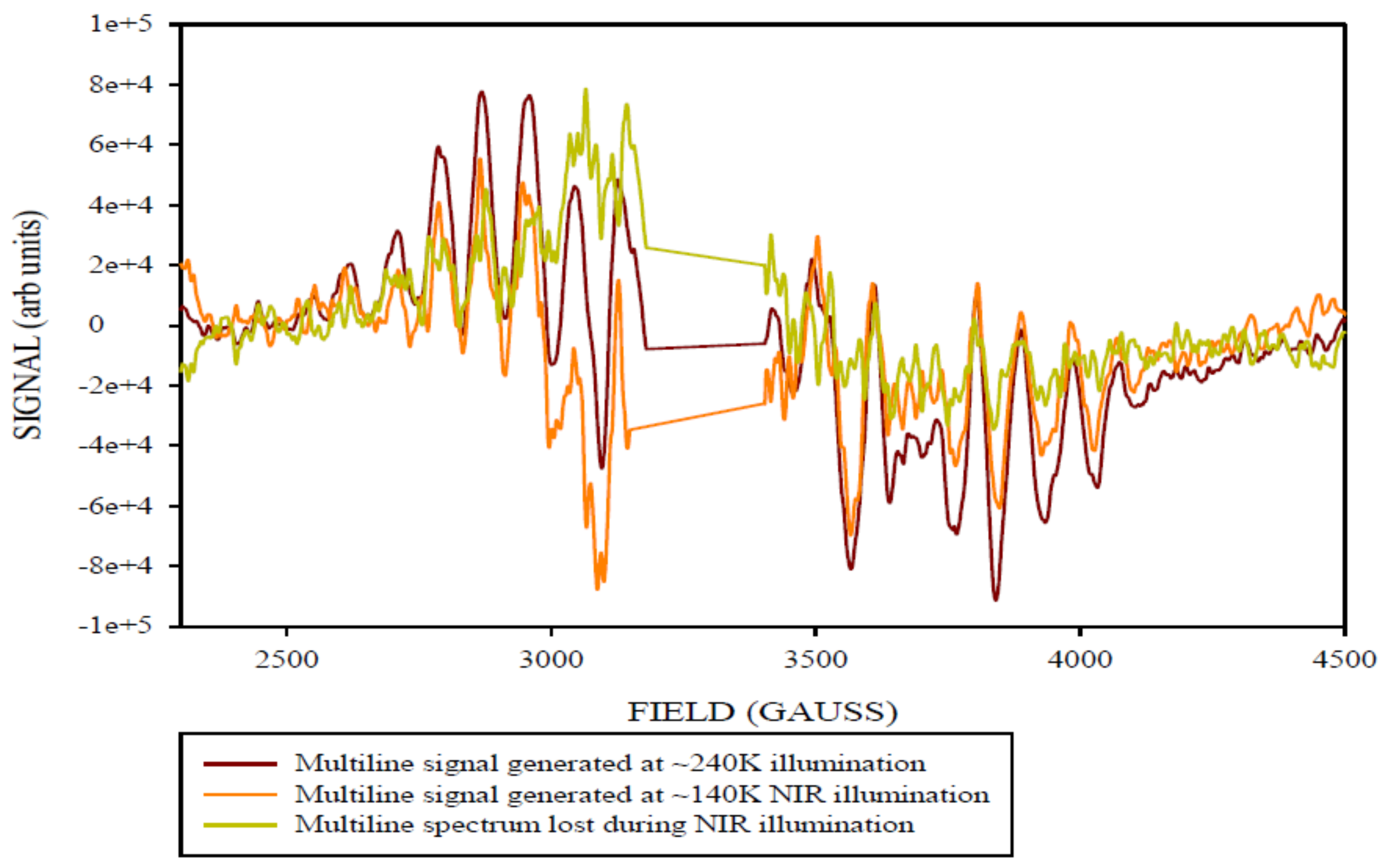
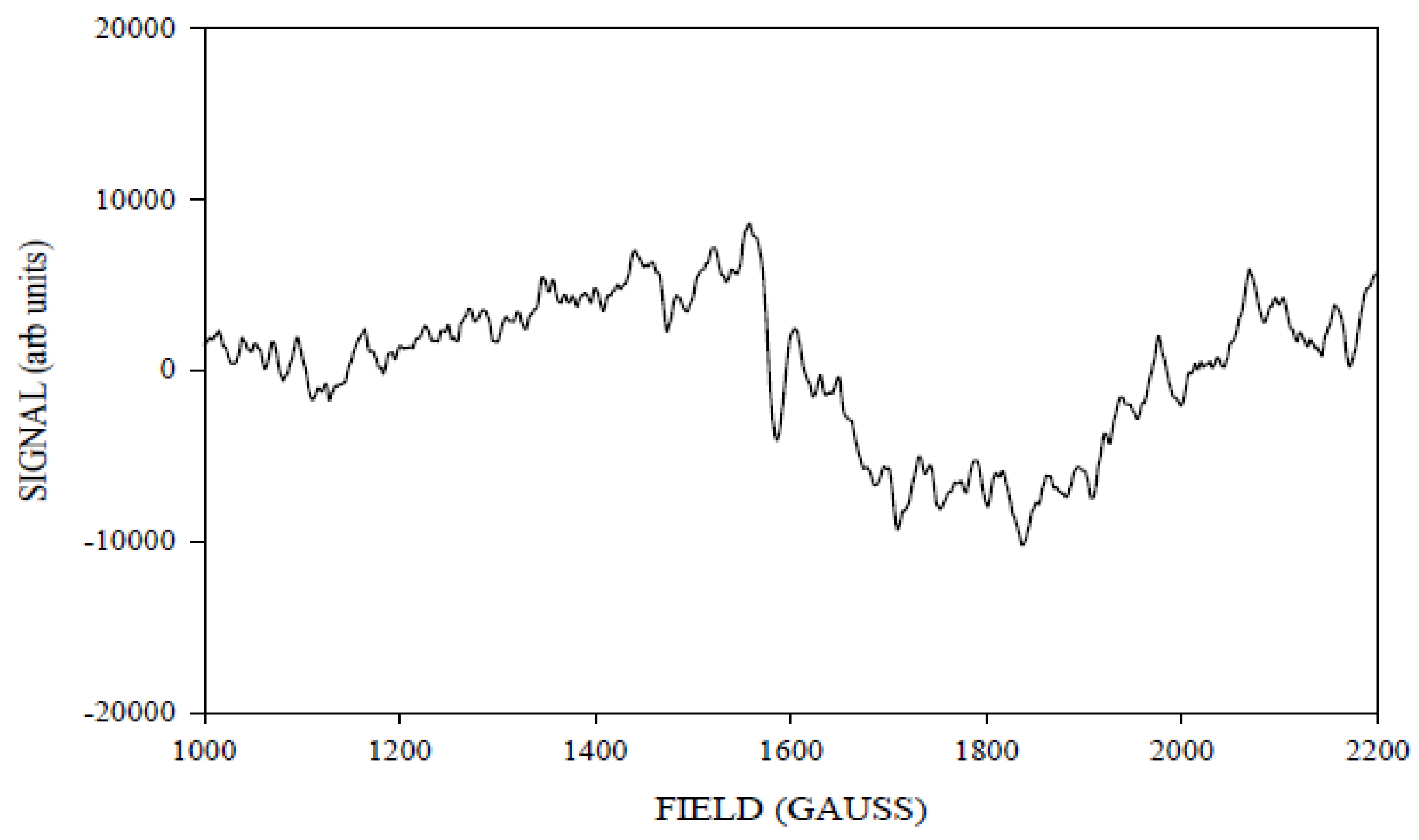
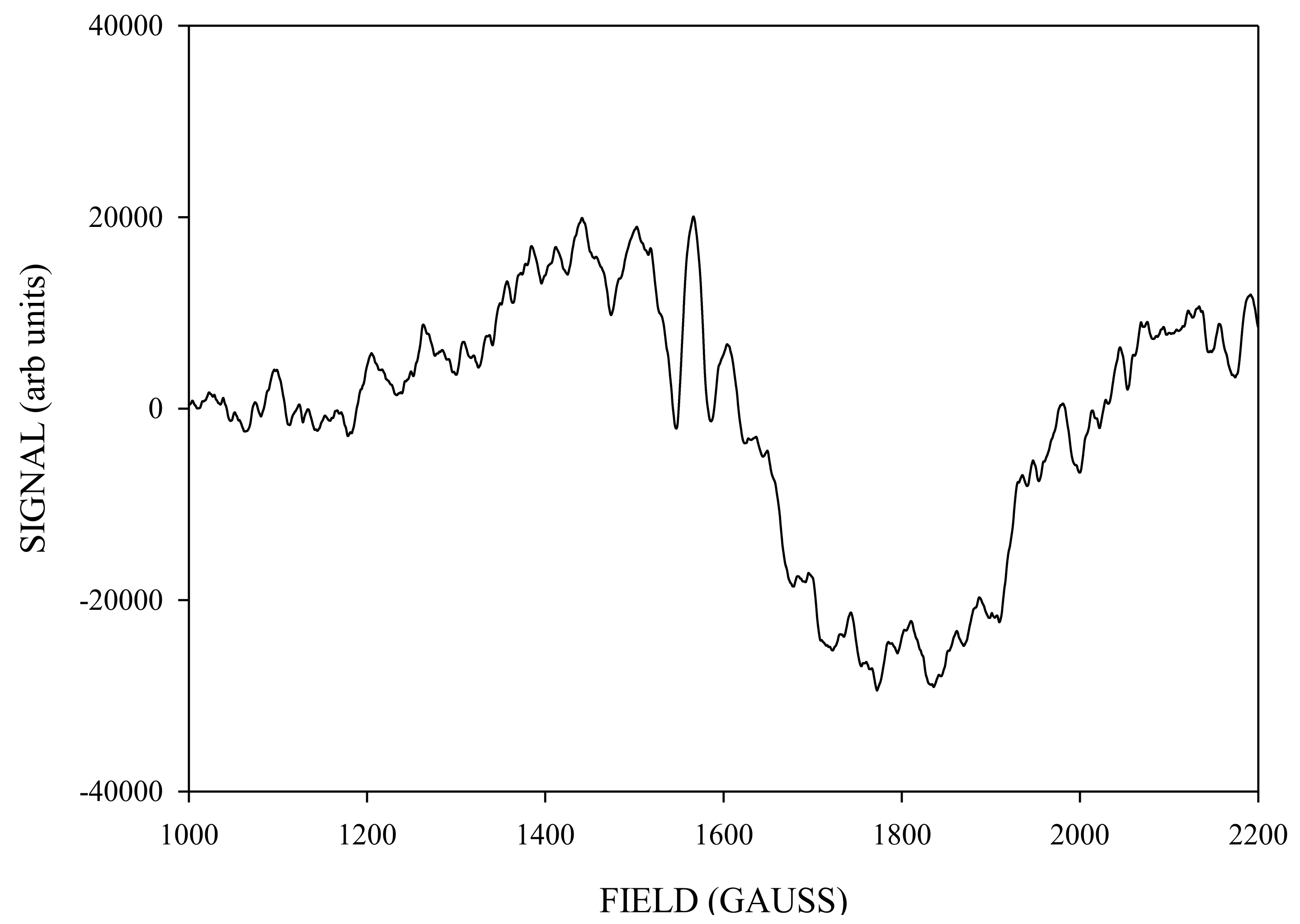
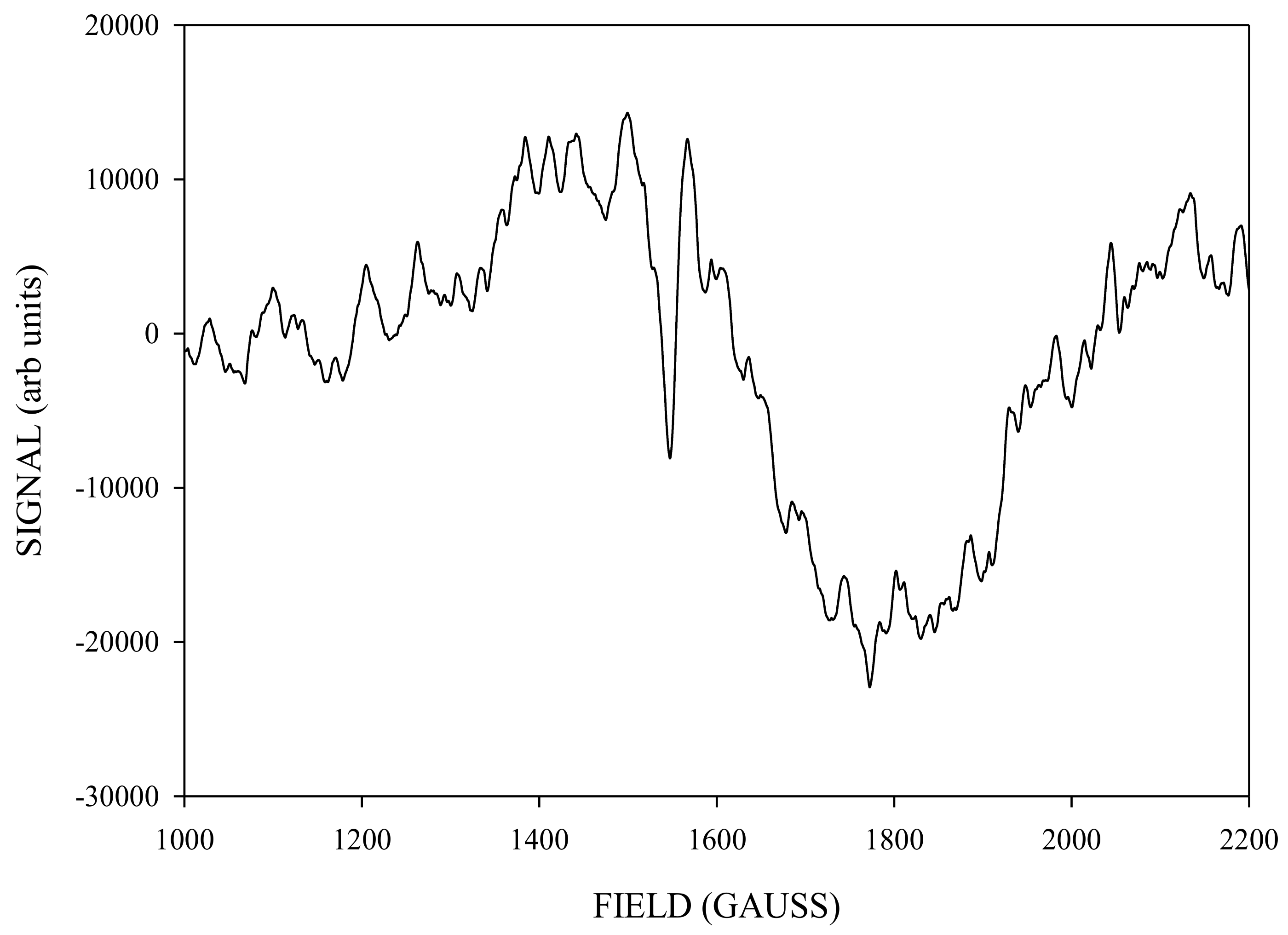
2. Results and Discussion
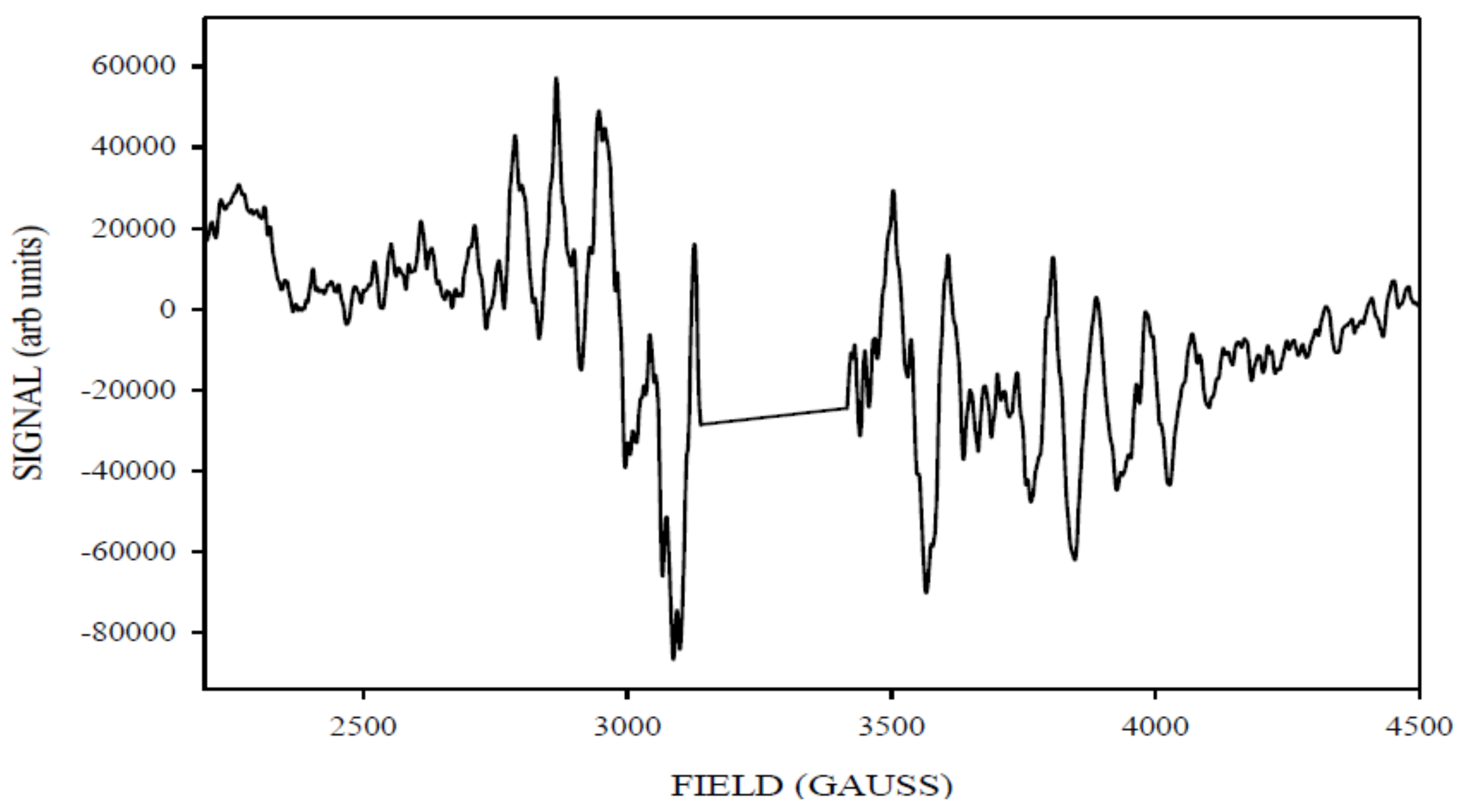
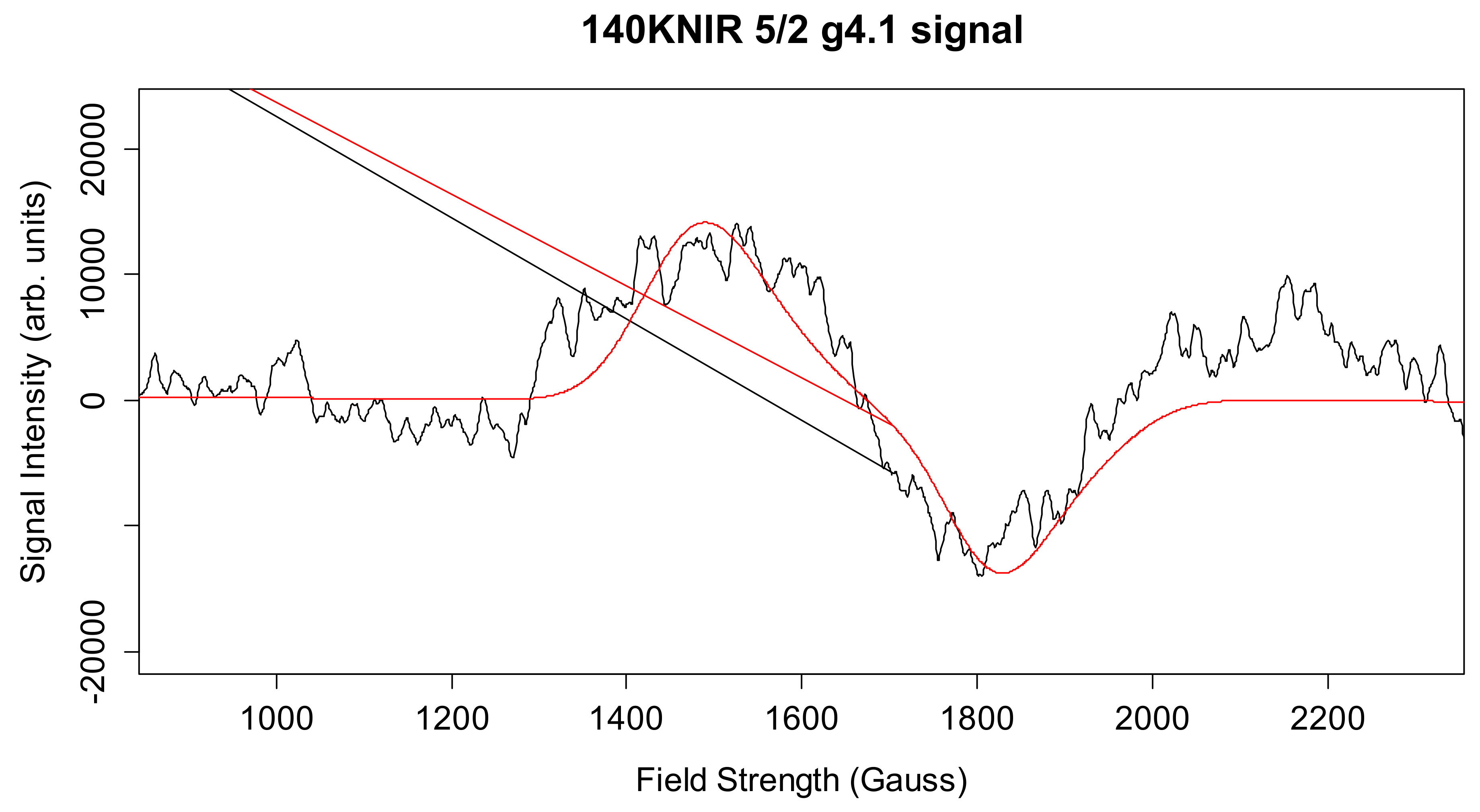
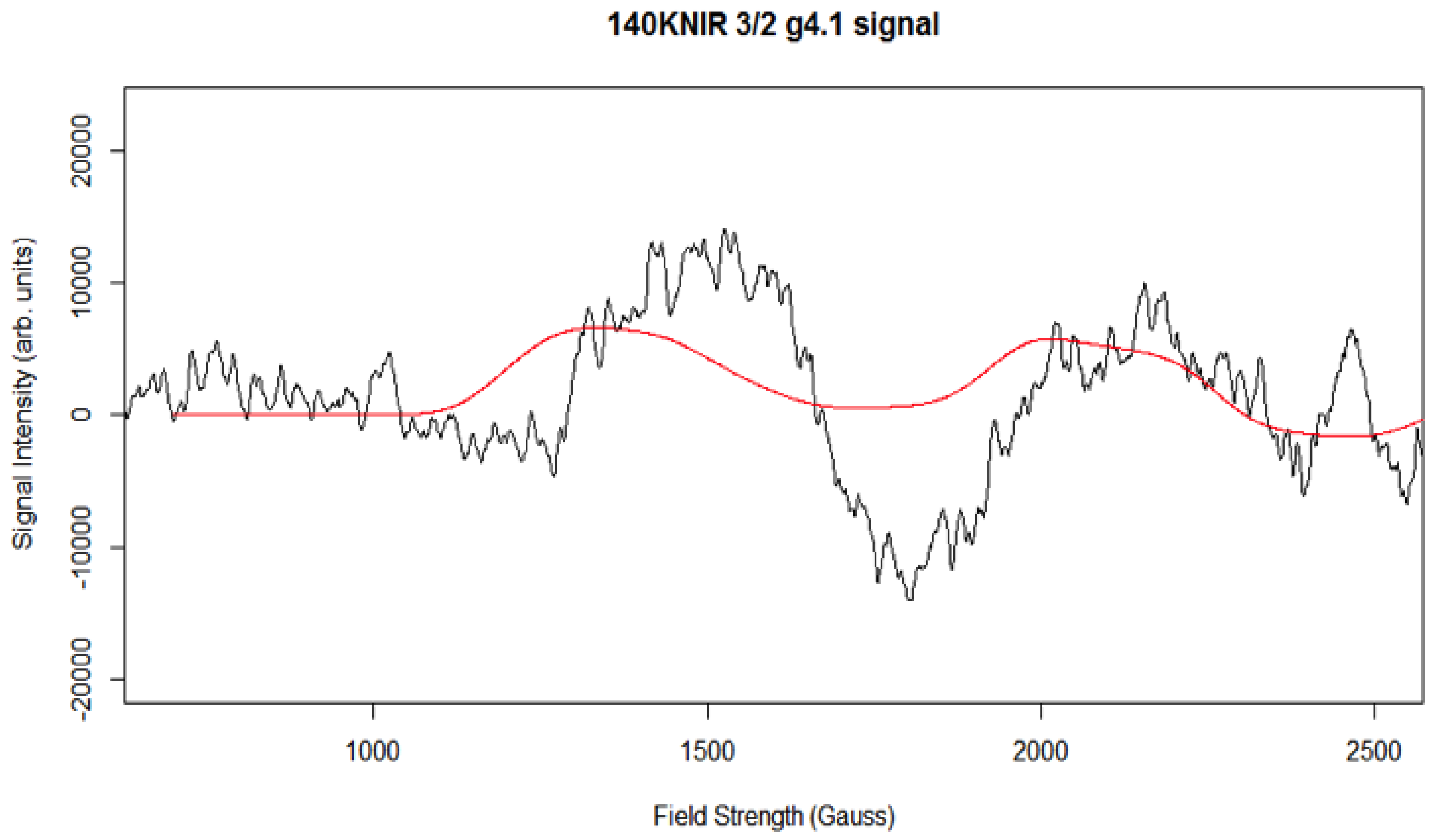
Simulation of X-Band CW-EPR-Generated 4.1 Signal of ≈140 K NIR-Illuminated PSII Core Samples
3. Materials and Methods
3.1. Illumination and Annealing Procedures
3.2. X-Band CW-EPR Spectrometer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Isobe, H.; Shoji, M.; Suzuki, T.; Shen, J.-R.; Yamaguchi, K. Spin, Valence, and Structural Isomerism in the S3 State of the Oxygen-Evolving Complex of Photosystem II as a Manifestation of Multimetallic Cooperativity. J. Chem. Theory Comput. 2019, 15, 2375–2391. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, S.; Shen, L.; Han, G.; Umena, Y.; Shen, J.-R.; Noguchi, T.; Mino, H. Formation of the High-Spin S2 State Related to the Extrinsic Proteins in the Oxygen Evolving Complex of Photosystem II. J. Phys. Chem. Lett. 2020, 11. [Google Scholar] [CrossRef]
- Shen, J.-R. The Structure of Photosystem II and the Mechanism of Water Oxidation in Photosynthesis. Annu. Rev. Plant Biol. 2015, 66, 23–48. [Google Scholar] [CrossRef] [PubMed]
- Cardona, T.; Rutherford, A.W. Evolution of Photochemical Reaction Centres: More Twists? Trends Plant Sci. 2019, 24, 1008–1021. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Nakagawa, M.; Ishikita, H. pKa of the ligand water molecules in the oxygen-evolving Mn4CaO5 cluster in photosystem II. Commun. Chem. 2020, 3, 1–7. [Google Scholar] [CrossRef]
- Suga, M.; Akita, F.; Hirata, K.; Ueno, G.; Murakami, H.; Nakajima, Y.; Shimizu, T.; Yamashita, K.; Yamamoto, M.; Ago, H.; et al. Native structure of photosystem II at 1.95 Å resolution viewed by femtosecond X-ray pulses. Nat. Cell Biol. 2015, 517, 99–103. [Google Scholar] [CrossRef]
- Umena, Y.; Kawakami, K.; Shen, J.-R.; Kamiya, N. Crystal Structure of Oxygen-Evolving Photosystem II at a Resolution of 1.9 Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef]
- Zouni, A.; Witt, H.-T.; Kern, J.; Fromme, P.; Krauss, N.; Saenger, W.; Orth, P.P. Crystal structure of photosystem II from Synechococcus elongatus at 3.8 Å resolution. Nat. Cell Biol. 2001, 409, 739–743. [Google Scholar] [CrossRef]
- Kamiya, N.; Shen, J.-R. Crystal structure of oxygen-evolving photosystem II from Thermosynechococcus vulcanus at 3.7-A resolution. Proc. Natl. Acad. Sci. USA 2003, 100, 98–103. [Google Scholar] [CrossRef]
- Guskov, A.; Kern, J.; Gabdulkhakov, A.; Broser, M.; Zouni, A.; Saenger, W. Cyanobacterial photosystem II at 2.9-Å resolution and the role of quinones, lipids, channels and chloride. Nat. Struct. Mol. Biol. 2009, 16, 334–342. [Google Scholar] [CrossRef]
- Ferreira, K.N.; Iverson, T.M.; Maghlaoui, K.; Barber, J.; Iwata, S. Architecture of the Photosynthetic Oxygen-Evolving Center. Science 2004, 303, 1831–1838. [Google Scholar] [CrossRef]
- Wei, X.; Su, X.; Cao, P.; Liu, X.; Chang, W.; Li, M.; Zhang, X.; Liu, Z. Structure of spinach photosystem II–LHCII supercomplex at 3.2 Å resolution. Nat. Cell Biol. 2016, 534, 69–74. [Google Scholar] [CrossRef]
- Ago, H.; Adachi, H.; Umena, Y.; Tashiro, T.; Kawakami, K.; Kamiya, N.; Tian, L.; Han, G.; Kuang, T.; Liu, Z.; et al. Novel Features of Eukaryotic Photosystem II Revealed by Its Crystal Structure Analysis from a Red Alga. J. Biol. Chem. 2016, 291, 5676–5687. [Google Scholar] [CrossRef]
- Nagao, R.; Kato, K.; Suzuki, T.; Ifuku, K.; Uchiyama, I.; Kashino, Y.; Dohmae, N.; Akimoto, S.; Shen, J.-R.; Miyazaki, N.; et al. Structural basis for energy harvesting and dissipation in a diatom PSII–FCPII supercomplex. Nat. Plants 2019, 5, 890–901. [Google Scholar] [CrossRef]
- Pi, X.; Zhao, S.; Wang, W.; Liu, D.; Xu, C.; Han, G.; Kuang, T.; Sui, S.-F.; Shen, J.-R. The pigment-protein network of a diatom photosystem II–light-harvesting antenna supercomplex. Science 2019, 365, eaax4406. [Google Scholar] [CrossRef]
- McEvoy, J.P.; Brudvig, G.W. Water-Splitting Chemistry of Photosystem II. Chem. Rev. 2006, 106, 4455–4483. [Google Scholar] [CrossRef]
- Diner, B.A.; Britt, R.D. The Redox-Active Tyrosines YZ and YD. In Photosystem II: The Light-Driven Water: Plastoquinone Oxidoreductase; Advances in Photosynthesis and Respiration; Wydrzynski, T.J., Satoh, K., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 22, pp. 207–233. [Google Scholar]
- Debus, R.J.; Barry, B.A.; Sithole, I.; Babcock, G.T.; McIntosh, L. Directed mutagenesis indicates that the donor to P 680+ in photosystem II is tyrosine-161 of the D1 polypeptide. Biochemistry 1988, 27, 9071–9074. [Google Scholar] [CrossRef]
- Metz, J.G.; Nixon, P.J.; Rögner, M.; Brudvig, G.W.; Diner, B.A. Directed alteration of the D1 polypeptide of photosystem II: Evidence that tyrosine-161 is the redox component, Z, connecting the oxygen-evolving complex to the primary electron donor, P680. Biochemistry 1989, 28, 6960–6969. [Google Scholar] [CrossRef]
- Dismukes, G.C.; Siderer, Y. Intermediates of a polynuclear manganese center involved in photosynthetic oxidation of water. Proc. Natl. Acad. Sci. USA 1981, 78, 274–278. [Google Scholar] [CrossRef]
- Brudvig, G.W.; Casey, J.L.; Sauer, K. The effect of temperature on the formation and decay of the multiline EPR signal species associated with photosynthetic oxygen evolution. Biochim. Biophys. Acta (BBA) Bioenerg. 1983, 723, 366–371. [Google Scholar] [CrossRef]
- Zimmermann, J.; Rutherford, A. EPR studies of the oxygen-evolving enzyme of Photosystem II. Biochim. Biophys. Acta (BBA) Bioenerg. 1984, 767, 160–167. [Google Scholar] [CrossRef]
- Kok, B.; Forbush, B.; McGloin, M. Cooperation of charges in photosynthetic O2 evolution-I. A linear four step mechanism. Photochem. Photobiol. 1970, 11, 457–475. [Google Scholar] [CrossRef]
- Bencini, A.; Gatteschi, D. Electron Paramagnetic Resonance of Exchange Coupled Systems. In Electron Paramagnetic Resonance of Exchange Coupled Systems; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Jin, L.; Smith, P.; Noble, C.J.; Stranger, R.; Hanson, G.R.; Pace, R.J. Electronic structure of the oxygen evolving complex in photosystem II, as revealed by 55Mn Davies ENDOR studies at 2.5 K. Phys. Chem. Chem. Phys. 2014, 16, 7799–7812. [Google Scholar] [CrossRef]
- Kurashige, Y.; Chan, G.K.-L.; Yanai, T. Entangled quantum electronic wavefunctions of the Mn4CaO5 cluster in photosystem II. Nat. Chem. 2013, 5, 660–666. [Google Scholar] [CrossRef]
- Asada, M.; Nagashima, H.; Koua, F.H.M.; Shen, J.-R.; Kawamori, A.; Mino, H. Electronic structure of S2 state of the oxygen-evolving complex of photosystem II studied by PELDOR. Biochim. Biophys. Acta (BBA) Bioenerg. 2013, 1827, 438–445. [Google Scholar] [CrossRef]
- Casey, J.L.; Sauer, K. EPR detection of a cryogenically photogenerated intermediate in photosynthetic oxygen evolution. Biochim. Biophys. Acta (BBA) Bioenerg. 1984, 767, 21–28. [Google Scholar] [CrossRef]
- Åhrling, K.A.; Pace, R.J.; Evans, M.C.W. The Catalytic Manganese Cluster: Implications from Spectroscopy. In Photosystem II: The Light-Driven Water: Plastoquinone Oxidoreductase; Advances in Photosynthesis and Respiration; Wydrzynski, T.J., Satoh, K., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 22, pp. 285–305. [Google Scholar]
- Boussac, A.; Girerd, J.-J.; Rutherford, A.W. Conversion of the Spin State of the Manganese Complex in Photosystem II Induced by Near-Infrared Light. Biochemistry 1996, 35, 6984–6989. [Google Scholar] [CrossRef]
- Haddy, A.; Dunham, W.; Sands, R.H.; Aasa, R. Multifrequency EPR investigations into the origin of the S2-state signal at g = 4 of the O2-evolving complex. Biochim. Biophys. Acta (BBA) Bioenerg. 1992, 1099, 25–34. [Google Scholar] [CrossRef]
- Åhrling, K.A.; Smith, P.J.; Pace, R.J. Nature of the Mn Centers in Photosystem II. Modeling and Behavior of the g = 4 Resonances and Related Signals. J. Am. Chem. Soc. 1998, 120, 13202–13214. [Google Scholar] [CrossRef]
- Carrington, A.; McLachlan, A.D. Introduction to Magnetic Resonance: With Applications to Chemistry and Chemical Physics; Chapman and Hall: London, UK, 1979. [Google Scholar]
- Castner, T., Jr.; Newell, G.S.; Holton, W.C.; Slichter, C.P. Note on the Paramagnetic Resonance of Iron in Glass. J. Chem. Phys. 1960, 32, 668–673. [Google Scholar] [CrossRef]
- Bricker, T.M.; Pakrasi, H.B.; Sherman, L.A. Characterization of a spinach photosystem II core preparation isolated by a simplified method. Arch. Biochem. Biophys. 1985, 237, 170–176. [Google Scholar] [CrossRef]
- Smith, P.J.; Åhrling, K.A.; Pace, R.J. Nature of the S2state electron paramagnetic resonance signals from the oxygen-evolving complex of photosystem II: Q-band and oriented X-band studies. J. Chem. Soc. Faraday Trans. 1993, 89, 2863–2868. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J.; Nieveen, M.C.; Van De Meent, E.J.; Dekker, J.P.; Van Gorkom, H.J. Rapid and simple isolation of pure photosystem II core and reaction center particles from spinach. Photosynth. Res. 1991, 28, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.J.; Peterson, S.; Masters, V.M.; Wydrzynski, T.; Styring, S.; Krausz, E.; Pace, R.J. Magneto-Optical Measurements of the Pigments in Fully Active Photosystem II Core Complexes from Plants. Biochemistry 2002, 41, 1981–1989. [Google Scholar] [CrossRef]
- Cooper, S.R.; Calvin, M. Mixed valence interactions in Di-μ-Oxo bridged manganese complexes. J. Am. Chem. Soc. 1977, 99, 6623–6630. [Google Scholar] [CrossRef]
- Gatt, P.; Petrie, S.; Stranger, R.; Pace, R.J. Rationalizing the 1.9 Å Crystal Structure of Photosystem II-A Remarkable Jahn-Teller Balancing Act Induced by a Single Proton Transfer. Angew. Chem. Int. Ed. 2012, 51, 12025–12028. [Google Scholar] [CrossRef]
- Baituti, B.; Akofang, L. The Two Alternative Oxidation State Assignments of Manganese Ions: What S2 CW-EPR Multiline (ML) Signal Simulations Reveal? Appl. Magn. Reson. 2020, 51, 389–407. [Google Scholar] [CrossRef]
- Baituti, B. Computational studies of the Mn4/Ca cluster in photosystem II. J. Theor. Comput. Chem. 2018, 17, 1850007. [Google Scholar] [CrossRef]
- Baituti, B. What the multiline signal (MLS) simulation data with average of weighted computations reveal about the Mn hyperfine interactions and oxidation states of the manganese cluster in OEC? Hyperfine Interact. 2017, 238, 1–14. [Google Scholar] [CrossRef]
- Terrett, R.; Pace, R.J.; Petrie, S.; Stranger, R. What computational chemistry and magnetic resonance reveal concerning the oxygen evolving centre in Photosystem II. J. Inorg. Biochem. 2016, 162, 178–189. [Google Scholar] [CrossRef]
- Petrie, S.; Terrett, R.; Stranger, R.; Pace, R.J. Rationalizing the Geometries of the Water Oxidising Complex in the Atomic Resolution, Nominal S3 State Crystal Structures of Photosystem II. ChemPhysChem 2020, 21, 785–801. [Google Scholar] [CrossRef]
- Petrie, S.; Stranger, R.; Pace, R.J. Explaining the Different Geometries of the Water Oxidising Complex in the Nominal S3 State Crystal Structures of Photosystem II at 2.25 Å and 2.35 Å. ChemPhysChem 2018, 19, 3296–3309. [Google Scholar] [CrossRef]
- Petrie, S.; Stranger, R.; Pace, R.J. What Mn Kβ Spectroscopy reveals concerning the oxidation states of the Mn cluster in photosystem II. Phys. Chem. Chem. Phys. 2017, 19, 27682–27693. [Google Scholar] [CrossRef]
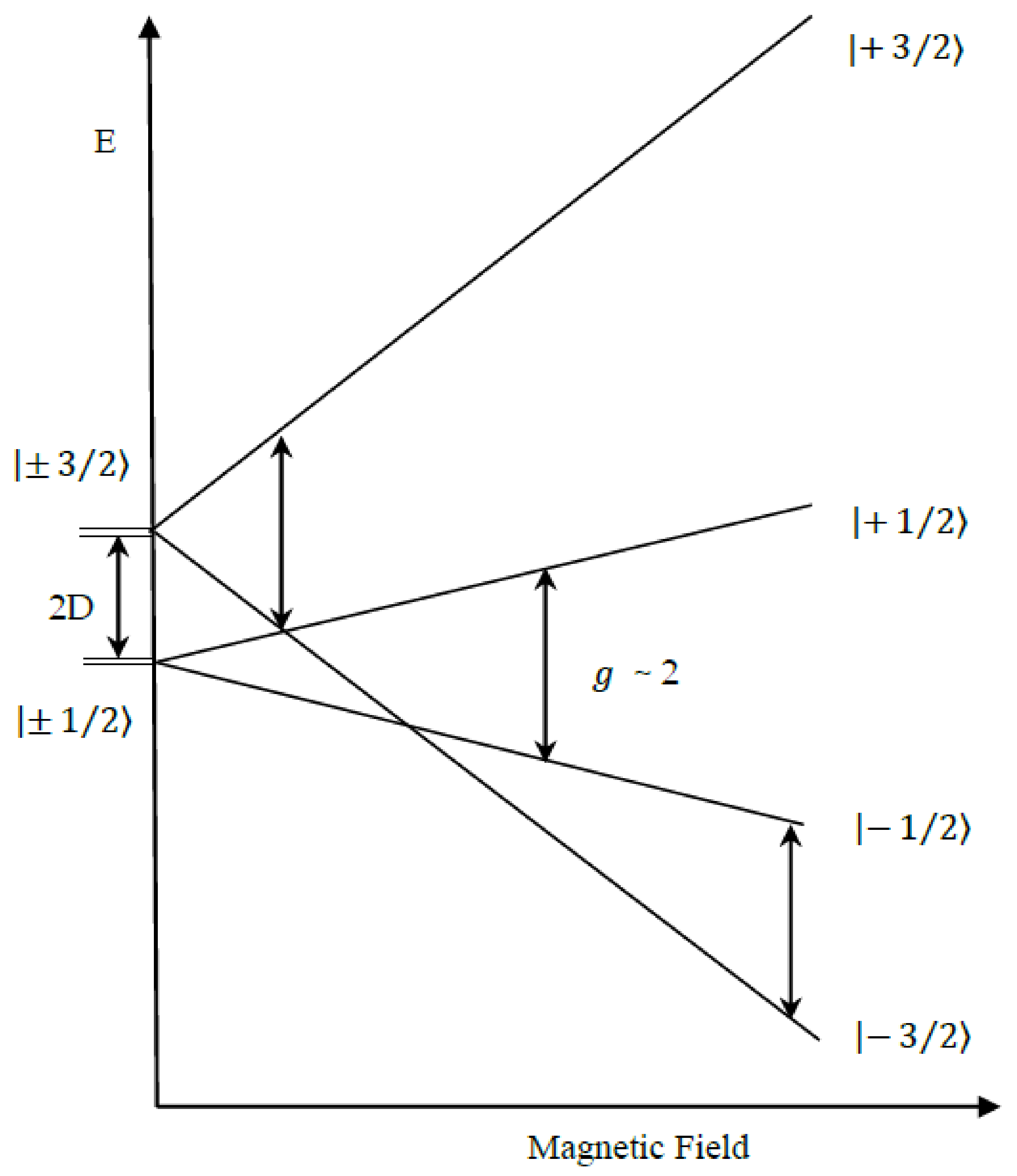
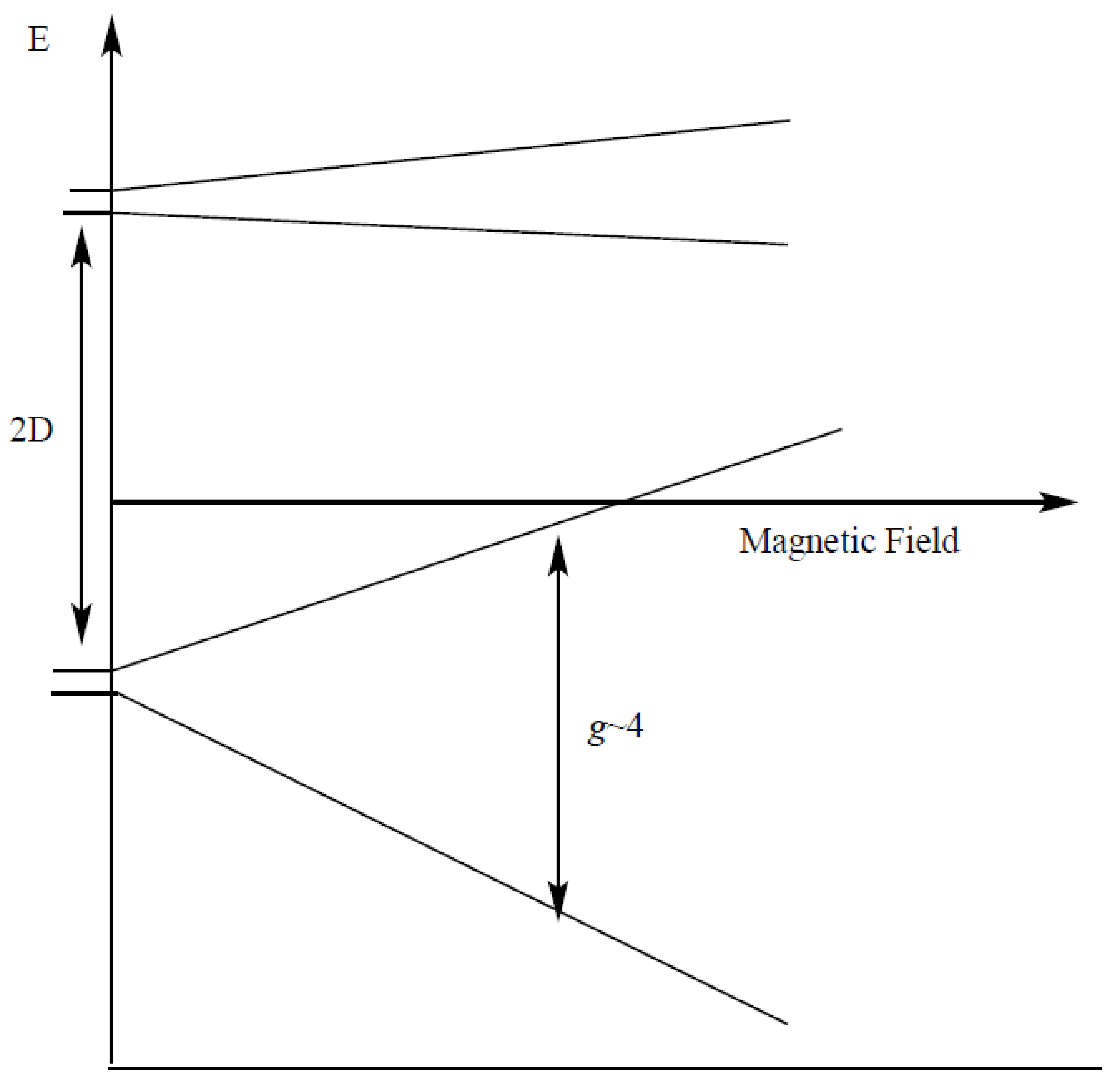
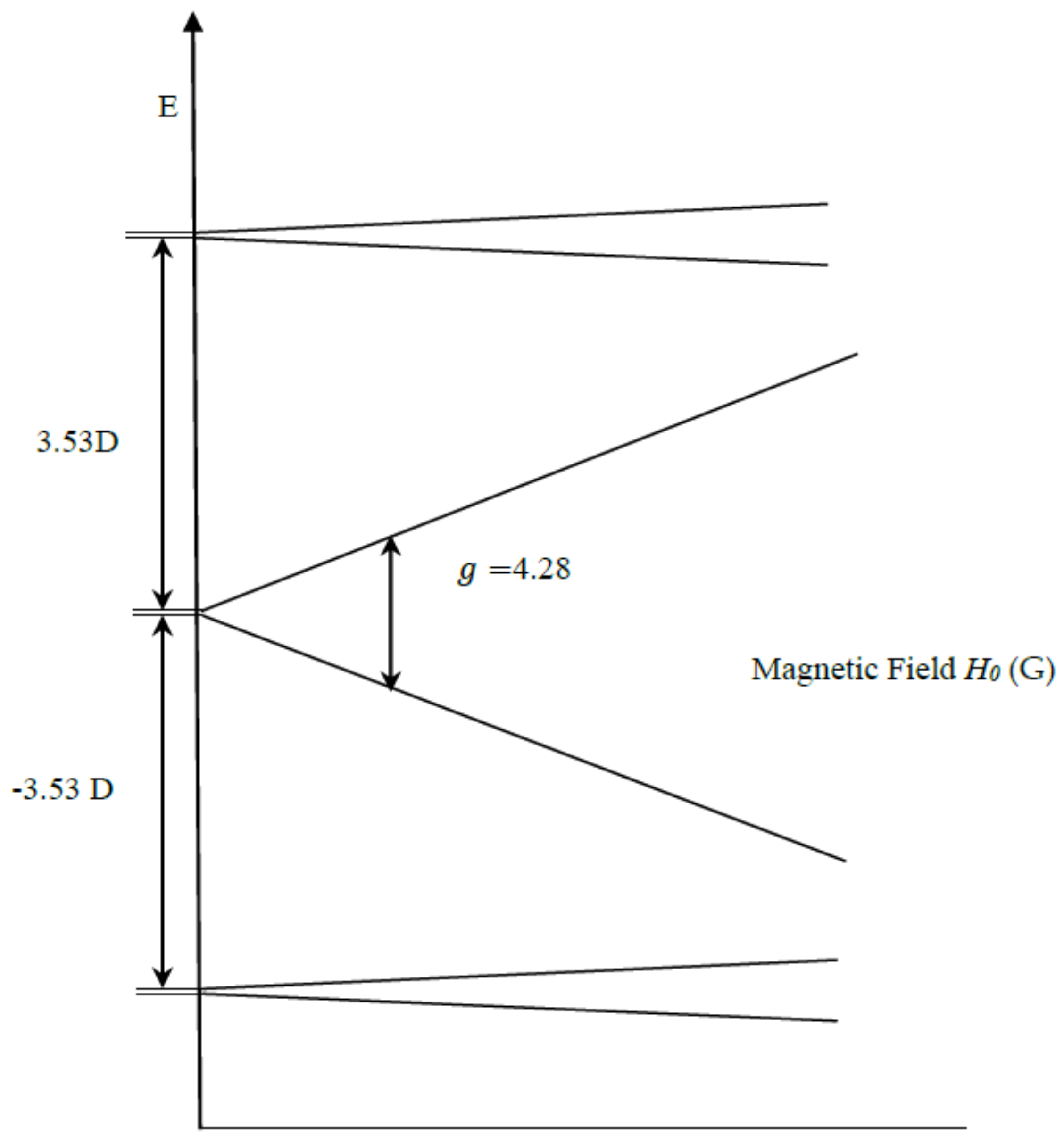
| gx, gy, gz | D (cm−1) | E/D | Mn1, Mn2 (MHz) | Linewidth (Gauss) | Spin | |
|---|---|---|---|---|---|---|
| g4.1 signal | 2.18, 2.16, 1.98 | * 0.45 | * 0.25 | 194.2, 45.2 | 140 | 5/2 |
| g4.1 signal | 2.18, 2.16, 1.98 | 0.3 | 0.3 | 194.2, 45.2 | 140 | 3/2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baituti, B.; Odisitse, S. A Computational Study of the S2 State in the Oxygen-Evolving Complex of Photosystem II by Electron Paramagnetic Resonance Spectroscopy. Molecules 2021, 26, 2699. https://doi.org/10.3390/molecules26092699
Baituti B, Odisitse S. A Computational Study of the S2 State in the Oxygen-Evolving Complex of Photosystem II by Electron Paramagnetic Resonance Spectroscopy. Molecules. 2021; 26(9):2699. https://doi.org/10.3390/molecules26092699
Chicago/Turabian StyleBaituti, Bernard, and Sebusi Odisitse. 2021. "A Computational Study of the S2 State in the Oxygen-Evolving Complex of Photosystem II by Electron Paramagnetic Resonance Spectroscopy" Molecules 26, no. 9: 2699. https://doi.org/10.3390/molecules26092699
APA StyleBaituti, B., & Odisitse, S. (2021). A Computational Study of the S2 State in the Oxygen-Evolving Complex of Photosystem II by Electron Paramagnetic Resonance Spectroscopy. Molecules, 26(9), 2699. https://doi.org/10.3390/molecules26092699






