Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars
Abstract
1. Introduction
2. Simulation Method and Process
2.1. Main Variables
2.2. Main Process of Simulations
3. Results and Analysis of Simulations
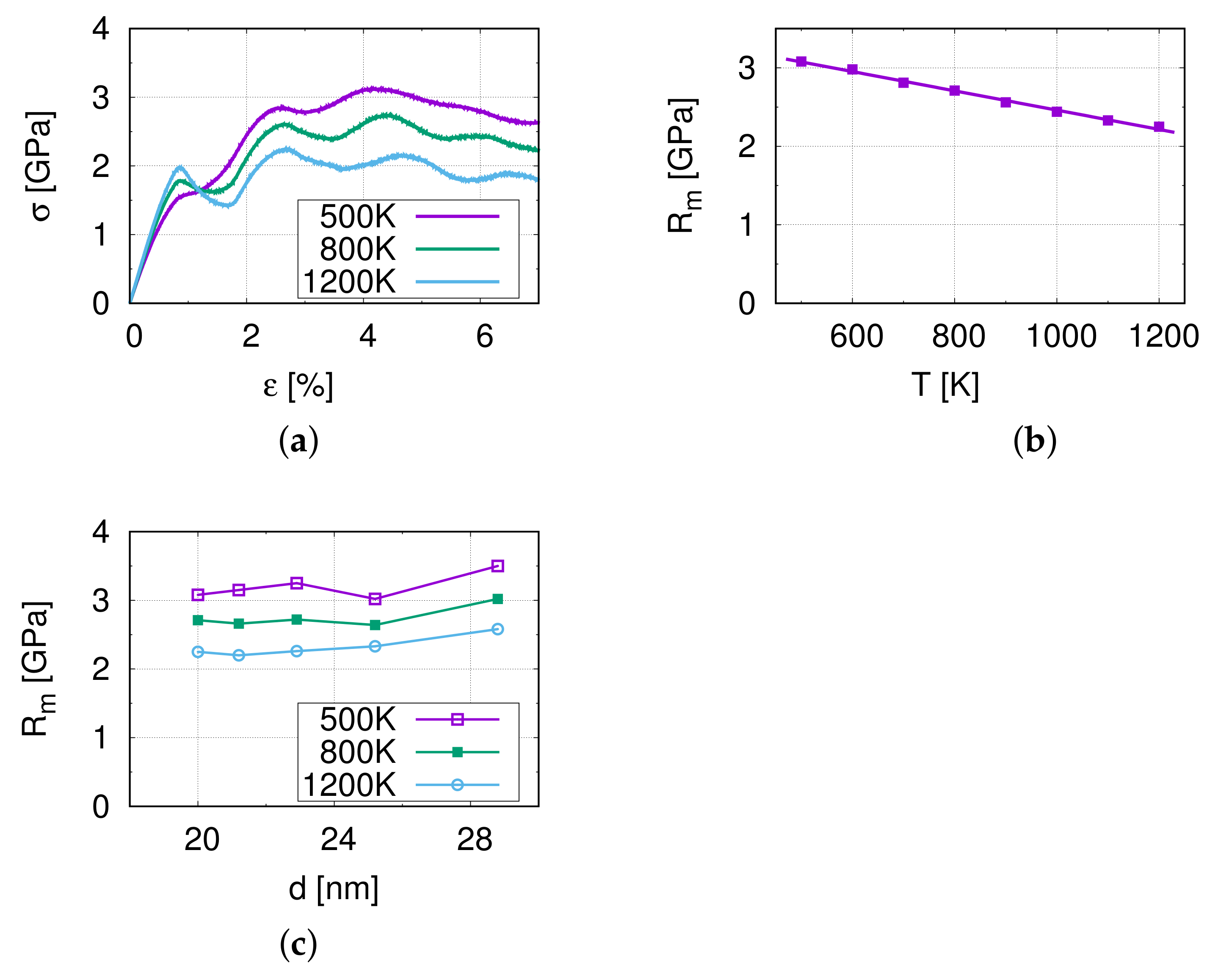
3.1. Nano-Tensile Test Simulations
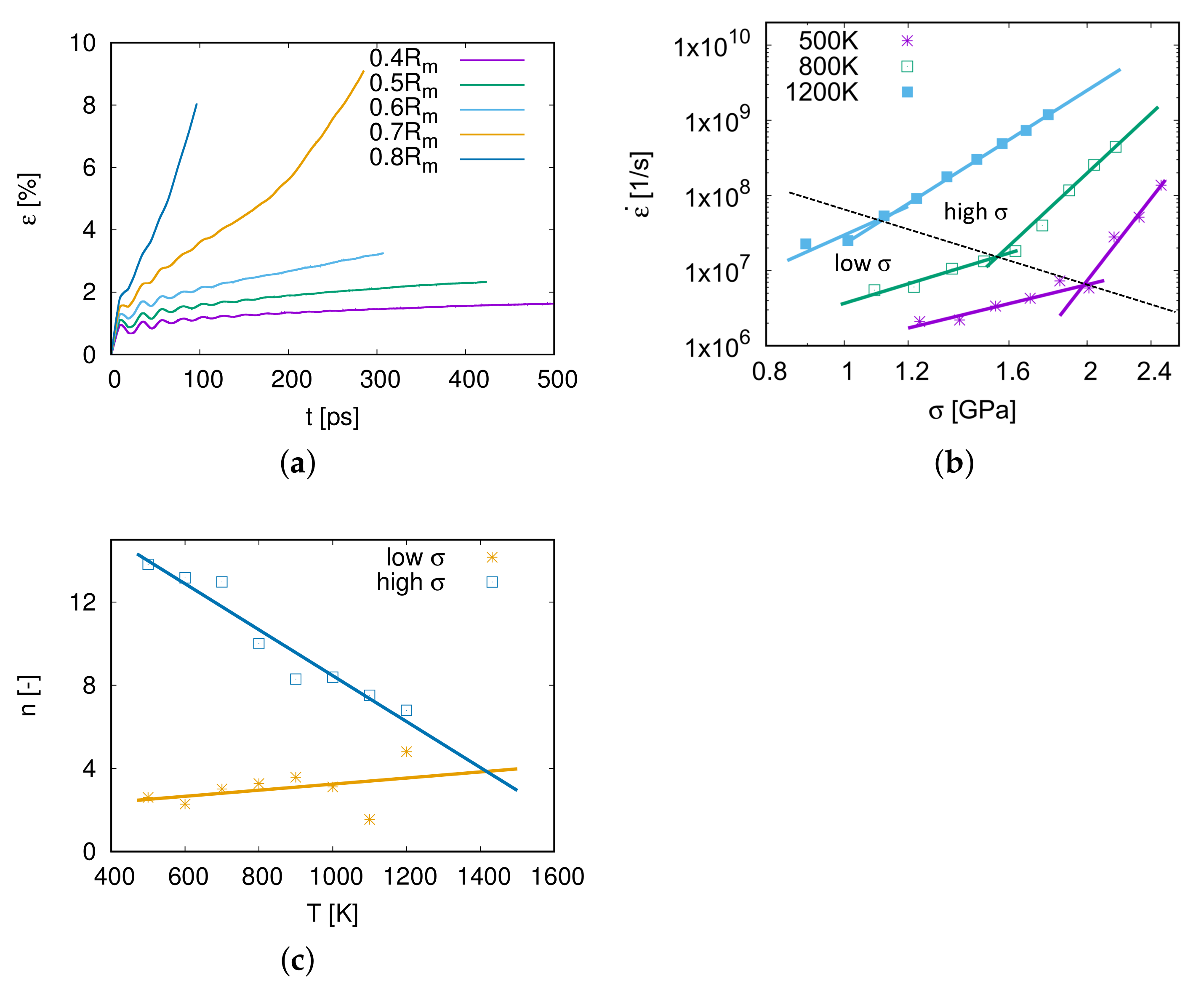
3.2. Nano-Creep Simulations
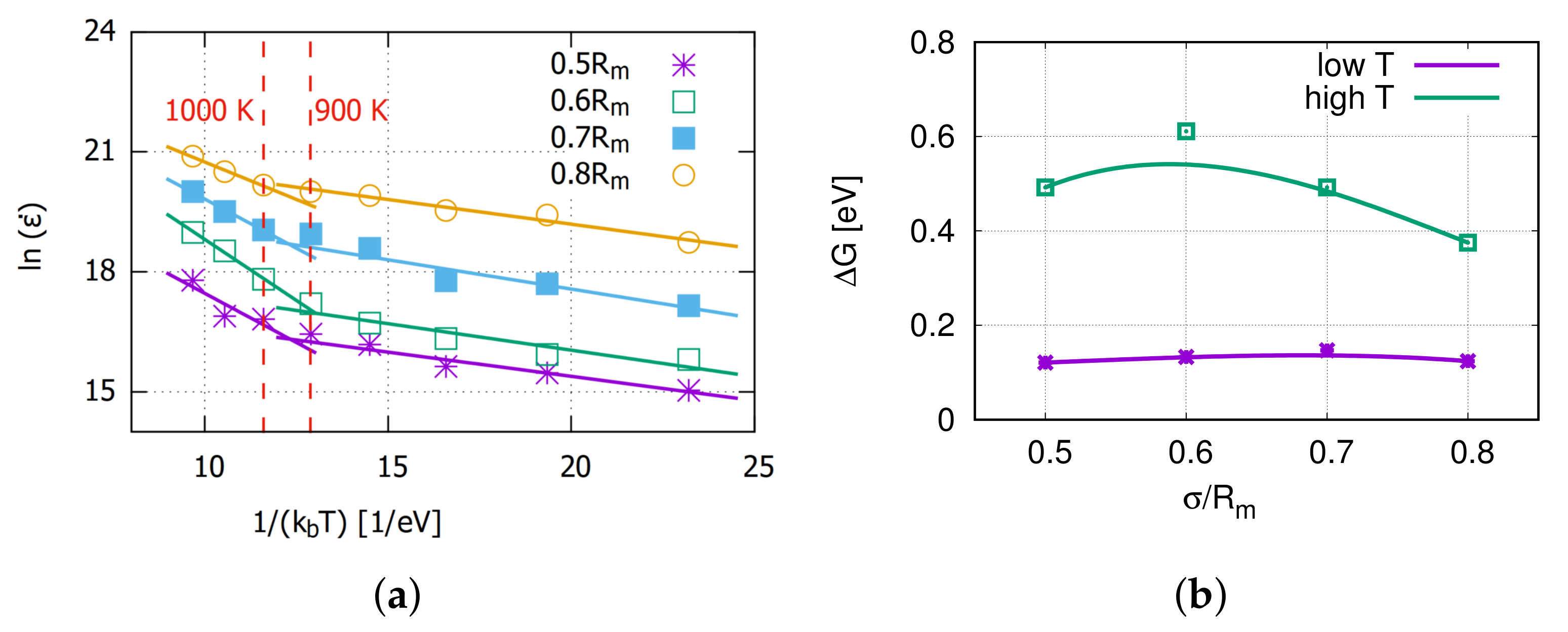
3.3. Thermally Activated Mechanisms
4. Discussion on Creep Mechanisms
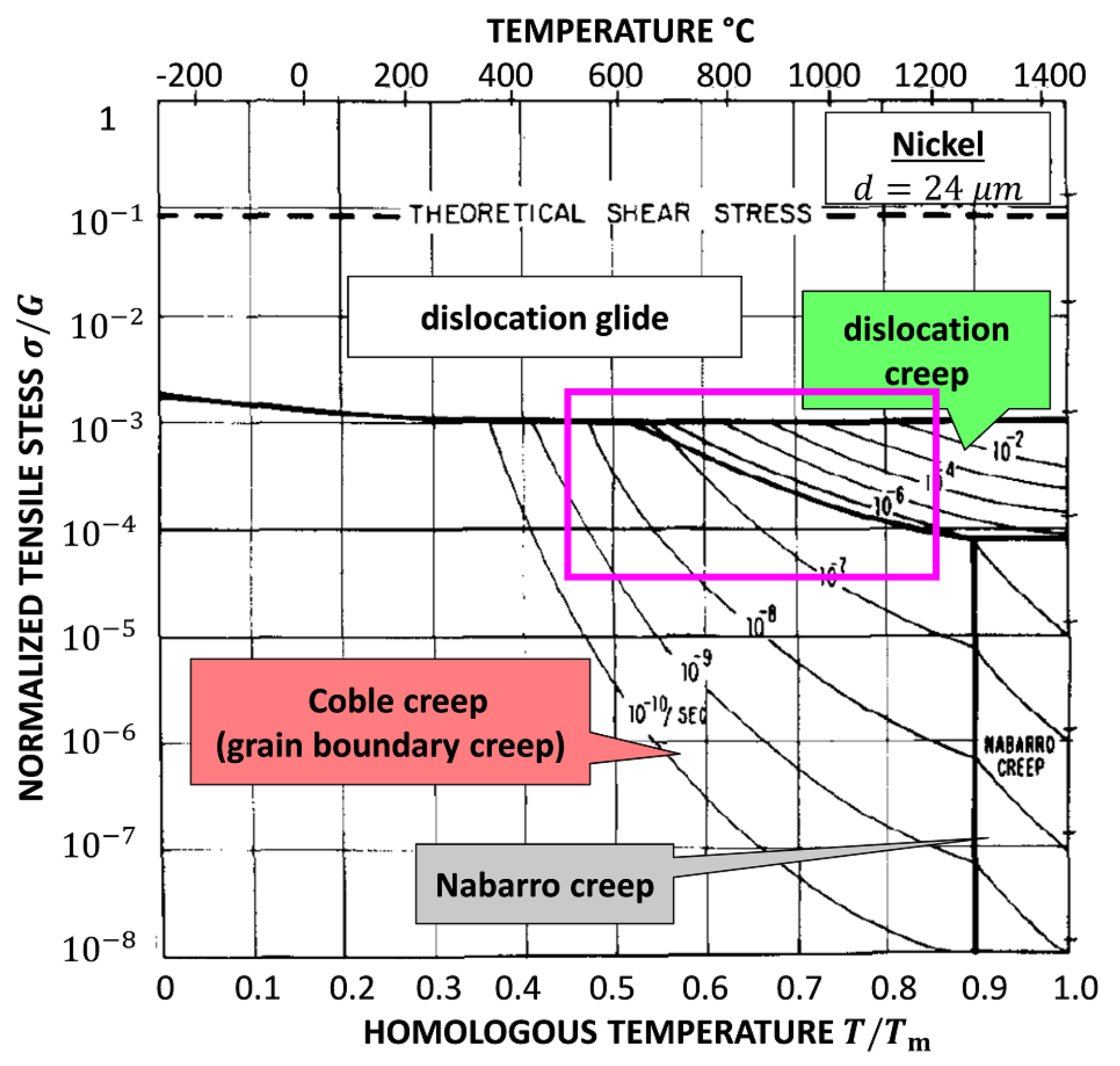
4.1. Deformation Diagram for NC Ni
4.2. Creep through Dislocations
4.3. Creep Through Grain Boundary Sliding
4.4. Grain Size Effect
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hahn, E.N.; Meyers, M.A. Grain-size dependent mechanical behavior of nanocrystalline metals. Mater. Sci. Eng. A 2015, 646, 101–134. [Google Scholar] [CrossRef]
- Wu, Z.; Sandlöbes, S.; Wang, Y.; Gibson, J.S.L.; Korte-Kerzel, S. Creep behaviour of eutectic Zn-Al-Cu-Mg alloys. Mater. Sci. Eng. A 2018, 724, 80–94. [Google Scholar] [CrossRef]
- Wu, J.; Tsai, W.; Huang, J.; Hsieh, C.; Huang, G.R. Sample size and orientation effects of single crystal aluminum. Mater. Sci. Eng. A 2016, 662, 296–302. [Google Scholar] [CrossRef]
- Carlton, C.; Ferreira, P. What is behind the inverse Hall–Petch effect in nanocrystalline materials? Acta Mater. 2007, 55, 3749–3756. [Google Scholar] [CrossRef]
- Mukherjee, A.K.; Bird, J.E.; Dorn, J.E. Experimental Correlations for High-Temperature Creep; Technical Report; University of California: Berkeley, CA, USA, 1968. [Google Scholar]
- Coble, R. A model for boundary diffusion controlled creep in polycrystalline materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
- Cahn, R.; Haasen, P.; Kramer, E. Plastic Deformation and Fracture of Materials. In Materials Science and Technology; Mughrabi, H., Ed.; WILEY–VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 1993; Volume 6. [Google Scholar]
- Ashby, M. Boundary defects, and atomistic aspects of boundary sliding and diffusional creep. Surf. Sci. 1972, 31, 498–542. [Google Scholar] [CrossRef]
- Keblinski, P.; Wolf, D.; Gleiter, H. Molecular-dynamics simulation of grain-boundary diffusion creep. Interface Sci. 1998, 6, 205–212. [Google Scholar] [CrossRef]
- Herring, C. Diffusional viscosity of a polycrystalline solid. J. Appl. Phys. 1950, 21, 437–445. [Google Scholar] [CrossRef]
- Berry, J.; Rottler, J.; Sinclair, C.W.; Provatas, N. Atomistic study of diffusion-mediated plasticity and creep using phase field crystal methods. Phys. Rev. B 2015, 92, 134103. [Google Scholar] [CrossRef]
- Nie, K.; Wu, W.P.; Zhang, X.L.; Yang, S.M. Molecular dynamics study on the grain size, temperature, and stress dependence of creep behavior in nanocrystalline nickel. J. Mater. Sci. 2017, 52, 2180–2191. [Google Scholar] [CrossRef]
- Jiao, S.; Kulkarni, Y. Molecular dynamics study of creep mechanisms in nanotwinned metals. Comput. Mater. Sci. 2015, 110, 254–260. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ishii, A.; Ogata, S. Transition of creep mechanism in nanocrystalline metals. Phys. Rev. B 2011, 84, 224102. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ishii, A.; Ogata, S. Grain size dependence of creep in nanocrystalline copper by molecular dynamics. Mater. Trans. 2012, 53, 1110171491. [Google Scholar] [CrossRef]
- Ashby, M.F. A first report on deformation-mechanism maps. Acta Metall. 1972, 20, 887–897. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Caro, A. Plastic behavior of nanophase Ni: A molecular dynamics computer simulation. Appl. Phys. Lett. 1997, 71, 1652–1654. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Caro, A. Plastic behavior of nanophase metals studied by molecular dynamics. Phys. Rev. B 1998, 58, 11246. [Google Scholar] [CrossRef]
- Reddy, K.V.; Meraj, M.; Pal, S. Mechanistic study of bending creep behaviour of bicrystal nanobeam. Comput. Mater. Sci. 2017, 136, 36–43. [Google Scholar] [CrossRef]
- Meraj, M.; Yedla, N.; Pal, S. The effect of porosity and void on creep behavior of ultra-fine grained nano crystalline nickel. Mater. Lett. 2016, 169, 265–268. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.; Mukherjee, A.; Gleiter, H. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nat. Mater. 2004, 3, 43–47. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Salazar, M.; Phillpot, S.; Gleiter, H. Length-scale effects in the nucleation of extended dislocations in nanocrystalline Al by molecular-dynamics simulation. Acta Mater. 2001, 49, 2713–2722. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.R.; Mukherjee, A.K.; Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nat. Mater. 2002, 1, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Yamakov, V.; Wolf, D.; Phillpot, S.; Gleiter, H. Grain-boundary diffusion creep in nanocrystalline palladium by molecular-dynamics simulation. Acta Mater. 2002, 50, 61–73. [Google Scholar] [CrossRef]
- Haslam, A.; Yamakov, V.; Moldovan, D.; Wolf, D.; Phillpot, S.; Gleiter, H. Effects of grain growth on grain-boundary diffusion creep by molecular-dynamics simulation. Acta Mater. 2004, 52, 1971–1987. [Google Scholar] [CrossRef]
- Pal, S.; Meraj, M.; Deng, C. Effect of Zr addition on creep properties of ultra-fine grained nanocrystalline Ni studied by molecular dynamics simulations. Comput. Mater. Sci. 2017, 126, 382–392. [Google Scholar] [CrossRef]
- Pinky, S.K. Molecular Dynamics Study of Creep Deformation in Nickel-Based Superalloy. Master’s Thesis, Missouri State University, Springfield, MO, USA, 2019. [Google Scholar]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Bonny, G.; Pasianot, R.C.; Castin, N.; Malerba, L. Ternary Fe–Cu–Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing. Philos. Mag. 2009, 89, 3531–3546. [Google Scholar] [CrossRef]
- Voter, A.F.; Chen, S.P. Accurate interatomic potentials for Ni, Al and Ni3Al. MRS Online Proc. Libr. OPL 1986, 82, 175. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Aidhy, D.S.; Lu, C.; Jin, K.; Bei, H.; Zhang, Y.; Wang, L.; Weber, W.J. Point defect evolution in Ni, NiFe and NiCr alloys from atomistic simulations and irradiation experiments. Acta Mater. 2015, 99, 69–76. [Google Scholar] [CrossRef]
- Anand, T.J.S. Nickel as an alternative automotive body material. J. Mech. Eng. 2012, 2, 187–197. [Google Scholar]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]



| Temperature | Bulk Modulus | Poisson’s Ratio | Young’s Modulus | Shear Modulus |
|---|---|---|---|---|
| T [K] | K [GPa] | [-] | E [GPa] | G [GPa] |
| 500 | 162.754 | 0.379 | 223.330 | 95.427 |
| 800 | 150.985 | 0.379 | 207.814 | 88.310 |
| 1200 | 135.164 | 0.381 | 189.529 | 77.88 |
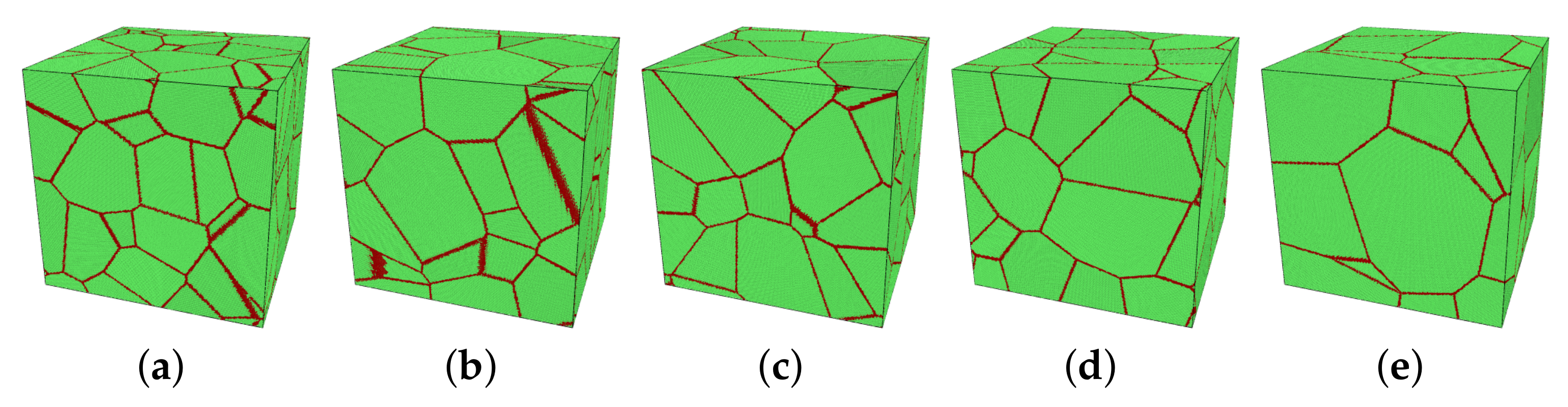
| Model | Number of Grains N | Averaged Grain Size d [nm] |
|---|---|---|
| M1 | 30 | 19.96 |
| M2 | 25 | 21.22 |
| M3 | 20 | 22.85 |
| M4 | 15 | 25.15 |
| M5 | 10 | 28.79 |
| 500 K | 600 K | 700 K | 800 K | 900 K | 1000 K | 1100 K | 1200 K | |
|---|---|---|---|---|---|---|---|---|
| low | 2.6 | 2.3 | 3.0 | 3.3 | 3.6 | 3.1 | 1.5 | 4.8 |
| high | 13.8 | 13.2 | 13.0 | 10.0 | 8.3 | 8.4 | 7.5 | 6.8 |
| Temperature [K] | 800 | 1200 |
| stress level | 0.65 | 0.4 |
| stress [GPa] | 1.76 | 0.90 |
| creep rate [] | ||
| stress exponent n | 10.0 | 4.8 |
| stacking fault ratio at 100 ps |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Binkele, P.; Verestek, W.; Schmauder, S. Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars. Molecules 2021, 26, 2606. https://doi.org/10.3390/molecules26092606
Xu X, Binkele P, Verestek W, Schmauder S. Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars. Molecules. 2021; 26(9):2606. https://doi.org/10.3390/molecules26092606
Chicago/Turabian StyleXu, Xiang, Peter Binkele, Wolfgang Verestek, and Siegfried Schmauder. 2021. "Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars" Molecules 26, no. 9: 2606. https://doi.org/10.3390/molecules26092606
APA StyleXu, X., Binkele, P., Verestek, W., & Schmauder, S. (2021). Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars. Molecules, 26(9), 2606. https://doi.org/10.3390/molecules26092606







