Integrating Rigidity Analysis into the Exploration of Protein Conformational Pathways Using RRT* and MC
Abstract
1. Introduction
1.1. RRT, RRT*, and Adaptive Sampling
- Create a random new sample (a new molecular conformation).
- Find ’s nearest neighbor () on the tree.
- Try to connect and by an edge. To do this, we incrementally rotate the neighbor’s relevant backbone dihedral angles in the direction of the new conformation.
- Stop when you reach an obstacle (a high energy barrier) or when you reach the newly created sample. The stopping point is .
- Add to the tree with as its parent.
- Stop when you reach an RMSD threshold distance from the goal or when the maximum number of iterations was reached.
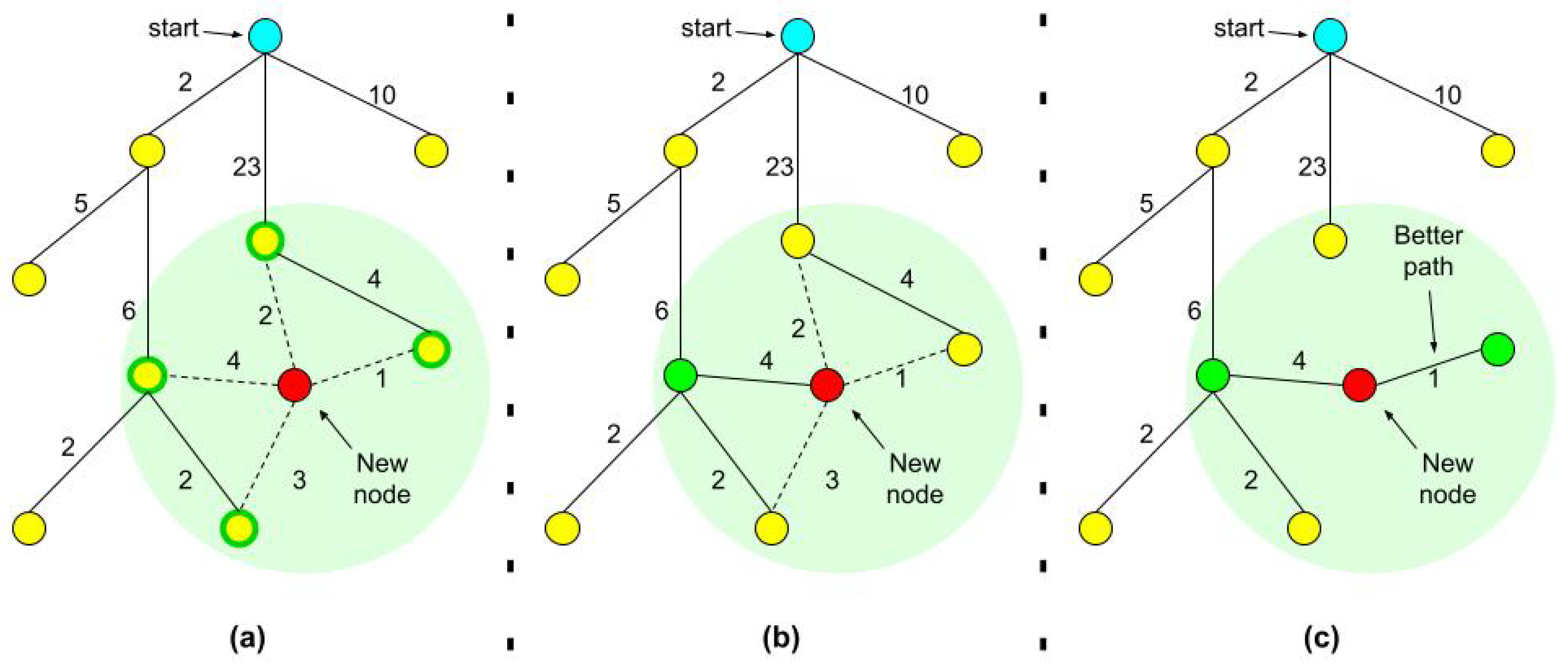
- For every node we also record the tree distance from the root. After finding the nearest neighbor on the tree, we examine the neighborhood of the new node in a fixed radius. If there is a node with a cheaper overall cost, it becomes the node’s parent instead of the original nearest neighbor.
- After adding the new node to its cheapest neighbor, the paths are rewired: The neighbors are checked if being rewired to the newly added vertex will decrease their overall cost.
- If the cost indeed decreases, the neighbor is rewired to the newly added vertex. This step makes the path smoother and less jagged looking.
1.2. Rigidity Analysis
1.3. Our Previous Work
1.4. This Contribution
2. Materials and Methods
2.1. Description of Algorithm
2.2. Integrating Rigidity Analysis
- We generate the start conformation’s rigid clusters of atoms, using a specified threshold for the minimum number of atoms per rigid cluster.
- The flexible residues are then produced using the rigid clusters extracted from the previous step.
- The list of flexible residues of the start conformation is given to the algorithm to be used as candidate residues for perturbation of their and dihedral angles.
2.3. Using the Kinari Software
2.4. Implementation Details
3. Results
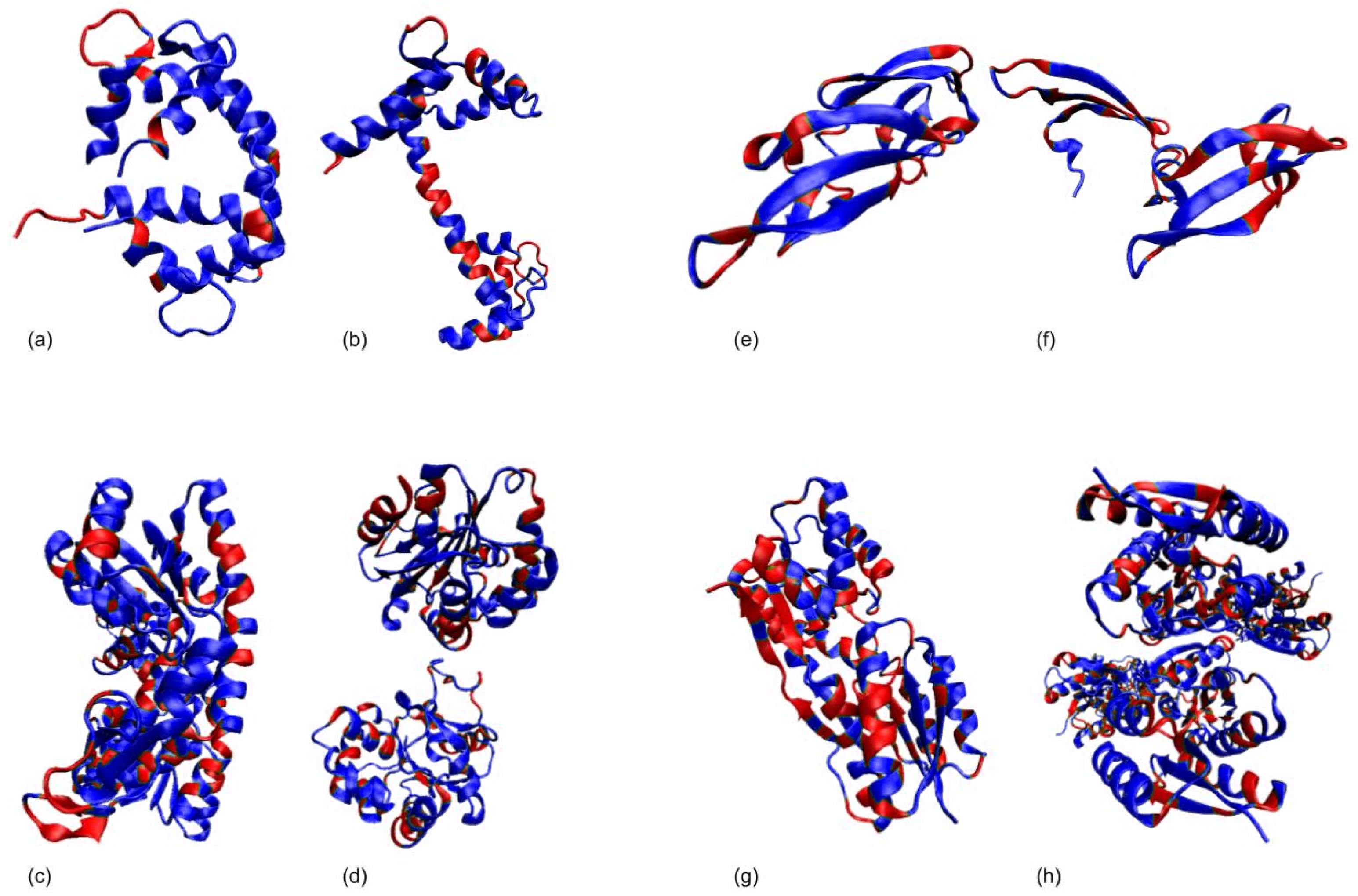
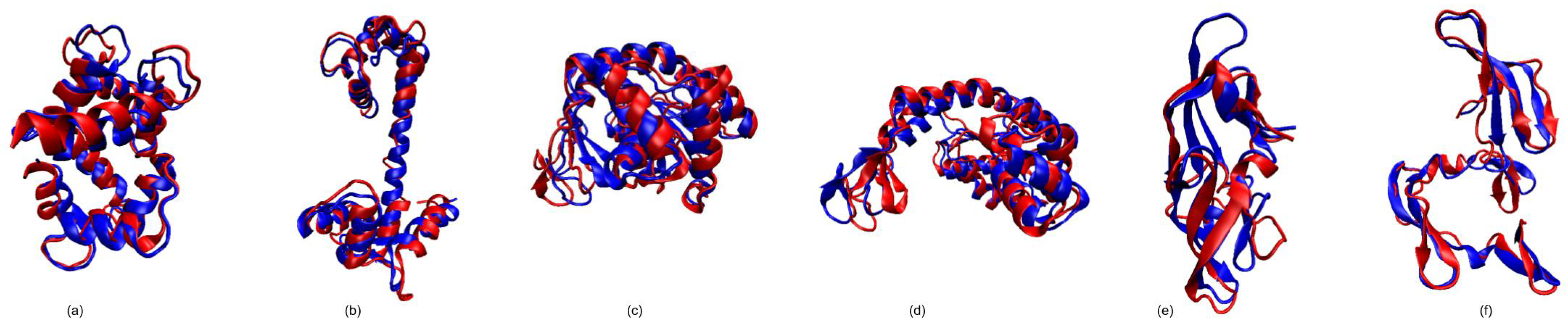
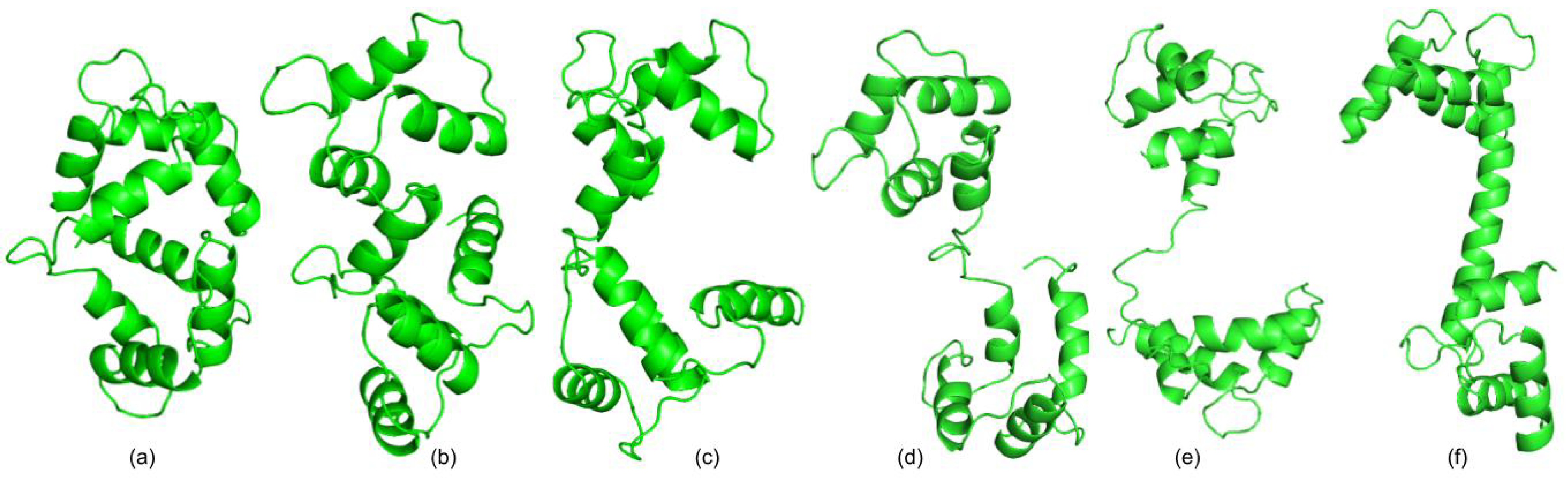
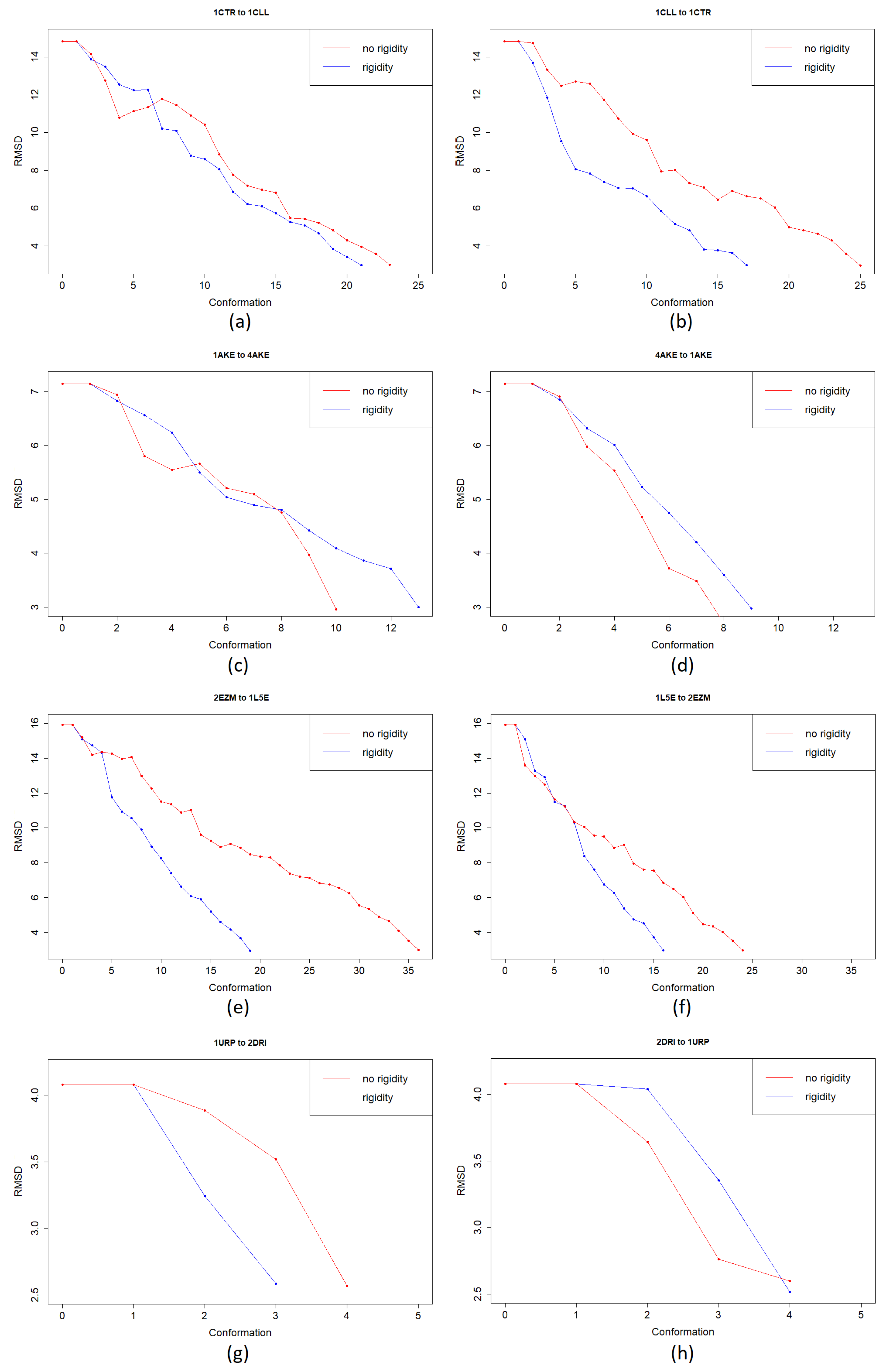
3.1. Test Cases
3.1.1. Calmodulin (CaM)
3.1.2. Adenylate Kinase (AdK)
3.1.3. Cyanovirin-N (CV-N)
3.1.4. Ribose Binding Protein (RBP)
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| RRT | Rapidly-Exploring Random Trees |
| CaM | Calmodulin |
| AdK | Adenylate Kinase |
| CVN | Cyanovirin-N |
| RBP | Ribose-binding Protein |
| MD | Molecular Dynamics |
References
- Frappier, V.; Chartier, M.; Najmanovich, R.J. ENCoM server: Exploring protein conformational space and the effect of mutations on protein function and stability. Nucleic Acids Res. 2015, 43, W395–W400. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, Y.; Shen, W.; Zhong, W. Fluorescamine Labeling for Assessment of Protein Conformational Change and Binding Affinity in Protein–Nanoparticle Interaction. Anal. Chem. 2017, 89, 12160–12167. [Google Scholar] [CrossRef] [PubMed]
- Mycroft-West, C.; Su, D.; Elli, S.; Li, Y.; Guimond, S.; Miller, G.; Turnbull, J.; Yates, E.; Guerrini, M.; Fernig, D.; et al. The 2019 coronavirus (SARS-CoV-2) surface protein (Spike) S1 Receptor Binding Domain undergoes conformational change upon heparin binding. bioRxiv 2020. [Google Scholar] [CrossRef]
- Ghosh, A.; Elber, R.; Scheraga, H.A. An atomically detailed study of the folding pathways of protein A with the stochastic difference equation. Proc. Natl. Acad. Sci. USA 2002, 99, 10394–10398. [Google Scholar] [CrossRef]
- Case, D.; Cheatham, T.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Brokaw, J.B.; Chu, J.W. On the Roles of Substrate Binding and Hinge Unfolding in Conformational Changes of Adenylate Kinase. Biophys. J. 2010, 99, 3420–3429. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhu, W. Zinc ion-induced conformational changes in new Delphi metallo-β-lactamase 1 probed by molecular dynamics simulations and umbrella sampling. Phys. Chem. Chem. Phys. 2017, 19, 3067–3075. [Google Scholar] [CrossRef]
- Zhang, Z.; Ehmann, U.; Zacharias, M. Monte Carlo replica-exchange based ensemble docking of protein conformations. Proteins Struct. Funct. Bioinform. 2017, 85, 924–937. [Google Scholar] [CrossRef]
- Karagöz, G.E.; Acosta-Alvear, D.; Nguyen, H.T.; Lee, C.P.; Chu, F.; Walter, P. An unfolded protein-induced conformational switch activates mammalian IRE1. Elife 2017, 6, e30700. [Google Scholar] [CrossRef]
- Guzman, H.V.; Tretyakov, N.; Kobayashi, H.; Fogarty, A.C.; Kreis, K.; Krajniak, J.; Junghans, C.; Kremer, K.; Stuehn, T. ESPResSo++ 2.0: Advanced methods for multiscale molecular simulation. Comput. Phys. Commun. 2019, 238, 66–76. [Google Scholar] [CrossRef]
- Schroeder, G.; Brunger, A.T.; Levitt, M. Combining Efficient Conformational Sampling with a Deformable Elastic Network Model Facilitates Structure Refinement at Low Resolution. Structure 2007, 15, 1630–1641. [Google Scholar] [CrossRef]
- Bauer, J.A.; Pavlović, J.; Bauerová-Hlinková, V. Normal Mode Analysis as a Routine Part of a Structural Investigation. Molecules 2019, 24, 3293. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Feng, Y.; Yang, L.; Kloczkowski, A.; Jernigan, R. The energy profiles of atomic conformational transition intermediates of adenylate kinase. Proteins 2009, 77, 551–558. [Google Scholar] [CrossRef]
- Hu, G.; Di Paola, L.; Liang, Z.; Giuliani, A. Comparative Study of Elastic Network Model and Protein Contact Network for Protein Complexes: The Hemoglobin Case. BioMed Res. Int. 2017, 2017, 2483264. [Google Scholar] [CrossRef]
- Guieysse, D.; Cortes, J.; Remaud-Simeon, M.; Simeon, T.; Ruiz de Angulo, V.; Tran, V. A path planning approach for computing large-amplitude motions of flexible molecules. Bioinformatics 2005, 21, 116–125. [Google Scholar] [CrossRef]
- Haspel, N.; Luo, D.; González, E. Detecting intermediate protein conformations using algebraic topology. BMC Bioinform. 2017, 18, 502. [Google Scholar] [CrossRef]
- Raveh, B.; Enosh, A.; Furman-Schueler, O.; Halperin, D. Rapid sampling of molecular motions with prior information constraints. PLoS Comp. Biol. 2009, 5, e1000295. [Google Scholar] [CrossRef]
- Al-Bluwi, I.; Vaisset, M.; Siméon, T.; Cortés, J. Modeling protein conformational transitions by a combination of coarse-grained normal mode analysis and robotics-inspired methods. BMC Struct. Biol. 2013, 13, S2. [Google Scholar] [CrossRef]
- Haspel, N.; Moll, M.; Baker, M.; Chiu, W.; Kavraki, L.E. Tracing Conformational Changes in Proteins. BMC Struct. Biol. 2010, 10, 1–11. [Google Scholar] [CrossRef]
- Molloy, K.; Shehu, A. Elucidating the ensemble of functionally-relevant transitions in protein systems with a robotics-inspired method. BMC Struct. Biol. 2013, 13, S8. [Google Scholar] [CrossRef]
- Hruska, E.; Abella, J.R.; Noeske, F.; Kavraki, L.E.; Clementi, C. Quantitative comparison of adaptive sampling methods for protein dynamics. J. Chem. Phys. 2018, 149, 244119. [Google Scholar] [CrossRef]
- Molloy, K.; Shehu, A. A General, Adaptive, Roadmap-Based Algorithm for Protein Motion Computation. IEEE Trans. Nanobiosci. 2016, 15, 158–165. [Google Scholar] [CrossRef] [PubMed]
- Zaman, A.B.; Shehu, A. Balancing multiple objectives in conformation sampling to control decoy diversity in template-free protein structure prediction. BMC Bioinform. 2019, 20, 211. [Google Scholar] [CrossRef] [PubMed]
- Estana, A.; Molloy, K.; Vaisset, M.; Sibille, N.; Simeon, T.; Bernadó, P.; Cortes, J. Hybrid parallelization of a multi-tree path search algorithm: Application to highly-flexible biomolecules. Parallel Comput. 2018, 77, 84–100. [Google Scholar] [CrossRef]
- Chon, L.; Saglam, A.S.; Zuckerman, D.M. Path-sampling strategies for simulating rare events in biomolecular systems. Elsevier’s Curr. Opin. Struct. Biol. 2017, 43, 88–94. [Google Scholar] [CrossRef] [PubMed]
- Ekenna, C.; Thomas, S.; Amato, N.M. Adaptive local learning in sampling based motion planning for protein folding. BMC Syst. Biol. 2016, 10, 49. [Google Scholar] [CrossRef]
- LaValle, S.M.; James, J.; Kuffner, J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Afrasiabi, F.; Haspel, N. Efficient Exploration of Protein Conformational Pathways using RRT* and MC. In Proceedings of the ACM-BCB (in CSBW 2020 Workshop), Virtual Event, Atlanta, GA, USA, 21–24 September 2020. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. IJRR 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Metlicka, M.; Bygi, M.N.; Streinu, I. Repairing gaps in Kinari-2 for large scale protein and flexibility analysis applications. In Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017; pp. 577–580. [Google Scholar] [CrossRef]
- Luo, D.; Haspel, N. Multi-Resolution Rigidity-Based Sampling of Protein Conformational Paths. In Proceedings of the International Conference on Bioinformatics, Computational Biology and Biomedical Informatics (BCB’13), Wshington, DC, USA, 22–25 September 2013; Association for Computing Machinery: New York, NY, USA; pp. 786–792. [Google Scholar] [CrossRef]
- Fox, N.; Jagodzinski, F.; Li, Y.; Streinu, I. KINARI-Web: A server for protein rigidity analysis. Nucleic Acids Res. 2011, 39, W177–W183. [Google Scholar] [CrossRef] [PubMed]
- Nouri Bygi, M.; Streinu, I. Efficient pebble game algorithms engineered for protein rigidity applications. In Proceedings of the 2017 IEEE 7th International Conference on Computational Advances in Bio- and Medical Sciences (ICCABS’17), Orlando, FL, USA, 19–21 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Vajdi, A.; Joshi, A.; Haspel, N. Integrating Co-Evolutionary Information in Monte Carlo Based Method for Proteins Trajectory Simulation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 7–10 September 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 598–603. [Google Scholar] [CrossRef]
- Papoian, G.A.; Ulander, J.; Eastwood, M.P.; Luthey-Schulten, Z.; Wolynes, P.G. Water in protein structure prediction. Proc. Natl. Acad. Sci. USA 2004, 101, 3352–3357. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef]
- Dehghanpoor, R.; Ricks, E.; Hursh, K.; Gunderson, S.; Farhoodi, R.; Haspel, N.; Hutchinson, B.; Jagodzinski, F. Predicting the Effect of Single and Multiple Mutations on Protein Structural Stability. Molecules 2018, 23, 251. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, Z.; Demirtas, A. Rigidity Analysis of Protein Molecules. J. Comput. Inf. Sci. Eng. 2015, 15, 031009. [Google Scholar] [CrossRef]
- Stevens, F.C. Calmodulin: An introduction. Can. J. Biochem. Cell Biol. 1983, 61, 906–910. [Google Scholar] [CrossRef] [PubMed]
- Hoeflich, K.P.; Ikura, M. Calmodulin in Action: Diversity in Target Recognition and Activation Mechanisms. Cell 2002, 108, 739–742. [Google Scholar] [CrossRef]
- Chang, H.Y.; Fu, C.Y. Adenylate Kinase. In Encyclopedia of Food Microbiology, 2nd ed.; Batt, C.A., Tortorello, M.L., Eds.; Academic Press: Oxford, UK, 2014; pp. 18–23. [Google Scholar] [CrossRef]
- Schrank, T.; Bolen, D.; Hilser, V. Rational modulation of conformational fluctuations in adenylate kinase reveals a local unfolding mechanism for allostery and functional adaptation in proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 16984–16989. [Google Scholar] [CrossRef]
- Daily, M.D.; Phillips, G.N.; Cui, Q. Many local motions cooperate to produce the adenylate kinase conformational transition. J. Mol. Biol. 2010, 400, 618–631. [Google Scholar] [CrossRef]
- Zappe, H.; Snell, M.; Bossard, M. PEGylation of cyanovirin-N, an entry inhibitor of HIV. Adv. Drug Deliv. Rev. 2008, 60, 79–87. [Google Scholar] [CrossRef]
- Björkman, A.J.; Mowbray, S.L. Multiple open forms of ribose-binding protein trace the path of its conformational change. J. Mol. Biol. 1998, 279. [Google Scholar] [CrossRef]
| Molecule | Path | Init. | min RMSD | |||
|---|---|---|---|---|---|---|
| CaM | ||||||
| 3 | ||||||
| 45 | 32 | |||||
| AdK | ||||||
| 307 | ||||||
| CVN | 56 | |||||
| 33 | ||||||
| RBP | ||||||
| 23 |
| Molecule | Path | Tree | Tree | Tree |
|---|---|---|---|---|
| CaM | 2209 | 2700 | 2137 | |
| 1597 | 1708 | 1166 | ||
| 1738 | 1603 | 1488 | ||
| 1432 | 1410 | 1354 | ||
| AdK | 2398 | 1661 | 1829 | |
| 1526 | 1491 | 1473 | ||
| Cvn | 3279 | 2886 | 3059 | |
| 1921 | 1680 | 1867 | ||
| Rbp | 100 | 91 | 84 | |
| 109 | 84 | 63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afrasiabi, F.; Dehghanpoor, R.; Haspel, N. Integrating Rigidity Analysis into the Exploration of Protein Conformational Pathways Using RRT* and MC. Molecules 2021, 26, 2329. https://doi.org/10.3390/molecules26082329
Afrasiabi F, Dehghanpoor R, Haspel N. Integrating Rigidity Analysis into the Exploration of Protein Conformational Pathways Using RRT* and MC. Molecules. 2021; 26(8):2329. https://doi.org/10.3390/molecules26082329
Chicago/Turabian StyleAfrasiabi, Fatemeh, Ramin Dehghanpoor, and Nurit Haspel. 2021. "Integrating Rigidity Analysis into the Exploration of Protein Conformational Pathways Using RRT* and MC" Molecules 26, no. 8: 2329. https://doi.org/10.3390/molecules26082329
APA StyleAfrasiabi, F., Dehghanpoor, R., & Haspel, N. (2021). Integrating Rigidity Analysis into the Exploration of Protein Conformational Pathways Using RRT* and MC. Molecules, 26(8), 2329. https://doi.org/10.3390/molecules26082329







