Expanding the Ligand Classes Used for Mn(II) Complexation: Oxa-aza Macrocycles Make the Difference
Abstract
1. Introduction
2. Results
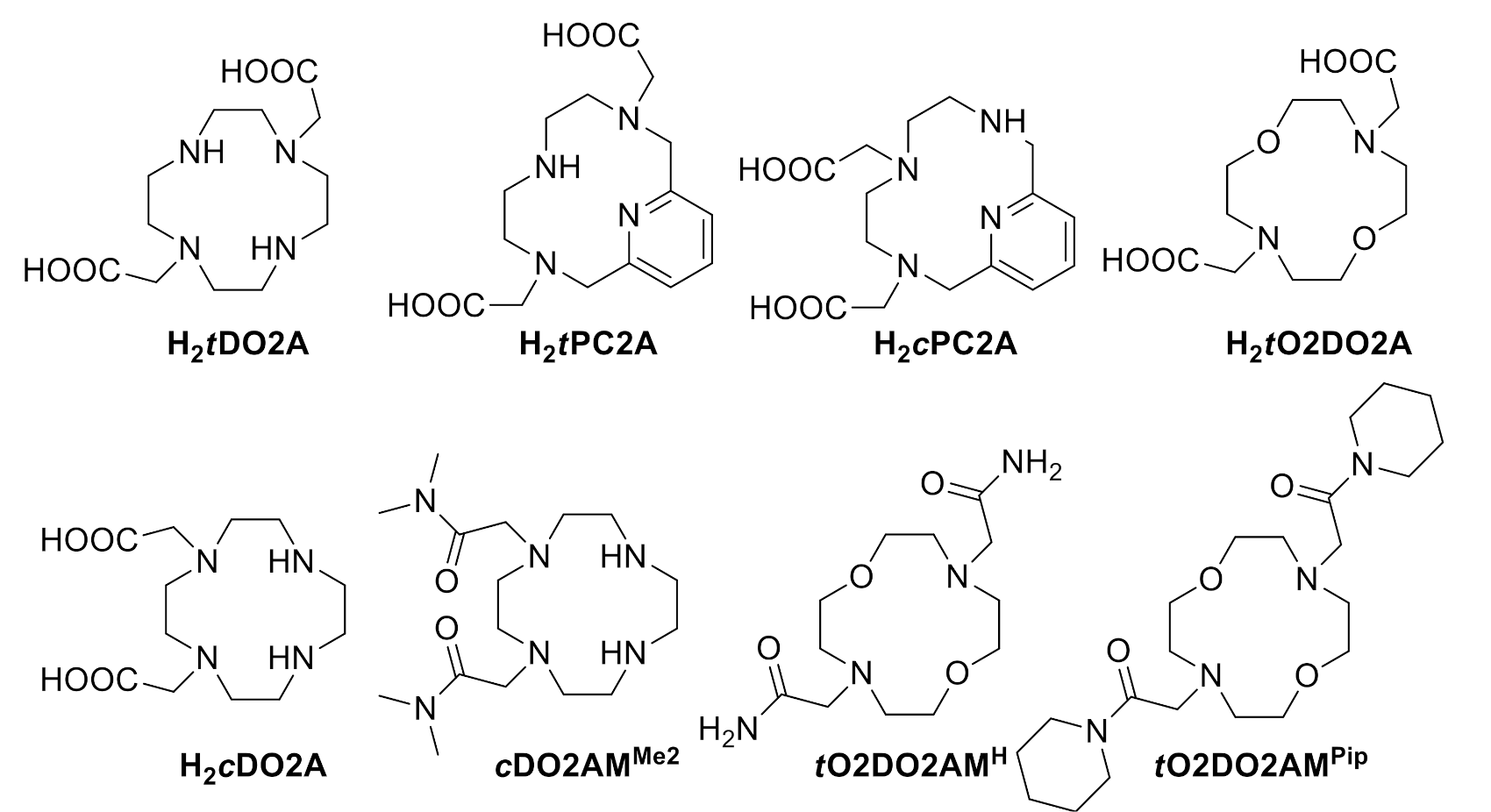
2.1. Synthesis of the Ligands
2.2. X-ray Crystal Structures
2.3. Protonation Constants of the Ligands
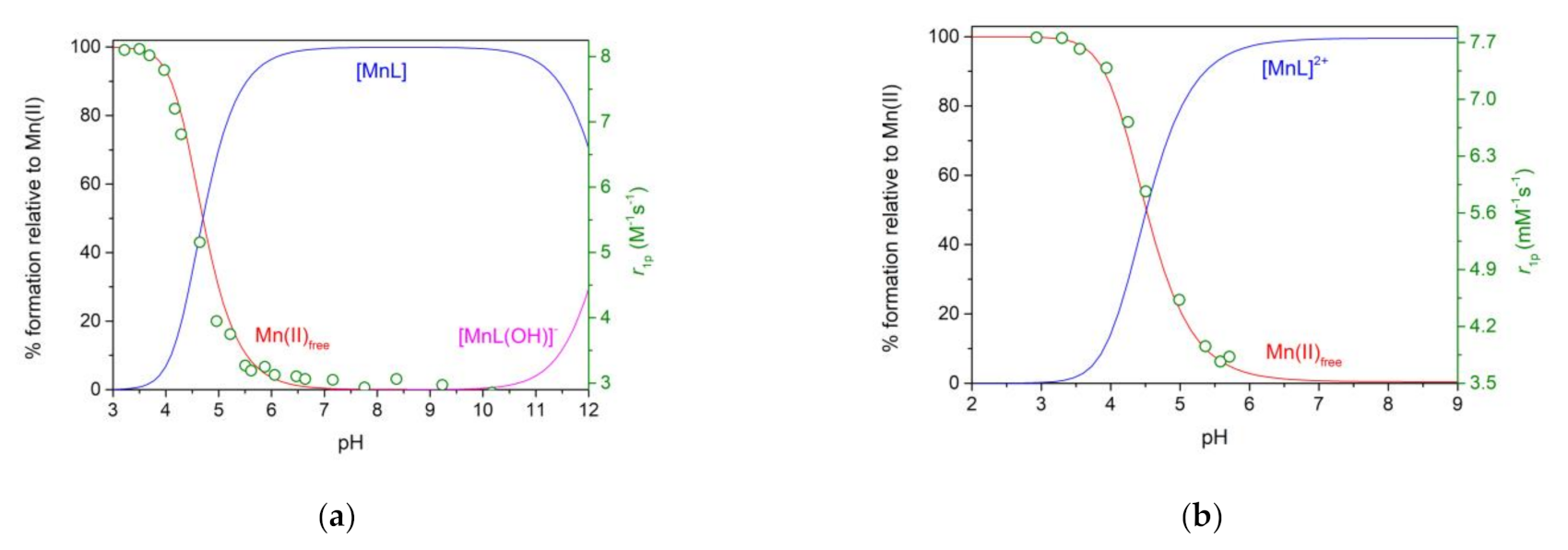
2.4. Stability Constants of Metal Complexes
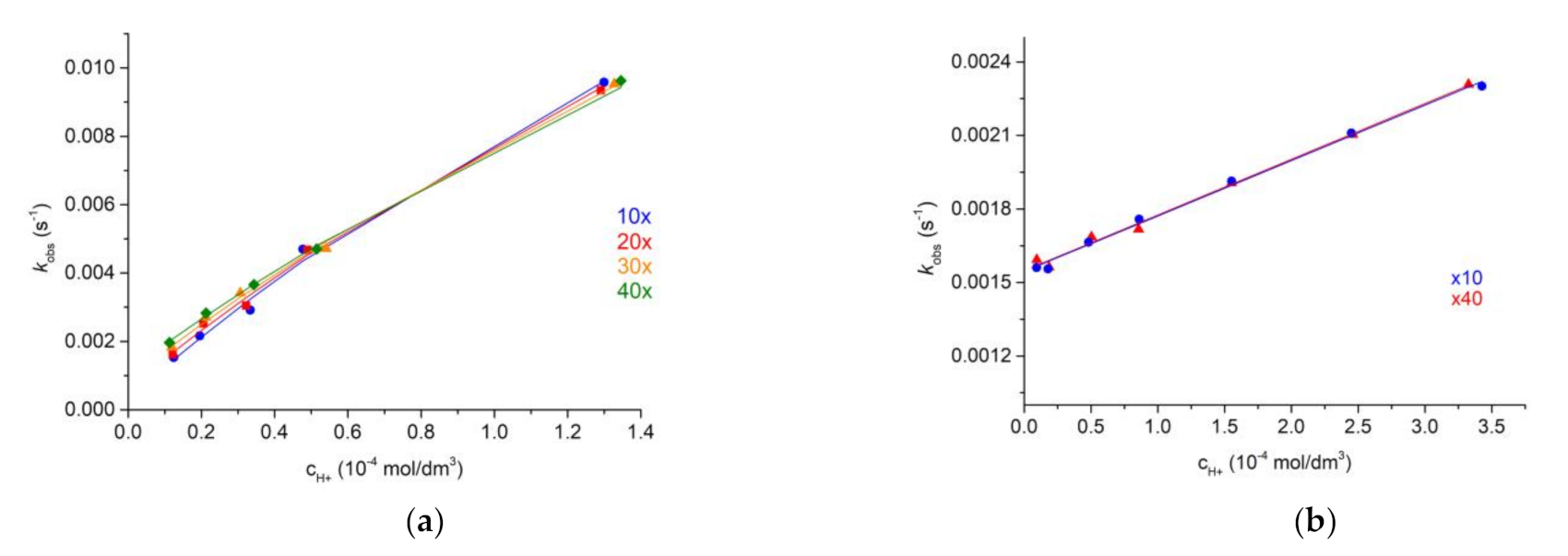
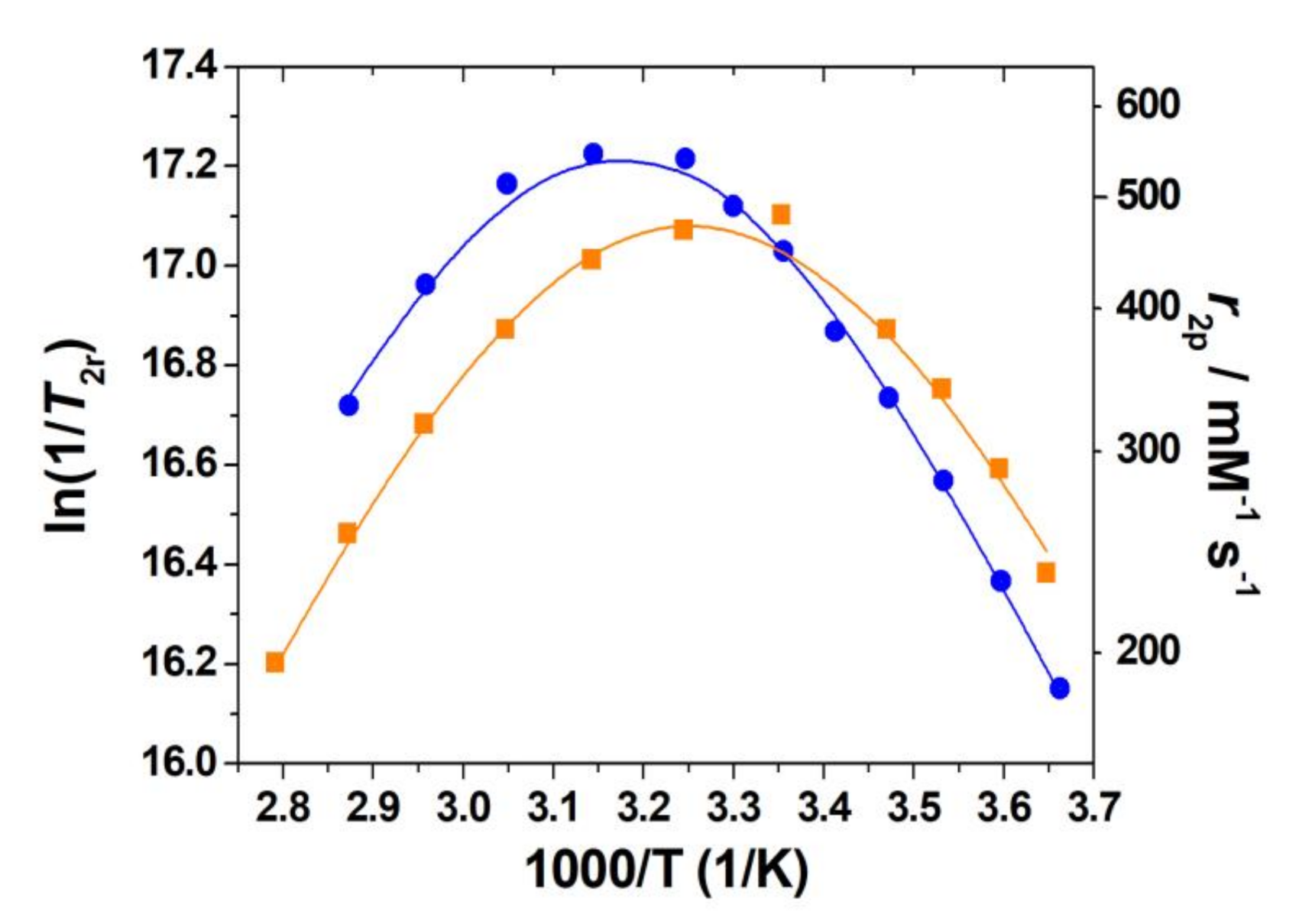
2.5. Dissociation Kinetics
2.6. Hydration Numbers
2.7. Water Exchange
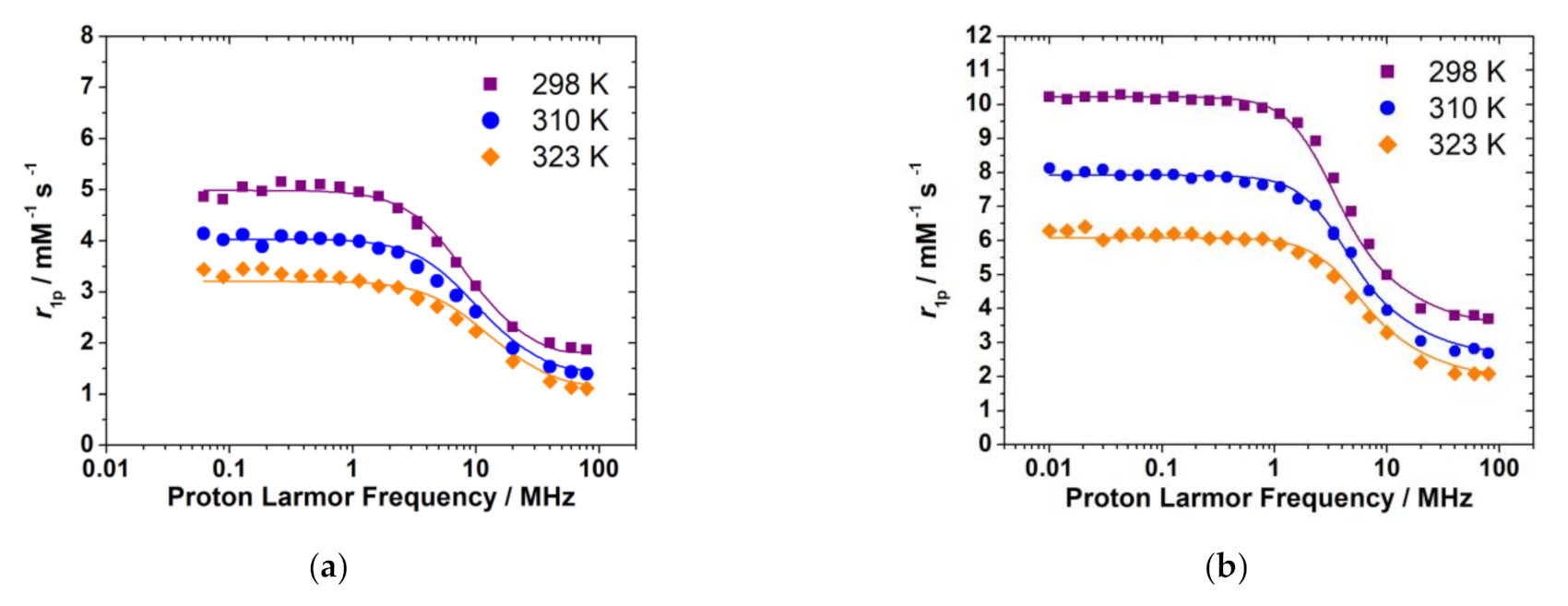
2.8. Analysis of the 1H NMRD Profiles
3. Materials and Methods
3.1. General Methods
Reagents
3.2. Synthesis
3.3. Equilibrium Studies
3.4. Kinetic Studies
H- and 17O Relaxometry
3.5. X-ray Diffraction Studies
3.6. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Wahsner, J.; Gale, E.M.; Rodríguez-Rodríguez, A.; Caravan, P. Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers. Chem. Rev. 2019, 119, 957–1057. [Google Scholar] [CrossRef]
- Merbach, A.; Helm, L.; Tóth, E. The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Hao, D.; Ai, T.; Goerner, F.; Hu, X.; Runge, V.M.; Tweedle, M. MRI Contrast Agents: Basic Chemistry and Safety. J. Magn. Reson. Imaging 2012, 36, 1060–1071. [Google Scholar] [CrossRef]
- Marckmann, P.; Skov, L.; Rossen, K.; Dupont, A.; Damholt, M.B.; Heaf, J.G.; Thomsen, H.S. Nephrogenic systemic fibrosis: Suspected causative role of gadodiamide used for contrast-enhanced magnetic resonance imaging. J. Am. Soc. Nephrol. 2006, 17, 2359–2362. [Google Scholar] [CrossRef]
- Grobner, T. Gadolinium—A specific trigger for the development of nephrogenic fibrosing dermopathy and nephrogenic systemic fibrosis? Nephrol. Dial. Transplant. 2006, 21, 1104–1108. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.L.; Qureshi, Z.P.; Sartor, A.O.; Norris, L.B.; Murday, A.; Xirasagar, S.; Thomsen, H.S. Gadolinium-induced nephrogenic systemic fibrosis: The rise and fall of an iatrogenic disease. Clin. Kidney J. 2012, 5, 82–88. [Google Scholar] [CrossRef] [PubMed]
- Kanda, T.; Ishii, K.; Kawaguchi, H.; Kitajima, K.; Takenaka, D. High signal intensity in the dentate nucleus and globus pallidus on unenhanced T1-weighted MR images: Relationship with increasing cumulative dose of a gadolinium-based contrast material. Radiology 2014, 270, 834–841. [Google Scholar] [CrossRef]
- Kanal, E.; Tweedle, M.F. Residual or Retained Gadolinium: Practical Implications for Radiologists and Our Patients. Radiology 2015, 275, 630–634. [Google Scholar] [CrossRef]
- Gupta, A.; Caravan, P.; Price, W.S.; Platas-Iglesias, C.; Gale, E.M. Applications for Transition-Metal Chemistry in Contrast-Enhanced Magnetic Resonance Imaging. Inorg. Chem. 2020, 59, 6648–6678. [Google Scholar] [CrossRef] [PubMed]
- Botta, M.; Carniato, F.; Esteban-Gómez, D.; Platas-Iglesias, C.; Tei, L. Mn(II) compounds as an alternative to Gd-based MRI probes. Future Med. Chem. 2019, 11, 1461–1483. [Google Scholar] [CrossRef]
- Drahos, B.; Lukes, I.; Tóth, E. Manganese(II) Complexes as Potential Contrast Agents for MRI. Eur. J. Inorg. Chem. 2012, 2012, 1975–1986. [Google Scholar] [CrossRef]
- Pan, D.; Schmieder, A.H.; Wickline, S.A.; Lanza, G.M. Manganese-Based MRI Contrast Agents: Past, Present, and Future. Tetrahedron 2011, 67, 8431–8444. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Mancía, S.; Ríos, C.; Montes, S. Manganese accumulation in the CNS and associated pathologies. Biometals 2011, 24, 811–825. [Google Scholar] [CrossRef]
- Ndiaye, D.; Sy, M.; Pallier, A.; Même; de Silva, I.; Lacerda, S.; Nonat, A.M.; Charbonnière, L.J.; Tóth, É. Unprecedented Kinetic Inertness for a Mn2+-Bispidine Chelate: A Novel Structural Entry for Mn2+-Based Imaging Agents. Angew. Chem. Int. Ed. 2020, 59, 11958–11963. [Google Scholar] [CrossRef] [PubMed]
- Caravan, P.; Farrar, C.T.; Frullano, L.; Uppal, R. Influence of molecular parameters and increasing magnetic field strength on relaxivity of gadolinium- and manganese-based T1 contrast agents. Contrast Media Mol. Imaging 2009, 4, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Rolla, G.A.; Platas-Iglesias, C.; Botta, M.; Tei, L.; Helm, L. 1H and 17O NMR Relaxometric and Computational Study on Macrocyclic Mn(II) Complexes. Inorg. Chem. 2013, 52, 3268–3279. [Google Scholar] [CrossRef]
- Garda, Z.; Forgács, A.; Do, Q.N.; Kálmán, F.K.; Timári, S.; Baranyai, Z.; Tei, L.; Tóth, I.; Kovács, Z.; Tircsó, G. Physico-chemical Properties of MnII Complexes Formed with cis- and trans-DO2A: Thermodynamic, Electrochemical and Kinetic studies. J. Inorg. Biochem. 2016, 163, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, A.; Calabi, L.; Giorgi, C.; Losi, P.; Mariani, P.; Palano, D.; Paoli, P.; Rossi, P.; Valtancoli, B. Thermodynamic and structural aspects of manganese(II) complexes with polyaminopolycarboxylic ligands based upon 1,4,7,10-tetraazacyclododecane (cyclen). Crystal structure of dimeric [MnL]2·2CH3OH containing the new ligand 1,4,7,10-tetraazacyclododecane-1,4-diacetate. J. Chem. Soc. Dalton Trans. 2001, (6), 917–922. [Google Scholar] [CrossRef]
- Garda, Z.; Molnár, E.; Hamon, N.; Barriada, J.L.; Esteban-Gómez, D.; Váradi, B.; Nagy, V.; Pota, K.; Kalman, F.K.; Tóth, I.; et al. Complexation of Mn(II) by Rigid Pyclen Diacetates: Equilibrium, Kinetic, Relaxometric, DFT and SOD Activity Studies. Inorg. Chem. 2021, 60, 1133–1148. [Google Scholar] [CrossRef]
- Devreux, M.; Henoumont, C.; Dioury, F.; Boutry, S.; Vacher, O.; Vander Elst, L.; Port, M.; Muller, R.N.; Sandre, O.; Laurent, S. Mn2+ Complexes with Pyclen-Based Derivatives as Contrast Agents for Magnetic Resonance Imaging: Synthesis and Relaxometry Characterization. Inorg. Chem. 2021. [Google Scholar] [CrossRef] [PubMed]
- Botár, R.; Molnár, E.; Trencsényi, G.; Kiss, J.; Kálmán, F.K.; Tircsó, G. Stable and Inert Mn(II)-Based and pH-Responsive Contrast Agents. J. Am. Chem. Soc. 2020, 142, 1662–1666. [Google Scholar] [CrossRef]
- Kálmán, F.K.; Nagy, V.; Váradi, B.; Garda, Z.; Molnár, E.; Trencsényi, G.; Kiss, J.; Même, S.; Même, W.; Tóth, E.; et al. Mn(II)-Based MRI Contrast Agent Candidate for Vascular Imaging. J. Med. Chem. 2020, 63, 6057–6065. [Google Scholar] [CrossRef] [PubMed]
- Drahos, B.; Pniok, M.; Havlickova, J.; Kotek, J.; Cısarova, I.; Hermann, P.; Lukes, I.; Tóth, É. Mn2+ complexes of 1-oxa-4,7-diazacyclononane based ligands with acetic, phosphonic and phosphinic acid pendant arms: Stability and relaxation studies. Dalton Trans. 2011, 40, 10131–10146. [Google Scholar] [CrossRef]
- Balogh, E.; He, Z.; Hsieh, W.; Liu, S.; Tóth, É. Dinuclear Complexes Formed with the Triazacyclononane Derivative ENOTA4-: High-Pressure 17O NMR Evidence of an Associative Water Exchange on [MnII2(ENOTA)(H2O)2]. Inorg. Chem. 2007, 46, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Pujales-Paradela, R.; Carniato, F.; Esteban-Gómez, D.; Botta, M.; Platas-Iglesias, C. Controlling water exchange rates in potential Mn2+-based MRI agents derived from NO2A2−. Dalton Trans. 2019, 48, 3962–3972. [Google Scholar] [CrossRef] [PubMed]
- Bond, C.J.; Sokolow, G.E.; Crawley, M.R.; Burns, P.J.; Cox, J.M.; Mayilmurugan, R.; Morrow, J.R. Exploring Inner-Sphere Water Interactions of Fe(II) and Co(II) Complexes of 12-Membered Macrocycles To Develop CEST MRI Probes. Inorg. Chem. 2019, 58, 8710–8719. [Google Scholar] [CrossRef] [PubMed]
- Forgács, A.; Tei, L.; Baranyai, Z.; Tóth, I.; Zékány, L.; Botta, M. A Bisamide Derivative of [Mn(1,4-DO2A)]—Solution Thermodynam-ic, Kinetic, and NMR Relaxometric Studies. Eur. J. Inorg. Chem. 2016, 1165–1174. [Google Scholar] [CrossRef]
- Amorim, M.T.S.; Ascenso, J.R.; Delgado, R.; Fraústo da Silva, J.J.R. Nuclear Magnetic Resonance Studies of the Protonation Sequence of Some Oxaaza Macrocyclic Compounds. J. Chem. Soc. Dalton Trans. 1990, 3440–3455. [Google Scholar] [CrossRef]
- Kaupang, Å.; Bonge-Hansen, T. α-Bromodiazoacetamides—A new class of diazo compounds for catalyst-free, ambient temperature intramolecular C–H insertion reactions. Beilstein J. Org. Chem. 2013, 9, 1407–1413. [Google Scholar] [CrossRef]
- Urbanczyk-Lipkowska, Z.; Krajewski, J.W.; Gluzinski, P.; Kolinski, R.A.; Andreetti, G.D.; Bocelli, G. Crystal and molecular structure of inner-chelate cis-1,7-dioxa-4,10-diazacyclododecane-4,10-diacetatocopper(II) dehydrate. J. Crystallogr. Spectrosc. Res. 1988, 18, 157–164. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE. Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools; Version 2.1; Universitat de Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Casanova, D.; Alemany, P.; Bofill, J.M.; Alvarez, A. Shape and Symmetry of Heptacoordinate Transition-Metal Complexes: Structural Trends. Chem. Eur. J. 2003, 9, 1281–1295. [Google Scholar] [CrossRef]
- Forgács, A.; Pujales-Paradela, R.; Regueiro-Figueroa, M.; Valencia, L.; Esteban-Gómez, D.; Botta, M.; Platas-Iglesias, C. Developing the family of picolinate ligands for Mn2+ complexation. Dalton Trans. 2017, 46, 1546–1558. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Gao, J.; Wang, J.; Zhang, Z.H.; Wang, Y.F.; Chen, L.J.; Sun, W.; Zhang, X.D. Crystal Structures of Seven-Coordinate (NH4)2[MnII(EDTA)(H2O)]·3H2O, (NH4)2[MnII(CYDTA)(H2O)]·4H2O and K2[MnII(HDTPA)]·3.5H2O Complexes. J. Struct. Chem. 2008, 49, 724–731. [Google Scholar] [CrossRef]
- Phukan, B.; Patel, A.B.; Mukherjee, C. A water-soluble and water-coordinated Mn(II) complex: Synthesis, characterization and phantom MRI image study. Dalton Trans. 2015, 44, 12990–12994. [Google Scholar] [CrossRef] [PubMed]
- Khannam, M.; Weyhermüller, T.; Goswami, U.; Mukherjee, C. A highly stable L-alanine-based mono(aquated) Mn(II) complex as a T1-weighted MRI contrast agent. Dalton Trans. 2017, 46, 10426–10432. [Google Scholar] [CrossRef]
- Wang, S.; Westmoreland, T.D. Correlation of Relaxivity with Coordination Number in Six-, Seven-, and Eight-Coordinate Mn(II) Complexes of Pendant-Arm Cyclen Derivatives. Inorg. Chem. 2009, 48, 719–727. [Google Scholar] [CrossRef]
- Riesen, A.; Zehnder, M.; Kaden, T.A. Synthesis, Properties, and Structures of Mononuclear Complexes with 12- and 14-Membered Tetraazamacrocycle-N,N′,N″,N‴-tetraacetic acids. Helv. Chim. Acta 1986, 69, 2067–2073. [Google Scholar] [CrossRef]
- Kumar, K.; Tweedle, M.F.; Malley, M.F.; Gougoutas, J.Z. Synthesis, Stability, and Crystal Structure Studies of Some Ca2+, Cu2+, and Zn2+ Complexes of Macrocyclic Polyamino Carboxylates. Inorg. Chem. 1995, 34, 6472–6480. [Google Scholar] [CrossRef]
- Beattie, J.K. Conformational Analysis of Tris(ethylenediamine) Complexes. Acc. Chem. Res. 1971, 4, 253–259. [Google Scholar] [CrossRef]
- Dale, J. Exploratory Calculations of Medium and Large Rings. Acta Chem. Scand. 1973, 27, 1115–1129. [Google Scholar] [CrossRef]
- Liao, L.; Ingram, C.W.; Bacsa, J.; Zhang, Z.J.; Dinadayalane, T. A hydrogen bonded Co(II) coordination complex and a triply interpenetrating 3-D manganes(II) coordination polymer from diaza crown ether with dibenzoate sidearms. Cryst. Eng. Commun. 2016, 18, 2425–2436. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, A.; Carreira-Barral, I.; Esteban-Gómez, D.; Platas-Iglesias, C.; de Blas, A.; Rodríguez-Blas, T. ‘‘Cinderella’’ elements: Strategies to increase the stability of group 1 complexes by tailoring crown macrocycles. Inorg. Chim. Acta 2014, 417, 155–162. [Google Scholar] [CrossRef][Green Version]
- Ferreirós-Martínez, R.; Esteban-Gómez, D.; de Blas, A.; Platas-Iglesias, C.; Rodríguez-Blas, T. Eight-Coordinate Zn(II), Cd(II), and Pb(II) Complexes Based on a 1,7-Diaza-12-crown-4 Platform Endowed with a Remarkable Selectivity over Ca(II). Inorg. Chem. 2009, 48, 11821–11831. [Google Scholar] [CrossRef] [PubMed]
- González-Lorenzo, M.; Platas-Iglesias, C.; Avecilla, F.; Faulkner, S.; Pope, S.J.A.; de Blas, A.; Rodríguez-Blas, T. Structural and Photophysical Properties of Lathanide(III) Complexes with a Novel Octadentate Iminophenolate Bibracchial Lariat Ether. Inorg. Chem. 2005, 44, 4254–4262. [Google Scholar] [CrossRef] [PubMed]
- Mato-Iglesias, M.; Roca-Sabio, A.; Pálinkás, Z.; Esteban-Gómez, D.; Platas-Iglesias, C.; Tóth, E.; de Blas, A.; Rodríguez-Blas, T. Lanthanide Complexes Based on a 1,7-Diaza-12-crown-4 Platform Containing Picolinate Pendants: A New Structural Entry for the Design of Magnetic Resonance Imaging Contrast Agents. Inorg. Chem. 2008, 47, 7840–7851. [Google Scholar] [CrossRef]
- Hormann, J.; van der Meer, M.; Sarkar, B.; Kulak, N. From Cyclen to 12-Crown-4 Copper(II) Complexes: Exchange of Donor Atoms Improves DNA Cleavage Activity. Eur. J. Inorg. Chem. 2015, 4722–4730. [Google Scholar] [CrossRef]
- Kim, W.D.; Hrncir, D.C.; Kiefer, G.E.; Sherry, A.D. Synthesis, Crystal Structure, and Potentiometry of Pyridine-Containing Tetraaza Macrocyclic Ligands with Acetate Pendant Arms. Inorg. Chem. 1995, 34, 2225–2232. [Google Scholar] [CrossRef]
- Amorim, M.T.S.; Delgado, R.; Frausto da Silva, J.J.R. N,N′-Diacetate derivatives of some polyoxa-polyaza macrocyclic compounds: Protonation and complexation studies. Polyhedron 1992, 11, 1891–1899. [Google Scholar] [CrossRef]
- Regueiro-Figueroa, M.; Bensenane, B.; Ruscsak, E.; Esteban-Gomez, D.; Charbonniere, L.J.; Tircsó, G.; Tóth, I.; de Blas, A.; Rodríguez-Blas, T.; Platas-Iglesias, C. Lanthanide dota-like complexes containing a picolinate pendant: Structural entry for the design of LnIII-based luminescent probes. Inorg. Chem. 2011, 50, 4125–4141. [Google Scholar] [CrossRef] [PubMed]
- Gündüz, S.; Vibhute, S.; Botár, R.; Kálmán, F.K.; Tóth, I.; Tircsó, I.; Regueiro-Figueroa, M.; Esteban-Gómez, D.; Platas-Iglesias, C.; Angelovski, G. Coordination properties of GdDO3A-based model compounds of bioresponsive MRI contrast agents. Inorg. Chem. 2018, 57, 5973–5986. [Google Scholar] [CrossRef] [PubMed]
- Pasha, A.; Tircsó, G.; Benyó, E.T.; Brücher, E.; Sherry, A.D. Synthesis and Characterization of DOTA-(amide)4 Derivatives: Equilibrium and Kinetic Behavior of Their Lanthanide(III) Complexes. Eur. J. Inorg. Chem. 2007, 4340–4349. [Google Scholar] [CrossRef] [PubMed]
- Forgács, A.; Tei, L.; Baranyai, Z.; Esteban-Gómez, D.; Platas-Iglesias, C.; Botta, M. Optimising the relaxivities of Mn2+ complexes by targeting human serum albumin (HSA). Dalton Trans. 2017, 46, 8494–8504. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, A.; Garda, Z.; Ruscsák, E.; Esteban-Gómez, D.; de Blas, A.; Rodríguez-Blas, T.; Lima, L.M.P.; Beyler, M.; Tripier, R.; Tircsó, G.; et al. Stable Mn2+, Cu2+ and Ln3+ complexes with cyclen-based ligands functionalized with picolinate pendant arms. Dalton Trans. 2015, 44, 5017–5031. [Google Scholar] [CrossRef] [PubMed]
- Nizou, G.; Molnár, E.; Hamon, N.; Kálmán, F.K.; Fougère, O.; Rousseaux, O.; Esteban Gòmez, D.; Platas-Iglesias, C.; Beyler, M.; Tircsó, G.; et al. Pyclen-Based Ligands Bearing Pendant Picolinate Arms for Gadolinium Complexation. Inorg. Chem. 2021, 60, 1133–1148. [Google Scholar] [CrossRef] [PubMed]
- Drahos, B.; Kotek, J.; Hermann, P.; Lukes, I.; Tóth, E. Mn2+ Complexes with Pyridine-Containing 15-Membered Macrocycles: Thermodynamic, Kinetic, Crystallographic, and 1H/17O Relaxation Studies. Inorg. Chem. 2010, 49, 3224–3238. [Google Scholar] [CrossRef] [PubMed]
- Gale, E.M.; Zhu, J.; Caravan, P. Direct Measurement of the Mn(II) Hydration State in Metal Complexes and Metalloproteins through 17O NMR Line Widths. J. Am. Chem. Soc. 2013, 135, 18600–18608. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.A.; Geraldes, C.F.G.C. A Semi-Empirical Method for the Estimation of the Hydration Number of Mn(II)-Complexes. Inorganics 2018, 6, 116. [Google Scholar] [CrossRef]
- Swift, T.J.; Connick, R.E. NMR-Relaxation Mechanisms of O17 in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere. J. Chem. Phys. 1962, 37, 307–320. [Google Scholar] [CrossRef]
- Swift, T.J.; Connick, R.E. Erratum: NMR-Relaxation Mechanisms of 17O in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere. J. Chem. Phys. 1964, 41, 2553. [Google Scholar] [CrossRef]
- Patinec, V.; Rolla, G.A.; Botta, M.; Tripier, R.; Esteban-Gómez, D.; Platas-Iglesias, C. Hyperfine Coupling Constants on Inner-Sphere Water Molecules of a Triazacyclononane-based Mn(II) Complex and Related Systems Relevant as MRI Contrast Agents. Inorg. Chem. 2013, 52, 11173–11184. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, C.D.; van Eldik, R. Mechanistic information on some inorganic and bioinorganic reactions from volume profile analysis. Inorg. Chim. Acta 2010, 363, 2357–2374. [Google Scholar] [CrossRef]
- Helm, L.; Merbach, A.E. Inorganic and Bioinorganic Solvent Exchange Mechanisms. Chem. Rev. 2005, 105, 1923–1959. [Google Scholar] [CrossRef]
- Esteban-Gómez, D.; Cassino, C.; Botta, M.; Platas-Iglesias, C. 17O and 1H relaxometric and DFT study of hyperfine coupling constants in [Mn(H2O)6]2+. RSC Adv. 2014, 4, 7094–7103. [Google Scholar] [CrossRef]
- Helm, L. Relaxivity in paramagnetic systems: Theory and mechanisms. Prog. Nucl. Magn. Reson. Spectrosc. 2006, 49, 45–64. [Google Scholar] [CrossRef]
- Martell, E.; Motekaitis, R.J. Determination and Use of Stability Constants; VCH Publishers: New York, NY, USA, 1992. [Google Scholar]
- Zékány, L.; Nagypál, I. Computational Method for Determination of Formation Constants; Legett, D.J., Ed.; Plenum: New York, NY, USA, 1985; p. 291. [Google Scholar]
- Raiford, D.S.; Fisk, C.L.; Becker, E.D. Calibration of methanol and ethylene glycol nuclear magnetic resonance thermometers. Anal. Chem. 1979, 51, 2050–2051. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Yerly, F. VISUALISEUR 3.3.7 and OPTIMISEUR 3.3.7. Lausanne, Switzerland, 2006. [Google Scholar]
- APEX3; Version 2016.1; Bruker AXS Inc.: Madison, WI, USA, 2016.
- SAINT; Version 8.38A.; Bruker AXS Inc: Madison, WI, USA, 2015.
- Sheldrick, C.M. SADABS; Version 2014/5; Bruker AXS Inc.: Madison, WI, USA.
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2008, A64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef] [PubMed]
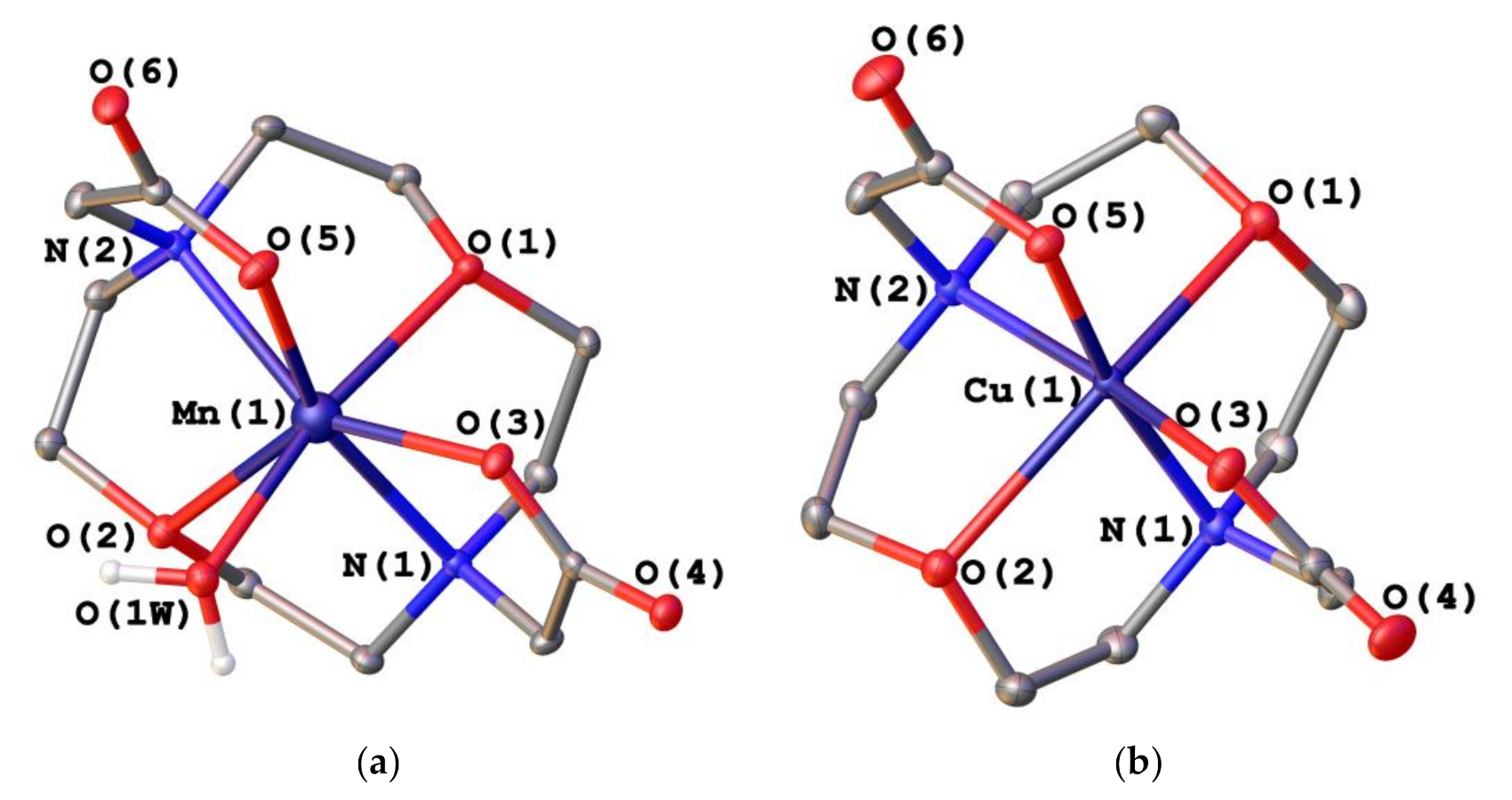
| Mn(1)–O(1) | 2.3124(17) | Cu(1)–O(1) | 2.3783(8) |
| Mn(1)–O(2) | 2.4542(17) | Cu(1)–O(2) | 2.3282(8) |
| Mn(1)–O(3) | 2.1518(16) | Cu(1)–O(3) | 1.9426(8) |
| Mn(1)–O(5) | 2.1566(17) | Cu(1)–O(5) | 1.9356(8) |
| Mn(1)–N(1) | 2.3756(19) | Cu(1)–N(1) | 2.1036(9) |
| Mn(1)–N(2) | 2.3855(18) | Cu(1)–N(2) | 2.0763(9) |
| Mn(1)–O(1W) | 2.2054(18) | - |
| tO2DO2A2− | tO2DO2AMPip | tDO2A2− | tPC2A2− | |
|---|---|---|---|---|
| logK1H | 8.05(2)/9.53 a | 7.19(2) | 11.69 b/11.29 c/11.66 d | 12.25 e/12.50 f |
| logK2H | 7.43(2)/7.46 a | 6.29(2) | 9.75 b/9.84 c/9.75 d | 5.97 e/5.75 f |
| logK3H | 2.06(2)/2.11 a | - | 3.97 b/3.97 c/4.06 d | 3.47 e/3.28 f |
| logK4H | - | - | 2.68 b/2.59 c/2.58 d | 1.99 e/2.38 f |
| ∑logKiH | 17.54/19.10 a | 13.48 | 28.09 b/27.69 c/28.05 d | 23.68 e/23.91 f |
| ∑logKiH, i = 1–2 | 15.48/16.99 a | 13.48 | 21.44 b/21.13 c/21.41 d | 18.22 e/18.25 f |
| tO2DO2A2− | tO2DO2AMPip | tDO2A2− | tPC2A2− | |
|---|---|---|---|---|
| logKMgL | 3.91(1)/5.62 a | 2.91(5) | - | 9.84 e |
| logKCaL | 6.96(1)/8.50 a | 5.78(1) | 8.86 d | 9.82 e |
| logKMnL | 9.38(1)/11.03 a | 7.76(3) | 14.64 b/14.54 c/15.07 d | 17.09e |
| logKMnHL | - | - | 4.40 b/4.25 c/4.48 d | 2.14 e |
| logKMnH2L | - | - | 4.45 c | - |
| logKMnLOH | 12.38(2) | - | 11.50 c | - |
| logKZnL | 10.55(3)/12.28 a | 8.69(2) | 18.86 d | 19.49 e |
| logKZnHL | - | - | 4.23 d | 2.74 e |
| logKZnH2L | - | - | 1.78 d | - |
| logKZnLOH | 11.40(4) | - | - | - |
| logKCuL | 14.56(2)/15.95 a | 10.66(3) | 24.24 d | 23.58 e |
| logKCuHL | 2.46(3) | - | 3.06 d | 2.12 e |
| logKCuLOH | 11.95(3) | - | - | - |
| pMn e | 6.67/6.79 a | 6.28 | 6.52 b/6.60 c/6.73 d | 8.64 e |
| tO2DO2A2− | tO2DO2AMPip | tDO2A2−a | tPC2A2−b | |
|---|---|---|---|---|
| k0 (s−1) | - | (1.54 ± 0.01) × 10−3 | - | - |
| k1 (M−1s−1) | 100 ± 5 | 2.3 ± 0.06 | 85 | 221 |
| k2 (M−2s−1) | - | - | 3 × 106 | - |
| k3 (M−1s−1) | (9 ± 1) × 10−2 | - | - | 3.6 × 10−2 |
| logKMn(HL) | 3.4 ± 0.1 | - | 4.4 | 3.6 |
| logKM(L)M | 1.2 ± 0.2 | - | - | 1.4 |
| t1/2 (h) c | 39 | 0.13 | 58 | 21 |
| tO2DO2A2− | tO2DO2AMPip | tPC2A2−e | |
|---|---|---|---|
| kex298/106 s−1 | 53.3 ± 0.9 | 34.7 ± 0.3 | 126 |
| ΔH‡/kJ mol−1 a | 29.7 ± 0.6 | 28.8 ± 0.3 | 37.5 |
| ΔS‡/J mol−1 K−1 a | 2.8 ± 1.6 | −3.9 ± 1.0 | |
| AO/ħ / 106 rad s−1 a | −45.3 ± 0.6 | −40.1 c | −42.4 |
| 1/T1e298/108 s−1 a | 0.72 ± 0.40 | 0.18 ± 0.02 | 1.1 |
| τR298/ps b | 46.7 ± 0.9 | 87 ± 1 | |
| ER/kJ mol−1 | 20 d | 19.3 ± 0.5 | |
| Δ2/1019 rad s−2 | 11.1 ± 11 | 0.25 ± 0.1 |
| [Cu(tO2DO2A)]·2H2O | [Mn(tO2DO2A)(H2O)]·2H2O | |
|---|---|---|
| formula | C12H24CuN2O8 | C12H26MnN2O9 |
| MW | 387.87 | 397.29 |
| crystal system | monoclinic | orthorhombic |
| space group | P21/n | Pca21 |
| T/K | 100(2) | 100(2) |
| a/Å | 11.2189(5) | 13.5220(3) |
| b/Å | 11.8336(6) | 16.7031(4) |
| c/Å | 12.3596(6) | 14.2920(3) |
| α/deg | 90 | 90 |
| β/deg | 112.853(2) | 90 |
| γ/deg | 90 | 90 |
| V/Å3 | 1512.06(13) | 3227.98(13) |
| F(000) | 812 | 1.672 |
| Z | 4 | 8 |
| λ, Å (Mo Kα) | 0.71073 | 0.71073 |
| Dcalc/g·cm−3 | 1.704 | 1.635 |
| μ/mm−1 | 1.490 | 0.869 |
| θ range/deg | 2.48–30.51 | 2.85–30.32 |
| Rint | 0.0279 | 0.0490 |
| reflns obsd | 4618 | 9852 |
| GOF on F2 | 1.063 | 1.033 |
| R1 a | 0.0204 | 0.0304 |
| wR2 (all data) b | 0.0544 | 0.0636 |
| Largest differences peax and hole/e Å−3 | 0.472 and −0.352 | 0.359 and −0.365 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kálmán, F.K.; Nagy, V.; Uzal-Varela, R.; Pérez-Lourido, P.; Esteban-Gómez, D.; Garda, Z.; Pota, K.; Mezei, R.; Pallier, A.; Tóth, É.; et al. Expanding the Ligand Classes Used for Mn(II) Complexation: Oxa-aza Macrocycles Make the Difference. Molecules 2021, 26, 1524. https://doi.org/10.3390/molecules26061524
Kálmán FK, Nagy V, Uzal-Varela R, Pérez-Lourido P, Esteban-Gómez D, Garda Z, Pota K, Mezei R, Pallier A, Tóth É, et al. Expanding the Ligand Classes Used for Mn(II) Complexation: Oxa-aza Macrocycles Make the Difference. Molecules. 2021; 26(6):1524. https://doi.org/10.3390/molecules26061524
Chicago/Turabian StyleKálmán, Ferenc K., Viktória Nagy, Rocío Uzal-Varela, Paulo Pérez-Lourido, David Esteban-Gómez, Zoltán Garda, Kristof Pota, Roland Mezei, Agnès Pallier, Éva Tóth, and et al. 2021. "Expanding the Ligand Classes Used for Mn(II) Complexation: Oxa-aza Macrocycles Make the Difference" Molecules 26, no. 6: 1524. https://doi.org/10.3390/molecules26061524
APA StyleKálmán, F. K., Nagy, V., Uzal-Varela, R., Pérez-Lourido, P., Esteban-Gómez, D., Garda, Z., Pota, K., Mezei, R., Pallier, A., Tóth, É., Platas-Iglesias, C., & Tircsó, G. (2021). Expanding the Ligand Classes Used for Mn(II) Complexation: Oxa-aza Macrocycles Make the Difference. Molecules, 26(6), 1524. https://doi.org/10.3390/molecules26061524






