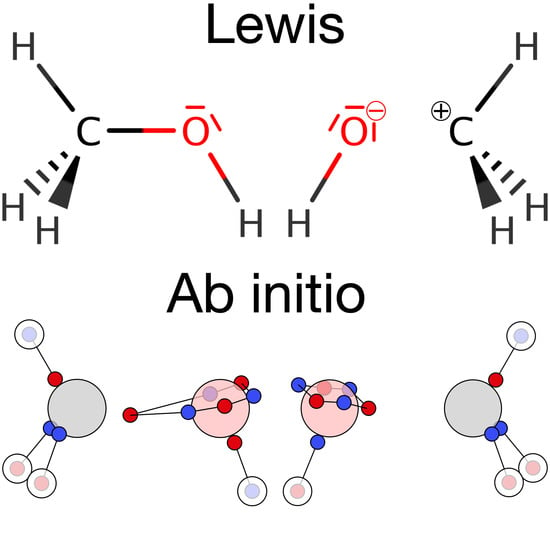
Ab Initio Dot Structures Beyond the Lewis Picture
Abstract
1. Introduction
2. Methods
2.1. The Probability Density
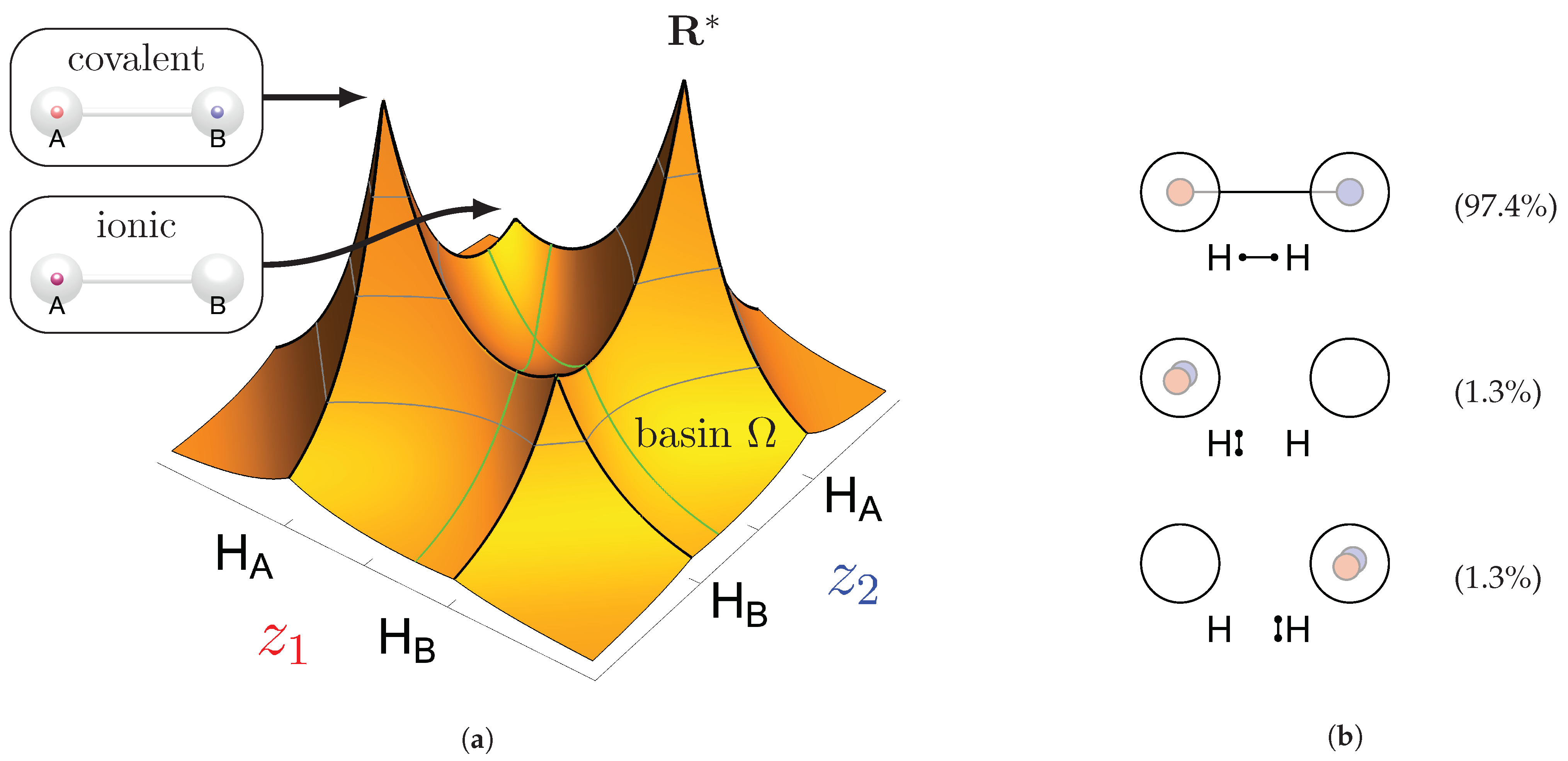
2.2. Maxima, Basins of Attraction, and Probabilities
2.3. Clustering of Maxima
2.4. Spin Correlation, Electron Motifs, and Ab Initio Dot Structures
3. Computational Approach
3.1. Wave Function Generation
3.2. Monte Carlo Integration of the Probability Density
3.3. Local Maximization
3.4. Clustering and Spin-Correlation Analysis
4. Results and Discussion
4.1. Single Bonds
4.2. Multiple Bonds
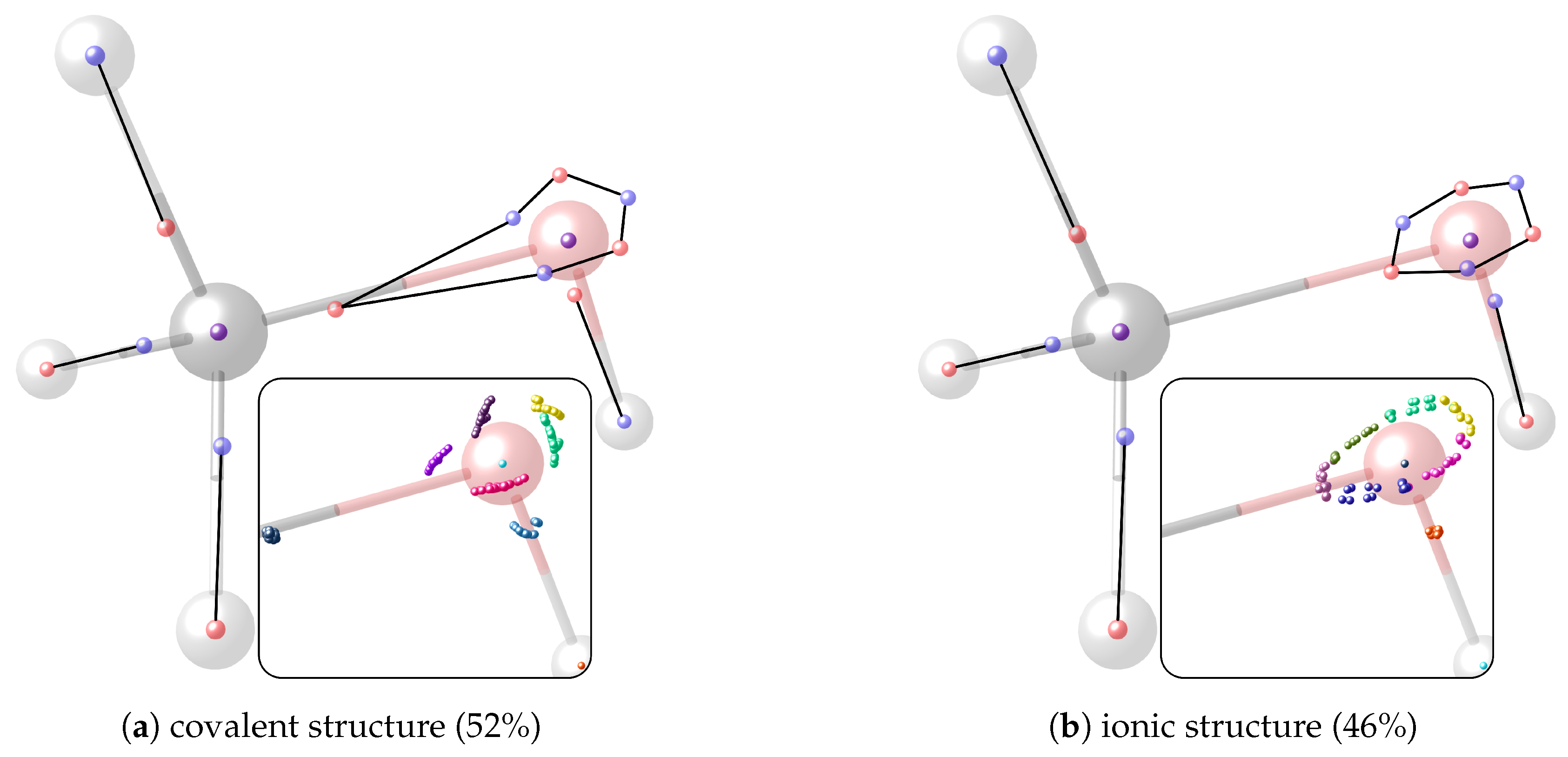
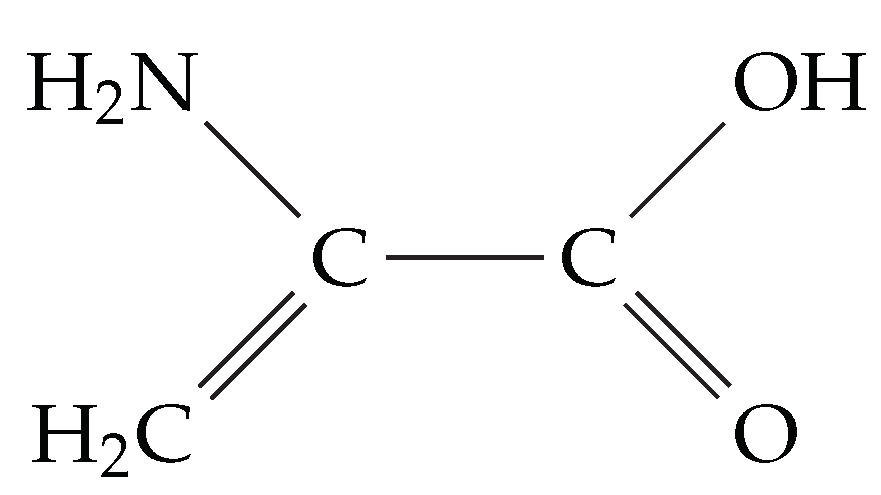
4.3. Motif Interaction in the Carboxyl Group of Acetic Acid
4.4. Motif Transferability in Dehydroalanine
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Structural Similarity

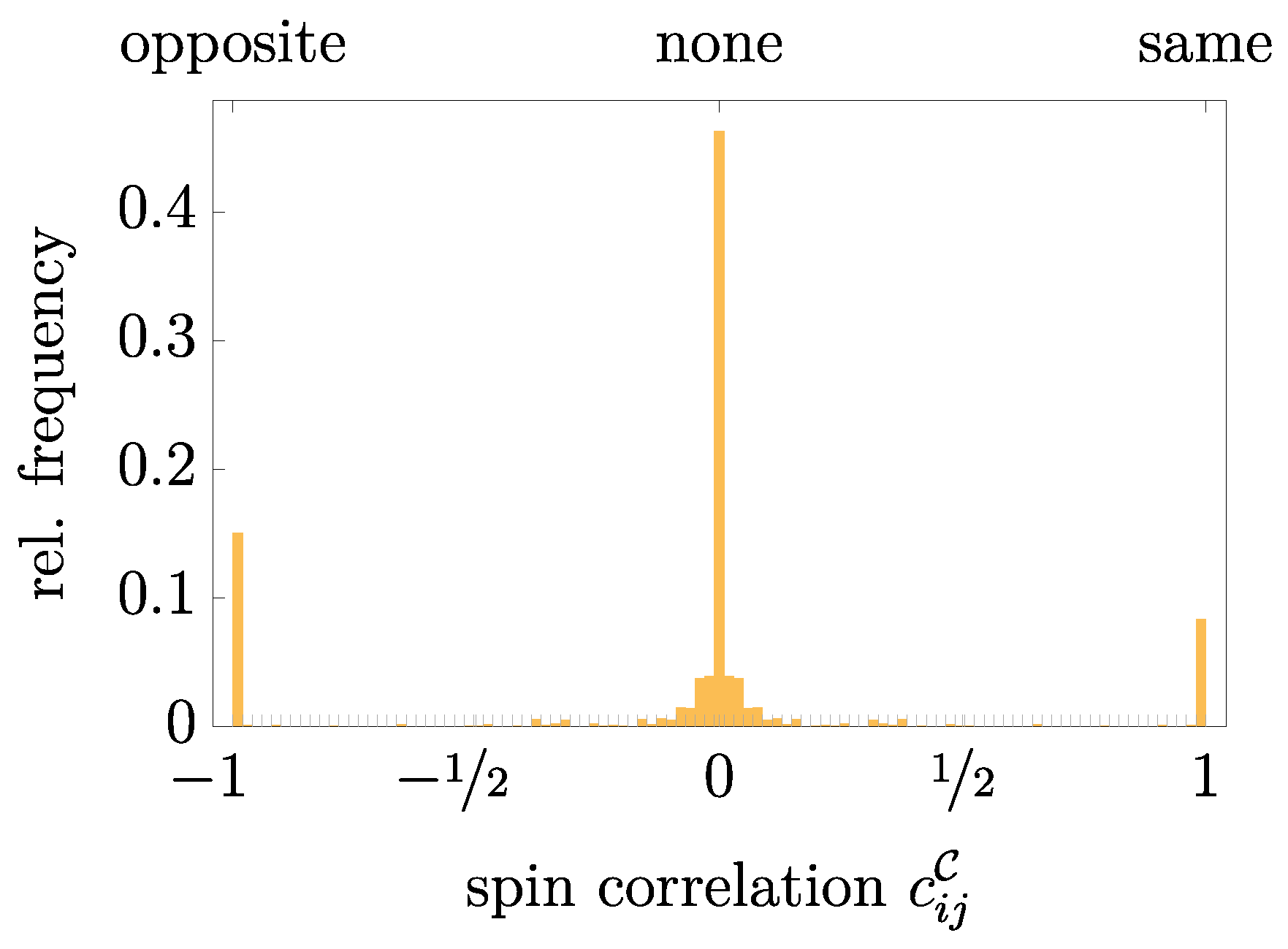
Appendix B. Spin-Correlation Distribution
Appendix C. Pre-Clustering
References
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. [Interaction of neutral atoms and homopolar bond according to quantum mechanics]. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the chemical bond. Applications of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Artmann, K. Zur Quantentheorie der gewinkelten Valenz, I. Mitteilung: Eigenfunktion und Valenzbetätigung des Zentralatoms. [On the quantum theory of angled valence, 1st report: Eigenfunctions and valence activity of the central atom]. Z. Naturforsch. A 1946, 1, 426–432. [Google Scholar] [CrossRef]
- Zimmerman, H.K.; Van Rysselberghe, P. Directed valence as a property of determinant wave functions. J. Chem. Phys. 1949, 17, 598–602. [Google Scholar] [CrossRef]
- Waitz, M.; Bello, R.Y.; Metz, D.; Lower, J.; Trinter, F.; Schober, C.; Keiling, M.; Lenz, U.; Pitzer, M.; Mertens, K.; et al. Imaging the square of the correlated two-electron wave function of a hydrogen molecule. Nat. Commun. 2017, 8, 2266. [Google Scholar] [CrossRef]
- Linnett, J.W. A modification of the Lewis–Langmuir octet rule. J. Am. Chem. Soc. 1961, 83, 2643–2653. [Google Scholar] [CrossRef]
- Scemama, A.; Caffarel, M.; Savin, A. Maximum probability domains from quantum Monte Carlo calculations. J. Comput. Chem. 2007, 28, 442–454. [Google Scholar] [CrossRef] [PubMed]
- Lüchow, A.; Petz, R. Single electron densities: A new tool to analyze molecular wavefunctions. J. Comput. Chem. 2011, 32, 2619–2626. [Google Scholar] [CrossRef]
- Lüchow, A.; Petz, R. Single Electron Densities from Quantum Monte Carlo Simulations. In Advances in Quantum Monte Carlo; American Chemical Society: Washington, DC, USA, 2012; pp. 65–75. [Google Scholar] [CrossRef]
- Lüchow, A. Maxima of |Ψ|2: A connection between quantum mechanics and Lewis structures. J. Comput. Chem. 2014, 35, 854–864. [Google Scholar] [CrossRef]
- Reuter, L.; Lüchow, A. On the connection between probability density analysis, QTAIM, and VB theory. Phys. Chem. Chem. Phys. 2020, 22, 25892–25903. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Beddall, P.M. Virial field relationship for molecular charge distributions and the spatial partitioning of molecular properties. J. Chem. Phys. 1972, 56, 3320–3329. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree–Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Liu, Y.; Frankcombe, T.J.; Schmidt, T.W. Chemical bonding motifs from a tiling of the many-electron wavefunction. Phys. Chem. Chem. Phys. 2016, 18, 13385–13394. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, J.R.; Rzepa, H.S. Foliacenes: Ab Initio Modeling of Metallocomplexes Exhibiting a Unique Form of 16-Electron, Metal-Induced Aromaticity. J. Am. Chem. Soc. 2004, 126, 14865–14870. [Google Scholar] [CrossRef] [PubMed]
- Peart, P.A.; Repka, L.M.; Tovar, J.D. Emerging Prospects for Unusual Aromaticity in Organic Electronic Materials: The Case for Methano[10]annulene. Eur. J. Org. Chem. 2008, 2008, 2193–2206. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. The molecular orbital theory of chemical valency I. The determination of molecular orbitals. Proc. R. Soc. Lond. A 1949, 198, 1–13. [Google Scholar] [CrossRef]
- England, W.; Salmon, L.S.; Ruedenberg, K. Localized molecular orbitals: A bridge between chemical intuition and molecular quantum mechanics. In Molecular Orbitals; Springer: Berlin/Heidelberg, Germany, 1970; pp. 31–123. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Lu, W.C.; Wang, C.Z.; Schmidt, M.W.; Bytautas, L.; Ho, K.M.; Ruedenberg, K. Molecule intrinsic minimal basis sets. I. Exact resolution of ab initio optimized molecular orbitals in terms of deformed atomic minimal-basis orbitals. J. Chem. Phys. 2004, 120, 2629–2637. [Google Scholar] [CrossRef]
- Knizia, G. Intrinsic atomic orbitals: An unbiased bridge between quantum theory and chemical concepts. J. Chem. Theory Comput. 2013, 9, 4834–4843. [Google Scholar] [CrossRef]
- Szalay, S. Multipartite entanglement measures. Phys. Rev. A 2015, 92, 042329. [Google Scholar] [CrossRef]
- Szalay, S.; Barcza, G.; Szilvási, T.; Veis, L.; Legeza, Ö. The correlation theory of the chemical bond. Sci. Rep. 2017, 7, 2237. [Google Scholar] [CrossRef] [PubMed]
- Savin, A.; Nesper, R.; Wengert, S.; Fässler, T.F. ELF: The electron localization function. Angew. Chem. Int. Ed. Engl. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
- Chamorro, E.; Fuentealba, P.; Savin, A. Electron probability distribution in AIM and ELF basins. J. Comput. Chem. 2003, 24, 496–504. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Francisco, E.; Blanco, M.A. An electron number distribution view of chemical bonds in real space. Phys. Chem. Chem. Phys. 2007, 9, 1087–1092. [Google Scholar] [CrossRef] [PubMed]
- Schulte, C.; Lüchow, A. Quantum Monte Carlo Calculations on the Anomeric Effect. Recent Prog. Quantum Monte Carlo 2016, 1955, 89–105. [Google Scholar] [CrossRef]
- Florek, K.; Łukaszewicz, J.; Perkal, J.; Steinhaus, H.; Zubrzycki, S. Sur la liaison et la division des points d’un ensemble fini. [On the connection and division of points of a finite set]. Colloq. Math. 1951, 2, 282–285. [Google Scholar] [CrossRef]
- Gower, J.C.; Ross, G.J.S. Minimum spanning trees and single linkage cluster analysis. Appl. Stat. 1969, 18, 54. [Google Scholar] [CrossRef]
- Kaufman, B.; Onsager, L. Crystal statistics. III. Short-range order in a binary Ising lattice. Phys. Rev. 1949, 76, 1244–1252. [Google Scholar] [CrossRef]
- Lüchow, A.; Sturm, A.; Schulte, C.; Haghighi Mood, K. Generic expansion of the Jastrow correlation factor in polynomials satisfying symmetry and cusp conditions. J. Chem. Phys. 2015, 142, 084111. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Correlation energy of an inhomogeneous electron gas: A coordinate-space model. J. Chem. Phys. 1988, 88, 1053–1062. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1-118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- O-ohata, K.; Taketa, H.; Huzinaga, S. Gaussian expansions of atomic orbitals. J. Phys. Soc. Jpn. 1966, 21, 2306–2313. [Google Scholar] [CrossRef]
- Petersson, G.A.; Zhong, S.; Montgomery, J.A.; Frisch, M.J. On the optimization of Gaussian basis sets. J. Chem. Phys. 2003, 118, 1101–1109. [Google Scholar] [CrossRef]
- Schmidt, K.E.; Moskowitz, J.W. Correlated Monte Carlo wave functions for the atoms He through Ne. J. Chem. Phys. 1990, 93, 4172–4178. [Google Scholar] [CrossRef]
- Güçlü, A.D.; Jeon, G.S.; Umrigar, C.J.; Jain, J.K. Quantum Monte Carlo study of composite fermions in quantum dots: The effect of Landau-level mixing. Phys. Rev. B 2005, 72, 205327. [Google Scholar] [CrossRef]
- Toulouse, J.; Umrigar, C.J. Optimization of quantum Monte Carlo wave functions by energy minimization. J. Chem. Phys. 2007, 126, 084102. [Google Scholar] [CrossRef]
- Lüchow, A.; Manten, S.; Diedrich, C.; Bande, A.; Scott, T.C.; Schwarz, A.; Berner, R.; Petz, R.; Sturm, A.; Hermsen, M.; et al. Amolqc. Zenodo 2021. [Google Scholar] [CrossRef]
- Kato, T. On the eigenfunctions of many-particle systems in quantum mechanics. Commun. Pure Appl. Math. 1957, 10, 151–177. [Google Scholar] [CrossRef]
- Lüchow, A. Quantum Monte Carlo methods. WIREs Comput. Mol. Sci. 2011, 1, 388–402. [Google Scholar] [CrossRef]
- Umrigar, C.J.; Nightingale, M.P.; Runge, K.J. A diffusion Monte Carlo algorithm with very small time-step errors. J. Chem. Phys. 1993, 99, 2865–2890. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Heuer, M.A.; Reuter, L. InPsights. Zenodo 2020. [Google Scholar] [CrossRef]
- Munkres, J. Algorithms for the assignment and transportation problems. J. Soc. Ind. Appl. Math. 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Wong, J.K. A new implementation of an algorithm for the optimal assignment problem: An improved version of Munkres’ algorithm. BIT Numer. Math. 1979, 19, 418–424. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Heuer, M.A.; Reuter, L.; Lüchow, A. A Dataset for Probability Density Analysis Containing 30 Small Molecules and Dehydroalanine. Nat. Human Behav. 2020. Available online: https://osf.io/6z2j9 (accessed on 31 December 2020). [CrossRef]
- Shaik, S.; Danovich, D.; Wu, W.; Hiberty, P.C. Charge-shift bonding and its manifestations in chemistry. Nat. Chem. 2009, 1, 443–449. [Google Scholar] [CrossRef]
- Wu, W.; Gu, J.; Song, J.; Shaik, S.; Hiberty, P.C. The inverted bond in [1.1.1]propellane is a charge-shift bond. Angew. Chem. 2009, 121, 1435–1438. [Google Scholar] [CrossRef]
- Shaik, S.; Danovich, D.; Wu, W.; Su, P.; Rzepa, H.S.; Hiberty, P.C. Quadruple bonding in C2 and analogous eight-valence electron species. Nat. Chem. 2012, 4, 195–200. [Google Scholar] [CrossRef]
- Edmiston, C.; Ruedenberg, K. Localized atomic and molecular orbitals. Rev. Mod. Phys. 1963, 35, 457–464. [Google Scholar] [CrossRef]
- Foster, J.M.; Boys, S.F. A quantum variational calculation for HCHO. Rev. Mod. Phys. 1960, 32, 303–304. [Google Scholar] [CrossRef]
- Boys, S.F. Construction of some molecular orbitals to be approximately invariant for changes from one molecule to another. Rev. Mod. Phys. 1960, 32, 296–299. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 94, 117, 125. [Google Scholar]


| H | B | C | N | O | F | |
|---|---|---|---|---|---|---|
| H | 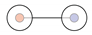 1c: (%) |  2c: (%) |  3c: (%) | 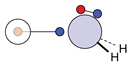 4c: (%) | 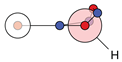 5c: (%) | 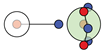 6c: (%) |
| B |  7c: (%) | 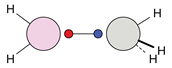 8c: (%) | ||||
| C | 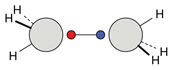 12c: (%) | 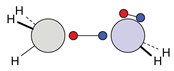 13c: (%) | 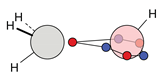 14c: (%) | 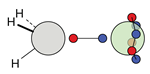 15c: (%) | ||
| N | 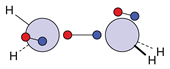 16c: (%) | 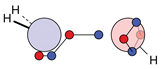 17c: (%) | 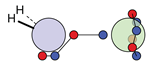 18c: (%) | |||
| O |  5c: (%) | 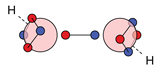 19c: (%) | 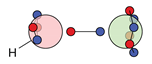 20c: (%) | |||
| F |  6c: (%) | 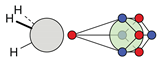 15c: (%) | 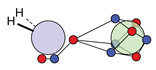 18c: (%) | 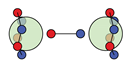 21c: (%) |
| H | B | C | N | O | F | |
|---|---|---|---|---|---|---|
| H |  1i: (%) |  2i (%) |  3i: (%) | 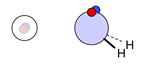 4i: (%) | 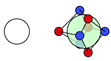 6i: (%) | |
| B |  9i: (%) | 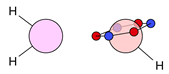 10i: (%) | 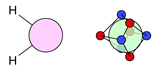 11i: (100%) | |||
| C | 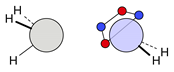 13i: (%) | 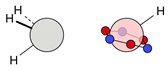 14i (%) | 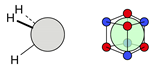 15i: (%) | |||
| N | 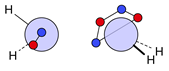 16i: (%) | 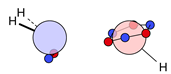 17i: (%) | 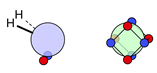 18i: (%) | |||
| O |  19i: (%) |  20i: (%) | ||||
| F | 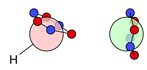 20i’: (%) | 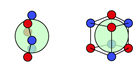 21i: (%) |
| C | N | O | |
|---|---|---|---|
| Covalent | |||
| C |  22c: (%) | 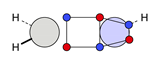 23c: (%) | 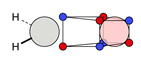 24c: (%) |
| N | 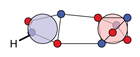 26c: (%) | ||
| C | 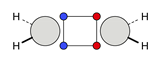 22c: (%) |  23c: (%) | 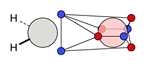 24c: (%) |
| N | 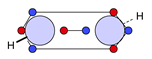 25c: (100%) | 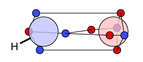 26c: (%) | |
| C |  22c: (%) | ||
| Ionic | |||
| C | 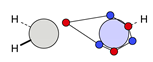 23i: (%) | 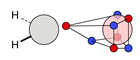 24i: (%) | |
| N | 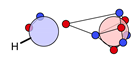 26i: (%) | ||
| C | N | |
|---|---|---|
| Covalent | ||
| C | 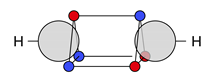 27c: (%) |  28c: (%) |
| N | 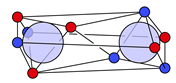 29c: (%) | |
| C | 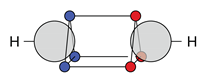 27c: (%) | 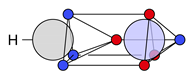 28c: (%) |
| N | 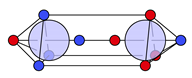 29c: (%) | |
| C |  27c: (%) |  28c: (%) |
| N | 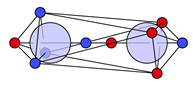 29c: (%) | |
| C | 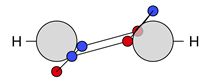 27c: (%) | |
| Ionic | ||
| C | 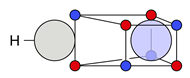 28i: (%) | |
| /% | ||
|---|---|---|
| 14i-5c | 24i | 30 |
| 14c-5i | 24i | 26 |
| 14c-5c | 24i | 22 |
| 14i-5i | 24i | 16 |
| 14i-5c | 24c | 4 |
| Group | Motif | /% | /% |
|---|---|---|---|
| 22c or 22c | 93 | 86 | |
| 22c | 6 | 14 | |
| 13c | 73 | 82 | |
| 13i | 27 | 18 | |
| 14i-5c and 24i | 43 | 30 | |
| 14c-5i and 24i | 25 | 26 | |
| 14c-5c and 24i | 11 | 22 | |
| 14i-5i and 24i | 19 | 16 | |
| 14i-5c and 24c | 3 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heuer, M.A.; Reuter, L.; Lüchow, A. Ab Initio Dot Structures Beyond the Lewis Picture. Molecules 2021, 26, 911. https://doi.org/10.3390/molecules26040911
Heuer MA, Reuter L, Lüchow A. Ab Initio Dot Structures Beyond the Lewis Picture. Molecules. 2021; 26(4):911. https://doi.org/10.3390/molecules26040911
Chicago/Turabian StyleHeuer, Michael A., Leonard Reuter, and Arne Lüchow. 2021. "Ab Initio Dot Structures Beyond the Lewis Picture" Molecules 26, no. 4: 911. https://doi.org/10.3390/molecules26040911
APA StyleHeuer, M. A., Reuter, L., & Lüchow, A. (2021). Ab Initio Dot Structures Beyond the Lewis Picture. Molecules, 26(4), 911. https://doi.org/10.3390/molecules26040911