Next Article in Journal
Effect of the Supporting Electrolyte on Chloroform Reduction at a Silver Electrode in Aqueous Solutions
Next Article in Special Issue
Non-Equilibrium Thermodynamics View on Kinetics of Autocatalytic Reactions—Two Illustrative Examples
Previous Article in Journal
Fate of Biodegradable Engineered Nanoparticles Used in Veterinary Medicine as Delivery Systems from a One Health Perspective
Previous Article in Special Issue
Hydrogenation of CO2 Promoted by Silicon-Activated H2S: Origin and Implications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 3
10.3390/molecules26030524
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

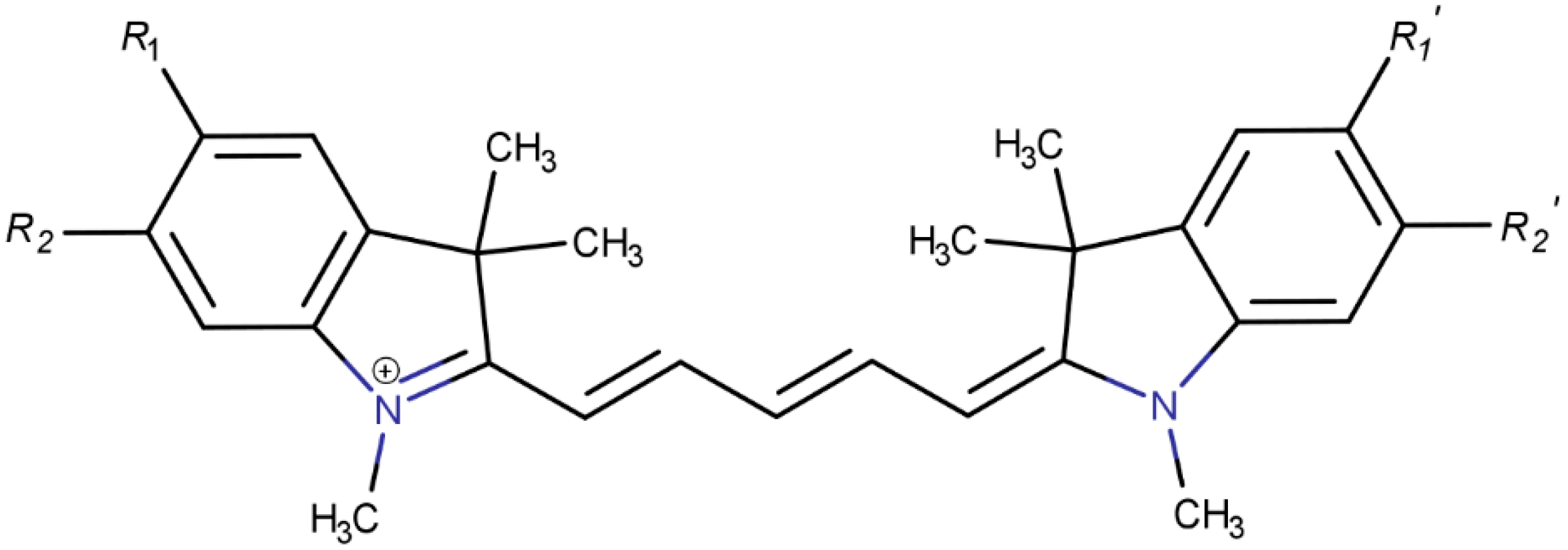
Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations

by
Austin Biaggne
1,
William B. Knowlton
1,2,
Bernard Yurke
1,2,
Jeunghoon Lee
1,3 and
Lan Li
1,4,*
1
Micron School of Materials Science and Engineering, Boise State University, Boise, ID 83725, USA
2
Department of Electrical and Computer Engineering, Boise State University, Boise, ID 83725, USA
3
Department of Chemistry and Biochemistry, Boise State University, Boise, ID 83725, USA
4
Center for Advanced Energy Studies, Idaho Falls, ID 83401, USA
*
Author to whom correspondence should be addressed.
Molecules 2021, 26(3), 524; https://doi.org/10.3390/molecules26030524
Submission received: 8 December 2020 / Revised: 11 January 2021 / Accepted: 15 January 2021 / Published: 20 January 2021
(This article belongs to the Special Issue 25th Anniversary of Molecules—Recent Advances in Physical Chemistry)
Browse Figures
Versions Notes

Abstract

:
The aggregation ability and exciton dynamics of dyes are largely affected by properties of the dye monomers. To facilitate aggregation and improve excitonic function, dyes can be engineered with substituents to exhibit optimal key properties, such as hydrophobicity, static dipole moment differences, and transition dipole moments. To determine how electron donating (D) and electron withdrawing (W) substituents impact the solvation, static dipole moments, and transition dipole moments of the pentamethine indocyanine dye Cy5, density functional theory (DFT) and time-dependent (TD-) DFT calculations were performed. The inclusion of substituents had large effects on the solvation energy of Cy5, with pairs of withdrawing substituents (W-W pairs) exhibiting the most negative solvation energies, suggesting dyes with W-W pairs are more soluble than others. With respect to pristine Cy5, the transition dipole moment was relatively unaffected upon substitution while numerous W-W pairs and pairs of donating and withdrawing substituents (D-W pairs) enhanced the static dipole difference. The increase in static dipole difference was correlated with an increase in the magnitude of the sum of the Hammett constants of the substituents on the dye. The results of this study provide insight into how specific substituents affect Cy5 monomers and which pairs can be used to engineer dyes with desired properties.

1. Introduction

Dyes in natural [1,2,3] and synthetic [4,5,6,7,8] systems have been shown to exhibit molecular aggregation behavior of which exciton delocalization is a signature. Exciton delocalization can be described as the collective sharing of an electronic excitation over dyes within an aggregate due to the transition dipole-dipole coupling between the dyes. Upon aggregation, the dyes can assume various stacking geometries that can be best described in the context of the simplest dye aggregate—the dimer. Three idealized dimer aggregate stacking geometry cases that are commonly presented, as related to the transition dipole moment of one dye relative to the other dye, are: head to tail (J-aggregates [9,10,11,12]), stacked or face-to-face (H-aggregates [10,11,13]), and oblique, in which the transition dipole moments (polarizations) of dyes are at 90 degrees to one another [10,11,14,15]. The geometric orientation of the transition dipole moments and subsequent transition dipole-dipole coupling manifests as changes in excitonic behavior. Potential applications of excitonic properties of dye aggregates include organic photovoltaics [16], non-linear optics [17], and quantum computing [18,19]. The functionality of excitonic devices utilizing dye aggregate properties is therefore determined by the dynamics of the excitons in the material, such as exciton exchange between the dye aggregates and exciton-exciton interactions.
The dynamics of excitons that exist in an aggregate of molecules are characterized by the Frenkel Hamiltonian [20], which describes the mechanisms and associated energy terms of exciton hopping and exciton-exciton interactions. The exciton exchange energy and two-body exciton interaction energy determine the Hamiltonian. Assuming the dipole approximation, the exciton exchange energy, associated with the transfer of an exciton between two adjacent dyes, is enhanced with increasing transition dipole moments (μ) of the dye monomers. Similarly, the two-body exciton interaction energy, associated with changes in the static dipole-dipole coupling of the dyes with differing ground and excited state charge distributions, increases with increasing static dipole difference (Δd) between the dye monomer’s ground and excited states [20]. Both energy terms also increase as the dye-dye separations decrease. Because of the dependence of the Frenkel Hamiltonian energies on dye monomer properties, enhancement of the aggregate’s excitonic properties can be facilitated by the increase of μ, Δd, and aggregation ability of the dye monomers.
Because of the strong excitonic coupling leading to exciton delocalization found in cyanine dye aggregates, the structural, photophysical, and excitonic properties of polymethine indocyanine dyes, such as Cy3 and Cy5, incorporated into DNA structures have been studied experimentally [7,8,21,22,23,24]. Cy3 and Cy5 both contain polymethine bridges connecting two indolenine groups with a delocalized charge. Cy3 and Cy5 have similar structures, their only difference is the number of carbons in the polymethine bridge (three for Cy3 and five for Cy5). In practice, DNA is used as a scaffold to better control the number and orientation of the dyes and bring them within close enough proximity to induce exciton delocalization. Markova et al. demonstrated that Cy5 dyes internalized in DNA duplexes exhibited J-like absorption properties [21]. Similarly, Cannon et al. measured the absorption of Cy5 dyes incorporated into DNA duplexes and found that at low salt concentrations, Cy5 dyes aggregated in J-dimers [7]. By increasing the salt concentration, the DNA coupled to form tetramer aggregates in which the dyes oriented in H-like aggregates and exhibited strong exciton delocalization. Furthermore, it was found that dyes brought within 2 base-pairs of each other exhibit Davydov splitting [7]. In a later study, Cannon et al. found that Cy5 dyes covalently bound in DNA Holliday Junctions exhibited strong Davydov splitting and exciton delocalization [8]. Cunningham et al. also found that Cy3 dyes brought within 2 base-pairs of each other exhibit Davydov splitting and exciton delocalization and that local DNA sequences in proximity to the dyes affected the resulting dye orientations [22]. Nicoli et al. demonstrated that Cy3 dyes covalently attached to DNA backbones exhibited H-like aggregate properties which could be varied by changing the dye-dye separations and DNA rigidity [23].
Studies have shown that the addition of substituents can alter the permanent molecular dipole moments and aggregation properties of molecules [25,26,27,28]. Misawa et al. measured large changes in the static dipole moments of pseudoisocyanine bromide (PIC-Br) upon J-aggregation, revealing that cyanine molecules had the ability to achieve large static dipole moments [25]. Utilizing Stark spectroscopy, Marder et al. measured large static dipole moments (~40 Debye) of a normally symmetric β-carotene molecule [26]. The large static dipole values were engineered by inducing electronic asymmetry into the β-carotene, which augmented the electron withdrawing ability of one side of the otherwise symmetric molecule. This could also happen to cyanine molecules. Garoff et al. found that alterations of the heterocyclic groups of cationic cyanine dyes yields varying aggregation on DNA [27]. Quinoline substituents outperformed benzothiazole, benzoxazole, and dimethylindole in terms of aggregation ability. By incorporating various substituent types into a cyanine dye, Stadler et al. demonstrated significant substituent effects on dye-aggregation [28]. Methoxy and fluoro groups attached to the ends of the cyanine dyes improved dimerization in an aqueous solution and in DNA.
In previous computational studies, researchers have used density functional theory (DFT) and time-dependent density functional theory (TD-DFT) methods to calculate the structural and electronic properties of organic molecules [29,30,31]. Fothergill et al. successfully used TD-DFT to calculate the vibrationally-resolved Cy5 monomer absorption spectrum that yielded a max absorption energy within 0.007 eV of experimental values [29]. Cao et al. used DFT and TD-DFT to perform a systematic analysis of the effects of an amino group on the electronic properties of Cy3, Cy5, Cy7, and Cy9 dyes when the amino group was placed at different locations along the polymenthinic chain [30]. The amino group substituent altered the geometry and spectral properties of the dyes, yielding a wide range of peak absorption energies [30]. The effects of single, double, and quadruple substitutions of substituents on the excitation properties of anthracene molecules were also explored using DFT and TD-DFT by Abou-Hatab et al. [31]. The addition of substituents to the anthracene molecule overall red-shifted excitation energies and raised oscillator strengths [31]. The excitation energies of modified anthracene were found to be correlated with the Hammett constants of the substituents [31]. Quantum chemical calculations of ground and excited state dipole moments of coumarin [32] and quinoline [33] molecules have also been shown to agree with experimentally derived values.
The purpose of this study is to quantify how substituents affect the solubility and electronic properties of Cy5 dye monomers using DFT-based methods. Dye aggregate simulations using molecular dynamics are ongoing and beyond the scope of this manuscript. In both experimental and computational studies, the impacts of substituents on dyes and their excited state properties are crucial but have not been fully addressed. Specifically, computational studies on the relationships of hydrophobicity, μ and Δd of substituted Cy5 dyes have not been performed. This paper demonstrates that the hydrophobicity and Δd of a Cy5 dye can be altered without degrading μ. The modification of Cy5 hydrophobicity is desirable to promote denser dye packing and the increase of Δd would promote larger exciton-exciton interactions in the Cy5 aggregates. However, to preserve exciton exchange energy, μ should not be decreased upon substitution. To understand the effects of various substituents on the electronic properties of Cy5, substituents with varying electron donating and withdrawing strengths were added to the dye. We performed DFT and TD-DFT calculations for each substituted Cy5 dye to calculate the Gibbs free energy of solvation (ΔGsolv), Δd, and μ in comparison with pristine (unsubstituted) Cy5. Substituted Cy5 dyes exhibiting large Δd were selected for further calculations, in which the number of substituents was doubled to determine the effects of multiple substituents on the solvation and dipole properties. Please note that our study focuses on the computational screening of potential Cy5 substituents that could increase the Δd value of pristine Cy5 but not decrease its μ value.

2. Computational Methods

Excited state properties are dependent on the exchange-correlation functionals chosen [34,35,36,37,38,39]. Jacquemin studied the viability of various exchange-correlation functionals for the ground and excited state calculations of 31 different molecules as well as increasingly long push-pull chains [35]. It was determined that the M06-2X and CAM-B3LYP functionals yielded excess dipoles (synonymous with static dipole differences) that strongly correlated to approximate second order coupled clusters double (CC2) methods [35]. Kawauchi et al. found that the prediction of absorption spectra for a set of organic dyes were more accurately predicted using the M06-2X functional than others [36]. Similarly, Laine et al. found that the M06-2X functional could be used to accurately predict experimental bathochromic shifts of BODIPY dyes [37]. Garcia et al. performed a series of TD-DFT calculations on a family of push-pull compounds and found that, out of the functionals tested, CAM-B3LYP was one of the functionals that yielded the best agreement with experimental vertical absorption energies [38]. Kerkines et al. also found that CAM-B3LYP gave good agreement with experiment for excited state properties for the push-pull organic dye DMA-DPH [39].
Due to the common and successful applications of M06-2X and CAM-B3LYP, both functionals were used for the calculations in the present work for comparison. All dyes were optimized in the ground state using the M06-2X functional [35,36,37,40] to a residual force of 4.5 × 10−4 Hartree/Bohr with a validation to be at minima through ground state vibrational analysis. Single point excited state calculations were performed on the optimized ground state structures to obtain vertical transitions to the lowest excited singlet states of the dyes using the M06-2X and CAM-B3LYP functionals. Both are hybrid functionals. However, M06-2X is defined as a global hybrid [40] while CAM-B3LYP is defined as a range-separated hybrid functional [41]. Calculations were performed using the 6 − 31 + g(d,p) basis set due to its common usage in similar studies [37,42,43] and to compromise between accuracy and computational resources. The Gaussian16 ab initio quantum chemistry package was employed [44] and initial molecule structures were built using the GaussView GUI [45].
To determine the effect of substituents on the solubility of Cy5, vacuum and implicit solvation calculations were conducted to determine the ΔGsolv of each substituted Cy5 dye. In general, ΔGsolv is the amount of energy required to dissolve a dye in solvent. Similar to prior DFT studies [46,47], ΔGsolv is correlated to solubility, where the more negative ΔGsolv is, the more soluble the molecule [46,47]. To calculate ΔGsolv, the dyes were fully relaxed in vacuum and solvent in the ground state. The universal Solvation Model based on Density (SMD) [48] variation of the integral equation formalism polarizable continuum model (IEFPCM) [49,50] was used to model the dyes in solvents for solvation energy calculations. Four solvents were used, including water, pyridine, quinoline and isoquinoline. The last three solvents were used to mimic the effect of surrounding DNA in comparison with water solvation due to their similar structures to DNA nucleobases. Pyridine, quinoline, and isoquinoline were used to roughly estimate how various substituents on Cy5 dyes affect the dye’s propensity to intercalate into DNA structures. Despite this being a relatively simple model, it could provide insight into dye-DNA interactions for further studies.
The ΔGsolv for pristine and substituted dyes was determined as [29,47]:
ΔGsolv = Esolvated − Evacuum
where Esolvated is the total energy of the dye in implicit solvent and Evacuum is the total energy of the dye in vacuum. A negative ΔGsolv signifies that the solvation is exothermic and an amount of energy is released. Calculations were also performed using the Gibbs free energies of the dyes in solvent and vacuum instead of the total energies, similar to Abdur Rauf et al. [46]. However, it was found that the energy corrections were minimal and trends between data sets remained the same, as shown in Figure S1.
Calculations of the ground and excited state electronic properties (i.e., dipole properties) were performed using the IEFPCM solvation model without SMD variation [51,52,53] in water solvent. The ground state optimized structures were used for linear-response, single-point, excited state calculations [54]. To quantify the effects of substituents on μ and Δd, the single point excited state calculations were used to determine excited state dipole moments and μ. Using the static ground state and excited state dipole moments, Δd was calculated as [35]:
Δd = [(dxES − dxGS)2 + (dyES − dyGS)2 + (dzES − dzGS)2]1/2
where dij is the Cartesian dipole moment vector component, i refers to the Cartesian x, y, or z direction, and j is either GS or ES (ground state or excited state).
Hydrogens at the ends of a Cy5 dye, labeled as R in Figure 1, were replaced with the substituents in Table 1. The substitution of the hydrogens at the R sites produces conjugated systems with increased polarity and asymmetry. As shown in Table 1, each substituent is identified as either a donating or withdrawing group based on its empirically derived Hammett Constant, σp [55,56]. The magnitude of σp quantifies the electron donating or withdrawing ability of a substituent. Negative values correspond to electron donating groups and positive values correspond to electron withdrawing groups [31,57]. In total, the substituents were paired into 54 combinations, which could be categorized as donating-donating (D-D), withdrawing-withdrawing (W-W), and donating-withdrawing (D-W) pairs. Firstly, hydrogens on the R1 and R1’ sites were replaced. In subsequent calculations, dyes that exhibited the largest Δd were doubled. The second pair of substituents were attached at the R2 and R2’ sites so that R1 = R2 and R1’ = R2’.

3. Results

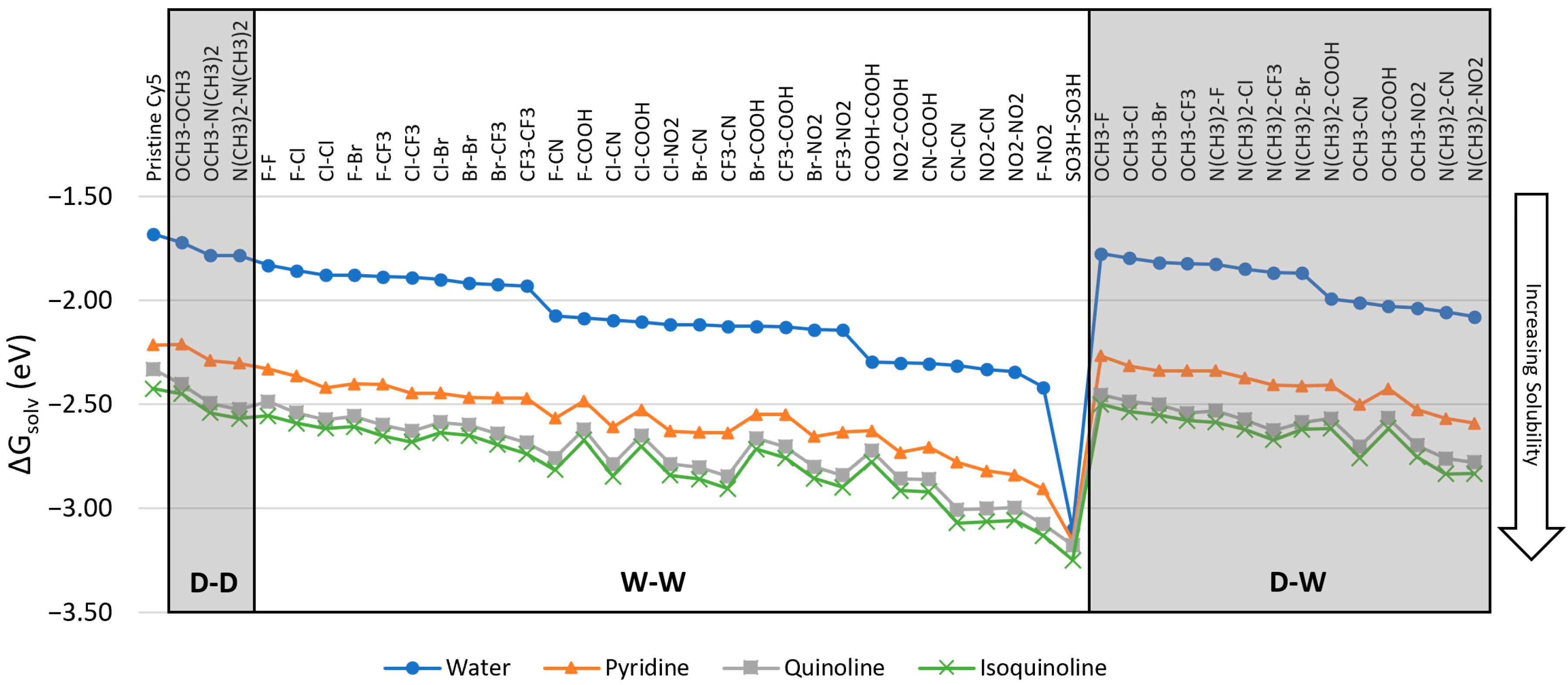
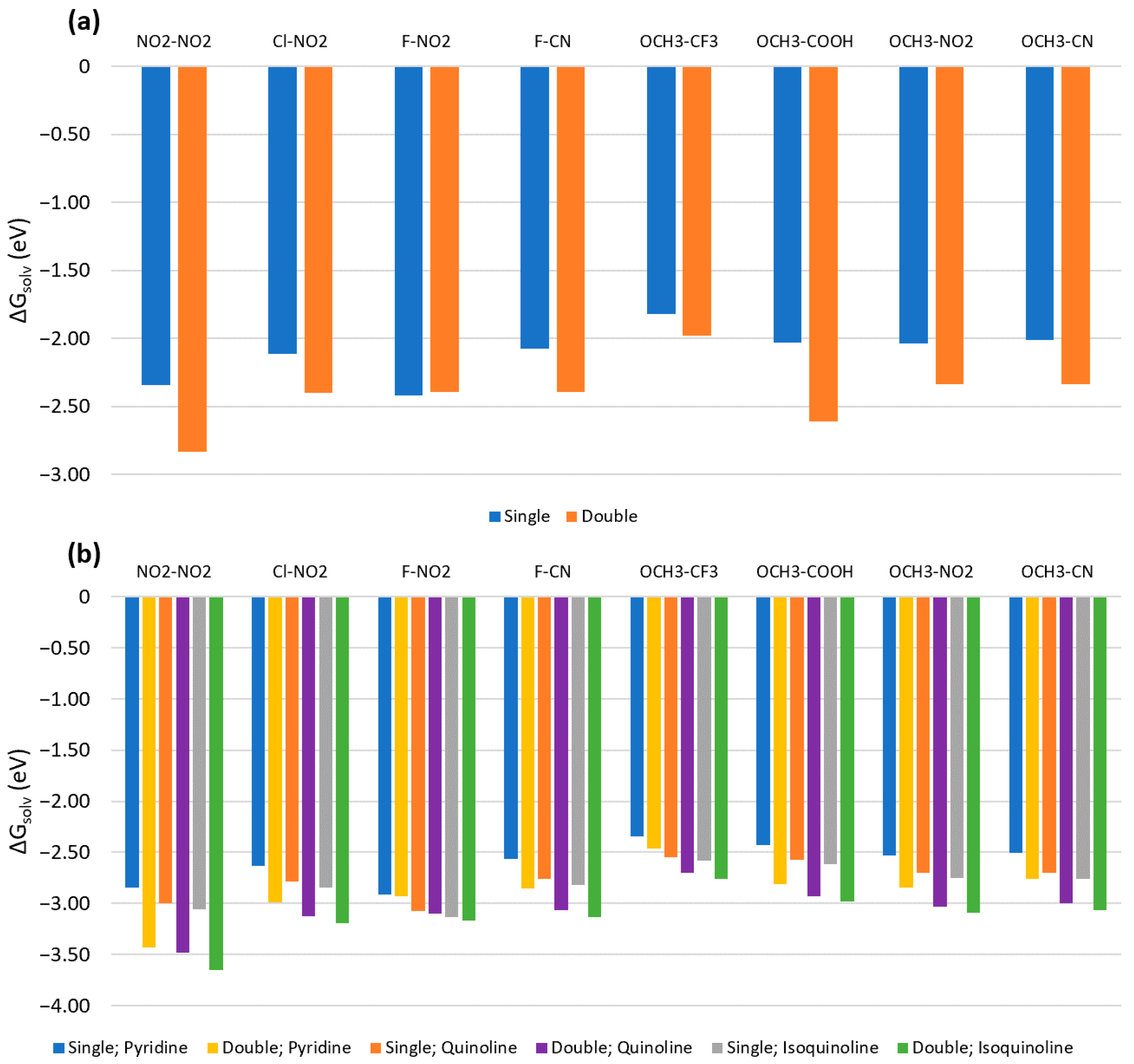
3.1. Solvation Energies

The calculated Gibbs free energies of solvation, ΔGsolv, are shown in Figure 2 for implicit water, pyridine, quinoline, and isoquinoline solvents. Values of ΔGsolv were calculated to estimate the solubility of the dyes in the given solvent. The dyes are grouped according to their substituent’s classification and ordered from less negative to more negative ΔGsolv values in water. All ΔGsolv values were calculated using Equation (1) with the substituent pairs located at the R1 and R1’ positions of Cy5 (Figure 1). The calculations for ΔGsolv, μ, and Δd were conducted using the M06-2X and CAM-B3LYP functionals. It was found that both M06-2X and CAM-B3LYP yield similar values and the overall same trends for ΔGsolv, μ, and Δd, and so only the results for M06-2X are presented. For a comparison between M06-2X and CAM-B3LYP, see the Supporting Information.
Pristine Cy5 has the least negative ΔGsolv. Like other studies [46,47], this indicates that pristine Cy5 is the most hydrophobic (i.e., least soluble). Many substituted Cy5 dyes containing D-D, W-W, and D-W pairs have comparable solubility to pristine Cy5, however, numerous substituent pairs make ΔGsolv more negative. A large number of W-W pairs exhibit the most negative solvation energies and are therefore taken to be the most hydrophilic (i.e., most aqueously soluble) and thus may hinder dye aggregation. However, numerous W-W pairs do not follow this trend, all of which are a combination of F, Cl, Br, and CF3 substituents. Specifically, the first 10 W-W pairs shown in Figure 2 exhibit ΔGsolv comparable to D-D and D-W pairs. The next 11 pairs have ΔGsolv similar to D-W pairs. The ΔGsolv values of the first 8 D-W pairs (which also contain F, Cl, Br, or CF3) are similar to those of the D-D pairs and the first 10 W-W pairs. The SO3H-SO3H-substituted Cy5 has the most negative ΔGsolv and is therefore the most soluble in water.
Comparing the values of ΔGsolv in water and other solvents, the dyes solvated in water exhibit less negative ΔGsolv than those in pyridine, quinoline, and isoquinoline. However, the substituents follow the same solubility trends as in water. In addition, the dyes prefer to form solutions in pyridine, quinoline, and isoquinoline due to the more negative ΔGsolv values of the dyes in these solvents compared to water. These three solvents are taken to mimic the structures of base pairs of DNA. It can therefore be inferred that substituted Cy5 dyes energetically prefer to be surrounded by DNA nucleobases (as mimicked by pyridine, quinoline, and isoquinoline) rather than to exist freely in aqueous solvent. Our predictions agree well with the molecular dynamics simulations conducted by Stennet et al. [58] and Cunningham et al. [22] in which cyanine dyes doubly linked to DNA duplexes solvated in water intercalated into the DNA structures to form dimers. Furthermore, the dyes with higher hydrophobicity may exhibit increased aggregation in DNA duplexes, leading to shorter dye-dye separations. This has been observed experimentally by Stadler et al. [28]. Our computational results suggest that D-D and D-W substituent pairs should exhibit denser dye packing than the other substituted dyes, resulting in comparatively enhanced dipole-dipole couplings, excitonic exchange energies, and two-body exciton interactions.

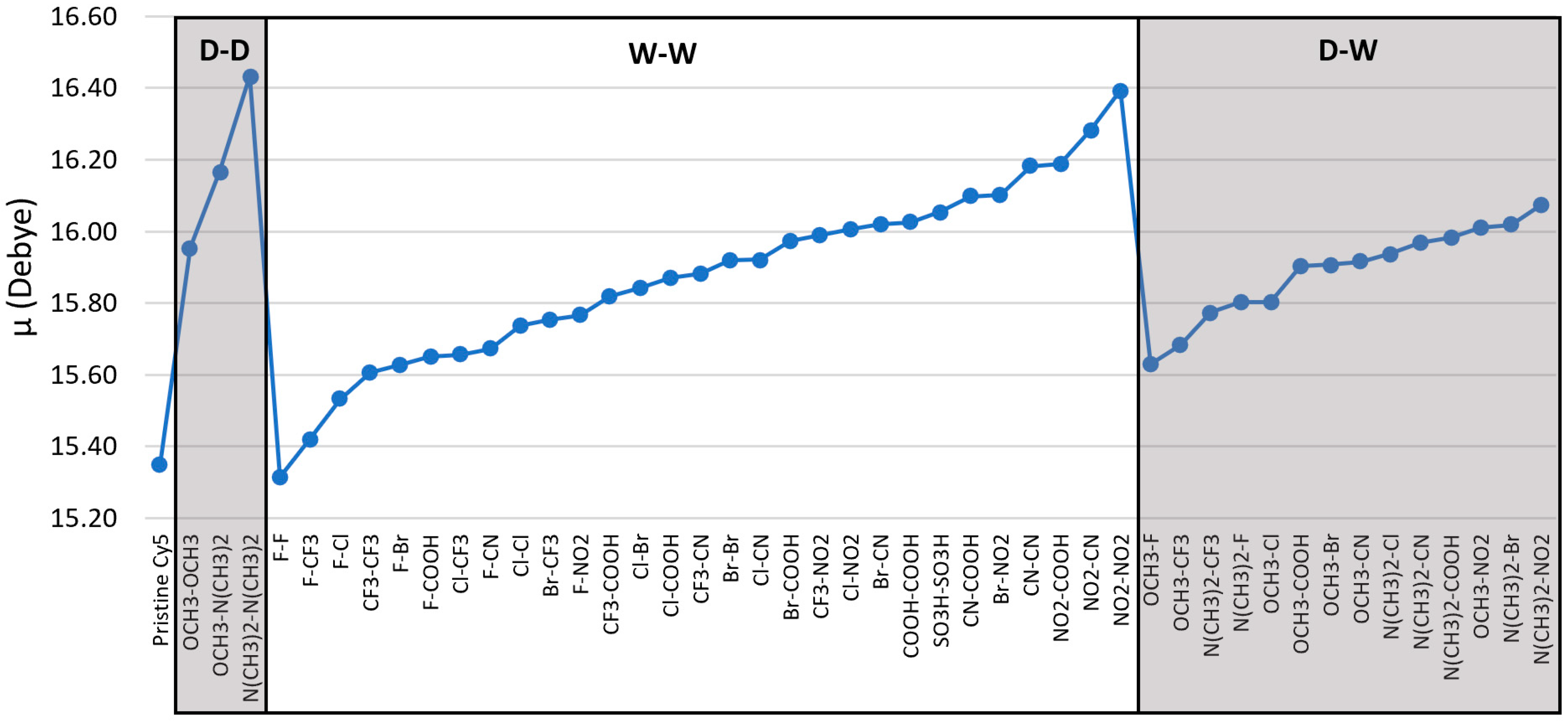
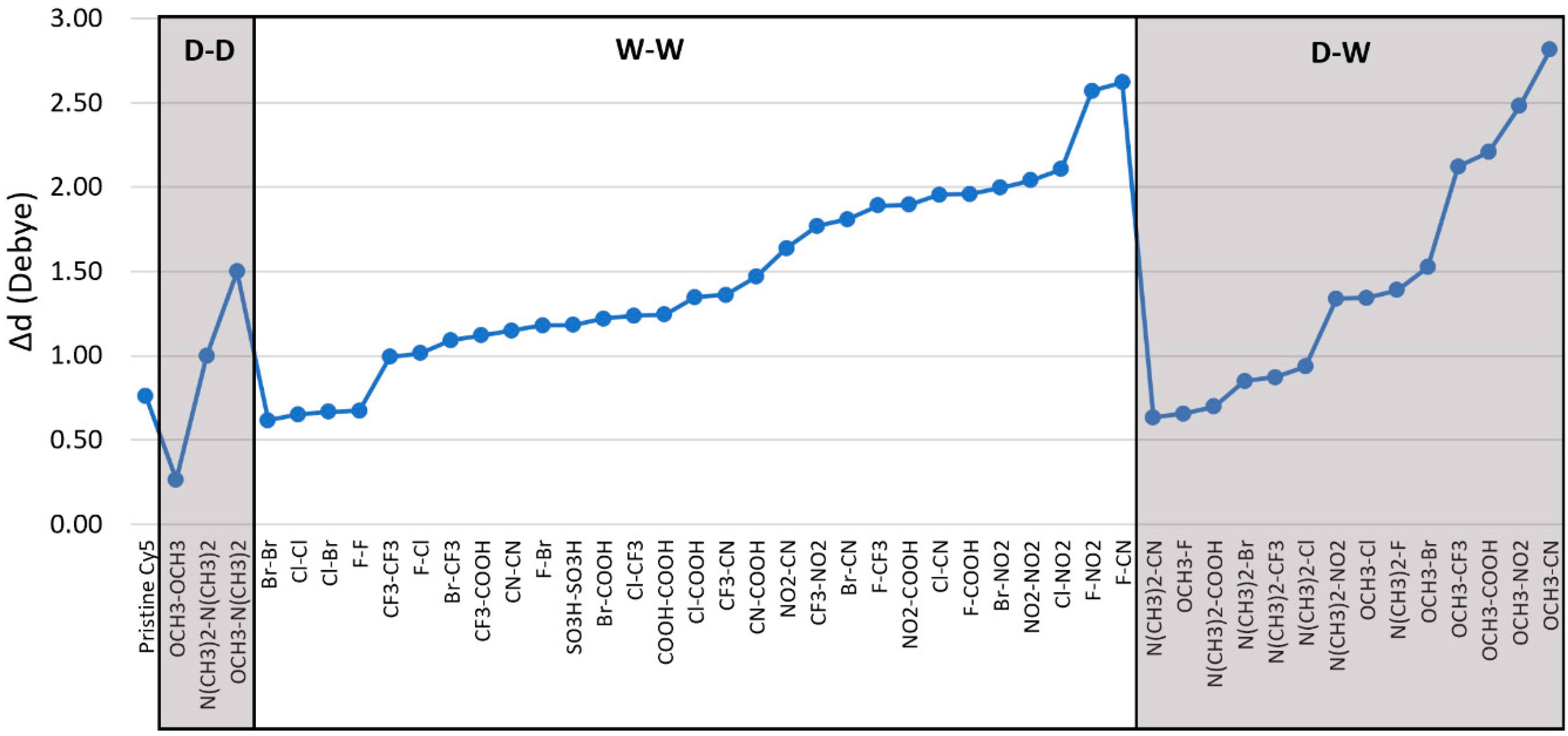
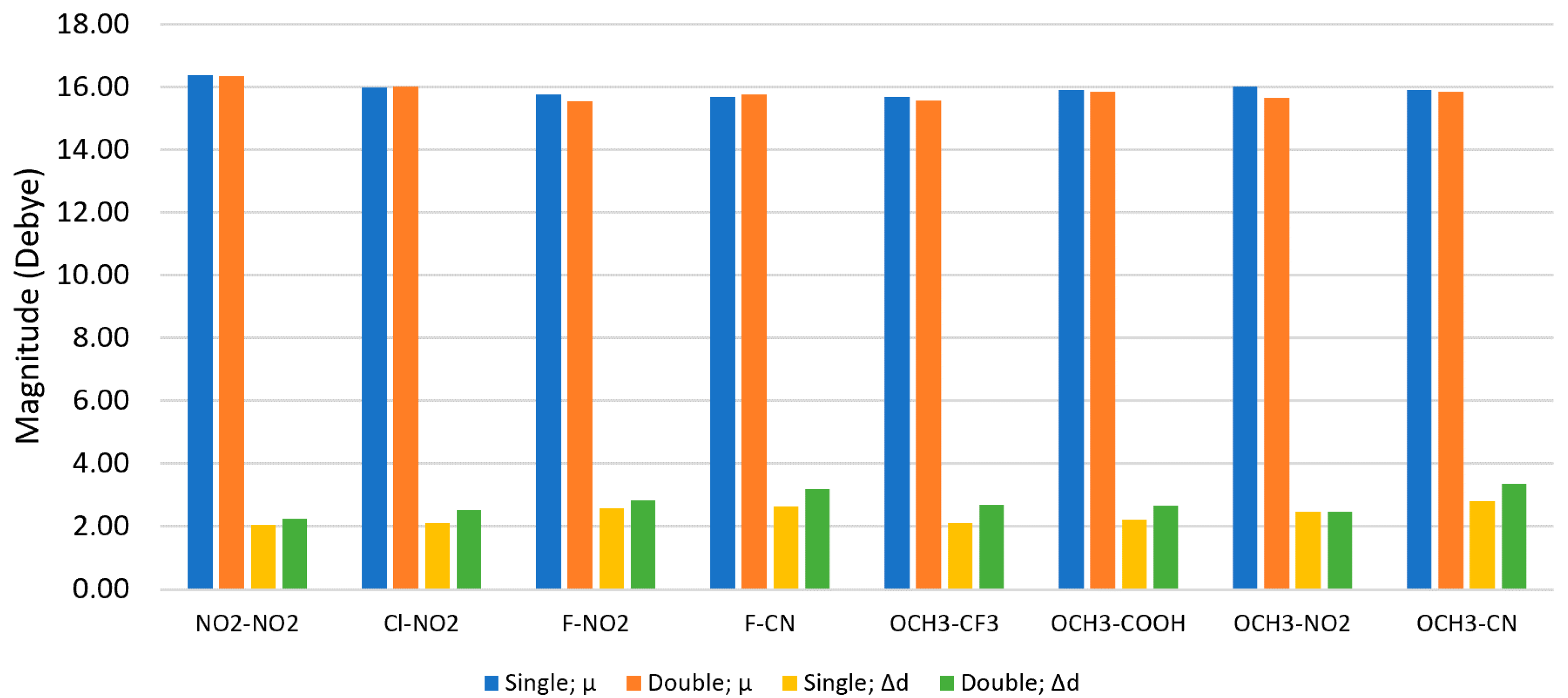
3.2. Dipole Moments

To determine the effects of electron donating and electron withdrawing substituents on the dipole properties of Cy5, DFT and TD-DFT methods were employed to calculate the μ and Δd of pristine and substituted Cy5 dyes. The μ and Δd shown were calculated using the M06-2X functional. The calculated value of μ for pristine Cy5 is 15.35 D, whose vector is primarily along the long axis (pentamethine chain) of the Cy5 dye. The calculated value of μ reasonably agrees with the experimental value of 13.4 D calculated from our colleague’s experimental monomer absorption data. Figure 3 shows that most of the substituent pairs increase μ, except the W-W pair F-F with a value of 15.32 D. N(CH3)2-N(CH3)2 has the largest μ of 16.43 D. Overall, the addition of substituents to the Cy5 dye has a minimal effect on μ—the largest change from pristine Cy5 is only 1.08 D. Since μ is relatively unaffected by the inclusion of different substituents, replacing H atoms with substituents in Cy5 should not decrease the excitonic exchange constant and may, in fact, increase it, which would be beneficial for excitonic applications.
Unlike μ, the addition of substituents on Cy5 has a greater effect on the static dipole difference magnitude, Δd. Pristine Cy5 has a Δd of 0.76 D. Figure 4 shows that multiple substituent pairs yield lower Δd values than pristine Cy5, including the D-D pair OCH3-OCH3 with a Δd of 0.27 D, the lowest Δd of all substituent pairs tested. Four W-W pairs have lower Δd than pristine Cy5, including Br-Br, Cl-Cl, Cl-Br, and F-F, with Δd of 0.62–0.67 D. Three D-W pairs also yield lower Δd than pristine Cy5, including N(CH3)2-CN, OCH3-F, and N(CH3)2-COOH with Δd of 0.63–0.70. Furthermore, dyes with higher symmetry (i.e., dyes with two of the same substituents) consistently exhibit some of the lowest values of Δd, an exception being the NO2-NO2 substituent pair.
Compared to pristine Cy5, most substituent pairs enhance Δd. For W-W pairs, the largest Δd belong to the pairs containing the strong electron withdrawing substituents NO2 and CN, where the F-CN pair exhibits the largest Δd of the W-W pairs, 2.62 D. Many D-W pairs also yield larger Δd than pristine Cy5, such as the pairs containing the OCH3 group, which is not the strongest electron donating substituent tested. Comparing W-W and D-W pairs, the substituent pair yielding the largest Δd is OCH3-CN with a value of 2.82 D, more than triple the Δd of pristine Cy5.
Overall, the addition of substituent pairs to pristine Cy5 can influence static dipole properties and increase static dipole differences. Recalling that an increase in Δd leads to an increase in the two-body exciton interaction energy, the substitution of Cy5 with pairs of strong electron withdrawing substituents or pairs of strong electron donating substituents and withdrawing substituents can augment the two-body exciton interaction energy between dyes.

3.3. Double Substituents

Figure 3 and Figure 4 indicate that the substitution of Cy5 with pairs of substituents that have strong electron donating or strong electron withdrawing properties is consistent with an increase in both μ and Δd. This finding led to the question as to would increasing the number of the same substituents further increase μ and Δd and how would these substituents influence the dye’s solubility—i.e., ΔGsolv. To investigate this question, the single substituents that were used on eight dyes that exhibited the largest Δd values in Figure 4 were then doubled on those dyes. Specifically, the added substituents were placed on the R2 and R2’ sites on Cy5 (Figure 1).
Comparing the water solvation between single and double substituents shown in Figure 5a, ΔGsolv values for most of the double substituents are more negative, indicating that by doubling the number of substituents, the dyes become slightly more hydrophilic. However, the F-NO2 doubly substituted Cy5 has a less negative ΔGsolv by about 0.02 eV. The decreases in ΔGsolv are minimal, however, with changes ranging from 0.16 eV (OCH3-CF3) to 0.58 eV (OCH3-COOH).
Similar to the water solvated dyes, ΔGsolv values for doubly substituted Cy5 dyes in pyridine, quinoline, and isoquinoline all become slightly more negative, as shown in Figure 5b. This implies that while the dyes become more hydrophilic with double substitution, solvation in pyridine, quinoline, and isoquinoline is also slightly improved. Besides ΔGsolv, other factors that were not considered, such as dye size or Coulombic effects between adjacent dyes or the dyes and DNA, may also influence dye intercalation into DNA.
For double substitutions, most of the calculated μ values slightly decrease, as shown in Figure 6. NO2-NO2 has the smallest decrease of 0.05 D, while OCH3-NO2 has the largest decrease of 0.36 D. Conversely, the double substitutions slightly increase Δd in all cases except for OCH3-NO2, for which Δd decreases by 0.02 D. The D-W pair OCH3-CF3 has the largest increase of 0.57 D. The D-W pair OCH3-CN also exhibits a large increase of Δd (2.82 D to 3.35 D), over four times that of pristine Cy5. Of all dyes tested in this study, doubly substituted OCH3-CN has the largest Δd.

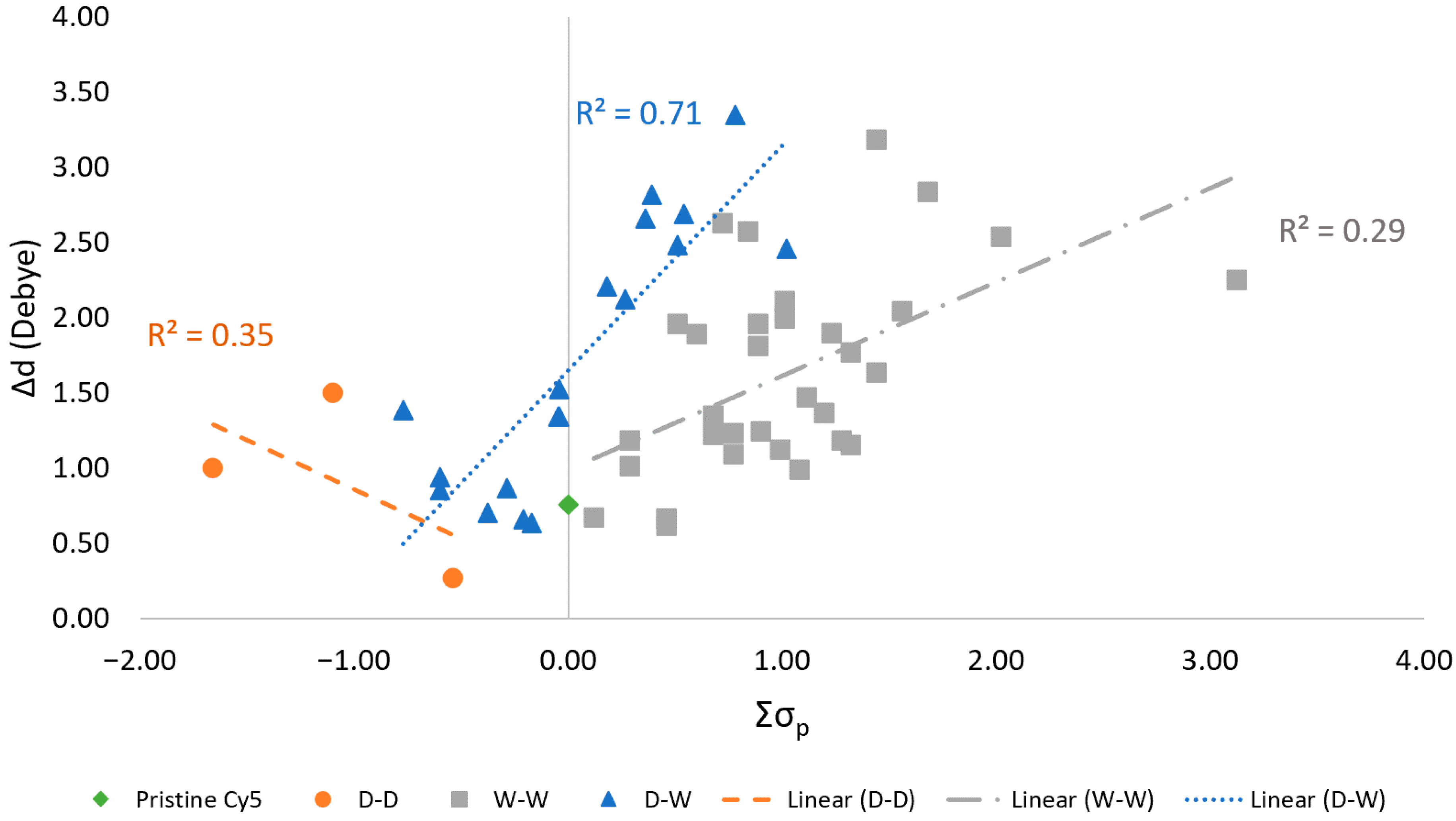
3.4. Relationships with Hammett Constants

Recall that a substituent can be identified as either an electron donating or an electron withdrawing substituent based on the empirically derived σp. Specifically, electron donating groups and electron withdrawing groups are associated with negative and positive values of σp, respectively [31,57]. Hence, we hypothesize that there exists a relationship between the experimentally derived σp parameters and calculated Δd values. For simplicity, we assume a linear correlation. To test this hypothesis, the Δd of the dyes were plotted against the sum of the σp (Σσp) of the substituents attached to the dyes, as shown in Figure 7. To determine the predictability of Δd based on Σσp, linear correlations are drawn for each data set (i.e., D-D, W-W, and D-W) and the variance between Δd and Σσp is quantified with the coefficient of determination, R2. A perfect linear correlation corresponds to an R2 of 1 and no correlation corresponds to an R2 of 0. Plots of the Δd values for D-D and W-W pairs against Σσp exhibit R2 values of 0.35 and 0.29, respectively. The D-W pairs exhibit a larger R2 value of 0.71. In general, within all three sets of data, the increase in the magnitude of Σσp values corresponds to a larger Δd.

4. Discussion

Upon substitution of the hydrogen atoms at the ends of Cy5, μ remains relatively unaffected, with the largest change being 1.08 D, shown in Figure 3. However, the values for ΔGsolv and Δd are altered compared to pristine Cy5, as shown in Figure 2 and Figure 4. Single atom W-W substituent pairs (F-F, Cl-Cl, Br-Br, F-Cl, F-Br, and Cl-Br) consistently exhibit less negative ΔGsolv (more hydrophobic) and lower Δd than multi-atom W-W pairs. The symmetry of the substituted Cy5 dyes also contributes to the calculated values of Δd, with more symmetric dyes (dyes with two of the same substituents) exhibiting smaller Δd values than asymmetric dyes, overall. The W-W pair NO2-NO2 does not follow this trend, however, signifying that symmetry is not the only factor to consider for Δd. Furthermore, asymmetry of substituted Cy5 does not always produce larger Δd values compared to pristine Cy5, as is the case for numerous D-W pairs.
As shown in Figure 2, pristine Cy5 has the least negative ΔGsolv, indicating that it is the least soluble in water, pyridine, quinoline, and isoquinoline. It is known that Cy5 and similar dyes exhibit limited solubility in water [59,60] and enhanced solubility in less polar solvents such as dimethyl sulfoxide (DMSO) and dimethyl formamide (DMF), both of which are used for experimental Cy5 sample preparation [61,62]. The relative solvation energies of Cy5 in water and the less polar pyridine, quinoline, and isoquinoline in the present study agree with the trend of Cy5 solubility in water, DMSO, and DMF. D-D and D-W substituted Cy5 dyes exhibit less negative ΔGsolv values compared to most W-W substituents. It is also found that the SO3H-SO3H substituted Cy5 has the most negative ΔGsolv, which agrees with the experiments showing that SO3H substituents increase a molecule’s hydrophilicity [63]. The increase in hydrophilicity of the dyes can be attributed to the increase in polarity upon substitution. The polarity of the dyes in the ground state is estimated with their ground state dipole moments [46] (see Table S2). Upon substitution, the ground state dipole moments increase with respect to pristine Cy5 (except for N(CH3)2-N(CH3)2), indicating an increase in polarity and solubility. Compared to dyes solvated in water, dyes solvated in DNA base mimicking pyridine, quinoline, and isoquinoline solvents exhibit more negative ΔGsolv, indicating that the dyes prefer to be solvated in those solvents rather than water. This may be correlated to the dye’s preference to intercalate into DNA structures, as observed in literature [7,22,28,58], rather than exist freely in an aqueous solution. However, this is a relatively simplistic view and further studies are ongoing.
Most substituent pairs exhibit larger values for Δd than pristine Cy5, as shown in Figure 4. Similar trends for substituted symmetric molecules have been studied experimentally. When added to symmetric molecules, electron withdrawing substituents [26] and electron donating substituents [32,33] are suggested to induce large Δd through charge separation and intramolecular charge transfer, shifting the charge density of the dyes. Two of the four largest Δd values for W-W pairs belong to dyes with one of the weakest withdrawing substituents (F, Br, or Cl) paired with the strongest withdrawing substituent, NO2. The other largest Δd values are for the F-CN substituted dye, with CN being the second strongest withdrawing substituent, and NO2-NO2. Interestingly, the four largest Δd values for D-W substituted dyes do not belong to ones with the strongest donating substituent, N(CH3)2, but rather OCH3. The withdrawing substituents in the D-W pairs exhibiting the largest Δd, however, are the strongest withdrawing substituents used. This indicates that withdrawing substituents have a larger effect on Δd, as has been shown in a study on a similar system [64]. However, despite that the largest Δd values for D-W pairs belong to dyes with OCH3, there is a positive linear correlation between Δd and Σσp of D-W pairs with an R2 value of 0.71, as shown in Figure 7. Conversely, the three D-D pairs have a weak negative linear correlation with an R2 value of 0.35, where the Δd values decrease as Σσp increases. W-W pairs also have a weak linear correlation, with an R2 value of 0.29. However, by visual inspection, as the magnitude of Σσp increases, so does Δd for all pair types. For the case of W-W and D-W pairs, this implies that electron withdrawing substituents have a larger impact on Δd for Cy5. The increase is greatest for D-W pairs and moderate for W-W pairs, as signified by the slopes of the linear fits.
Based on the results of this study, the addition of substituents can enhance excitonic properties of Cy5 aggregates. The inclusion of substituents decreases the value of ΔGsolv indicating that some substituents (most prevalently W-W substituents) make Cy5 more hydrophilic than others, thus hindering the aggregation of these dyes. Compared to most W-W pairs, D-D and D-W pairs are shown to be more hydrophobic, meaning aggregation may occur more readily for those dyes compared to W-W substituted Cy5. Furthermore, the inclusion of substituents does not degrade μ, indicating that the exciton exchange energy should remain relatively unaffected. W-W and D-W substituents can increase the Δd of Cy5 by more than triple that of pristine Cy5. Assuming with a pristine Cy5 dimer orientation obtained from experiment [7,29] and that the exciton-exciton interaction energies increase with the square of Δd [20], the exciton-exciton interaction energies of F-CN, F-NO2, OCH3-CN, and OCH3-NO2 substituted Cy5 dyes could be potentially increased by about ten times in comparison with that of the pristine Cy5 due to the increase in their Δd values.

5. Conclusions

We performed DFT and TD-DFT calculations to determine the effects various substituents had on the ΔGsolv, μ, and Δd of Cy5. By substituting the hydrogens at the ends of a Cy5 dye, the ΔGsolv and Δd of the dye can be altered. W-W substituent pairs were found to have the most negative values of ΔGsolv and therefore made Cy5 more soluble in water compared to D-D and D-W. Dyes solvated in pyridine, quinoline, and isoquinoline, taken to mimic DNA bases, were found to have more negative values than those solvated in water, suggesting that intercalation into DNA structures is favorable. Overall, the addition of substituents did not have a substantial impact on μ, with the largest difference between a substituted Cy5 and pristine Cy5 being 1.08 D. However, substituents did have a large impact on the Δd of the dye. Numerous W-W and D-W substituent pairs increased Δd by up to three times that of pristine Cy5. The W-W pair with the largest Δd value was F-CN (2.62 D) and the D-W pair with the largest Δd value was OCH3-CN (2.82 D). Doubling the substituents on the Cy5 dye did not appreciably make ΔGsolv more negative or increase Δd overall, with the largest increase of Δd being around 0.57 D for OCH3-CF3. The substituted Cy5 dye with the largest Δd was doubly substituted OCH3-CN (3.35 D). Finally, correlations were made between the sum of experimentally derived σp parameters and Δd values. Overall, an increase in the magnitude of Σσp of the substituents correlated to an increase in Δd. This trend was more pronounced for D-W pairs than W-W pairs and D-D pairs. D-W pairs exhibited a positive linear correlation with an R2 of 0.71, signifying that the sum of σp values can be used to approximate the relative magnitudes of Δd for substituted Cy5 dyes.
The substitution of Cy5 can enhance electronic properties for improved excitonic applications. D-D and D-W pairs have less negative ΔGsolv compared to W-W pairs, indicating that dye aggregation may be less favorable for W-W pairs. Furthermore, the substituents did not decrease μ of the dyes so that the excitonic exchange constant should not be degraded. Both W-W and D-W pairs increased Δd and thus may enhance the two-exciton interaction term of the Frenkel Hamiltonian. The results of this study could help select the dye candidates with optimized electronic properties for desired applications. Specifically, these results will guide the synthesis and experimental studies for tailoring the dipole properties of Cy5 dyes via substituent engineering towards applications that exploit dye aggregates and exciton dynamics.

Supplementary Materials

The following are available online. Figure S1: Gibbs free energies of solvation (ΔGsolv) for pristine and substituted Cy5 using the M06-2X functional calculated using the Gibbs free energies of the dyes in solvent and vacuum (instead of total energies), Figure S2: Gibbs free energies of solvation (ΔGsolv) for pristine and substituted Cy5 using the M06-2X and CAM-B3LYP functionals, Figure S3: Transition dipole moments (μ) for pristine and substituted Cy5 using the M06-2X and CAM-B3LYP functionals, Figure S4: Static dipole moment differences (Δd) for pristine and substituted Cy5 using the M06-2X and CAM-B3LYP functionals, Table S1: Solvation energies of pristine and substituted Cy5 dyes in water, pyridine, quinoline, and isoquinoline solvents, Table S2: Magnitudes of the ground state dipole moments (GSDM) and excited state dipole moments (ESDM) calculated for each Cy5 dye with the M06-2X and CAM-B3LYP functionals.

Author Contributions

Conceptualization, W.B.K., B.Y. and J.L.; Methodology, B.Y. and J.L.; Supervision, W.B.K., B.Y. and L.L.; Project administration, W.B.K. and B.Y.; Data curation, A.B.; Formal analysis, A.B. and L.L.; Writing—original draft; A.B.; Writing—review and editing, W.B.K., B.Y., J.L. and L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported fully by the Department of Navy award No. N00014-19-1-2615 issued by the Office of Naval Research, except for resources provided by the High Performance Computing Center at Idaho National Laboratory that are supported by the Office of Nuclear Energy of the U.S. Department of Energy and the Nuclear Science User Facilities under Contract No. DE-AC07-05ID14517.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Select solvation energy and dipole moment data presented in this study are available in the Supporting Information. In the near-term, all other data presented are available upon request from the corresponding author. Within six months, we plan to make all data available in a publicly accessible data repository.

Acknowledgments

We would like to thank Joseph Melinger and Youngchan Kim at the U.S. Naval Research Laboratory for their helpful discussion of dye and substituent structures and properties. We would also like to thank Kimo Wilson and Simon Roy from the Nanoscale Materials and Device Group at Boise State University who provided experimental Cy5 monomer absorbance data.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Monshouwer, R.; Abrahamsson, M.; Van Mourik, F.; Van Grondelle, R. Superradiance and Exciton Delocalization in Bacterial Photosynthetic Light-Harvesting Systems. J. Phys. Chem. B 1997, 101, 7241–7248. [Google Scholar] [CrossRef] [Green Version]
  2. Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.K.; Mančal, T.; Cheng, Y.C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef] [PubMed]
  3. Mirkovic, T.; Ostroumov, E.E.; Anna, J.M.; Van Grondelle, R.; Govindjee; Scholes, G.D. Light absorption and energy transfer in the antenna complexes of photosynthetic organisms. Chem. Rev. 2017, 117, 249–293. [Google Scholar] [CrossRef] [PubMed]
  4. Lim, J.M.; Kim, P.; Yoon, M.C.; Sung, J.; Dehm, V.; Chen, Z.; Würthner, F.; Kim, D. Exciton delocalization and dynamics in helical π-stacks of self-assembled perylene bisimides. Chem. Sci. 2013, 4, 388–397. [Google Scholar] [CrossRef]
  5. Bialas, D.; Zitzler-Kunkel, A.; Kirchner, E.; Schmidt, D.; Würthner, F. Structural and quantum chemical analysis of exciton coupling in homo-and heteroaggregate stacks of merocyanines. Nat. Commun. 2016, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
  6. Kaufmann, C.; Kim, W.; Nowak-Król, A.; Hong, Y.; Kim, D.; Würthner, F. Ultrafast Exciton Delocalization, Localization, and Excimer Formation Dynamics in a Highly Defined Perylene Bisimide Quadruple π-Stack. J. Am. Chem. Soc. 2018, 140, 4253–4258. [Google Scholar] [CrossRef]
  7. Cannon, B.L.; Kellis, D.L.; Patten, L.K.; Davis, P.H.; Lee, J.; Graugnard, E.; Yurke, B.; Knowlton, W.B. Coherent Exciton Delocalization in a Two-State DNA-Templated Dye Aggregate System. J. Phys. Chem. A 2017, 121, 6905–6916. [Google Scholar] [CrossRef]
  8. Cannon, B.L.; Patten, L.K.; Kellis, D.L.; Davis, P.H.; Lee, J.; Graugnard, E.; Yurke, B.; Knowlton, W.B. Large Davydov Splitting and Strong Fluorescence Suppression: An Investigation of Exciton Delocalization in DNA-Templated Holliday Junction Dye Aggregates. J. Phys. Chem. A 2018, 122, 2086–2095. [Google Scholar] [CrossRef]
  9. Jelley, E.E. Spectral absorption and fluorescence of dyes in the molecular state. Nature 1936, 138, 1009–1010. [Google Scholar] [CrossRef]
  10. Kasha, M. Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates. Radiat. Res. 1963, 20, 55–70. [Google Scholar] [CrossRef]
  11. Kasha, M.; Rawls, H.R.; Ashraf El-Bayoumi, M. The Exciton Model in Molecular Spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. [Google Scholar] [CrossRef] [Green Version]
  12. Würthner, F.; Kaiser, T.E.; Saha-Möller, C.R. J-aggregates: From serendipitous discovery to supramolecular engineering of functional dye materials. Angew. Chemie Int. Ed. 2011, 50, 3376–3410. [Google Scholar] [CrossRef] [PubMed]
  13. Nüesch, F.; Grätzel, M. H-aggregation and correlated absorption and emission of a merocyanine dye in solution, at the surface and in the solid state. A link between crystal structure and photophysical properties. Chem. Phys. 1995, 193, 1–17. [Google Scholar] [CrossRef]
  14. Davydov, A.S. The Theory of Molecular Excitons. Sov. Phys. Uspekhi 1964, 7, 393–448. [Google Scholar] [CrossRef]
  15. Pajusalu, M.; Rätsep, M.; Trinkunas, G.; Freiberg, A. Davydov Splitting of Excitons in Cyclic Bacteriochlorophyll a Nanoaggregates of Bacterial Light-Harvesting Complexes between 4.5 and 263 K. ChemPhysChem 2011, 12, 634–644. [Google Scholar] [CrossRef]
  16. Collado-Fregoso, E.; Boufflet, P.; Fei, Z.; Gann, E.; Ashraf, S.; Li, Z.; McNeill, C.R.; Durrant, J.R.; Heeney, M.; Ashraf, R.S. Increased Exciton Dipole Moment Translates into Charge-Transfer Excitons in Thiophene-Fluorinated Low-Bandgap Polymers for Organic Photovoltaic Applications. Chem. Mater. 2015, 27, 7934–7944. [Google Scholar] [CrossRef] [Green Version]
  17. Markov, R.V.; Plekhanov, A.I.; Shelkovnikov, V.V.; Knoester, J. Giant Nonlinear Optical Response of Interacting One-Dimensional Frenkel Excitons in Molecular Aggregates. Phys. Status Solidi 2000, 221, 529–533. [Google Scholar] [CrossRef]
  18. Cannon, B.L.; Kellis, D.L.; Davis, P.H.; Lee, J.; Kuang, W.; Hughes, W.L.; Graugnard, E.; Yurke, B.; Knowlton, W.B. Excitonic AND Logic Gates on DNA Brick Nanobreadboards. ACS Photonics 2015, 2, 398–404. [Google Scholar] [CrossRef] [Green Version]
  19. Kellis, D.L.; Sarter, C.; Cannon, B.L.; Davis, P.H.; Graugnard, E.; Lee, J.; Pensack, R.D.; Kolmar, T.; Jäschke, A.; Yurke, B.; et al. An All-Optical Excitonic Switch Operated in the Liquid and Solid Phases. ACS Nano 2019, 13, 2986–2994. [Google Scholar] [CrossRef]
  20. Abramavicius, D.; Palmieri, B.; Mukamel, S. Extracting single and two-exciton couplings in photosynthetic complexes by coherent two-dimensional electronic spectra. Chem. Phys. 2009, 357, 79–84. [Google Scholar] [CrossRef] [Green Version]
  21. Markova, L.I.; Malinovskii, V.L.; Patsenker, L.D.; Häner, R. J- vs. H-type assembly: Pentamethine cyanine (Cy5) as a near-IR chiroptical reporter. Chem. Commun. 2013, 49, 5298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Cunningham, P.D.; Kim, Y.C.; Díaz, S.A.; Buckhout-White, S.; Mathur, D.; Medintz, I.L.; Melinger, J.S. Optical Properties of Vibronically Coupled Cy3 Dimers on DNA Scaffolds. J. Phys. Chem. B 2018, 122, 5020–5029. [Google Scholar] [CrossRef] [PubMed]
  23. Nicoli, F.; Roos, M.K.; Hemmig, E.A.; Di Antonio, M.; de Vivie-Riedle, R.; Liedl, T. Proximity-Induced H-Aggregation of Cyanine Dyes on DNA-Duplexes. J. Phys. Chem. A 2016, 120, 9941–9947. [Google Scholar] [CrossRef] [PubMed]
  24. Huff, J.S.; Davis, P.H.; Christy, A.; Kellis, D.L.; Kandadai, N.; Toa, Z.S.D.; Scholes, G.D.; Yurke, B.; Knowlton, W.B.; Pensack, R.D. DNA-Templated Aggregates of Strongly Coupled Cyanine Dyes: Nonradiative Decay Governs Exciton Lifetimes. J. Phys. Chem. Lett. 2019, 10, 2386–2392. [Google Scholar] [CrossRef]
  25. Misawa, K.; Minoshima, K.; Ono, H.; Kobayashi, T. Giant static dipole moment change on electronic excitation in highly oriented J-aggregates. Chem. Phys. Lett. 1994, 220, 251–256. [Google Scholar] [CrossRef]
  26. Marder, S.R.; Torruellas, W.E.; Blanchard-Desce, M.; Ricci, V.; Stegeman, G.I.; Gilmour, S.; Brédas, J.L.; Li, J.; Bublitz, G.U.; Boxer, S.G. Large molecular third-order optical nonlinearities in polarized carotenoids. Science (80-) 1997, 276, 1233–1236. [Google Scholar] [CrossRef] [Green Version]
  27. Garoff, R.A.; Litzinger, E.A.; Connor, R.E.; Fishman, I.; Armitage, B.A. Helical Aggregation of Cyanine Dyes on DNA Templates: Effect of Dye Structure on Formation of Homo-and Heteroaggregates. Langmuir 2002, 18, 6330–6337. [Google Scholar] [CrossRef]
  28. Stadler, A.L.; Renikuntla, B.R.; Yaron, D.; Fang, A.S.; Armitage, B.A. Substituent effects on the assembly of helical cyanine dye aggregates in the minor groove of a DNA template. Langmuir 2011, 27, 1472–1479. [Google Scholar] [CrossRef]
  29. Fothergill, J.W.; Hernandez, A.C.; Knowlton, W.B.; Yurke, B.; Li, L. Ab Initio Studies of Exciton Interactions of Cy5 Dyes. J. Phys. Chem. A 2018, 122, 8989–8997. [Google Scholar] [CrossRef]
  30. Cao, J.; Fan, J.; Sun, W.; Guo, Y.; Wu, H.; Peng, X. The photoprocess effects of an amino group located at different positions along the polymethine chain in indodicarbocyanine dyes. RSC Adv. 2017, 7, 30740–30746. [Google Scholar] [CrossRef] [Green Version]
  31. Abou-Hatab, S.; Spata, V.A.; Matsika, S. Substituent Effects on the Absorption and Fluorescence Properties of Anthracene. J. Phys. Chem. A 2017, 121, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
  32. Chandrasekhar, K.; Naik, L.R.; Kumar, S.; Math, N.N. Steady-state absorption and fluorescence study: Dipole moments of coumarins. Indian J. Pure Appl. Phys. 2006, 44, 292–299. [Google Scholar]
  33. Bridhkoti, J.P.; Gahlaut, R.; Joshi, H.C.; Pant, S. Effect of positional substitution of amino group on excited state dipole moments of quinoline. J. Lumin. 2011, 131, 1869–1873. [Google Scholar] [CrossRef]
  34. Jacquemin, D.; Zhao, Y.; Valero, R.; Adamo, C.; Ciofini, I.; Truhlar, D.G. Verdict: Time-dependent density functional theory “not guilty” of large errors for cyanines. J. Chem. Theory Comput. 2012, 8, 1255–1259. [Google Scholar] [CrossRef]
  35. Jacquemin, D. Excited-State Dipole and Quadrupole Moments: TD-DFT versus CC2. J. Chem. Theory Comput. 2016, 12, 3993–4003. [Google Scholar] [CrossRef]
  36. Kawauchi, S.; Antonov, L.; Okuno, Y. Prediction of the color of dyes by using time-dependent density functional theory (TD-DFT). Bulg. Chem. Commun. 2014, 46, 228–237. [Google Scholar]
  37. Laine, M.; Barbosa, N.A.; Wieczorek, R.; Melnikov, M.Y.; Filarowski, A. Calculations of BODIPY dyes in the ground and excited states using the M06-2X and PBE0 functionals. J. Mol. Model. 2016, 22, 1–7. [Google Scholar] [CrossRef] [Green Version]
  38. García, G.; Adamo, C.; Ciofini, I. Evaluating push-pull dye efficiency using TD-DFT and charge transfer indices. Phys. Chem. Chem. Phys. 2013, 15, 20210–20219. [Google Scholar] [CrossRef]
  39. Kerkines, I.S.K.; Petsalakis, I.D.; Argitis, P.; Theodorakopoulos, G. Fluorescence properties of organic dyes: Quantum chemical studies on the green/blue neutral and protonated DMA-DPH emitters in polymer matrices. Phys. Chem. Chem. Phys. 2011, 13, 21273–21281. [Google Scholar] [CrossRef]
  40. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
  41. Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
  42. Yesudas, K. Cationic cyanine dyes: Impact of symmetry-breaking on optical absorption and third-order polarizabilities. Phys. Chem. Chem. Phys. 2013, 15, 19465–19477. [Google Scholar] [CrossRef] [PubMed]
  43. Chen, J.; Gao, Y.; Xu, Y.; Xu, F.; Zhang, Q.; Lu, X. Theoretical study of novel porphyrin D-π-A conjugated organic dye sensitizer in solar cells. Mater. Chem. Phys. 2019, 225, 417–425. [Google Scholar] [CrossRef]
  44. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A. 03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  45. Dennington, R.; Keith, T.A.; Millam, J. GaussView Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
  46. Rauf, S.M.A.; Arvidsson, P.I.; Albericio, F.; Govender, T.; Maguire, G.E.M.; Kruger, H.G.; Honarparvar, B. The effect of N-methylation of amino acids (Ac-X-OMe) on solubility and conformation: A DFT study. Org. Biomol. Chem. 2015, 13, 9993–10006. [Google Scholar] [CrossRef]
  47. Mananghaya, M.R.; Santos, G.N.; Yu, D.N. Solubility of amide functionalized single wall carbon nanotubes: A quantum mechanical study. J. Mol. Liq. 2017, 242, 1208–1214. [Google Scholar] [CrossRef]
  48. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
  49. Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to Isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
  50. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
  51. Budzák, Š.; Medved, M.; Mennucci, B.; Jacquemin, D. Unveiling solvents effect on excited-state polarizabilities with the corrected linear-response model. J. Phys. Chem. A 2014, 118, 5652–5656. [Google Scholar] [CrossRef]
  52. Selvam, K.; Gandhi, S.; Krishnamurty, S.; Gopalakrishnan, G. Effect of substitution on the excited state photophysical and spectral properties of boron difluoride curcumin complex dye and their derivatives: A time dependent-DFT study. J. Photochem. Photobiol. B Biol. 2019, 199, 111595. [Google Scholar] [CrossRef]
  53. Heid, E.; Hunt, P.A.; Schröder, C. Evaluating excited state atomic polarizabilities of chromophores. Phys. Chem. Chem. Phys. 2018, 20, 8554–8563. [Google Scholar] [CrossRef] [PubMed]
  54. Bamgbelu, A.; Wang, J.; Leszczynski, J. TDDFT study of the optical properties of Cy5 and its derivatives. J. Phys. Chem. A 2010, 114, 3551–3555. [Google Scholar] [CrossRef] [PubMed]
  55. Hansch, C.; Leo, A.; Taft, R.W. A Survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
  56. Imaizumi, H.; Koyanagi, T.; Zhao, D. Reactivity of sulfonic acid group and estimation of its substituent-effect in T-for-H exchange reaction. J. Radioanal. Nucl. Chem. 2002, 252, 467–472. [Google Scholar] [CrossRef]
  57. Paschoal, D.; Santos, H.F. Dos Assessing the quantum mechanical level of theory for prediction of linear and nonlinear optical properties of push-pull organic molecules. J. Mol. Model 2013, 19, 2079–2090. [Google Scholar] [CrossRef] [PubMed]
  58. Stennett, E.M.S.; Ma, N.; van der Vaart, A.; Levitus, M. Photophysical and Dynamical Properties of Doubly Linked Cy3–DNA Constructs. J. Phys. Chem. B 2014, 118, 152–163. [Google Scholar] [CrossRef]
  59. Yang, S.K.; Shi, X.; Park, S.; Ha, T.; Zimmerman, S.C. A dendritic single-molecule fluorescent probe that is monovalent, photostable and minimally blinking. Nat. Chem. 2013, 5, 692–697. [Google Scholar] [CrossRef] [Green Version]
  60. Liu, W.; McGarraugh, H.H.; Smith, B.D. Fluorescent thienothiophene-containing squaraine dyes and threaded supramolecular complexes with tunable wavelengths between 600–800 nm. Molecules 2018, 23, 2229. [Google Scholar] [CrossRef] [Green Version]
  61. Toutchkine, A.; Nalbant, P.; Hahn, K.M. Facile synthesis of thiol-reactive Cy3 and Cy5 derivatives with enhanced water solubility. Bioconjug. Chem. 2002, 13, 387–391. [Google Scholar] [CrossRef]
  62. Kang, J.; Kaczmarek, O.; Liebscher, J.; Dähne, L. Prevention of H-aggregates formation in Cy5 labeled macromolecules. Int. J. Polym. Sci. 2010, 2010. [Google Scholar] [CrossRef]
  63. Markova, L.I.; Terpetschnig, E.A.; Patsenker, L.D. Comparison of a series of hydrophilic squaraine and cyanine dyes for use as biological labels. Dye. Pigment. 2013, 99, 561–570. [Google Scholar] [CrossRef]
  64. Karaca, S.; Elmaci, N. A theoretical study on the ground and excited state behaviors of TTBC related carbocyanine dyes. J. Mol. Struct. Theochem. 2009, 915, 149–159. [Google Scholar] [CrossRef] [Green Version]
Molecules 26 00524 g001 550
Figure 1. Molecular structure of a Cy5 (1,1′-dimethyl-3,3,3′,3′-tetramethylindocarbocyanine) dye. Hydrogens at ‘R’ locations were replaced with substituents.
Figure 1. Molecular structure of a Cy5 (1,1′-dimethyl-3,3,3′,3′-tetramethylindocarbocyanine) dye. Hydrogens at ‘R’ locations were replaced with substituents.
Molecules 26 00524 g001
Molecules 26 00524 g002 550
Figure 2. Solvation energies of substituted Cy5 dyes in water, pyridine, quinoline, and isoquinoline calculated using Equation (1). The geometry was optimized and the energies were calculated using the M06-2X functional. D-D is donating-donating, W-W is withdrawing-withdrawing, and D-W is donating-withdrawing. Substituted dyes are grouped according to substituent classification and ordered by decreasing ΔGsolv. The lines added to the data are to highlight the trends of the data and are not meant to infer a quantitative behavior.
Figure 2. Solvation energies of substituted Cy5 dyes in water, pyridine, quinoline, and isoquinoline calculated using Equation (1). The geometry was optimized and the energies were calculated using the M06-2X functional. D-D is donating-donating, W-W is withdrawing-withdrawing, and D-W is donating-withdrawing. Substituted dyes are grouped according to substituent classification and ordered by decreasing ΔGsolv. The lines added to the data are to highlight the trends of the data and are not meant to infer a quantitative behavior.
Molecules 26 00524 g002
Molecules 26 00524 g003 550
Figure 3. Transition dipole moment magnitudes (μ) of pristine and substituted Cy5 dyes. The given substituent groups are placed on R1 and R1’ sites in Figure 1. Geometry optimizations and excited state calculations were performed using the M06-2X functional. The dyes are grouped according to substituent classification and ordered by increasing μ. The lines added to the data are to highlight the trends of the data and are not meant to infer a quantitative behavior.
Figure 3. Transition dipole moment magnitudes (μ) of pristine and substituted Cy5 dyes. The given substituent groups are placed on R1 and R1’ sites in Figure 1. Geometry optimizations and excited state calculations were performed using the M06-2X functional. The dyes are grouped according to substituent classification and ordered by increasing μ. The lines added to the data are to highlight the trends of the data and are not meant to infer a quantitative behavior.
Molecules 26 00524 g003
Molecules 26 00524 g004 550
Figure 4. Static dipole difference magnitudes (Δd) of pristine and substituted Cy5 dyes calculated using Equation (2). The given substituent groups are placed on R1 and R1’ sites in Figure 1. Ground state optimizations and excited state single point calculations were performed using the M06-2X functional. The dyes are grouped according to substituent classification and ordered according to increasing Δd. The lines added to the data are to highlight trends and are not meant to infer a quantitative behavior.
Figure 4. Static dipole difference magnitudes (Δd) of pristine and substituted Cy5 dyes calculated using Equation (2). The given substituent groups are placed on R1 and R1’ sites in Figure 1. Ground state optimizations and excited state single point calculations were performed using the M06-2X functional. The dyes are grouped according to substituent classification and ordered according to increasing Δd. The lines added to the data are to highlight trends and are not meant to infer a quantitative behavior.
Molecules 26 00524 g004
Molecules 26 00524 g005 550
Figure 5. Gibbs free energy of solvation (ΔGsolv) calculated using Equation (1) for singly and doubly substituted Cy5 dyes in (a) water and (b) pyridine, quinoline, and isoquinoline. Singly and doubly substituted Cy5 dyes were made by adding the given substituent pair to the R positions in Figure 1. For doubly substituted Cy5, two of the same substituent were added on the same side of the dye. All calculations were performed using the M06-2X functional.
Figure 5. Gibbs free energy of solvation (ΔGsolv) calculated using Equation (1) for singly and doubly substituted Cy5 dyes in (a) water and (b) pyridine, quinoline, and isoquinoline. Singly and doubly substituted Cy5 dyes were made by adding the given substituent pair to the R positions in Figure 1. For doubly substituted Cy5, two of the same substituent were added on the same side of the dye. All calculations were performed using the M06-2X functional.
Molecules 26 00524 g005
Molecules 26 00524 g006 550
Figure 6. Magnitudes of transition dipole moments (μ) and static dipole differences (Δd) for singly and doubly substituted Cy5 dyes. For doubly substituted Cy5, two of the same substituent were added on the same side of the dye. Ground state optimizations and excited state single point calculations to the first excited state were performed using the M06-2X functional.
Figure 6. Magnitudes of transition dipole moments (μ) and static dipole differences (Δd) for singly and doubly substituted Cy5 dyes. For doubly substituted Cy5, two of the same substituent were added on the same side of the dye. Ground state optimizations and excited state single point calculations to the first excited state were performed using the M06-2X functional.
Molecules 26 00524 g006
Molecules 26 00524 g007 550
Figure 7. Static dipole difference magnitudes (Δd) found using the M06-2X functional plotted against the sum of the Hammett constants of the substituents attached to Cy5 dyes. Linear fits of the separate sets of data are shown along with corresponding R2 values.
Figure 7. Static dipole difference magnitudes (Δd) found using the M06-2X functional plotted against the sum of the Hammett constants of the substituents attached to Cy5 dyes. Linear fits of the separate sets of data are shown along with corresponding R2 values.
Molecules 26 00524 g007
Table
Table 1. Substituents, their corresponding Hammett constants (σp), and the classifications used in the current study. Negative values correspond to electron donating substituents and positive values correspond to electron withdrawing substituents.
Table 1. Substituents, their corresponding Hammett constants (σp), and the classifications used in the current study. Negative values correspond to electron donating substituents and positive values correspond to electron withdrawing substituents.
SubstituentσpClassification
N(CH3)2−0.83 aDonating
OCH3−0.27 a
F0.06 aWithdrawing
Cl0.23 a
Br0.23 a
COOH0.45 a
CF30.54 a
SO3H0.64 b
CN0.66 a
NO20.78 a
a Values taken from Hansch et al. [55]. b Values taken from Imaizumi et al. [56].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Biaggne, A.; Knowlton, W.B.; Yurke, B.; Lee, J.; Li, L. Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations. Molecules 2021, 26, 524. https://doi.org/10.3390/molecules26030524

AMA Style

Biaggne A, Knowlton WB, Yurke B, Lee J, Li L. Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations. Molecules. 2021; 26(3):524. https://doi.org/10.3390/molecules26030524

Chicago/Turabian Style

Biaggne, Austin, William B. Knowlton, Bernard Yurke, Jeunghoon Lee, and Lan Li. 2021. "Substituent Effects on the Solubility and Electronic Properties of the Cyanine Dye Cy5: Density Functional and Time-Dependent Density Functional Theory Calculations" Molecules 26, no. 3: 524. https://doi.org/10.3390/molecules26030524

Article Metrics

Back to TopTop