Deuterium Isotope Effects on Acid-Base Equilibrium of Organic Compounds
Abstract
:1. Introduction
2. Theoretical Background
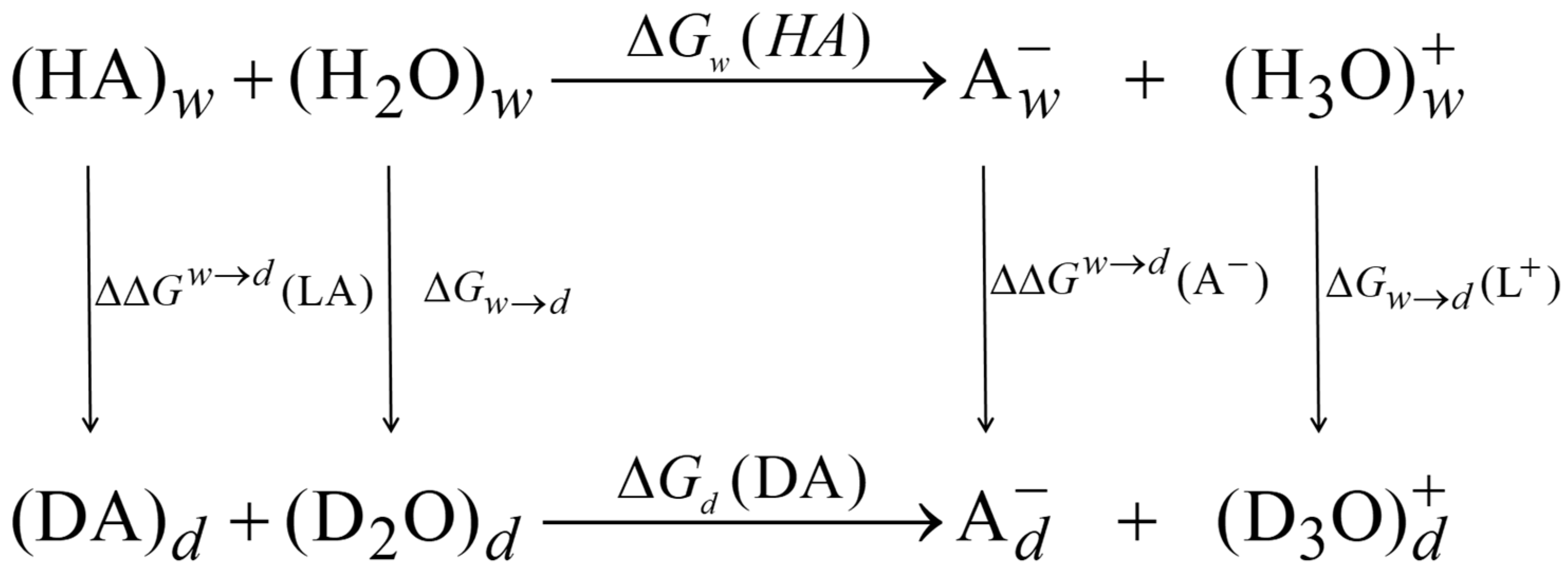
2.1. Theoretical Models for Solvent Isotope Effects on Acid–Base Equilibrium
- Model 1: Since the difference is computed relative to that of , the small isotope effects in different media in each term of Equation (5) can be all lumped into the constant reference free energy term in Equation (4), , as long as the computational results for AcOL are obtained in exactly the same way as that for other acids. Then, the Model-1 (M1) is determined bywhere has a combined value of −0.7895 kcal/mol in the present study (Table 1), and is the free energy difference associated with the exchange effect (EE) of acid LA:
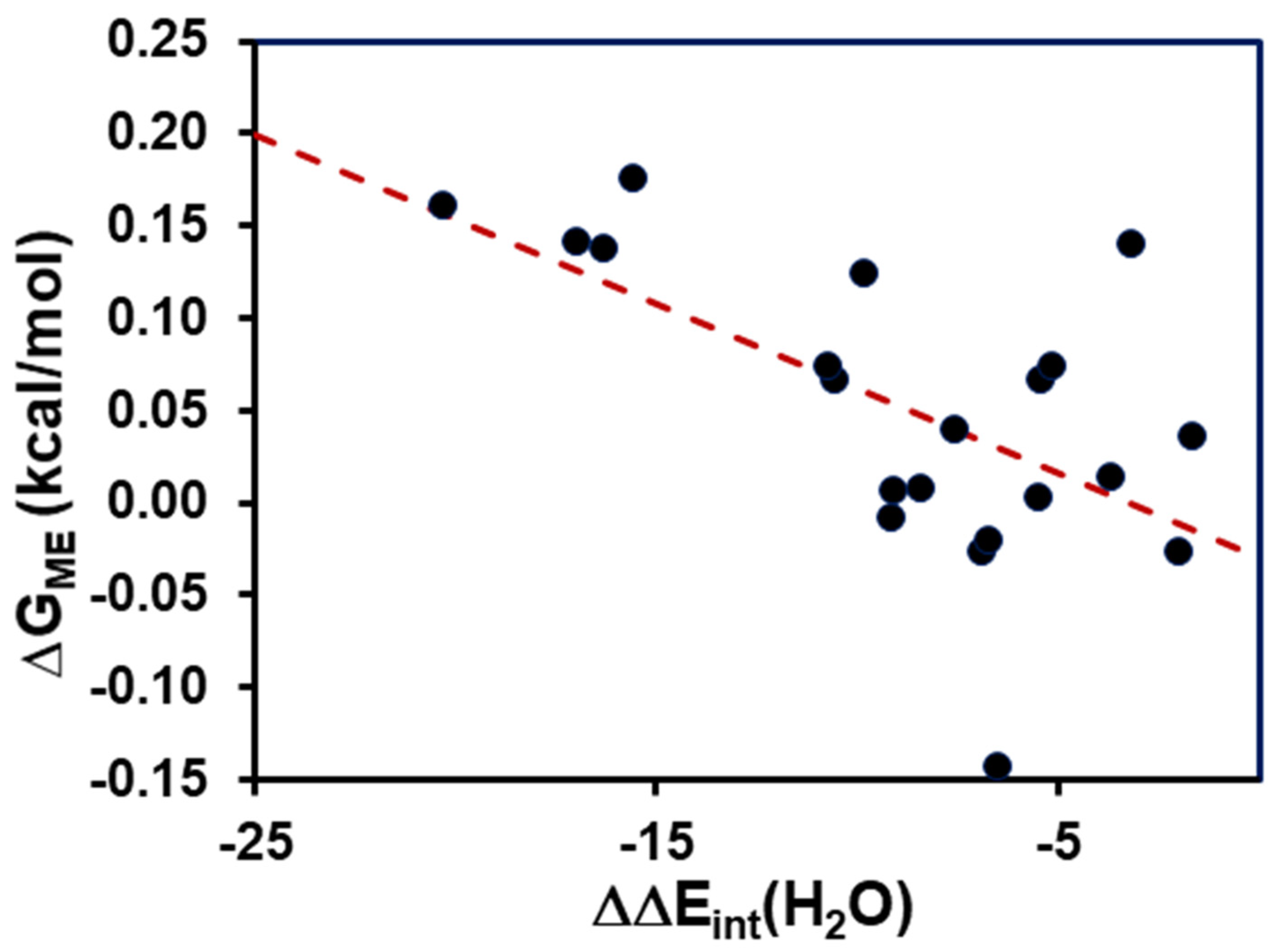
- Model 2: The isotope effects on the med ium terms (Equation (5)) can be incorporated into calculations by approximating the NQE with the inclusion of one solvent molecule that directly forms a hydrogen bond with the acid and its conjugate base explicitly. Therefore, Model 2 (M2) can be expressed as follows:where is the free energy difference due to the medium effect (ME) on acid and base interactions with the solvent:
2.2. Isotope Effects from Path Integral-Free Energy Perturbation Simulations
3. Computational Details
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Schowen, K.B.; Schowen, R.L. Solvent Isotope Effects on Enzyme-Systems. Methods Enzymol. 1982, 87, 551–606. [Google Scholar] [PubMed]
- Jancso, G.; Van Hook, W.A. Condensed Phase Isotope-Effects (Especially Vapor-Pressure Isotope-Effects). Chem. Rev. 1974, 74, 689–750. [Google Scholar] [CrossRef]
- Bell, R.P.; Kuhn, A.T. Dissociation Constants of Some Acids in Deuterium Oxide. T Faraday Soc. 1963, 59, 1789–1793. [Google Scholar] [CrossRef]
- Robinson, R.A.; Paabo, M.; Bates, R.G. Deuterium Isotope Effect on Dissociation of Weak Acids in Water and Deuterium Oxide. J. Res. Nat. Bur. Stand. Sect. A-Phys. Chem. 1969, 73, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Cook, P.F. Enzyme Mechanism from Isotope Effects; CRC Press: Boca Raton, FL, USA, 1991; p. 500. [Google Scholar]
- Gao, J.; Ma, S.H.; Major, D.T.; Nam, K.; Pu, J.Z.; Truhlar, D.G. Mechanisms and free energies of enzymatic reactions. Chem. Rev. 2006, 106, 3188–3209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Raffele, D.; Marti, S.; Moliner, V. QM/MM Theoretical Studies of a de Novo Retro-Aldolase Design. ACS Catal. 2019, 9, 2482–2492. [Google Scholar] [CrossRef]
- Fernandez, P.L.; Murkin, A.S. Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions. Molecules 2020, 25, 1933. [Google Scholar] [CrossRef] [Green Version]
- Hodge, E.A.; Benhaim, M.A.; Lee, K.K. Bridging protein structure, dynamics, and function using hydrogen/deuterium-exchange mass spectrometry. Prot. Sci. 2020, 29, 843–855. [Google Scholar] [CrossRef]
- Borysik, A.J. Simulated Isotope Exchange Patterns Enable Protein Structure Determination. Angew. Chem. Int. Ed. 2017, 56, 9396–9399. [Google Scholar] [CrossRef]
- Connelly, G.P.; Bai, Y.W.; Jeng, M.F.; Englander, S.W. Isotope Effects in Peptide Group Hydrogen-Exchange. Proteins-Struct. Funct. Gen. 1993, 17, 87–92. [Google Scholar] [CrossRef]
- Harijan, R.K.; Zoi, I.; Antoniou, D.; Schwartz, S.D.; Schramm, V.L. Catalytic-site design for inverse heavy-enzyme isotope effects in human purine nucleoside phosphorylase. Proc. Nat. Acad. Sci. USA 2017, 114, 6456–6461. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, M.M.; Gamarra, B.; Kahmen, A.; Siegwolf, R.T.W.; Saurer, M. Oxygen isotope fractionations across individual leaf carbohydrates in grass and tree species. Plant Cell Environ. 2017, 40, 1658–1670. [Google Scholar] [CrossRef] [PubMed]
- Rule, C.K.; La Mer, V.K. Dissociation constants of deutero acids by E. MF measurements. J. Am. Chem. Soc. 1938, 60, 1974–1981. [Google Scholar] [CrossRef]
- Wehry, E.L.; Rogers, L.B. Deuterium Isotope Effects on Protolytic Dissociation of Organic Acids in Electronically Excited States. J. Am. Chem. Soc. 1966, 88, 351–354. [Google Scholar] [CrossRef]
- Salomaa, P.; Hakala, R.; Vesala, S.; Aalto, T. Solvent Deuterium Isotope Effects on Acid-Base Reactions. Part III. Relative Acidity Constants of Inorganic Oxyacids in Light and Heavy Water. Kinetic Applications. Acta Chem. Scan. 1969, 23, 2116–2126. [Google Scholar] [CrossRef]
- Jencks, W.P.; Salvesen, K. Equilibrium Deuterium Isotope Effects on Ionization of Thiol Acids. J. Am. Chem. Soc. 1971, 93, 4433–4436. [Google Scholar] [CrossRef]
- Thomsen, B.; Shiga, M. Nuclear quantum effects on autoionization of water isotopologs studied by ab initio path integral molecular dynamics. J. Chem. Phys. 2021, 154, 084117. [Google Scholar] [CrossRef] [PubMed]
- Mora-Diez, N.; Egorova, Y.; Plommer, H.; Tremaine, P.R. Theoretical study of deuterium isotope effects on acid-base equilibria under ambient and hydrothermal conditions. RSC Adv. 2015, 5, 9097–9109. [Google Scholar] [CrossRef]
- Liu, M.; Youmans, K.N.; Gao, J. Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution. Molecules 2018, 23, 2644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krzan, M.; Vianello, R.; Marsavelski, A.; Repic, M.; Zaksek, M.; Kotnik, K.; Fijan, E.; Mavri, J. The Quantum Nature of Drug-Receptor Interactions: Deuteration Changes Binding Affinities for Histamine Receptor Ligands. PLoS ONE 2016, 11, e0154002. [Google Scholar] [CrossRef] [Green Version]
- Hok, L.; Mavri, J.; Vianello, R. The Effect of Deuteration on the H-2 Receptor Histamine Binding Profile: A Computational Insight into Modified Hydrogen Bonding Interactions. Molecules 2020, 25, 6017. [Google Scholar] [CrossRef]
- Krzan, M.; Keuschler, J.; Mavri, J.; Vianello, R. Relevance of Hydrogen Bonds for the Histamine H2 Receptor-Ligand Interactions: A Lesson from Deuteration. Biomolecules 2020, 10, 196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jorgensen, W.L.; Briggs, J.M.; Gao, J. A priori calculations of pKa’s for organic compounds in water. The pKa of ethane. J. Am. Chem. Soc. 1987, 109, 6857–6858. [Google Scholar] [CrossRef]
- Paabo, M.; Bates, R.G.; Robinson, R.A. Dissociation of Acetic Acid-D4 in Deuterium Oxide from 5 to 50 Degrees and Related Isotope Effects. J. Phys. Chem. 1966, 70, 2073. [Google Scholar] [CrossRef]
- Braude, E.A.; Nachod, F.C. Determination of Organic Structures by Physical Methods; Academic Press: New York, NY, USA, 1955. [Google Scholar]
- Guthrie, J.P. Hydration of Thioesters—Evaluation of Free-Energy Changes for Addition of Water to Some Thioesters, Rate-Equilibrium Correlations over Very Wide Ranges in Equilibrium-Constants, and a New Mechanistic Criterion. J. Am. Chem. Soc. 1978, 100, 5892–5904. [Google Scholar] [CrossRef]
- Guthrie, J.P.; Pike, D.C. Hydration of Acylimidazoles—Tetrahedral Intermediates in Acylimidazole Hydrolysis and Nucleophilic-Attack by Imidazole on Esters—The Question of Concerted Mechanisms for Acyl Transfers. Can. J. Chem. 1987, 65, 1951–1969. [Google Scholar] [CrossRef]
- Stewart, R. The Proton, Applications to Organic Chemistry; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Ballinger, P.; Long, F.A. The Reaction of Chlorohydrins and Hydroxide Ion in the Solvents H2O and D2O. J. Am. Chem. Soc. 1959, 81, 2347–2352. [Google Scholar] [CrossRef]
- Ballinger, P.; Long, F.A. Acid Ionization Constants of Alcohols.1. Trifluoroethanol in the Solvents H2O and D2O. J. Am. Chem. Soc. 1959, 81, 1050–1053. [Google Scholar] [CrossRef]
- Martin, D.C.; Butler, J.A.V. The dissociation constants of some nitrophenols in deuterium oxide. J. Chem. Soc. 1939, 1366–1371. [Google Scholar] [CrossRef]
- Bolton, P.D.; Hall, F.M.; Kudrynsk, J. Additive Substituent Effects on Ionization of Meta-Substituted Phenols. Aust. J. Chem. 1968, 21, 1541–1549. [Google Scholar] [CrossRef]
- Major, D.T.; Gao, J. An Integrated Path Integral and Free-Energy Perturbation-Umbrella Sampling Method for Computing Kinetic Isotope Effects of Chemical Reactions in Solution and in Enzymes. J. Chem.Theory Comput. 2007, 3, 949–960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J. Enzymatic Kinetic Isotope Effects from Path-Integral Free Energy Perturbation Theory. Methods Enzymol. 2016, 577, 359–388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zwanzig, R. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Hwang, J.K.; Warshel, A. A quantized classical path approach for calculations of quantum mechanical rate constants. J. Phys. Chem. 1993, 97, 10053–10058. [Google Scholar] [CrossRef]
- Sprik, M.; Klein, M.L.; Chandler, D. Simulation of an excess electron in a hard sphere fluid. J. Chem. Phys. 1985, 83, 3042–3049. [Google Scholar] [CrossRef]
- Major, D.T.; Gao, J. Implementation of the bisection sampling method in path integral simulations. J. Mol. Graph. Model. 2005, 24, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Major, D.T.; Garcia-Viloca, M.; Gao, J. Path Integral Simulations of Proton Transfer Reactions in Aqueous Solution Using Combined QM/MM Potentials. J. Chem. Theory Comput. 2006, 2, 236–245. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Wong, K.-Y.; Major, D.T. Combined QM/MM and path integral simulations of kinetic isotope effects in the proton transfer reaction between nitroethane and acetate ion in water. J. Comput. Chem. 2008, 29, 514–522. [Google Scholar] [CrossRef] [Green Version]
- Major, D.T.; Heroux, A.; Orville, A.M.; Valley, M.P.; Fitzpatrick, P.F.; Gao, J. Differential quantum tunneling contributions in nitroalkane oxidase catalyzed and the uncatalyzed proton transfer reaction. Proc. Natl. Acad. Sci. USA 2009, 106, 20736–20739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.-L.; Gao, J.; Rubinstein, A.; Major, D.T. Molecular dynamics simulations of the intramolecular proton transfer and carbanion stabilization in the pyridoxal 5′-phosphate dependent enzymesl-dopa decarboxylase and alanine racemase. Biochim. Biophys. Acta-Prot. Proteom. 2011, 1814, 1438–1446. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Cembran, A.; Ma, S.; Gao, J. Connecting Protein Conformational Dynamics with Catalytic Function As Illustrated in Dihydrofolate Reductase. Biochemistry 2013, 25, 2036–2049. [Google Scholar] [CrossRef] [Green Version]
- Bauer, P.; Barrozo, A.; Purg, M.; Amrein, B.A.; Esguerra, M.; Wilson, P.B.; Major, D.T.; Aqvist, J.; Kamerlin, S.C.L. Q6: A comprehensive toolkit for empirical valence bond and related free energy calculations. Softwarex 2018, 7, 388–395. [Google Scholar] [CrossRef]
- Pollock, E.L.; Ceperley, D.M. Simulation of quantum many-body systems by path-integral methods. Phys. Rev. B 1984, 30, 2555–2568. [Google Scholar] [CrossRef]
- Ceperley, D.M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 1995, 67, 279–355. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Gao, J.; York, D.M. An Efficient Linear-Scaling Ewald Method for Long-Range Electrostatic Interactions in Combined QM/MM Calculations. J. Chem. Theory Comput. 2005, 1, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.P.; Cicotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–337. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Wong, K.-Y.; Major, D.T.; Cembran, A.; Song, L.; Lin, Y.-L.; Fan, Y.; Ma, S. Kinetic isotope effects from hybrid classical and quantum path integral computations. In Quantum Tunneling in Enzyme-Catalysed Reactions; RSC Biomolecular Sciences; Allemann, R.K., Scrutton, N.S., Eds.; Royal Society of Chemistry: London, UK, 2009; pp. 105–131. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. M06 DFT functionals. Theor. Chem. Acc. 2008, 120, 215. [Google Scholar] [CrossRef] [Green Version]
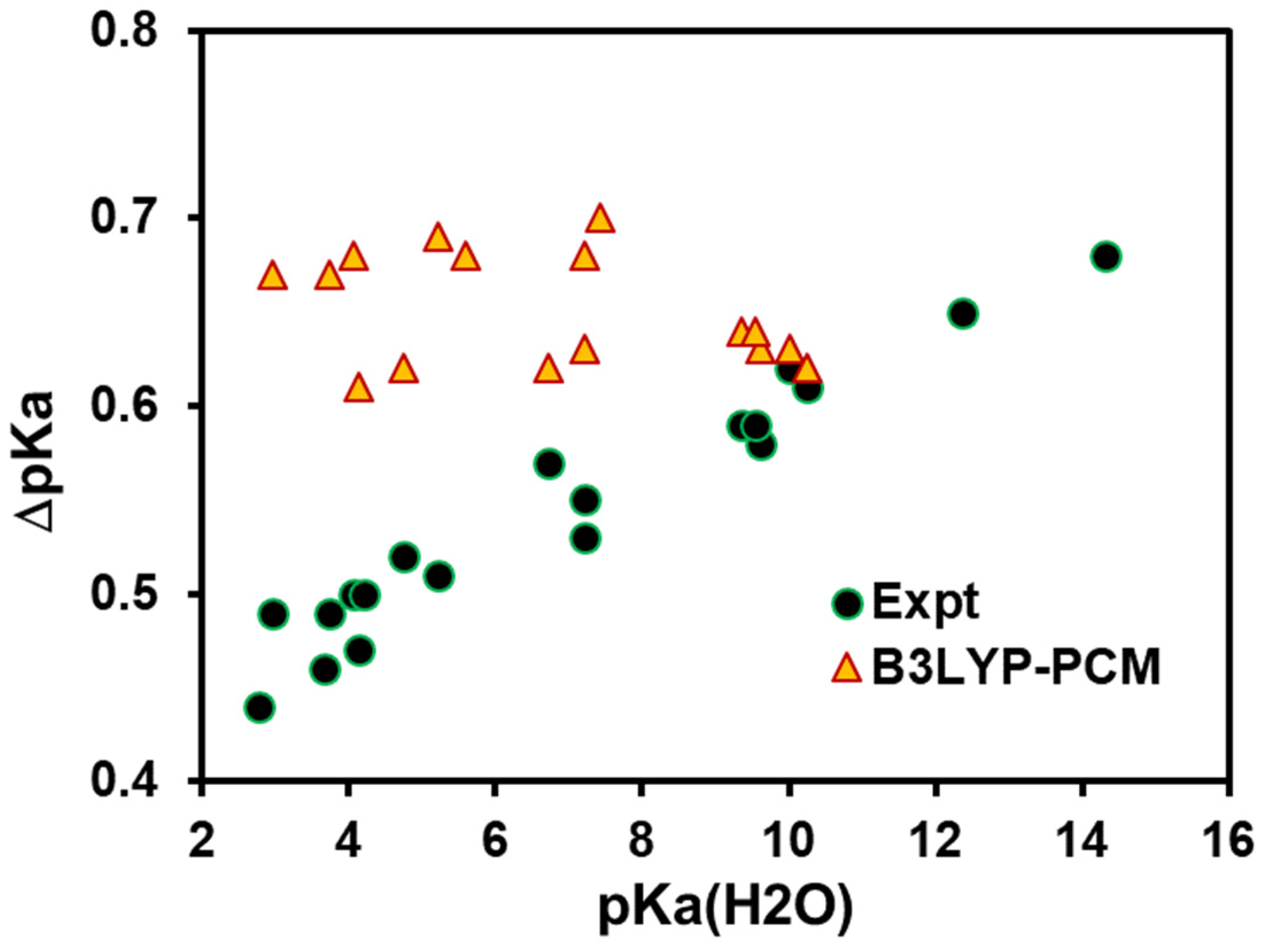

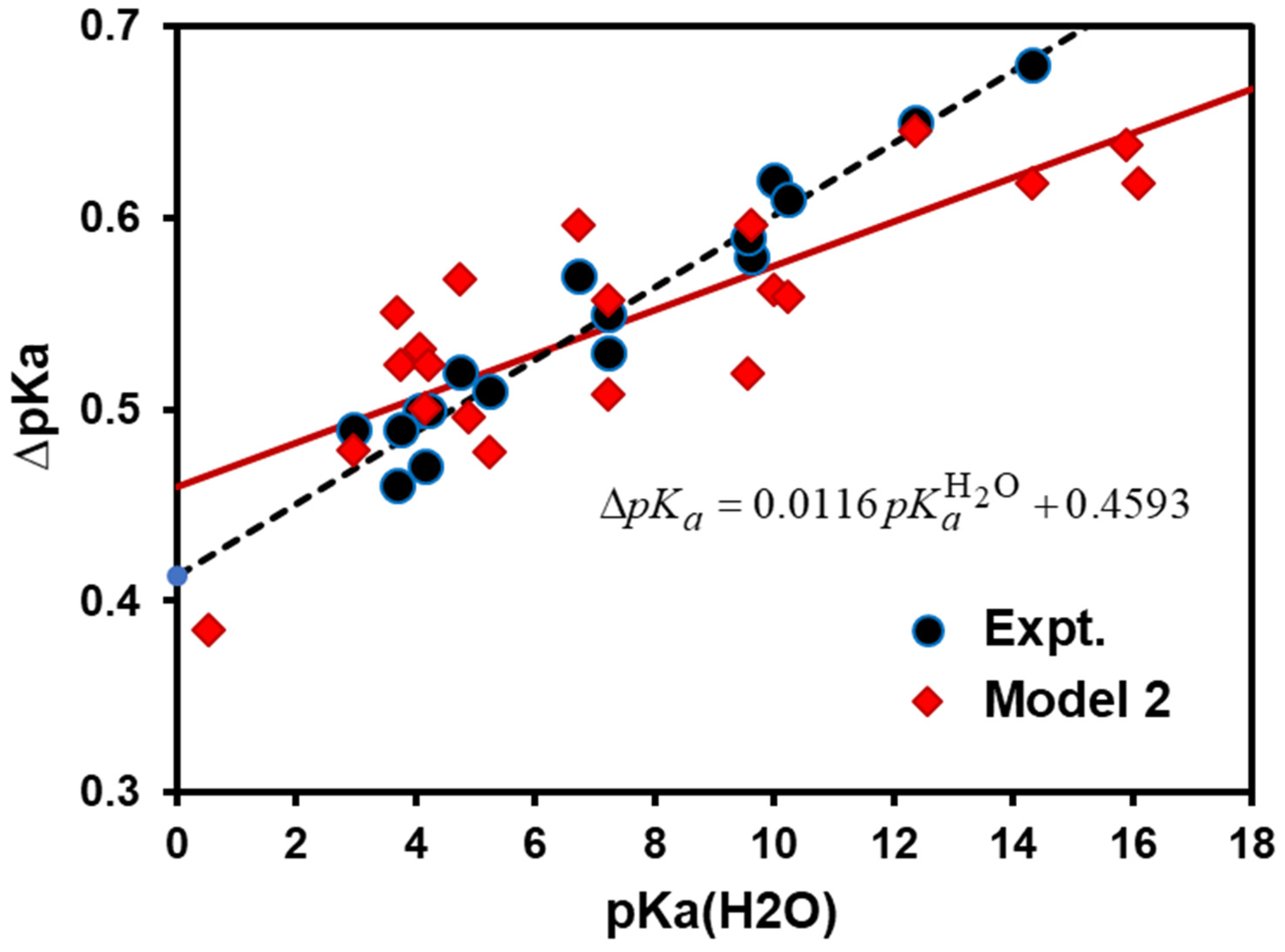
| Expt. | Calc. b | PI-FEP | |||||
|---|---|---|---|---|---|---|---|
| Acid (HA) | Model 1 | Model 2 | |||||
| MeCO2H | 4.75 a | 0.52 a,b | 0.62 | 1.4988 | 0.0656 | 0.52 | 0.57 |
| HCO2H | 3.67 c | 0.46 c | 1.5360 | 0.0052 | 0.55 | 0.55 | |
| EtCO2H | 4.88 d | 1.4754 | −0.0094 | 0.50 | 0.50 | ||
| F3CCO2H | 0.52 e | 1.4583 | −0.1444 | 0.49 | 0.38 | ||
| PhCO2H | 4.21 f | 0.50 f | 1.4909 | 0.0127 | 0.51 | 0.52 | |
| β-NaphCO2H | 4.14 g | 0.47g | 0.61 | 1.4994 | −0.0274 | 0.52 | 0.50 |
| EtOH | 15.9 h | 1.4998 | 0.1605 | 0.52 | 0.64 | ||
| PrOH | 16.1 i | 1.4966 | 0.1362 | 0.52 | 0.62 | ||
| 2-ClEtOH | 14.3 j | 0.68 j | 1.4925 | 0.1401 | 0.52 | 0.62 | |
| CF3CH2OH | 12.4 k | 0.65 k | 1.4953 | 0.1742 | 0.52 | 0.65 | |
| PhOH | 10.0 g | 0.62 g | 0.63 | 1.4913 | 0.0656 | 0.51 | 0.56 |
| 3-MeOPhOH | 9.62 g | 0.58 g | 0.63 | 1.4805 | 0.1228 | 0.51 | 0.60 |
| 4-MeOPhOH | 10.2 g | 0.61 g | 0.62 | 1.4793 | 0.0726 | 0.51 | 0.56 |
| 2-NitroPhOH | 7.22 b,l | 0.55 b,l | 0.68 | 1.4801 | 0.0018 | 0.51 | 0.51 |
| 4-NitroPhOH | 7.22 g | 0.53 g | 0.63 | 1.4757 | 0.0733 | 0.50 | 0.56 |
| 3,5-diNitroPhOH | 6.73 m | 0.57 a,b | 0.62 | 1.4629 | 0.1394 | 0.49 | 0.60 |
| 2,5-diNitroPhOH | 5.22 g,n | 0.51 g,n | 0.69 | 1.4681 | −0.0271 | 0.50 | 0.48 |
| 2,4-diNitroPhOH | 4.07 g,n | 0.50 b,g | 0.68 | 1.4794 | 0.0355 | 0.51 | 0.53 |
| 2,6-diNitroPhOH | 3.73 n | 0.49 n | 0.67 | 1.4647 | 0.0392 | 0.50 | 0.52 |
| 4-Cl-2,6-diNitroPhOH | 2.96 a,n | 0.49 a,n | 0.67 | 1.4631 | −0.0209 | 0.49 | 0.48 |
| β-Naphthol | 9.55 g | 0.59 g | 0.64 | 1.4907 | 0.0065 | 0.51 | 0.52 |
| Acid (HA) | |||
|---|---|---|---|
| MeCO2H | −11.1 | −16.5 | 0.0656 |
| HCO2H | −11.2 | −20.2 | 0.0052 |
| EtCO2H | −11.1 | −20.2 | −0.0094 |
| F3CCO2H | −10.5 | −17.0 | −0.1444 |
| PhCO2H | −11.3 | −14.9 | 0.0127 |
| β-NaphCO2H | −11.3 | −18.1 | −0.0274 |
| EtOH | −5.0 | −25.2 | 0.1605 |
| PrOH | −3.5 | −19.8 | 0.1362 |
| 2-ClEtOH | −5.9 | −22.9 | 0.1401 |
| CF3CH2OH | −7.0 | −22.5 | 0.1742 |
| PhOH | −7.0 | −17.5 | 0.0656 |
| 3-MeOPhOH | −6.9 | −16.7 | 0.1228 |
| 4-MeOPhOH | −6.8 | −17.5 | 0.0726 |
| 2-NitroPhOH | −8.8 | −14.2 | 0.0018 |
| 4-NitroPhOH | −8.7 | −13.8 | 0.0733 |
| 3,5-diNitroPhOH | −9.9 | −13.0 | 0.1394 |
| 2,5-diNitroPhOH | −10.2 | −12.2 | −0.0271 |
| 2,4-diNitroPhOH | −10.3 | −12.0 | 0.0355 |
| 2,6-diNitroPhOH | −5.6 | −13.2 | 0.0392 |
| 4-Cl-2,6-diNitroPhOH | −5.9 | −12.6 | −0.0209 |
| β-Naphthol | −7.2 | −15.6 | 0.0065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Gao, J. Deuterium Isotope Effects on Acid-Base Equilibrium of Organic Compounds. Molecules 2021, 26, 7687. https://doi.org/10.3390/molecules26247687
Liu M, Gao J. Deuterium Isotope Effects on Acid-Base Equilibrium of Organic Compounds. Molecules. 2021; 26(24):7687. https://doi.org/10.3390/molecules26247687
Chicago/Turabian StyleLiu, Meiyi, and Jiali Gao. 2021. "Deuterium Isotope Effects on Acid-Base Equilibrium of Organic Compounds" Molecules 26, no. 24: 7687. https://doi.org/10.3390/molecules26247687
APA StyleLiu, M., & Gao, J. (2021). Deuterium Isotope Effects on Acid-Base Equilibrium of Organic Compounds. Molecules, 26(24), 7687. https://doi.org/10.3390/molecules26247687





