Alkyne-Functionalized Cyclooctyne on Si(001): Reactivity Studies and Surface Bonding from an Energy Decomposition Analysis Perspective
Abstract
:1. Introduction
2. Methods
2.1. Structural Optimizations and Ab Initio Molecular Dynamic Calculations
2.2. Bonding Analysis
3. Results and Discussion
3.1. Gas Phase Structure and Adsorption Modes
3.2. Singly Bonded States
3.3. Bonding Analysis of Singly Bonded States
3.4. Conformer Space
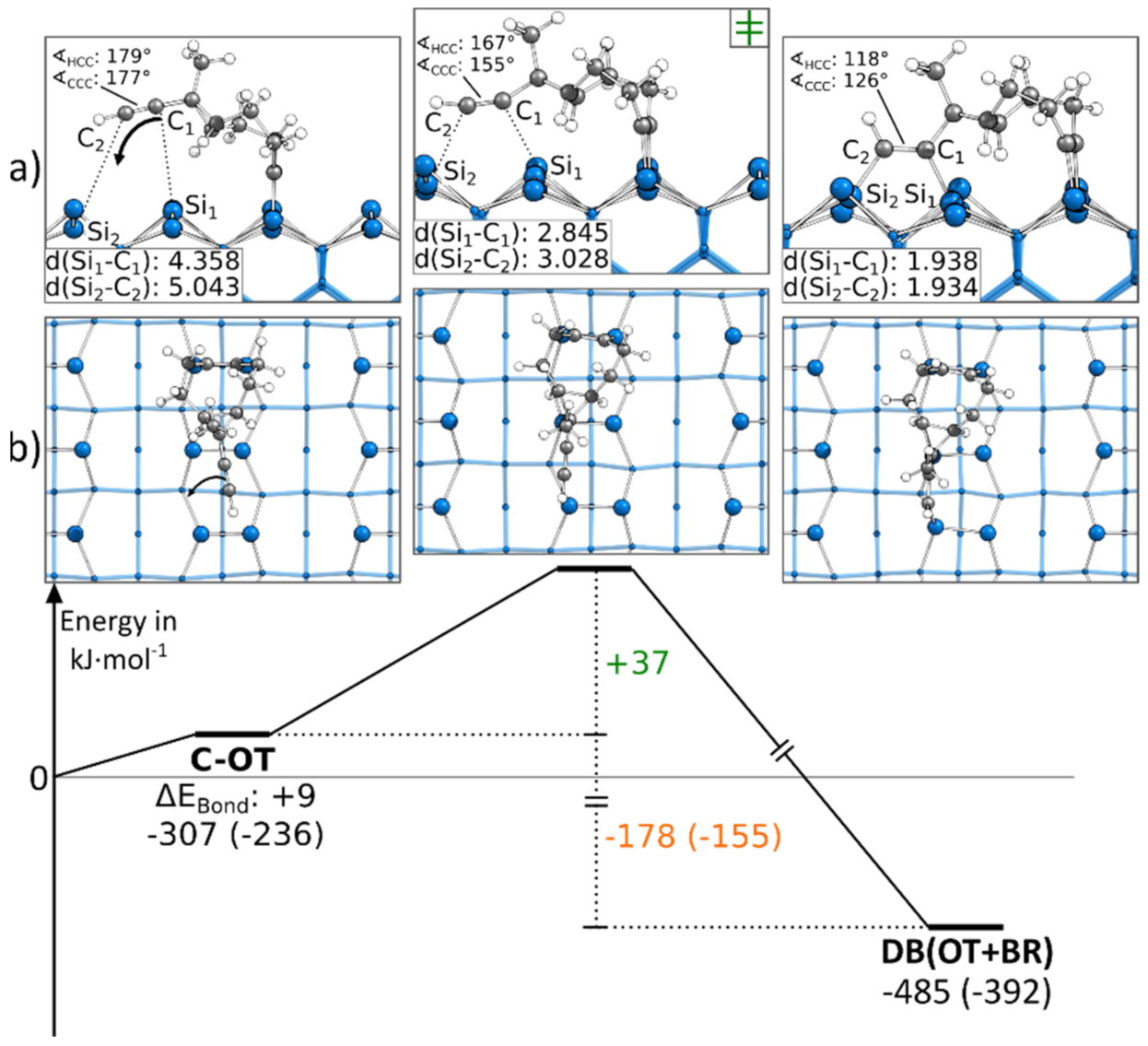
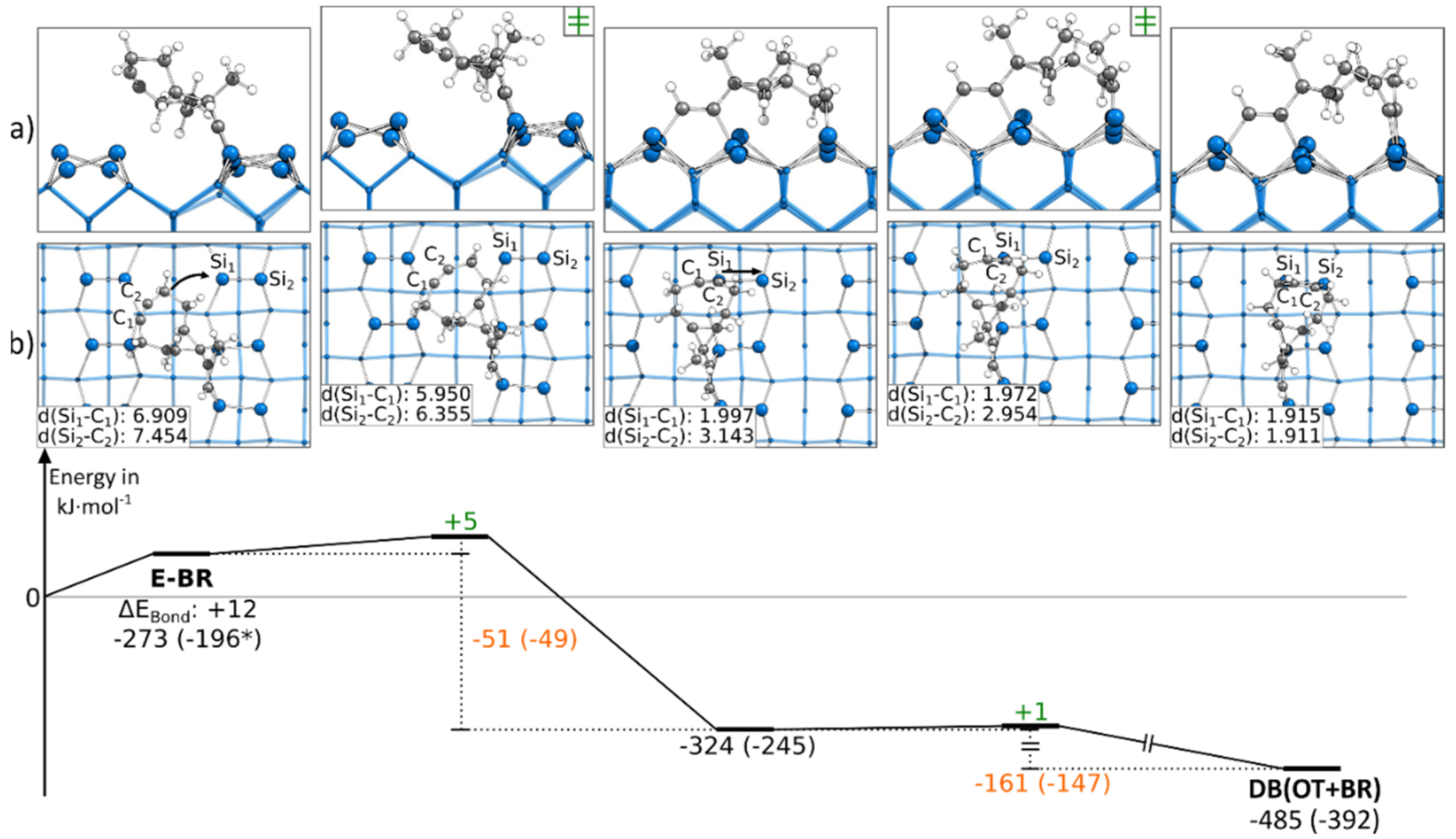
3.5. Doubly Bonded States
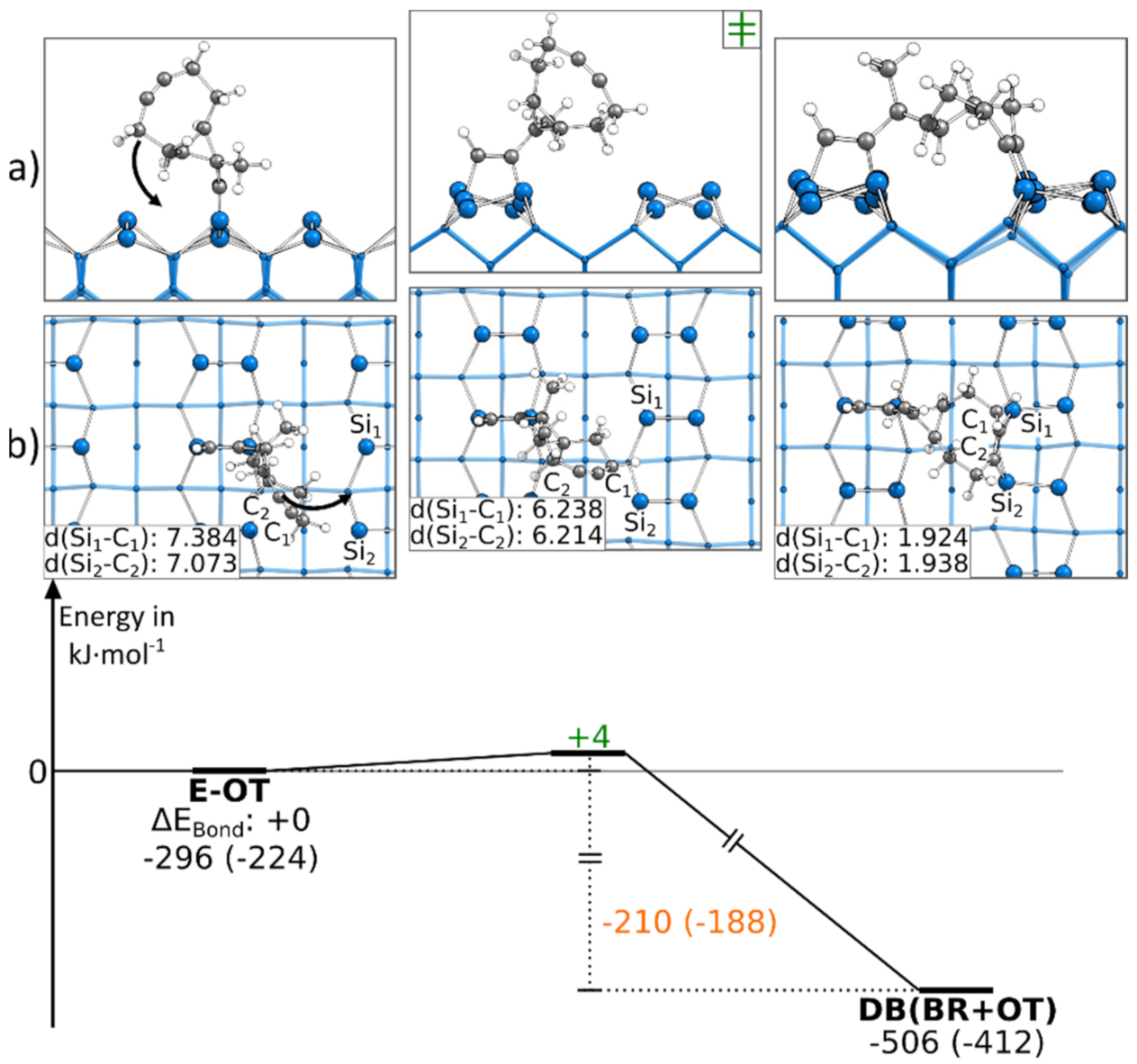
3.5.1. Reaction Paths to DB(OT+BR)
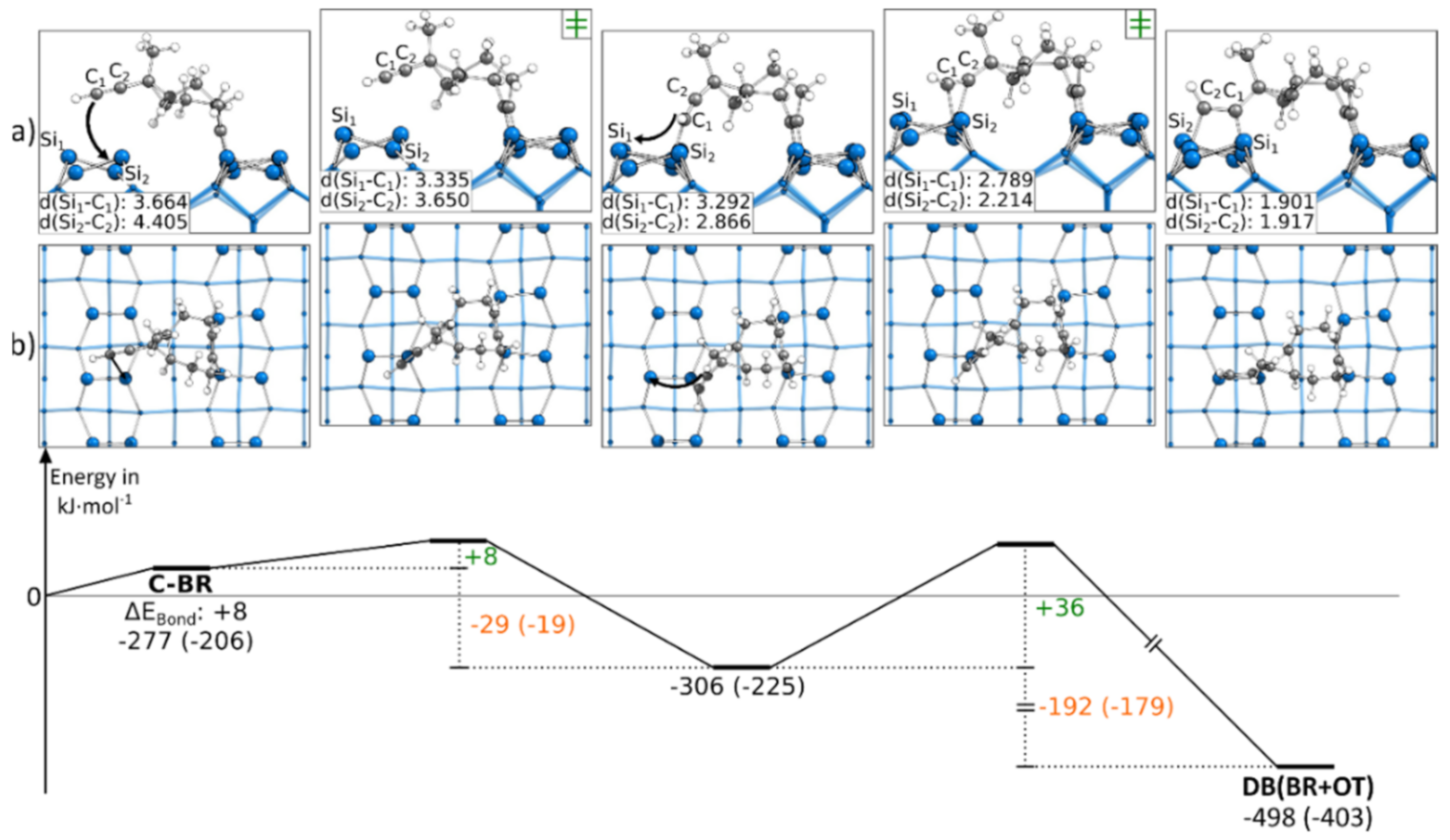
3.5.2. Reaction Paths to DB(BR+OT)
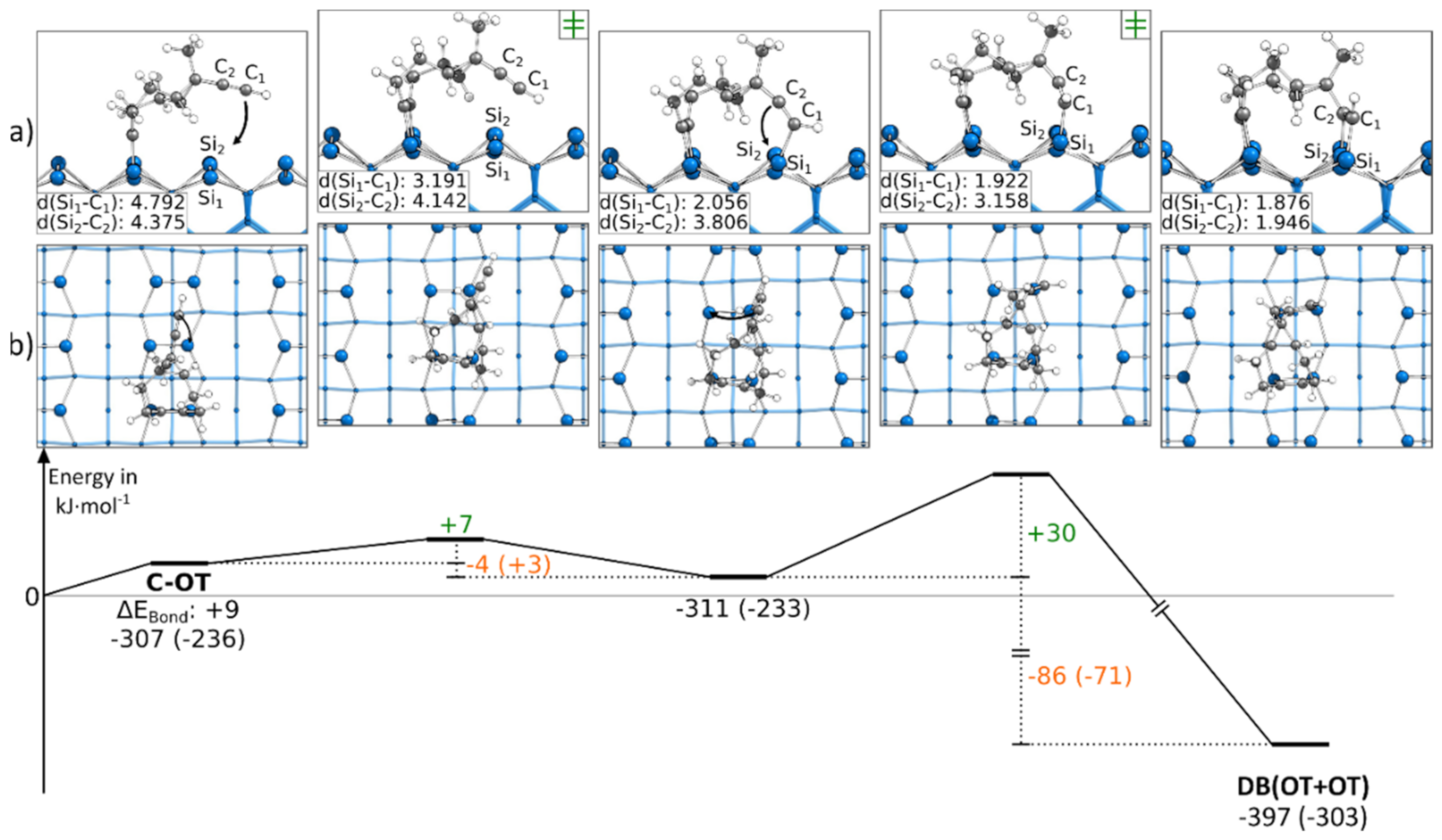
3.5.3. Reaction Paths to DB(OT+OT)
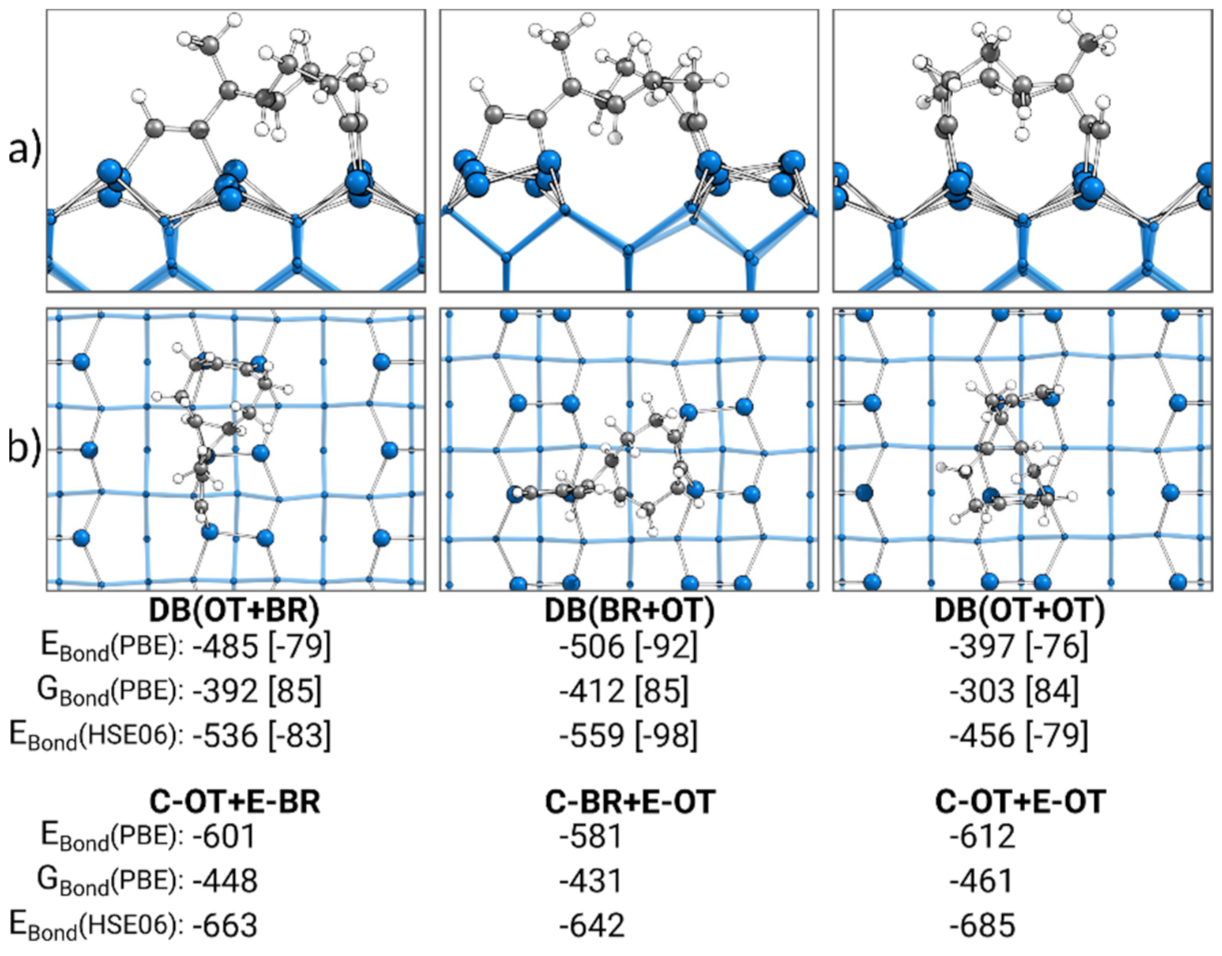
3.6. Comparison of Doubly Bonded Structures
3.7. Bonding Analysis of Doubly Bonded States
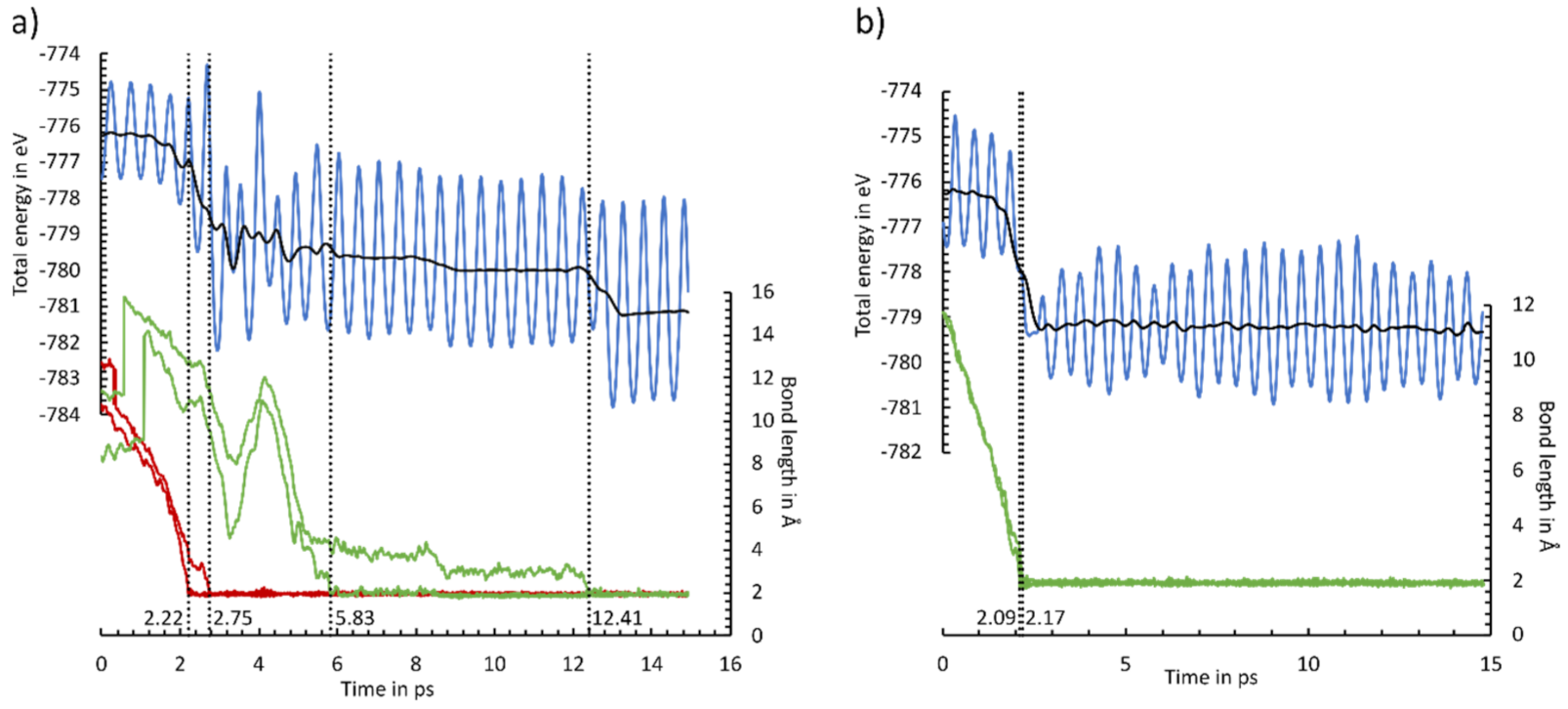
3.8. Ab Initio Molecular Dynamics
3.9. Comparison to the Experiment
3.9.1. Low T, Low θ
3.9.2. High T, High θ and High T, Low θ
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- International Roadmap for Devices and Systems (IRDSTM). 2020. Available online: https://irds.ieee.org (accessed on 29 October 2021).
- Aradhya, S.; Venkataraman, L. Single-molecule junctions beyond electronic transport. Nat. Nanotechnol. 2013, 8, 399–410. [Google Scholar] [CrossRef]
- Yates, J.T. A New Opportunity in Silicon-Based Microelectronics. Science 1998, 279, 335–336. [Google Scholar] [CrossRef]
- Zhou, H.; Bent, S.F. Fabrication of organic interfacial layers by molecular layer deposition: Present status and future opportunities. J. Vac. Sci. Technol. A 2013, 31, 040801. [Google Scholar] [CrossRef]
- Hills, G.; Lau, C.; Wright, A.; Fuller, S.; Bishop, M.D.; Srimani, T.; Kanhaiya, P.; Ho, R.; Amer, A.; Stein, Y.; et al. Modern microprocessor built from complementary carbon nanotube transistors. Nature 2019, 572, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Miozzo, L.; Yassar, A.; Horowitz, G. Surface engineering for high performance organic electronic devices: The chemical approach. J. Mater. Chem. 2010, 20, 2513–2538. [Google Scholar] [CrossRef]
- Wolkow, R.A. Controlled Molecular Adsorption on Silicon: Laying a Foundation for Molecular Devices. Annu. Rev. Phys. Chem. 1999, 50, 413–441. [Google Scholar] [CrossRef] [PubMed]
- Teplyakov, A.V.; Bent, S.F. Semiconductor surface functionalization for advances in electronics, energy conversion, and dynamic systems. J. Vac. Sci. Technol. A 2013, 31, 050810. [Google Scholar] [CrossRef]
- Bent, S.F. Organic functionalization of group IV semiconductor surfaces: Principles, examples, applications, and prospects. Surf. Sci. 2002, 500, 879–903. [Google Scholar] [CrossRef]
- Kachian, J.S.; Wong, K.T.; Bent, S.F. Periodic Trends in Organic Functionalization of Group IV Semiconductor Surfaces. Acc. Chem. Res. 2010, 43, 346–355. [Google Scholar] [CrossRef] [PubMed]
- Yates, J.T., Jr. Surface chemistry of silicon-the behaviour of dangling bonds. J. Phys. Condens. Matter 1991, 3, S143–S156. [Google Scholar] [CrossRef]
- Filler, M.A.; Bent, S.F. The surface as molecular reagent: Organic chemistry at the semiconductor interface. Prog. Surf. Sci. 2003, 73, 1–56. [Google Scholar] [CrossRef]
- Yoshinobu, J. Physical properties and chemical reactivity of the buckled dimer on Si(100). Prog. Surf. Sci. 2004, 77, 37–70. [Google Scholar] [CrossRef]
- Leftwich, T.; Teplyakov, A. Chemical manipulation of multifunctional hydrocarbons on silicon surfaces. Surf. Sci. Rep. 2008, 63, 1–71. [Google Scholar] [CrossRef]
- Hossain, Z.; Yamashita, Y.; Mukai, K.; Yoshinobu, J. Selective functionalization of the Si(100) surface by switching the adsorption linkage of a bifunctional organic molecule. Chem. Phys. Lett. 2004, 388, 27–30. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Leung, K. Selective surface chemistry of allyl alcohol and allyl aldehyde on Si(100) 2×1: Competition of [2 + 2] C=C cycloaddition with O–H dissociation and with [2 + 2] CO cycloaddition in bifunctional molecules. Surf. Sci. 2009, 603, 1203–1211. [Google Scholar] [CrossRef]
- Shao, Y.X.; Cai, Y.H.; Dong, D.; Wang, S.; Ang, S.G.; Xu, G.Q. Spectroscopic study of propargyl chloride attachment on Si(100)−2×1. Chem. Phys. Lett. 2009, 482, 77–80. [Google Scholar] [CrossRef]
- Reutzel, M.; Münster, N.; Lipponer, M.A.; Länger, C.; Höfer, U.; Koert, U.; Dürr, M. Chemoselective Reactivity of Bifunctional Cyclooctynes on Si(001). J. Phys. Chem. C 2016, 120, 26284–26289. [Google Scholar] [CrossRef] [Green Version]
- Kolb, H.C.; Finn, M.G.; Sharpless, K.B. Click Chemistry: Diverse Chemical Function from a Few Good Reactions. Angew. Chem. Int. Ed. 2001, 40, 2004–2021. [Google Scholar] [CrossRef]
- Devaraj, N.K.; Finn, M.G. Introduction: Click Chemistry. Chem. Rev. 2021, 121, 6697–6698. [Google Scholar] [CrossRef] [PubMed]
- Sletten, E.M.; Bertozzi, C.R. Bioorthogonal Chemistry: Fishing for Selectivity in a Sea of Functionality. Angew. Chem. Int. Ed. 2009, 48, 6974–6998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glaser, T.; Meinecke, J.; Länger, C.; Heep, J.; Koert, U.; Dürr, M. Solution-Based Alkyne–Azide Coupling on Functionalized Si(001) Prepared under UHV Conditions. J. Phys. Chem. C 2021, 125, 4021–4026. [Google Scholar] [CrossRef]
- Glaser, T.; Meinecke, J.; Freund, L.; Länger, C.; Luy, J.-N.; Tonner, R.; Koert, U.; Dürr, M. Click Chemistry in Ultra-high Vacuum—Tetrazine Coupling with Methyl Enol Ether Covalently Linked to Si(001). Chem. Eur. J. 2021, 27, 8082–8087. [Google Scholar] [CrossRef] [PubMed]
- Luy, J.-N.; Tonner, R. Complementary Base Lowers the Barrier in SuFEx Click Chemistry for Primary Amine Nucleophiles. ACS Omega 2020, 5, 31432–31439. [Google Scholar] [CrossRef] [PubMed]
- Meinecke, J.; Koert, U. Copper-Free Click Reaction Sequence: A Chemoselective Layer-by-Layer Approach. Org. Lett. 2019, 21, 7609–7612. [Google Scholar] [CrossRef]
- Pecher, J.; Mette, G.; Dürr, M.; Tonner, R. Site-Specific Reactivity of Ethylene at Distorted Dangling-Bond Configurations on Si(001). Chem. Phys. Chem. 2017, 18, 357–365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, J.-H.; Kleinman, L. Adsorption kinetics of acetylene and ethylene on Si(001). Phys. Rev. B 2004, 69, 075303. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Precursor States of Organic Adsorbates on Semiconductor Surfaces are Chemisorbed and Immobile. Chem. Phys. Chem. 2017, 18, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-W.; Lee, J.-H.; Kim, H.-J.; Cho, J.-H. Contribution of van der Waals interactions to the adsorption energy of C2H2, C2H4, and C6H6 on Si(100). Chem. Phys. Lett. 2013, 557, 159–162. [Google Scholar] [CrossRef]
- Luy, J.-N.; Tonner, R. Organic Functionalization at the Si(001) Dimer Vacancy Defect—Structure, Bonding and Reactivity. J. Phys. Chem. C 2021, 125, 5635–5646. [Google Scholar] [CrossRef]
- Mette, G.; Schwalb, C.; Dürr, M.; Höfer, U. Site-selective reactivity of ethylene on clean and hydrogen precovered Si(001). Chem. Phys. Lett. 2009, 483, 209–213. [Google Scholar] [CrossRef]
- Matsui, F.; Yeoim, H.; Imanishi, A.; Isawa, K.; Matsuda, I.; Ohta, T. Adsorption of acetylene and ethylene on the Si(001)2×1 surface studied by NEXAFS and UPS. Surf. Sci. 1998, 401, L413–L419. [Google Scholar] [CrossRef]
- Lipponer, M.A.; Armbrust, N.; Dürr, M.; Höfer, U. Adsorption dynamics of ethylene on Si(001). J. Chem. Phys. 2012, 136, 144703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pecher, J.; Schober, C.; Tonner, R. Chemisorption of a Strained but Flexible Molecule: Cyclooctyne on Si(001). Chem. Eur. J. 2017, 23, 5459–5466. [Google Scholar] [CrossRef] [PubMed]
- Silvestrelli, P.L.; Pulci, O.; Palummo, M.; Del Sole, R.; Ancilotto, F. First-principles study of acetylene adsorption on Si(100): The end-bridge structure. Phys. Rev. B 2003, 68, 235306. [Google Scholar] [CrossRef]
- Liu, Q.; Hoffmann, R. The Bare and Acetylene Chemisorbed Si(001) Surface, and the Mechanism of Acetylene Chemisorption. J. Am. Chem. Soc. 1995, 117, 4082–4092. [Google Scholar] [CrossRef]
- Miotto, R.; Ferraz, A.C.; Srivastava, G.P. Acetylene adsorption on the Si(001) surface. Phys. Rev. B 2002, 65, 075401. [Google Scholar] [CrossRef] [Green Version]
- Mezhenny, S.; Lyubinetsky, I.; Choyke, W.; Wolkow, R.; Yates, J. Multiple bonding structures of C2H2 chemisorbed on Si(100). Chem. Phys. Lett. 2001, 344, 7–12. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Jordan, K.D. Theoretical Study of the Adsorption of Acetylene on the Si(001) Surface. J. Phys. Chem. B 2000, 104, 8259–8267. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics 2018, 6, 17. [Google Scholar] [CrossRef] [Green Version]
- Länger, C.; Heep, J.; Nikodemiak, P.; Bohamud, T.; Kirsten, P.; Höfer, U.; Koert, U.; Dürr, M. Formation of Si/organic interfaces using alkyne-functionalized cyclooctynes—Precursor-mediated adsorption of linear alkynes versus direct adsorption of cyclooctyne on Si(001). J. Phys. Condens. Matter 2019, 31, 034001. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Kim, H.; Lee, G.; Hong, Y.-K.; Lee, K.; Hwang, C.; Kim, D.-H.; Koo, J.-Y. Initial adsorption configurations of acetylene molecules on the Si(001) surface. Phys. Rev. B 2001, 64, 193313. [Google Scholar] [CrossRef]
- Czekala, P.T.; Lin, H.; Hofer, W.A.; Gulans, A. Acetylene adsorption on silicon (100)-(4 × 2) revisited. Surf. Sci. 2011, 605, 1341–1346. [Google Scholar] [CrossRef]
- Zhang, Q.J.; Fan, X.L.; Lau, W.M.; Liu, Z.-F. Sublayer Si atoms as reactive centers in the chemisorption on Si(100): Adsorption of C2H2 and C2H4. Phys. Rev. B 2009, 79, 195303. [Google Scholar] [CrossRef] [Green Version]
- Taylor, P.A.; Wallace, R.M.; Cheng, C.C.; Weinberg, W.H.; Dresser, M.J.; Choyke, W.J.; Yates, J.T. Adsorption and decomposition of acetylene on silicon (100)-(2 × 1). J. Am. Chem. Soc. 1992, 114, 6754–6760. [Google Scholar] [CrossRef]
- Takeuchi, N. First principles calculations of the adsorption of acetylene on the Si(001) surface at low and full coverage. Surf. Sci. 2007, 601, 3361–3365. [Google Scholar] [CrossRef]
- Kim, W.; Kim, H.; Lee, G.; Chung, J.; You, S.-Y.; Hong, Y.-K.; Koo, J.-Y. Acetylene molecules on the Si(001) surface: Room-temperature adsorption and structural modification upon annealing. Surf. Sci. 2002, 514, 376–382. [Google Scholar] [CrossRef]
- Pecher, L.; Schmidt, S.; Tonner, R. Dispersion-mediated steering of organic adsorbates on a precovered silicon surface. Beilstein J. Org. Chem. 2018, 14, 2715–2721. [Google Scholar] [CrossRef] [PubMed]
- Mette, G.; Dürr, M.; Bartholomäus, R.; Koert, U.; Höfer, U. Real-space adsorption studies of cyclooctyne on Si(001). Chem. Phys. Lett. 2012, 556, 70–76. [Google Scholar] [CrossRef]
- Pecher, L.; Schmidt, S.; Tonner, R. Modeling the Complex Adsorption Dynamics of Large Organic Molecules: Cyclooctyne on Si(001). J. Phys. Chem. C 2017, 121, 26840–26850. [Google Scholar] [CrossRef]
- Mette, G.; Reutzel, M.; Bartholomäus, R.; Laref, S.; Tonner, R.; Dürr, M.; Koert, U.; Höfer, U. Complex Surface Chemistry of an Otherwise Inert Solvent Molecule: Tetrahydrofuran on Si(001). Chem. Phys. Chem. 2014, 15, 3725–3728. [Google Scholar] [CrossRef]
- Reutzel, M.; Mette, G.; Stromberger, P.; Koert, U.; Dürr, M.; Höfer, U. Dissociative Adsorption of Diethyl Ether on Si(001) Studied by Means of Scanning Tunneling Microscopy and Photoelectron Spectroscopy. J. Phys. Chem. C 2015, 119, 6018–6023. [Google Scholar] [CrossRef]
- Pecher, L.; Laref, S.; Raupach, M.; Tonner, R. Ethers on Si(001): A Prime Example for the Common Ground between Surface Science and Molecular Organic Chemistry. Angew. Chem. Int. Ed. 2017, 56, 15150–15154. [Google Scholar] [CrossRef] [PubMed]
- Reutzel, M.; Lipponer, M.; Dürr, M.; Höfer, U. Binding Energy and Dissociation Barrier: Experimental Determination of the Key Parameters of the Potential Energy Curve of Diethyl Ether on Si(001). J. Phys. Chem. Lett. 2015, 6, 3971–3975. [Google Scholar] [CrossRef] [PubMed]
- Turner, R.B.; Jarrett, A.D.; Goebel, P.; Mallon, B.J. Heats of hydrogenation. IX. Cyclic acetylenes and some miscellaneous olefins. J. Am. Chem. Soc. 1973, 95, 790–792. [Google Scholar] [CrossRef]
- Luy, J.-N.; Molla, M.; Pecher, L.; Tonner, R. Efficient hierarchical models for reactivity of organic layers on semiconductor surfaces. J. Comput. Chem. 2021, 42, 827–839. [Google Scholar] [CrossRef]
- Glaser, T.; Länger, C.; Heep, J.; Meinecke, J.; Silly, M.G.; Koert, U.; Dürr, M. Starting from a Fixed Geometry: Real-Time XPS Investigation of a Surface Reaction with Controlled Molecular Configurations. J. Phys. Chem. C 2020, 124, 22619–22624. [Google Scholar] [CrossRef]
- Glaser, T.; Meinecke, J.; Länger, C.; Luy, J.-N.; Tonner, R.; Koert, U.; Dürr, M. Combined XPS and DFT investigation of the adsorption modes of methyl enol ether functionalized cyclooctyne on Si(001). Chem. Phys. Chem. 2021, 22, 404–409. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Computational analysis of the competitive bonding and reactivity pattern of a bifunctional cyclooctyne on Si(001). Theor. Chem. Acc. 2018, 137, 48. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initiomolecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initiomolecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.1996, 77, 1395. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Uberuaga, B.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef] [Green Version]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Verlet, L. Computer "Experiments" on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. Constant Temperature Molecular Dynamics Methods. Prog. Theor. Phys. Suppl. 1991, 103, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Bylander, D.M.; Kleinman, L. Energy fluctuations induced by the Nosé thermostat. Phys. Rev. B 1992, 46, 13756–13761. [Google Scholar] [CrossRef] [PubMed]
- Boyd, D.R.J. Infrared Spectrum of Trideuterosilane and the Structure of the Silane Molecule. J. Chem. Phys. 1955, 23, 922–926. [Google Scholar] [CrossRef]
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Raupach, M.; Tonner, R. A periodic energy decomposition analysis method for the investigation of chemical bonding in extended systems. J. Chem. Phys. 2015, 142, 194105. [Google Scholar] [CrossRef] [Green Version]
- Pecher, L.; Tonner, R. Deriving bonding concepts for molecules, surfaces, and solids with energy decomposition analysis for extended systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1401. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chem. Acc. 1977, 46, 1–10. [Google Scholar] [CrossRef]
- Franchini, M.; Philipsen, P.H.T.; van Lenthe, E.; Visscher, L. Accurate Coulomb Potentials for Periodic and Molecular Systems through Density Fitting. J. Chem. Theory Comput. 2014, 10, 1994–2004. [Google Scholar] [CrossRef] [PubMed]
- Wiesenekker, G.; Velde, G.T.; Baerends, E.J. Analytic quadratic integration over the two-dimensional Brillouin zone. J. Phys. C Solid State Phys. 1988, 21, 4263–4283. [Google Scholar] [CrossRef]
- Velde, G.T.; Baerends, E.J. Precise density-functional method for periodic structures. Phys. Rev. B 1991, 44, 7888–7903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiesenekker, G.; Baerends, E.J. Quadratic integration over the three-dimensional Brillouin zone. J. Phys. Condens. Matter 1991, 3, 6721–6742. [Google Scholar] [CrossRef]
- Franchini, M.; Philipsen, P.H.T.; Visscher, L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1-118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef] [Green Version]
- Philipsen, P.H.T.; van Lenthe, E.; Snijders, J.G.; Baerends, E.J. Relativistic calculations on the adsorption of CO on the (111) surfaces of Ni, Pd, and Pt within the zeroth-order regular approximation. Phys. Rev. B 1997, 56, 13556–13562. [Google Scholar] [CrossRef] [Green Version]
- Philipsen, P.H.T.; Baerends, E.J. Relativistic calculations to assess the ability of the generalized gradient approximation to reproduce trends in cohesive properties of solids. Phys. Rev. B 2000, 61, 1773–1778. [Google Scholar] [CrossRef] [Green Version]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
- Michalak, A.; Mitoraj, M.; Ziegler, T. Bond Orbitals from Chemical Valence Theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef]
- Perdew, J.P. Climbing the ladder of density functional approximations. MRS Bull. 2013, 38, 743–750. [Google Scholar] [CrossRef]
- Cohen, A.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2011, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]

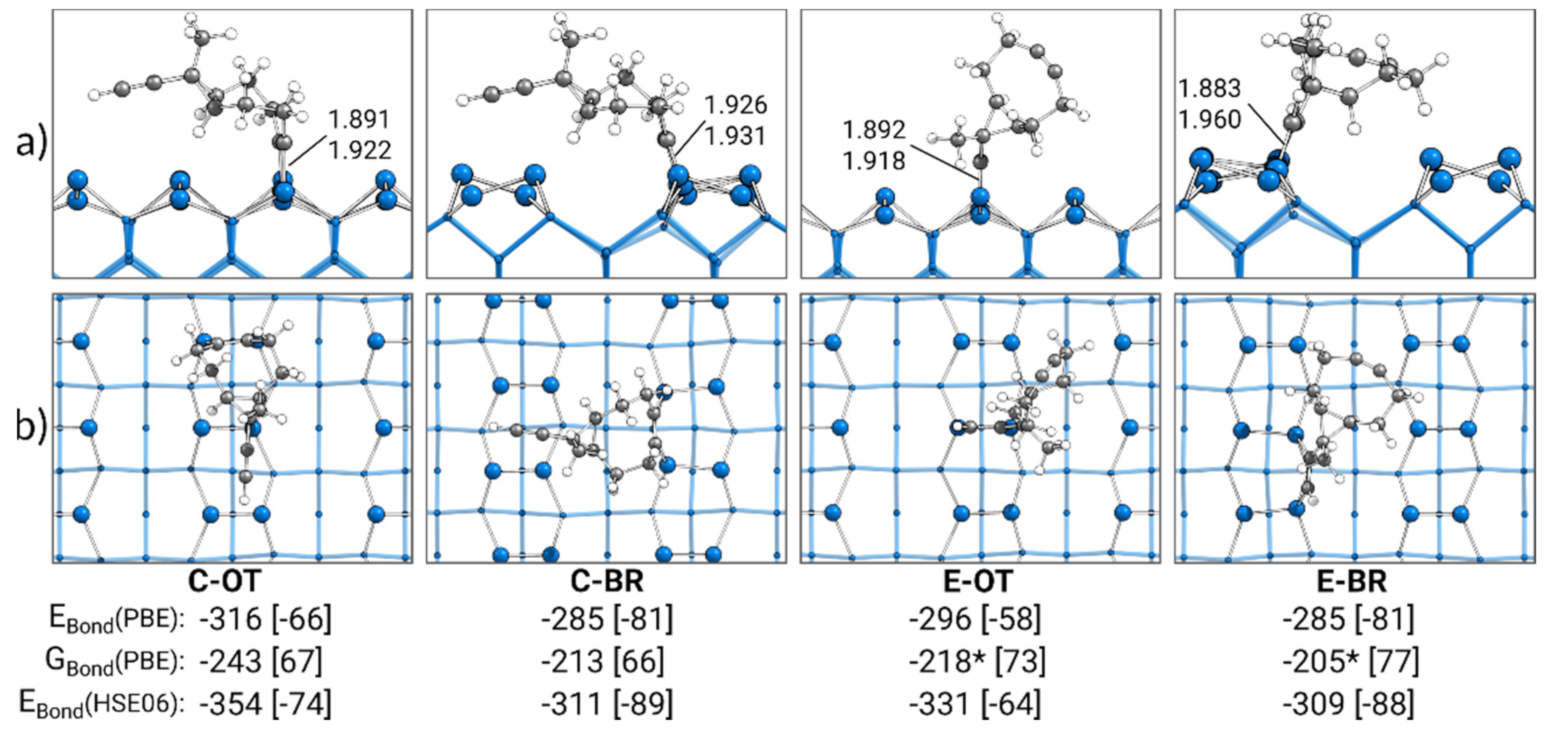
| C-OT | C-BR | E-OT | E-BR | Cyclo. OT | Acet. OT | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔEint | −681 | −723 | −677 | −757 | −658 | −668 | ||||||
| ΔE int(disp) (b) | −62 | (9%) | −74 | (10%) | −53 | (8%) | −74 | (10%) | −43 | (7%) | −12 | (2%) |
| ΔEint(elec) (b) | −619 | (91%) | −649 | (90%) | −624 | (92%) | −683 | (90%) | −615 | (93%) | −656 | (98%) |
| ΔEPauli | 1500 | 1406 | 1482 | 1393 | 1468 | 1323 | ||||||
| ΔEelstat (c) | −940 | (44%) | −923 | (45%) | −924 | (44%) | −913 | (44%) | −936 | (45%) | −828 | (42%) |
| ΔEorb (c) | −1179 | (56%) | −1132 | (55%) | −1182 | (56%) | −1163 | (56%) | −1148 | (55%) | −1152 | (58%) |
| ΔEorb (M→S) (d) | −364 | (31%) | −339 | (30%) | −367 | (31%) | −339 | (29%) | ||||
| ΔEorb (S→M) (d) | −610 | (52%) | −603 | (53%) | −621 | (53%) | −610 | (52%) | ||||
| ΔEprep | 352 | 429 | 370 | 464 | 339 | 389 | ||||||
| ΔEprep (M) (e) | 324 | 329 | 345 | 367 | 313 | 364 | ||||||
| ΔEprep (S) (e) | 28 | 100 | 25 | 97 | 26 | 25 | ||||||
| EBond | −329 | −294 | −307 | −293 | −319 | −279 | ||||||
| EBond (PAW) | −316 | −285 | −296 | −285 | −308 | −268 | ||||||
| d(Si-C) | 1.891 | 1.926 | 1.892 | 1.883 | 1.900 | 1.896 | ||||||
| d(Si-C) | 1.922 | 1.931 | 1.918 | 1.960 | 1.916 | 1.913 | ||||||
| DB(OT+BR) | DB(BR+OT) | DB(OT+OT) | ||||
|---|---|---|---|---|---|---|
| ΔΔEint | +96 | +50 | +89 | |||
| ΔΔEint(disp) (b) | +65 | (−4%) | +45 | (-3%) | +49 | (-3%) |
| ΔΔEint(elec) (b) | +31 | (+4%) | +5 | (+3%) | +40 | (+3%) |
| ΔΔEPauli | −77 | −48 | +39 | |||
| ΔΔEelstat (c) | +57 | (±0%) | +43 | (±0%) | +43 | (−1%) |
| ΔΔEorb (c) | +51 | (±0%) | +10 | (±0%) | −42 | (+1%) |
| ΔΔEorb (M→S) (d) | +31 | (−1%) | +11 | (±0%) | +6 | (−1%) |
| ΔΔEorb (S→M) (d) | −21 | (+2%) | −7 | (+1%) | −57 | (+1%) |
| ΔΔEprep | +26 | +26 | +136 | |||
| ΔΔEprep (M) (e) | +21 | +21 | +100 | |||
| ΔΔEprep (S) (e) | +5 | +5 | +36 | |||
| ΔEBond | +122 | +76 | +225 | |||
| ΔEBond (PAW) | +116 | +75 | +215 | |||
| Final Adsorption Structure | Number of Observations |
|---|---|
| C-OT | 2 |
| DB(OT+BR) | 1 |
| DB(OT+“OT”) | 1 |
| DB(BR+OT) | 4 |
| Hydrogen abstraction | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieck, F.; Tonner-Zech, R. Alkyne-Functionalized Cyclooctyne on Si(001): Reactivity Studies and Surface Bonding from an Energy Decomposition Analysis Perspective. Molecules 2021, 26, 6653. https://doi.org/10.3390/molecules26216653
Pieck F, Tonner-Zech R. Alkyne-Functionalized Cyclooctyne on Si(001): Reactivity Studies and Surface Bonding from an Energy Decomposition Analysis Perspective. Molecules. 2021; 26(21):6653. https://doi.org/10.3390/molecules26216653
Chicago/Turabian StylePieck, Fabian, and Ralf Tonner-Zech. 2021. "Alkyne-Functionalized Cyclooctyne on Si(001): Reactivity Studies and Surface Bonding from an Energy Decomposition Analysis Perspective" Molecules 26, no. 21: 6653. https://doi.org/10.3390/molecules26216653
APA StylePieck, F., & Tonner-Zech, R. (2021). Alkyne-Functionalized Cyclooctyne on Si(001): Reactivity Studies and Surface Bonding from an Energy Decomposition Analysis Perspective. Molecules, 26(21), 6653. https://doi.org/10.3390/molecules26216653






