Defect Structures of Magnetic Nanoparticles in Smectic A Liquid Crystals
Abstract
1. Introduction
2. Preparation of the Hybrid System
3. Results
3.1. Defects Observed in Polarised Light
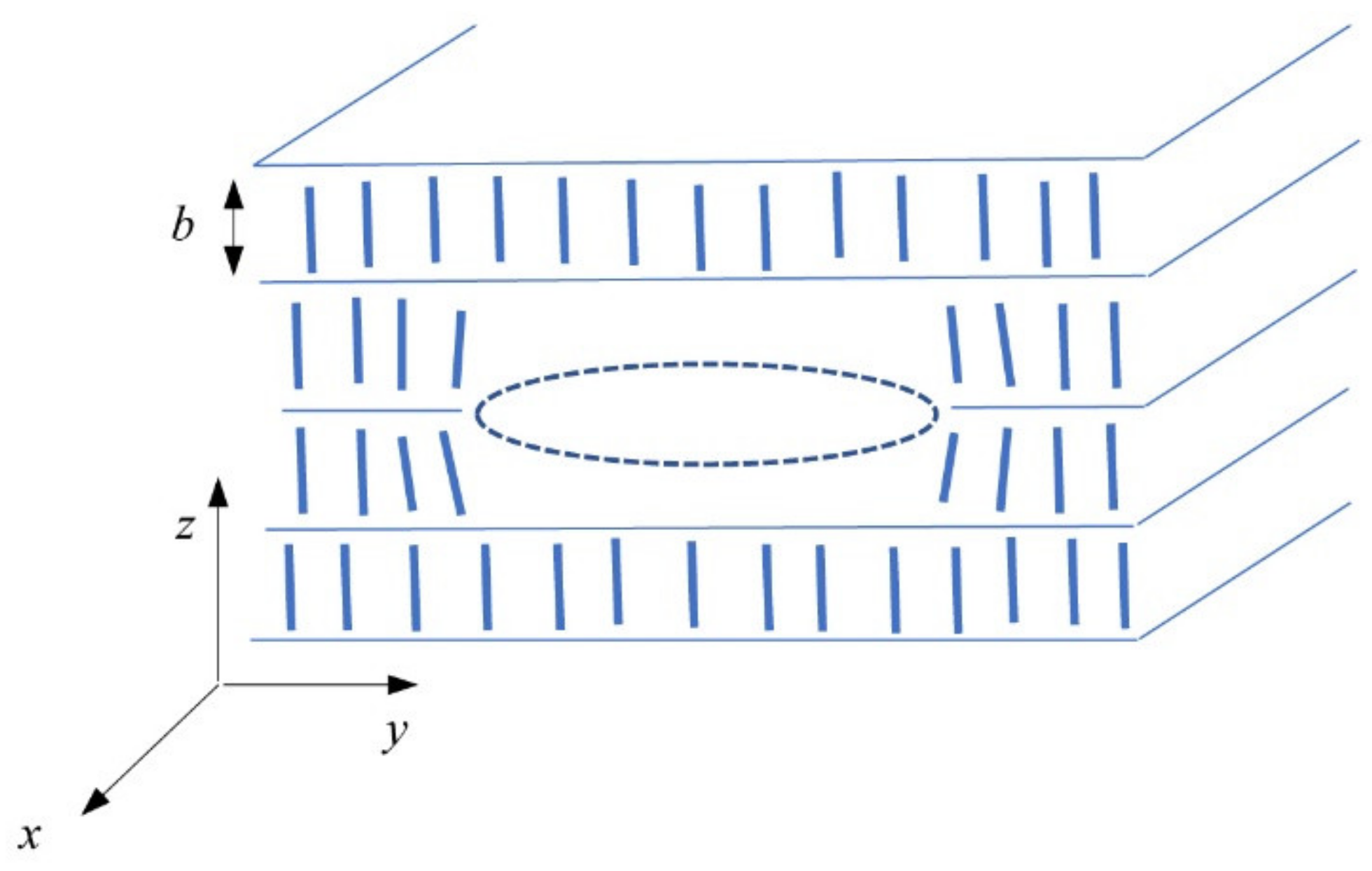
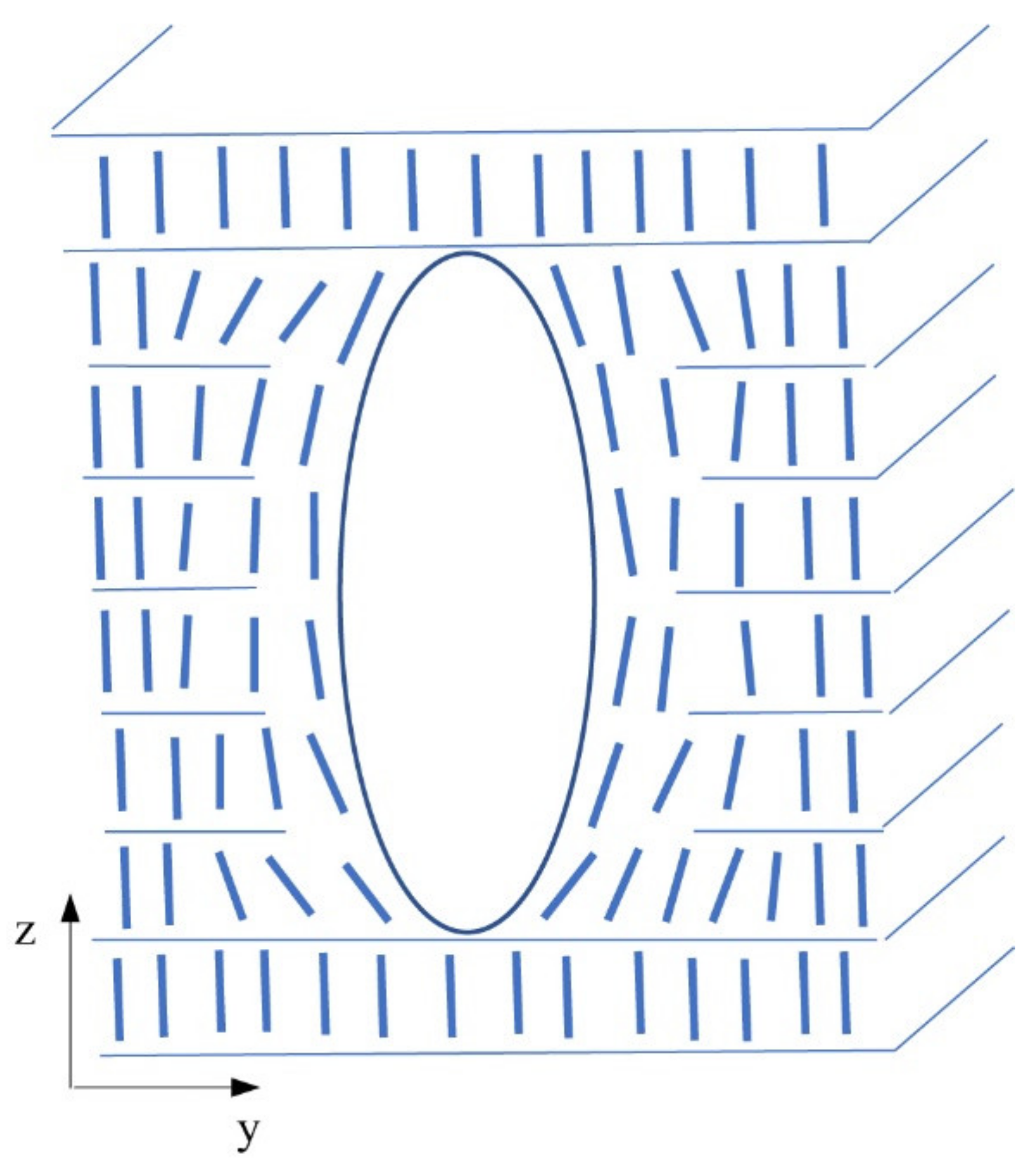
3.2. Model and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Goodby, J.W.; Collings, P.J.; Kato, T.; Tschierske, C.; Gleeson, H.F.; Raynes, P. Handbook of Liquid Crystals; Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar]
- Lagerwall, J.P.F.; Scalia, G. Liquid Crystals with Nano and Microparticles; World Scientific: Singapore, 2016. [Google Scholar]
- Hegmann, T.; Qi, H.; Marx, V.M. Nanoparticles in Liquid Crystals: Synthesis, Self-Assembly, Defect Formation and Potential Applications. J. Inorg. Organomet. Polym. 2007, 17, 483–508. [Google Scholar] [CrossRef]
- Bisoyi, H.K.; Kumar, S. Liquid-crystal nanoscience: An emerging avenue of soft self-assembly. Chem. Soc. Rev. 2011, 40, 306–319. [Google Scholar] [CrossRef] [PubMed]
- Coursault, D.; Grand, J.; Zappone, B.; Ayeb, H.; Lévi, G.; Félidj, N.; Lacaze, E. Linear Self-Assembly of Nanoparticles within Liquid Crystal Defect Arrays. Adv. Mater. 2012, 24, 1461–1465. [Google Scholar] [CrossRef]
- Loudet, J.C. Colloidal inclusions in liquid crystals: Phase separation mechanisms and some dynamical aspects. Liq. Cryst. Today 2005, 14, 1–14. [Google Scholar] [CrossRef]
- Wittmann, R.; Cortes, L.B.G.; Löwen, H.; Aarts, D.G.A.L. Particle-resolved topological defects of smectic colloidal liquid crystals in extreme confinement. Nat. Commun. 2021, 12, 623. [Google Scholar] [CrossRef] [PubMed]
- Do, S.; Missaoui, A.; Coati, A.; Resta, A.; Goubet, N.; Royer, S.; Guida, G.; Briand, E.; Lhuillier, E.; Garreau, Y.; et al. Interactions Between Topological Defects and Nanoparticles. Front. Phys. 2020, 7, 234. [Google Scholar] [CrossRef]
- Stark, H. Physics of colloidal dispersions in nematic liquid crystals. Phys. Rep. 2001, 351, 387–474. [Google Scholar] [CrossRef]
- Poulin, P.; Stark, H.; Lubensky, T.C.; Weitz, D.A. Novel colloidal interactions in anisotropic fluids. Science 1997, 275, 1770–1773. [Google Scholar] [CrossRef]
- Musevic, I.; Skarabot, M.; Tkalec, U.; Ravnik, M.; Zumer, S. Two-Dimensional Nematic Colloidal Crystals Self-Assembled by Topological Defects. Science 2006, 313, 954–957. [Google Scholar] [CrossRef]
- Maximean, M. New grafted ferrite particles/liquid crystal composite under magnetic field. J. Magn. Magn. Mater. 2018, 452, 343–348. [Google Scholar] [CrossRef]
- Blanc, C.; Coursault, D.; Lacaze, E. Ordering nano-and microparticles assemblies with liquid crystals. Liq. Cryst. Rev. 2013, 1, 83–109. [Google Scholar] [CrossRef]
- Oswald, P. Dynamics of Dislocations in Smectic A Liquid Crystals Doped with Nanoparticles. Crystals 2019, 9, 400. [Google Scholar] [CrossRef]
- Lejček, L.; Novotná, V.; Glogarová, M. Molecular tilt near nanoparticles in the smectic-A phase of a de Vries liquid-crystalline compounds. Phys. Rev. E 2014, 89, 12505. [Google Scholar] [CrossRef]
- Persan, P.S.; Prost, J. Dislocation and impurity effects in smectic-A liquid crystals. J. Appl. Phys. 1975, 46, 2343. [Google Scholar] [CrossRef]
- Lejcek, L. Point-like impurity-dislocation interactions in smectic A liquid crystals. Liq. Cryst. 1986, 1, 473–482. [Google Scholar] [CrossRef]
- Terentjev, E.M. Point defect condensation in smectic A liquid crystals. Kristallografiya 1988, 33, 1077–1083. [Google Scholar]
- Turner, M.S.; Sens, P. Interactions between particulate inclusions in a smectic-A liquid crystal. Phys. Rev. E 1997, 55, R1275–R1278. [Google Scholar] [CrossRef]
- Dolganov, P.V.; Cluzeau, P.; Dolganov, V.K. Interaction and self-organization of inclusions in two-dimensional free-standing films. Liq. Cryst. Rev. 2019, 7, 1–29. [Google Scholar] [CrossRef]
- Cluzeau, P.; Poulin, P.; Joly, G.; Nguyen, H.T. Interactions between colloidal inclusions in two-dimensional smectic-C* films. Phys. Rev. E 2001, 63, 31702. [Google Scholar] [CrossRef] [PubMed]
- Patricio, P.; Tasinkevych, M.; Da Gama, M.T. Colloidal dipolar interactions in 2D smectic-C films. Eur. Phys. J. E 2002, 7, 117–120. [Google Scholar] [CrossRef][Green Version]
- Silvestre, N.M.; Patrício, P.; Telo da Gama, M.M. Interactions between circular inclusions in smectic-C films. with planar anchoring. Mol. Cryst. Liq. Cryst. 2008, 495, 266–618. [Google Scholar] [CrossRef]
- Dolganov, P.V.; Kats, E.I.; Cluzeau, P. Stepwise transition of a topological defect from the smectic film to the boundary of a dipolar inclusion. Phys. Rev. E 2010, 81, 31709. [Google Scholar] [CrossRef]
- Martínez-Miranda, L.J.; McCarthy, K.; Kurihara, L.K.; Harry, J.J.; Noel, A. Effect of the surface coating on the magnetic nanoparticle smectic-A liquid crystal interaction. Appl. Phys. Lett. 2006, 89, 161917. [Google Scholar] [CrossRef]
- Walton, D.; Shibli, S.M.; Vega, M.L.; Oliveira, E. Magnetic nanoparticle size constraints in ferronematic liquid crystals. J. Magn. Magn. Mater. 2005, 292, 310–316. [Google Scholar] [CrossRef]
- Peroukidis, S.D.; Klapp, S.H.L. Spontaneous ordering of magnetic particles in liquid crystals: From chains to biaxial lamellae. Phys. Rev. E 2015, 92, 10501. [Google Scholar] [CrossRef] [PubMed]
- Shrivastav, G.P. Self-Assembly of an Equimolar Mixture of Liquid Crystals and Magnetic Nanoparticles. Crystals 2021, 11, 834. [Google Scholar] [CrossRef]
- Kašpar, M.; Hamplová, V.; Novotná, V.; Pacherová, O. The effect of the alkyl chain length on the mesomorphic properties of new lactic acid derivatives. Liq. Cryst. 2014, 41, 1179–1187. [Google Scholar] [CrossRef]
- Repko, A.; Niznansky, D.; Poltierova-Vejpravova, J. A study of oleic acid-based hydrothermal preparation of CoFe2O4 nanoparticles. J. Nanoparticle Res. 2011, 13, 5021–5031. [Google Scholar] [CrossRef]
- Oswald, P.; Pieranski, P. Smectic and Columnar Liquid Crystals; Taylor and Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Oswald, P.; Milette, J.; Relaix, S.; Reven, L.; Dequit, A.; Lejcek, L. Alloy hardening of a smectic A liquid crystal doped with gold nanoparticles. EPL 2013, 103, 46004. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novotná, V.; Lejček, L.; Hamplová, V.; Vejpravová, J. Defect Structures of Magnetic Nanoparticles in Smectic A Liquid Crystals. Molecules 2021, 26, 5717. https://doi.org/10.3390/molecules26185717
Novotná V, Lejček L, Hamplová V, Vejpravová J. Defect Structures of Magnetic Nanoparticles in Smectic A Liquid Crystals. Molecules. 2021; 26(18):5717. https://doi.org/10.3390/molecules26185717
Chicago/Turabian StyleNovotná, Vladimíra, Lubor Lejček, Věra Hamplová, and Jana Vejpravová. 2021. "Defect Structures of Magnetic Nanoparticles in Smectic A Liquid Crystals" Molecules 26, no. 18: 5717. https://doi.org/10.3390/molecules26185717
APA StyleNovotná, V., Lejček, L., Hamplová, V., & Vejpravová, J. (2021). Defect Structures of Magnetic Nanoparticles in Smectic A Liquid Crystals. Molecules, 26(18), 5717. https://doi.org/10.3390/molecules26185717






