Density-Based Descriptors of Redox Reactions Involving Transition Metal Compounds as a Reality-Anchored Framework: A Perspective
Abstract
:1. Introduction
2. Oxidation and Charge Self-Regulation
2.1. Formal Oxidation State Ansatz
2.2. Relation to Projection Approaches
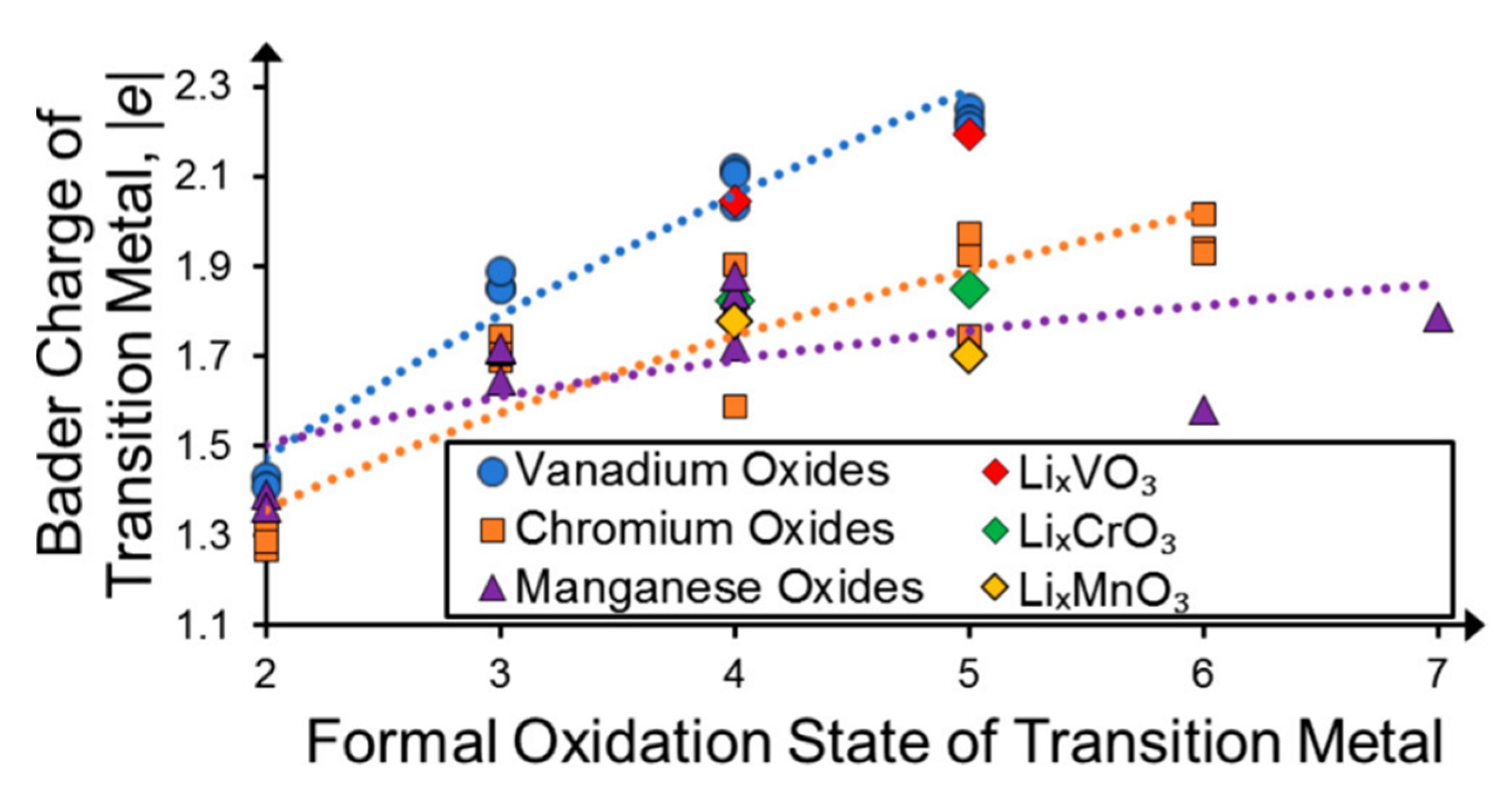
2.3. Charge Self-Regulation
3. Density-Based Descriptors as Observables-Based Framework
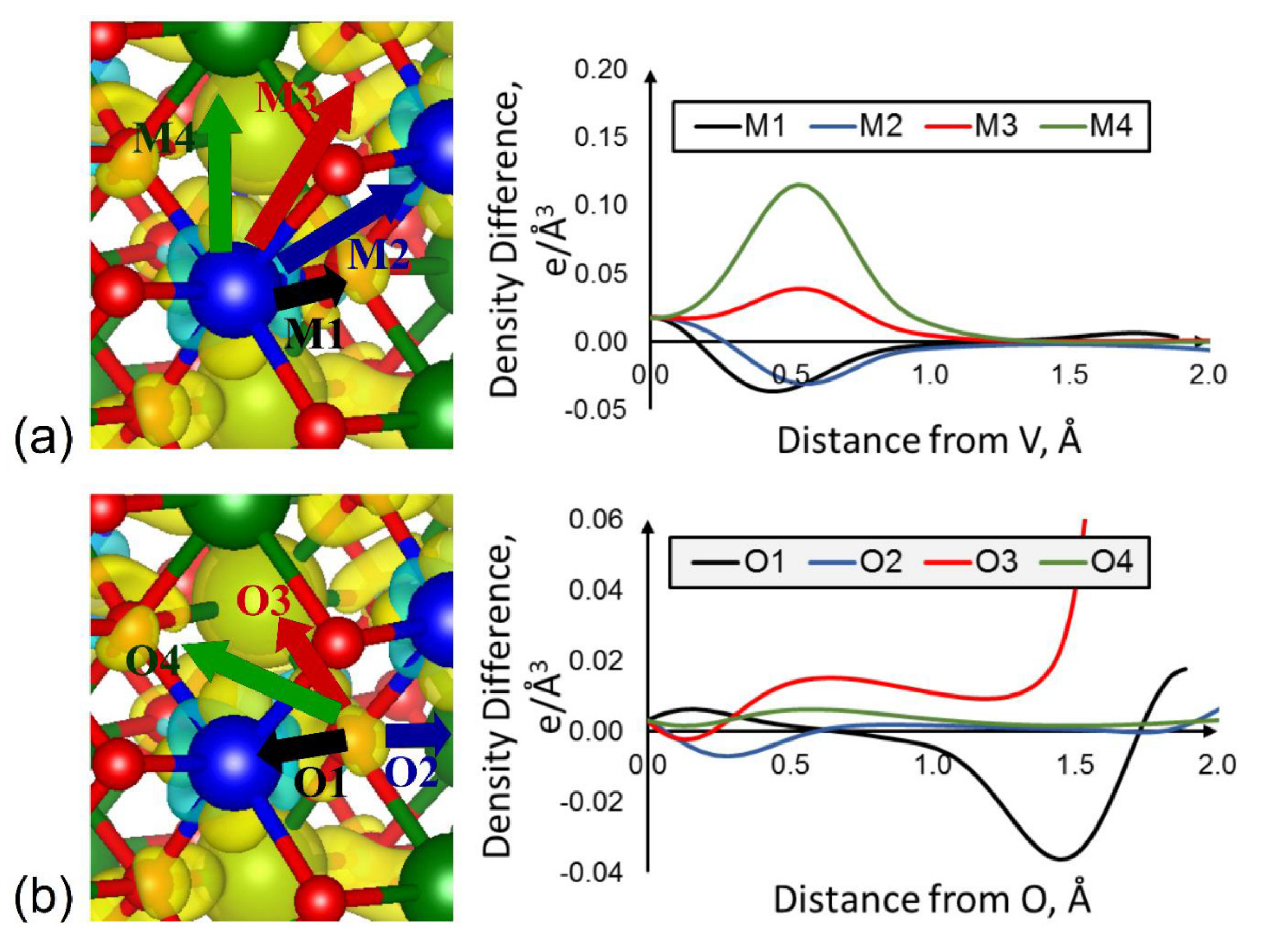
3.1. Charge Distribution in Titanium Dioxide and Its Changes upon Reduction
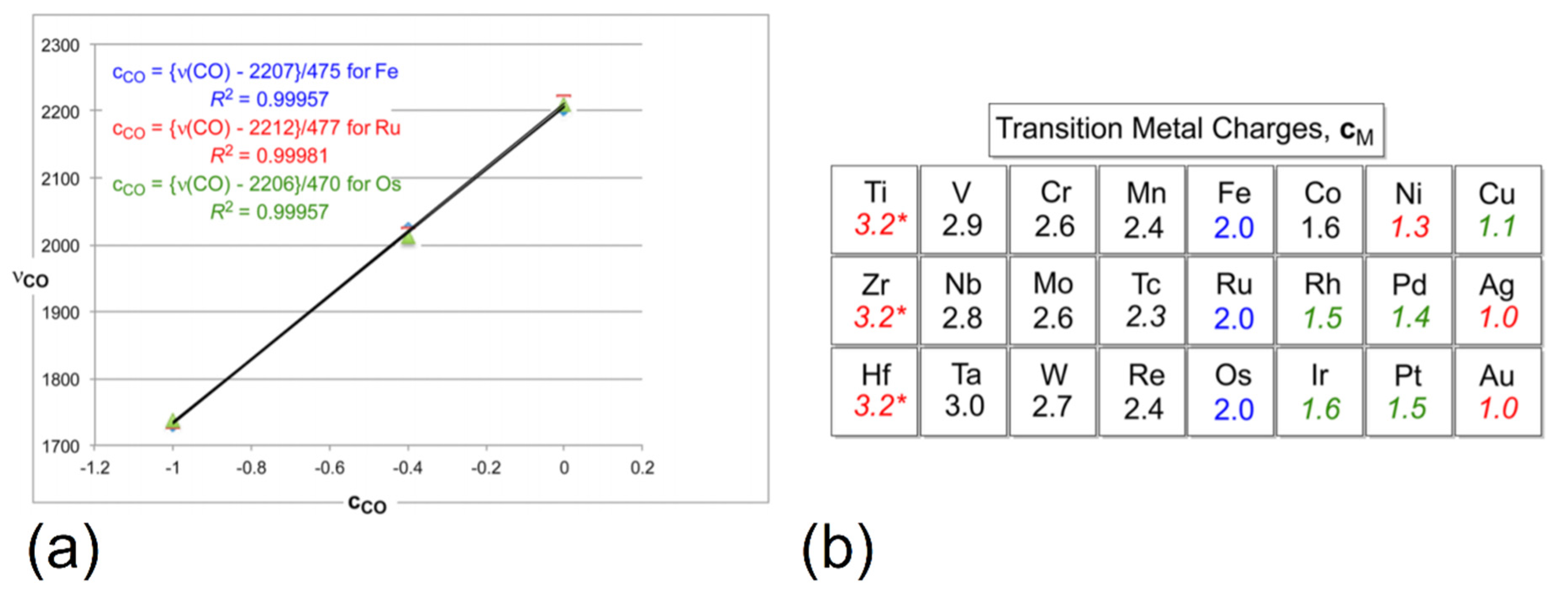
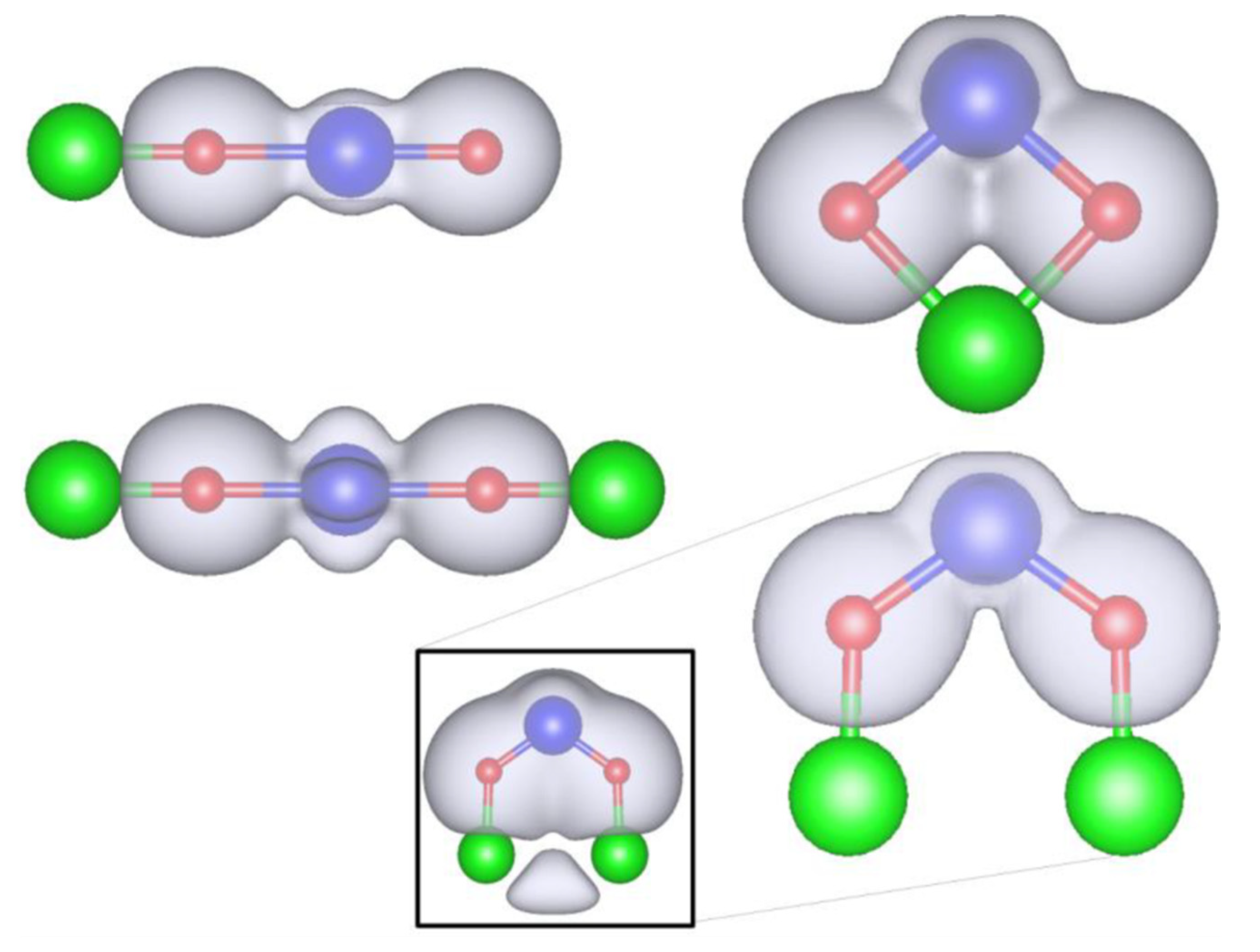
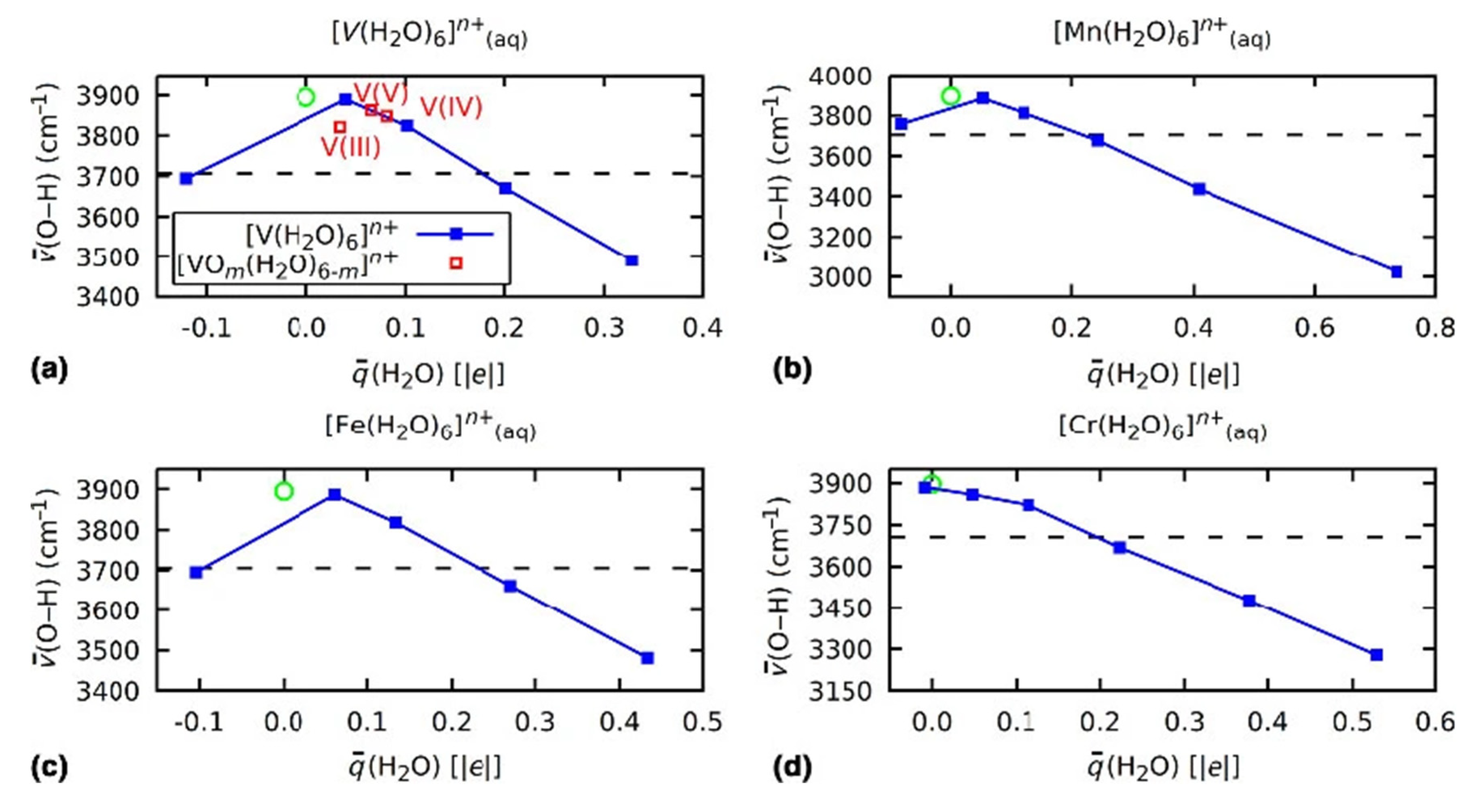
3.2. Role of Ligands in the Stabilization of Metal Ions
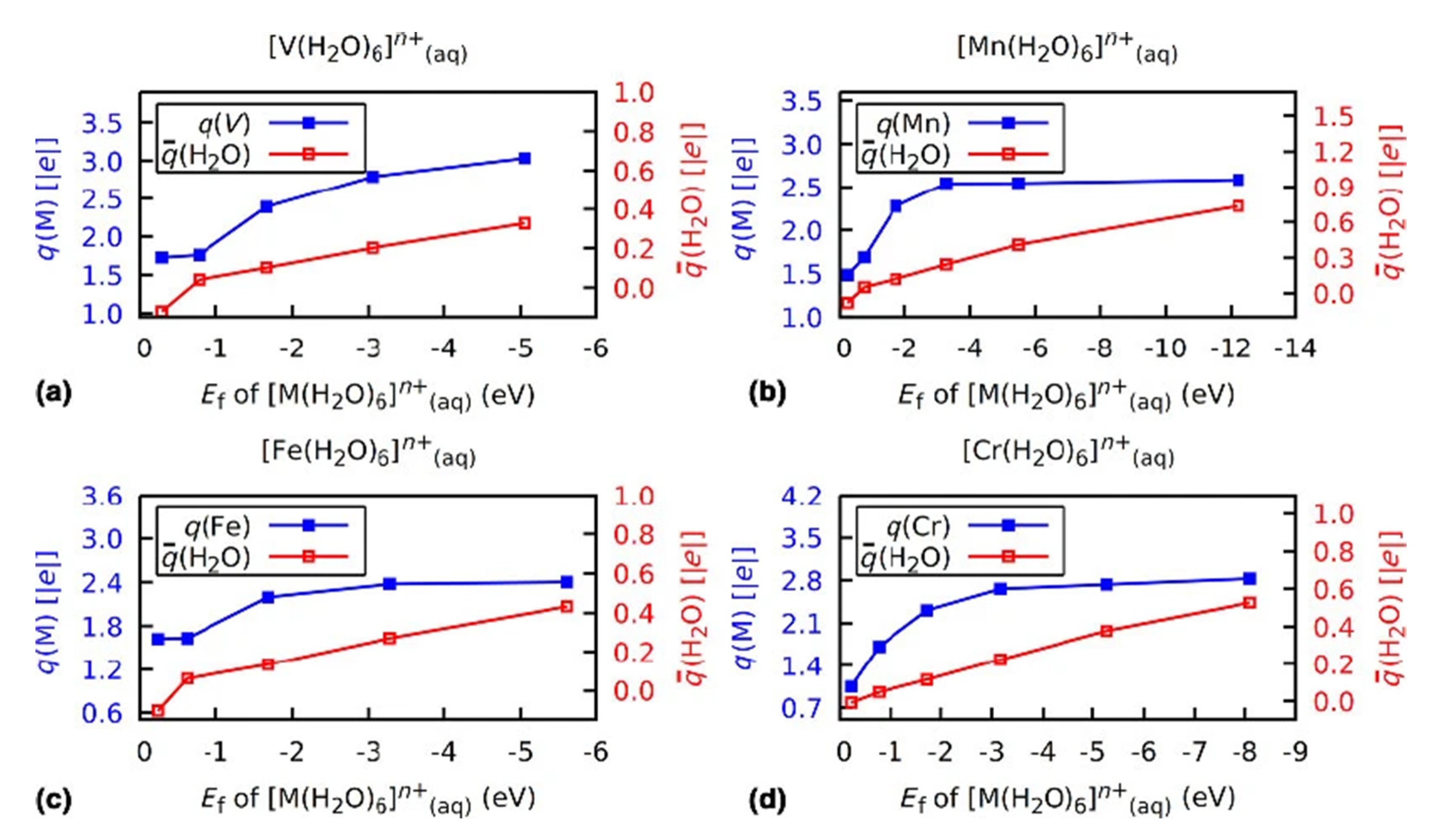
3.3. Impurity Charge Stabilization
3.4. Oxygen Redox and PDOS
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cohen, M.; Kelly, P.S. Hartree-Fock wave functions for excited states: II. Simplification of the orbital equations. Can. J. Phys. 1966, 44, 3227–3240. [Google Scholar] [CrossRef]
- McEachran, R.P.; Tull, C.E.; Cohen, M. Frozen core approximation for atoms and atomic ions. Can. J. Phys. 1968, 46, 2675–2678. [Google Scholar] [CrossRef]
- Von Barth, U.; Gelatt, C.D. Validity of the frozen-core approximation and pseudopotential theory for cohesive energy calculations. Phys. Rev. B 1980, 21, 2222–2228. [Google Scholar] [CrossRef]
- Chambers, C.; Holliday, A.K. Modern Inorganic Chemistry: An Intermediate Text, 1st ed.; Butterworth & Co Ltd.: London, UK, 1975. [Google Scholar]
- Heslop, R.B.; Robinson, P.L. Inorganic Chemistry: A Guide to Advanced Study, 3rd ed.; Elsevier Publishing Company: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Karen, P.; McArdle, P.; Takats, J. Toward a comprehensive definition of oxidation state (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1017–1081. [Google Scholar] [CrossRef] [Green Version]
- Karen, P.; McArdle, P.; Takats, J. Comprehensive definition of oxidation state (IUPAC Recommendations 2016). Pure Appl. Chem. 2016, 88, 831–839. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Zhu, Y.; Vogt, T.; Su, H.; Davenport, J.W.; Tafto, J. Valence-electron distribution in MgB2 by accurate diffraction measurements and first-principles calculations. Phys. Rev. B 2004, 69, 064501. [Google Scholar] [CrossRef]
- González-Navarrete, P.; Andrés, J.; Berski, S. How a Quantum Chemical Topology Analysis Enables Prediction of Electron Density Transfers in Chemical Reactions. The Degenerated Cope Rearrangement of Semibullvalene. J. Phys. Chem. Lett. 2012, 3, 2500–2505. [Google Scholar] [CrossRef]
- Rombouts, J.A.; Ehlers, A.W.; Lammertsma, K. A quantitative analysis of light-driven charge transfer processes using voronoi partitioning of time dependent DFT-derived electron densities. J. Comput. Chem. 2017, 38, 1811–1818. [Google Scholar] [CrossRef] [Green Version]
- Zalazar, M.F.; Peruchena, N.M. Topological description of the bond-breaking and bond-forming processes of the alkene protonation reaction in zeolite chemistry: An AIM study. J. Mol. Model. 2011, 17, 2501–2511. [Google Scholar] [CrossRef] [PubMed]
- Resta, R. Charge states in transition. Nature 2008, 453, 735. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, S.A.; Hussain, M.S.; Ilyas, B.; Rafique, M.; Dogar, A.H.; Qayyum, A. Characterization of highly charged titanium ions produced by nanosecond pulsed laser. Laser Part. Beams 2015, 33, 81–86. [Google Scholar] [CrossRef] [Green Version]
- Khaydarov, R.T.; Beisinbaeva, H.B.; Sabitov, M.M.; Kalal, M.; Berdiyorov, G.R. Effect of light gas atom inclusions on the characteristics of laser-produced plasma ions. Nucl. Fusion 2011, 51, 103041. [Google Scholar] [CrossRef]
- Koch, D.; Manzhos, S. On the Charge State of Titanium in Titanium Dioxide. J. Phys. Chem. Lett. 2017, 8, 1593–1598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koch, D.; Chen, Y.; Golub, P.; Manzhos, S. Revisiting π backbonding: The influence of d orbitals on metal–CO bonds and ligand red shifts. Phys. Chem. Chem. Phys. 2019, 21, 20814–20821. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhao, L.; Jin, J.; Pan, S.; Li, W.; Jin, X.; Wang, G.; Zhou, M.; Frenking, G. Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals. Science 2018, 361, 912. [Google Scholar] [CrossRef] [Green Version]
- Alippi, P.; Filippone, F.; Mattioli, G.; Bonapasta, A.A.; Fiorentini, V. Bound states of the Fe impurity in wurtzite GaN from hybrid density-functional calculations. Phys. Rev. B 2011, 84, 033201. [Google Scholar] [CrossRef]
- Christensen, A.; Carter, E.A. First-principles characterization of a heteroceramic interface: ZrO2(001) deposited on an α-Al2O3(11-02) substrate. Phys. Rev. B 2000, 62, 16968–16983. [Google Scholar] [CrossRef] [Green Version]
- Dalpian, G.M.; Liu, Q.; Varignon, J.; Bibes, M.; Zunger, A. Bond disproportionation, charge self-regulation, and ligand holes in s-p and in d-electron ABX3 perovskites by density functional theory. Phys. Rev. B 2018, 98, 075135. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M.; Anderson, P.W. Simple model of multiple charge states of transition-metal impurities in semiconductors. Phys. Rev. B 1976, 13, 2553–2559. [Google Scholar] [CrossRef]
- Koch, D.; Golub, P.; Manzhos, S. Stability of charges in titanium compounds and charge transfer to oxygen in titanium dioxide. J. Phys. Conf. Ser. 2018, 1136, 012017. [Google Scholar] [CrossRef]
- Koch, D.; Manzhos, S. The role of solvent charge donation in the stabilization of metal ions in aqueous solution. MRS Commun. 2018, 8, 1139–1144. [Google Scholar] [CrossRef]
- Koch, D.; Manzhos, S. Oxygen Redox Activity in Cathodes: A Common Phenomenon Calling for Density-Based Descriptors. J. Phys. Chem. C 2020, 124, 19962–19968. [Google Scholar] [CrossRef]
- Raebiger, H. Theory of defect complexes in insulators. Phys. Rev. B 2010, 82, 073104. [Google Scholar] [CrossRef]
- Raebiger, H.; Lany, S.; Zunger, A. Charge self-regulation upon changing the oxidation state of transition metals in insulators. Nature 2008, 453, 763–766. [Google Scholar] [CrossRef]
- Wolczanski, P.T. Flipping the Oxidation State Formalism: Charge Distribution in Organometallic Complexes As Reported by Carbon Monoxide. Organometallics 2017, 36, 622–631. [Google Scholar] [CrossRef]
- Zunger, A.; Lindefelt, U. Substitutional 3d impurities in silicon: A self-regulating system. Solid State Commun. 1983, 45, 343–346. [Google Scholar] [CrossRef]
- Pauling, L. The modern theory of valency. J. Chem. Soc. 1948, 1461–1467. [Google Scholar] [CrossRef] [PubMed]
- Haque, F.; Daeneke, T.; Kalantar-zadeh, K.; Ou, J.Z. Two-Dimensional Transition Metal Oxide and Chalcogenide-Based Photocatalysts. Nano-Micro Lett. 2017, 10, 23. [Google Scholar] [CrossRef] [Green Version]
- Liao, P.; Carter, E.A. New concepts and modeling strategies to design and evaluate photo-electro-catalysts based on transition metal oxides. Chem. Soc. Rev. 2013, 42, 2401–2422. [Google Scholar] [CrossRef]
- Marschall, R.; Wang, L. Non-metal doping of transition metal oxides for visible-light photocatalysis. Catal. Today 2014, 225, 111–135. [Google Scholar] [CrossRef]
- Li, D.; Shi, J.; Li, C. Transition-Metal-Based Electrocatalysts as Cocatalysts for Photoelectrochemical Water Splitting: A Mini Review. Small 2018, 14, 1704179. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, J. Structural engineering of transition metal-based nanostructured electrocatalysts for efficient water splitting. Front. Chem. Sci. Eng. 2018, 12, 838–854. [Google Scholar] [CrossRef]
- Yang, Y.; Niu, S.; Han, D.; Liu, T.; Wang, G.; Li, Y. Progress in Developing Metal Oxide Nanomaterials for Photoelectrochemical Water Splitting. Adv. Energy Mater. 2017, 7, 1700555. [Google Scholar] [CrossRef]
- Ren, H.; Koshy, P.; Chen, W.-F.; Qi, S.; Sorrell, C.C. Photocatalytic materials and technologies for air purification. J. Hazard. Mater. 2017, 325, 340–366. [Google Scholar] [CrossRef]
- Royer, S.; Duprez, D. Catalytic Oxidation of Carbon Monoxide over Transition Metal Oxides. ChemCatChem 2011, 3, 24–65. [Google Scholar] [CrossRef]
- Gao, C.; Han, Q.; Wu, M. Review on transition metal compounds based counter electrode for dye-sensitized solar cells. J. Energy Chem. 2018, 27, 703–712. [Google Scholar] [CrossRef] [Green Version]
- Haque, M.A.; Sheikh, A.D.; Guan, X.; Wu, T. Metal Oxides as Efficient Charge Transporters in Perovskite Solar Cells. Adv. Energy Mater. 2017, 7, 1602803. [Google Scholar] [CrossRef]
- Yeoh, M.-E.; Chan, K.-Y. Recent advances in photo-anode for dye-sensitized solar cells: A review. Int. J. Energy Res. 2017, 41, 2446–2467. [Google Scholar] [CrossRef]
- Granqvist, C.G. Electrochromics for smart windows: Oxide-based thin films and devices. Thin Solid Films 2014, 564, 1–38. [Google Scholar] [CrossRef]
- Wu, W.; Wang, M.; Ma, J.; Cao, Y.; Deng, Y. Electrochromic Metal Oxides: Recent Progress and Prospect. Adv. Electron. Mater. 2018, 4, 1800185. [Google Scholar] [CrossRef]
- He, P.; Yu, H.; Li, D.; Zhou, H. Layered lithium transition metal oxide cathodes towards high energy lithium-ion batteries. J. Mater. Chem. 2012, 22, 3680–3695. [Google Scholar] [CrossRef]
- Su, H.; Jaffer, S.; Yu, H. Transition metal oxides for sodium-ion batteries. Energy Storage Mater. 2016, 5, 116–131. [Google Scholar] [CrossRef]
- Zheng, M.; Tang, H.; Li, L.; Hu, Q.; Zhang, L.; Xue, H.; Pang, H. Hierarchically Nanostructured Transition Metal Oxides for Lithium-Ion Batteries. Adv. Sci. 2018, 5, 1700592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.K.; Mahapatra, S.; Lahan, H. Aluminium-ion batteries: Developments and challenges. J. Mater. Chem. A 2017, 5, 6347–6367. [Google Scholar] [CrossRef]
- Gummow, R.J.; Vamvounis, G.; Kannan, M.B.; He, Y. Calcium-Ion Batteries: Current State-of-the-Art and Future Perspectives. Adv. Mater. 2018, 30, 1801702. [Google Scholar] [CrossRef]
- Huie, M.M.; Bock, D.C.; Takeuchi, E.S.; Marschilok, A.C.; Takeuchi, K.J. Cathode materials for magnesium and magnesium-ion based batteries. Coord. Chem. Rev. 2015, 287, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Koch, D.; Manzhos, S. Ab initio modeling and design of vanadia-based electrode materials for post-lithium batteries. J. Phys. D Appl. Phys. 2019, 53, 083001. [Google Scholar] [CrossRef]
- Assat, G.; Tarascon, J.-M. Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries. Nat. Energy 2018, 3, 373–386. [Google Scholar] [CrossRef]
- Grimaud, A.; Hong, W.T.; Shao-Horn, Y.; Tarascon, J.M. Anionic redox processes for electrochemical devices. Nat. Mater. 2016, 15, 121–126. [Google Scholar] [CrossRef]
- Wu, J.; Zhuo, Z.; Rong, X.; Dai, K.; Lebens-Higgins, Z.; Sallis, S.; Pan, F.; Piper, L.F.J.; Liu, G.; Chuang, Y.-D.; et al. Dissociate lattice oxygen redox reactions from capacity and voltage drops of battery electrodes. Sci. Adv. 2020, 6, eaaw3871. [Google Scholar] [CrossRef]
- Seo, D.-H.; Lee, J.; Urban, A.; Malik, R.; Kang, S.; Ceder, G. The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials. Nat. Chem. 2016, 8, 692–697. [Google Scholar] [CrossRef]
- Kulish, V.V.; Koch, D.; Manzhos, S. Ab initio study of Li, Mg and Al insertion into rutile VO2: Fast diffusion and enhanced voltages for multivalent batteries. Phys. Chem. Chem. Phys. 2017, 19, 22538–22545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Legrain, F.; Malyi, O.; Manzhos, S. Insertion energetics of lithium, sodium, and magnesium in crystalline and amorphous titanium dioxide: A comparative first-principles study. J. Power Sources 2015, 278, 197–202. [Google Scholar] [CrossRef]
- Jiang, B.; Zuo, J.M.; Jiang, N.; O’Keeffe, M.; Spence, J.C.H. Charge density and chemical bonding in rutile, TiO2. Acta Crystallogr. Sect. A 2003, 59, 341–350. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.-C.; Frenkel, A.I.; Wu, L.; Hanson, J.; Ku, W.; Božin, E.S.; Billinge, S.J.L.; Zhu, Y. Nanoscale disorder and local electronic properties of CaCu3Ti4O12: An integrated study of electron, neutron, and x-ray diffraction, x-ray absorption fine structure, and first-principles calculations. Phys. Rev. B 2010, 81, 144203. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Yao, Y. Positioning Organic Electrode Materials in the Battery Landscape. Joule 2018, 2, 1690–1706. [Google Scholar] [CrossRef]
- Carvalho, R.P.; Marchiori, C.F.N.; Oltean, V.-A.; Renault, S.; Willhammar, T.; Pay Gómez, C.; Araujo, C.M.; Brandell, D. Structure–property relationships in organic battery anode materials: Exploring redox reactions in crystalline Na- and Li-benzene diacrylate using combined crystallography and density functional theory calculations. Mater. Adv. 2021, 2, 1024–1034. [Google Scholar] [CrossRef]
- Pahlevaninezhad, M.; Leung, P.; Velasco, P.Q.; Pahlevani, M.; Walsh, F.C.; Roberts, E.P.L.; Ponce de León, C. A nonaqueous organic redox flow battery using multi-electron quinone molecules. J. Power Sources 2021, 500, 229942. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, Y.; Niu, Z.; Ye, J.; Dai, G.; Zhang, X.; Zhao, Y. Tailoring the Voltage Gap of Organic Battery Materials Based on a Multi-Electron Redox Chemistry. ChemElectroChem 2020, 7, 1781–1788. [Google Scholar] [CrossRef]
- Duffy, J.A. Ionic−Covalent Character of Metal and Nonmetal Oxides. J. Phys. Chem. A 2006, 110, 13245–13248. [Google Scholar] [CrossRef]
- Frenking, G. Understanding the nature of the bonding in transition metal complexes: From Dewar’s molecular orbital model to an energy partitioning analysis of the metal–ligand bond. J. Organomet. Chem. 2001, 635, 9–23. [Google Scholar] [CrossRef]
- NIST X-ray Photoelectron Spectroscopy Database. NIST Standard Reference Database Number 20. 2000, 20899. [CrossRef]
- Biesinger, M.C.; Lau, L.W.M.; Gerson, A.R.; Smart, R.S.C. Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Sc, Ti, V, Cu and Zn. Appl. Surf. Sci. 2010, 257, 887–898. [Google Scholar] [CrossRef]
- Biesinger, M.C.; Payne, B.P.; Hart, B.R.; Grosvenor, A.P.; McIntryre, N.S.; Lau, L.W.; Smart, R.S. Quantitative chemical state XPS analysis of first row transition metals, oxides and hydroxides. J. Phys. Conf. Ser. 2008, 100, 012025. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Qi, Y. Energy landscape of the charge transfer reaction at the complex Li/SEI/electrolyte interface. Energy Environ. Sci. 2019, 12, 1286–1295. [Google Scholar] [CrossRef]
- Lian, R.; Wang, D.; Ming, X.; Zhang, R.; Wei, Y.; Feng, J.; Meng, X.; Chen, G. Phase transformation, ionic diffusion, and charge transfer mechanisms of KVOPO4 in potassium ion batteries: First-principles calculations. J. Mater. Chem. A 2018, 6, 16228–16234. [Google Scholar] [CrossRef]
- Würger, T.; Feiler, C.; Vonbun-Feldbauer, G.B.; Zheludkevich, M.L.; Meißner, R.H. A first-principles analysis of the charge transfer in magnesium corrosion. Sci. Rep. 2020, 10, 15006. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons Ltd: Chichester, UK, 2007. [Google Scholar]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Stone, A.J.; Alderton, M. Distributed multipole analysis. Mol. Phys. 1985, 56, 1047–1064. [Google Scholar] [CrossRef]
- Walsh, A.; Sokol, A.A.; Buckeridge, J.; Scanlon, D.O.; Catlow, C.R.A. Oxidation states and ionicity. Nat. Mater. 2018, 17, 958–964. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef] [Green Version]
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. II. Overlap Populations, Bond Orders, and Covalent Bond Energies. J. Chem. Phys. 1955, 23, 1841–1846. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. III. Effects of Hybridization on Overlap and Gross AO Populations. J. Chem. Phys. 1955, 23, 2338–2342. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. IV. Bonding and Antibonding in LCAO and Valence-Bond Theories. J. Chem. Phys. 1955, 23, 2343–2346. [Google Scholar] [CrossRef]
- Löwdin, P.O. On the Non-Orthogonality Problem Connected with the Use of Atomic Wave Functions in the Theory of Molecules and Crystals. J. Chem. Phys. 1950, 18, 365–375. [Google Scholar] [CrossRef]
- Chen, K.; Luo, D.; Dronskowski, R. Exploring the Possible Anionic Redox Mechanism in Li-Rich Transition-Metal Carbodiimides. J. Phys. Chem. C 2021, 125, 8479–8487. [Google Scholar] [CrossRef]
- Wang, H.; Emanuelsson, R.; Banerjee, A.; Ahuja, R.; Strømme, M.; Sjödin, M. Effect of Cycling Ion and Solvent on the Redox Chemistry of Substituted Quinones and Solvent-Induced Breakdown of the Correlation between Redox Potential and Electron-Withdrawing Power of Substituents. J. Phys. Chem. C 2020, 124, 13609–13617. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, L.; Zhan, W.; Wang, X.; Han, X. Separated redox site strategies for engineering highly efficient photocatalysts: A pagoda-like In2O3/CuO heteroepitaxial structure coated with a N-doped C layer. J. Mater. Chem. A 2021, 9, 4310–4316. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; van Eikema Hommes, N.J.R.; Fonseca Guerra, C.; Baerends, E.J. The Carbon−Lithium Electron Pair Bond in (CH3Li)n (n = 1, 2, 4). Organometallics 1996, 15, 2923–2931. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Handgraaf, J.-W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi deformation density (VDD) charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. The Quantum Mechanical Basis of Conceptual Chemistry. Monatsh. Chem. 2005, 136, 819–854. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. In Encyclopedia of Computational Chemistry; von Ragué Schleyer, P.N.L.A., Clark, T., Gasteiger, J., Kollman, P.A., Schaefer, H.F., Schreiner, P.R., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Ayed, O.; Loutellier, A.; Manceron, L.; Perchard, J.P. Interaction between lithium and carbon monoxide. 1. A matrix infrared study. J. Am. Chem. Soc. 1986, 108, 8138–8147. [Google Scholar] [CrossRef]
- Feltrin, A.; Guido, M.; Nunziante Cesaro, S. Fourier transform infrared study and matrix effects of aluminum and gallium carbonyls isolated in argon and nitrogen. Vib. Spectrosc. 1995, 8, 175–183. [Google Scholar] [CrossRef]
- Ellis, J.E.; Beck, W. New Surprises in Metal Carbonyl Chemistry. Angew. Chem. Int. Ed. Engl. 1995, 34, 2489–2491. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, L.; Jiang, D.; Fernández, I.; Berger, R.; Zhou, M.; Frenking, G. Barium as Honorary Transition Metal in Action: Experimental and Theoretical Study of Ba(CO)+ and Ba(CO)−. Angew. Chem. Int. Ed. 2018, 57, 3974–3980. [Google Scholar] [CrossRef] [PubMed]
- Low, F.W.; Lai, C.W. Recent developments of graphene-TiO2 composite nanomaterials as efficient photoelectrodes in dye-sensitized solar cells: A review. Renew. Sustain. Energy Rev. 2018, 82, 103–125. [Google Scholar] [CrossRef]
- Park, N.G.; van de Lagemaat, J.; Frank, A.J. Comparison of Dye-Sensitized Rutile- and Anatase-Based TiO2 Solar Cells. J. Phys. Chem. B 2000, 104, 8989–8994. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhu, K. Charge Transport and Recombination in Perovskite (CH3NH3)PbI3 Sensitized TiO2 Solar Cells. J. Phys. Chem. Lett. 2013, 4, 2880–2884. [Google Scholar] [CrossRef]
- Madian, M.; Eychmüller, A.; Giebeler, L. Current Advances in TiO2-Based Nanostructure Electrodes for High Performance Lithium Ion Batteries. Batteries 2018, 4, 7. [Google Scholar] [CrossRef] [Green Version]
- Opra, D.P.; Gnedenkov, S.V.; Sinebryukhov, S.L. Recent efforts in design of TiO2(B) anodes for high-rate lithium-ion batteries: A review. J. Power Sources 2019, 442, 227225. [Google Scholar] [CrossRef]
- Aravindan, V.; Lee, Y.-S.; Yazami, R.; Madhavi, S. TiO2 polymorphs in ‘rocking-chair’ Li-ion batteries. Mater. Today 2015, 18, 345–351. [Google Scholar] [CrossRef]
- Humayun, M.; Raziq, F.; Khan, A.; Luo, W. Modification strategies of TiO2 for potential applications in photocatalysis: A critical review. Green Chem. Lett. Rev. 2018, 11, 86–102. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.G.; Devi, L.G. Review on Modified TiO2 Photocatalysis under UV/Visible Light: Selected Results and Related Mechanisms on Interfacial Charge Carrier Transfer Dynamics. J. Phys. Chem. A 2011, 115, 13211–13241. [Google Scholar] [CrossRef] [PubMed]
- Kumaravel, V.; Mathew, S.; Bartlett, J.; Pillai, S.C. Photocatalytic hydrogen production using metal doped TiO2: A review of recent advances. Appl. Catal. B 2019, 244, 1021–1064. [Google Scholar] [CrossRef]
- Catlow, C.R.A.; Stoneham, A.M. Ionicity in solids. J. Phys. C Solid State Phys. 1983, 16, 4321–4338. [Google Scholar] [CrossRef]
- Deng, S.; Wang, L.; Hou, T.; Li, Y. Two-Dimensional MnO2 as a Better Cathode Material for Lithium Ion Batteries. J. Phys. Chem. C 2015, 119, 28783–28788. [Google Scholar] [CrossRef]
- Kulish, V.V.; Manzhos, S. Comparison of Li, Na, Mg and Al-ion insertion in vanadium pentoxides and vanadium dioxides. RSC Adv. 2017, 7, 18643–18649. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Liu, L.-M.; Zhao, S.-J.; Li, B.-H.; Liu, H.; Lang, X.-F. β-MnO2 as a cathode material for lithium ion batteries from first principles calculations. Phys. Chem. Chem. Phys. 2013, 15, 9075–9083. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Q.; Deng, H. Single-layered V2O5 a promising cathode material for rechargeable Li and Mg ion batteries: An ab initio study. Phys. Chem. Chem. Phys. 2013, 15, 8705–8709. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.; Zhang, X.; Zhao, X.; Zhang, H.; Ding, F.; Xie, Z.; Zhou, Z. First-principles computational studies on layered Na2Mn3O7 as a high-rate cathode material for sodium ion batteries. J. Mater. Chem. A 2017, 5, 12752–12756. [Google Scholar] [CrossRef]
- Legrain, F.; Manzhos, S. Aluminum doping improves the energetics of lithium, sodium, and magnesium storage in silicon: A first-principles study. J. Power Sources 2015, 274, 65–70. [Google Scholar] [CrossRef] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
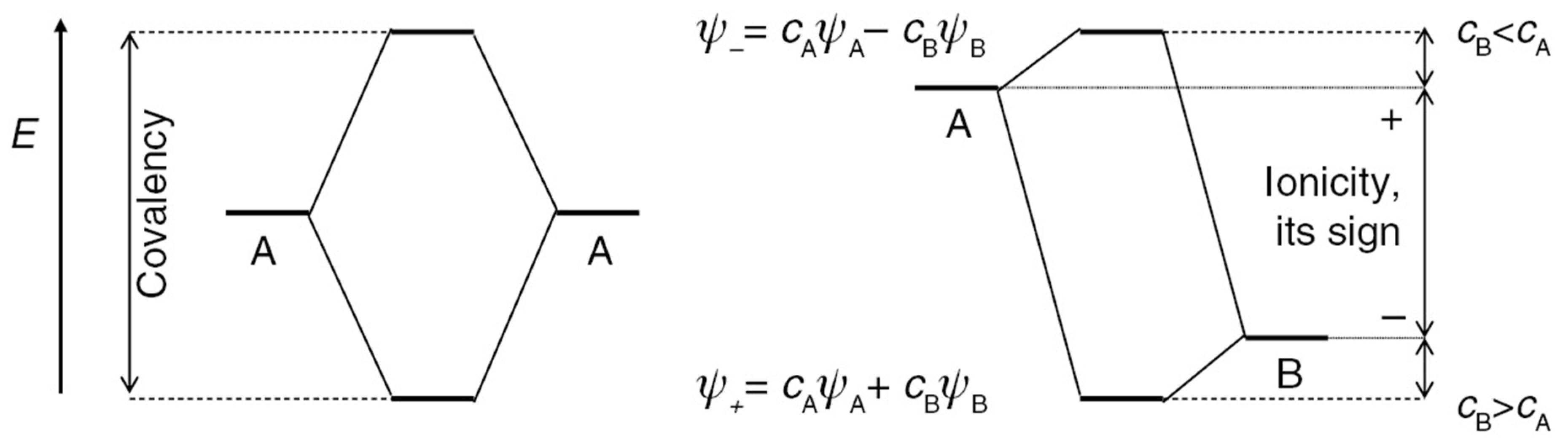




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, D.; Chaker, M.; Ihara, M.; Manzhos, S. Density-Based Descriptors of Redox Reactions Involving Transition Metal Compounds as a Reality-Anchored Framework: A Perspective. Molecules 2021, 26, 5541. https://doi.org/10.3390/molecules26185541
Koch D, Chaker M, Ihara M, Manzhos S. Density-Based Descriptors of Redox Reactions Involving Transition Metal Compounds as a Reality-Anchored Framework: A Perspective. Molecules. 2021; 26(18):5541. https://doi.org/10.3390/molecules26185541
Chicago/Turabian StyleKoch, Daniel, Mohamed Chaker, Manabu Ihara, and Sergei Manzhos. 2021. "Density-Based Descriptors of Redox Reactions Involving Transition Metal Compounds as a Reality-Anchored Framework: A Perspective" Molecules 26, no. 18: 5541. https://doi.org/10.3390/molecules26185541
APA StyleKoch, D., Chaker, M., Ihara, M., & Manzhos, S. (2021). Density-Based Descriptors of Redox Reactions Involving Transition Metal Compounds as a Reality-Anchored Framework: A Perspective. Molecules, 26(18), 5541. https://doi.org/10.3390/molecules26185541






