New In Vitro-In Silico Approach for the Prediction of In Vivo Performance of Drug Combinations
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Cell Culture
2.3. Evaluation of Cell Growth Inhibition with the MTT Assay
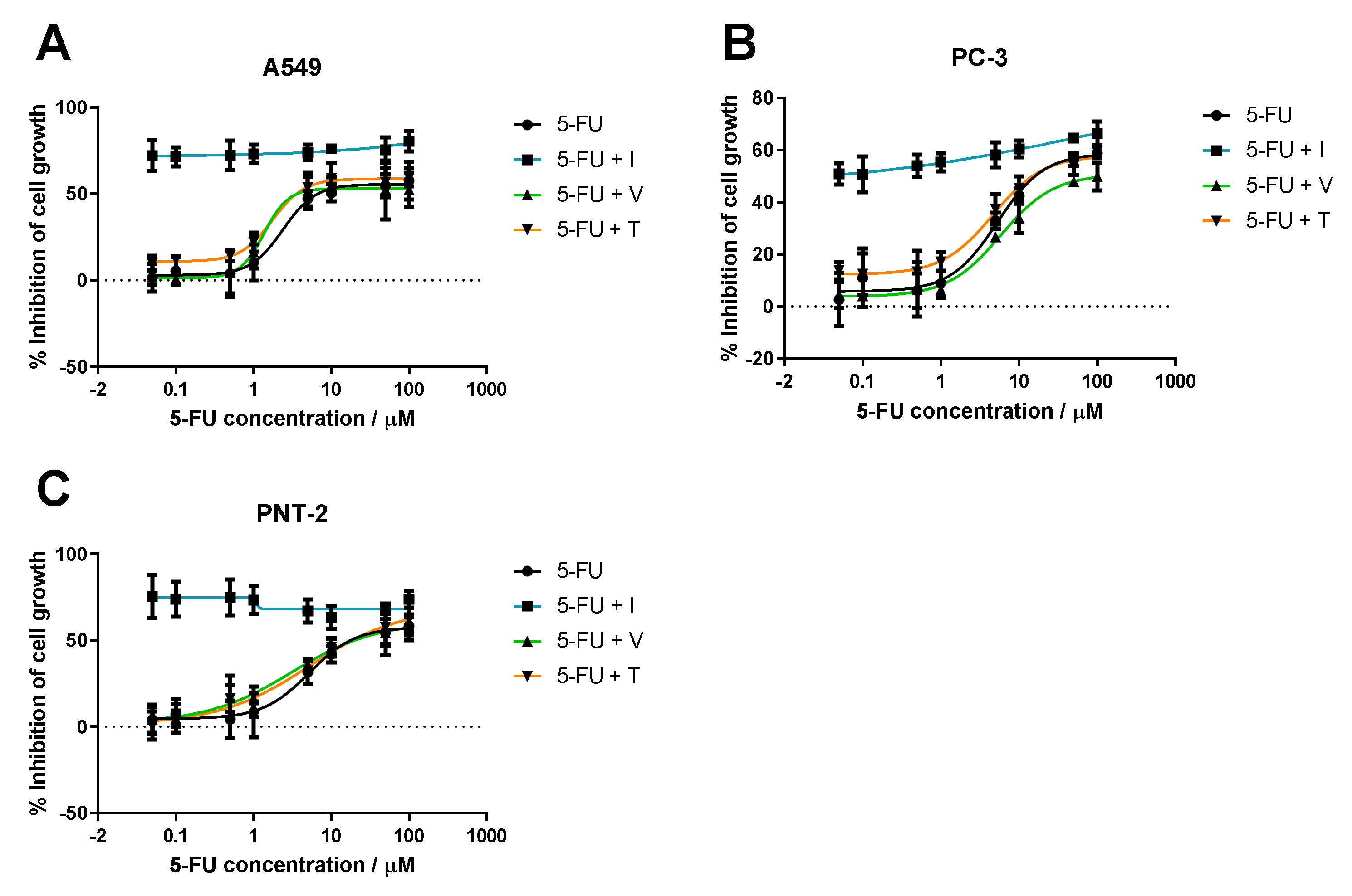
2.3.1. Dose-Response Curve Determination for ACDs and ACD-RD Combinations
2.3.2. Further Studies with Itraconazole in Combination with Gemcitabine or 5-FU
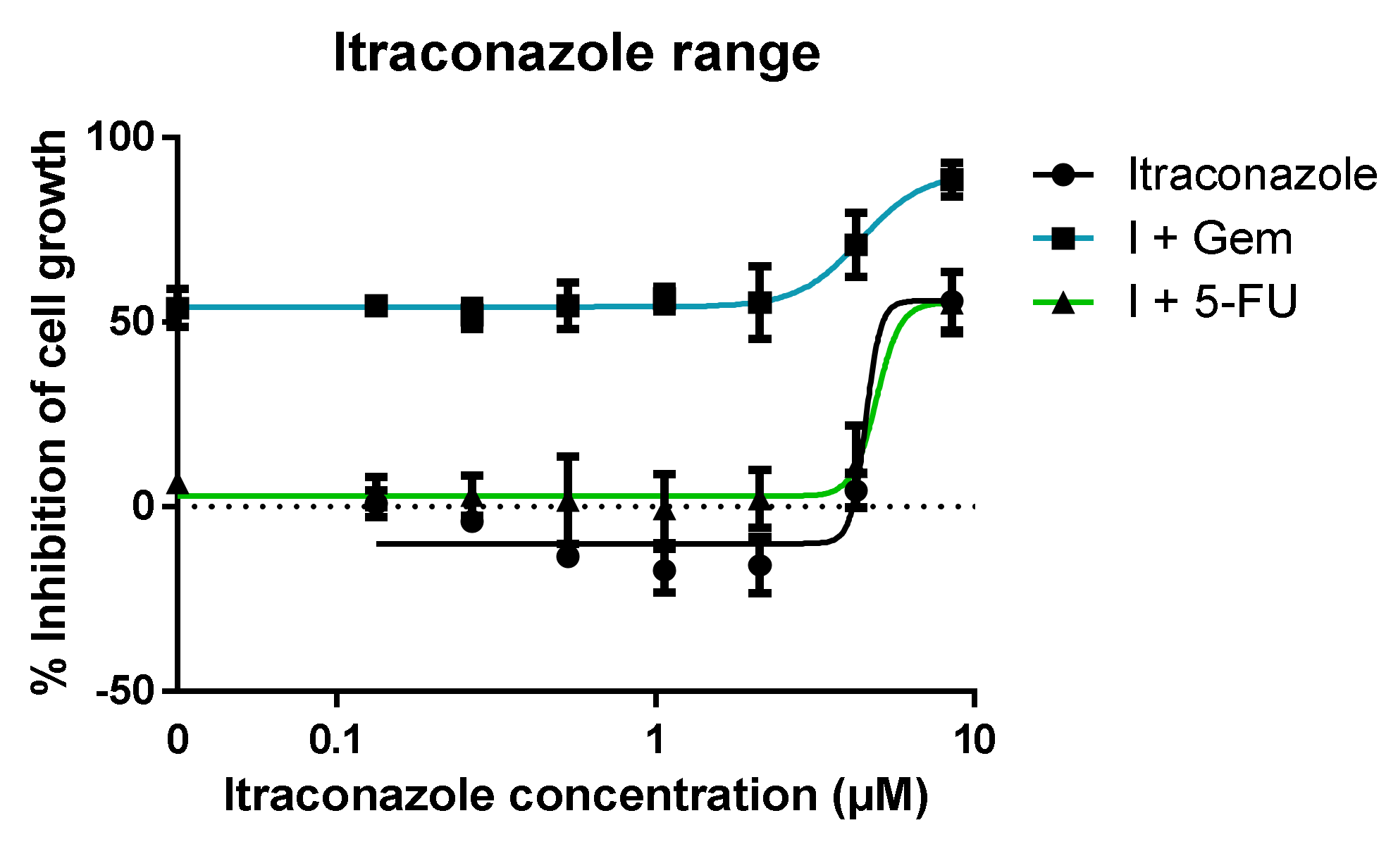
- Range of itraconazole concentrations + fixed concentration of ACD (Gem or 5-FU); itraconazole’s concentrations ranged from 0.07 to 4.25 μM, since the concentration used in the previous experiments was 8.5 μM (note dilution factor of 2 in the well). The concentration chosen for Gem and 5-FU was the one that showed the lowest effect in the previous experiments: 0.01 and 1 μM, respectively. The ACDs were also tested alone for control purposes;
- Range of ACD (Gem or 5-FU) concentrations + fixed concentration of itraconazole (three different concentrations were tested). Different concentrations of ACD (Gem or 5-FU) were added to the wells, as well as a fixed concentration of itraconazole. The multiple serial dilutions tested for ACD ranged from 0.005 to 10 μM for Gem (since in the previous experiments the resulting dose-response curve did not have the ideal shape), and the range was maintained for 5-FU. The concentrations for itraconazole were 2, 4 and 6 μM (concentrations within the range that showed an effect when administered with a very low concentration of ACD). Itraconazole was also tested alone for control purposes.
2.4. Model Development
2.4.1. WinNonlin: PK Analysis
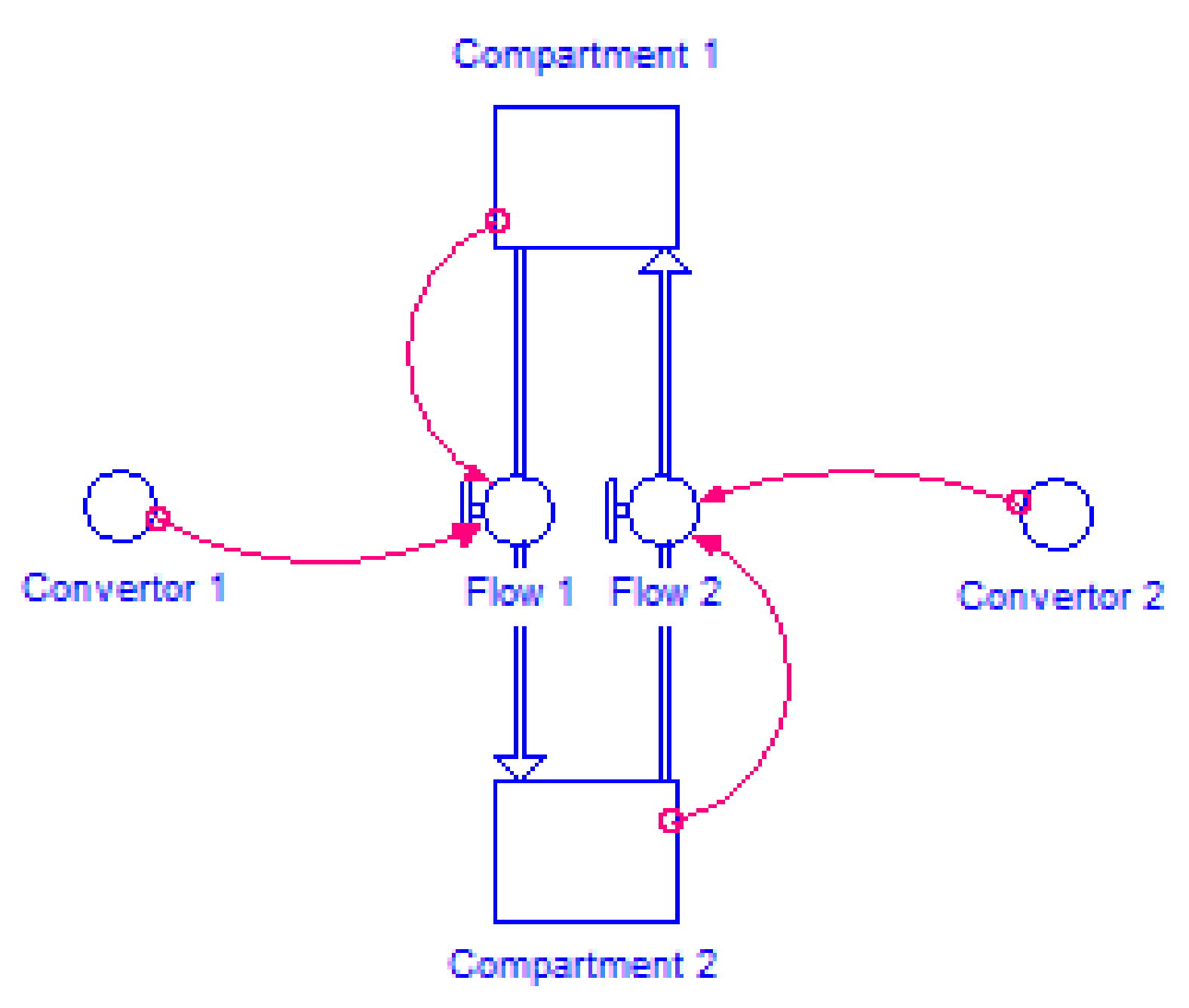
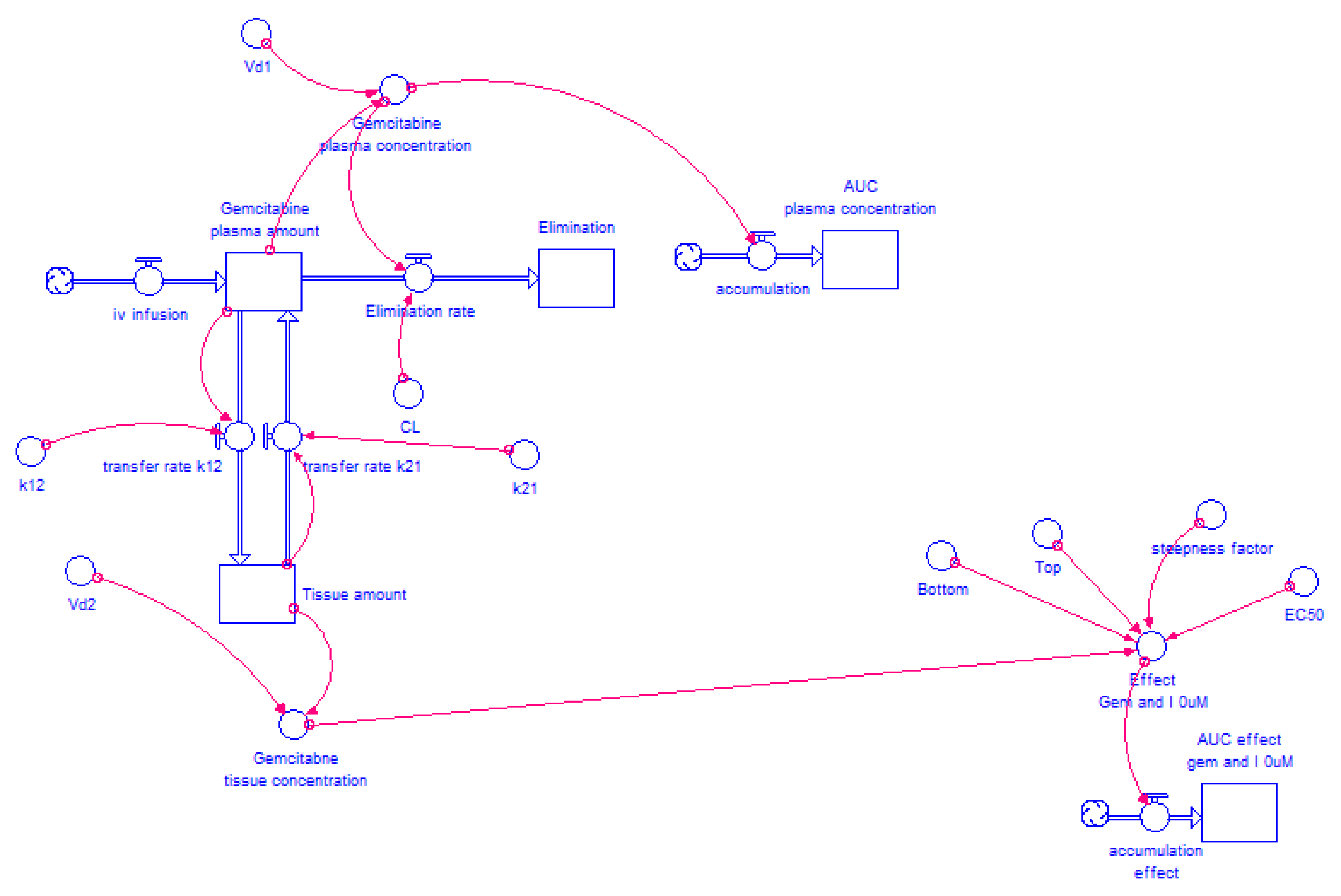
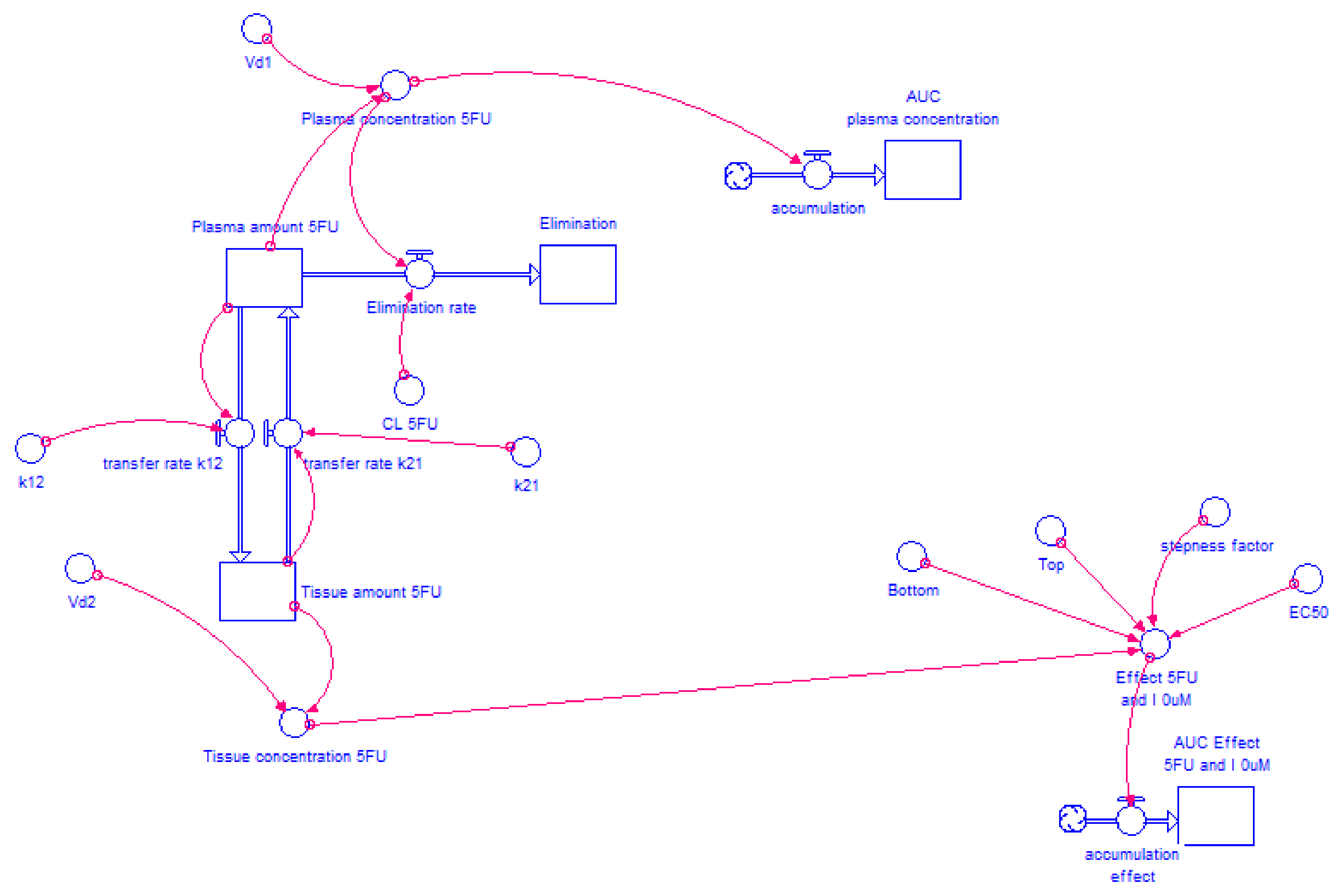
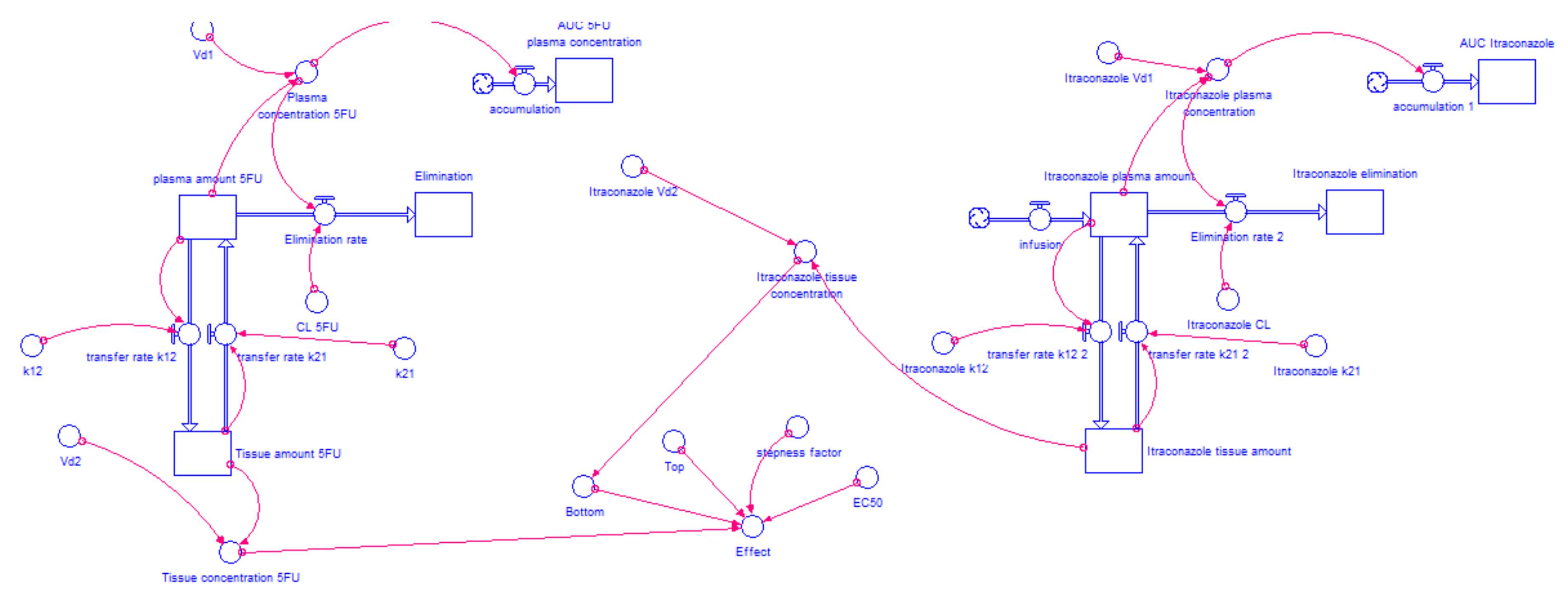
2.4.2. Model Structure
2.4.3. Determination of the AUC for Each Drug Combination Effect in Humans
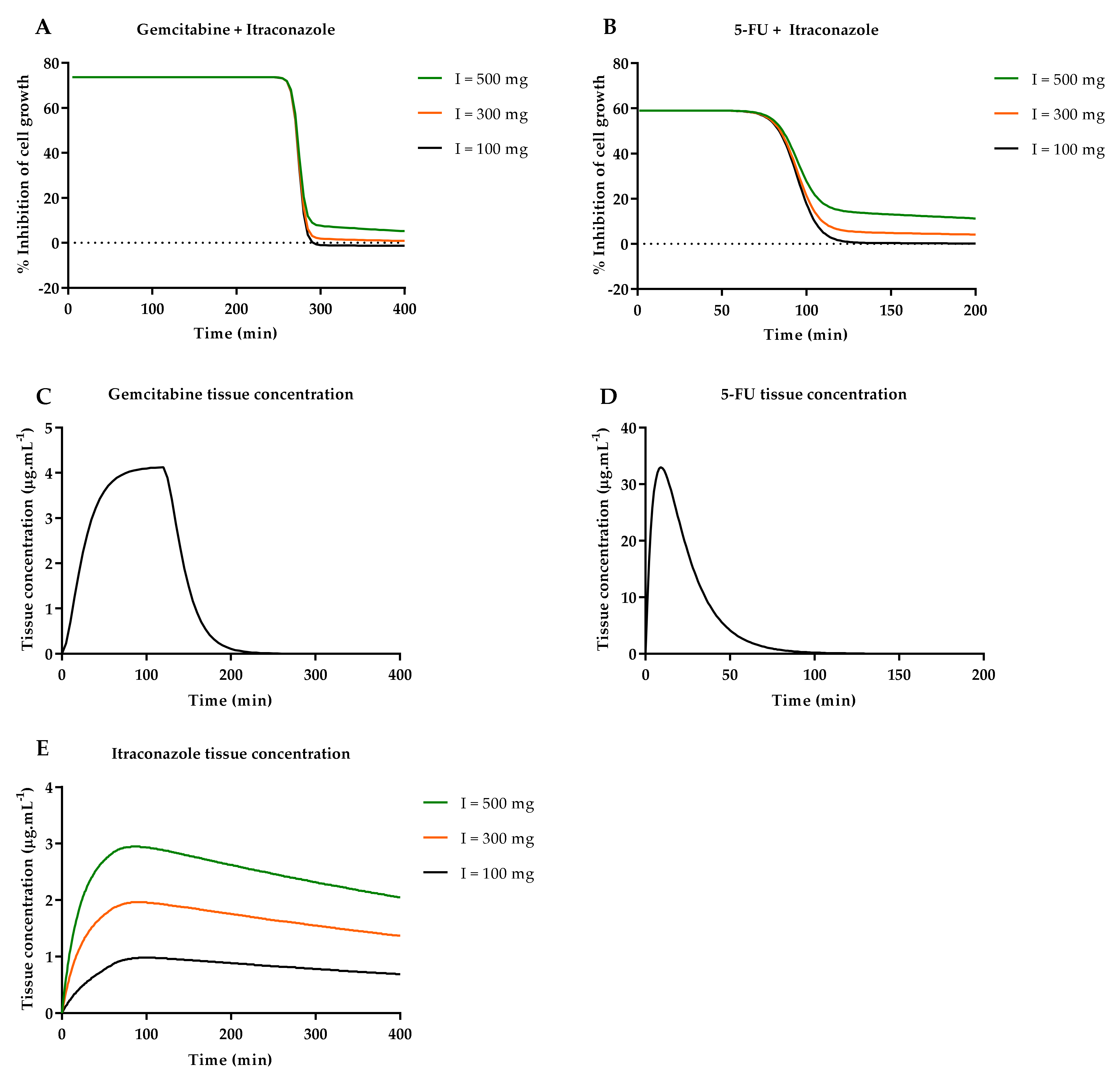
2.4.4. Itraconazole’s Dose-Dependent Effect, when Combined with Gemcitabine or 5-FU
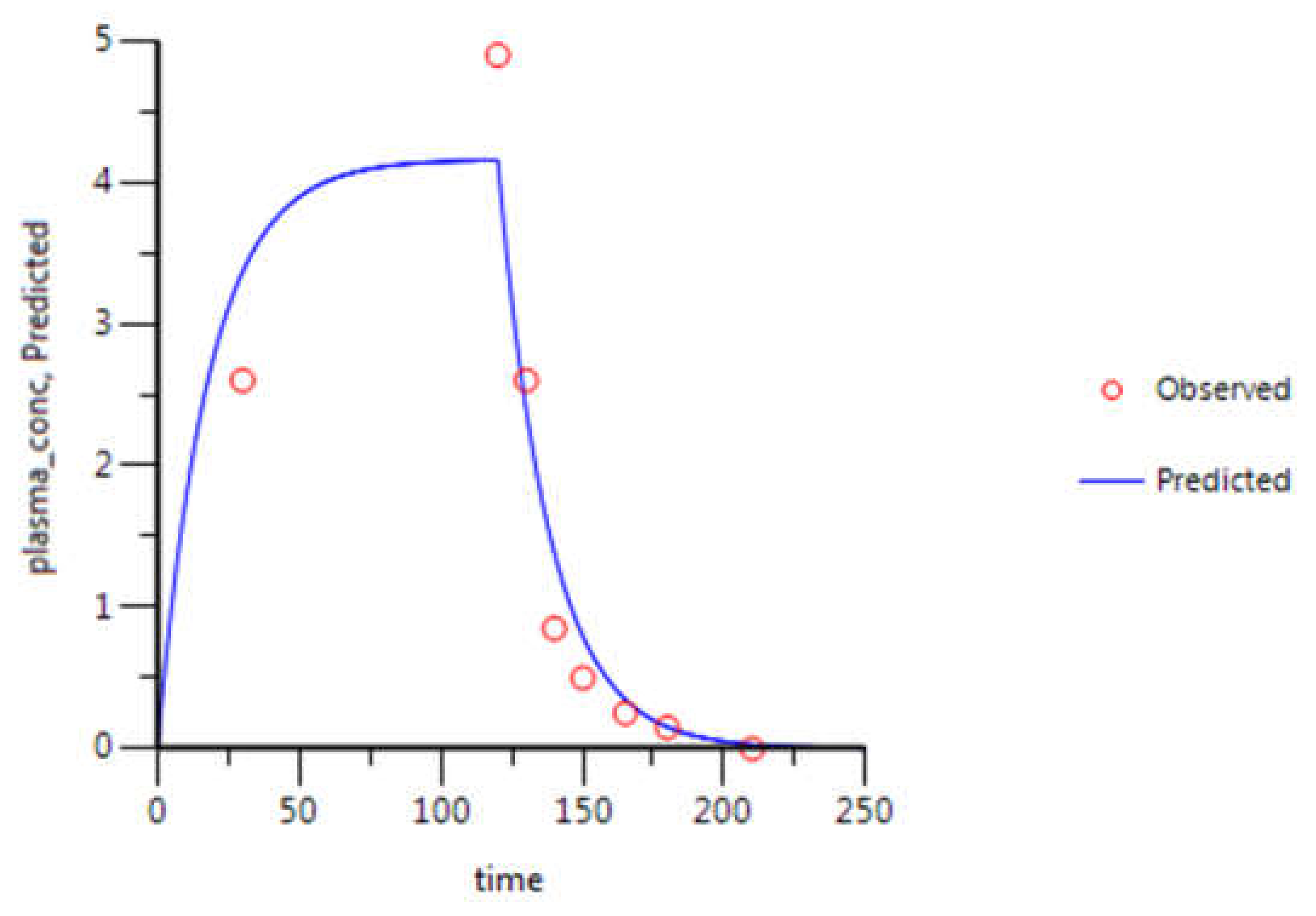
2.5. Model Validation
3. Results and Discussion
3.1. In Vitro Experiments—Evaluation of Inhibition of Cell Growth
3.1.1. Range of ACD Concentrations + Fixed Concentration of RD
3.1.2. Range of Itraconazole Concentrations + Fixed Concentration of ACD
3.1.3. Range of ACD Concentrations + Fixed Concentration of Itraconazole
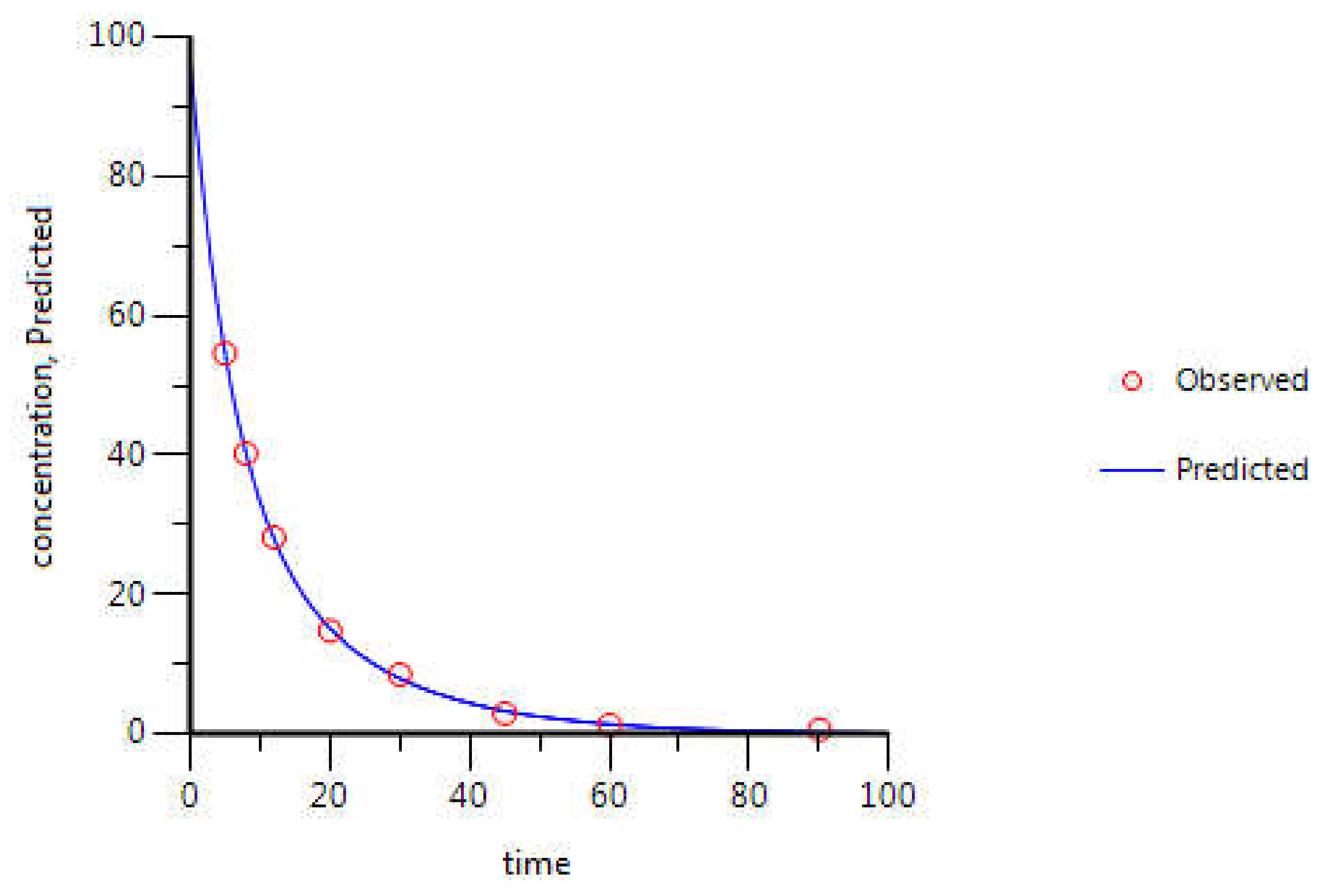
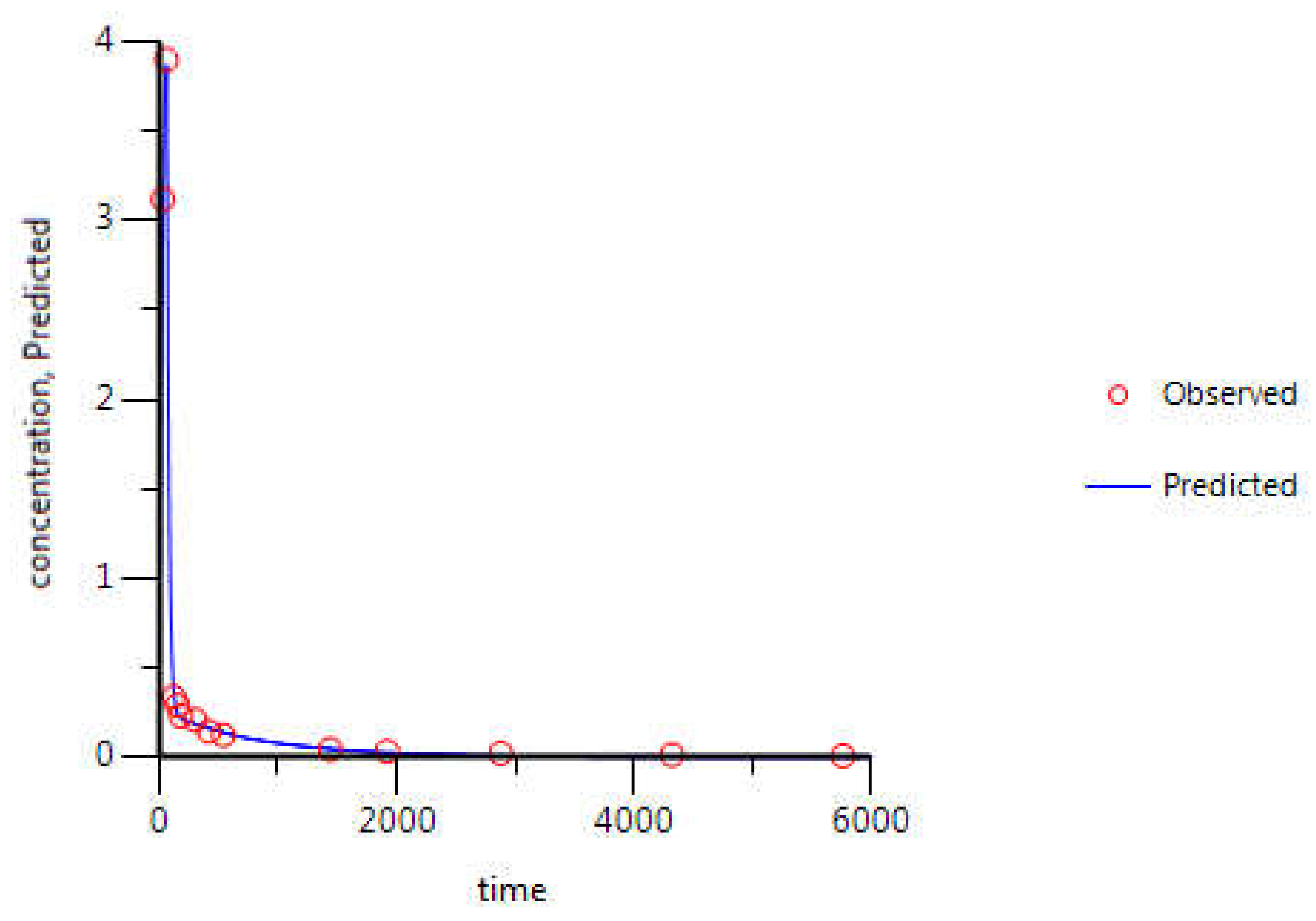
3.2. WinNonlin: PK Analysis
3.3. STELLA® Models
3.3.1. Input Data for the Model
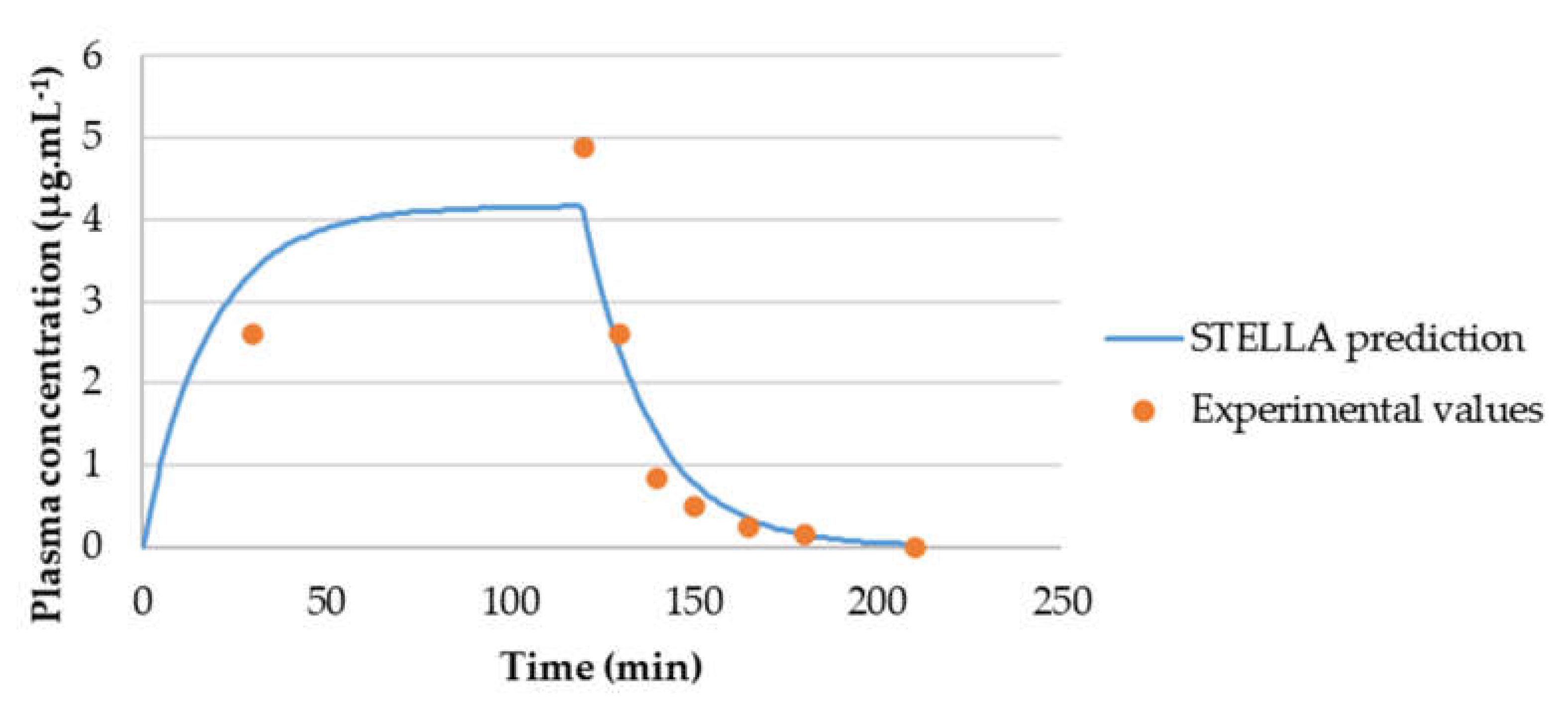
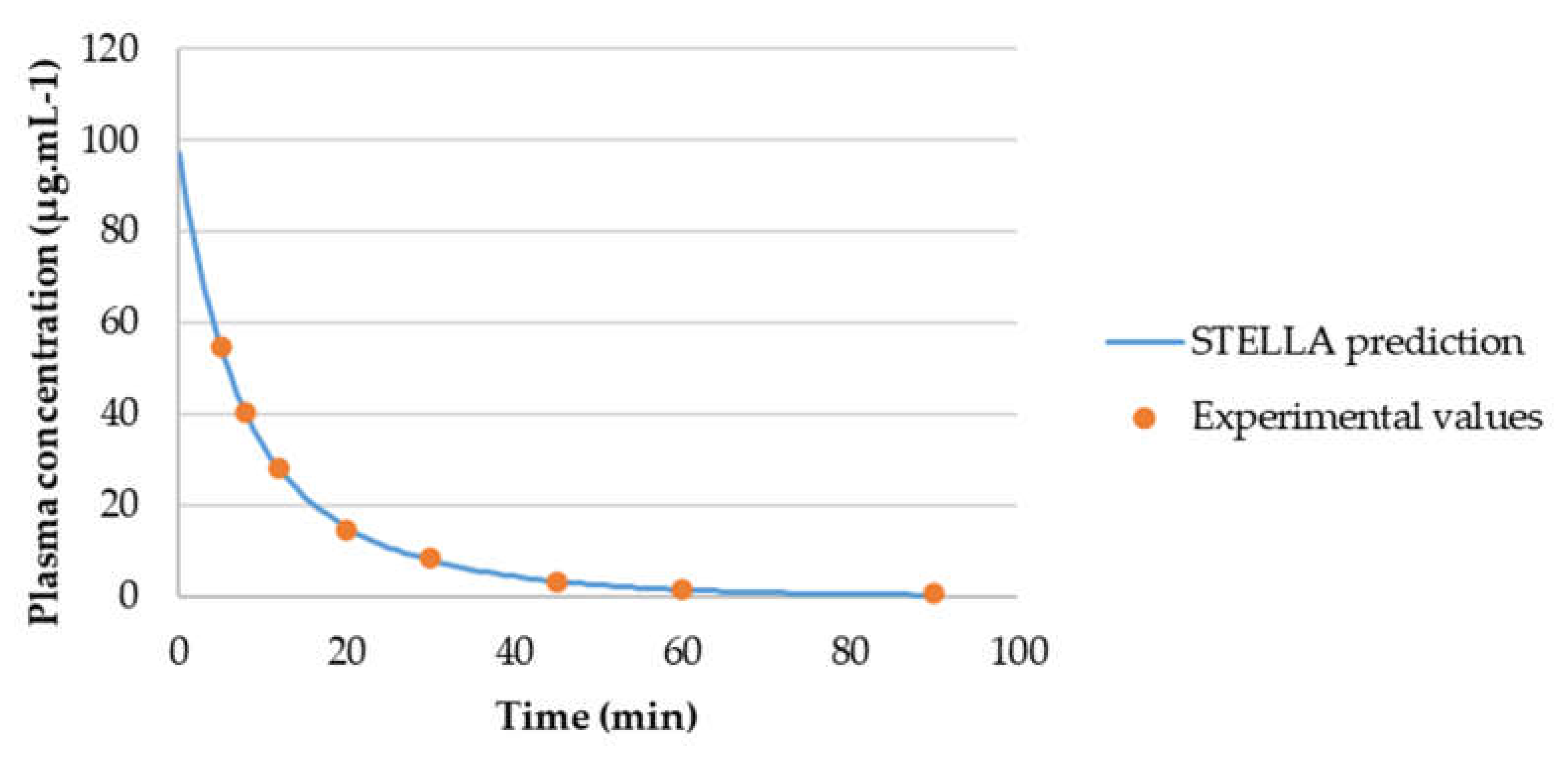
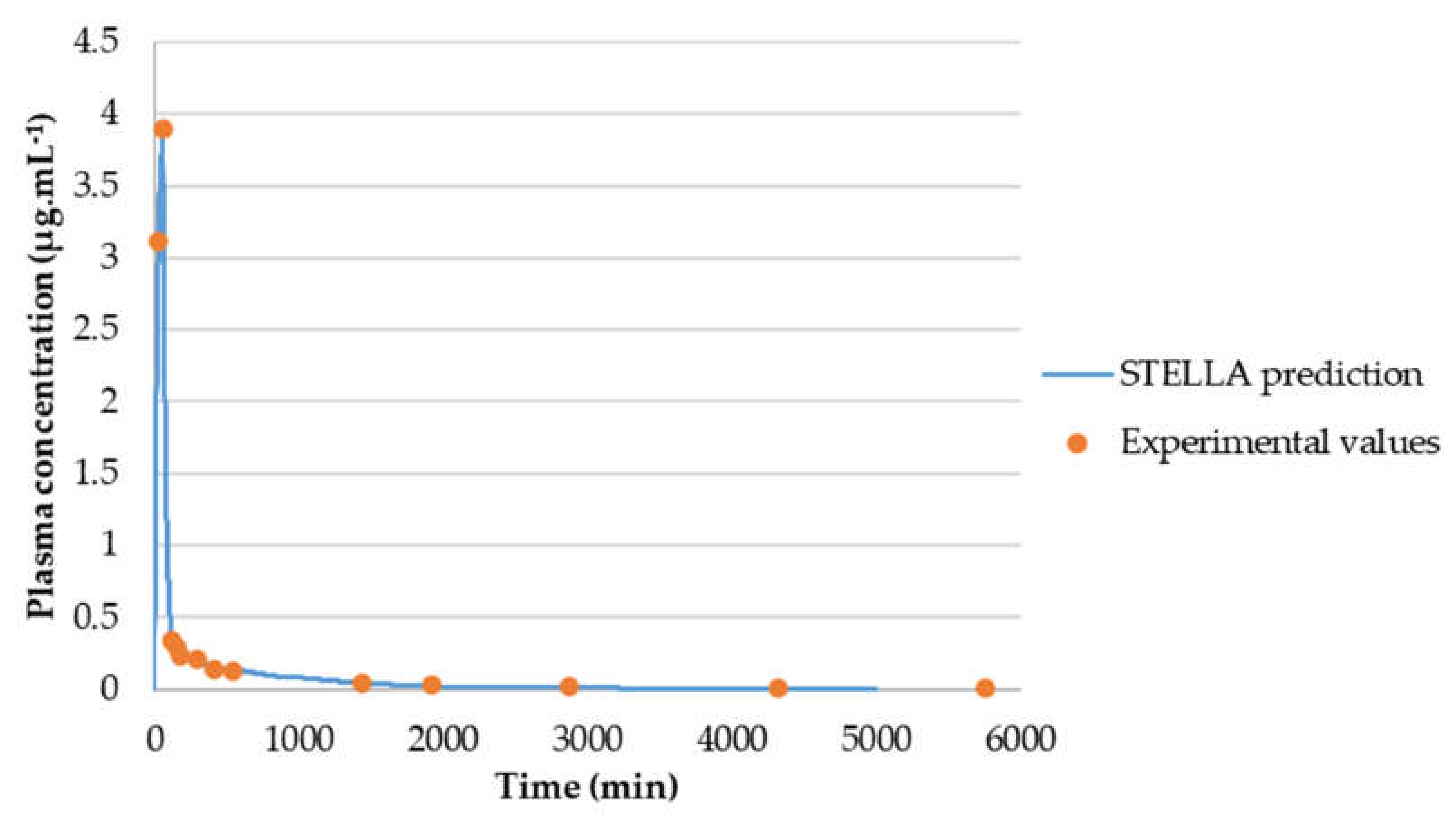
3.3.2. Model Validation
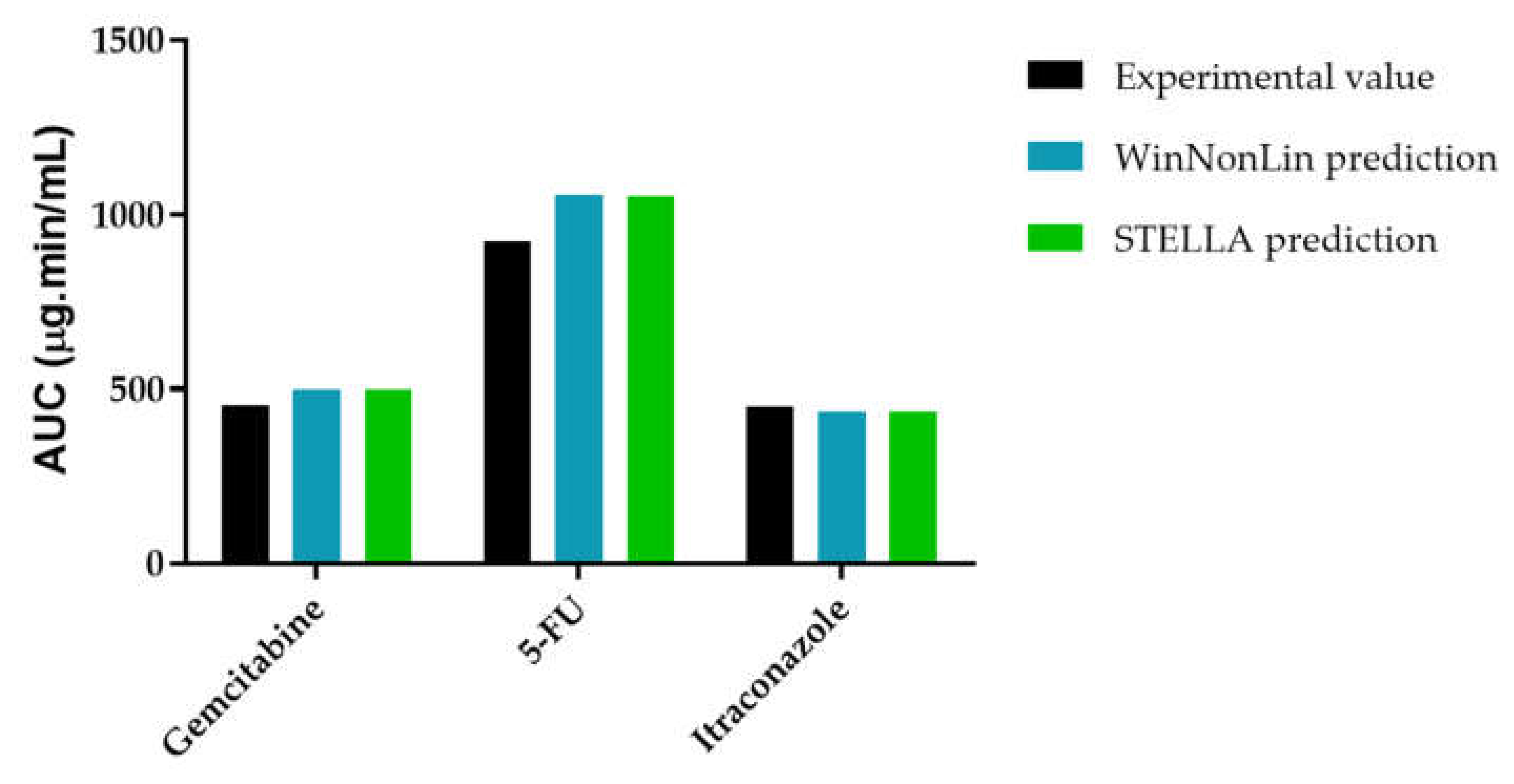
3.3.3. AUCeffect: Drug Combination Effect Comparison
4. Discussing the Limitations in Pharmacokinetics Modeling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Jambhekar, S.S.; Breen, P.J. Basic Pharmacokinetics; Pharmaceutical Press: London, UK, 2009; Volume 76. [Google Scholar]
- DiMasi, J.A.; Hansen, R.W.; Grabowski, H.G. The price of innovation: New estimates of drug development costs. J. Health Econ. 2003, 22, 151–185. [Google Scholar] [CrossRef]
- Box, G.E.; Draper, N.R. Empirical Model-Building and Response Surfaces; Wiley: New York, NY, USA, 1987; Volume 424. [Google Scholar]
- Rooney, K.F.; Snoeck, E.; Watson, P.H. Modelling and simulation in clinical drug development. Drug Discov. Today 2001, 6, 802–806. [Google Scholar] [CrossRef]
- Gieschke, R.; Steimer, J. Pharmacometrics: Modelling and simulation tools to improve decision making in clinical drug development. Eur. J. Metabol. Pharmacokinet. 2000, 25, 49–58. [Google Scholar] [CrossRef]
- Shargel, L.; Wu-Pong, S.; Yu, A.B. Applied Biopharmaceutics & Pharmacokinetics; Mcgraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Zhuang, X.; Lu, C. PBPK modeling and simulation in drug research and development. Acta Pharm. Sin. B 2016, 6, 430–440. [Google Scholar] [CrossRef]
- De Biasi, J.; Rekik, L. Four compartment mammillary model applied to the pharmacokinetics of a spiroarsorane administered orally to rabbits. J. Biomed. Eng. 1991, 13, 439–440. [Google Scholar] [CrossRef]
- Gabrielsson, J.; Weiner, D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill Higher Education: Boston, MA, USA, 2010. [Google Scholar]
- Otsuka, K.; Wagner, C.; Selen, A.; Dressman, J. Prediction of in-vivo pharmacokinetic profile for immediate and modified release oral dosage forms of furosemide using an in-vitro–in-silico–in-vivo approach. J. Pharm. Pharmacol. 2015, 67, 651–665. [Google Scholar] [CrossRef]
- Vellonen, K.-S.; Soini, E.-M.; Del Amo, E.M.; Urtti, A. Prediction of ocular drug distribution from systemic blood circulation. Mol. Pharm. 2016, 13, 2906–2911. [Google Scholar] [CrossRef] [PubMed]
- Hargrove, J.; Hulsey, M.; Summers, A. From genotype to phenotype: Computer-based modeling of gene expression with STELLA II. BioTechniques 1993, 15, 1096–1101. [Google Scholar] [PubMed]
- Miller, N.A.Y.; Reddy, M.B.; Heikkinen, A.T.; Lukacova, V.; Parrott, N. Physiologically Based Pharmacokinetic Modelling for First-In-Human Predictions: An Updated Model Building Strategy Illustrated with Challenging Industry Case Studies. Clin. Pharmacokinet. 2019, 58, 727–746. [Google Scholar] [CrossRef] [PubMed]
- DeVita, V.T., Jr. Single agent versus combination chemotherapy. CA Cancer J. Clin. 1975, 25, 152–158. [Google Scholar]
- Perelson, A.S.; Essunger, P.; Cao, Y.; Vesanen, M.; Hurley, A.; Saksela, K.; Markowitz, M.; Ho, D.D. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 1997, 387, 188–191. [Google Scholar] [CrossRef]
- Armand, J.; Dormont, J.; Schwebig, A. Recommendations for the study of drug combination therapy for the treatment of AIDS and cancer. Round Table No 7 at Giens XIII. Therapie 1998, 53, 385–389. [Google Scholar]
- Ai, N.; Fan, X.; Ekins, S. In silico methods for predicting drug–drug interactions with cytochrome P-450s, transporters and beyond. Adv. Drug Deliv. Rev. 2015, 86, 46–60. [Google Scholar] [CrossRef] [PubMed]
- Tallarida, R.J. An overview of drug combination analysis with isobolograms. J. Pharmacol. Exp. Ther. 2006, 319, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.-C. Drug combination studies and their synergy quantification using the Chou-Talalay method. Cancer Res. 2010, 70, 440–446. [Google Scholar] [CrossRef]
- Skeel, R.T.; Khleif, S.N. Handbook of Cancer Chemotherapy; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2011. [Google Scholar]
- Correia, A.; Silva, D.; Correia, A.; Vilanova, M.; Gärtner, F.; Vale, N. Study of new therapeutic strategies to combat breast cancer using drug combinations. Biomolecules 2018, 8, 175. [Google Scholar] [CrossRef]
- Hamann, S.R.; Blouin, R.A.; McAllister, R. Clinical pharmacokinetics of verapamil. Clin. Pharmacokinet. 1984, 9, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Heykants, J.; Van Peer, A.; Van de Velde, V.; Van Rooy, P.; Meuldermans, W.; Lavrijsen, K.; Woestenborghs, R.; Van Cutsem, J.; Cauwenbergh, G. The clinical pharmacokinetics of itraconazole: An overview. Mycoses 1989, 32, 67–87. [Google Scholar] [CrossRef]
- Madden, S.; Spaldin, V.; Park, B.K. Clinical pharmacokinetics of tacrine. Clin. Pharmacokinet. 1995, 28, 449–457. [Google Scholar] [CrossRef]
- Milroy, R. A randomised clinical study of verapamil in addition to combination chemotherapy in small cell lung cancer. Br. J. Cancer 1993, 68, 813–818. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.R.; Huang, M.Z.; Xu, N.; Shentu, J.Z.; Liu, J.; Cai, J. Pharmacokinetics of gemcitabine in Chinese patients with non-small-cell lung cancer. J. Zhejiang Univ. Sci. B 2005, 6, 446–450. [Google Scholar] [CrossRef] [PubMed]
- Mouton, J.W.; van Peer, A.; de Beule, K.; Van Vliet, A.; Donnelly, J.P.; Soons, P.A. Pharmacokinetics of itraconazole and hydroxyitraconazole in healthy subjects after single and multiple doses of a novel formulation. Antimicrob. Agents Chemother. 2006, 50, 4096–4102. [Google Scholar] [CrossRef] [PubMed]
- Heggie, G.D.; Sommadossi, J.P.; Cross, D.S.; Huster, W.J.; Diasio, R.B. Clinical pharmacokinetics of 5-fluorouracil and its metabolites in plasma, urine, and bile. Cancer Res. 1987, 47, 2203–2206. [Google Scholar] [PubMed]
- Soria, I.; Myhre, P.; Horton, V.; Ellefson, P.; McCarville, S.; Schmitt, K.; Owens, M. Effect of food on the pharmacokinetics and bioavailability of oral imiquimod relative to a subcutaneous dose. Int. J. Clin. Pharmacol. Ther. 2000, 38, 476–481. [Google Scholar] [CrossRef]
- Ince, P.; Appleton, D.; Finney, K.; Sunter, J.; Watson, A. Verapamil increases the sensitivity of primary human colorectal carcinoma tissue to vincristine. Br. J. Cancer 1986, 53, 137. [Google Scholar] [CrossRef][Green Version]
- Mansouri, A.; Haouzi, D.; Descatoire, V.; Demeilliers, C.; Sutton, A.; Vadrot, N.; Fromenty, B.; Feldmann, G.; Pessayre, D.; Berson, A. Tacrine inhibits topoisomerases and DNA synthesis to cause mitochondrial DNA depletion and apoptosis in mouse liver. Hepatology 2003, 38, 715–725. [Google Scholar] [CrossRef]
- Merry, S.; Fetherston, C.; Kaye, S.; Freshney, R.; Plumb, J. Resistance of human glioma to adriamycin in vitro: The role of membrane transport and its circumvention with verapamil. Br. J. Cancer 1986, 53, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Morrow, M.; Wait, R.; Rosenthal, R.; Gamelli, R. Verapamil enhances antitumor activity without increasing myeloid toxicity. Surgery 1987, 101, 63–68. [Google Scholar]
- Tsuruo, T.; Iida, H.; Tsukagoshi, S.; Sakurai, Y. Overcoming of vincristine resistance in P388 leukemia in vivo and in vitro through enhanced cytotoxicity of vincristine and vinblastine by verapamil. Cancer Res. 1981, 41, 1967–1972. [Google Scholar]
- Ambudkar, S.V.; Dey, S.; Hrycyna, C.A.; Ramachandra, M.; Pastan, I.; Gottesman, M.M. Biochemical, cellular, and pharmacological aspects of the multidrug transporter. Annu. Rev. Pharmacol. Toxicol. 1999, 39, 361–398. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, D.; Zhang, Q.; Chen, Y.; Zheng, D.; Hao, L.; Duan, C.; Jia, L.; Liu, G.; Liu, Y. Synergistic effect of folate-mediated targeting and verapamil-mediated P-gp inhibition with paclitaxel-polymer micelles to overcome multi-drug resistance. Biomaterials 2011, 32, 9444–9456. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Y.; Schwarz, B.; Mysliwietz, J.; Hartig, R.; Camaj, P.; Bao, Q.; Jauch, K.-W.; Guba, M.; Ellwart, J.W. Verapamil inhibits tumor progression of chemotherapy-resistant pancreatic cancer side population cells. Int. J. Oncol. 2016, 49, 99–110. [Google Scholar] [CrossRef]
- Chong, C.R.; Xu, J.; Lu, J.; Bhat, S.; Sullivan Jr, D.J.; Liu, J.O. Inhibition of angiogenesis by the antifungal drug itraconazole. ACS Chem. Biol. 2007, 2, 263–270. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Tang, J.Y.; Gong, R.; Kim, J.; Lee, J.J.; Clemons, K.V.; Chong, C.R.; Chang, K.S.; Fereshteh, M.; Gardner, D. Itraconazole, a commonly used antifungal that inhibits Hedgehog pathway activity and cancer growth. Cancer Cell 2010, 17, 388–399. [Google Scholar] [CrossRef] [PubMed]
- Nacev, B.A.; Grassi, P.; Dell, A.; Haslam, S.M.; Liu, J.O. The antifungal drug itraconazole inhibits vascular endothelial growth factor receptor 2 (VEGFR2) glycosylation, trafficking, and signaling in endothelial cells. J. Biol. Chem. 2011, 286, 44045–44056. [Google Scholar] [CrossRef]
- Kim, J.; Aftab, B.T.; Tang, J.Y.; Kim, D.; Lee, A.H.; Rezaee, M.; Kim, J.; Chen, B.; King, E.M.; Borodovsky, A. Itraconazole and arsenic trioxide inhibit Hedgehog pathway activation and tumor growth associated with acquired resistance to smoothened antagonists. Cancer Cell 2013, 23, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, J.; Zhang, T.; Zou, L.; Chen, Y.; Wang, K.; Lei, Y.; Yuan, K.; Li, Y.; Lan, J. Itraconazole suppresses the growth of glioblastoma through induction of autophagy: Involvement of abnormal cholesterol trafficking. Autophagy 2014, 10, 1241–1255. [Google Scholar] [CrossRef]
- Wang, E.-j.; Lew, K.; Casciano, C.N.; Clement, R.P.; Johnson, W.W. Interaction of common azole antifungals with P glycoprotein. Antimicrob. Agents Chemother. 2002, 46, 160–165. [Google Scholar] [CrossRef]
- Toutain, P.-L.; Bousquet-Mélou, A. Volumes of distribution. J. Vet. Pharmacol. Ther. 2004, 27, 441–453. [Google Scholar] [CrossRef]


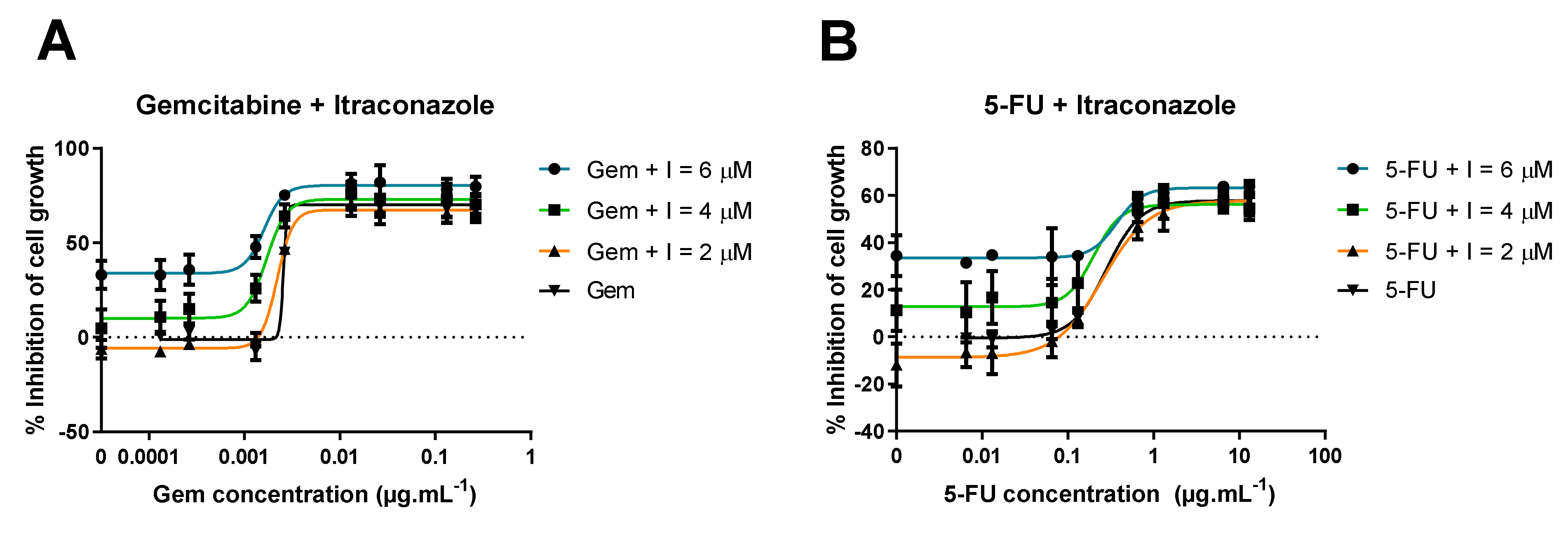


| Gem + I a | Bottom (%) | Top (%) | Steepness Factor | EC50 (μg·mL−1) |
|---|---|---|---|---|
| I = 6 μM | 34.33 ± 2.43 | 80.39 ± 1.71 | 4.30 ± 1.30 | 0.0016 ± 3.2 × 10−7 |
| I = 4 μM | 12.83 ± 2.79 | 73.07 ± 1.97 | 4.37 ± 0.99 | 0.0018 ± 3.1 × 10−7 |
| I = 2 μM | −5.51 ± 1.83 | 67.47 ± 1.29 | 5.35 ± 1.12 | 0.0022 ± 1.6 × 10−7 |
| I = 0 μM | −1.06 ± 2.35 | 70.12 ± 1.67 | 23.14 ± 4.20 × 105 | 0.0026 ± 2.2 × 105 |
| Average | N.A. | 72.76 | 4.67 | 0.0021 |
| 5-FU + I a | Bottom (%) | Top (%) | Steepness Factor | EC50 (μg·mL−1) |
|---|---|---|---|---|
| I = 6 μM | 33.22 ± 1.58 | 63.24 ± 1.62 | 2.77 ± 1.23 | 0.36 ± 0.01 |
| I = 4 μM | 13.42 ± 3.09 | 56.05 ± 2.87 | 2.90 ± 2.40 | 0.20 ± 0.0071 |
| I = 2 μM | −6.99 ± 2.14 | 57.52 ± 2.11 | 1.70 ± 0.26 | 0.27 ± 0.002 |
| I = 0 μM | −0.47 ± 1.32 | 57.80 ± 1.32 | 2.19 ± 0.27 | 0.28 ± 0.001 |
| Average | N.A. | 58.65 | 2.39 | 0.28 |
| Gemcitabine Parameters | Estimate | CV (%) | Literature Values [27] |
|---|---|---|---|
| k10 (min−1) | 5.54 × 10−2 | 144.9 | 7.00 × 10−2 |
| k12 (min−1) | 6.64 × 10−4 | 45,998.6 | - |
| k21 (min−1) | 1.02 × 10−1 | 29,203.6 | - |
| AUC (μg·mL−1·min) | 499.58 | 10.3 | 453.00 |
| Cmax (μg·mL−1) | 4.16 | 10.5 | 4.92 |
| CL (mL·min−1) | 3771.20 | 10.3 | 3940.05 |
| Vss (mL) | 68,464.40 | 37.4 | - |
| Vd1 (mL) | 68,019.62 | 148.8 | - |
| Vd2 (mL) | 444.79 | 19,137.5 | - |
| 5-FU Parameters | Estimate | CV (%) | Literature Values [29] |
|---|---|---|---|
| k10 (min−1) | 9.17 × 10−2 | 4.9 | - |
| k12 (min−1) | 3.21 × 10−2 | 29.5 | - |
| k21 (min−1) | 1.07 × 10−1 | 28.1 | - |
| AUC (μg·mL−1·min) | 1058.81 | 1.6 | 926.80 |
| Cmax (μg·mL−1) | 97.14 | 5.1 | - |
| CL (mL·min−1) | 850.01 | 1.6 | 1069.20 |
| Vss (mL) | 12,056.99 | 4.9 | 15,912.00 |
| Vd1 (mL) | 9265.14 | 5.1 | - |
| Vd2 (mL) | 2791.84 | 14.2 | - |
| Itraconazole Parameters | Estimate | CV (%) | Literature Values [28] |
|---|---|---|---|
| k10 (min−1) | 2.80 × 10−2 | 8.8 | 2.66 × 10−2 |
| k12 (min−1) | 2.38 × 10−2 | 9.4 | - |
| k21 (min−1) | 2.34 × 10−3 | 15.3 | - |
| AUC (μg·mL−1·min) | 437.73 | 7.9 | 449.88 |
| Cmax (μg·mL−1) | 3.88 | 0.6 | - |
| CL (mL·min−1) | 228.45 | 7.9 | 246.67 |
| Vss (mL) | 90,922.24 | 20.9 | 558,000.00 |
| Vd1 (mL) | 8145.37 | 2.6 | - |
| Vd2 (mL) | 82,776.88 | 22.9 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correia, C.; Ferreira, A.; Santos, J.; Lapa, R.; Yliperttula, M.; Urtti, A.; Vale, N. New In Vitro-In Silico Approach for the Prediction of In Vivo Performance of Drug Combinations. Molecules 2021, 26, 4257. https://doi.org/10.3390/molecules26144257
Correia C, Ferreira A, Santos J, Lapa R, Yliperttula M, Urtti A, Vale N. New In Vitro-In Silico Approach for the Prediction of In Vivo Performance of Drug Combinations. Molecules. 2021; 26(14):4257. https://doi.org/10.3390/molecules26144257
Chicago/Turabian StyleCorreia, Cristiana, Abigail Ferreira, Joana Santos, Rui Lapa, Marjo Yliperttula, Arto Urtti, and Nuno Vale. 2021. "New In Vitro-In Silico Approach for the Prediction of In Vivo Performance of Drug Combinations" Molecules 26, no. 14: 4257. https://doi.org/10.3390/molecules26144257
APA StyleCorreia, C., Ferreira, A., Santos, J., Lapa, R., Yliperttula, M., Urtti, A., & Vale, N. (2021). New In Vitro-In Silico Approach for the Prediction of In Vivo Performance of Drug Combinations. Molecules, 26(14), 4257. https://doi.org/10.3390/molecules26144257







