Computational NMR Spectroscopy of Ionic Liquids: [C4C1im]Cl/Water Mixtures
Abstract
1. Introduction
2. Results
2.1. Molecular Dynamics Simulations
2.2. DFT-NMR Calculations
3. Discussion
4. Computational Methods
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Grimblat, N.; Sarotti, A.M. Computational Chemistry to the Rescue: Modern Toolboxes for the Assignment of Complex Molecules by GIAO NMR Calculations. Chem.-A Eur. J. 2016, 22, 12246–12261. [Google Scholar] [CrossRef] [PubMed]
- Bagno, A.; Saielli, G. Addressing the stereochemistry of complex organic molecules by density functional theory-NMR. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 228–240. [Google Scholar] [CrossRef]
- Tantillo, D.J. Walking in the woods with quantum chemistry-applications of quantum chemical calculations in natural products research. Nat. Prod. Rep. 2013, 30, 1079–1086. [Google Scholar] [CrossRef] [PubMed]
- Bagno, A.; Saielli, G. Computational NMR spectroscopy: Reversing the information flow. Theor. Chem. Acc. 2007, 117, 603–619. [Google Scholar] [CrossRef]
- Sarotti, A.M. Successful combination of computationally inexpensive GIAO 13C NMR calculations and artificial neural network pattern recognition: A new strategy for simple and rapid detection of structural misassignments. Org. Biomol. Chem. 2013, 11, 4847–4859. [Google Scholar] [CrossRef]
- Kwan, E.E.; Liu, R.Y. Enhancing NMR Prediction for Organic Compounds Using Molecular Dynamics. J. Chem. Theory Comput. 2015, 11, 5083–5089. [Google Scholar] [CrossRef]
- Iron, M.A. Evaluation of the Factors Impacting the Accuracy of 13C NMR Chemical Shift Predictions using Density Functional Theory—The Advantage of Long-Range Corrected Functionals. J. Chem. Theory Comput. 2017, 13, 5798–5819. [Google Scholar] [CrossRef]
- Saielli, G.; Bagno, A. Can two molecules have the same NMR spectrum? Hexacyclinol revisited. Org. Lett. 2009, 11, 1409–1412. [Google Scholar] [CrossRef]
- Saielli, G. Computational Spectroscopy of Ionic Liquids for Bulk Structure Elucidation. Adv. Theory Simulations 2018, 1, 1800084. [Google Scholar] [CrossRef]
- Bagno, A.; D’Amico, F.; Saielli, G. Computing the NMR Spectrum of a Bulk Ionic Liquid Phase by QM/MM Methods. J. Phys. Chem. B 2006, 110, 23004–23006. [Google Scholar] [CrossRef]
- Bagno, A.; D’Amico, F.; Saielli, G. Computing the 1H NMR spectrum of a bulk ionic liquid from snapshots of car-parrinello molecular dynamics simulations. ChemPhysChem 2007, 8, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Saielli, G.; Bagno, A.; Castiglione, F.; Simonutti, R.; Mauri, M.; Mele, A. Understanding cage effects in imidazolium ionic liquids by 129Xe NMR: MD simulations and relativistic DFT calculations. J. Phys. Chem. B 2014, 118, 13963–13968. [Google Scholar] [CrossRef] [PubMed]
- Charpentier, T. The PAW/GIPAW approach for computing NMR parameters: A new dimension added to NMR study of solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Pavan, B.; Ceresoli, D.; Tecklenburg, M.M.J.; Fornari, M. First principles NMR study of fluorapatite under pressure. Solid State Nucl. Magn. Reson. 2012, 45–46, 59–65. [Google Scholar] [CrossRef][Green Version]
- Pigliapochi, R.; Pell, A.J.; Seymour, I.D.; Grey, C.P.; Ceresoli, D.; Kaupp, M. DFT investigation of the effect of spin-orbit coupling on the NMR shifts in paramagnetic solids. Phys. Rev. B 2017, 95, 54412. [Google Scholar] [CrossRef]
- Pedone, A. Recent advances in solid-state NMR computational spectroscopy: The case of alumino-silicate glasses. Int. J. Quantum Chem. 2016, 116, 1520–1531. [Google Scholar] [CrossRef]
- Mastrorilli, P.; Todisco, S.; Bagno, A.; Gallo, V.; Latronico, M.; Fortuño, C.; Gudat, D. Multinuclear Solid-State NMR and DFT Studies on Phosphanido-Bridged Diplatinum Complexes. Inorg. Chem. 2015, 54, 5855–5863. [Google Scholar] [CrossRef]
- Todisco, S.; Saielli, G.; Gallo, V.; Latronico, M.; Rizzuti, A.; Mastrorilli, P. 31P and 195Pt solid-state NMR and DFT studies on platinum(i) and platinum(ii) complexes. Dalt. Trans. 2018, 47, 8884–8891. [Google Scholar] [CrossRef]
- Holmes, S.T.; Iuliucci, R.J. Modeling NMR Chemical Shift Tensors. In Modern Magnetic Resonance; Webb, G.A., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 959–993. ISBN 978-3-319-28388-3. [Google Scholar]
- Neves, C.M.S.S.; Dinis, T.B.V.; Carvalho, P.J.; Schröder, B.; Santos, L.M.N.B.F.; Freire, M.G.; Coutinho, J.A.P. Binary Mixtures of Ionic Liquids in Aqueous Solution: Towards an Understanding of Their Salting-In/Salting-Out Phenomena. J. Solution Chem. 2019, 48, 983–991. [Google Scholar] [CrossRef]
- Shi, R.; Wang, Y. Dual Ionic and Organic Nature of Ionic Liquids. Sci. Rep. 2016, 6, 19612–19644. [Google Scholar] [CrossRef]
- Wang, Y.; Voth, G.A. Tail Aggregation and Domain Diffusion in Ionic Liquids. J. Phys. Chem. B 2006, 110, 18601–18608. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Voth, G.A. Unique Spatial Heterogeneity in Ionic Liquids. J. Am. Chem. Soc. 2005, 127, 12192–12193. [Google Scholar] [CrossRef] [PubMed]
- Dhakal, P.; Shah, J.K. Recent advances in molecular simulations of ionic liquid–ionic liquid mixtures. Curr. Opin. Green Sustain. Chem. 2019, 18, 90–97. [Google Scholar] [CrossRef]
- Cha, S.; Ao, M.; Sung, W.; Moon, B.; Ahlström, B.; Johansson, P.; Ouchi, Y.; Kim, D. Structures of ionic liquid–water mixtures investigated by IR and NMR spectroscopy. Phys. Chem. Chem. Phys. 2014, 16, 9591–9601. [Google Scholar] [CrossRef] [PubMed]
- Bagno, A.; Butts, C.; Chiappe, C.; D’Amico, F.; Lord, J.C.D.; Pieraccini, D.; Rastrelli, F. The effect of the anion on the physical properties of trihalide-based N,N-dialkylimidazolium ionic liquids. Org. Biomol. Chem. 2005, 3, 1624–1630. [Google Scholar] [CrossRef] [PubMed]
- Cesare Marincola, F.; Piras, C.; Russina, O.; Gontrani, L.; Saba, G.; Lai, A. NMR Investigation of Imidazolium-Based Ionic Liquids and Their Aqueous Mixtures. ChemPhysChem 2012, 13, 1339–1346. [Google Scholar] [CrossRef] [PubMed]
- Ermanis, K.; Parkes, K.E.B.; Agback, T.; Goodman, J.M. The optimal DFT approach in DP4 NMR structure analysis—Pushing the limits of relative configuration elucidation. Org. Biomol. Chem. 2019, 17, 5886–5890. [Google Scholar] [CrossRef]
- Chen, S.; Izgorodina, E.I. Prediction of 1H NMR chemical shifts for clusters of imidazolium-based ionic liquids. Phys. Chem. Chem. Phys. 2017, 19, 17411–17425. [Google Scholar] [CrossRef]
- Chen, S.; Vijayaraghavan, R.; MacFarlane, D.R.; Izgorodina, E.I. Ab Initio Prediction of Proton NMR Chemical Shifts in Imidazolium Ionic Liquids. J. Phys. Chem. B 2013, 117, 3186–3197. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Köddermann, T.; Paschek, D.; Ludwig, R. Molecular Dynamic Simulations of Ionic Liquids: A Reliable Description of Structure, Thermodynamics and Dynamics. ChemPhysChem 2007, 8, 2464–2470. [Google Scholar] [CrossRef] [PubMed]
- Lopes, J.N.C.; Deschamps, J.; Padua, A.A.H.A.H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 11250. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Wang, D.; Wang, X.; Liu, Z. Volumetric Properties of 1-Butyl-3-methylimidazolium Chloride with Organic Solvents. J. Chem. Eng. Data 2017, 62, 3958–3966. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, H.; Su, B.; Yang, Y.; Ren, Q.; Xing, H. Volumetric Properties of Binary Mixtures of 1-Butyl-3-methylimidazolium Chloride + Water or Hydrophilic Solvents at Different Temperatures. J. Chem. Eng. Data 2010, 55, 1750–1754. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS-A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD--Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Rickard, G.A.; Karadakov, P.B.; Webb, G.A.; Morokuma, K. Calculation of NMR Chemical Shifts in Carbohydrates with ONIOM: A Study of the Conformers of β-d-Glucopyranose. J. Phys. Chem. A 2003, 107, 292–300. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
Sample Availability: Samples of the compounds are not available from the authors. |
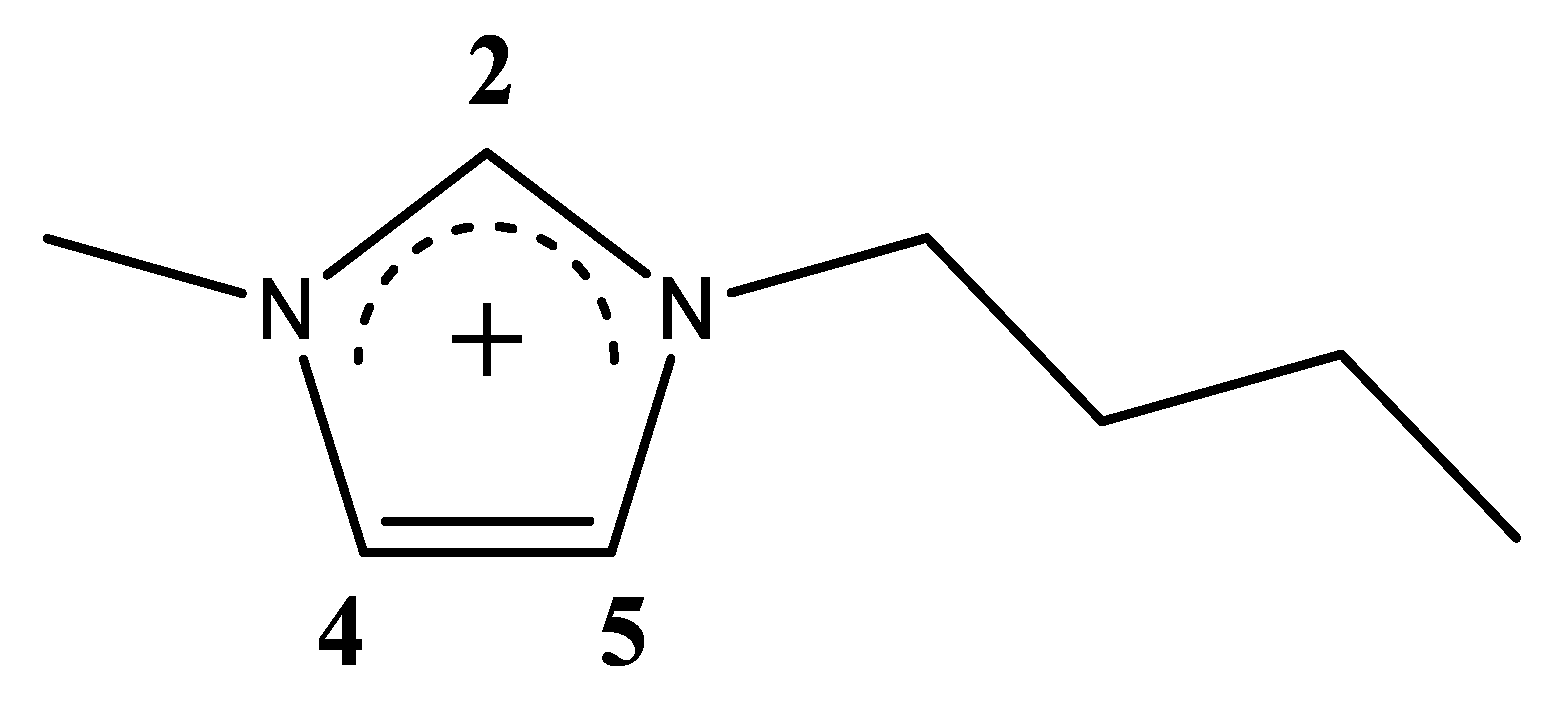


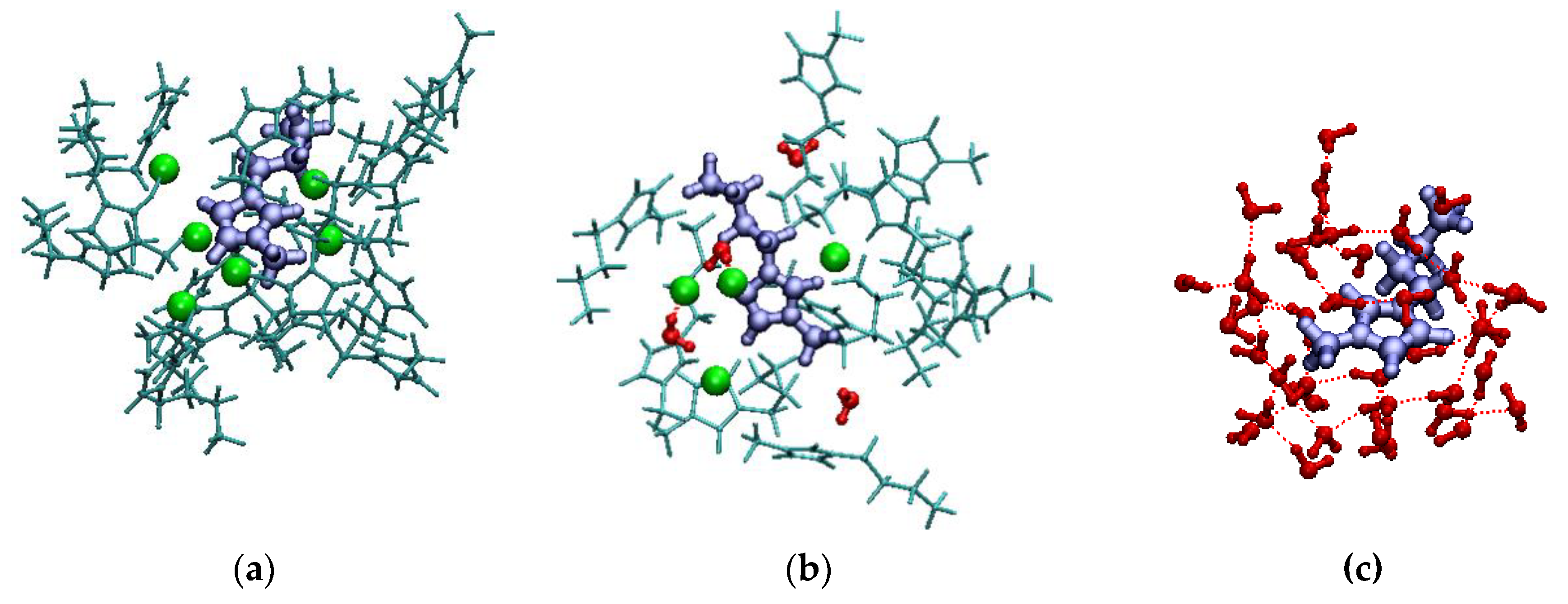
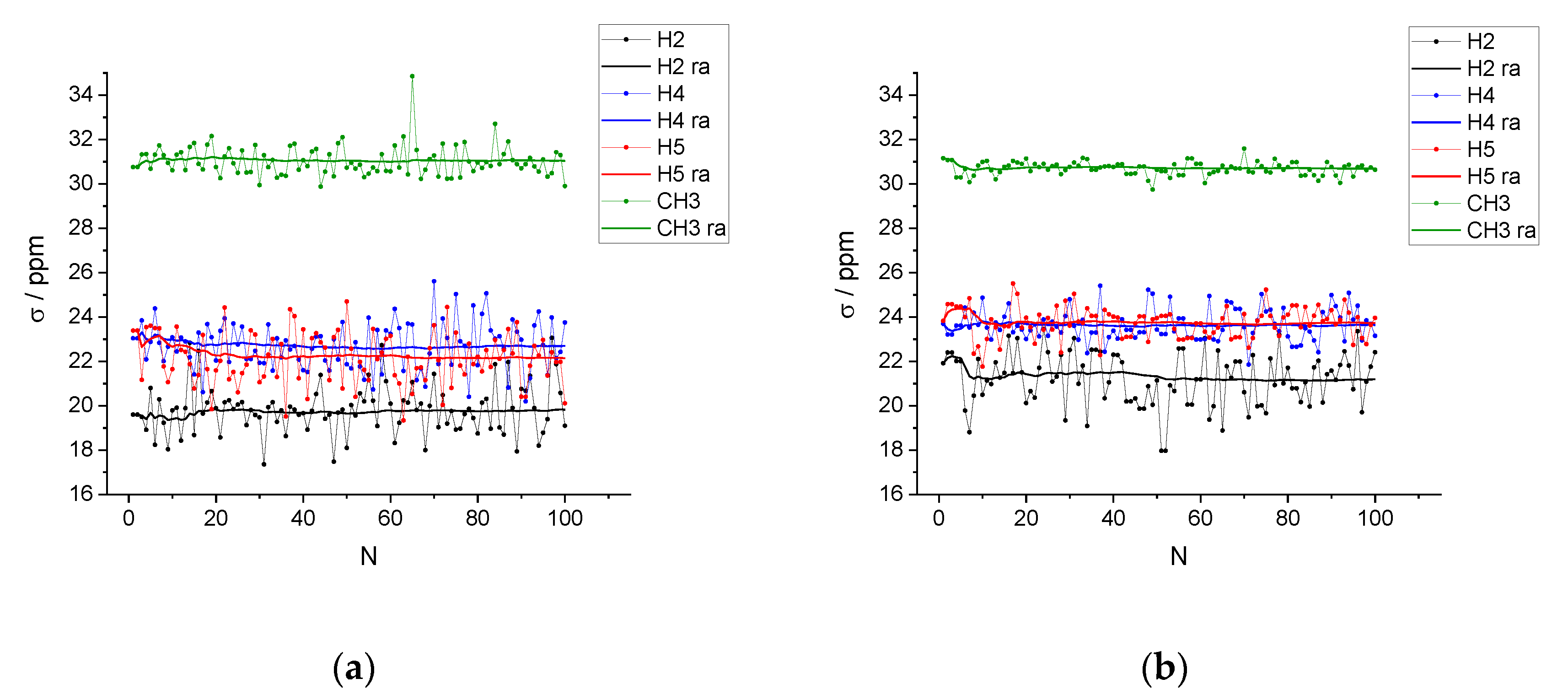
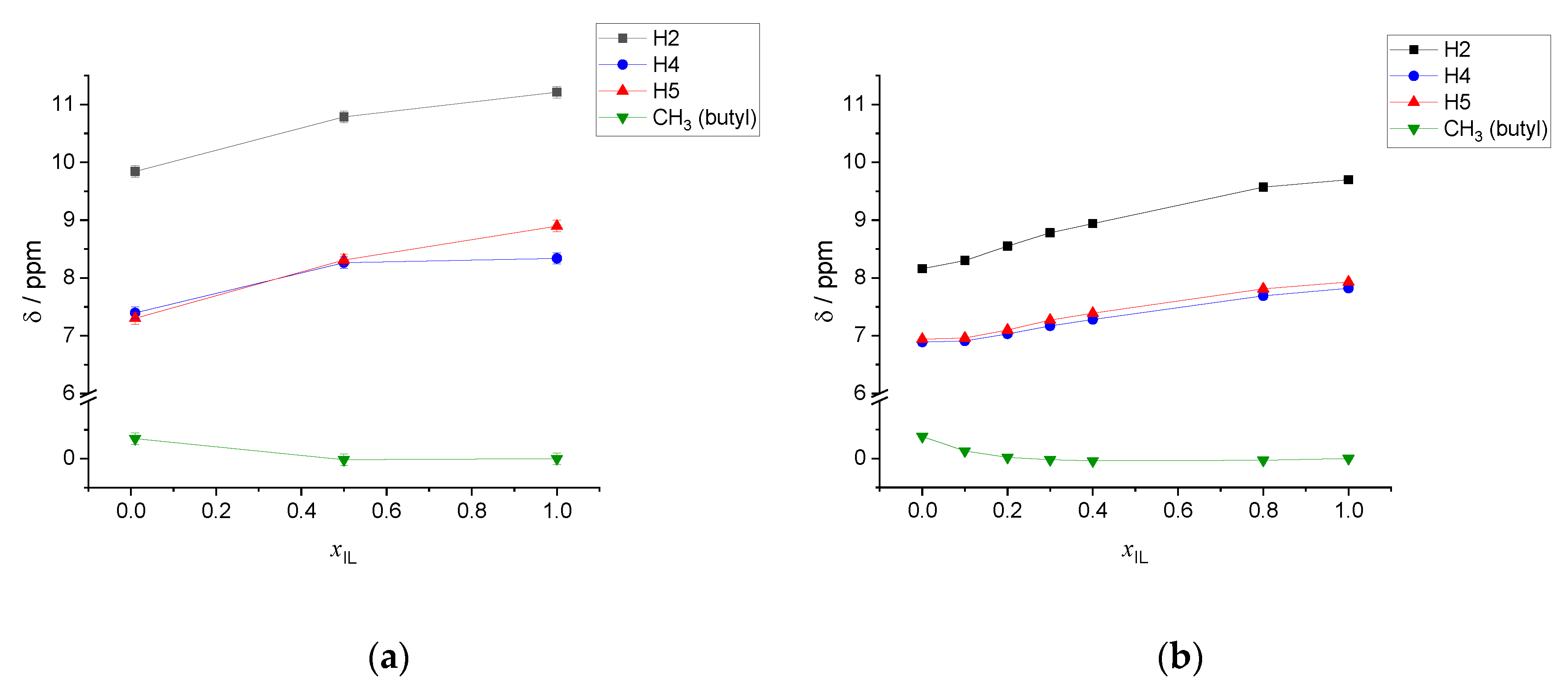

| xIL | <NCAT> | <NAN> | <NW> | <q> |
|---|---|---|---|---|
| 1.00 | 12.9 | 5.1 | 0 | +7.8 |
| 0.50 | 11.9 | 4.9 | 5.6 | +7.0 |
| 0.01 | 1.3 | 0.2 | 38.8 | +1.1 |
| xIL | σ (δ) H2 | σ (δ) H4 | σ (δ) H5 | σ (δ) CH3 Butyl |
|---|---|---|---|---|
| 1.00 | 19.82 (11.21) | 22.70 (8.34) | 22.14 (8.90) | 31.04 (0.00) |
| 0.50 | 20.25 (10.79) | 22.77 (8.26) | 22.72 (8.31) | 31.05 (−0.02) |
| 0.01 | 21.19 (9.84) | 23.64 7.40 | 23.73 (7.30) | 30.69 (0.35) |
| xIL | <d> (g/mL) | <L> (Å) | N Atoms | NIP + NW |
|---|---|---|---|---|
| 1.00 | 1.11 a | 47.04 | 10,025 | 400 + 0 |
| 0.50 | 1.15 b | 38.16 | 5800 | 200 + 200 |
| 0.01 | 1.01 c | 31.96 | 3260 | 10 + 1000 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saielli, G. Computational NMR Spectroscopy of Ionic Liquids: [C4C1im]Cl/Water Mixtures. Molecules 2020, 25, 2085. https://doi.org/10.3390/molecules25092085
Saielli G. Computational NMR Spectroscopy of Ionic Liquids: [C4C1im]Cl/Water Mixtures. Molecules. 2020; 25(9):2085. https://doi.org/10.3390/molecules25092085
Chicago/Turabian StyleSaielli, Giacomo. 2020. "Computational NMR Spectroscopy of Ionic Liquids: [C4C1im]Cl/Water Mixtures" Molecules 25, no. 9: 2085. https://doi.org/10.3390/molecules25092085
APA StyleSaielli, G. (2020). Computational NMR Spectroscopy of Ionic Liquids: [C4C1im]Cl/Water Mixtures. Molecules, 25(9), 2085. https://doi.org/10.3390/molecules25092085






