Choline Hydrogen Dicarboxylate Ionic Liquids by X-ray Scattering, Vibrational Spectroscopy and Molecular Dynamics: H-Fumarate and H-Maleate and Their Conformations
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Details
2.1.1. Synthesis
2.1.2. X-ray Scattering
2.1.3. Infrared and Raman Spectra
2.2. Computational Details
3. Results and Discussion
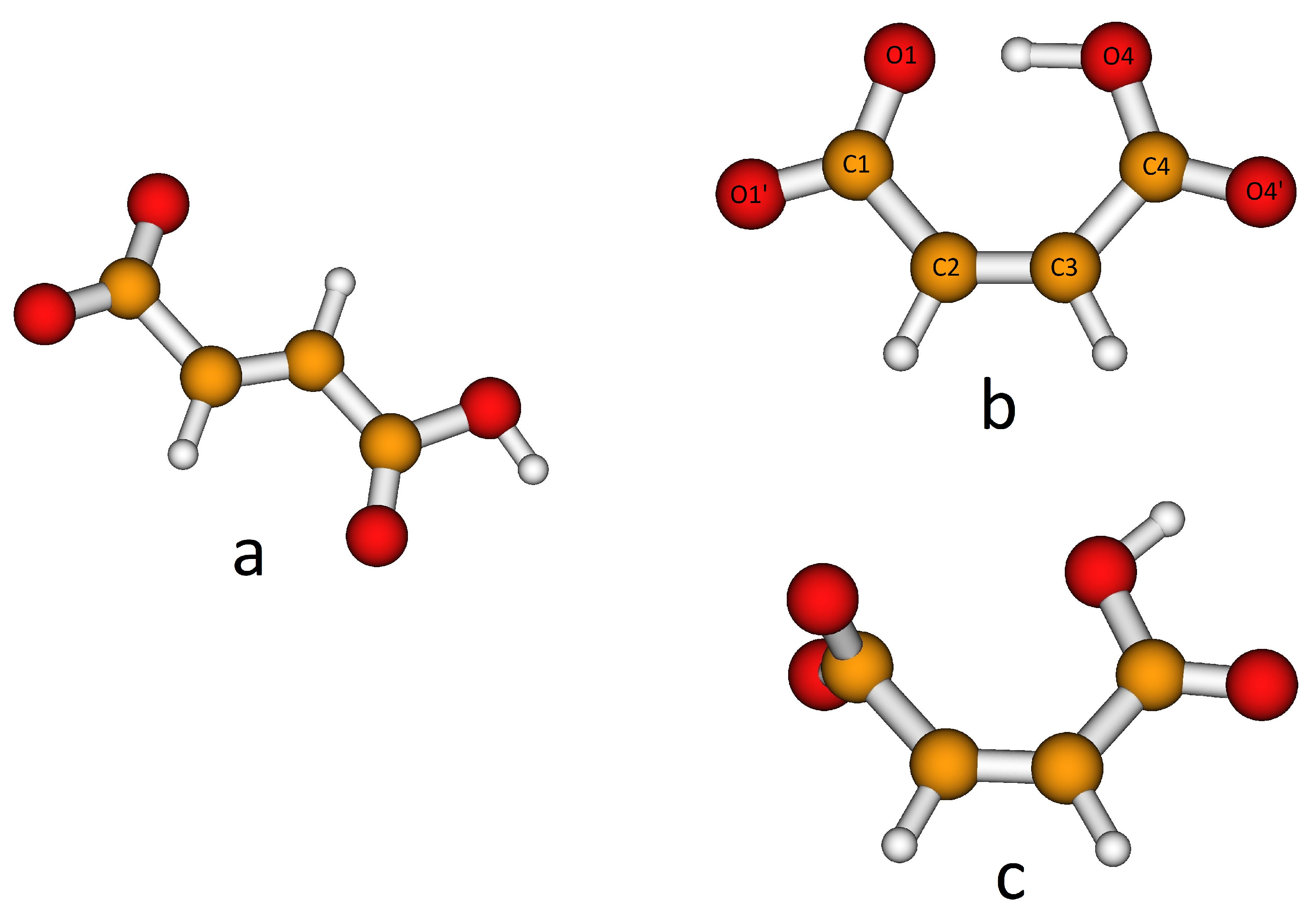
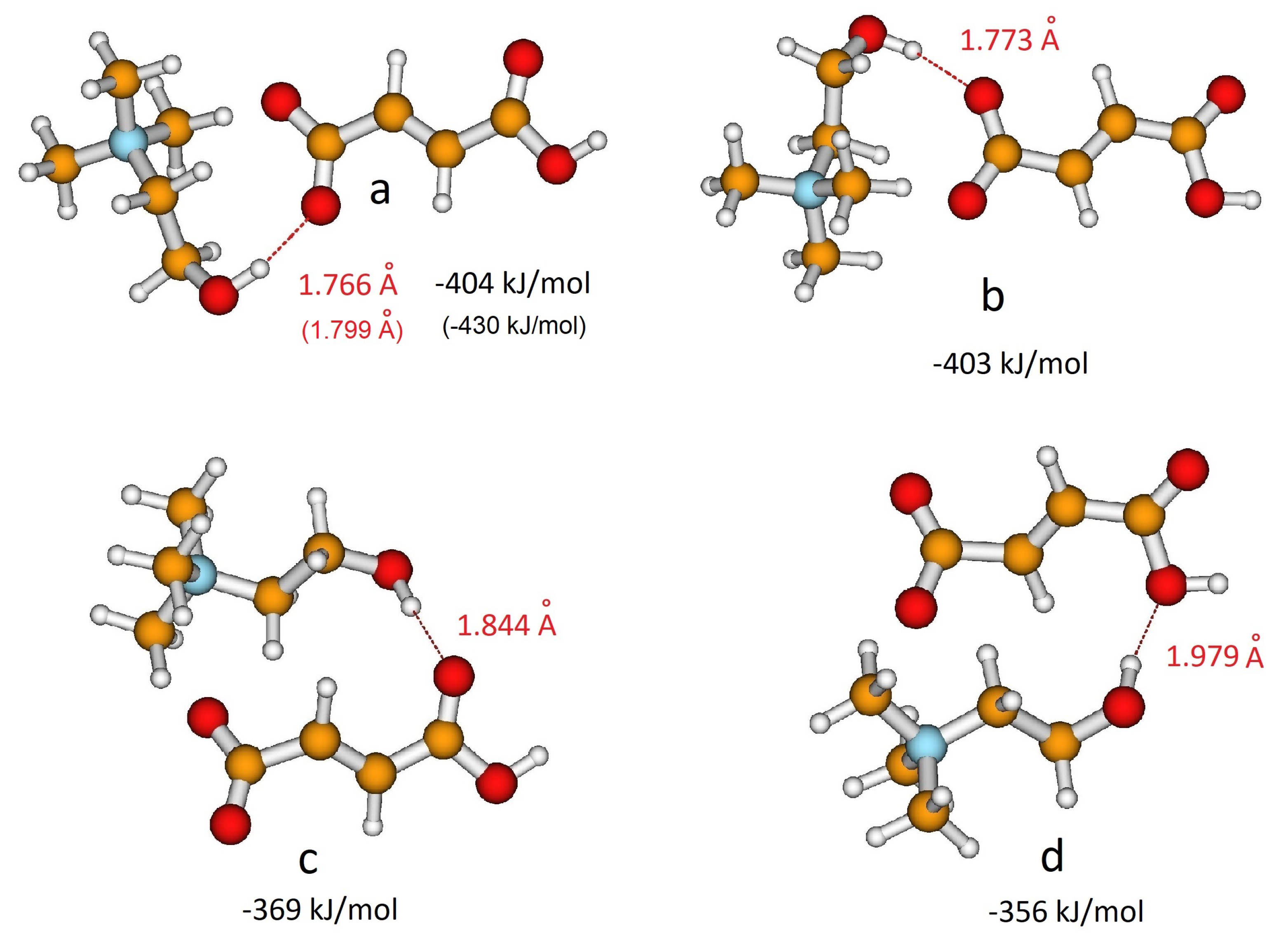
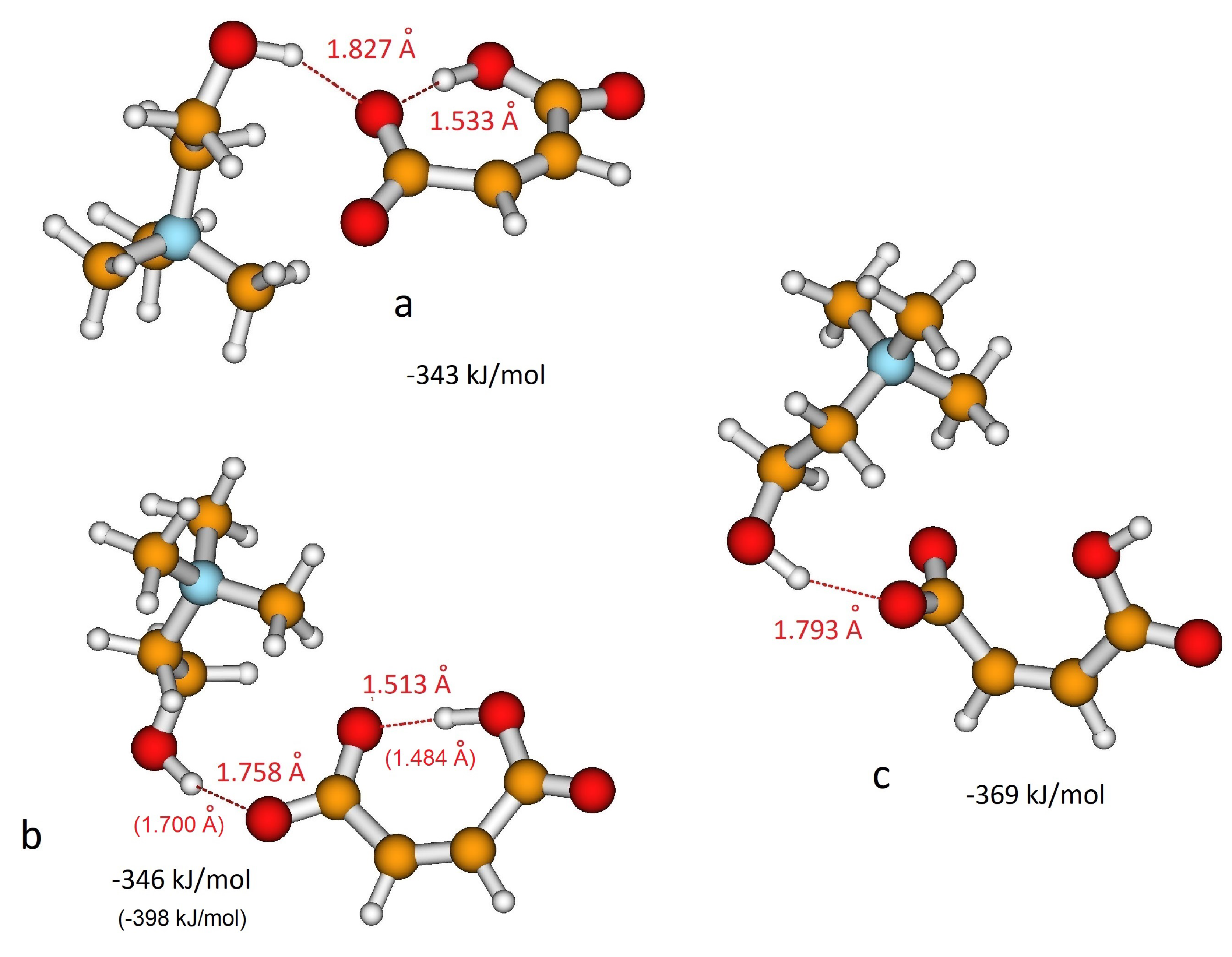
3.1. QM Ion Pair
3.2. AIMD Results
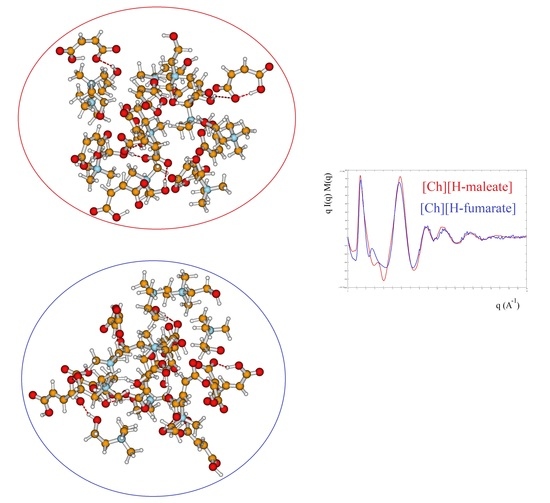
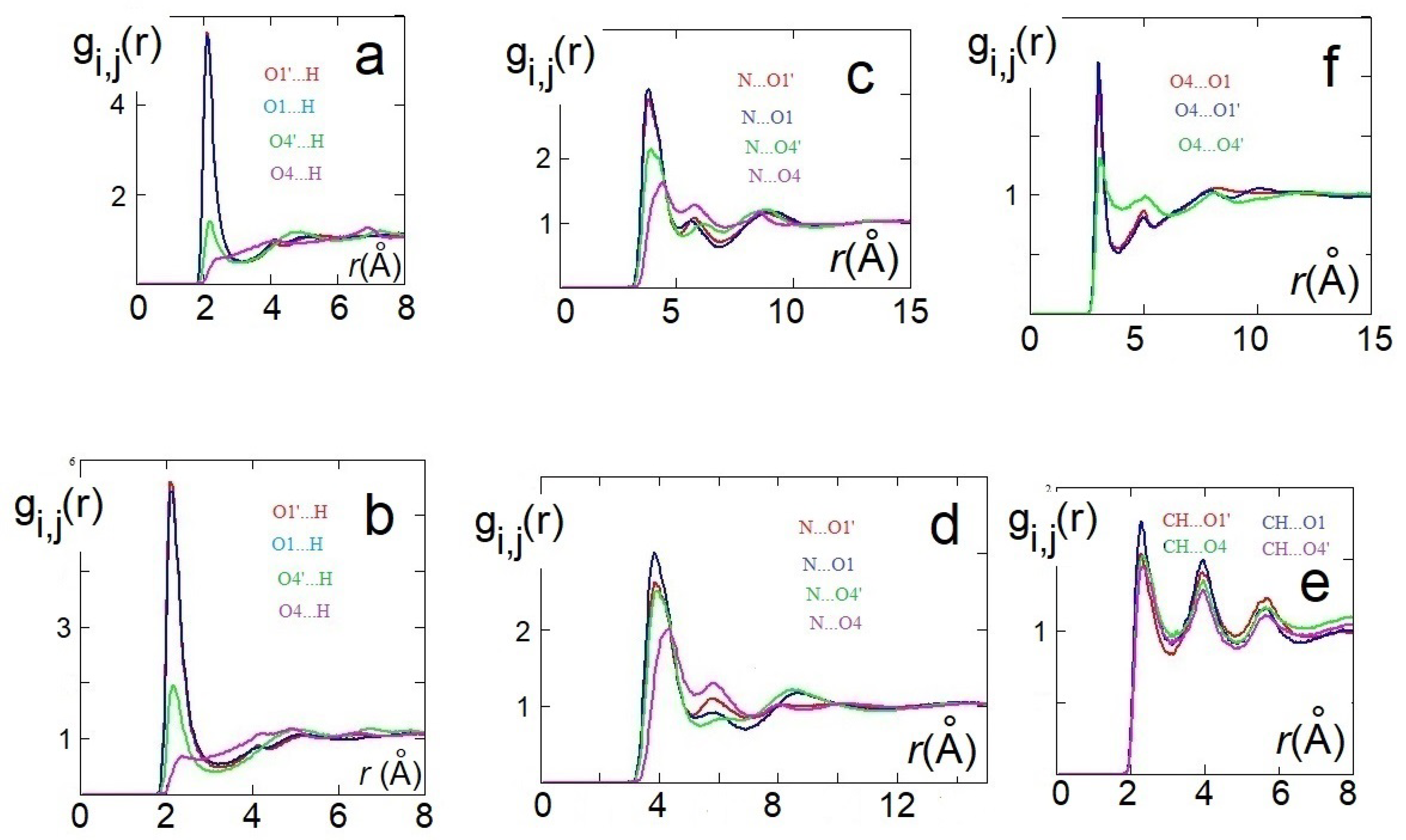
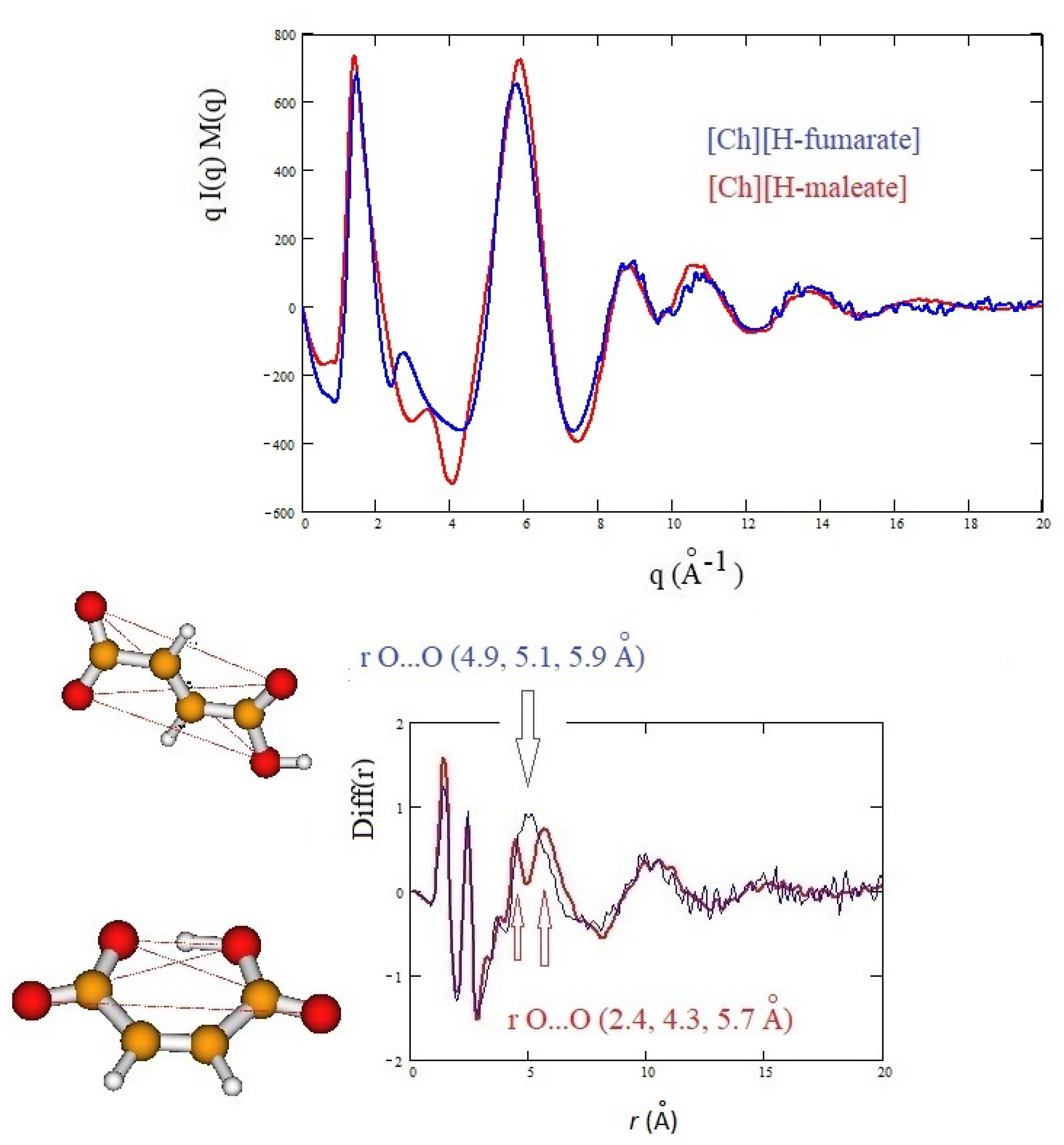
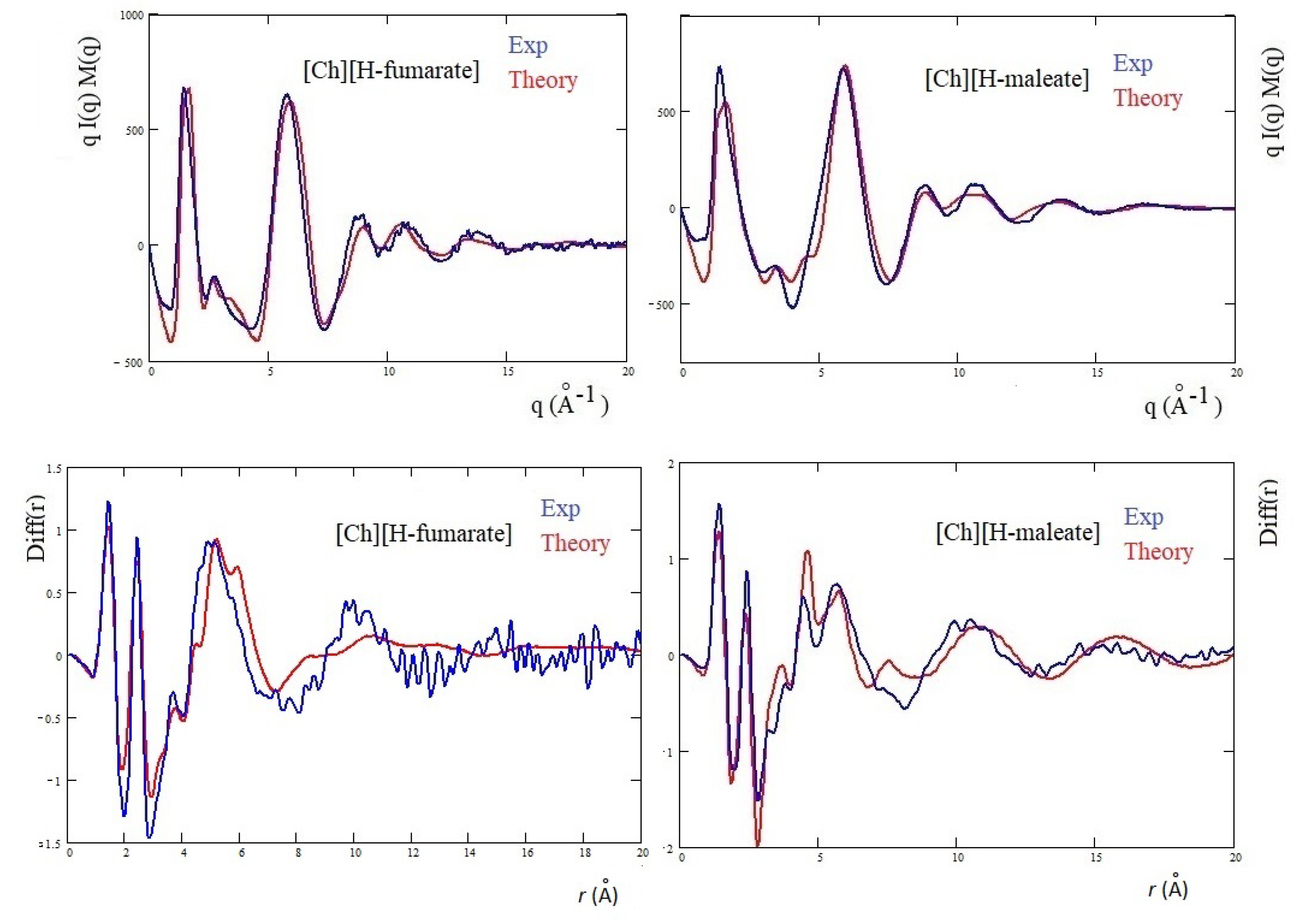
3.3. X-ray Results and MD Simulations
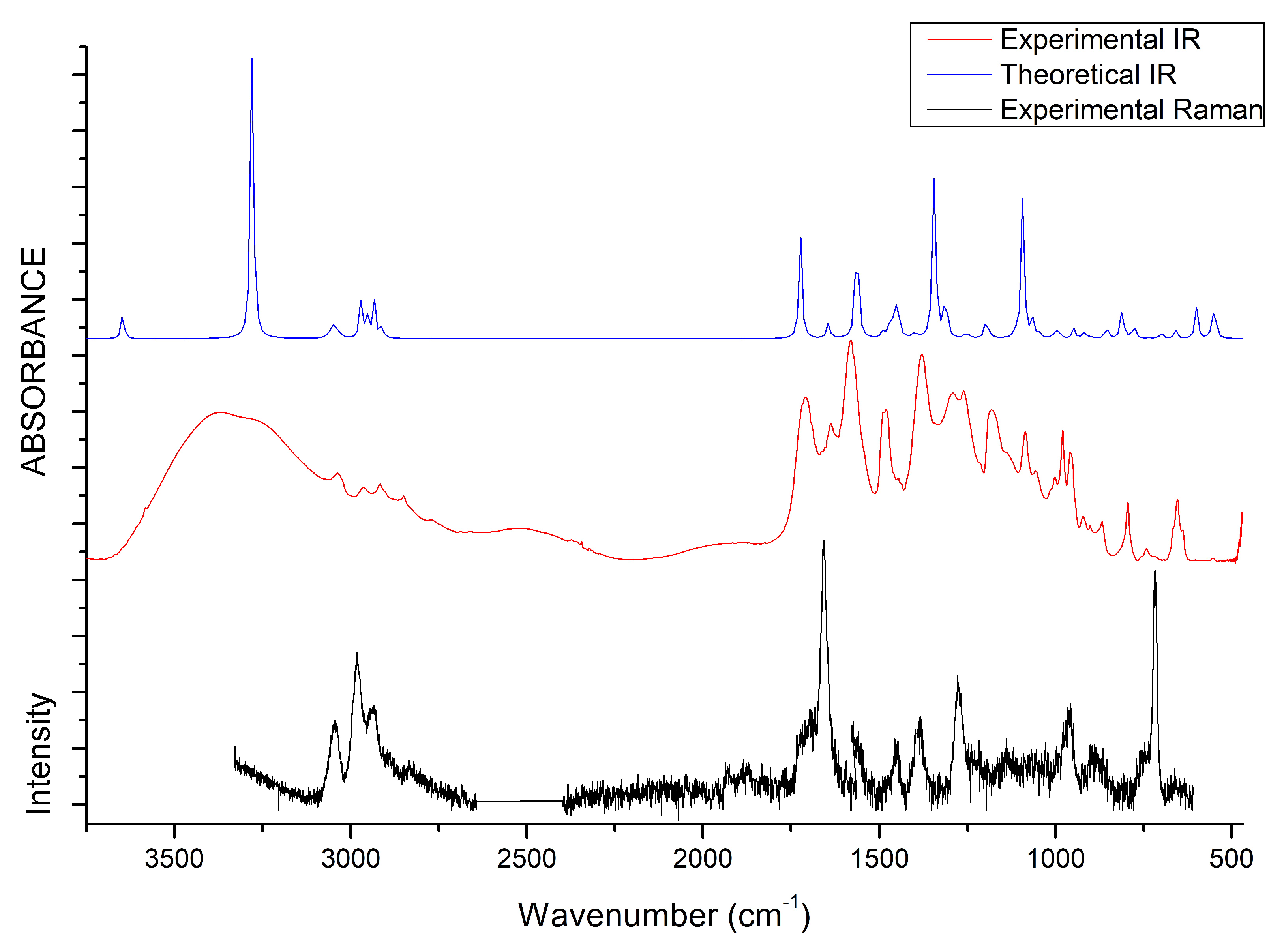
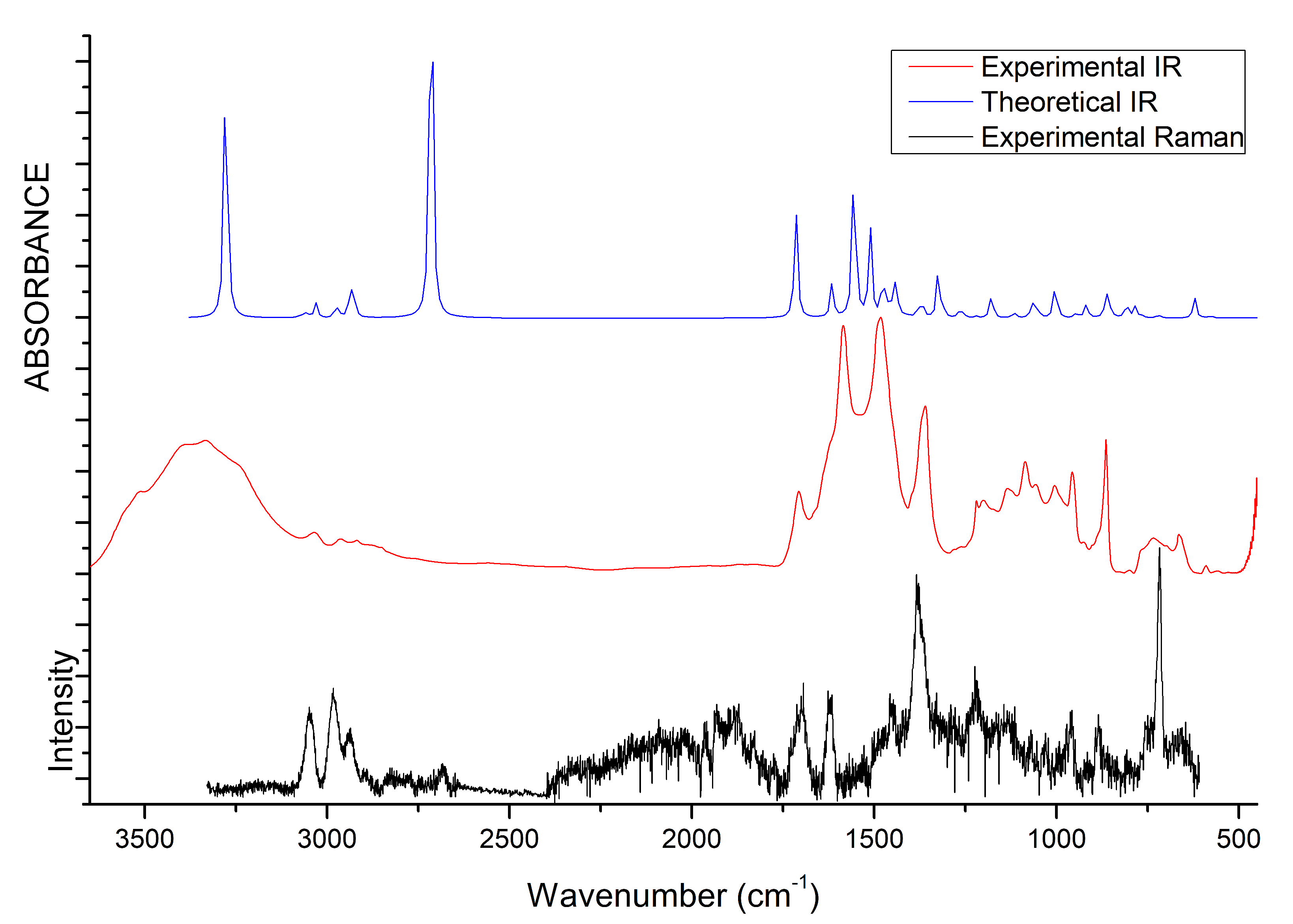
3.4. IR and Raman Spectra
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Graves, T.L.; Drummond, C.J. Protic Ionic Liquids: Properties and Applications. Chem. Rev. 2008, 108, 206–237. [Google Scholar] [CrossRef] [PubMed]
- Wilkes, J.S. A short history of ionic liquids from molten salts to neoteric solvents. Green Chem. 2002, 4, 73–80. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Koo, Y.M. Introduction: Ionic Liquids. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef]
- Angell, C.A.; Ansaria, Y.; Zhaoa, Z. Ionic liquids: Past, present and future. Faraday Discuss. 2012, 154, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Castner, E.W., Jr.; Wishart, J.F. Spotlight on ionic liquids. J. Chem. Phys. 2010, 132, 120901–120909. [Google Scholar] [CrossRef] [PubMed]
- Wasserscheid, P.; Keim, W. Ionic Liquids-New “Solutions” for Transition Metal Catalysis. Angew. Chem. Int. Ed. 2000, 39, 3772–3789. [Google Scholar] [CrossRef]
- Welton, T. Ionic liquids: A brief history. Biophys. Rev. 2018, 10, 691–706. [Google Scholar] [CrossRef]
- Graves, T.L.; Drummond, C.J. Protic Ionic Liquids: Properties and Applications. Chem. Rev. 2015, 115, 11379–11448. [Google Scholar] [CrossRef]
- Gathergood, N.; Scammells, P.J.; Garca, M.T. Biodegradable ionic liquids Part III. The first readily biodegradable ionic liquids. Green Chem. 2006, 8, 156–160. [Google Scholar] [CrossRef]
- Petkovic, M.; Seddon, K.R.; Rebelo, L.P.N.; Pereira, C.S. Ionic liquids: A pathway to environmental acceptability. Chem. Soc. Rev. 2011, 40, 1383–1403. [Google Scholar] [CrossRef] [PubMed]
- Fukaya, Y.; Iizuka, Y.; Sekikawa, K.; Ohno, H. Bio ionic liquids: Room temperature ionic liquids composed wholly of biomaterials. Green Chem. 2007, 9, 1155–1157. [Google Scholar] [CrossRef]
- Fukumoto, K.; Yoshizawa, M.; Ohno, H. Room Temperature ionic Liquids from 20 Natural Amino Acids. J. Am. Chem. Soc. 2005, 127, 2398–2399. [Google Scholar] [CrossRef] [PubMed]
- Fukumoto, K.; Ohno, H. Design and synthesis of hydrophobic and chiral anions from amino acids as precursor for functional ionic liquids. Chem. Comm. 2006, 3081–3083. [Google Scholar] [CrossRef] [PubMed]
- Kagimoto, J.; Fukumoto, K.; Ohno, H. Effect of tetrabutylphosphonium cation on the physico-chemical properties of amino-acid ionic liquids. Chem. Comm. 2006, 2254–2256. [Google Scholar] [CrossRef]
- Liu, Q.P.; Hou, X.D.; Li, N.; Zong, M.H. Ionic liquids from renewable biomaterials: Synthesis, characterization and application in the pretreatment of biomass. Green Chem. 2012, 14, 304–307. [Google Scholar] [CrossRef]
- Hou, X.D.; Liu, Q.P.; Smith, T.J.; Li, N.; Zong, M.H. Evaluation of Toxicity and Biodegradability of Cholinium Amino Acids Ionic Liquids. PLoS ONE 2013, 8, e59145. [Google Scholar] [CrossRef]
- Pernak, J.; Syguda, A.; Mirska, I.; Pernak, A.; Nawrot, J.; Pradzynska, A.; Griffin, S.; Rogers, R.D. Choline-Derivative-Based Ionic Liquids. Chem. Eur. J. 2007, 13, 6817–6827. [Google Scholar] [CrossRef]
- Muhammad, N.; Hossain, M.I.; Man, Z.; El-Harbawi, M.; Bustam, M.A.; Noaman, Y.A.; Alitheen, N.B.M.; Ng, M.K.; Hefter, G.; Yin, C.Y. Synthesis and Physical Properties of Choline Carboxylate Ionic Liquids. J. Chem. Eng. Data 2012, 57, 2191–2196. [Google Scholar] [CrossRef]
- Gadilohar, B.L.; Shankarling, G.S. Choline based ionic liquids and their applications in organic transformation. J. Mol. Liq. 2017, 227, 234–261. [Google Scholar] [CrossRef]
- Tanzi, L.; Benassi, P.; Nardone, M.; Ramondo, F. Choline salicylate ionic liquid by X-ray scattering, vibrational spectroscopy and molecular dynamics. J. Phys. Chem. A 2014, 118, 12229–12240. [Google Scholar] [CrossRef]
- Tanzi, L.; Ramondo, F.; Caminiti, R.; Campetella, M.; Di Luca, A.; Gontrani, L. Structural studies on choline-carboxylate bio-ionic liquids by X-ray scattering and molecular dynamics. J. Chem. Phys. 2015, 143, 114506–114510. [Google Scholar] [CrossRef] [PubMed]
- Tanzi, L.; Nardone, M.; Benassi, P.; Ramondo, F.; Caminiti, R.; Gontrani, L. Choline salicylate ionic liquid by X-ray scattering, vibrational spectroscopy and molecular dynamics. J. Mol. Liq. 2016, 218, 39–49. [Google Scholar] [CrossRef]
- Benedetto, A.; Bodo, E.; Gontrani, L.; Ballone, P.; Caminiti, R. Amino acid anions in organic ionic compounds. An ab initio study of selected ion pairs. J. Phys. Chem. B 2014, 118, 2471–2486. [Google Scholar] [CrossRef] [PubMed]
- Campetella, M.; Bodo, E.; Caminiti, R.; Martino, A.; D’Apuzzo, F.; Lupi, S.; Gontrani, L. Interaction and dynamics of ionic liquids based on choline and amino acid anions. J. Chem. Phys. 2015, 142, 234502–234510. [Google Scholar] [CrossRef]
- Campetella, M.; Le Donne, A.; Daniele, M.; Gontrani, L.; Lupi, S.; Bodo, E.; Leonelli, F. Hydrogen Bonding as a Clustering Agent in Protic Ionic Liquids. Like-charge vs Opposite-charge dimers formation. J. Phys. Chem. B 2018, 122, 2635–2645. [Google Scholar] [CrossRef] [PubMed]
- Gontrani, L. Choline-amino acid ionic liquids: Past and recent achievements about the structure and properties of these really “green” chemicals. Biophys. Rev. 2018, 10, 873–880. [Google Scholar] [CrossRef] [PubMed]
- Perakis, F.; De Marco, L.; Shalit, A.; Tang, F.; Kann, Z.R.; Kühne, T.D.; Torre, R.; Bonn, M.; Nagata, Y. Vibrational Spectroscopy and Dynamics of Water. Chem. Rev. 2016, 116, 7590–7607. [Google Scholar] [CrossRef]
- Ojha, D.; Karhan, K.; Kühne, T.D. On the Hydrogen Bond Strength and Vibrational Spectroscopy of Liquid Water. Sci. Rep. 2018, 8, 16888–16895. [Google Scholar] [CrossRef]
- Woo, H.K.; Wang, X.B.; Wang, L.S.; Lau, K.C. Probing the Low-Barrier Hydrogen Bond in Hydrogen Maleate in the Gas Phase: A Photoelectron Spectroscopy and ab Initio Study. J. Phys. Chem. A 2005, 109, 10633–10636. [Google Scholar] [CrossRef]
- Fillaux, F.; Leygue, N.; Tomkinson, J.; Cousson, A.; Paulus, W. Structure and dynamics of the symmetric hydrogen bond in potassium hydrogen maleate: A neutron scattering study. Chem. Phys. 1999, 244, 387–403. [Google Scholar] [CrossRef]
- Vener, M.V.; Manaev, A.V.; Tsirelson, V.G. Proton Dynamics in Strong (Short) Intramolecular H-Bond. DFT Study of the KH Maleate Crystal. J. Phys. Chem. A 2008, 112, 13628–13632. [Google Scholar] [CrossRef] [PubMed]
- Vener, M.V.; Manaev, A.V.; Hadzi, D.; Tsirelson, V.G. QTAIM Study of Strong H-Bonds with the O-H⋯A Fragment (A=O, N) in Three-Dimensional Periodical Crystals. Z. Phys. Chem. 2008, 222, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
- Carbone, M.; Caminiti, R.; Sadun, C. Structural study by energy dispersive X-ray diffraction of amorphous mixed hydroxycarbonates containing Co, Cu, Zn, Al. J. Mater. Chem. 1996, 6, 1709–1716. [Google Scholar] [CrossRef]
- Caminiti, R.; Carbone, M.; Sadun, C. Palladium (II) and platinum (II) aqueous solutions. Evidence for the solvation of the [PdCl4]2− and [PtCl4]2− ions. J. Mol. Liq. 1998, 75, 149–158. [Google Scholar] [CrossRef]
- Gontrani, L.; Caminiti, R.; Bencivenni, L.; Sadun, C. Molecular aggregation phenomena in solution: An energy dispersive X-ray diffraction study of concentrated imidazole water solutions. Chem. Phys. Lett. 1999, 301, 131–137. [Google Scholar] [CrossRef]
- Gontrani, L.; Ramondo, F.; Caminiti, R. Energy dispersive X-ray diffraction and molecular dynamics meet: The structure of liquid pyrrole. Chem. Phys. Lett. 2006, 417, 200–205. [Google Scholar] [CrossRef]
- Gontrani, L.; Ramondo, F.; Caracciolo, G.; Caminiti, R. A study of cyclohexane, piperidine and morpholine with X-ray diffraction and molecular simulations. J. Mol. Liq. 2008, 139, 23–28. [Google Scholar] [CrossRef]
- Gontrani, L.; Russina, O.; Marincola, F.C.; Caminiti, R. An energy dispersive x-ray scattering and molecular dynamics study of liquid dimethyl carbonate. J. Chem. Phys. 2009, 131, 244503–244509. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Jamroz, M.H. Vibrational Energy Distribution Analysis (VEDA): Scopes and limitations. Spectrochim. Acta Part A 2013, 114, 220–230. [Google Scholar] [CrossRef] [PubMed]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; He, X. Accurate prediction of energetic properties of ionic liquid clusters using a fragment-based quantum mechanical method. Phys. Chem. Chem. Phys. 2017, 19, 20657–20666. [Google Scholar] [CrossRef] [PubMed]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package— Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103–194146. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.; Caldwell, J.; Kollman, P.; Case, D. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Campetella, M.; Macchagodena, M.; Gontrani, L.; Kirchnen, B. Effect of alkyl chain length in protic ionic liquids: An AIMD perspective. Mol. Phys. 2017, 115, 1582–1589. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoen, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Dupradeau, F.Y.; Pigache, A.; Zaffran, T.; Savineau, C.; Lelong, R.; Grivel, N.; Lelong, D.; Rosanski, W.; Cieplak, P. The R.E.D. tools: Advances in RESP and ESP charge derivation and force field library building. Phys. Chem. Chem. Phys. 2010, 12, 7821–7839. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M., Jr.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraajie, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Martinez, L.; Antrade, R.; Birgin, E.G.; Martinez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef]
- Hollòczki, O.; Macchiagodena, M.; Weber, H.; Thomas, M.; Brehm, M.; Stark, A.; Russina, O.; Triolo, A.; Kirchner, B. Triphilic Ionic-Liquid Mixtures: Fluorinated and Non-fluorinated Aprotic Ionic-Liquid Mixtures. ChemPhysChem 2015, 16, 3325–3333. [Google Scholar] [CrossRef]
- Viloca, M.G.; Gonzales-Lafont, A.; Lluch, J.M. Theoretical Study of the Low-Barrier Hydrogen Bond in the Hydrogen Maleate Anion in the Gas Phase. Comparison with Normal Hydrogen Bonds. J. Am. Chem. Soc. 1997, 119, 1081–1086. [Google Scholar] [CrossRef]
- Xi Tian, S.; Li, H.B. A theoretical study of the photodetachment and intramolecular hydrogen-bonding energies of hydrogen maleate anions. J. Phys. Chem. A 2007, 111, 4404–4410. [Google Scholar] [CrossRef] [PubMed]
- Gontrani, L.; Bodo, E.; Triolo, A.; Leonelli, F.; D’Angelo, P.; Migliorati, V.; Caminiti, R. The interpretation of diffraction patterns of Protic Ionic Liquids: A challenging task for classical molecular dynamics simulations. J. Phys. Chem. B 2012, 116, 13024–13032. [Google Scholar] [CrossRef]
- Ramondo, F.; Gontrani, L.; Campetella, M. Coupled hydroxyl and ether functionalisation in EAN derivatives: The effect of hydrogen bond donor/acceptor groups on the structural heterogeneity studied with X-ray diffractions and fixed charge/polarizable simulations. Phys. Chem. Chem. Phys. 2019, 21, 11464–11475. [Google Scholar] [CrossRef]
- Andersson, M.P.; Uvdal, P. New Scale Factors for Harmonic Vibrational Frequencies Using the B3LYP Density Functional Method with the Triple-z Basis Set 6-311+G(d,p). J. Phys. Chem. A 2005, 109, 12, 2937–2941. [Google Scholar] [CrossRef] [PubMed]
- Pohle, W.; Gauger, D.R.; Fritzsche, H.; Rattay, B.; Selle, C.; Binder, H.; Bohlig, H. FTIR-spectroscopic characterization of phosphocholine-headgroup model compounds. J. Mol. Struct. 2001, 563–564, 463–467. [Google Scholar] [CrossRef]

| Experiment | Theory | Assignment | |||
|---|---|---|---|---|---|
| IR | Raman | Frequency | Intensity | Intensity | |
| IR (km/mol) | Raman (Å/amu) | ||||
| 630 | 572 | 78 | 1 | CO | |
| 651 | 620 | 97 | 3 | OCC, OCO | |
| 750 | 716 | 723 | 21 | 9 | OCO, OCO |
| 796 | 803 | 30 | 0 | OCO | |
| 850 | 850 | 837 | 102 | 3 | CO choline |
| 920 | 884 | 42 | 8 | CN choline | |
| 954 | 960 | 980 | 31 | 5 | CN choline |
| 980 | 1026 | 39 | 0 | CH | |
| 1085 | 1101 | 55 | 3 | CO choline | |
| 1189 | 1129 | 441 | 0 | CO | |
| 1251 | 1237 | 64 | 7 | HCC | |
| 1277 | 1288 | 9 | 35 | HCC | |
| 1292 | 1355 | 122 | 4 | HCC, HOC | |
| 1389 | 1384 | 1388 | 335 | 49 | |
| 1453 | 1492 | 59 | 33 | HCH choline | |
| 1485 | 1505, 1498 | 44, 48 | 3, 11 | HCH choline | |
| 1582 | 1580 | 1615 | 407 | 10 | |
| 1637 | 1661 | 1698 | 50 | 332 | C=C |
| 1706 | ≈1700 | 1780 | 317 | 52 | C=O |
| 2930 | 2938 | 3048, 3030 | 36, 115 | 115, 169 | CH choline |
| 2980 | 2983 | 3069 | 114 | 350 | CH choline |
| 3164, 3152, 3148 | 18, 25, 15 | 62, 71, 83 | CH choline | ||
| 3036 | 3050 { | ||||
| 3200, 3180 | 0, 2 | 32, 55 | CH |
| Experiment | Theory | Assignment | |||
|---|---|---|---|---|---|
| IR | Raman | Frequency | Intensity | Intensity | |
| IR (km/mol) | Raman (Å/amu) | ||||
| 594 | 595 | 6 | 1 | OCO, CC | |
| 664 | 641 | 66 | 2 | CC, OCC, OCO | |
| 734 | 716 | 744 | 10 | 14 | CN choline |
| 865 | 850 | 834 | 51 | 0 | CO choline |
| 910 | 893 | 46 | 7 | CN choline | |
| 961 | 960 | 950 | 24 | 1 | CN choline |
| 1001 | 1039 | 70 | 2 | CO | |
| 1050 | 1035 | 24 | 2 | CH | |
| 1085 | 1100 | 49 | 4 | CO choline | |
| 1127 | 1136 | 1154 | 13 | 3 | CH3 choline |
| 1200 | 1216 | 29 | 6 | CH3 choline | |
| 1209 | 1222 | 1218 | 51 | 8 | HCC |
| 1361 | 1382 | 1368 | 153 | 49 | |
| 1482 | 1460 | 1489, 1517 | 85, 49 | 10, 1 | HOC, HCC choline |
| 1588 | 1561 | 293 | 2 | HOC | |
| ≈1580 | 1607 | 563 | 2 | ||
| 1623 | 1669 | 112 | 126 | C=C | |
| 1712 | 1694 | 1772 | 353 | 121 | C=O |
| 2680-2650 | 2804 | 1495 | 46 | OH | |
| 2930 | 2938 | 3033 | 117 | 226 | CH choline |
| 2980 | 2983 | 3070, 3076 | 8, 20 | 132, 170 | CH choline |
| 3160, 3156 | 6, 11 | 52, 100 | CH choline | ||
| 3036 | 3050 { | ||||
| 3175, 3154 | 12, 0 | 155, 50 | CH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Muzio, S.; Ramondo, F.; Gontrani, L.; Ferella, F.; Nardone, M.; Benassi, P. Choline Hydrogen Dicarboxylate Ionic Liquids by X-ray Scattering, Vibrational Spectroscopy and Molecular Dynamics: H-Fumarate and H-Maleate and Their Conformations. Molecules 2020, 25, 4990. https://doi.org/10.3390/molecules25214990
Di Muzio S, Ramondo F, Gontrani L, Ferella F, Nardone M, Benassi P. Choline Hydrogen Dicarboxylate Ionic Liquids by X-ray Scattering, Vibrational Spectroscopy and Molecular Dynamics: H-Fumarate and H-Maleate and Their Conformations. Molecules. 2020; 25(21):4990. https://doi.org/10.3390/molecules25214990
Chicago/Turabian StyleDi Muzio, Simone, Fabio Ramondo, Lorenzo Gontrani, Francesco Ferella, Michele Nardone, and Paola Benassi. 2020. "Choline Hydrogen Dicarboxylate Ionic Liquids by X-ray Scattering, Vibrational Spectroscopy and Molecular Dynamics: H-Fumarate and H-Maleate and Their Conformations" Molecules 25, no. 21: 4990. https://doi.org/10.3390/molecules25214990
APA StyleDi Muzio, S., Ramondo, F., Gontrani, L., Ferella, F., Nardone, M., & Benassi, P. (2020). Choline Hydrogen Dicarboxylate Ionic Liquids by X-ray Scattering, Vibrational Spectroscopy and Molecular Dynamics: H-Fumarate and H-Maleate and Their Conformations. Molecules, 25(21), 4990. https://doi.org/10.3390/molecules25214990