Equilibrium Bond Lengths from Orbital-Free Density Functional Theory
Abstract
1. Introduction
2. Theory
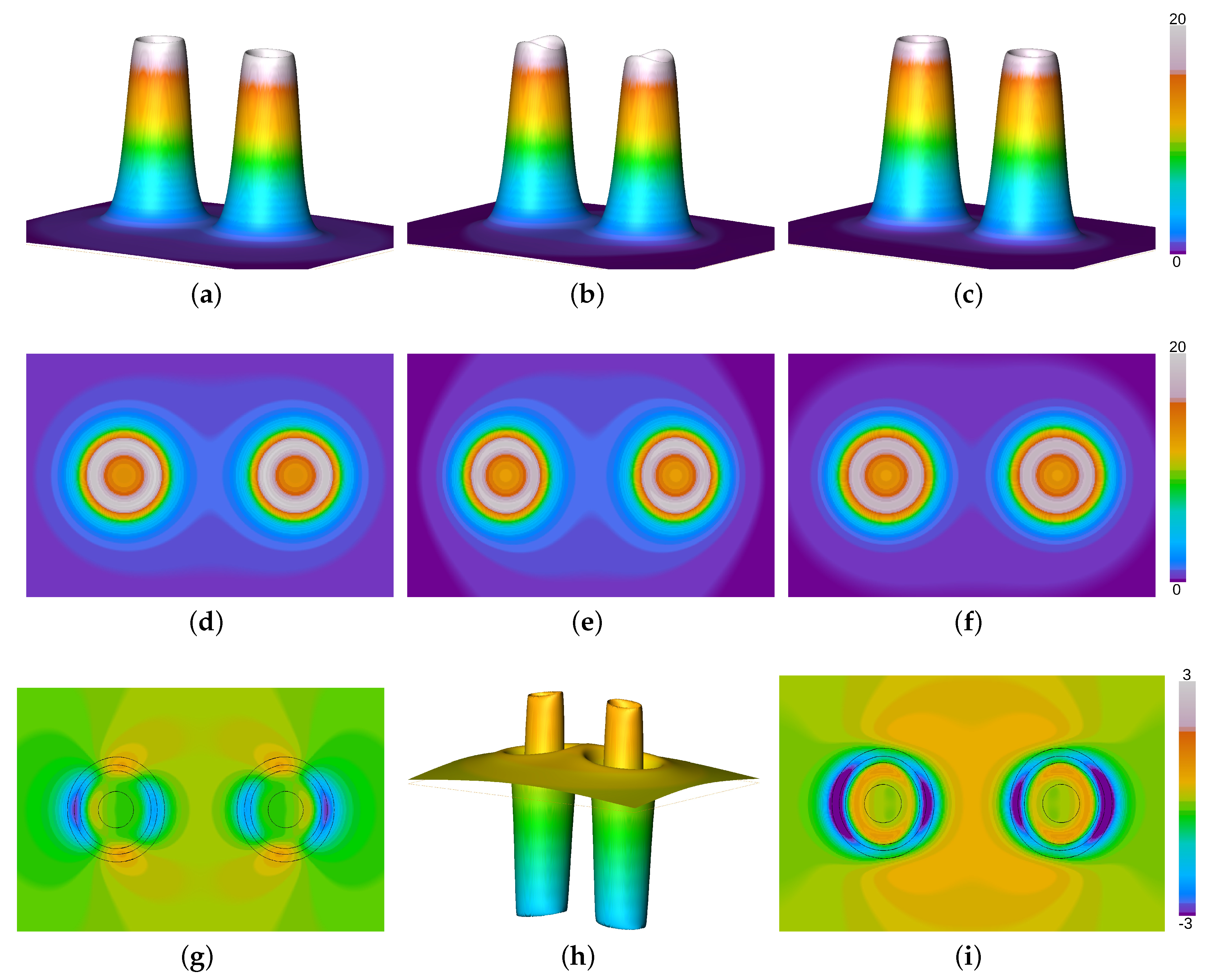
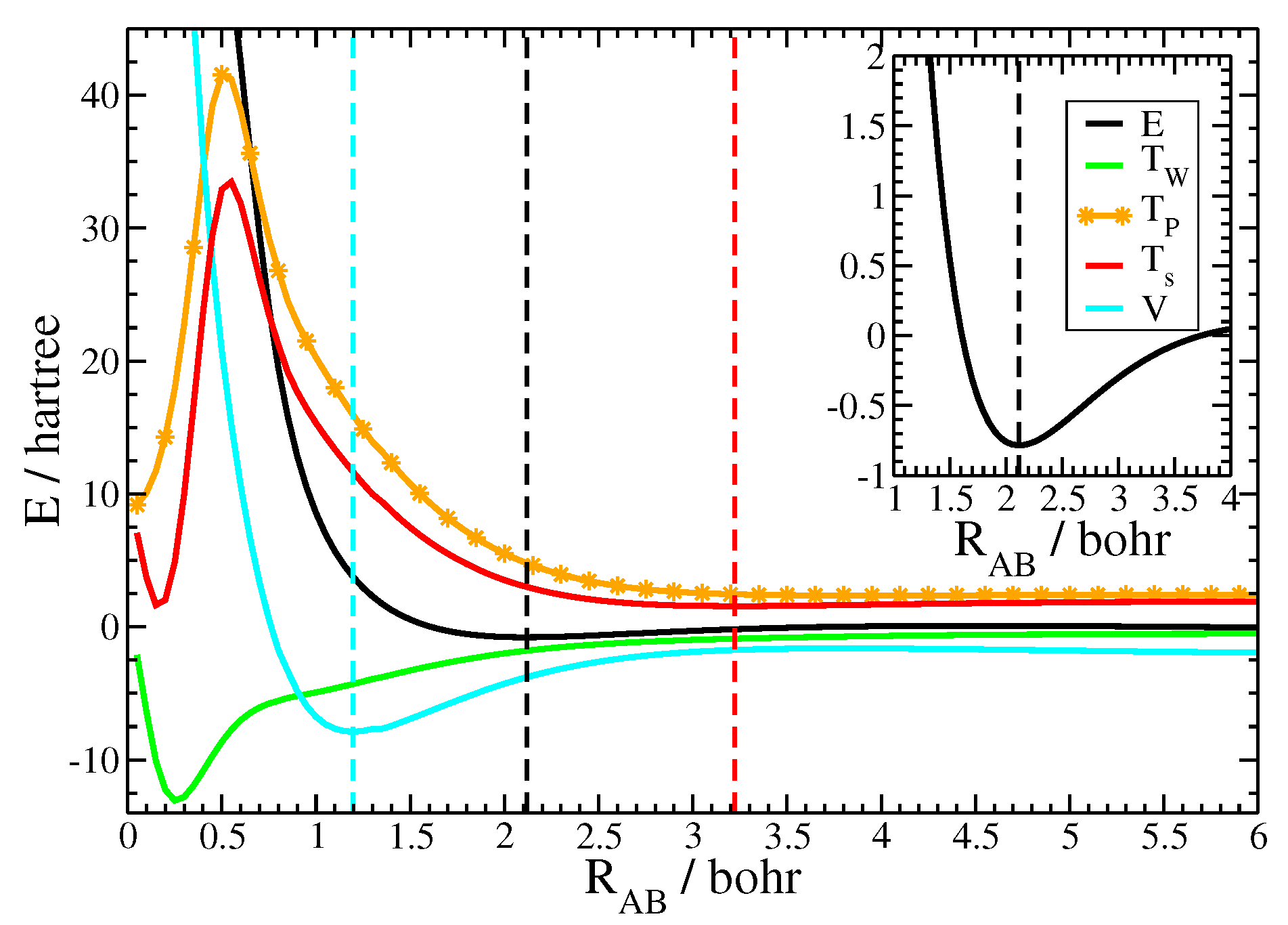
3. Results and Discussion
4. Materials and Methods
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeous Electron Gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Ho, G.S.; Lignères, V.L.; Carter, E.A. Introducing PROFESS: A new program for orbital-free density functional calculations. Comput. Phys. Commun. 2008, 179, 839–854. [Google Scholar] [CrossRef]
- Wang, Y.A.; Wesolowski, T.A. Recent Progress in Orbital-Free Density Functional Theory; World Scientific: Singapore, 2013. [Google Scholar]
- Karasiev, V.; Sjostrom, T.; Trickey, S.B. Finite-temperature orbital-free DFT molecular dynamics: Coupling Profess and Quantum Espresso. Comput. Phys. Commun. 2014, 185, 3240. [Google Scholar] [CrossRef]
- Lehtomäki, J.; Makkonen, I.; Caro, M.A.; Harju, A.; Lopez-Acevedo, O. Orbital-free density functioal theory implementation with the projector augmented-wave method. J. Chem. Phys. 2014, 141, 234102. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Suryanarayana, P. Higher-order finite-difference formulation of Periodic Orbital-free Density Functional Theory. J. Comput. Phys. 2016, 307, 634–652. [Google Scholar] [CrossRef]
- Witt, W.C.; del Rio, B.G.; Dieterich, J.M.; Carter, E.A. Orbital-free density functional theory for materials research. J. Mat. Res. 2018, 33, 777–795. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Karasiev, V.; Trickey, S.B. Frank Discussion of the Status of Ground-state Orbital-free DFT. Adv. Quantum Chem. 2015, 71, 221–245. [Google Scholar]
- Thomas, L.H. The calculation of atomic fields. Proc. Camb. Philos. Soc. 1927, 23, 542–548. [Google Scholar] [CrossRef]
- Fermi, E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Z. Phys. 1928, 48, 73–79. [Google Scholar] [CrossRef]
- Von Weizsäcker, C.F. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431–458. [Google Scholar] [CrossRef]
- Kirzhnits, D.A. Quantum Corrections to the Thomas-Fermi Equation. Sov. Phys. JETP 1957, 5, 64–71. [Google Scholar]
- Hodges, C.H. Quantum Corrections to the Thomas-Fermi Approximation—The Kirzhnits Method. Can. J. Phys. 1973, 51, 1428–1437. [Google Scholar] [CrossRef]
- Murphy, D.R. Sixth-order term of the gradient expansion of the kinetic-energy density functional. Phys. Rev. A 1981, 24, 1682–1688. [Google Scholar] [CrossRef]
- Yang, W. Gradient correction in Thomas-Fermi theory. Phys. Rev. A 1986, 34, 4575–4585. [Google Scholar] [CrossRef]
- Yang, W.; Parr, R.G.; Lee, C. Various functionals for the kinetic energy density of an atom or molecule. Phys. Rev. A 1986, 34, 4586–4590. [Google Scholar] [CrossRef]
- Lee, C.L.; Ghosh, S.K. Density gradient expansion of the kinetic-energy functional for molecules. Phys. Rev. A 1986, 33, 3506–3507. [Google Scholar] [CrossRef]
- Kozlowski, P.M.; Nalewajski, R.F. A Graph Approach to the Gradient Expansion of Density Functionals. Int. J. Quantum Chem. 1986, 30, 219–226. [Google Scholar] [CrossRef]
- Thakkar, A.J. Comparison of kinetic-energy density functionals. Phys. Rev. A 1992, 46, 6920–6924. [Google Scholar] [CrossRef]
- Chai, J.D.; Weeks, J.D. Modified Statistical Treatment of Kinetic Energy in the Thomas-Fermi Model. J. Phys. Chem. B 2004, 108, 6870–6876. [Google Scholar] [CrossRef]
- Dreizler, R.M.; Gross, E.K.U. Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Lee, H.; Lee, C.; Parr, R.G. Conjoint gradient correction to the Hartree-Fock kinetic- and exchange-energy density functionals. Phys. Rev. A 1991, 44, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Wesolowski, T.A. Link between the Kinetic- and Exchange-Energy Functionals in the Generalized Gradient Approximation. Int. J. Quantum Chem. 2002, 89, 441–446. [Google Scholar] [CrossRef]
- Lee, D.; Constantin, L.A.; Perdew, J.P.; Burke, K. Condition on the Kohn-Sham kinetic energy and modern parametrization of the Thomas-Fermi density. J. Chem. Phys. 2009, 130, 034107. [Google Scholar] [CrossRef] [PubMed]
- Karasiev, V.; Chakraborty, D.; Trickey, S.B. Progress on new approaches to old ideas: Orbital-free Density Functionals. In Many-Electron Approaches in Physics, Chemistry and Mathematics; Delle Site, L., Bach, V., Eds.; Springer: Heidelberg, Germany, 2014; pp. 113–134. [Google Scholar]
- Ayers, P.W.; Lucks, J.B.; Parr, R.G. Constructing exact density functionals from the moments of the electron density. Acta Chim. Phys. Debrecina 2002, 34, 223–248. [Google Scholar]
- Wang, Y.A.; Carter, E.A. Orbital-free kinetic-energy density functional theory. In Theoretical Methods in Condensed Phase Chemistry; Schwarz, S.D., Ed.; Kluwer: New York, NY, USA, 2000; pp. 117–184. [Google Scholar]
- Shin, I.; Carter, E.A. Enhanced von Weizsäcker Wang-Govind-Carter kinetic energy density functional for semiconductors. J. Chem. Phys. 2014, 140, 18A531. [Google Scholar] [CrossRef]
- Liu, S.; Parr, R.G. Expansion of density functionals in terms of homogeneous functionals: Justification and nonlocal representation of the kinetic energy, exchange energy and classical Coulomb repulsion energy for atoms. Phys. Rev. A 1997, 55, 1792–1798. [Google Scholar] [CrossRef]
- Salazar, E.X.; Guarderas, P.F.; Ludeña, E.V.; Cornejo, M.H.; Karasiev, V.V. Study of some simple approximations to the non-interacting kinetic energy functional. Int. J. Quantum Chem. 2016, 116, 1313–1321. [Google Scholar] [CrossRef]
- Ludeña, E.V.; Salazar, E.X.; Cornejo, M.H.; Arroyo, D.E.; Karasiev, V.V. The Liu-Parr power series expansion of the Pauli kinetic energy functional with the incorporation of shell-inducing traits: Atoms. Int. J. Quantum Chem. 2018, 118, e25601. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Delle Site, L. Design of kinetic functionals for many body electron systems: Combining analytical theory with Monte Carlo sampling of electronic configurations. Phys. Rev. B 2008, 77, 073104. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Hamilton, I.P.; Delle Site, L. Interacting electrons, spin statistics, and information theory. J. Chem. Phys. 2010, 132, 014106. [Google Scholar] [CrossRef]
- Trickey, S.; Karasiev, V.V.; Vela, A. Positivity constraints and information-theoretical kinetic energy functionals. Phys. Rev. B 2011, 84, 075146. [Google Scholar] [CrossRef]
- March, N.H. The local potential determining the square root of the ground-state electron density of atoms and molecules from the Schrödinger equation. Phys. Lett. A 1986, 113, 476–478. [Google Scholar] [CrossRef]
- Levy, M.; Ou-Yang, H. Exact properties of the Pauli potential for the square root of the electron density and the kinetic energy functional. Phys. Rev. A 1988, 38, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Nagy, A. Analysis of the Pauli potential of atoms and ions. Acta Phys. Hung. 1991, 70, 321–331. [Google Scholar]
- Nagy, A.; March, N.H. The exact form of the Pauli potential for the ground state of two- and three-level atoms and Ions. Int. J. Quantum Chem. 1991, 39, 615–623. [Google Scholar] [CrossRef]
- Nagy, A.; March, N.H. Relation between the Pauli potential and the Pauli energy density in an inhomogeneous electron liquid. Phys. Chem. Liq. 1992, 25, 37–42. [Google Scholar] [CrossRef]
- Holas, A.; March, N.H. Exact theorems concerning non-interacting kinetic energy density functional in D dimensions and their implications for gradient expansions. Int. J. Quantum Chem. 1995, 56, 371–383. [Google Scholar] [CrossRef]
- Amovilli, C.; March, N.H. Kinetic energy density in terms of electron density for closed-shell atoms in a bare Coulomb field. Int. J. Quantum Chem. 1998, 66, 281–283. [Google Scholar] [CrossRef]
- Nagy, A. Alternative descriptors of Coulomb systems and their relationship to the kinetic energy. Chem. Phys. Lett. 2008, 460, 343–346. [Google Scholar] [CrossRef][Green Version]
- Nagy, A. The Pauli potential from the differential virial theorem. Int. J. Quantum Chem. 2010, 110, 2117–2120. [Google Scholar] [CrossRef]
- Nagy, A. Functional derivative of the kinetic energy functional for spherically symmetric systems. J. Chem. Phys. 2011, 135, 044106. [Google Scholar] [CrossRef] [PubMed]
- Kraisler, E.; Schild, A. Discontinous behavior of the Pauli potential in density functional theory as a function of the electron number. Phys. Rev. Res. 2020, 2, 013159. [Google Scholar] [CrossRef]
- Finzel, K.; Baranov, A.I. A simple model for the Slater exchange potential and its performance for solids. Int. J. Quantum Chem. 2016, 117, 40–47. [Google Scholar] [CrossRef]
- Finzel, K. Chemical bonding without orbitals. Comput. Theor. Chem. 2018, 1144, 50–55. [Google Scholar] [CrossRef]
- Finzel, K. A fragment-based approximation of the Pauli kinetic energy. Theor. Chem. Acc. 2018, 137, 182. [Google Scholar] [CrossRef]
- Finzel, K.; Kohout, M. A study of the basis set dependence of the bifunctional expression of the non-interacting kinetic energy for atomic systems. Comput. Theor. Chem. 2019, 1155, 56–60. [Google Scholar] [CrossRef]
- Finzel, K. The first order atomic fragment approach—An orbital-free implementation of density functional theory. J. Chem. Phys. 2019, 151, 024109. [Google Scholar] [CrossRef]
- Levy, M.; Perdew, J.P. Hellmann-Feynman, virial, and scaling requisites for the exact universal density functionals. Shape of the correlation potential and diamagnetic susceptibility for atoms. Phys. Rev. A 1985, 32, 2010–2021. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Jones, R.S.; Trickey, S.B.; Harris, F.E. Properties of constraint-based single-point approximate kinetic energy functionals. Phys. Rev. B 2009, 80, 245120. [Google Scholar] [CrossRef]
- ADF2017 01; SCM, Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, 2017; Available online: http://www.scm.com (accessed on 9 April 2020).
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules; Van Nostrand: Princenton, NJ, USA, 1979. [Google Scholar]
- Røeggen, I.; Veseth, L. Interatomic potential for the Ξ1 state of Be2, revisited. Int. J. Quantum Chem. 2005, 101, 201–210. [Google Scholar] [CrossRef]
- Ruedenberg, K. The physical nature of the chemical bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
- Finzel, K. Local conditions for the Pauli potential in order to yield self-consistent electron densities exhibiting proper atomic shell structure. J. Chem. Phys. 2016, 144, 034108. [Google Scholar] [CrossRef] [PubMed]
- Finzel, K. About the atomic shell structure in real space and the Pauli exclusion principle. Theor. Chem. Acc. 2016, 135, 148. [Google Scholar] [CrossRef]
- Finzel, K. Reinvestigation of the ideal atomic shell structure and its application in orbital-free density functional theory. Theor. Chem. Acc. 2016, 135, 87. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Einführung in die Theoretische Chemie; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2002. [Google Scholar]
- Francisco, E.; Martín Pendás, A.; Blanco, M.A.; Francisco, E. Chemical fragments in real space: Definitions, properties and energetic decompositions. J. Comput. Chem. 2007, 28, 161–184. [Google Scholar]
- Kohout, M.; Savin, A. Atomic Shell Structure and Electron Numbers. Int. J. Quantum Chem. 1996, 60, 875–882. [Google Scholar] [CrossRef]
- Zener, C. Analytic atomic wave functions. Phys. Rev. 1930, 36, 51–56. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic shielding constants. Phys. Rev. 1930, 36, 57–64. [Google Scholar] [CrossRef]
| OF-DFT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Recent Work | |||||||||||
| Exp. [55,56] | KS | 0th [48] | 1th [51] | gs PP | cs PP | ||||||
| N | 2.07 | 2.09 | 0.8 | 2.9 | 39.8 | 2.30 | 10.9 | 2.26 | 8.7 | 2.12 | 2.1 |
| O | 2.28 | 2.31 | 1.0 | 2.6 | 13.9 | 1.85 | −18.9 | 1.84 | −19.1 | 1.83 | −19.6 |
| CO | 2.13 | 2.15 | 0.9 | 3.0 | 40.7 | 2.20 | 3.2 | 2.14 | 0.4 | 2.09 | −2.0 |
| Be | 4.63 | 4.69 | 1.2 | 4.4 | −5.0 | 4.15 | −10.4 | 4.14 | −10.7 | 4.14 | −10.7 |
| B | 3.00 | 3.08 | 2.6 | – | – | – | – | 3.16 | 5.3 | 3.01 | 0.0 |
| C | 2.35 | 2.66 | 13.1 | – | – | – | – | 2.64 | 12.4 | 2.49 | 6.2 |
| NO | 2.17 | 2.19 | 0.7 | – | – | – | – | 2.02 | −7.0 | 1.96 | −9.9 |
| CN | 2.21 | 2.23 | 0.5 | – | – | – | – | 2.42 | 9.3 | 2.28 | 3.1 |
| BeO | 2.52 | 2.54 | 1.2 | – | – | – | – | 2.53 | 0.6 | 2.52 | 0.3 |
| MAPE | 2.4 | 24.9 | 10.8 | 8.2 | 6.0 | ||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finzel, K. Equilibrium Bond Lengths from Orbital-Free Density Functional Theory. Molecules 2020, 25, 1771. https://doi.org/10.3390/molecules25081771
Finzel K. Equilibrium Bond Lengths from Orbital-Free Density Functional Theory. Molecules. 2020; 25(8):1771. https://doi.org/10.3390/molecules25081771
Chicago/Turabian StyleFinzel, Kati. 2020. "Equilibrium Bond Lengths from Orbital-Free Density Functional Theory" Molecules 25, no. 8: 1771. https://doi.org/10.3390/molecules25081771
APA StyleFinzel, K. (2020). Equilibrium Bond Lengths from Orbital-Free Density Functional Theory. Molecules, 25(8), 1771. https://doi.org/10.3390/molecules25081771






