Abstract
A computational study of the iodide discrimination by different neutral and cationic iodotriazole halogen bonding hosts was carried out by means of Density Functional Theory. The importance of the size of the scaffold was highlighted and its impact observed in the binding energies and intermolecular X⋯I distances. Larger scaffolds were found to reduce the electronic repulsion and increase the overlap between the halide electron lone pair and the corresponding I-C antibonding orbital, increasing the halogen bonding interactions. Additionally, the planarity plays an important role within the interaction, and can be tuned using hydroxyl to perform intramolecular hydrogen bonds (IMHB) between the scaffold and the halogen atoms. Structures with IMHB exhibit stronger halogen bond interactions, as evidenced by the shorter intramolecular distances, larger electron density values at the bond critical point and more negative binding energies.
1. Introduction
Interest in anion recognition and anion transporters, particularly in supramolecular chemistry, has increased in the last two decades. [1,2,3,4,5] Different varieties of anions play a fundamental role in chemical, biological, medical, industrial, and environmental processes. However, the field concerning anion transporters has suffered from a slower development in comparison to the cation analogous field. This is mainly because of the intrinsic properties of anions, presenting poorly defined coordination preferences in contrast with the parallel coordination found for cations. In order to address this anion-binding conundrum, halogen bonding (XB) has emerged as an attractive noncovalent interaction with tuneable features which make it a promising approach by which to enhance anion transportation. Commonly, there is a wide range of available noncovalent interactions which can be used within the ion transport field to trap or stabilise anion-host complexes such as hydrogen bonds [6] or chalcogen bonds [7], anion-π etc. Hydrogen bonding interactions are, traditionally, the most prevalent noncovalent interaction found in anion recognition, but some works point to the use of a scaffold with chalcogen atoms (S) as potential anion transporters through tuneable chalcogen interactions between halides and sulphur [7,8]. On the other hand, halogen bonds, which are often described as analogous to hydrogen bonds, present comparable binding strength and similar directionality (at least 175° in the gas phase). Scheiner reported theoretical anion transporter scaffolds establishing not only chalcogen bonds, but also tetrel, pnicogen and halogen bonds [2,3,4].
A halogen-based scaffold capacity to behave as a good anion transporter is also highlighted in the literature, not only from an experimental perspective, but also based upon a theoretical approach [9,10,11,12]. Those scaffolds establish halogen bonds with the anions due to the existence of a σ-hole on the halogen atom, described by Politzer et al. [13,14,15]. This well-known “σ-hole” accounts for the electron-deficient outer lobe of a p orbital involved in forming a covalent bond. It is also well-established that the strength of noncovalent interactions, particularly halogen bonds, can be tuned by a) varying the nature of the halogen donor atom (Cl, Br, I), and b) with the electron-withdrawing capacity of the atoms/group covalently bonded to the halogen atom. Halogen atoms down a group, which are more polarizable and less electronegative, are more likely to present deeper σ-holes and therefore facilitate the formation of halogen bonds with anions. Among the halogens, only the heavier elements (Br and I) present the most effective σ-hole.
Halogen-bonding host molecules for anion recognition contain XB-donor motifs, which present a heavy halogen donor atom covalently bonded to a highly electron-deficient group. These factors account for the dominance of aromatic XB-donor groups substituted on aromatic motifs for anion binding over aliphatic scaffolds, as the latter is often susceptible to nucleophilic substitution in the presence of anions. Two of the most common neutral and cationic XB motifs that fulfil these criteria in general are collected in Figure 1.
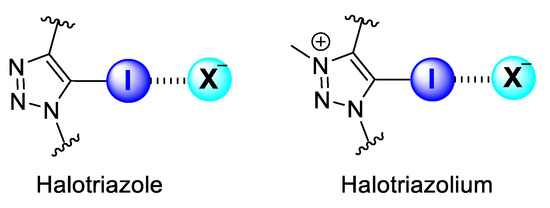
Figure 1.
Common neutral (halotriazole) and cationic (halotriazolium) XB motifs for anion binding.
Herein, in this work, neutral and cationic XB-donor motifs are studied considering the receptor design features required for optimizing XB-anion binding strength. The anion recognition properties of XB-anion receptors of varying structural complexities are discussed, and optimization of XB-anion binding geometries is highlighted. It is worth noting that experimental work on those anion transporters has been carried out in different solvent environments. It is well-known that gas-phase calculations can be greatly affected by the inclusion of the solvent. Noncovalent interactions such as chalcogen or halogen bonds, particularly in charged systems where the charges are shielded by the solvent, can be very affected or compete with other interactions due to the presence of a solvent [9], even when using raw or very approximative models [7,8]. For this reason, all the structures were obtained under solvent conditions mimicking the experimental conditions reported.
2. Results
In order to explore a wide range of XB donor motifs, two scaffolds were considered: firstly bis-iodotriazole carbazole-based XB donor motif (Figure 2), and secondly bis-iodotriazole pyridinium-based XB donor motif (Figure 5). In both cases, the neutral and cationic XB-donor groups, halotriazole and halotriazolium respectively, were taken into account.
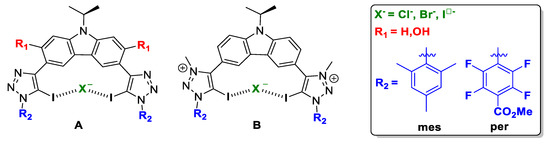
Figure 2.
Schematic representation of the compound subject to study: (A) neutral XB donor motif and (B) cationic XB donor motif.
2.1. Bis-Iodotriazole Carbazole-Based XB Donor Motif
It has been experimentally shown by Schubert et al. [12] that bidentated carbazole-based XB donor scaffolds present the ideal space and angle to act as a host for anions. They found that forbidding the flexibility of the XB donor part (halotriazole in that particular case) by an intramolecular hydrogen bond increases the halogen-bonding interaction between the host molecule and the different halogen anions.
Herein, a thorough computational study has been performed in order to rationalise the experimental outcome, and to enable the prediction and better design of the XB donor motif increasing the halogen-bonding interaction involved, and therefore, enhancing the anion transporter ability. Two scaffolds have been proposed, A and B (Figure 2). For host molecule A, we different possibilities have been studied, named A_R1_R2:X, where R1 can be H or OH. These groups will account for the flexibility/rigidity of the scaffold respectively due to the absence or presence of an intramolecular hydrogen bond; R2 substituents were selected in terms of the electrodonating (mes), or electrowithdrawing (per) capacity; and finally, X stands for the halogen anion to be trapped, i.e., Cl-, Br- and I-. For host molecule B, no R1 groups but H were studied due to methyl groups on the pyridinium motif which prevents intramolecular hydrogen-bonding interactions. Therefore the nomenclature followed was: B_H_R2:X.
2.1.1. MEPs Monomers
We began by calculating the molecular electrostatic potential (MEP) surfaces for the four neutral different monomers (A) to analyse the areas susceptible of halogen-bonding. The maxima of the MEP on the 0.001 a.u. electron density isosurface are plotted in Figure 3 (and Figure S1) and summarised in Table 1.
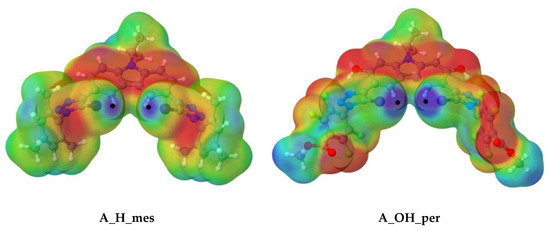
Figure 3.
Molecular electrostatic potential on the 0.001 a.u electron density isosurface for A_H_mes and A_OH_per scaffolds at the m062x/aug–cc–pVDZ computational level. Colour scheme range: Red (−0.015 a.u.) to Blue (+0.05 a.u.).

Table 1.
Maxima (Vmax,I) values of the molecular electrostatic potential (in a.u.) on the 0.001 a.u. electron density isosurface for all the monomers (A) calculated at m062x/aug–cc–pVDZ level. Due to the lack of symmetry slight variations are found the two different iodine atoms (1 and 2).
Two MEP maxima values (black dots) were found for the halogen atoms, (Vmax,I), corresponding to a σ-hole on the C-I bond axis.
As observed, the depth of Vmax,I increases with the electro-withdrawing substituent (from mes to per), as well as with the rigidity of structure, in which an intermolecular hydrogen bond is presented (H to OH). Therefore, the deepest σ-hole of the four (0.705 au) was found for A_OH_per, so, in principle, one would expect that the interaction between A_OH_per and the corresponding anion would be the strongest.
2.1.2. Structural Analysis
We began by performing a conformational analysis for two monomers, A_H_mes and A_OH_per, studying the corresponding stability and barriers between the two different conformations, cis and trans (Figure S2 and Table S2). In both cases, the cis conformer is more stable than the trans one. When the scaffold does not exhibit an intramolecular hydrogen bond, A_H_mes, the difference between both conformers is only 1 kJ/mol, while when the intramolecular HB takes place, A_OH_per, the difference between both conformations increases 12 kJ/mol, favouring isomer cis. This is in agreement with what was found in crystal structures in which the scaffold interacts with the corresponding anion using the cis conformer.
A total of 18 complexes were found due to the interaction between scaffolds A and B with three different halides, i.e., Cl−, Br−, and I−. Two of the optimised geometries obtained for each A and B scaffolds are depicted in Figure 4 for illustrative purposes, while the rest have been included in the ESI (Table S1).
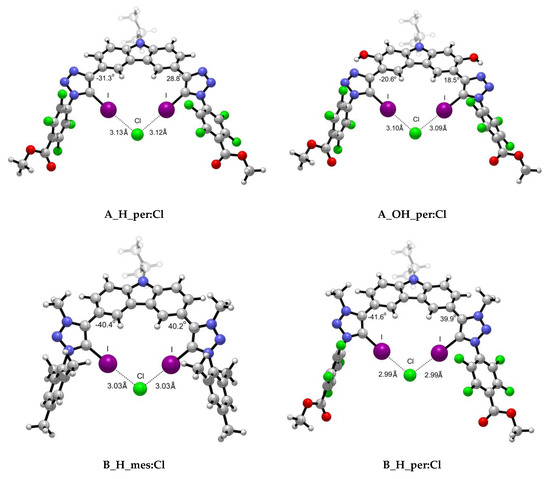
Figure 4.
Representative optimised structures for the interaction between scaffolds A and B with Cl− anion.
As observed from the structures in Figure 4 and the collected data in Table 2, the intermolecular distance between the X− anion and each of the iodine atoms is almost identical for both X-⋯I interactions, despite the slight variations on the MEP maxima values on the σ-hole. The highest degree of asymmetry regarding the dihedral angle formed between the scaffold and the halide atom (Figure 4) is associated to the iodine anion and the cationic XB motif. The rigid structures in which an intramolecular hydrogen bond is involved exhibit the highest planarity. The X⋯I intermolecular distances were found to be shorter in the per than in the mes complexes in alignment with the MEP maxima found for the σ-holes. Also, shorter distances were found for complexes with intramolecular hydrogen bonds (H vs. OH) concomitantly with more planarity shown by the dihedral angles between both rings (as per Figure 4). Finally, the shortest intermolecular X⋯I distances were found for the cationic XB (B) complexes, in agreement with the electrostatic nature of the interaction. As expected, the distances correspond to halide radii: Cl < Br < I. Tepper et al.’s [12] experimental data indicate that A_H_mes:Cl complex exhibits a I⋯Cl- intermolecular distance of 3.11 Å, which is in fair agreement with our computational value 3.17 Å. In the same work, the authors studied the influence of the OH group in the arrangement and I⋯Cl- distance. Their crystallographic data shows a trimer complex (A_OH_mes)2:Cl in which four simultaneous XB are taking place. The intermolecular distances reported vary from 3.09 to 3.23 Å due to the orientation of the scaffolds. Our theoretical distance, i.e., 3.14 Å, is in good agreement with one of the distances reported (3.13 Å) and with the average of all of them (3.135 Å).

Table 2.
Electron density at the BCP (ρ), Laplacian (∇2ρ), and interaction distance (Å) for all the complexes studied at m062x/aug–cc–pVDZ computational level. Dihedral angles (Figure 4).
The geometric patterns of Table 2 are reflected in the trend of the electron density values at the bond critical points (BCPs) corresponding to the halogen-bonding interactions (Table 2). Molecular graphs for all the complexes are summarised in Table S1, and the values of the Laplacian (∇2ρ) in Table 2 indicate that all the interaction considered are within the closed shell range. Therefore, from the geometric perspective, complex B_H_per scaffold manifest the strongest electron density value, as well as the shortest X-I distance, revealing halotriazolium as a highly potent anion-binding XB motif, and therefore, allowing strong coordination to occur with the halide ions.
2.1.3. Energetic Analysis
The binding energies (Eb) reported in Table 3 obey a systematic trend. These complexes are strongest for Cl and weakest for I, presenting almost the same gap between Cl and Br atoms and Br and I atoms. This pattern mirrors the noncovalent bond lengths in Table 2.

Table 3.
Binding energies (Eb) and binding free energy (ΔGb, at 298K) (kJ/mol) upon complexation at m062x/aug–cc–pVTZ computational level. Equilibrium constants for the halogen-bonding interaction.
It is commonly found that binding energies are substantially diminished when vibrational and entropic factors are included in the formulation. The Gibbs free energies of the association reactions reported in Table 3 do indeed indicate a weakening by less negative quantities. But this weakening is relatively modest, and the binding free energies are still quite substantial. In fact, all quantities in Table 3 are negative, indicating spontaneous association processes. The evolution of the free energy values in Table 3 closely mimics those of Eb, except in one case, B_H_mes, in which the trend is the opposite, obtaining the lowest ΔGb when the iodide ion is interacting with the host.
The anion-scaffold binding has important implications for the selectivity of these receptors. The selectivity for Cl- over the other two anions can be evaluated by the equilibrium constant, k = exp , and the resulting quantities are reported in the last column of Table 3. In all cases, the values > 1 indicate that the binding of the/a chloride ion to the receptor is favoured over the other two, i.e., bromide and iodine, ions. The only exception is the B_H_mes complex, in which the opposite was found. Additionally, the equilibrium constant for the halogen-bonding interaction upon complexation for all complexes A and B was calculated and gathered in Table S3, ranging from a minimum of 84.7 for A_H_mes:I up to 4.73 × 1016 for B_H_per:Cl. It is observed that the largest equilibrium constant corresponds to the complexes B, in which ks range on the order of 1013–1016 according to the binding energy trend.
Finally, an NBO analysis of the wave function in order to characterise the intramolecular halogen–bonding was performed. To describe these bonds, a charge transfer from the lone pair(s) of the halide to σ*(X-C) antibonding orbital has to be localised. The energetic component of these charge transfers, E(2), is displayed in Table 4. All the E(2) are quite large and, as expected, diminish with the size of the halide: Cl > Br > I. A nice and clear correlation is found between the binding energies (Eb) and the magnitude of E(2). The only exception to this trend is the complex A_H_mes, presenting a higher values of E(2) than expected. However, it is well-known that the E(2) charge-transfer energies are not the only factor in the binding of the halides.

Table 4.
NBO values of charge transfer energy E(2), in kJ/mol, from lone pairs of halide to σ*(X-C) antibonding orbital.
2.2. Bis-Iodotriazole Pyridinium-Based XB Donor Motif
In the second part of this work, bis-iodotriazole-pyridinium motif based receptors were studied, since those molecules are capable of binding anions by two bifurcated halogen bonds. Beer et al. showed, from an experimental perspective, the evidence of the halogen bond interactions involving those pyridinium based scaffolds and halide atoms [11].
Two different XB donor motif were studied, i.e., halotriazole (neutral) and halotriazolium (cationic), and therefore, two families of compounds were optimised, C and D (Figure 5).
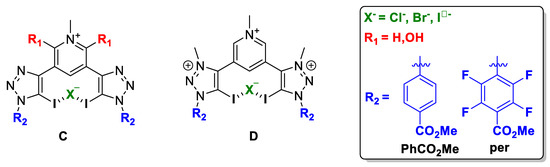
Figure 5.
Schematic representation of the compound subject to study: (C) neutral XB donor motif and (D) cationic XB donor motif.
2.2.1. Structural Analysis
A total of 18 complexes were found due to the interaction between scaffolds C and D with three different halides, Cl−, Br− and. Two of the optimised complexes obtained, one for each C and D, are depicted in Figure 6 for illustrative purposes, while the rest are included in the ESI (Table S1).
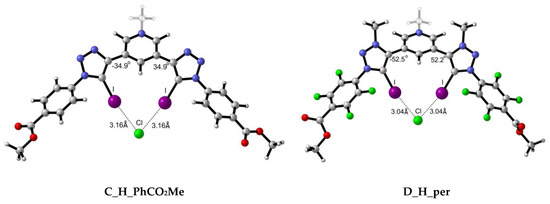
Figure 6.
Representative optimised structures for the interaction between scaffolds C and D with Cl− anion.
Intermolecular X⋯I distances (Table 5) for C complexes are in the same range as those for A complexes, with slightly shorter distances for A_H_per complexes with respect to the C_H_per ones. Despite the fact that C complexes present a positive formal charge, the larger scaffold presented in complexes A allow for a better orientation of the XB donor motifs in C complexes. This can be noticed by the I⋯I intramolecular distance, for example in A_OH_per:Cl (4.69 Å) and C_OH_per:Cl (3.85 Å) complexes. The larger scaffold in the former allows longer I⋯I separation, resulting in less electronic repulsion between the two I atoms and, therefore, better accommodation of the halide. Also, as observed by the dihedral angles, intramolecular hydrogen bond-driven rigid systems allow for better orientations and, therefore, shorter X⋯I distances. Bunchuay et al. [16] provided structural information about the mono cationic acyclic XB bis-iodotriazole pyridinium (C_H_per) receptor with Cl− and I−. The intramolecular distances reported for C_H_per:Cl are 3.007 and 3.142 Å, since neither donor motif is symmetric. Our theoretical I⋯Cl− of 3.14 is in good agreement with the experimental ones. In case of C_H_per:I, slightly larger discrepancies are found in the I⋯I− distances between Bunchuay’s work (3.401–3.357 Å) and the computed distances in the present work (3.50 Å), although they are still within the same range.

Table 5.
Electron density at the BCP (ρ), Laplacian (∇2ρ), and interaction distance (Å) for all the complexes studied at m062x/aug–cc–pVDZ computational level. Dihedral angles (Figure 6).
Triply charged complexes, D, present shorter distances than C and A complexes, but slightly longer than B ones, where, intuitively, one would expect the opposite. Again, the larger the scaffold, the better the orientation; the lower electronic repulsion explains why B complexes exhibit shorter X⋯I than D complexes. Electron density and Laplacian values (Table 5) are consistent with the intermolecular distances pattern found as well.
2.2.2. Energetic Analysis
The binding and free energies for C and D complexes are gathered in Table 6. Value analysis indicated that the general trend on both ΔEb and ΔGb is as follows: A< C < D < B. In spite of binding energies for C complexes being stronger than A complexes, both families have very close binding energy values. Again, this can be explained in terms of the size of the scaffold which accommodates the halide better in A than in C. The positive charge in C complexes will increase the interaction with the halide, but somehow, it suffers for some penalty due to the electronic repulsion between I atoms in the XB donor motif. This explains why the interaction energy in C complexes is stronger than A, but not as strong as one should expect. When moving to more charged systems, the binding energies are much larger (see C and D complexes in Table 6). As with the A and C complexes, the D < B difference can be explained in the same scaffold-size/electronic repulsion terms.

Table 6.
Binding energies (Eb) and binding free energy (ΔGb, at 298K) (kJ/mol) upon complexation at m062x/aug–cc–pVTZ computational level. Equilibrium constants for the halogen-bonding interaction.
Regarding the equilibrium constants with respect to the chloride anion, bromide is more competitive in C and D complexes than in B or A ones. Chloride is in almost all cases favoured over iodine. Finally, and similar to what was observed for the A and B complexes, the NBO E(2) values trend (Table 7) is in agreement with the binding energies found across the halide anion.

Table 7.
NBO values of charge transfer energy E(2), in kJ/mol, from lone pairs of halide to σ*(X-C) antibonding orbital.
3. Discussion
A total of 36 compounds were characterised, four different organic scaffolds interacting with three different halide atoms. Very good exponential relationships between the electron density values at the BCPs and the intramolecular X⋯I distance (X=Cl−, Br− or I−) were found (Figure 7). As observed, when the anion involved in the interaction is chloride, all the distances are shorter, and therefore, present the highest density values for all the families.
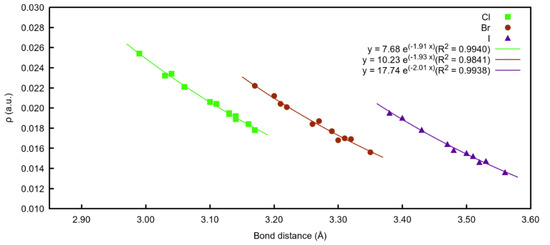
Figure 7.
Exponential correlation density at BCPs vs. bond distances (X⋯I) regarding the three different halide atoms involved.
When the same relationship between density and X⋯I distances is made regarding the 12 different families (Figure S4), the same trend was found for the three halide atoms. Additionally, B and D complexes with electro withdrawing substituent, per, appear to be the best options in order to get the strongest halogen bonding interaction, following the scaffolds that establish an intramolecular hydrogen bond (A_OH_per and C_OH_per).
In terms of binding energies, chloride-based complexes are the strongest ones, and the binding energies evolve with the electron donor capacity of the anion as Cl− > Br− > I−.
It is clear that the scaffold plays an important role in establishing halogen bond interactions. Larger scaffolds accommodate the halide better than smaller scaffolds. This reduces the electronic repulsion between iodine atoms (XB donors) and increases the overlap between the halide electron lone pairs and the I-C σ* antibonding orbital, as evidenced by the larger E(2) values for A_per complexes with respect to the C_per ones.
Also, the presence of OH groups and the possibility of forming intramolecular hydrogen bonds increases the planarity of the molecule, particularly between the scaffold and XB donor motifs, increasing the rigidity and enhancing the halogen bond.
4. Computational Methods
Structures of the complexes were optimized at the m062x/aug–cc–pVDZ [17,18] computational level. Harmonic vibrational frequencies were computed at the same level used for the geometry optimizations in order to confirm that the stationary points are local minima. For the heavy atom I, the aug-cc-pVDZ-PP pseudopotential [19,20] was used to incorporate relativistic effects. Calculations were performed using the Gaussian16 software [21]. Single point energies for lowest energy small basis set calculations were computed using m062x/aug–cc–pVTZ. Binding energies (Eb) were calculated as a difference of the energy of the optimised complex minus the energy of each monomer in their optimised geometry. The free energies reported in the document were obtained by adding the free energy correction from the small basis set calculations to the potential energy obtained from the high-level single-point energy calculations.
Solvent effects (THF for A and B complexes and DMSO for C and D complexes) were included in the optimization by means of a continuum method, the Solvation Model based on Density (SMD) approach [22], and the refined SMD18 [23] version for Br and I atoms, implemented in Gaussian16.
The molecular electrostatic potential (MEP) of the isolated monomers were calculated on the electron density isosurface of 0.001 au. This isosurface has been shown to resemble the van der Waals surface [24]. These calculations were carried out with the Gaussian-16 software and the numerical results analysed using the Multiwfn [25] and plotted using Jmol [26].
The Atoms in Molecules (AIM) methodology [27,28] was used to analyse the electron density of the systems with the AIMAll program [29]. The Natural Bond Orbital (NBO) method [30] was employed to evaluate atomic charges using the NBO-3 program, and to analyse charge-transfer interactions between the occupied and unoccupied orbitals.
Supplementary Materials
The following are available online, Table S1: Molecular graphs and optimized geometries for all complexes, Figure S1: Molecular electrostatic potential for selected monomers (A), Figure S2: Optimised trans isomer for scaffolds A_H_mes and A_OH_per, Table2: Relative energies (ΔE) and binding free energy (ΔG,) for cis and trans conformers, Table S3: Equilibrium constants for the halogen-bonding interaction for complexes A and B, Figure S3: Molecular electrostatic potential for selected monomers(C), Table S4. Maxima (Vmax,X) values of the molecular electrostatic potential for all the monomers (C), Table S5. Equilibrium constants for the halogen-bonding interaction for complexes C and D, Figure S4. Relationship density at BCPs vs bond distances (I-X) for all the families under study.
Author Contributions
Conceptualization, C.T. and G.S.-S.; methodology, C.T., G.S.-S., I.I.; formal analysis, C.T., G.S.-S., I.I.; investigation, C.T., G.S.-S., I.I.; writing—original draft preparation, C.T., G.S.-S.; writing—review and editing, C.T., G.S.-S., I.I.; supervision, C.T.; project administration, C.T..; funding acquisition, C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science Foundation of Ireland (SFI), grant number 18/SIRG/5517.
Acknowledgments
We are grateful to the Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and Dr. Lee O’Riordan for his careful reading and help.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lim, J.Y.C.; Beer, P.D. Sigma-Hole Interactions in Anion Recognition. Chem 2018, 4, 731–783. [Google Scholar] [CrossRef]
- Scheiner, S. Highly Selective Halide Receptors Based on Chalcogen, Pnicogen, and Tetrel Bonds. Chem. Eur. J. 2016, 22, 18850–18858. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Assembly of Effective Halide Receptors from Components. Comparing Hydrogen, Halogen, and Tetrel Bonds. J. Phys. Chem. A 2017, 121, 3606–3615. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Comparison of halide receptors based on H, halogen, chalcogen, pnicogen, and tetrel bonds. Faraday Discuss. 2017, 203, 213–226. [Google Scholar] [CrossRef]
- Decato, D.A.; Riel, A.M.S.; Berryman, O.B. Anion Influence on the Packing of 1,3-Bis(4-Ethynyl-3-Iodopyridinium)-Benzene Halogen Bond Receptors. Crystals 2019, 9, 522. [Google Scholar] [CrossRef]
- Sánchez-Sanz, G.; Trujillo, C. Cyclohexane-Based Scaffold Molecules Acting as Anion Transport, Anionophores, via Noncovalent Interactions. J. Chem. Inf. Model. 2019, 59, 2212–2217. [Google Scholar] [CrossRef]
- Sánchez-Sanz, G.; Trujillo, C. Improvement of Anion Transport Systems by Modulation of Chalcogen Interactions: The influence of solvent. J. Phys. Chem. A 2018, 122, 1369–1377. [Google Scholar] [CrossRef]
- Benz, S.; Macchione, M.; Verolet, Q.; Mareda, J.; Sakai, N.; Matile, S. Anion Transport with Chalcogen Bonds. J. Am. Chem. Soc. 2016, 138, 9093–9096. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Sansotera, M.; Terraneo, G. Halogen bonding: A general route in anion recognition and coordination. Chem. Soc. Rev. 2010, 39, 3772–3783. [Google Scholar] [CrossRef]
- Tepper, R.; Schulze, B.; Jäger, M.; Friebe, C.; Scharf, D.H.; Görls, H.; Schubert, U.S. Anion Receptors Based on Halogen Bonding with Halo-1,2,3-triazoliums. J. Org. Chem. 2015, 80, 3139–3150. [Google Scholar] [CrossRef]
- Robinson, S.W.; Mustoe, C.L.; White, N.G.; Brown, A.; Thompson, A.L.; Kennepohl, P.; Beer, P.D. Evidence for Halogen Bond Covalency in Acyclic and Interlocked Halogen-Bonding Receptor Anion Recognition. J. Am. Chem. Soc. 2015, 137, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Tepper, R.; Schulze, B.; Görls, H.; Bellstedt, P.; Jäger, M.; Schubert, U.S. Preorganization in a Cleft-Type Anion Receptor Featuring Iodo-1,2,3-Triazoles As Halogen Bond Donors. Org. Lett. 2015, 17, 5740–5743. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. A predicted new type of directional noncovalent interaction. Int. J. Quantum Chem. 2007, 107, 2286–2292. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.; Concha, M. σ-hole bonding between like atoms; a fallacy of atomic charges. J. Mol. Model. 2008, 14, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Mohajeri, A.; Pakiari, A.H.; Bagheri, N. Theoretical studies on the nature of bonding in σ-hole complexes. Chem. Phys. Lett. 2009, 467, 393–397. [Google Scholar] [CrossRef]
- Bunchuay, T.; Docker, A.; Martinez-Martinez, A.J.; Beer, P.D. A Potent Halogen-Bonding Donor Motif for Anion Recognition and Anion Template Mechanical Bond Synthesis. Angew. Chem. Int. Ed. 2019, 58, 13823–13827. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. 1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian, version 16; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Engelage, E.; Schulz, N.; Heinen, F.; Huber, S.M.; Truhlar, D.G.; Cramer, C.J. Refined SMD Parameters for Bromine and Iodine Accurately Model Halogen-Bonding Interactions in Solution. Chem. Eur. J. 2018, 24, 15983–15987. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Jmol: An Open-source Java Viewer for Chemical Structures in 3D. Available online: http://www.jmol.org/ (accessed on 10 December 2019).
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A.; Aicken, F.M.; O’Brien, S.E. Atoms In Molecules: An introduction, Prentice Hall, Harlow, England. Chem. Model. Appl. Theory 2000, 1, 143–198. [Google Scholar]
- Keith, T.A. TK Gristmill Software. Available online: Aim.tkgristmill.com (accessed on 10 December 2019).
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
Sample Availability: Not available |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).