Factors Impacting σ- and π-Hole Regions as Revealed by the Electrostatic Potential and Its Source Function Reconstruction: The Case of 4,4′-Bipyridine Derivatives
Abstract
1. Introduction
2. Results and Discussion
2.1. Calculation of VS,max Values
2.2. Impact of Chemical and Conformational Features on VS Values
2.2.1. σ-Holes Located on the Elongation of C-X Bonds (X = Cl, Br)
2.2.2. Phenyl π-Holes
2.2.3. 3-Ch σ-Holes
2.3. Source Function (SF) Reconstruction of VS,max
2.3.1. Cpyridyl–Ch σ-Holes
2.3.2. CR–Ch σ-Holes
2.3.3. Aryl π-Holes
2.4. Analysis of VS,max and Source Function (SF) Contributions Changes
2.4.1. S→Se Substitutions
2.4.2. R→R’ Substitutions
2.4.3. S→Se and R→R’ Substitutions
2.4.4. Conformational Changes
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scrocco, E.; Tomasi, J. The electrostatic molecular as a tool for the interpretation of molecular properties. Top. Curr. Chem. 1973, 42, 95–170. [Google Scholar] [CrossRef]
- Clark, T. Halogen bonds and σ-holes. Faraday Discuss. 2017, 203, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Politzer, P. Molecular electrostatic potentials and noncovalent interactions. WIREs Comput. Mol. Sci. 2017, 7, e1326. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface electrostatic potentials of halogenated methanes as indicators of directional intermolecular interactions. Int. J. Quantum Chem. 1992, 44, 57–64. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. An overview of strengths and directionalities of noncovalent interactions: σ-hole and π-holes. Crystals 2019, 9, 165. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Shing Ho, P.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013. Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Kopylovich, M.N.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. Chalcogen bonding in synthesis, catalysis and design of materials. Dalton Trans. 2017, 46, 10121–10138. [Google Scholar] [CrossRef] [PubMed]
- Vogel, L.; Wonner, P.; Huber, S.M. Chalcogen bonding: An overview. Angew. Chem. Int. Ed. 2019, 58, 1880–1891. [Google Scholar] [CrossRef] [PubMed]
- Biot, N.; Bonifazi, D. Chalcogen-bond driven molecular recognition at work. Coord. Chem. Rev. 2020, 413, 213243. [Google Scholar] [CrossRef]
- Murray, J.S.; Macaveiu, L.; Politzer, P. Factor affecting the strengths of σ-hole electrostatic potentials. J. Comput. Sci. 2014, 5, 590–596. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Houk, K.N. Through-space effects of substituents dominate molecular electrostatic potentials of substituted arenes. J. Chem. Theory Comput. 2009, 5, 2301–2312. [Google Scholar] [CrossRef] [PubMed]
- Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F., Cl, Br, I). J. Mol. Mod. 2013, 19, 2739–2746. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Tran, K.–A.; Lane, P.; Murray, J.S.; Politzer, P. Comparative analysis of electrostatic potential maxima and minima on molecular surface, as determined by three methods and a variety of basis sets. J. Comput. Sci. 2016, 17, 273–284. [Google Scholar] [CrossRef]
- Kolář, M.H.; Hobza, P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Chopade, P.D.; Desper, J. Establishing a hierarchy of halogen bonding by engineering crystals without disorder. Cryst. Growth Des. 2013, 13, 4145–4150. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Wijethunga, T.K.; Desper, J.; Đaković, M. Electrostatic potential differences and halogen-bond selectivity. Cryst. Growth Des. 2016, 16, 2662–2670. [Google Scholar] [CrossRef]
- Lange, A.; Heidrich, J.; Zimmermann, M.O.; Exner, T.E.; Boeckler, F.M. Scaffold effects on halogen bonding strength. J. Chem. Inf. Model. 2019, 59, 885–894. [Google Scholar] [CrossRef] [PubMed]
- Dessì, A.; Peluso, P.; Dallocchio, R.; Weiss, R.; Andreotti, G.; Allocca, M.; Aubert, E.; Pale, P.; Mamane, V.; Cossu, S. Rational design, synthesis, characterization and evaluation of 4,4′-bipyridines as new transthyretin fibrillogenesis inhibitors. Molecules 2020, 25, 2213. [Google Scholar] [CrossRef]
- Lim, J.Y.C.; Marques, I.; Thompson, A.L.; Christensen, K.E.; Félix, V.; Beer, P.D. Chalcogen bonding macrocycles and [2] rotaxanes for anion recognition. J. Am. Chem. Soc. 2017, 139, 3122–3133. [Google Scholar] [CrossRef] [PubMed]
- Ams, M.R.; Trapp, N.; Schwab, A.; Milić, J.V.; Diederich, F. Chalcogen bonding “2S-2N squares” versus competing interactions: Exploring the recognition properties of sulfur. Chem. Eur. J. 2019, 25, 323–333. [Google Scholar] [CrossRef] [PubMed]
- Nayak, S.K.; Kumar, V.; Murray, J.S.; Politzer, P.; Terraneo, G.; Pilati, T.; Metrangolo, P.; Resnati, G. Fluorination promotes chalcogen bonding in crystalline solids. CrystEngComm 2017, 19, 4955–4959. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-holes and π-holes: Similarities and differences. J. Comput. Chem. 2018, 39, 464–471. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A.; Mooibroek, T.J. π-Hole interactions involving nitro aromatic ligands in protein structures. Chem. Eur. J. 2019, 25, 13436–13443. [Google Scholar] [CrossRef]
- Abboud, M.; Mamane, V.; Aubert, E.; Lecomte, C.; Fort, Y. Synthesis of polyhalogenated 4, 4′-bipyridines via a simple dimerization procedure. J. Org. Chem. 2010, 75, 3224–3231. [Google Scholar] [CrossRef]
- Mamane, V.; Peluso, P.; Aubert, E.; Cossu, S.; Pale, P. Chiral hexahalogenated 4, 4′-bipyridines. J. Org. Chem. 2016, 81, 4576–4587. [Google Scholar] [CrossRef]
- Peluso, P.; Mamane, V.; Aubert, E.; Dessì, A.; Dallocchio, R.; Dore, A.; Pale, P.; Cossu, S. Insights into halogen bond-driven enantioseparations. J. Chromatogr. A 2016, 1467, 228–238. [Google Scholar] [CrossRef]
- Peluso, P.; Mamane, V.; Dallocchio, R.; Dessì, A.; Villano, R.; Sanna, D.; Aubert, E.; Pale, P.; Cossu, S. Polysaccharide-based chiral stationary phases as halogen bond acceptors: A novel strategy for detection of stereoselective σ-hole bonds in solution. J. Sep. Sci. 2018, 41, 1247–1256. [Google Scholar] [CrossRef] [PubMed]
- Peluso, P.; Gatti, C.; Dessì, A.; Dallocchio, R.; Weiss, R.; Aubert, E.; Pale, P.; Cossu, S.; Mamane, V. Enantioseparation of fluorinated 3-arylthio-4, 4′-bipyridines: Insights into chalcogen and π-hole bonds in high-performance liquid chromatography. J. Chromatogr. A 2018, 1567, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Weiss, R.; Aubert, E.; Peluso, P.; Cossu, S.; Pale, P.; Mamane, V. Chiral chalcogen bond donors based on the 4, 4′-bipyridine scaffold. Molecules 2019, 24, 4484. [Google Scholar] [CrossRef] [PubMed]
- Benz, S.; López-Andarias, J.; Mareda, J.; Sakai, N.; Matile, S. Catalysis with chalcogen bonds. Angew. Chem. Int. Ed. 2017, 56, 812–815. [Google Scholar] [CrossRef]
- O’Hair, R.A.J.; Williams, C.M.; Clark, T. Neighboring group stabilization by σ-holes. J. Mol. Model. 2010, 16, 559–565. [Google Scholar] [CrossRef]
- Riel, A.M.S.; Huynh, H.-T.; Jeannin, O.; Berryman, O.; Fourmigué, M. Organic selenocyanates as halide receptors: From chelation to one-dimensional systems. Cryst. Growth Des. 2019, 19, 1418–1425. [Google Scholar] [CrossRef]
- Trujillo, C.; Rozas, I.; Elguero, J.; Alkorta, I.; Sánchez-Sanz, G. Modulating intramolecular chalcogen bonds in aromatic (thio)(seleno) phene-based derivatives. Phys. Chem. Chem. Phys. 2019, 21, 23645–23650. [Google Scholar] [CrossRef]
- Lu, T.; Zheng, Y.; Gou, Q.; Hou, G.–L.; Feng, G. Rotational characterization of S⋯ F chalcogen bonds in the complex of 2, 2, 4, 4-tetrafluoro-1, 3-dithietane and difluoromethane. Phys. Chem. Chem. Phys. 2019, 21, 24659–24665. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Gatti, C. A Green’s function for the density. Chem. Phys. Lett. 1998, 287, 233–238. [Google Scholar] [CrossRef]
- Gatti, C.; Cargnoni, F.; Bertini, L. Chemical information from the source function. J. Comput. Chem. 2003, 24, 422–436. [Google Scholar] [CrossRef]
- Gatti, C. The source function descriptor as a tool to extract chemical information from theoretical and experimental electron densities. Struct. Bond. 2012, 147, 193–286. [Google Scholar] [CrossRef]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the fluorine in molecules dispersive? Is molecular electrostatic potential a valid property to explore fluorine-centered non-covalent interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. On the importance of halogen–halogen interactions in the solid state of fullerene halides: A combined theoretical and crystallographic study. Crystals 2017, 7, 191. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Allred, A.L. Electronegativity values from thermochemical data. Inorg. Nucl. Chem. 1961, 17, 215–221. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics, 87th ed.; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Kirshenboim, O.; Kozuch, S. How to twist, split and warp a σ-hole with hypervalent halogens. J. Phys. Chem. A 2016, 120, 9431–9445. [Google Scholar] [CrossRef]
- Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.B.; Slipchenko, L.V.; Levchenko, S.V.; O’Neil, D.P.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision, B. 01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyser. J. Comp. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Quantitative analysis of molecular surface based on improved marching tetrahedra algorithm. J. Mol. Graph. Model. 2012, 38, 314–323. [Google Scholar] [CrossRef]
- Gatti, C. VEXTLOC Code; CNR-ISTM: Milano, Italy, 2018. [Google Scholar]
- Gatti, C. SF-ESI Codes; CNR-ISTM: Milano, Italy, 2015. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory, International Series of Monographs on Chemistry 22; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Gatti, C. SF_ED_EP_ESI Codes; CNR-ISTM: Milano, Italy, 2018. [Google Scholar]
- Kosov, D.S.; Popelier, P.L.A. Atomic Partitioning of Molecular Electrostatic Potentials. J. Phys. Chem. A 2000, 104, 7339–7345. [Google Scholar] [CrossRef]
- Gatti, C. ANASFR_EP Code; CNR-ISTM: Milano, Italy, 2018. [Google Scholar]
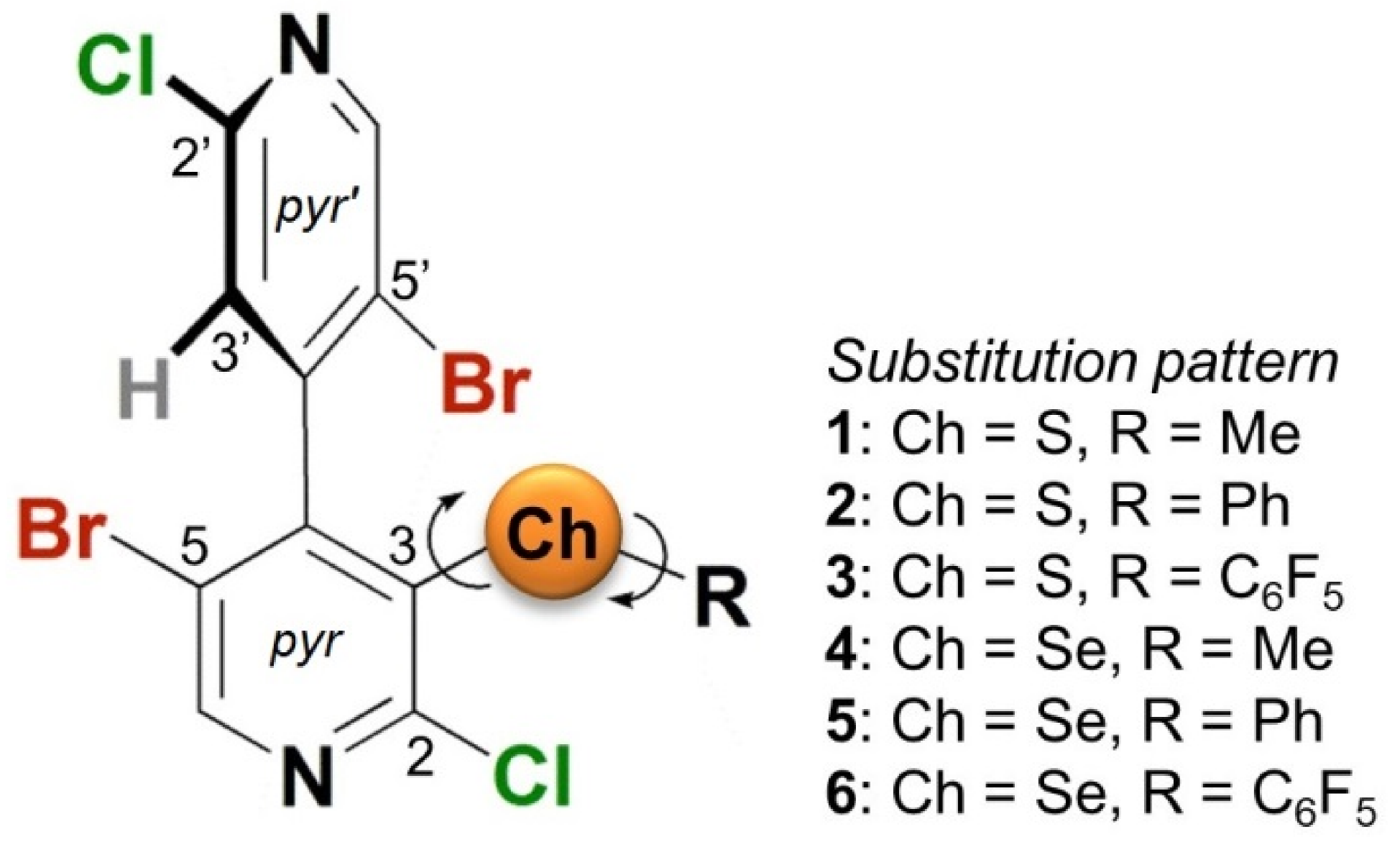
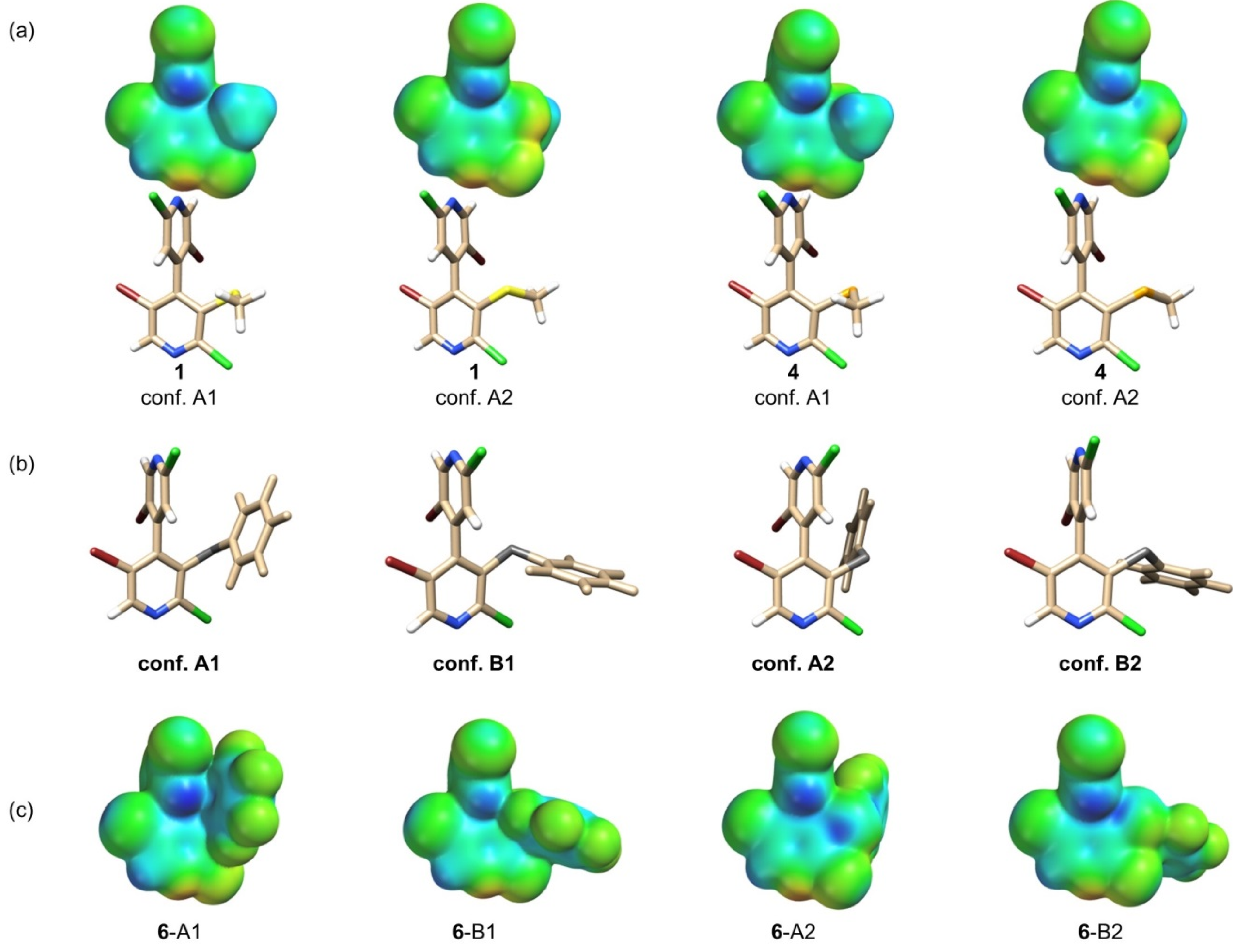
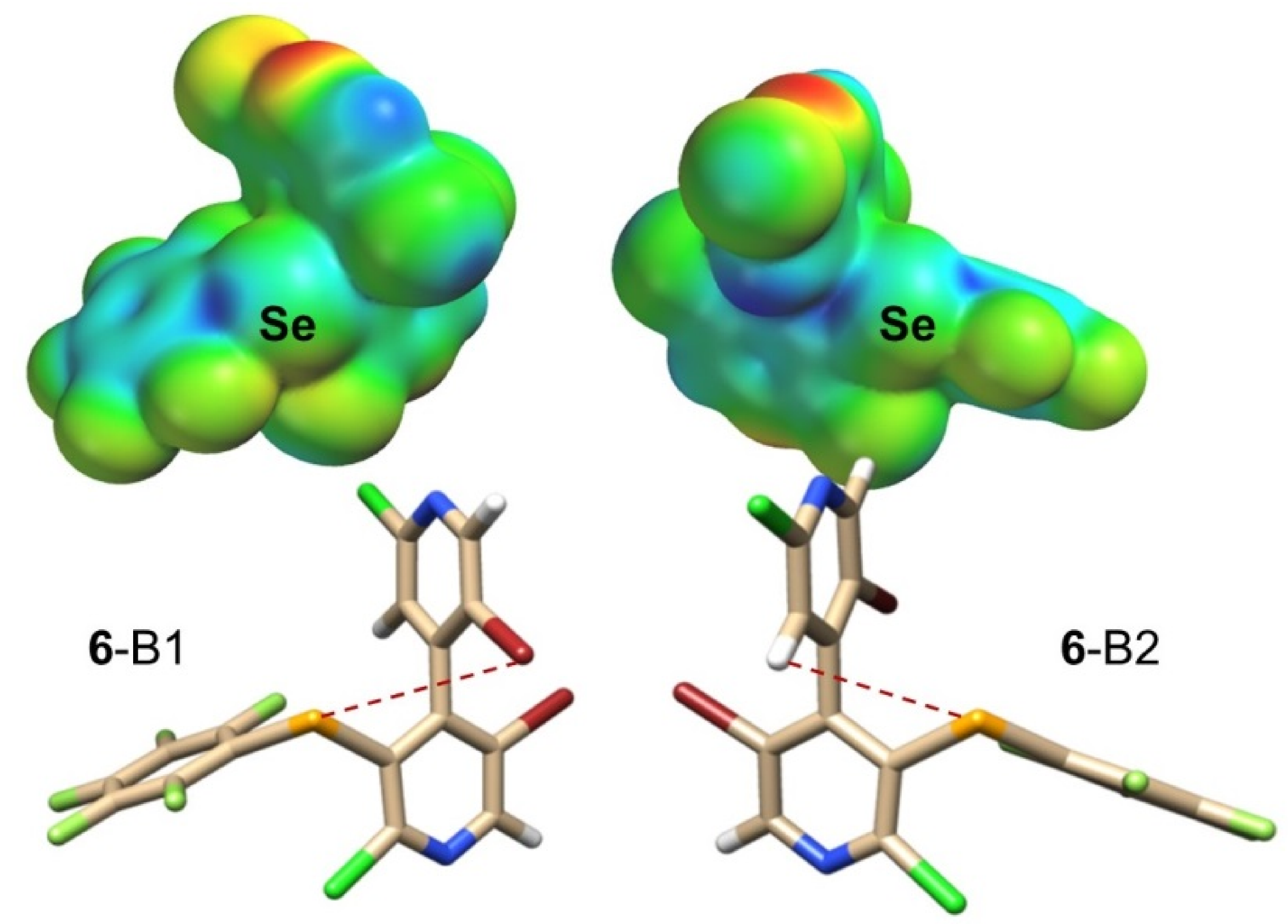
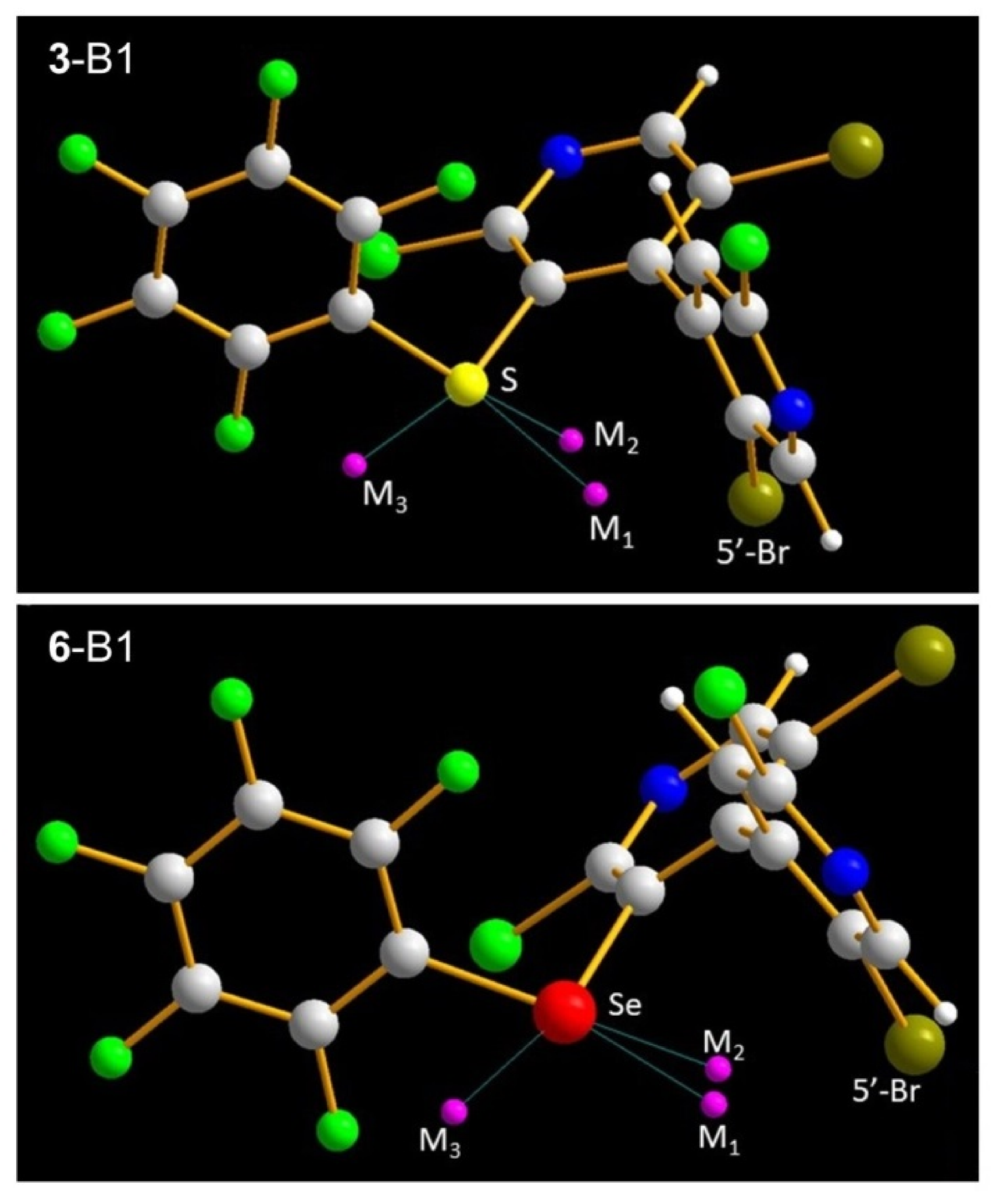


| Conf. | R (3-ChR) | Ch | 2′-Cl | 2-Cl | 5′-Br | 5-Br | Ch (Cpyridyl–Ch) | Ch (CR–Ch) | π-Hole External 1 | π-Hole Internal 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| ΔVS,max 2 | 0.0046 | 0.0106 | 0.0078 | 0.0055 | 0.0326 | 0.0434 | 0.0597 | 0.0685 | ||
| 1-A1 | Me | S | 0.0233 | 0.0259 | 0.0449 | 0.0478 | 0.0428 | 0.0193 | ||
| 1-A2 | 0.0219 | 0.0262 | 0.0493 | 0.0476 | 0.0423 | - | ||||
| 2-A1 | Ph | S | 0.0224 | 0.0230 | 0.0445 | 0.0475 | 0.0285 | 0.0268 | −0.0080 | - |
| 2-A2 | 0.0215 | 0.0231 | 0.0451 | 0.0471 | 0.0267 | 0.0340 | −0.0090 | −0.0138 | ||
| 2-B1 | 0.0221 | 0.0222 | 0.0446 | 0.0469 | 0.0307 | 0.0169 | −0.0115 | −0.0087 | ||
| 2-B2 | 0.0215 | 0.0220 | 0.0491 | 0.0464 | 0.0286 | - | −0.0127 | −0.0093 | ||
| 3-A1 | C6F5 | S | 0.0258 | 0.0269 | 0.0520 | 0.0492 | 0.0491 | 0.0445 | 0.0466 | 0.0538 |
| 3-A2 | 0.0246 | 0.0271 | 0.0519 | 0.0518 | 0.0491 | 0.0501 | 0.0456 | - | ||
| 3-B1 | 0.0235 | 0.0307 | 0.0486 | 0.0512 | 0.0495 | 0.0272 3 | 0.0470 | 0.0444 | ||
| 3-B2 | 0.0250 | 0.0326 | 0.0475 | 0.0512 | 0.0512 | 0.0553 | 0.0452 | 0.0404 | ||
| 4-A1 | Me | Se | 0.0229 | 0.0253 | 0.0452 | 0.0471 | 0.0521 | 0.0260 | ||
| 4-A2 | 0.0219 | 0.0256 | 0.0486 | 0.0470 | 0.0518 | 0.0463 | ||||
| 5-A1 | Ph | Se | 0.0225 | 0.0224 | 0.0443 | 0.0466 | 0.0401 | 0.0352 | −0.0072 | - |
| 5-A2 | 0.0212 | 0.0225 | 0.0441 | 0.0463 | 0.0391 | 0.0414 | −0.0082 | −0.0147 | ||
| 6-A1 | C6F5 | Se | 0.0251 | 0.0266 | 0.0493 | 0.0514 | 0.0584 | 0.0559 | 0.0454 | 0.0527 |
| 6-A2 | 0.0244 | 0.0267 | 0.0512 | 0.0512 | 0.0577 | 0.0609 | 0.0448 | - | ||
| 6-B1 | 0.0235 | 0.0294 | 0.0496 | 0.0510 | 0.0582 | 0.0319 4 | 0.0455 | 0.0425 | ||
| 6-B2 | 0.0258 | 0.0314 | 0.0476 | 0.0510 | 0.0593 | 0.0603 | 0.0438 | 0.0390 |
| σ-hole | 0.001 | 0.002 | 0.003 | 0.004 |
|---|---|---|---|---|
| σ-hole (Cpyridyl–S) | - | 0.0422 | 0.0502 | 0.0590 |
| σ-hole (CMe–S) | - | - | - | 0.0578 |
| Conf.,M | VS,max (au) | dCh-M (Å) | dBr-M (Å) | C5′-Br-M (°) | CArF-Br-M (°) |
|---|---|---|---|---|---|
| 3-B1,M1 | 0.0202 | 2.098 | 2.268 | 61.9 | 156.2 |
| 3-B1,M2 | 0.0272 | 2.016 | 2.431 | 87.2 | 154.5 |
| 3-B2,M | 0.0553 | 2.095 | 1.616 1 | 97.6 2 | 162.7 |
| 6-B1,M1 | 0.0309 | 2.035 | 2.410 | 73.7 | 163.3 |
| 6-B1,M2 | 0.0319 | 2.057 | 2.418 | 88.8 | 154.5 |
| 6-B2,M | 0.0603 | 2.105 | 1.696 1 | 94.6 2 | 161.6 |
| Conf. | VS,max | SF(Ch) | SF(R) | SF(BiPy) | SF(pyr) | SF(pyr’) | SF(5′-Br) | SF(3′-H) | Err% |
|---|---|---|---|---|---|---|---|---|---|
| S (σ-hole, Cpyridyl–S) | |||||||||
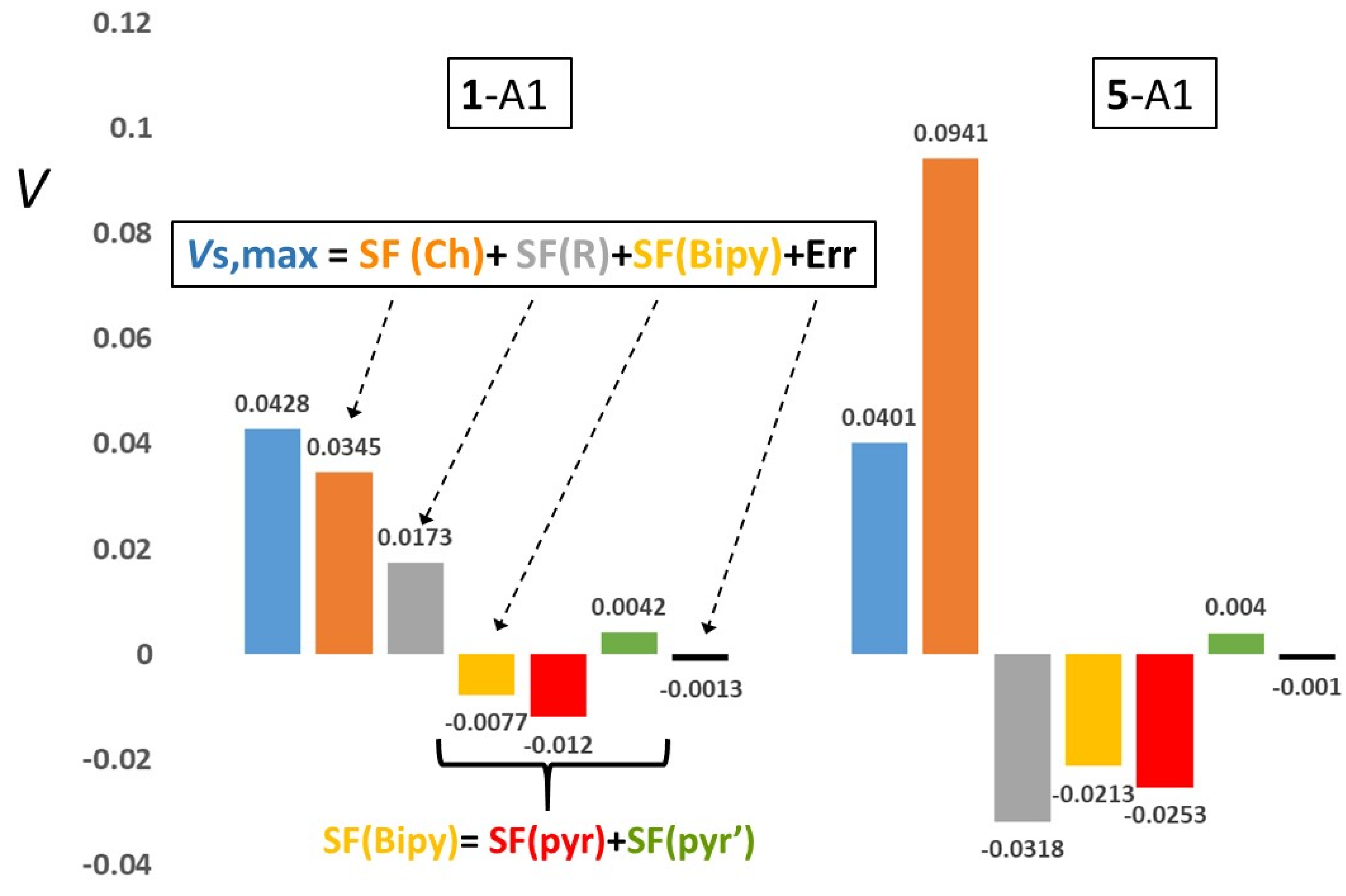
| 1-A1 | 0.0428 | 0.0345 (80.7) | 0.0173 (40.4) | −0.0077 (−18.1) | −0.0120 (−28.0) | 0.0042 (9.9) | −0.0016 (−3.8) | 0.0101 (23.6) | 3.0 |
| 1-A2 | 0.0423 | 0.0324 (76.5) | 0.0185 (43.9) | −0.0071 (−16.8) | −0.0118 (−28.0) | 0.0047 (11.2) | −0.0028 (−6.6) | 0.0106 (25.1) | 3.6 |
| 2-A1 | 0.0285 | 0.0359 (125.9) | −0.0022 (−7.6) | −0.0040 (−14.1) | −0.0088 (−31.0) | 0.0048 (16.9) | −0.0017 (−5.8) | 0.0115 (40.3) | 4.2 |
| 2-B1 | 0.0307 | 0.0369 (120.2) | 0.0006 (2.0) | −0.0058 (−19.1) | −0.0100 (−32.6) | 0.0041 (13.5) | −0.0022 (−7.1) | 0.0099 (32.3) | 3.1 |
| 2-A2 | 0.0267 | 0.0340 (127.0) | −0.0027 (−9.9) | −0.0038 (−14.3) | −0.0095 (−35.5) | 0.0057 (21.3) | −0.0000 (−0.0) | 0.0118 (44.0) | 2.9 |
| 2-B2 | 0.0286 | 0.0352 (123.1) | −0.0007 (−2.5) | −0.0056 (−19.4) | −0.0104 (−36.4) | 0.0049 (17.0) | −0.0018 (−6.2) | 0.0111 (38.9) | 1.1 |
| 3-A1 | 0.0491 | 0.0656 (133.7) | −0.0197 (−40.2) | 0.0042 (8.5) | −0.0023 (−4.7) | 0.0065 (13.2) | −0.0010 (−2.1) | 0.0107 (21.7) | 2.0 |
| 3-B1 | 0.0495 | 0.0665 (134.3) | −0.0184 (−37.1) | 0.0019 (3.8) | −0.0046 (−9.3) | 0.0065 (13.1) | −0.0024 (−4.6) | 0.0118 (23.7) | 1.0 |
| 3-A2 | 0.0491 | 0.0639 (130.2) | −0.0186 (−37.9) | 0.0040 (8.2) | −0.0026 (−5.3) | 0.0067 (13.5) | −0.0012 (−2.5) | 0.0156 (31.2) | 0.5 |
| 3-B2 | 0.0512 | 0.0656 (128.3) | −0.0161 (−31.4) | 0.0019 (3.6) | −0.0046 (−9.0) | 0.0064 (12.6) | 0.0009 (1.8) | 0.0111 (21.6) | 0.5 |
| Se (σ-hole, Cpyridyl–Se) | |||||||||
| 4-A1 | 0.0521 | 0.0897 (172.2) | −0.0122 (−23.5) | −0.0240 (−46.0) | −0.0275 (−52.7) | 0.0035 (6.7) | −0.0021 (−4.1) | 0.0100 (19.3) | 2.7 |
| 4-A2 | 0.0518 | 0.0877 (169.4) | −0.0108 (−20.9) | −0.0239 (−46.3) | −0.0276 (−53.4) | 0.0037 (7.1) | −0.0026 (−5.1) | 0.0102 (19.8) | 2.3 |
| 5-A1 | 0.0401 | 0.0941 (234.8) | −0.0318 (−79.2) | −0.0213 (−53.1) | −0.0253 (−63.1) | 0.0040 (10.0) | −0.0018 (−4.6) | 0.0112 (28.1) | 2.4 |
| 5-A2 | 0.0391 | 0.0916 (234.2) | −0.0308 (−78.7) | −0.0210 (−53.6) | −0.0257 (−65.8) | 0.0048 (12.2) | −0.0002 (−0.5) | 0.0110 (28.2) | 1.9 |
| 6-A1 | 0.0584 | 0.1227 (210.0) | −0.0495 (−84.6) | −0.0143 (−24.5) | −0.0197 (−33.7) | 0.0053 (9.1) | −0.0015 (−2.5) | 0.0103 (17.7) | 0.8 |
| 6-B1 | 0.0582 | 0.1232 (211.7) | −0.0483 (−83.0) | −0.0167 (−28.6) | −0.0219 (−37.7) | 0.0052 (9.0) | −0.0027 (−4.6) | 0.0115 (19.7) | 0.0 |
| 6-A2 | 0.0577 | 0.1207 (209.0) | −0.0480 (−83.2) | −0.0144 (−24.9) | −0.0201 (−34.9) | 0.0057 (9.9) | −0.0015 (−2.6) | 0.0111 (19.3) | 0.9 |
| 6-B2 | 0.0593 | 0.1238 (208.7) | −0.0486 (−81.9) | −0.0160 (−27.0) | −0.0210 (−35.4) | 0.0050 (8.4) | 0.0007 (1.2) | 0.0106 (17.9) | −0.3 |
| Conf. | VS,max | SF(Ch) | SF(R) | SF(BiPy) | SF(pyr) | SF(pyr’) | SF(5′-Br) | SF(3′-H) | Err% |
|---|---|---|---|---|---|---|---|---|---|
| S (σ-hole, CR–S) | |||||||||
| 1-A1 | 0.0193 | 0.0312 (161.1) | 0.0107 (55.1) | −0.0215 (−111.1) | −0.0286(−147.6) | 0.0071 (36.5) | −0.0150 (−77.4) | 0.0114 (58.7) | 5.1 |
| 1-A2 | Absent | ||||||||
| 2-A1 | 0.0268 | 0.0416 (155.4) | 0.0038 (14.1) | −0.0175 (−65.1) | −0.0261 (−97.3) | 0.0086 (32.2) | −0.0101 (−37.6) | 0.0114 (42.6) | 4.4 |
| 2-B1 | 0.0169 | 0.0342 (202.8) | 0.0041 (24.6) | −0.0204 (−120.7) | −0.0263 (−155.8) | 0.0059 (35.1) | −0.0166 (−98.1) | 0.0115 (68.0) | 6.7 |
| 2-A2 | 0.0340 | 0.0385 (113.2) | 0.0049 (14.5) | −0.0085 (−25.0) | −0.0294 (−86.6) | 0.0210 (61.7) | 0.0008 (2.3) | 0.0168 (49.3) | 2.8 |
| 2-B2 | Absent | ||||||||
| 3-A1 | 0.0445 | 0.0634 (142.5) | −0.0130 (−29.2) | −0.0051 (−11.6) | −0.0149 (−33.4) | 0.0097 (21.8) | −0.0085 (−19.2) | 0.0102 (22.9) | 1.8 |
| 3-B1 | 0.0272 | 0.0515 (189.4) | −0.0119 (−43.8) | −0.0118 (−43.5) | −0.0186 (−68.5) | 0.0068 (25.0) | −0.0176 (−64.8) | 0.0133 (49.0) | 2.1 |
| 0.0202 | 0.0267 (132.2) | −0.0121 (−59.7) | 0.0062 (30.9) | −0.0004 (−2.2) | 0.0067 (33.2) | −0.0064 (−31.8) | 0.0153 (75.9) | 3.4 | |
| 3-A2 | 0.0500 | 0.0607 (121.2) | −0.0121 (−24.1) | 0.0019 (3.8) | −0.0175 (−35.0) | 0.0194 (38.8) | −0.0006 (−1.1) | 0.0119 (24.3) | 0.9 |
| 3-B2 | 0.0553 | 0.0523 (94.6) | −0.0107 (−19.4) | 0.0144 (26.0) | −0.0162 (−29.4) | 0.0306 (55.4) | 0.0044 (7.9) | 0.0262 (47.4) | 1.2 |
| Se (σ-hole, CR–Se) | |||||||||
| 4-A1 | 0.0260 | 0.0784 (302.0) | −0.0057 (−22.1) | −0.0457 (−176.0) | −0.0495 (−190.4) | 0.0037 (14.4) | −0.0167 (−64.3) | 0.0115 (44.4) | 3.9 |
| 4-A2 | 0.0463 | 0.0810 (175.0) | −0.0048 (−10.4) | −0.0290 (−62.7) | −0.0516 (−111.4) | 0.0225 (48.7) | 0.0011 (2.4) | 0.0235 (50.8) | 1.8 |
| 5-A1 | 0.0352 | 0.0934 (265.3) | −0.0135 (−38.3) | −0.0437 (−124.1) | −0.0501(−142.2) | 0.0064 (18.1) | −0.0104 (−29.6) | 0.0113 (32.2) | 2.9 |
| 5-A2 | 0.0414 | 0.0899 (216.9) | −0.0124 (−29.9) | −0.0352 (−84.9) | −0.0532 (−128.3) | 0.0180 (43.4) | 0.0006 (1.6) | 0.0158 (38.1) | 2.0 |
| 6-A1 | 0.0559 | 0.1212 (216.9) | −0.0301 (−53.9) | −0.0346 (−62.0) | −0.0421(−75.3) | 0.0074 (13.3) | −0.0093 (-16.7) | 0.0101 (18.1) | 1.0 |
| 6-B1 | 0.0309 | 0.0839 (271.6) | −0.0286 (−92.6) | −0.0242 (−78.3) | −0.0244 (−79.0) | 0.0002 (0.7) | −0.0147 (−47.5) | 0.0137 (44.3) | 0.7 |
| 0.0319 | 0.1011 (317.0) | −0.0288 (−90.4) | −0.0400 (−125.6) | −0.0425 (−133.4) | 0.0025 (7.7) | −0.0195 (−61.3) | 0.0130 (40.6) | 0.9 | |
| 6-A2 | 0.0609 | 0.1176 (193.1) | −0.0288 (−47.4) | −0.0272 (−44.7) | −0.0444 (−72.9) | 0.0172 (28.2) | −0.0007 (−1.2) | 0.0149 (24.5) | 1.0 |
| 6-B2 | 0.0603 | 0.1059 (175.5) | −0.0284 (−47.1) | −0.0161 (−26.8) | −0.0391 (−64.9) | 0.0230 (38.1) | 0.0043 (7.2) | 0.0254 (42.1) | 1.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gatti, C.; Dessì, A.; Dallocchio, R.; Mamane, V.; Cossu, S.; Weiss, R.; Pale, P.; Aubert, E.; Peluso, P. Factors Impacting σ- and π-Hole Regions as Revealed by the Electrostatic Potential and Its Source Function Reconstruction: The Case of 4,4′-Bipyridine Derivatives. Molecules 2020, 25, 4409. https://doi.org/10.3390/molecules25194409
Gatti C, Dessì A, Dallocchio R, Mamane V, Cossu S, Weiss R, Pale P, Aubert E, Peluso P. Factors Impacting σ- and π-Hole Regions as Revealed by the Electrostatic Potential and Its Source Function Reconstruction: The Case of 4,4′-Bipyridine Derivatives. Molecules. 2020; 25(19):4409. https://doi.org/10.3390/molecules25194409
Chicago/Turabian StyleGatti, Carlo, Alessandro Dessì, Roberto Dallocchio, Victor Mamane, Sergio Cossu, Robin Weiss, Patrick Pale, Emmanuel Aubert, and Paola Peluso. 2020. "Factors Impacting σ- and π-Hole Regions as Revealed by the Electrostatic Potential and Its Source Function Reconstruction: The Case of 4,4′-Bipyridine Derivatives" Molecules 25, no. 19: 4409. https://doi.org/10.3390/molecules25194409
APA StyleGatti, C., Dessì, A., Dallocchio, R., Mamane, V., Cossu, S., Weiss, R., Pale, P., Aubert, E., & Peluso, P. (2020). Factors Impacting σ- and π-Hole Regions as Revealed by the Electrostatic Potential and Its Source Function Reconstruction: The Case of 4,4′-Bipyridine Derivatives. Molecules, 25(19), 4409. https://doi.org/10.3390/molecules25194409














