“On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface
Abstract
1. Introduction
2. Results
2.1. Anisotropic Wannier Polarizability Method
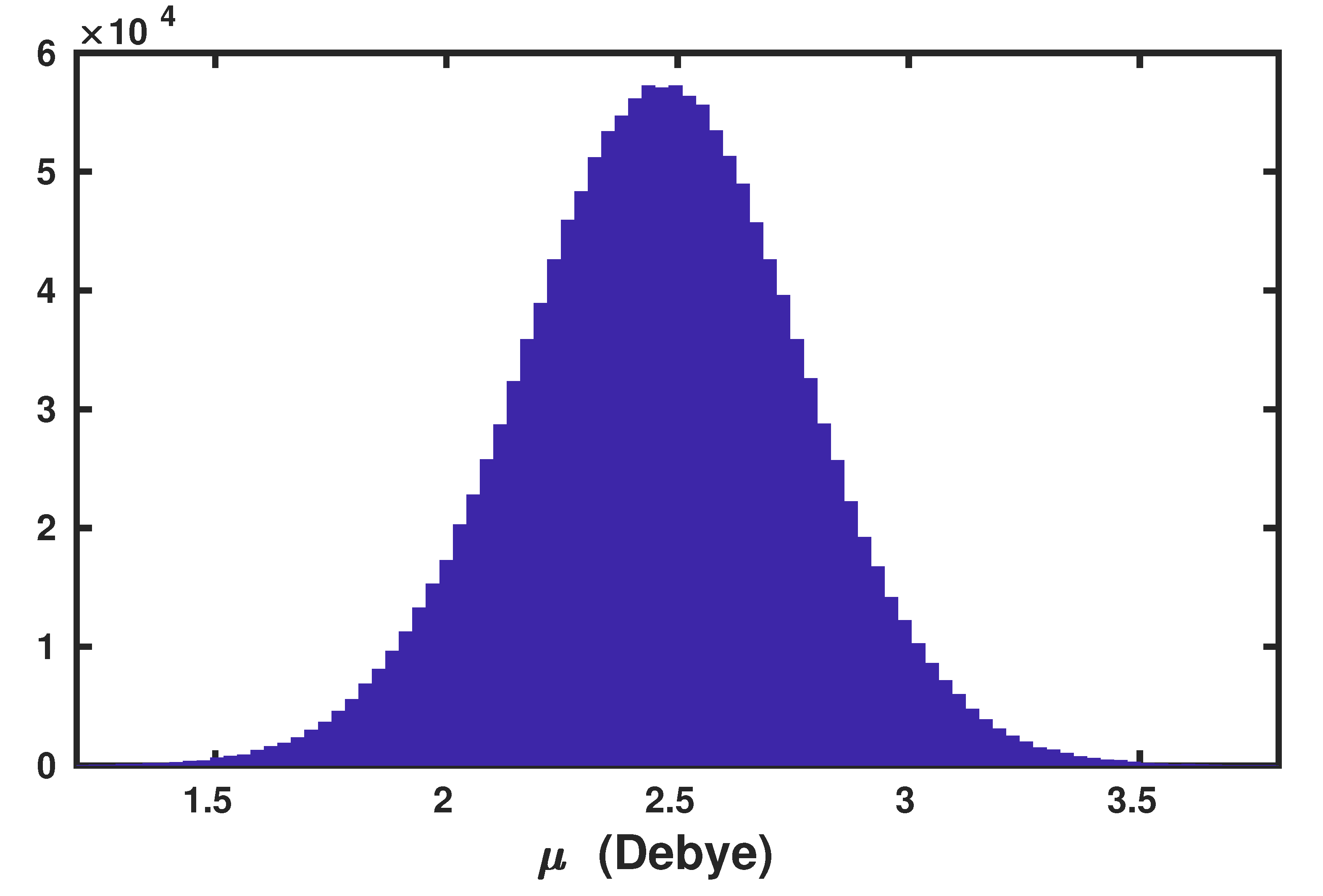
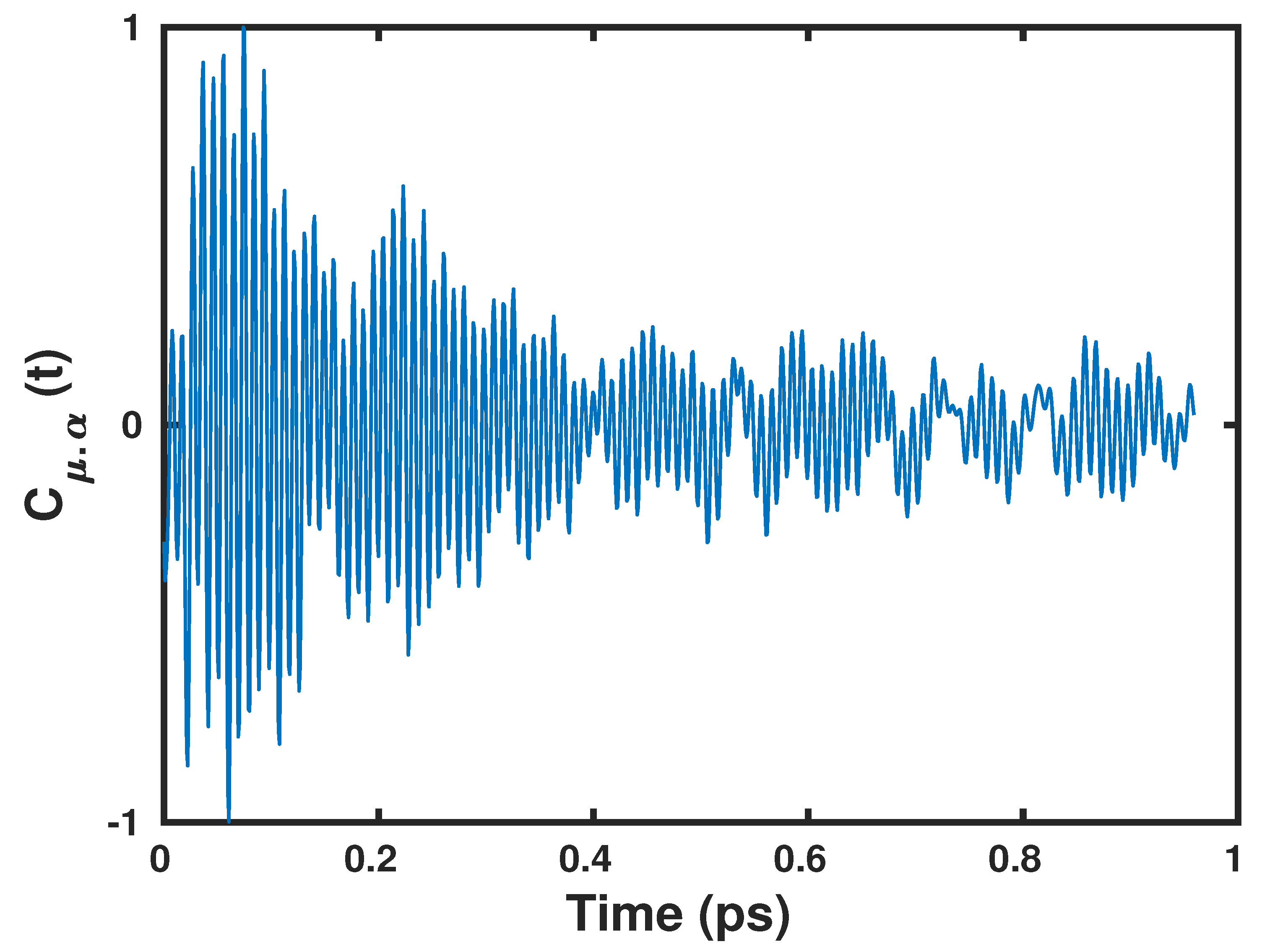
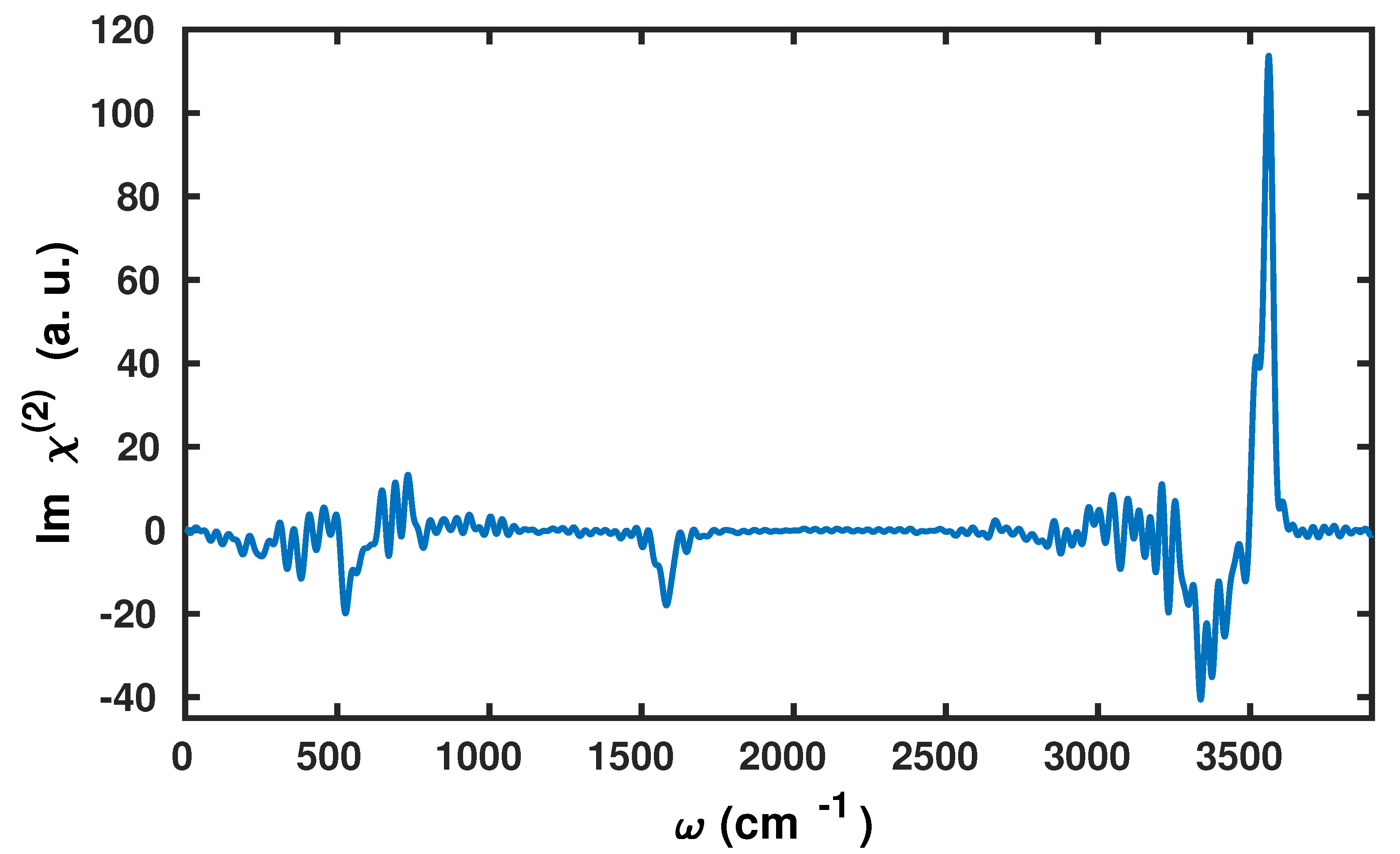
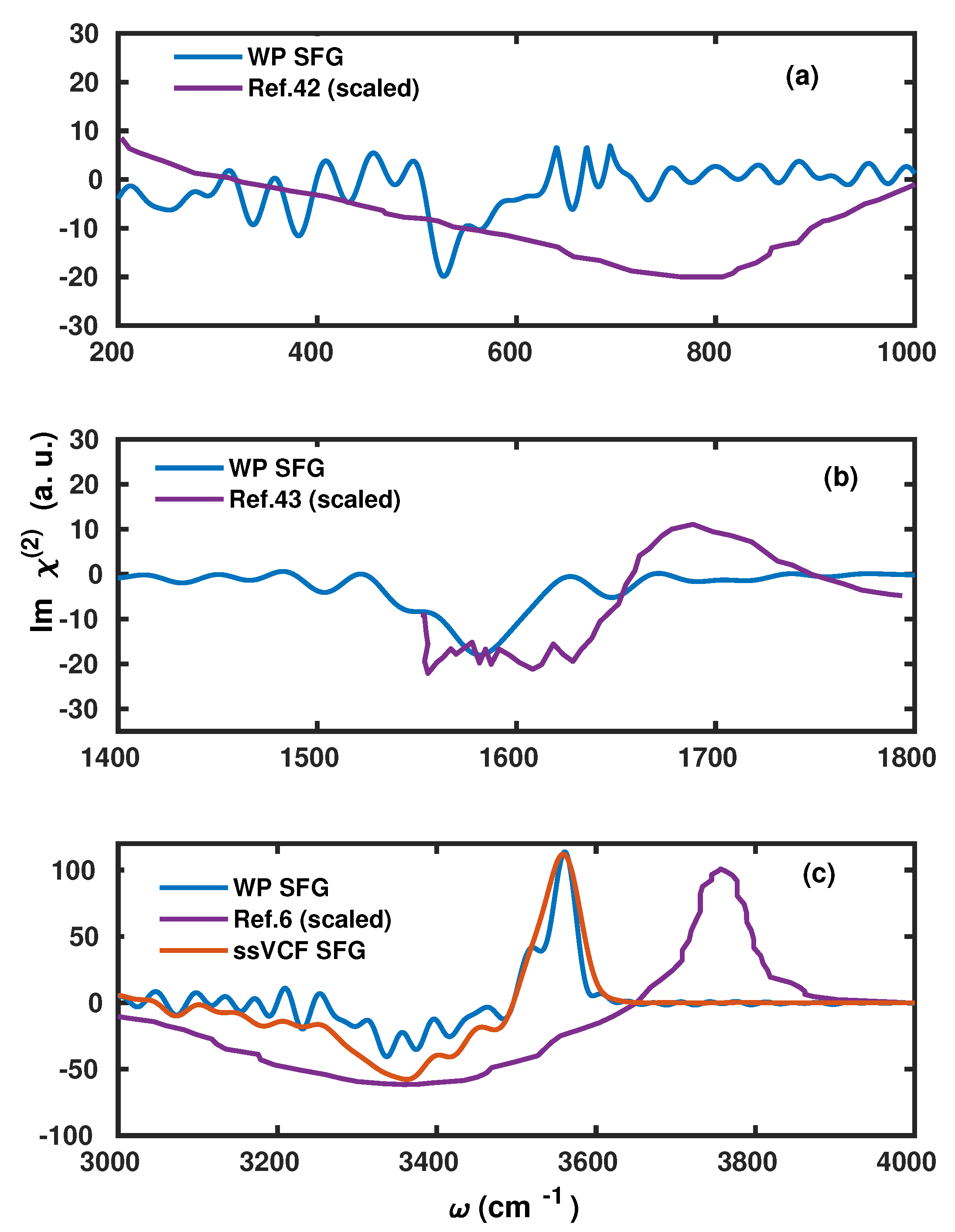
2.2. Application to the Air–Water Interface
3. Computational Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Ultrafast Dynamics at Water Interfaces Studied by Vibrational Sum Frequency Generation Spectroscopy. Chem. Rev. 2017, 16, 10665. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Superfine, R.; Freysz, E.; Shen, Y.R. Vibrational Spectroscopy of Water at the Vapor-Water Interface. Phys. Rev. Lett. 1993, 70, 2313. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.R.; Ostroverkhov, V. Sum-Frequency Vibrational Spectroscopy on Water Interfaces: Polar Orientation of Water Molecules at Interfaces. Chem. Rev. 2006, 106, 1140. [Google Scholar] [CrossRef] [PubMed]
- Bakker, H.J.; Skinner, J.L. Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water. Chem. Rev. 2010, 110, 1498. [Google Scholar] [CrossRef] [PubMed]
- Richmond, G.L. Molecular Bonding and Interactions at Aqueous Surfaces as Probed by Vibrational Sum Frequency Spectroscopy. Chem. Rev. 2002, 102, 2693. [Google Scholar] [CrossRef]
- Raymond, E.A.; Tarbuck, T.L.; Brown, M.G.; Richmond, G.L. Hydrogen-Bonding Interactions at the Vapor/Water Interface Investigated by Vibrational Sum-Frequency Spectroscopy of HOD/H2O/D2O Mixtures and Molecular Dynamics Simulations. J. Phys. Chem. B 2003, 107, 546. [Google Scholar] [CrossRef]
- Perakis, F.; Marco, L.D.; Shalit, A.; Tang, F.; Kann, Z.R.; Kühne, T.D.; Torre, R.; Bonn, M.; Nagata, Y. Vibrational Spectroscopy and Dynamics of Water. Chem. Rev. 2016, 116, 7590. [Google Scholar] [CrossRef]
- Ojha, D.; Karhan, K.; Kühne, T.D. On the Hydrogen Bond Strength and Vibrational Spectroscopy of Liquid Water. Sci. Rep. 2018, 8, 16888. [Google Scholar] [CrossRef]
- John, C.; Spura, T.; Habershon, S.; Kühne, T.D. Quantum Ring-Polymer Contraction Method: Including Nuclear Quantum Effects at no Additional Computational Cost in comparison to ab initio Molecular Dynamics. Phys. Rev. E 2016, 93, 043305. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kühne, T.D. Second generation Car–Parrinello Molecular Dynamics. WIREs Comput. Mol. Sci. 2014, 4, 391. [Google Scholar] [CrossRef]
- Souza, I.; Marzari, N.; Vanderbilt, D. Maximally Localized Wannier Functions for entangled Energy Bands. Phys. Rev. B 2001, 65, 035109. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally Localized Generalized Wannier Functions for Composite Energy Bands. Phys. Rev. B 1997, 56, 12847. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier Functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419. [Google Scholar] [CrossRef]
- Silvestrelli, P.L. Maximally Localized Wannier Functions for Simulations with Supercells of General Symmetry. Phys. Rev. B 1999, 59, 9703. [Google Scholar] [CrossRef]
- Berghold, G.; Mundy, C.J.; Romero, A.H.; Hutter, J.; Parrinello, M. General and Efficient Algorithms for obtaining Maximally Localized Wannier Functions. Phys. Rev. B 2000, 61, 10040. [Google Scholar] [CrossRef]
- Resta, R. Quantum-Mechanical Position Operator in Extended Systems. Phys. Rev. Lett. 1998, 80, 1800. [Google Scholar] [CrossRef]
- Chen, W.; Sharma, M.; Resta, R.; Galli, G.; Car, R. Role of Dipolar Correlations in the Infrared Spectra of Water and Ice. Phys. Rev. B 2008, 77, 245114. [Google Scholar] [CrossRef]
- Gaigeot, M.-P.; Sprik, M. Ab Initio Molecular Dynamics Computation of the Infrared Spectrum of Aqueous Uracil. J. Phys. Chem. B 2003, 107, 10344. [Google Scholar] [CrossRef]
- Heyden, M.; Sun, J.; Funkner, S.; Mathias, G.; Forbert, H.; Havenith, M.; Marx, D. Dissecting the THz Spectrum of Liquid Water from First Principles via Correlations in Time and Space. Proc. Natl. Acad. Sci. USA 2010, 107, 12068. [Google Scholar] [CrossRef]
- Zhang, C.; Khaliullin, R.Z.; Bovi, D.; Guidoni, L.; Kühne, T.D. Vibrational signature of water molecules in asymmetric hydrogen bonding environments. J. Phys. Chem. Lett. 2013, 4, 3245. [Google Scholar] [CrossRef]
- Ojha, D.; Henao, A.; Kühne, T.D. Nuclear quantum effects on the vibrational dynamics of liquid water. J. Chem. Phys. 2018, 148, 102328. [Google Scholar] [CrossRef] [PubMed]
- Ojha, D.; Chandra, A. Phys. Temperature dependence of the ultrafast vibrational echo spectroscopy of OD modes in liquid water from first principles simulations. Phys. Chem. Chem. Phys. 2019, 21, 6485. [Google Scholar] [CrossRef] [PubMed]
- Ojha, D.; Chandra, A. Two-dimensional infrared spectroscopy of aqueous solutions from first principles simulations. Chem. Phys. Lett. 2020, 751, 137493. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic Polarization in Crystalline Dielectrics: the Geometric Phase Approach. Rev. Mod. Phys. 1994, 66, 899. [Google Scholar] [CrossRef]
- King-Smith, R.D.; Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651. [Google Scholar] [CrossRef]
- Umari, P.; Pasquarello, A. Ab initio Molecular Dynamics in a Finite Homogeneous Electric Field. Phys. Rev. Lett. 2002, 89, 157602. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Putrino, A.; Parrinello, M. Anharmonic Raman Spectra in High-Pressure Ice from Ab Initio Simulations. Phys. Rev. Lett. 2002, 88, 176401. [Google Scholar] [CrossRef]
- Luber, S.; Iannuzzi, M.; Hutter, J. Raman spectra from ab initio molecular dynamics and its application to liquid S-methyloxirane. J. Chem. Phys. 2014, 141, 094503. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.D.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- Azar, P.P.; Kühne, T.D. Efficient “On-the-Fly” calculation of Raman Spectra from Ab-Initio molecular dynamics: Application to hydrophobic/hydrophilic solutes in bulk water. J. Comput. Chem. 2015, 36, 2188. [Google Scholar] [CrossRef]
- Morita, A.; Hynes, J.T. A theoretical analysis of the sum frequency generation spectrum of the water surface. Chem. Phys. 2000, 258, 371. [Google Scholar] [CrossRef]
- Morita, A.; Hynes, J.T. A theoretical analysis of the sum frequency generation spectrum of the water surface. II. Time-dependent approach. J. Phys. Chem. B 2002, 106, 673. [Google Scholar] [CrossRef]
- Ishiyama, T.; Imamura, T.; Morita, A. Theoretical Studies of Structures and Vibrational Sum Frequency Generation Spectra at Aqueous Interfaces. Chem. Rev. 2014, 114, 8447. [Google Scholar] [CrossRef] [PubMed]
- Pieniazek, P.A.; Tainter, C.J.; Skinner, J.L. Surface of Liquid Water: Three-Body Interactions and Vibrational Sum-Frequency Spectroscopy. J. Am. Chem. Soc. 2011, 133, 10360. [Google Scholar] [CrossRef]
- Li, Y.; Skinner, J.L. IR spectra of water droplets in no man’s land and the location of the liquid-liquid critical point. J. Chem. Phys. 2016, 145, 124509. [Google Scholar]
- Li, Y.; Skinner, J.L. Communication: Vibrational sum-frequencyspectrum of the air-water interface, revisited. J. Chem. Phys. 2016, 145, 031103. [Google Scholar]
- Pieniazek, P.A.; Tainter, C.J.; Skinner, J.L. Interpretation of the water surface vibrational sum-frequency spectrum. J. Chem. Phys. 2011, 135, 044701. [Google Scholar] [CrossRef]
- Li, Y.; Gruenbaum, M.; Skinner, J.L. Slow hydrogen-bond switching dynamics at the water surface revealed by theoretical two-dimensional sum-frequency spectroscopy. Proc. Natl. Acad. Sci. USA 2013, 110, 1992. [Google Scholar]
- Ohta, T.; Usui, K.; Hasegawa, T.; Bonn, M.; Nagata, Y. Toward ab initio molecular dynamics modeling for sum-frequency generation spectra; an efficient algorithm based on surface-specific velocity-velocity correlation function. J. Chem. Phys. 2015, 143, 124702. [Google Scholar] [CrossRef]
- Khatib, R.; Hasegawa, T.; Sulpizi, M.; Backus, E.H.G.; Bonn, M.; Nagata, Y. Molecular Dynamics Simulations of SFG Librational Modes Spectra of Water at the Water–Air Interface. J. Phys. Chem. C 2016, 120, 18665. [Google Scholar] [CrossRef]
- Nagata, Y.; Hsieh, C.-S.; Hasegawa, T.; Voll, J.; Backus, E.H.G.; Bonn, M. Water Bending Mode at the Water–Vapor Interface Probed by Sum-Frequency Generation Spectroscopy: A Combined Molecular Dynamics Simulation and Experimental Study. J. Phys. Chem. Lett. 2013, 11, 1872. [Google Scholar] [CrossRef] [PubMed]
- Kaliannan, N.K.; Henao, A.; Wiebeler, H.; Zysk, F.; Ohto, T.; Nagata, Y.; Kühne, T.D. Impact of intermolecular vibrational coupling effects on the sum-frequency generation spectra of the water/air interface. Mol. Phys. 2020, 118, 1620358. [Google Scholar] [CrossRef]
- Sulpizi, M.; Salanne, M.; Sprik, M.; Gaigeot, M.P. Vibrational sum frequency generation spectroscopy of the water liquid–vapor interface from density functional theory-based molecular dynamics simulations. J. Phys. Chem. Lett. 2013, 4, 83. [Google Scholar] [CrossRef]
- Khatib, R.; Sulpizi, M. Sum Frequency Generation Spectra from Velocity–Velocity Correlation Functions. J. Phys. Chem. Lett. 2017, 8, 1310. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Jeon, J.; Cho, M. Ab initio Modeling of the Vibrational Sum-Frequency Generation Spectrum of Interfacial Water. J. Phys. Chem. Lett. 2019, 10, 1153. [Google Scholar] [CrossRef]
- Ohto, T.; Dodia, M.; Xu, J.; Imoto, S.; Tang, F.; Zysk, F.; Kühne, T.D.; Shigeta, Y.; Bonn, M.; Wu, X.; et al. Accessing the accuracy of density functional theory through structure and dynamics of the water–air interface. J. Phys. Chem. Lett. 2019, 10, 4914. [Google Scholar] [CrossRef]
- Partovi-Azar, P.; Kühne, T.D.; Kaghazchi, P. Evidence for the existence of Li2S2 clusters in lithium–sulfur batteries: ab initio Raman spectroscopy simulation. Phys. Chem. Chem. Phys. 2015, 17, 22009. [Google Scholar] [CrossRef]
- Laidig, K.E.; Bader, R.F.W. Properties of atoms in molecules: Atomic polarizabilities. J. Chem. Phys. 1990, 93, 7213. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471. [Google Scholar] [CrossRef]
- Hutter, J.; Alavi, A.; Deutsch, T.; Bernasconi, M.; Goedecker, S.; Marx, D.; Tuckerman, M.; Parrinello, M. CPMD Program, MPI für Festkörperforschung and IBM Zurich Research Laboratory. Available online: www.cpmd.org (accessed on 28 August 2020).
- Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; Taylor & Francis: Abingdon, UK, 2003. [Google Scholar]
- Vanderbilt, D. Car-Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a Long-range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef] [PubMed]
- McGrath, M.J.; Kuo, I.F.; Siepmann, J.I. Liquid Structures of Water, Methanol, and Hydrogen Fluoride at Ambient Conditions from first principles Molecular Dynamics Simulations with a Dispersion Corrected Density Functional. Phys. Chem. Chem. Phys. 2011, 13, 19943. [Google Scholar] [CrossRef] [PubMed]
- Kühne, T.D.; Pascal, T.A.; Kaxiras, E.; Jung, Y. New insights into the Structure of the Vapor/water Interface from Large-scale First-principles Simulations. J. Phys. Chem. Lett. 2011, 2, 105. [Google Scholar] [CrossRef] [PubMed]
- McGrath, M.J.; Kuo, I.F.; Ghogomu, J.N.; Mundy, C.J.; Siepmann, J.I. Vapor-Liquid Coexistence Curves for Methanol and Methane Using Dispersion-Corrected Density Functional Theory. J. Phys. Chem. B 2011, 115, 11688. [Google Scholar] [CrossRef]
- Nagata, Y.; Ohto, T.; Bonn, M.; Kühne, T.D. Surface Tension of ab initio Liquid Water at the Water-air Interface. J. Chem. Phys. 2016, 144, 204705. [Google Scholar] [CrossRef]
- Nose, S. A Unified Formulation of the Constant Temperature Molecular-Dynamics Methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Pártay, L.B.; Hantal, G.; Jedlovszky, P.; Vincze, Á.; Horvai, G. A new method for determining the interfacial molecules and characterizing the surface roughness in computer simulations. Application to the liquid–vapor interface of water. J. Comp. Chem. 2008, 29, 945. [Google Scholar] [CrossRef] [PubMed]
- Sega, M.; Kantorovich, S.S.; Jedlovszky, P.; Jorge, M. A Python Package for the Interfacial Analysis of Molecular Simulations. J. Chem. Phys. 2013, 138, 044110. [Google Scholar] [CrossRef] [PubMed]
- Bredenbeck, J.; Ghosh, A.; Nienhuys, H.-K.; Bonn, M. Interface-specific Ultrafast Two-dimensional Vibrational Spectroscopy. Acc. Chem. Res. 2009, 42, 1332. [Google Scholar] [CrossRef]
- Ojha, D.; Kaliannan, N.K.; Kühne, T.D. Time-dependent Vibrational Sum-frequency Generation Spectroscopy of the Air-water Interface. Commun. Chem. 2019, 2, 116. [Google Scholar] [CrossRef]
- Savolainen, J.; Ahmed, S.; Hamm, P. Two-dimensional Raman-terahertz Spectroscopy of Water. Proc. Natl. Acad. Sci. USA 2013, 110, 20402. [Google Scholar] [CrossRef] [PubMed]
- Elgabarty, H.; Kampfrath, T.; Bonthuis, D.J.; Balos, V.; Kaliannan, N.K.; Loche, P.; Netz, R.R.; Wolf, M.; Kühne, T.D.; Sajadi, M. Energy Transfer within the Hydrogen Bonding Network of Water following Resonant Terahertz Excitation. Sci. Adv. 2020, 6, eaay7074. [Google Scholar] [CrossRef]
- Tanimura, Y.; Mukamel, S. Two-dimensional Femtosecond Vibrational Spectroscopy of Liquids. J. Chem. Phys. 1993, 99, 9496. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojha, D.; Kühne, T.D. “On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface. Molecules 2020, 25, 3939. https://doi.org/10.3390/molecules25173939
Ojha D, Kühne TD. “On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface. Molecules. 2020; 25(17):3939. https://doi.org/10.3390/molecules25173939
Chicago/Turabian StyleOjha, Deepak, and Thomas D. Kühne. 2020. "“On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface" Molecules 25, no. 17: 3939. https://doi.org/10.3390/molecules25173939
APA StyleOjha, D., & Kühne, T. D. (2020). “On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface. Molecules, 25(17), 3939. https://doi.org/10.3390/molecules25173939






