Magnetization Characteristics of Oriented Single-Crystalline NiFe-Cu Nanocubes Precipitated in a Cu-Rich Matrix
Abstract
1. Introduction
2. Results
2.1. Materials
2.2. Measurements
3. Discussion
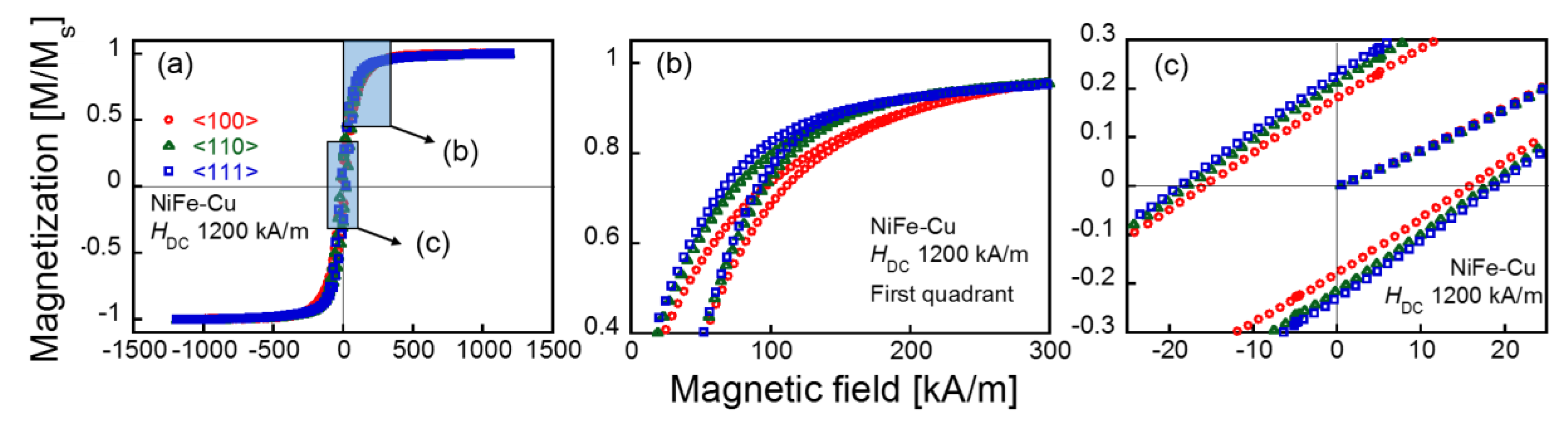
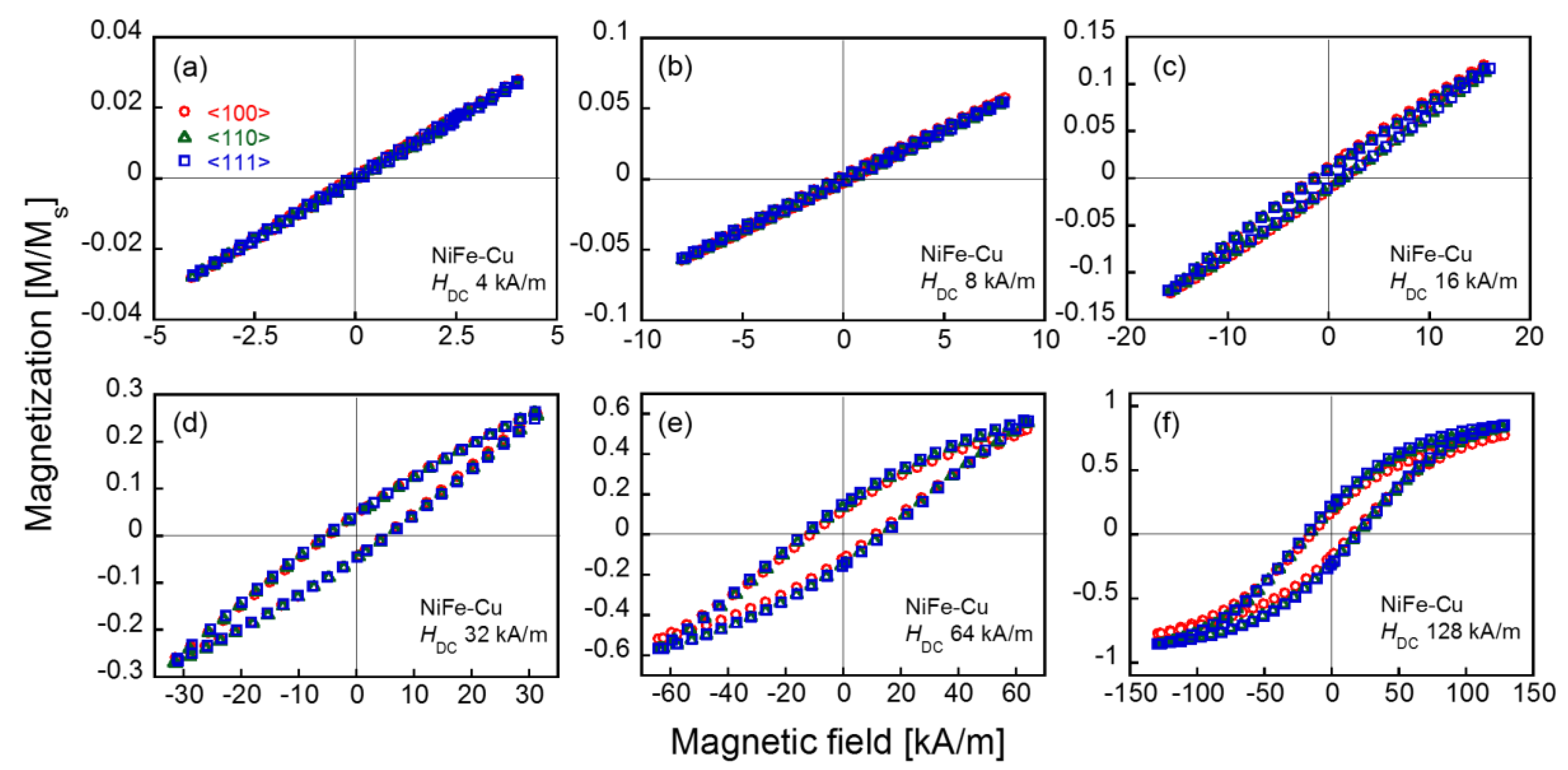
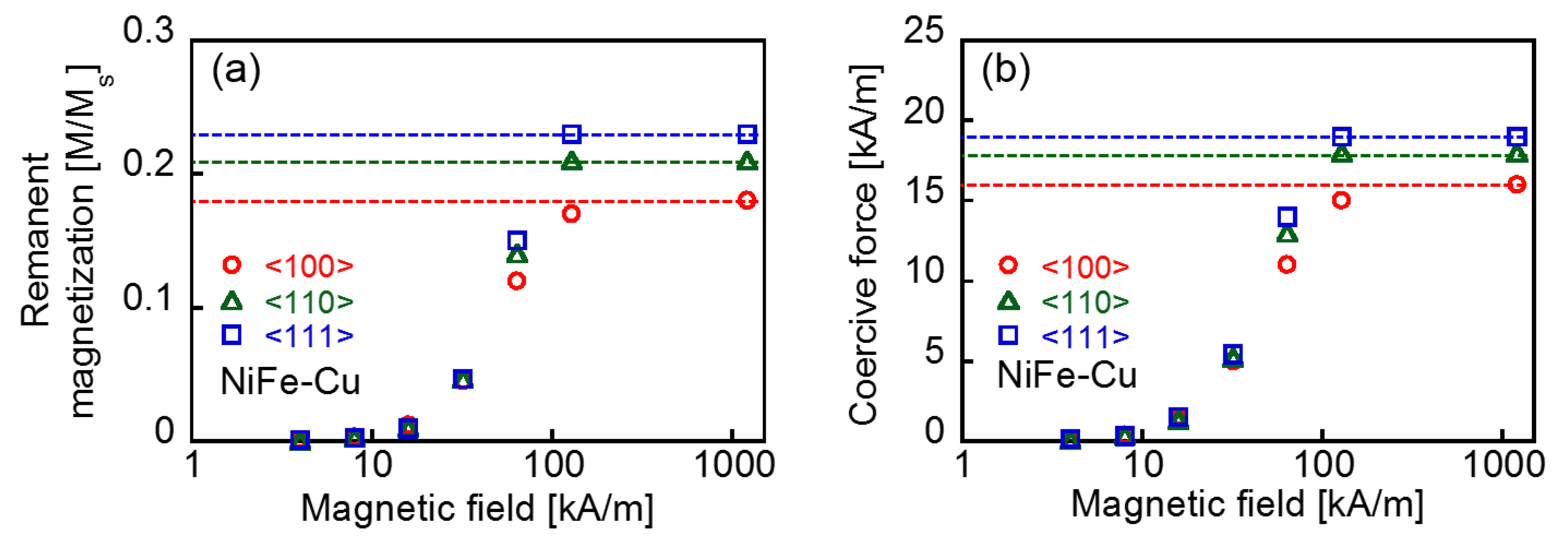
3.1. DC Magnetization Curves
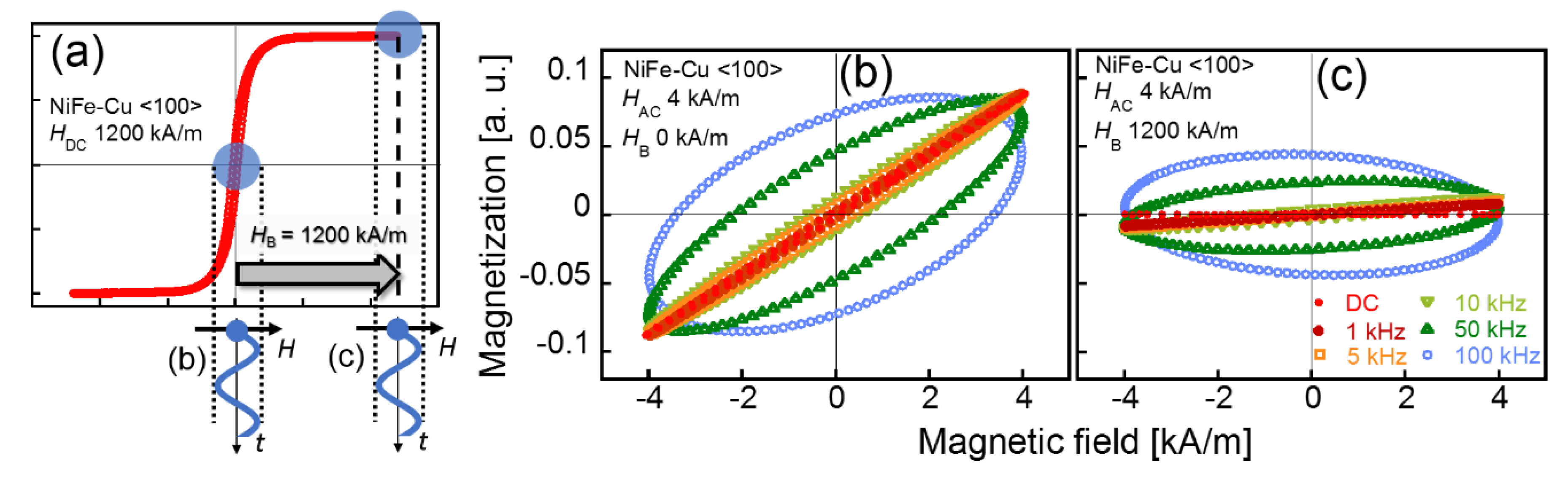
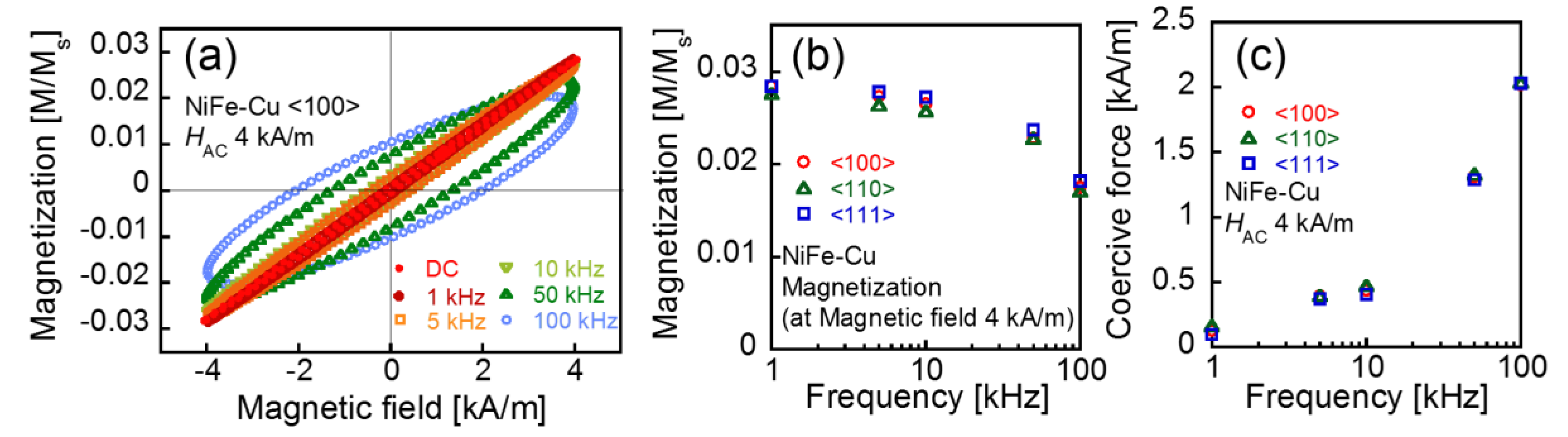
3.2. AC Magnetization Curves
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Palzer, R.J.; Heiderger, C. Studies on the quantitative biology of hyperthermic killing of hela cells. Cancer Res. 1973, 33, 415–421. [Google Scholar] [PubMed]
- Pankhurst, Q.A.; Thanh, N.K.T.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Mamiya, H. Recent advances in understanding magnetic nanoparticles in AC magnetic fields and optimal design for targeted hyperthermia. J. Nanomater. 2013, 2013, 752973. [Google Scholar] [CrossRef]
- Shi, G.; Takeda, R.; Trisnanto, S.B.; Yamada, T.; Ota, S.; Takemura, Y. Enhanced specific loss power from Resovist® achieved by aligning magnetic easy axes of nanoparticles for hyperthermia. J. Magn. Magn. Mater. 2019, 473, 148–154. [Google Scholar] [CrossRef]
- Khurshid, H.; Alonso, J.; Nemati, Z.; Phan, M.H.; Mukherjee, P.; Fdez-Gubieda, M.L.; Barandiarán, J.M.; Srikanth, H. Anisotropy effects in magnetic hyperthermia: A comparison between spherical and cubic exchange-coupled FeO/Fe3O4 nanoparticles. J. Appl. Phys. 2015, 117, 17A337. [Google Scholar] [CrossRef]
- Oyarzún, S.; Tamion, A.; Tournus, F.; Dupuis, V.; Hillenkamp, M. Size effects in the magnetic anisotropy of embedded cobalt nanoparticles: From shape to surface. Sci. Rep. 2015, 5, 14749. [Google Scholar] [CrossRef]
- Ota, S.; Takemura, Y. Characterization of Néel and Brownian relaxations isolated from complex dynamics influenced by dipole interactions in magnetic nanoparticles. J. Phys. Chem. C. 2019, 123, 28859–28866. [Google Scholar] [CrossRef]
- Trisnanto, S.B.; Ota, S.; Takemura, Y. Two-step relaxation process of colloidal magnetic nanoclusters under pulsed fields. Appl. Phys. Express 2018, 11, 075001. [Google Scholar] [CrossRef]
- Martinez-Boubeta, C.; Simeonidis, K.; Makridis, A.; Angelakeris, M.; Iglesias, O.; Guardia, P.; Cabot, A.; Yedra, L.; Estradé, S.; Peiró, F.; et al. Learning from nature to improve the heat generation of iron-oxide nanoparticles for magnetic hyperthermia applications. Sci. Rep. 2013, 3, 1652. [Google Scholar] [CrossRef]
- Branquinho, L.C.; Carrião, M.S.; Costa, A.S.; Zufelato, N.; Sousa, M.H.; Miotto, R.; Ivkov, R.; Bakuzis, A.F. Effect of magnetic dipolar interactions on nanoparticle heating efficiency: Implications for cancer hyperthermia. Sci. Rep. 2013, 3, 2887. [Google Scholar] [CrossRef]
- Yoshida, T.; Matsugi, Y.; Tsujimura, N.; Sasayama, T.; Enpuku, K.; Viereck, T.; Schilling, M.; Ludwig, F. Effect of alignment of easy axes on dynamic magnetization of immobilized magnetic nanoparticles. J. Magn. Magn. Mater. 2017, 427, 162–167. [Google Scholar] [CrossRef]
- Ota, S.; Matsugi, Y.; Nakamura, T.; Takeda, R.; Takemura, Y.; Kato, I.; Nohara, S.; Sasayama, T.; Yoshida, T.; Enpuku, K. Effects of size and anisotropy of magnetic nanoparticles associated with dynamics of easy axis for magnetic particle imaging. J. Magn. Magn. Mater. 2019, 474, 311–318. [Google Scholar] [CrossRef]
- Ota, S.; Takemura, Y. Dynamics of magnetization and easy axis of individual ferromagnetic nanoparticle subject to anisotropy and thermal fluctuations. J. Magn. Soc. Jpn. 2019, 43, 34–41. [Google Scholar] [CrossRef]
- Suzuki, T.; Yanase, S.; Honda, N.; Ouchi, K. Recording characteristics of ordered Fe-Pt high-density perpendicular magnetic recording media. J. Magn. Soc. Jpn. 1999, 23, 957–960. [Google Scholar] [CrossRef]
- Bozorth, R.M. The Permalloy Problem. Rev. Mod. Phys. 1953, 25, 42–48. [Google Scholar] [CrossRef]
- Graham, C.D., Jr. Magnetocrystalline anisotropy constants of iron at room temperature and below. Phys. Rev. 1958, 112, 1117–1120. [Google Scholar] [CrossRef]
- Paige, D.M.; Szpunar, B.; Tanner, B.K. The magnetocrystalline anisotropy of cobalt. J. Magn. Magn. Mater. 1984, 44, 239–248. [Google Scholar] [CrossRef]
- Franse, J.J.M.; De Vries, G. The magnetocrystalline anisotropy energy of nickel. Physica 1968, 39, 477–498. [Google Scholar] [CrossRef]
- Usov, N.A.; Nesmeyanov, M.S.; Gubanova, E.M.; Epshtein, N.B. Heating ability of magnetic nanoparticles with cubic and combined anisotropy. Beilstein J. Nanotechnol. 2019, 10, 305–314. [Google Scholar] [CrossRef]
- Kim, J.S.; Taniuchi, T.; Mizuguchi, M.; Shin, S.; Takanashi, K.; Takeda, M. Microstructural evolution and correlated magnetic domain configuration of nanoparticles embedded in a single crystal of Cu75–Ni20–Fe5 alloy. J. Phys. D Appl. Phys. 2016, 49, 335006. [Google Scholar] [CrossRef]
- Kim, J.S.; Takeda, M.; Bae, D.S. Microstructural evolution and magnetic properties of ultrafine solute-atom particles formed in a Cu75–Ni20–Fe5 alloy on isothermal annealing. Jpn. J. Appl. Phys. 2016, 55, 123002. [Google Scholar] [CrossRef]
- Matai, S.; Sakakura, H.; Takeda, M. Relationship between microstructure and magnetic properties of nano-scale particles formed in Cu-Ni-(FeCo) alloys. Mater. Sci. Forum 2018, 941, 1324–1329. [Google Scholar] [CrossRef]
- Sakakura, H.; Matai, S.; Takeda, M. Spontaneous microstructural evolution and magnetic properties of nano-scale particles comprising ferromagnetic element atoms in Cu-Ni-Fe and Cu-Ni-Co alloys. Mater. Sci. Forum 2018, 941, 1222–1227. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism, Reissued; IEEE Press: New York, NY, USA, 1993; pp. 154–155. [Google Scholar]
- Trygg, J.; Johansson, B.; Eriksson, O.; Wills, J.M. Total energy calculation of the magnetocrystalline anisotropy energy in the ferromagnetic 3d metals. Phys. Rev. Lett. 1995, 75, 2871–2874. [Google Scholar] [CrossRef]
- Bozorth, R.M. Determination of ferromagnetic anisotropy in single crystals and in polycrystalline sheets. Phys. Rev. 1936, 50, 1076–1081. [Google Scholar] [CrossRef]
- Williams, H.J. Magnetic properties of single crystals of silicon iron. Phys. Rev. 1937, 52, 747–751. [Google Scholar] [CrossRef]
- Krishnan, K.M. Fundamentals and Applications of Magnetic Materials; Oxford Univ. Press: Oxford, UK, 2016; pp. 193–212. [Google Scholar]
- Ota, S.; Takemura, Y. Evaluation of easy-axis dynamics in a magnetic fluid by measurement and analysis of the magnetization curve in an alternating magnetic field. Appl. Phys. Express 2017, 10, 085001. [Google Scholar] [CrossRef]
- Ota, S.; Yamada, T.; Takemura, Y. Dipole-dipole interaction and its concentration dependence of magnetic fluid evaluated by alternating current hysteresis measurement. J. Appl. Phys. 2015, 117, 17D713. [Google Scholar] [CrossRef]
- Ota, S.; Kitaguchi, R.; Takeda, R.; Yamada, T.; Takemura, Y. Rotation of magnetization derived from Brownian relaxation in magnetic fluids of different viscosity evaluated by dynamic hysteresis measurements over a wide frequency range. Nanomaterials 2016, 6, 170. [Google Scholar] [CrossRef]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Hergt, R.; Hiergeist, R.; Hilger, I.; Kaiser, W.A.; Lapatnikov, Y.; Margel, S.; Richter, U. Maghemite nanoparticles with very high AC-losses for application in RF-magnetic hyperthermia. J. Magn. Magn. Mater. 2004, 270, 345–357. [Google Scholar] [CrossRef]
- Chung, S.H.; Hoffmann, A.; Bader, S.D.; Liu, C.; Kay, B.; Makowski, L.; Chen, L. Biological sensors based on Brownian relaxation of magnetic nanoparticles. Appl. Phys. Lett. 2004, 85, 2971. [Google Scholar] [CrossRef]
- Trisnanto, S.B.; Takemura, Y. Complex magnetization harmonics of polydispersive magnetic nanoclusters. Nanomaterials 2018, 8, 424. [Google Scholar] [CrossRef]
- Shah, S.A.; Reeves, D.B.; Ferguson, R.M.; Weaver, J.B.; Krishnan, K.M. Mixed Brownian alignment and Néel rotations in superparamagnetic iron oxide nanoparticle suspensions driven by an ac field. Phys. Rev. B 2015, 92, 094438. [Google Scholar] [CrossRef]
- Simeonidis, K.; Morales, M.P.; Marciello, M.; Angelakeris, M.; de la Presa, P.; Lazaro-Carrillo, A.; Tabero, A.; Villanueva, A.; Chubykalo, O.; Serantes, D. In-situ particles reorientation during magnetic hyperthermia application: Shape matters twice. Sci. Rep. 2016, 6, 38382. [Google Scholar] [CrossRef]
- Takeda, R.; Ota, S.; Yamada, T.; Takemura, Y. Dynamic hysteresis measurement of magnetic nanoparticles with aligned easy axes. J. Magn. Soc. Jpn. 2018, 42, 55–61. [Google Scholar] [CrossRef]


| Base Material: Cu75Ni20Fe5 | Cu | Ni | Fe | μB |
|---|---|---|---|---|
| Matrix | 80.9 | 16.6 | 2.5 | 0.04 |
| Nanocubic precipitates | 21.2 | 51.4 | 27.4 | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, S.; Yamaminami, T.; Sakakura, H.; Takeda, M.; Yamada, T.; Sakuma, H.; Trisnanto, S.B.; Ota, S.; Takemura, Y. Magnetization Characteristics of Oriented Single-Crystalline NiFe-Cu Nanocubes Precipitated in a Cu-Rich Matrix. Molecules 2020, 25, 3282. https://doi.org/10.3390/molecules25143282
Kobayashi S, Yamaminami T, Sakakura H, Takeda M, Yamada T, Sakuma H, Trisnanto SB, Ota S, Takemura Y. Magnetization Characteristics of Oriented Single-Crystalline NiFe-Cu Nanocubes Precipitated in a Cu-Rich Matrix. Molecules. 2020; 25(14):3282. https://doi.org/10.3390/molecules25143282
Chicago/Turabian StyleKobayashi, Shota, Tsuyoshi Yamaminami, Hibiki Sakakura, Mahoto Takeda, Tsutomu Yamada, Hiroshi Sakuma, Suko Bagus Trisnanto, Satoshi Ota, and Yasushi Takemura. 2020. "Magnetization Characteristics of Oriented Single-Crystalline NiFe-Cu Nanocubes Precipitated in a Cu-Rich Matrix" Molecules 25, no. 14: 3282. https://doi.org/10.3390/molecules25143282
APA StyleKobayashi, S., Yamaminami, T., Sakakura, H., Takeda, M., Yamada, T., Sakuma, H., Trisnanto, S. B., Ota, S., & Takemura, Y. (2020). Magnetization Characteristics of Oriented Single-Crystalline NiFe-Cu Nanocubes Precipitated in a Cu-Rich Matrix. Molecules, 25(14), 3282. https://doi.org/10.3390/molecules25143282






