A Fractional Diffusion Model for Dye-Sensitized Solar Cells
Abstract
1. Introduction
2. Mathematical Model
3. Finite Difference Method
3.1. Nodes Determined by Boundary Conditions
3.2. Iteration Algorithm
3.3. Estimate for Short-Circuit Current Density
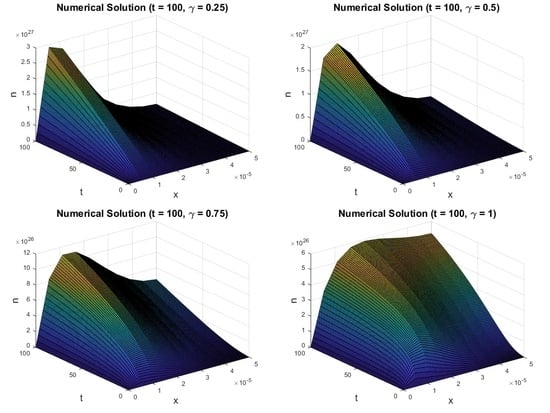
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DSSC | Dye-Sensitized Solar Cell |
| FPDE | Fractional Partial Differential Equation |
| Titanium Dioxide |
References
- O’Regan, B.; Grätzel, M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar] [CrossRef]
- Chapin, D.L.; Fuller, C.S.; Pearson, G.L. A new Silicon junction photocell for converting solar radiation into electrical power. J. Appl. Phys. 1954, 25, 676–677. [Google Scholar] [CrossRef]
- Ferber, J.; Stangl, R.; Luther, J. An electrical model of the dye-sensitized solar cell. Sol. Energy Mater. Sol. Cells 1998, 53, 29–54. [Google Scholar] [CrossRef]
- Gregg, B.A. Comment on “Diffusion impedance and space charge capacitance in the nanoporous dye-sensitized electrochemical solar cell” and “Electronic transport in dye-sensitized nanoporous TiO2 solar cells—Comparison of electrolyte and solid-state devices”. J. Phys. Chem. B 2003, 107, 13540. [Google Scholar] [CrossRef]
- Södergren, S.; Hagfeldt, A.; Olsson, J.; Lindquist, S. Theoretical Models for the Action Spectrum and the Current-Voltage Characteristics of Microporous Semiconductor Films in Photoelectrochemical Cells. J. Phys. Chem. 1994, 98, 5552–5556. [Google Scholar] [CrossRef]
- Cao, F.; Oskam, G.; Meyer, G.J.; Searson, P.C. Electron Transport in Porous Nanocrystalline TiO2 Photoelectrochemical Cells. J. Phys. Chem. 1996, 100, 17021–17027. [Google Scholar] [CrossRef]
- Anta, J.A.; Casanueva, F.; Oskam, G. A numerical model for charge transport and recombination in dye-sensitized solar cells. J. Phys. Chem. B 2006, 110, 5372–5378. [Google Scholar] [CrossRef]
- Maldon, B.; Thamwattana, N.; Edwards, M. Exploring nonlinear diffusion equations for modelling dye-sensitized solar cells. Entropy 2020, 22, 248. [Google Scholar] [CrossRef]
- Andrade, L.; Sousa, J.; Ribeiro, H.A.; Mendes, A. Phenomenological modeling of dye-sensitized solar cells under transient conditions. Sol. Energy 2020, 85, 781–793. [Google Scholar] [CrossRef]
- Gacemi, Y.; Cheknane, A.; Hilal, H.S. Simulation and modelling of charge transport in dye-sensitized solar cells based on carbon nano-tube electrodes. Phys. Scr. 2013, 87, 035703–035714. [Google Scholar] [CrossRef]
- Maldon, B.; Thamwattana, N. An analytical solution for charge carrier densities in dye-sensitized solar cells. J. Photoch. Photobiol. A 2019, 370, 41–60. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific Publishing Co. Pty. Ltd.: Singapore, 2014. [Google Scholar]
- Nigmatullin, R. The realization of the generalised transfer equation in a medium with fractal geometry. Phys. Status Solidi B 1986, 133, 425–430. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Fractional reaction-diffusion. Phys. A 2000, 276, 448–455. [Google Scholar] [CrossRef]
- Nelson, J. Continuous-Time Random-Walk Model of Electron Transport in Nanocrystalline TiO2 Electrodes. Phys. Rev. B 1999, 59, 15374–15380. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Svetukhin, V.V.; Uchaikin, V.V.; Morozova, E.V. Fractional Model of Electron Diffusion in Dye-Sensitized Nanocrystalline Solar Cells. In Proceedings of the International Conference on Mathematical Models and Methods in Applied Sciences, Saint Petersburg, Russia, 23–25 September 2014; pp. 118–121. [Google Scholar]
- Koster, L.J.A.; Smits, E.C.P.; Mihailetchi, V.D.; Blom, P.W.M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 2005, 72, 085205.1–085205.9. [Google Scholar] [CrossRef]
- Duan, J.S.; Fu, S.Z.; Wang, Z. Fractional diffusion-wave equations on finite interval by Laplace transform. Integral Transform. Spec. Funct. 2014, 25, 220–229. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency indepdendent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M.; Meerschaert, M.; Sankaranarayanan, H. Reprint of: Boundary conditions for fractional diffusion. J. Comput. Appl. Math. 2018, 339, 414–430. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of fractional integrals and derivatives of elementary functions: Overview and tutorial. Mathematics 2019, 7, 407. [Google Scholar] [CrossRef]
- Benkstein, K.D.; Kopidakis, N.; van de Lagemaat, J.; Frank, A.J. Influence of the percolation network geometry on electron transport in dye-sensitized titanium dioxide solar cells. J. Phys. Chem. B 2003, 107, 7759–7767. [Google Scholar] [CrossRef]
- Hu, Y.; Li, C.; Li, H. The finite difference method for Caputo-type parabolic equation with fractional Laplacian: One dimension case Chaos Soliton. Fract. 2017, 102, 319–326. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Yoshimoto, Y.; Suda, R. Second order accuracy finite difference methods for space-fractional partial differential equations. J. Comput. Appl. Math. 2017, 320, 101–109. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. The finite difference methods for fractional ordinary differential equations. Numer. Funct. Anal. Opt. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration of Arbitrary Order; Academic Press: San Diego, CA, USA, 1974. [Google Scholar]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C.; Sumathy, K. An analytical study of the porosity effect on dye-sensitized solar cell performance. Sol. Energy Mater. Sol. Cells 2006, 90, 1331–1344. [Google Scholar] [CrossRef]
- Gómez, R.; Salvador, P. Photovoltage Dependence on Film Thickness and Type of Illumination in Nanoporous Thin Flim Electrodes According to a Simple Diffusion Model. Sol. Energy Mater. Sol. Cells 2005, 88, 377–388. [Google Scholar] [CrossRef]

| Parameter | Value | Unit | Reference |
|---|---|---|---|
| [7] | |||
| [10] | |||
| d | m | [7] | |
| [7] | |||
| m | 1 | - | [5] |
| [27] | |||
| 10 | [10] | ||
| [28] |
| 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldon, B.; Thamwattana, N. A Fractional Diffusion Model for Dye-Sensitized Solar Cells. Molecules 2020, 25, 2966. https://doi.org/10.3390/molecules25132966
Maldon B, Thamwattana N. A Fractional Diffusion Model for Dye-Sensitized Solar Cells. Molecules. 2020; 25(13):2966. https://doi.org/10.3390/molecules25132966
Chicago/Turabian StyleMaldon, B., and N. Thamwattana. 2020. "A Fractional Diffusion Model for Dye-Sensitized Solar Cells" Molecules 25, no. 13: 2966. https://doi.org/10.3390/molecules25132966
APA StyleMaldon, B., & Thamwattana, N. (2020). A Fractional Diffusion Model for Dye-Sensitized Solar Cells. Molecules, 25(13), 2966. https://doi.org/10.3390/molecules25132966